当期目录

2019年, 第39卷, 第4期　刊出日期：2019-08-25 上一期    下一期

本期栏目： 论文　

全选:

合并摘要

导出引用 EndNote Reference Manager ProCite BibTeX RefWorks

隐藏/显示图片

论文

Select

THE SCHWARZ LEMMA AT THE BOUNDARY OF THE NON-CONVEX COMPLEX ELLIPSOIDS 何乐, 涂振汉 数学物理学报(英文版). 2019 (4):  915-926.  DOI: 10.1007/s10473-019-0401-5 摘要 ( 122 )   PDF   收藏 Let B2,p:={z∈C2:|z1|2+|z2|p<1} (0 < p < 1). Then, B2,p (0 < p < 1) is a non-convex complex ellipsoid in C2 without smooth boundary. In this article, we establish a boundary Schwarz lemma at z0 ∈ ∂B2,p for holomorphic self-mappings of the non-convex complex ellipsoid B2,p, where z0 is any smooth boundary point of B2,p. 参考文献 | 相关文章 | 计量指标

Select

A STUDY OF A FULLY COUPLED TWO-PARAMETER SYSTEM OF SEQUENTIAL FRACTIONAL INTEGRO-DIFFERENTIAL EQUATIONS WITH NONLOCAL INTEGRO-MULTIPOINT BOUNDARY CONDITIONS Ahmed ALSAEDI, Bashir AHMAD, Shorog ALJOUDI, Sotiris K. NTOUYAS 数学物理学报(英文版). 2019 (4):  927-944.  DOI: 10.1007/s10473-019-0402-4 摘要 ( 111 )   PDF   收藏 In this article, we discuss the existence and uniqueness of solutions for a coupled two-parameter system of sequential fractional integro-differential equations supplemented with nonlocal integro-multipoint boundary conditions. The standard tools of the fixed-point theory are employed to obtain the main results. We emphasize that our results are not only new in the given configuration, but also correspond to several new special cases for specific values of the parameters involved in the problem at hand. 参考文献 | 相关文章 | 计量指标

Select

THE ORLICZ BRUNN-MINKOWSKI INEQUALITY FOR DUAL HARMONIC QUERMASSINTEGRALS 吴翔, 李寿贵 数学物理学报(英文版). 2019 (4):  945-954.  DOI: 10.1007/s10473-019-0403-3 摘要 ( 89 )   PDF   收藏 Within the framework of Orlicz Brunn-Minkowski theory recently introduced by Lutwak, Yang, and Zhang[20, 21], Gardner, Hug, and Weil[5, 6] et al, the dual harmonic quermassintegrals of star bodies are studied, and a new Orlicz Brunn-Minkowski type inequality is proved for these geometric quantities. 参考文献 | 相关文章 | 计量指标

Select

DENSITY ESTIMATES FOR SOLUTIONS OF STOCHASTIC FUNCTIONAL DIFFERENTIAL EQUATIONS Nguyen Tien DUNG, Ta Cong SON, Tran Manh CUONG, Nguyen Van TAN, Trinh Nhu QUYNH 数学物理学报(英文版). 2019 (4):  955-970.  DOI: 10.1007/s10473-019-0404-2 摘要 ( 86 )   PDF   收藏 In this article, we investigate the density of the solution to a class of stochastic functional differential equations by means of Malliavin calculus. Our aim is to provide upper and lower Gaussian estimates for the density. 参考文献 | 相关文章 | 计量指标

Select

ECONOMICAL DIFFERENCE SCHEME FOR ONE MULTI-DIMENSIONAL NONLINEAR SYSTEM Temur JANGVELADZE, Zurab KIGURADZE, Mikheil GAGOSHIDZE 数学物理学报(英文版). 2019 (4):  971-988.  DOI: 10.1007/s10473-019-0405-1 摘要 ( 86 )   PDF   收藏 The multi-dimensional system of nonlinear partial differential equations is considered. In two-dimensional case, this system describes process of vein formation in higher plants. Variable directions finite difference scheme is constructed. The stability and convergence of that scheme are studied. Numerical experiments are carried out. The appropriate graphical illustrations and tables are given. 参考文献 | 相关文章 | 计量指标

Select

LEAST SQUARES TYPE ESTIMATION FOR DISCRETELY OBSERVED NON-ERGODIC GAUSSIAN ORNSTEIN-UHLENBECK PROCESSES Khalifa ES-SEBAIY, Fares ALAZEMI, Mishari AL-FORAIH 数学物理学报(英文版). 2019 (4):  989-1002.  DOI: 10.1007/s10473-019-0406-0 摘要 ( 123 )   PDF   收藏 In this article, we consider the drift parameter estimation problem for the nonergodic Ornstein-Uhlenbeck process defined as dXt=θXtdt + dGt, t ≥ 0 with an unknown parameter θ > 0, where G is a Gaussian process. 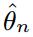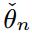We assume that the process {Xt, t ≥ 0} is observed at discrete time instants t1=△n,…, tn=n△n, and we construct two least squares type estimators and for θ on the basis of the discrete observations {Xti, i=1,…, n} as n → ∞. 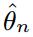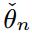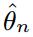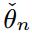Then, we provide sufficient conditions, based on properties of G, which ensure that and  are strongly consistent and the sequences √n△n(-θ) and √n△n(-θ) are tight. Our approach offers an elementary proof of[11], which studied the case when G is a fractional Brownian motion with Hurst parameter H ∈ (1/2, 1). As such, our results extend the recent findings by[11] to the case of general Hurst parameter H ∈ (0, 1). We also apply our approach to study subfractional Ornstein-Uhlenbeck and bifractional Ornstein-Uhlenbeck processes. 参考文献 | 相关文章 | 计量指标

Select

POINTWISE MULTIPLICATION OPERATORS FROM HARDY SPACES TO WEIGHTED BERGMAN SPACES IN THE UNIT BALL OF Cn 彭茹, 邢晓蕾, 江良英 数学物理学报(英文版). 2019 (4):  1003-1016.  DOI: 10.1007/s10473-019-0407-z 摘要 ( 79 )   PDF   收藏 This article is devoted to characterizing the boundedness and compactness of multiplication operators from Hardy spaces to weighted Bergman spaces in the unit ball of Cn. 参考文献 | 相关文章 | 计量指标

Select

HYPERSTABILITY OF THE GENERALIZED CAUCHY-JENSEN FUNCTIONAL EQUATION IN ULTRAMETRIC SPACES Prondanai KASKASEM, Chakkrid KILN-EAM 数学物理学报(英文版). 2019 (4):  1017-1032.  DOI: 10.1007/s10473-019-0408-y 摘要 ( 67 )   PDF   收藏 In this article, we prove hyperstability results of the generalized Cauchy-Jensen functional equation αf(x+y/α+ z)=f(x) + f(y) + αf(z) for any fixed positive integer α ≥ 2 in ultrametric Banach spaces by using fixed point method. 参考文献 | 相关文章 | 计量指标

Select

(S, T)-WEAK TRACTABILITY OF MULTIVARIATE LINEAR PROBLEMS IN THE AVERAGE CASE SETTING 刘永平, 许贵桥 数学物理学报(英文版). 2019 (4):  1033-1052.  DOI: 10.1007/s10473-019-0409-x 摘要 ( 131 )   PDF   收藏 The purpose of this article is to investigate (s,t)-weak tractability of multivariate linear problems in the average case setting. The considered algorithms use finitely many evaluations of arbitrary linear functionals. Generally, we obtained matching necessary and sufficient conditions for (s,t)-weak tractability in terms of the corresponding non-increasing sequence of eigenvalues. Specifically, we discussed (s,t)-weak tractability of linear tensor product problems and obtained necessary and sufficient conditions in terms of the corresponding one-dimensional problem. As an example of applications, we discussed also (s,t)-weak tractability of a multivariate approximation problem. 参考文献 | 相关文章 | 计量指标

Select

A PICARD-TYPE THEOREM AND A UNIQUENESS THEOREM OF NON-ARCHIMEDEAN ANALYTIC CURVES IN PROJECTIVE SPACE 王中华, 颜启明 数学物理学报(英文版). 2019 (4):  1053-1064.  DOI: 10.1007/s10473-019-0410-4 摘要 ( 79 )   PDF   收藏 In this article, we prove a Picard-type Theorem and a uniqueness theorem for non-Archimedean analytic curves in the projective space Pn(F), where the characteristic of F is 0 or positive. In the main results of this article, we ignore the zeros with large multiplicities. 参考文献 | 相关文章 | 计量指标

Select

EQUIVARIANT MINIMAL IMMERSIONS FROM S3 INTO CP3 胡泽君, 尹佳斌 数学物理学报(英文版). 2019 (4):  1065-1080.  DOI: 10.1007/s10473-019-0411-3 摘要 ( 62 )   PDF   收藏 Associated with an immersion φ:S3 → CP3, we can define a canonical bundle endomorphism F:TS3→TS3 by the pull back of the Kähler form of CP3. In this article, related to F we study equivariant minimal immersions from S3 into CP3 under the additional condition (▽XF)X=0 for all X ∈ ker (F). As main result, we give a complete classification of such kinds of immersions. Moreover, we also construct a typical example of equivariant non-minimal immersion φ:S3 → CP3 satisfying (▽XF)X=0 for all X ∈ ker (F), which is neither Lagrangian nor of CR type. 参考文献 | 相关文章 | 计量指标

Select

VECTOR FIELDS FOR CONTACT PAIRS 何跃, 赫海龙 数学物理学报(英文版). 2019 (4):  1081-1088.  DOI: 10.1007/s10473-019-0412-2 摘要 ( 89 )   PDF   收藏 Let M be a (2k+2l+2)-dimensional smooth manifold. For such M, Bande and Hadjar introduce a new geometric structure called contact pair which roughly is a couple of 1-forms of constant classes with complementary kernels and foliations. We show the relationship between a pair of vector fields for a contact pair and a quadruple of functions on M. This is a generalization of the classical result for contact manifolds. 参考文献 | 相关文章 | 计量指标

Select

DISJOINT SUPERCYCLIC WEIGHTED PSEUDO-SHIFTS ON BANACH SEQUENCE SPACES 王亚, 梁玉霞 数学物理学报(英文版). 2019 (4):  1089-1102.  DOI: 10.1007/s10473-019-0413-1 摘要 ( 86 )   PDF   收藏 In this article, we present several equivalent conditions ensuring the disjoint supercyclicity of finite weighted pseudo-shifts acting on an arbitrary Banach sequence space. The disjoint supercyclic properties of weighted translations on locally compact discrete groups, the direct sums of finite classical weighted backward shifts, and the bilateral backward operator weighted shifts can be viewed as special cases of our main results. Furthermore, we exhibit an interesting fact that any finite bilateral weighted backward shifts on the space l2(Z) never satisfy the d-Supercyclicity Criterion by a simple proof. 参考文献 | 相关文章 | 计量指标

Select

THE INVARIANCE OF SUBCLASSES OF BIHOLOMORPHIC MAPPINGS ON BERGMAN-HARTOGS DOMAINS 崔艳艳, 刘浩 数学物理学报(英文版). 2019 (4):  1103-1120.  DOI: 10.1007/s10473-019-0414-0 摘要 ( 83 )   PDF   收藏 We mainly discuss the invariance of some subclasses of biholomorphic mappings under the generalized Roper-Suffridge operators on Bergman-Hartogs domains which are based on the unit ball Bn. Using the geometric properties and the distortion results of subclasses of biholomorphic mappings, we obtain the geometric characters of almost spirallike mappings of type β and order α, SΩ*(β, A, B), strong and almost spirallike mappings of type β and order α maintained under the generalized Roper-Suffridge operators on Bergman-Hartogs domains. Sequentially, we conclude that the generalized operators and the known operators preserve the same properties under some conditions. The conclusions generalize some known results. 参考文献 | 相关文章 | 计量指标

Select

THE REAL HYPER-ELLIPTIC SUBSPACES OF TEICHMÜLLER SPACE AND MODULI SPACE 胡光明, 漆毅 数学物理学报(英文版). 2019 (4):  1121-1135.  DOI: 10.1007/s10473-019-0415-z 摘要 ( 93 )   PDF   收藏 Although the existence and uniqueness of Strebel differentials are proved by Jenkins and Strebel, the specific constructions of Strebel differentials are difficult. Two special kinds of special Strebel differentials are constructed in [5, 6]. The Strebel rays [3] and the eventually distance minimizing rays [9] are important in Teichmüller spaces and moduli spaces, respectively. Motivated by the study of [3, 9], two special kinds of Strebel rays in the real hyper-elliptic subspace of Teichmüller space and two special kinds of EDM rays in the real hyper-elliptic subspace of moduli space are studied in this article. 参考文献 | 相关文章 | 计量指标

Select

ON THE CAUCHY PROBLEM FOR IMBQ SYSTEM ARISING FROM DNA 王玉柱, 田乃文 数学物理学报(英文版). 2019 (4):  1136-1148.  DOI: 10.1007/s10473-019-0416-y 摘要 ( 66 )   PDF   收藏 In this article, we focus on the Cauchy problem for the generalized IMBq system in n-dimensional space, which arises from DNA. We show the global existence and decay estimates of solution for a class of initial velocity, provided that the initial value is suitably small. 参考文献 | 相关文章 | 计量指标

Select

QUANTITATIVE WEIGHTED BOUNDS FOR A CLASS OF SINGULAR INTEGRAL OPERATORS 高文华, 胡国恩 数学物理学报(英文版). 2019 (4):  1149-1162.  DOI: 10.1007/s10473-019-0417-x 摘要 ( 127 )   PDF   收藏 In this article, the authors consider the weighted bounds for the singular integral operator defined by where Ω is homogeneous of degree zero and has vanishing moment of order one, and A is a function on Rn such that ▽A ∈ BMO(Rn). By sparse domination, the authors obtain some quantitative weighted bounds for TA when Ω satisfies regularity condition of Lr-Dini type for some r ∈ (1, ∞). 参考文献 | 相关文章 | 计量指标

Select

STABILITY OF A PAIR OF BANACH SPACES FOR ε-ISOMETRIES 戴端旭, 郑本拓 数学物理学报(英文版). 2019 (4):  1163-1172.  DOI: 10.1007/s10473-019-0418-9 摘要 ( 82 )   PDF   收藏 A pair of Banach spaces (X, Y) is said to be stable if for every ε-isometry f:X → Y, there exist γ > 0 and a bounded linear operator T:L(f) → X with ||T|| ≤ α such that ||Tf(x)-x|| ≤ γε for all x ∈ X, where L(f) is the closed linear span of f(X). In this article, we study the stability of a pair of Banach spaces (X, Y) when X is a C(K) space. This gives a new positive answer to Qian's problem. Finally, we also obtain a nonlinear version for Qian's problem. 参考文献 | 相关文章 | 计量指标

Select

VALUE DISTRIBUTION OF MEROMORPHIC SOLUTIONS OF CERTAIN NON-LINEAR DIFFERENCE EQUATIONS 陈敏风, 高宗升, 张继龙 数学物理学报(英文版). 2019 (4):  1173-1184.  DOI: 10.1007/s10473-019-0419-8 摘要 ( 101 )   PDF   收藏 In this article, we consider the non-linear difference equation (f(z + 1)f(z)-1)(f(z)f(z-1)-1)=P(z, f(z))/Q(z, f(z)), where P(z, f(z)) and Q(z, f(z)) are relatively prime polynomials in f(z) with rational coefficients. For the above equation, the order of growth, the exponents of convergence of zeros and poles of its transcendental meromorphic solution f(z), and the exponents of convergence of poles of difference △f(z) and divided difference △f(z)/f(z) are estimated. Furthermore, we study the forms of rational solutions of the above equation. 参考文献 | 相关文章 | 计量指标

Select

A NOTE ON LI-YAU-TYPE GRADIENT ESTIMATE 余成杰, 赵菲菲 数学物理学报(英文版). 2019 (4):  1185-1194.  DOI: 10.1007/s10473-019-0420-2 摘要 ( 84 )   PDF   收藏 In this article, we obtain Li-Yau-type gradient estimates with time dependent parameter for positive solutions of the heat equation that are different with the estimates by Li-Xu[21] and Qian[23]. As an application of the estimate, we also obtained slight improvements of Davies' Li-Yau-type gradient estimate. 参考文献 | 相关文章 | 计量指标

Select

ASYMPTOTIC STABILITY OF THE RAREFACTION WAVE FOR THE NON-VISCOUS AND HEAT-CONDUCTIVE IDEAL GAS IN HALF SPACE 侯美晨 数学物理学报(英文版). 2019 (4):  1195-1212.  DOI: 10.1007/s10473-019-0421-1 摘要 ( 82 )   PDF   收藏 This article is concerned with the impermeable wall problem for an ideal polytropic model of non-viscous and heat-conductive gas in one-dimensional half space. It is shown that the 3-rarefaction wave is stable under some smallness conditions. The proof is given by an elementary energy method and the key point is to do the higher order derivative estimates with respect to t because of the less dissipativity of the system and the higher order derivative boundary terms. 参考文献 | 相关文章 | 计量指标