Table of Content

25 December 2018, Volume 38 Issue 6 Previous Issue    Next Issue

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

NONLINEAR SEMIGROUP APPROACH TO TRANSPORT EQUATIONS WITH DELAYED NEUTRONS Abdul-Majeed AL-IZERI, Khalid LATRACH Acta mathematica scientia,Series B. 2018, 38 (6):  1637-1654.  Abstract ( 130 )   PDF   Save This paper deal with a nonlinear transport equation with delayed neutron and general boundary conditions. We establish, via the nonlinear semigroups approach, the existence and uniqueness of the mild solution, weak solution, strong solution and local solution on Lp-spaces (1 ≤ p<+∞). Local and non local evolution problems are discussed. References | Related Articles | Metrics

Select

THE COMBINED INVISCID AND NON-RESISTIVE LIMIT FOR THE NONHOMOGENEOUS INCOMPRESSIBLE MAGNETOHYDRODYNAMIC EQUATIONS WITH NAVIER BOUNDARY CONDITIONS Zhipeng ZHANG Acta mathematica scientia,Series B. 2018, 38 (6):  1655-1677.  Abstract ( 89 )   PDF   Save In this paper, we establish the existence of the global weak solutions for the nonhomogeneous incompressible magnetohydrodynamic equations with Navier boundary conditions for the velocity field and the magnetic field in a bounded domain Ω ⊂ R3. Furthermore, we prove that as the viscosity and resistivity coefficients go to zero simultaneously, these weak solutions converge to the strong one of the ideal nonhomogeneous incompressible magnetohydrodynamic equations in energy space. References | Related Articles | Metrics

Select

A NOTE ON q-DIFFERENCE OPERATOR AND RELATED LIMIT DIRECTION Yezhou LI, Ningfang SONG Acta mathematica scientia,Series B. 2018, 38 (6):  1678-1688.  Abstract ( 95 )   PDF   Save The growth of entire functions under the q-difference operators is studied in this paper, and then some properties of Julia set of entire functions under the higher order q-difference operators are obtained. References | Related Articles | Metrics

Select

ALTERNATING DIRECTION IMPLICIT OSC SCHEME FOR THE TWO-DIMENSIONAL FRACTIONAL EVOLUTION EQUATION WITH A WEAKLY SINGULAR KERNEL Haixiang ZHANG, Xuehua YANG, Da XU Acta mathematica scientia,Series B. 2018, 38 (6):  1689-1711.  Abstract ( 94 )   PDF   Save In this paper, a new kind of alternating direction implicit (ADI) Crank-Nicolson-type orthogonal spline collocation (OSC) method is formulated for the two-dimensional fractional evolution equation with a weakly singular kernel arising in the theory of linear viscoelasticity. The novel OSC method is used for the spatial discretization, and ADI Crank-Nicolson-type method combined with the second order fractional quadrature rule are considered for the temporal component. The stability of proposed scheme is rigourously established, and nearly optimal order error estimate is also derived. Numerical experiments are conducted to support the predicted convergence rates and also exhibit expected super-convergence phenomena. References | Related Articles | Metrics

Select

SIGN-CHANGING SOLUTIONS FOR THE STATIONARY KIRCHHOFF PROBLEMS INVOLVING THE FRACTIONAL LAPLACIAN IN RN Kun CHENG, Qi GAO Acta mathematica scientia,Series B. 2018, 38 (6):  1712-1730.  Abstract ( 101 )   PDF   Save In this paper, we study the existence of least energy sign-changing solutions for a Kirchhoff-type problem involving the fractional Laplacian operator. By using the constraint variation method and quantitative deformation lemma, we obtain a least energy nodal solution ub for the given problem. Moreover, we show that the energy of ub is strictly larger than twice the ground state energy. We also give a convergence property of ub as b↘ 0, where b is regarded as a positive parameter. References | Related Articles | Metrics

Select

DYNAMICS OF A HEPATITIS B MODEL WITH SATURATED INCIDENCE Liya LIU, Daqing JIANG, Tasawar HAYAT, Bashir AHMAD Acta mathematica scientia,Series B. 2018, 38 (6):  1731-1750.  Abstract ( 81 )   PDF   Save In this article, we present a hepatitis B epidemic model with saturated incidence. The dynamic behaviors of the deterministic and stochastic system are studied. To this end, we first establish the local and global stability conditions of the equilibrium of the deterministic model. Second, by constructing suitable stochastic Lyapunov functions, the sufficient conditions for the existence of ergodic stationary distribution as well as extinction of hepatitis B are obtained. References | Related Articles | Metrics

Select

HARNACK AND MEAN VALUE INEQUALITIES ON GRAPHS Yong LIN, Hongye SONG Acta mathematica scientia,Series B. 2018, 38 (6):  1751-1758.  Abstract ( 66 )   PDF   Save We prove a Harnack inequality for positive harmonic functions on graphs which is similar to a classical result of Yau on Riemannian manifolds. Also, we prove a mean value inequality of nonnegative subharmonic functions on graphs. References | Related Articles | Metrics

Select

LOCAL EXISTENCE AND BLOW-UP CRITERION OF 3D IDEAL MAGNETOHYDRODYNAMICS EQUATIONS Jae-Myoung KIM Acta mathematica scientia,Series B. 2018, 38 (6):  1759-1766.  Abstract ( 64 )   PDF   Save We investigate the local existence of smooth solutions of a 3D ideal magnetohydrodynamics (MHD) equations in a bounded domain and give a blow-up criteria to this equations with respect to vorticists. References | Related Articles | Metrics

Select

EXISTENCE OF SOLUTIONS FOR GRADIENT SYSTEMS WITH APPLICATION TO DIFFUSION PROBLEMS INVOLVING NONCONVEX ENERGIES Sahbi BOUSSANDEL Acta mathematica scientia,Series B. 2018, 38 (6):  1767-1778.  Abstract ( 70 )   PDF   Save In this paper, we establish the existence of solutions for gradient systems of evolution under some type (M) and semi-coerciveness conditions. The main result is applied in order to solve nonlinear diffusion equations involving nonconvex energies. References | Related Articles | Metrics

Select

CARLESON MEASURES AND THE GENERALIZED CAMPANATO SPACES OF VECTOR-VALUED MARTINGALES Lin YU, Ruhui WANG, Shoujiang ZHAO Acta mathematica scientia,Series B. 2018, 38 (6):  1779-1788.  Abstract ( 62 )   PDF   Save In this paper, the so-called (p, φ)-Carleson measure is introduced and the relationship between vector-valued martingales in the general Campanato spaces Lp,φ(X) and the (p, φ)-Carleson measures is investigated. Specifically, it is proved that for q ∈[2, ∞), the measure dμ:=||dfk||qdP ⊗ dm is a (q, φ)-Carleson measure on Ω×N for every f ∈ Lq,φ(X) if and only if X has an equivalent norm which is q-uniformly convex; while for p ∈ (1, 2], the measure dμ:=||dfk||pdP⊗dm is a (p, φ)-Carleson measure on Ω×N implies that f ∈ Lp,φ(X) if and only if X admits an equivalent norm which is p-uniformly smooth. This result extends an earlier result in the literature from BMO spaces to general Campanato spaces. References | Related Articles | Metrics

Select

THE Cn WP-BAILEY CHAIN Zhizheng ZHANG, Junli HUANG Acta mathematica scientia,Series B. 2018, 38 (6):  1789-1804.  Abstract ( 61 )   PDF   Save The purpose of this paper is to introduce the concept of Cn WP-Bailey pairs. The Cn WP-Bailey transform is obtained by applying the Cn 6φ5 summation formula. From this result, the Cn WP-Bailey lemma is deduced by making use of the Cn q-Dougall summation formula. Some applications are investigated. Finally, the case of elliptic Cn WP-Bailey pairs is discussed. References | Related Articles | Metrics

Select

ALGORITHMS FOR A SYSTEM OF GENERALIZED MIXED EQUILIBRIUM PROBLEMS AND A COUNTABLE FAMILY OF SOME NONLINEAR MULTI-VALUED NONEXPANSIVE-TYPE MAPS Ogonnaya Michael ROMANUS, Ukamaka Victoria NNYABA, Monday Ogudu NNAKWE Acta mathematica scientia,Series B. 2018, 38 (6):  1805-1820.  Abstract ( 56 )   PDF   Save In this paper, relaxed iterative algorithms of Krasnoselskii-type and Halpern-type that approximate a solution of a system of a generalized mixed equilibrium problem and a common fixed point of a countable family of totally quasi-φ-asymptotically nonexpansive multi-valued maps are constructed. Strong convergence of the sequence generated by these algorithms is proved in uniformly smooth and strictly convex real Banach spaces with Kadec-Klee property. Furthermore, several applications of our theorems are also presented. Finally, our theorems are significant improvements on several important recent results for this class of nonlinear problems. References | Related Articles | Metrics

Select

EXISTENCE OF MULTIPLE SOLUTIONS FOR A FRACTIONAL p-LAPLACIAN SYSTEM WITH CONCAVE-CONVEX TERM Junhui XIE, Xiaozhong HUANG, Yiping CHEN Acta mathematica scientia,Series B. 2018, 38 (6):  1821-1832.  Abstract ( 80 )   PDF   Save In this article, we study the existence of multiple solutions for the following system driven by a nonlocal integro-differential operator with zero Dirichlet boundary conditions where Ω is a smooth bounded domain in Rn, n > ps with s ∈ (0, 1) fixed, a(x), b(x), c(x) ≥ 0 and a(x), b(x), c(x) ∈ L∞(Ω), 1< q < p and α, β > 1 satisfy p < α +β < p*, p*=np/n-ps. By Nehari manifold and fibering maps with proper conditions, we obtain the multiplicity of solutions to problem (0.1). References | Related Articles | Metrics

Select

GLOBAL WELL-POSEDNESS FOR THE DENSITY-DEPENDENT INCOMPRESSIBLE MAGNETOHYDRODYNAMIC FLOWS IN BOUNDED DOMAINS Defu CHEN, Xia YE Acta mathematica scientia,Series B. 2018, 38 (6):  1833-1845.  Abstract ( 40 )   PDF (191KB) ( 18 )   Save In this paper, we study the three-dimensional incompressible magnetohydrodynamic equations in a smooth bounded domains, in which the viscosity of the fluid and the magnetic diffusivity are concerned with density. The existence of global strong solutions is established in vacuum cases, provided the assumption that (||▽μ(ρ0)||Lp +||▽ν(ρ0)||Lq +||b0||L3+||ρ0||L∞) (p, q > 3) is small enough, there is not any smallness condition on the velocity. References | Related Articles | Metrics

Select

THE GLM REPRESENTATION OF THE TWO-COMPONENT NONLINEAR SCHRÖDINGER EQUATION ON THE HALF-LINE Qiaozhen ZHU, Engui FAN, Jian XU Acta mathematica scientia,Series B. 2018, 38 (6):  1846-1860.  Abstract ( 58 )   PDF   Save The Gelfand-Levitan-Marchenko representation is used to analyze the initial-boundary value problem of two-component nonlinear Schrödinger equation on the half-line. It has shown that the global relation can be effectively analyzed by the Gelfand-Levitan-Marchenko representation. we also derive expressions for the Dirichlet-to-Neumann map to characterize the unknown boundary values. References | Related Articles | Metrics

Select

AN INTEGRAL ESTIMATE AND THE EQUIVALENT NORMS ON F(p, q, s, k) SPACES IN THE UNIT BALL Xuejun ZHANG, Shenlian LI, Qingli SHANG, Yuting GUO Acta mathematica scientia,Series B. 2018, 38 (6):  1861-1880.  Abstract ( 65 )   PDF   Save In this article, the authors give a typical integral's bidirectional estimates for all cases. At the same time, several equivalent characterizations on the F(p,q,s,k) space in the unit ball of Cn are given. References | Related Articles | Metrics

Select

BOUNDARY FEEDBACK STABILIZATION OF BOUSSINESQ EQUATIONS Hanbing LIU, Haijun XIAO Acta mathematica scientia,Series B. 2018, 38 (6):  1881-1902.  Abstract ( 58 )   PDF   Save The aim of this work is to design oblique boundary feedback controller for stabilizing the equilibrium solutions to Boussinesq equations on a bounded and open domain in R2. Two kinds of such feedback controller are provided, one is the proportional stabilizable feedback control, which is obtained by spectrum decomposition method, while another one is constructed via the Ricatti operator for an infinite time horizon optimal control problem. An example of periodic Boussinesq flow in 2-D channel is also given. References | Related Articles | Metrics

Select

LICHNEROWICZ-OBATA THEOREM FOR KOHN LAPLACIAN ON THE REAL ELLIPSOID Guijuan LIN Acta mathematica scientia,Series B. 2018, 38 (6):  1903-1911.  Abstract ( 223 )   PDF   Save We give the sharp lower bound for Ricci curvature on the real ellipsoid in Cn+1, and prove the Lichnerowicz-Obata theorem for Kohn Laplacian. References | Related Articles | Metrics

Select

ON BANACH-STONE TYPE THEOREMS IN UNIFORM MULTIPLICATIVE SUBGROUPS OF C(K)-SPACES Yunbai DONG, Pei-Kee LIN, Bentuo ZHENG Acta mathematica scientia,Series B. 2018, 38 (6):  1912-1920.  Abstract ( 64 )   PDF   Save In this article, we study the preservation properties of (Šilov) boundary of multiplicative subgroups in C(X) spaces for non-surjective norm-preserving multiplicative maps. We also show a sufficient condition for surjective maps between groups of positive continuous functions to be a composition operator. References | Related Articles | Metrics

Select

ROBUST EXPONENTIAL STABILITY OF SWITCHED DELAY INTERCONNECTED SYSTEMS UNDER ARBITRARY SWITCHING Huanbin XUE, Jiye ZHANG Acta mathematica scientia,Series B. 2018, 38 (6):  1921-1938.  Abstract ( 64 )   PDF   Save The problem of robust exponential stability for a class of switched nonlinear dynamical systems with uncertainties and unbounded delay is addressed. On the assumption that the interconnected functions of the studied systems satisfy the Lipschitz condition, by resorting to vector Lyapunov approach and M-matrix theory, the sufficient conditions to ensure the robust exponential stability of the switched interconnected systems under arbitrary switching are obtained. The proposed method, which neither require the individual subsystems to share a Common Lyapunov Function (CLF), nor need to involve the values of individual Lyapunov functions at each switching time, provide a new way of thinking to study the stability of arbitrary switching. In addition, the proposed criteria are explicit, and it is convenient for practical applications. Finally, two numerical examples are given to illustrate the correctness and effectiveness of the proposed theories. References | Related Articles | Metrics

Select

FINITE EXTENSIONS OF GENERALIZED BESSEL SEQUENCES TO GENERALIZED FRAMES Dengfeng LI, Yanting LI Acta mathematica scientia,Series B. 2018, 38 (6):  1939-1950.  Abstract ( 83 )   PDF   Save The objective of this paper is to investigate the question of modifying a given generalized Bessel sequence to yield a generalized frame or a tight generalized frame by finite extension. Some necessary and sufficient conditions for the finite extensions of generalized Bessel sequences to generalized frames or tight generalized frames are provided, and every result is illustrated by the corresponding example. References | Related Articles | Metrics

Select

HERMAN RINGS WITH SMALL PERIODS AND OMITTED VALUES Tarun Kumar CHAKRA, Gorachand CHAKRABORTY, Tarakanta NAYAK Acta mathematica scientia,Series B. 2018, 38 (6):  1951-1965.  Abstract ( 89 )   PDF   Save All possible arrangements of cycles of three periodic as well as four periodic Herman rings of transcendental meromorphic functions having at least one omitted value are determined. It is shown that if p=3 or 4, then the number of p-cycles of Herman rings is at most one. We have also proved a result about the non-existence of a 3-cycle and a 4-cycle of Herman rings simultaneously. Finally some examples of functions having no Herman ring are discussed. References | Related Articles | Metrics

Select

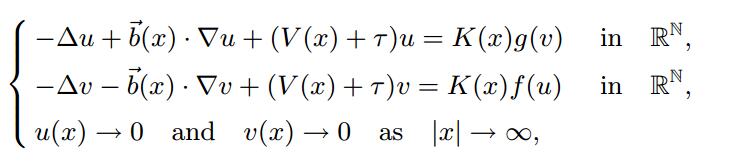
EXISTENCE OF GROUND STATE SOLUTIONS TO HAMILTONIAN ELLIPTIC SYSTEM WITH POTENTIALS Wenbo WANG, Quanqing LI Acta mathematica scientia,Series B. 2018, 38 (6):  1966-1980.  Abstract ( 81 )   PDF   Save In this paper, we investigate nonlinear Hamiltonian elliptic system where N ≥ 3, τ > 0 is a positive parameter and V, K are nonnegative continuous functions, f and g are both superlinear at 0 with a quasicritical growth at infinity. By establishing a variational setting, the existence of ground state solutions is obtained. References | Related Articles | Metrics