Table of Content

25 June 2019, Volume 39 Issue 3 Previous Issue    Next Issue

For Selected:

View Abstracts

Download Citations EndNote Reference Manager ProCite BibTeX RefWorks

Toggle Thumbnails

Articles

Select

PREFACE Yaozhong HU Acta mathematica scientia,Series B. 2019, 39 (3):  627-628.  DOI: 10.1007/s10473-019-0301-8 Abstract ( 101 )   PDF (103KB) ( 95 )   Save References | Related Articles | Metrics

Select

PRECISE MOMENT ASYMPTOTICS FOR THE STOCHASTIC HEAT EQUATION OF A TIME-DERIVATIVE GAUSSIAN NOISE Heyu LI, Xia CHEN Acta mathematica scientia,Series B. 2019, 39 (3):  629-644.  DOI: 10.1007/s10473-019-0302-7 Abstract ( 141 )   PDF   Save This article establishes the precise asymptotics Eum(t, x) (t→∞ or m→∞) for the stochastic heat equation with the time-derivative Gaussian noise W/t (t, x) that is fractional in time and homogeneous in space. References | Related Articles | Metrics

Select

NONLINEAR STOCHASTIC HEAT EQUATION DRIVEN BY SPATIALLY COLORED NOISE: MOMENTS AND INTERMITTENCY Le CHEN, Kunwoo KIM Acta mathematica scientia,Series B. 2019, 39 (3):  645-668.  DOI: 10.1007/s10473-019-0303-6 Abstract ( 150 )   PDF   Save In this article, we study the nonlinear stochastic heat equation in the spatial domain Rd subject to a Gaussian noise which is white in time and colored in space. The spatial correlation can be any symmetric, nonnegative and nonnegative-definite function that satisfies Dalang's condition. We establish the existence and uniqueness of a random field solution starting from measure-valued initial data. We find the upper and lower bounds for the second moment. With these moment bounds, we first establish some necessary and sufficient conditions for the phase transition of the moment Lyapunov exponents, which extends the classical results from the stochastic heat equation on Zd to that on Rd. Then, we prove a localization result for the intermittency fronts, which extends results by Conus and Khoshnevisan[9] from one space dimension to higher space dimension. The linear case has been recently proved by Huang et al[17] using different techniques. References | Related Articles | Metrics

Select

ON THE NECESSARY AND SUFFICIENT CONDITIONS TO SOLVE A HEAT EQUATION WITH GENERAL ADDITIVE GAUSSIAN NOISE Yaozhong HU, Yanghui LIU, Samy TINDEL Acta mathematica scientia,Series B. 2019, 39 (3):  669-690.  DOI: 10.1007/s10473-019-0304-5 Abstract ( 92 )   PDF   Save In this note, we consider stochastic heat equation with general additive Gaussian noise. Our aim is to derive some necessary and sufficient conditions on the Gaussian noise in order to solve the corresponding heat equation. We investigate this problem invoking two different methods, respectively, based on variance computations and on path-wise considerations in Besov spaces. We are going to see that, as anticipated, both approaches lead to the same necessary and sufficient condition on the noise. In addition, the path-wise approach brings out regularity results for the solution. References | Related Articles | Metrics

Select

LEAST SQUARES ESTIMATOR FOR PATH-DEPENDENT MCKEAN-VLASOV SDES VIA DISCRETE-TIME OBSERVATIONS Panpan REN, Jiang-Lun WU Acta mathematica scientia,Series B. 2019, 39 (3):  691-716.  DOI: 10.1007/s10473-019-0305-4 Abstract ( 109 )   PDF   Save In this article, we are interested in least squares estimator for a class of path-dependent McKean-Vlasov stochastic differential equations (SDEs). More precisely, we investigate the consistency and asymptotic distribution of the least squares estimator for the unknown parameters involved by establishing an appropriate contrast function. Comparing to the existing results in the literature, the innovations of this article lie in three aspects:(i) We adopt a tamed Euler-Maruyama algorithm to establish the contrast function under the monotone condition, under which the Euler-Maruyama scheme no longer works; (ii) We take the advantage of linear interpolation with respect to the discrete-time observations to approximate the functional solution; (iii) Our model is more applicable and practice as we are dealing with SDEs with irregular coefficients (for example, Hölder continuous) and path-distribution dependent. References | Related Articles | Metrics

Select

HÖLDER CONTINUITY FOR THE PARABOLIC ANDERSON MODEL WITH SPACE-TIME HOMOGENEOUS GAUSSIAN NOISE Raluca M BALAN, Lluís QUER-SARDANYONS, Jian SONG Acta mathematica scientia,Series B. 2019, 39 (3):  717-730.  DOI: 10.1007/s10473-019-0306-3 Abstract ( 80 )   PDF   Save In this article, we consider the Parabolic Anderson Model with constant initial condition, driven by a space-time homogeneous Gaussian noise, with general covariance function in time and spatial spectral measure satisfying Dalang's condition. First, we prove that the solution (in the Skorohod sense) exists and is continuous in Lp(Ω). Then, we show that the solution has a modification whose sample paths are Hölder continuous in space and time, under the minimal condition on the spatial spectral measure of the noise (which is the same as the condition encountered in the case of the white noise in time). This improves similar results which were obtained in [6, 10] under more restrictive conditions, and with sub-optimal exponents for H¨older continuity. References | Related Articles | Metrics

Select

ASYMPTOTICS OF THE SOLUTIONS TO STOCHASTIC WAVE EQUATIONS DRIVEN BY A NON-GAUSSIAN LEVY PROCESS Yiming JIANG, Suxin WANG, Xingchun WANG Acta mathematica scientia,Series B. 2019, 39 (3):  731-746.  DOI: 10.1007/s10473-019-0307-2 Abstract ( 91 )   PDF   Save In this article, we consider the long time behavior of the solutions to stochastic wave equations driven by a non-Gaussian Lévy process. We shall prove that under some appropriate conditions, the exponential stability of the solutions holds. Finally, we give two examples to illustrate our results. References | Related Articles | Metrics

Select

EULER SCHEME FOR FRACTIONAL DELAY STOCHASTIC DIFFERENTIAL EQUATIONS BY ROUGH PATHS TECHNIQUES Johanna GARZÓN, Samy TINDEL, Soledad TORRES Acta mathematica scientia,Series B. 2019, 39 (3):  747-763.  DOI: 10.1007/s10473-019-0308-1 Abstract ( 83 )   PDF   Save In this note, we study a discrete time approximation for the solution of a class of delayed stochastic differential equations driven by a fractional Brownian motion with Hurst parameter H∈ (1/2, 1). In order to prove convergence, we use rough paths techniques. Theoretical bounds are established and numerical simulations are displayed. References | Related Articles | Metrics

Select

JOINT HÖLDER CONTINUITY OF PARABOLIC ANDERSON MODEL Yaozhong HU, Khoa LÊ Acta mathematica scientia,Series B. 2019, 39 (3):  764-780.  DOI: 10.1007/s10473-019-0309-0 Abstract ( 94 )   PDF   Save We obtain the Holder continuity and joint Holder continuity in space and time for the random field solution to the parabolic Anderson equation (t-1/2△)u=u◇W in d-dimensional space, where W is a mean zero Gaussian noise with temporal covariance γ0 and spatial covariance given by a spectral density μ(ξ). We assume that γ0(t) ≤ c|t|-α0 and |μ(ξ)| ≤ c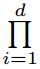|ξi|-αi or |μ(ξ)| ≤ c|ξ|-α, where αi, i=1,…, d (or α) can take negative value. References | Related Articles | Metrics

Select

MOMENTS OF CONTINUOUS-STATE BRANCHING PROCESSES IN LÉVY RANDOM ENVIRONMENTS Lina JI, Xiangqi ZHENG Acta mathematica scientia,Series B. 2019, 39 (3):  781-796.  DOI: 10.1007/s10473-019-0310-7 Abstract ( 88 )   PDF   Save For continuous-state branching processes in Lévy random environments, the recursion of n-moments and the equivalent condition for the existence of general f-moments are established, where f is a positive continuous function satisfying some standard conditions. References | Related Articles | Metrics

Select

COMPLEX WIENER-ITÔ CHAOS DECOMPOSITION REVISITED Yong CHEN, Yong LIU Acta mathematica scientia,Series B. 2019, 39 (3):  797-818.  DOI: 10.1007/s10473-019-0311-6 Abstract ( 97 )   PDF   Save In this article, some properties of complex Wiener-Itô multiple integrals and complex Ornstein-Uhlenbeck operators and semigroups are obtained. Those include Stroock's formula, Hu-Meyer formula, Clark-Ocone formula, and the hypercontractivity of complex Ornstein-Uhlenbeck semigroups. As an application, several expansions of the fourth moments of complex Wiener-Itô multiple integrals are given. References | Related Articles | Metrics

Select

REFLECTED BACKWARD STOCHASTIC DIFFERENTIAL EQUATION WITH JUMPS AND VISCOSITY SOLUTION OF SECOND ORDER INTEGRO-DIFFERENTIAL EQUATION WITHOUT MONOTONICITY CONDITION: CASE WITH THE MEASURE OF LÉVY INFINITE Lamine SYLLA Acta mathematica scientia,Series B. 2019, 39 (3):  819-844.  DOI: 10.1007/s10473-019-0312-5 Abstract ( 98 )   PDF   Save We consider the problem of viscosity solution of integro-partial differential equation(IPDE in short) with one obstacle via the solution of reflected backward stochastic differential equations(RBSDE in short) with jumps. We show the existence and uniqueness of a continuous viscosity solution of equation with non local terms, if the generator is not monotonous and Levy's measure is infinite. References | Related Articles | Metrics

Select

UNIQUENESS PROBLEM FOR SPDES FROM POPULATION MODELS Jie XIONG, Xu YANG Acta mathematica scientia,Series B. 2019, 39 (3):  845-856.  DOI: 10.1007/s10473-019-0313-4 Abstract ( 81 )   PDF   Save This is a survey on the strong uniqueness of the solutions to stochastic partial differential equations (SPDEs) related to two measure-valued processes:superprocess and Fleming-Viot process which are given as rescaling limits of population biology models. We summarize recent results for Konno-Shiga-Reimers' and Mytnik's SPDEs, and their related distribution-function-valued SPDEs. References | Related Articles | Metrics

Select

UNIQUENESS OF VISCOSITY SOLUTIONS OF STOCHASTIC HAMILTON-JACOBI EQUATIONS Jinniao QIU, Wenning WEI Acta mathematica scientia,Series B. 2019, 39 (3):  857-873.  DOI: 10.1007/s10473-019-0314-3 Abstract ( 80 )   PDF   Save This article is devoted to the study of fully nonlinear stochastic Hamilton-Jacobi (HJ) equations for the optimal stochastic control problem of ordinary differential equations with random coefficients. Under the standard Lipschitz continuity assumptions on the coefficients, the value function is proved to be the unique viscosity solution of the associated stochastic HJ equation. References | Related Articles | Metrics

Select

SOME RECENT PROGRESS ON STOCHASTIC HEAT EQUATIONS Yaozhong HU Acta mathematica scientia,Series B. 2019, 39 (3):  874-914.  DOI: 10.1007/s10473-019-0315-2 Abstract ( 97 )   PDF   Save This article attempts to give a short survey of recent progress on a class of elementary stochastic partial differential equations (for example, stochastic heat equations) driven by Gaussian noise of various covariance structures. The focus is on the existence and uniqueness of the classical (square integrable) solution (mild solution, weak solution). It is also concerned with the Feynman-Kac formula for the solution; Feynman-Kac formula for the moments of the solution; and their applications to the asymptotic moment bounds of the solution. It also briefly touches the exact asymptotics of the moments of the solution. References | Related Articles | Metrics