1 引言
其中
本文安排如下:第2节,得出方程(1.1)的精确解,并且研究方程(1.1)精确解的振动性;第3节,讨论方程(1.1)的数值解的振动性;第4节,研究
2 方程解析解的振动性与非振动性
定义2.1[6] 设
1)
2)
3)对任意
4)
下面的定理给出了方程(1.1)的解.
定理2.1 令
且
令
且
其中
证 假设
一般解为
令
则有
即
令
(2.3)式成立.由脉冲条件
(2.4)式成立.证毕.
由方程(2.4)得出方程(2.3)的差分方程,即
它的特征方程为
引理2.1[8] 方程(1.1)的每一个解振动的充要条件是差分方程(2.5)的特征方程(2.6)无正根,方程(1.1)存在一个非振动解的充要条件是差分方程(2.5)的特征方程(2.6)至少有一个正根.
根据引理
定理2.2 方程(1.1)的每一个解振动的充要条件是满足下列条件之一
当
当
当
当
方程(1.1)存在一个非振动解的充要条件是满足下列条件之一
当
当
当
当
证 我们只证
由
即
或者
得出
由
即
或者
得出
整理得
证毕.
3 方程数值解的振动性与非振动性
3.1 $ a = 0 $
当
其中
则有
由脉冲条件得到
得出(3.1)式的差分方程,即
它的特征方程为
定理3.1 假设
(1)
证 显然,若
代入方程(3.2)有
由脉冲条件得出
定理3.2 方程(3.1)的每一个解振动的充要条件是满足下列条件之一
当
当
方程(3.1)存在一个非振动解的充要条件是满足下列条件之一
当
(1)
(4)
当
证 由定理
由
即
或者
所以
由
即
或者
所以
整理得
证毕.
3.2 $ a \neq 0 $
其中
其中
由脉冲条件
它的特征方程为
定理3.3 假设
证 显然,若
由(3.7)式有
代入(3.6)式有
若
若
因此有
定理3.4 方程(3.5)的每一个解振动的充要条件是满足下列条件之一
当
当
方程(3.5)存在一个非振动解的充要条件是满足下列条件之一
当
当
证 由引理
若
即
或者
所以
由
即
或者
所以
整理得
证毕.
引理3.1[7] 对所有
由引理
定理3.5
证 我们只证
(ⅰ)当
又因为
因为
由定理
(ⅱ)当
又因为
因为
由定理
4 方程数值解的保持性
4.1 $ a = 0 $
定义4.1[8] 若方程(1.1)振动,存在一个
定理4.1 由定理
4.2 $ a \neq 0 $
定理4.2 记
●
●
●
●
证 我们只证
当
从而有
当
从而有
同理有
定理4.3 由定理
证 我们只证
当
由定理
定理4.4
(2)对任意
证 我们只证
当
即
●
●
当
即
●
●
综上,当
5 数值算例
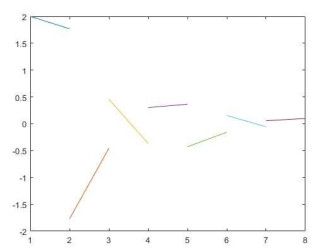
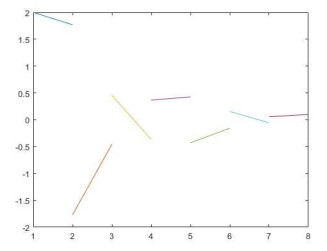
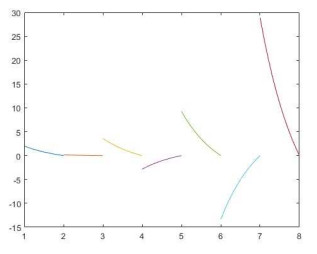
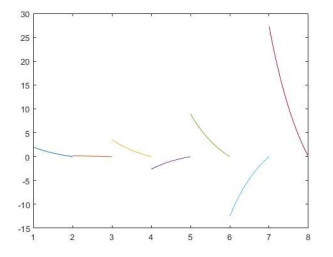
例1 考虑方程
其中
图 1
图 2
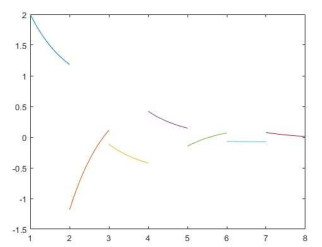
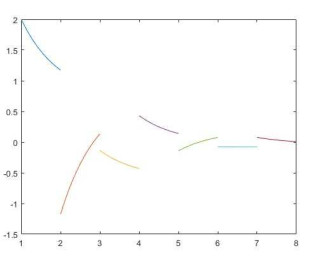
例2 考虑方程
其中
图 3
图 4
例3 考虑方程
其中
图 5
图 6
参考文献
Retarded differential equations with piecewise constant delays
DOI:10.1016/0022-247X(84)90248-8 [本文引用: 1]
The Euler scheme and its convergence for impulsive delay differential equations
Convergence and stability of Euler method for impulsive stochastic delay differential equations
Advanced impulsive differential equations with piecewise constant arguments
DOI:10.3846/1392-6292.2010.15.175-187 [本文引用: 2]