1 引言
目前, 分数阶微分方程的算法还不够成熟, 主要表现在算法需要长时间的计算历程和大空间域的计算, 成熟的算法较少, 主要集中在有限差分法与有限元方法. 因此发展新的数值算法, 提高计算效率, 解决分数阶微分方程计算量大和存储量过大等问题是学者们迫切关注的课题.
分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] .
在本文中, 我们将研究具有变系数的时间分数阶对流-扩散模型
(1.1) $\begin{equation} D_{t}^{\alpha}u(x,t)+c(x)\frac{\partial u(x,t)}{\partial x}+d(x)\frac{\partial^{2} u(x,t)}{\partial x^{2}}=r(x,t),\qquad (x,t)\in\Omega\times J, \end{equation}$
(1.2) $\begin{equation} u(0,t)=\zeta_{0}(t), u(1,t)=\zeta_{1}(t),\qquad t\in J, \end{equation}$
(1.3) $\begin{equation} u(x,0)=\phi(x), \qquad x\in\Omega. \end{equation}$
在这里, $\Omega\times J=[0,1]\times[T]$ $c(x)$ $d(x)$ $\zeta_{0}(t)$ $\zeta_{1}(t)$ $\phi(x)$ $ 0<\alpha<1$ $D_{t}^{\alpha}u(x,t)$ $u(x,t)$
(1.4) $\begin{equation} D_{t}^{\alpha}u(x,t)=\frac{1}{\Gamma(1-\alpha)}\int_0^{t}\frac{\partial u(x,s)}{\partial s}\frac{{\rm d}s}{(t-s)^{\alpha}},\qquad 0<\alpha<1. \end{equation}$
崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法.
本文包括介绍在内, 可分为 5 个部分. 第 2 部分是预备知识, 构造了再生核空间 $W_{2}^{3}[0,1]$
2 预备知识
2.1 方程的半离散格式
首先将上述方程的边值条件 $u(0,t)=\zeta_{0}(t)$ $u(1,t)=\zeta_{1}(t)$
(2.1) $ \begin{matrix} D_{t}^{\alpha}u(x,t)+c(x)\frac{\partial u(x,t)}{\partial x}+d(x)\frac{\partial^{2} u(x,t)}{\partial x^{2}} =f(x,t),\qquad (x,t)\in\Omega\times J, \end{matrix}$
(2.2) $\begin{equation} u(0,t)=0, u(1,t)=0, \qquad t\in J, \end{equation}$
(2.3) $\begin{equation} u(x,0)=\Phi(x), \qquad x\in\Omega, \end{equation}$
其中 $f(x,t)=r(x,t)-D_{t}^{\alpha}h(x,t)-c(x)\frac{\partial h(x,t)}{\partial x}-d(x)\frac{\partial^{2} h(x,t)}{\partial x^{2}} $ $h(x,t)=x\zeta_{1}(t)+(1-x)\zeta_{0}(t)$ .
引理2.1 [8 ] 对任意的 $0<\alpha<1$ $b_{j}$
(1) $b_{j}>0, j=0,1,\cdots,n$
(2) $ 1=b_{0}>b_{1}>\cdots>b_{n}$ $ b_{n} \rightarrow 0, (n\rightarrow \infty)$
(3) $ \sum\limits_{j=0}^{n}(b_{j}-b_{j+1})=1$ .
令 $\Delta t=\frac{1}{N}$ $(N\in\mathbb{N})$ $t_{n}=n \Delta t$ $(n=0$ $1$ $\cdots$ $N)$ . 为了简化, 定义 $u^{n}(x)=u(x,t_{n})$ $D_{t}^{\alpha}u(x,t_{n+1})$
(2.4) $\begin{aligned} D_{t}^{\alpha} u\left(x, t_{n+1}\right) & =\frac{1}{\Gamma(1-\alpha)} \int_{0}^{t} \frac{\partial u(x, s)}{\partial s} \frac{\mathrm{~d} s}{\left(t_{n+1}-s\right)^{\alpha}}=\frac{1}{\Gamma(1-\alpha)} \sum_{j=0}^{n} \int_{t_{j}}^{t_{j+1}} \frac{\partial u(x, s)}{\partial s} \frac{\mathrm{~d} s}{\left(t_{n+1}-s\right)^{\alpha}} \\ & =\frac{1}{\Gamma(1-\alpha)} \sum_{j=0}^{n} \int_{t_{j}}^{t_{j+1}}\left(\frac{u\left(x, t_{j+1}\right)-u\left(x, t_{j}\right)}{\Delta t}+o(\Delta t)\right) \frac{\mathrm{d} s}{\left(t_{n+1}-s\right)^{\alpha}} \\ & \approx \frac{1}{\Gamma(1-\alpha)} \sum_{j=0}^{n} \frac{u\left(x, t_{n-j+1}\right)-u\left(x, t_{n-j}\right)}{\Delta t} \int_{t_{j}}^{t_{j+1}} \frac{\mathrm{~d} t}{t^{\alpha}} \\ & \approx \frac{1}{\Gamma(1-\alpha)} \sum_{j=0}^{n} \frac{u\left(x, t_{n-j+1}\right)-u\left(x, t_{n-j}\right)}{\Delta t}\left((j+1)^{1-\alpha}-j^{1-\alpha}\right) \\ & \approx a(\Delta t, \alpha) \sum_{j=0}^{n} b_{j}\left(u\left(x, t_{n-j+1}\right)-u\left(x, t_{n-j}\right)\right) \end{aligned}$
这里 $ a(\Delta t, \alpha)=\frac{1}{\Gamma(2-\alpha)(\Delta t)^{\alpha}}$ $b_{j}=(j+1)^{1-\alpha}-j^{1-\alpha}$ .
将公式 (2.4) 代入公式 (2.1) 中, 则公式 (2.1) 可转化为如下形式
(2.5) $ \begin{matrix} &~~~~c(x)\frac{\partial u^{n+1}(x)}{\partial x}+d(x)\frac{\partial^{2} u^{n+1}(x)}{\partial x^{2}}+a(\Delta t,\alpha)\sum\limits_{j=0}^{n}b_{j}(u^{n-j+1}(x) -u^{n-j}(x))\\ &=f^{n+1}(x),\quad 0\leq n\leq N, \end{matrix}$
(2.6) $\begin{equation} u^{n+1}(x)\mid_{\partial\Omega}=0, \quad 0\leq n\leq N. \end{equation}$
2.2 两个再生核空间 $H_{2}^{3}[0,1]$ $W_{2}^{1}[0,1]$
下面建立并求解本节中所用到的再生核空间及再生核函数.
定义2.1 再生核空间 $H_{2}^{3}[0,1]$
定理2.1 $R_{x}(y)$ $H_{2}^{3}[0,1]$
定义2.2 再生核空间 $W_{2}^{1}[0,1]$
定理2.2 $Q_{x}(y)$ $W_{2}^{1}[0,1]$
3 数值方法
3.1 再生核方法求解方程 (2.5)
引入一个线性算子 $L:H_{2}^{3}[0,1]\rightarrow W_{2}^{1}[0,1]$ $ \forall u^{n+1}(x) \in H_{2}^{3}[0,1]$
(3.1) $\begin{equation} Lu^{n+1}(x)=a(\Delta t,\alpha)u^{n+1}(x)+c(x)\frac{\partial u^{n+1}(x)}{\partial x}+d(x)\frac{\partial^{2} u^{n+1}(x)}{\partial x^{2}}. \end{equation}$
(3.2) $\begin{equation} Lu^{n+1}(x)=F^{n+1}(x),\qquad 0\leq n \leq N-1, \end{equation}$
定理3.1 $L$ $H_{2}^{3}[0,1]$ $W_{2}^{1}[0,1]$
因为 $a(\Delta t,\alpha)$ $c(x)$ $d(x)$ $[0,1]$
令$\{x_{i}\}_{i=1}^{\infty}$ $\psi_{x}(y)=L^\ast Q_{x}(y)$ $L^\ast$ $L$ $\psi_{i}(x)=L_{y}R_{x}(y)\mid_{y=x_{i}}$ .
定理3.2 $\{\psi_{i}(x)\}_{i=1}^{\infty}$ $H_{2}^{3}[0,1]$
证 令 $\langle u(x),\psi_{i}(x)\rangle_{H_{2}^{3}[0,1]}=0, (i=1, 2, \cdots)$ $\forall$ $u(x) \in H_{2}^{3}[0,1]$
因为 $\{x_{i}\}_{i=1}^{\infty}$ $(Lu)(x)=0$ . 又由 $L^{-1}$ $u(x)=0$ .
在空间 $H_{2}^{3}[0,1]$ ${\{\psi_{i}}(x)\}_{i=1}^{\infty}$ ${\{\overline{\psi_{i}}(x)}\}_{i=1}^{\infty}$
定理3.3 假定 $u^{n+1}(x)$ $u^{n+1}(x)$
(3.3) $\begin{equation} u^{n+1}(x)=\sum\limits_{i=1}^{\infty}\sum\limits_{k=1}^{i}\beta_{ik}F^{n+1}(x_{k})\overline{\psi}_{i}(x). \end{equation}$
其中 $\{x_{i}\}_{i=1}^{\infty}$
我们对精确解 $u^{n+1}(x)=\sum\limits_{i=1}^{\infty}\sum\limits_{k=1}^{i}\beta_{ik}F^{n+1}(x_{k})\overline{\psi}_{i}(x)$ $m$ $u_{m}^{n+1}(x)$
(3.4) $\begin{equation} u_{m}^{n+1}(x)=\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{i}\beta_{ik}F^{n+1}(x_{k})\overline{\psi}_{i}(x), (n=0,1,\cdots, N-1). \end{equation}$
3.2 稳定性与收敛性分析
引理3.1 假定 $u^{n+1}(x)$ $u^{n+1}_{m}(x)$ $\{x_{k}\}_{k=1}^{\infty}$ $Lu^{n+1}(x_{k})=Lu^{n+1}_{m}(x_{k})$ .
因此, $\sum\limits_{k=1}^{i}\beta_{ik}F^{n+1}(x_{k})=\sum\limits_{k=1}^{i}\beta_{ik}Lu^{n}_{m}(x_{k})$ . 可得知 $Lu^{n}_{m}(x_{k})=F^{n+1}(x_{k})$ .
定理3.4 若 $\{x_{i}\}_{i=1}^{\infty}$ $\left\|u^{n+1}(x)-u^{n+1}_{m}(x)\right\|_{H_{2}^{3}[0,1]}\rightarrow0$ $(m\rightarrow\infty)$ .
证 令 $B=\{u^{n+1}_{m}(x)|\left\|u^{n+1}_{m}(x)\right\|_{H_{2}^{3}[0,1]}^{2}\leq c\}$ $c>0$ $\{u^{n+1}_{m}(x)\}_{m=1}^{\infty}\in B$ $p^{n+1}(x)\in B$
则 $Lp^{n+1}(x_{i})=F^{n+1}(x_{i})$ .
由于 $\{x_{i}\}_{i=1}^{\infty}$ $Lp^{n+1}(x)=F^{n+1}(x)$ . 因此 $p^{n+1}(x)$ $u^{n+1}(x)$
进而 $Lu^{n+1}_{m}(x)\rightarrow Lu^{n+1}(x)$ . 又因 $L^{-1}$
定理3.5 $u^{n+1}(x)$
证 令 $u^{n+1}(x)$ $\overline{u}^{n+1}(x)$
其中 $\varepsilon(x)\rightarrow0$
$u^{n+1}(x)$ $\overline{u}^{n+1}(x)$
令 $ \tilde{\varepsilon}=\max\limits_{0\leq x\leq1}\varepsilon(x), $
4 数值算例
在本节中, 通过算例证明了方法的有效性, 数值运算结果由 Mathmatica 11.0 给出. 最大绝对误差 $E_{\infty}$ $e_{m,n}(x)$ $C.O.$
${\bf 例 4.1}$
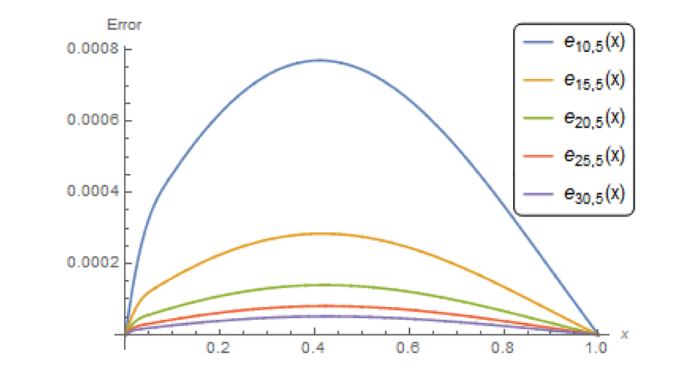
精确解为 $u(x,t)=x^{2}+2\frac{\Gamma(\alpha+1)}{\Gamma(2\alpha+1)}t^{2\alpha}$ $r(x,t)=2t^{\alpha}+2x^{2}+2$ . 当 $\alpha=0.5$ $t=0.5$ $m=64$ 6 ] 进行比较, 运算结果见表 1 . 表 2 展示了当 $n=6$ $\alpha=0.2$ $0.5$ $0.8 $ $m=10$ $15$ $20$ $25$ $30$ $m = 5 $ $\alpha = 0.5 $ $n=10$ $15$ $20$ $25$ $30$ 图 1 所示.
图1
${\bf 例 4.2}$
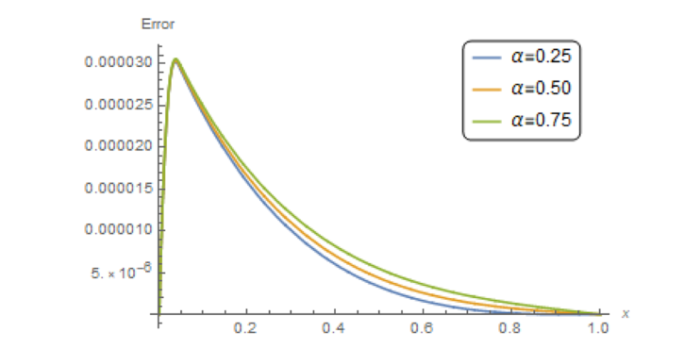
这里 $r(x,t)=\frac{2t^{\alpha}}{\Gamma(3-\alpha)}+2x-2$ $u(x,t)=x^{2}+t^{2}$ $T=1$ $n=5$ 表 3 展示了我们的方法在 $\alpha=0.2$ $0.5$ $0.8$ $m=10$ $15$ $20$ $25$ $30$ $\alpha=0.7$ $m=20$ $n=5$ $10$ $15$ $20 $ $x=0.2$ $0.4$ $0.6$ $0.8$ 表 4 所示. 图 2 展示了当 $m=20$ $t=1$ $\alpha=0.25$ $0.5$ $0.75$ 表 5 展示了当 $T=2$ $\alpha=0.5$ 28 ] 的方法进行比较, 从而证得所提方法的有效性.
图2
${\bf 例 4.3}$
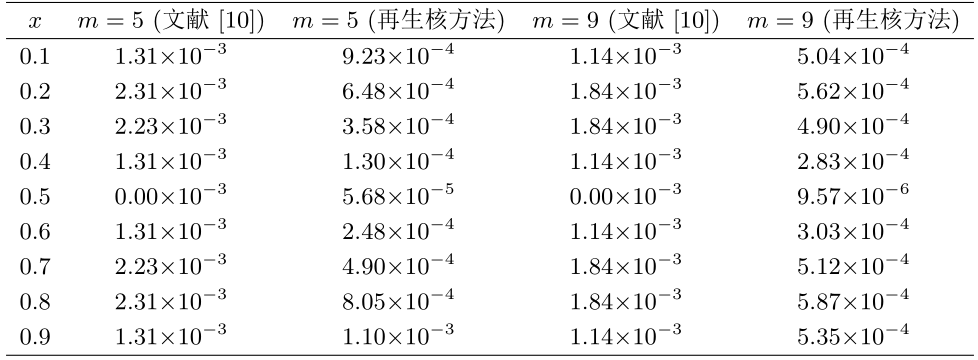
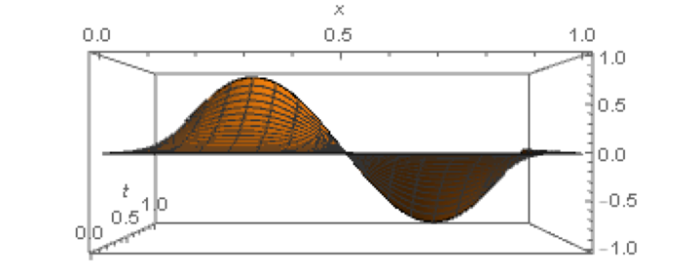
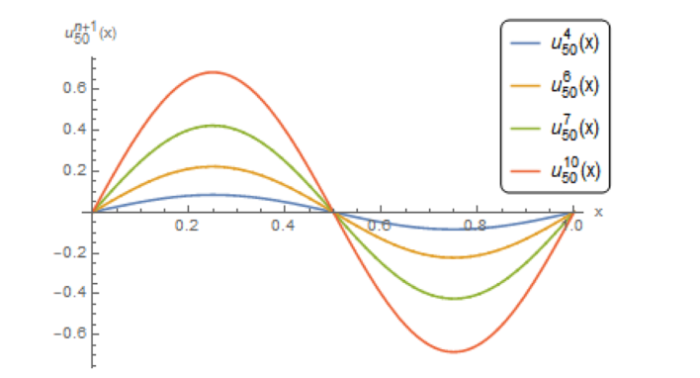
精确解是 $u(x,t)=t^{2}\sin(2\pi x)$ $f(x,t)=\frac{2}{\Gamma(3-\alpha)}t^{2-\alpha}\sin(2\pi x)+4\pi^{2}t^{2}\sin(2 \pi x)$ . 当 $\alpha=0.7$ $t=0.1$ [10 ] 的对比情况如表 6 所示. 图 3 展示了真解 $u(x,t)$ $m=50$ $t=0.3$ $0.5$ $0.7$ $0.9$ $u^{n+1}_{50}(x)$ $(n=3$ $5$ $7$ $9)$ 图 4 所示. 通过观察发现, 当 $t$ $n$ $u^{n+1}_{50}(x)$
图3
图4
图4
不同 $n$ $u^{n+1}_{50}$
5 总结
针对变系数的时间分数阶对流-扩散方程, 首先, 使用有限差分法, 将时间变量离散化, 得到了该方程的半离散格式. 之后再利用再生核方处理空间变量, 得到了方程的精确解 $u(x,t_{n})$ . 然后将精确解 $u(x,t_{n})$ $m$ $u_{m}(x,t_{n})$ . 通过证明, 知道该方法是稳定的. 最后, 给出了几个数值例子, 并与其他文献中的方法进行了比较, 表明该算法是有效的. 在未来的工作中, 可结合再生核方法与 $\varepsilon$ - 最优解概念来求解更高阶的微分方程, 也可用于求解积分方程, 界面问题等. 结合再生核方法与有限差分法也可被用来求解高维的时间分数阶对流-扩散方程及其他的分数阶偏微分方程. 同时, 也可将再生核方法与其他经典的数值方法相结合来提高算法的有效性.
参考文献
View Option
[1]
Gupta S Thakur B . Extended Legendre wavelet method for solving fractional order time hyperbolic partial differential equation
Int J Appl Comput Math , 2023 , 9 3 ): 41 -64
[本文引用: 1]
[2]
Osman M Xia Y Marwan M Omer O A . Novel approaches for solving fuzzy fractional partial differential equations
Fractal Fract 2022 , 6 11 ): Article 656
[本文引用: 1]
[3]
An X Y Liu F W Zheng M L , et al . A space-time spectral method for time-fractional Black-Scholes equation
Appl Numer Math , 2021 , 165 152 -166
[本文引用: 1]
[4]
Prakash A Veeresha P Prakasha D G Goyal M . A homotopy technique for a fractional order multi-dimensional telegraph equation via the Laplace transform
Eur Phys J Plus , 2019 , 134 1 -18
[本文引用: 1]
[5]
Lin Y Xu C . Finite difference/spectral approximations for the time-fractional diffusion equation
J Comput Phys , 2007 , 225 2 ): 1533 -1552
[本文引用: 1]
[6]
Chen Y Wu Y Cui Y , et al . Wavelet method for a class of fractional convection-diffusion equation with variable coefficients
J Comput Sci , 2010 , 1 3 ): 146 -149
[本文引用: 3]
[7]
Saadatmandi A Dehghan M Azizi M R . The Sinc-Legendre collocation method for a class of fractional convection-diffusion equations with variable coefficients
Commun Nonlinear Sci Numer Simul , 2012 , 17 11 ): 4125 -4136
[本文引用: 1]
[8]
Yaseen M Abbas M Nazir T Baleanu D . A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation
Adv Difference Equ , 2017 , 2017 1 -18
[本文引用: 2]
[9]
Ren L Wang Y M . A fourth-order extrapolated compact difference method for time-fractional convection-reaction-diffusion equations with spatially variable coefficients
Appl Math Comput , 2017 , 312 1 -22
[本文引用: 1]
[10]
Saw V Kumar S . Collocation method for time fractional diffusion equation based on the Chebyshev polynomials of second kind
Int J Appl and Comput Math , 2020 , 6 4 ): 117 -129
[本文引用: 3]
[11]
Saw V Kumar S . The Chebyshev collocation method for a class of time fractional convection-diffusion equation with variable coefficients
Math Methods Appl Sci , 2021 , 44 8 ): 6666 -6678
[本文引用: 1]
[12]
Uddin M Haq S . RBFs approximation method for time fractional partial differential equations
Commun Nonlinear Sci Numer Simul , 2011 , 16 11 ): 4208 -4214
[本文引用: 1]
[13]
Zhang J Zhang X Yang B . An approximation scheme for the time fractional convection-diffusion equation
Appl Math Comput , 2018 , 335 305 -312
[本文引用: 1]
[14]
Ravi Kanth A S V Garg N . Numerical simulation of time fractional advection-diffusion-reaction equation using exponential B-Splines // Kumar A, Srivastava S, Singh S. Renewable Energy Towards Smart Grid: Select Proceedings of SGESC 2021. Singapore : Springer , 2022 : 133 -143
[本文引用: 1]
[15]
Li J C Qin X Q . Finite point method for the time fractional convection-diffusion equation Xiong N, Xiao Z, Tong Z, et al. Advances in Computational Science and Computing . Cham : Springer , 2019 : 28 -36
[本文引用: 1]
[16]
傅博 , 王世宇 , 高婷婷 , 吕学琴 . 带有 Caputo-Fabrizio 导数的分数阶微分方程的快速高阶算法的研究
数学物理学报 , 2023 , 43A 3 ): 896 -912
[本文引用: 1]
Fu B Wang S Y Gao T T Lv X Q . A fast high order method for fractional differential equations with the Caputo-Fabrizio derivative
Acta Math Sci , 2023 , 43A 3 ): 896 -912
[本文引用: 1]
[17]
Cui M Deng Z H . Numerical Functional Method in Reproducing Kernel Space . Harbin : The Publication of Harbin Institute of Technology , 1988
[本文引用: 1]
[18]
Cui M Yan Y . The representation of the solution of a kind of operator equation Au=f
Numer Math J Chin Univ , 1995 , 1 82 -86
[本文引用: 1]
[19]
Li X Y Li H X Wu B Y . Piecewise reproducing kernel method for linear impulsive delay differential equations with piecewise constant arguments
Appl Math Comput , 2019 , 349 304 -313
[本文引用: 1]
[20]
Mei L . A novel method for nonlinear impulsive differential equations in broken reproducing kernel space
Acta Math Sci , 2020 , 40 723 -733
[本文引用: 1]
[21]
Lv X Cui M . An efficient computational method for linear fifth-order two-point boundary value problems
J Comput Appl Math , 2010 , 234 5 ): 1551 -1558
[本文引用: 1]
[22]
Sahihi H Allahviranloo T Abbasbandy S . Solving system of second-order BVPs using a new algorithm based on reproducing kernel Hilbert space
Appl Numer Math , 2020 , 151 27 -39
[本文引用: 1]
[23]
Niu J Sun L Xu M Hou J . A reproducing kernel method for solving heat conduction equations with delay
Appl Math Lett , 2020 , 100 106036
[本文引用: 1]
[24]
Chen Z Jiang W Du H . A new reproducing kernel method for Duffing equations
Int J Comput Math , 2021 , 98 11 ): 2341 -2354
[本文引用: 1]
[25]
Mei L Wu B Lin Y . Shifted-Legendre orthonormal method for high-dimensional heat conduction equations
AIMS Math , 2022 , 7 5 ): 9463 -9478
[本文引用: 1]
[26]
Fardi M Al-Omari S K Q Araci S . A pseudo-spectral method based on reproducing kernel for solving the time-fractional diffusion-wave equation
Adv Contin Discrete Models , 2022 , 2022 1 ): 54 -67
[本文引用: 1]
[27]
Li Z Chen Q Wang Y Li X . Solving two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces
Fractal Fract , 2022 , 6 9 ): 492 -502
[本文引用: 1]
[28]
Mercer J . Functions of positive and negative type and their connection with theory of integral equations
Proc R Soc Lond , 1909 : 83 559 ): 69 -70
[本文引用: 2]
Extended Legendre wavelet method for solving fractional order time hyperbolic partial differential equation
1
2023
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
Novel approaches for solving fuzzy fractional partial differential equations
1
2022
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
A space-time spectral method for time-fractional Black-Scholes equation
1
2021
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
A homotopy technique for a fractional order multi-dimensional telegraph equation via the Laplace transform
1
2019
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
Finite difference/spectral approximations for the time-fractional diffusion equation
1
2007
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
Wavelet method for a class of fractional convection-diffusion equation with variable coefficients
3
2010
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
... 精确解为 $u(x,t)=x^{2}+2\frac{\Gamma(\alpha+1)}{\Gamma(2\alpha+1)}t^{2\alpha}$ $r(x,t)=2t^{\alpha}+2x^{2}+2$ . 当 $\alpha=0.5$ $t=0.5$ $m=64$ 6 ] 进行比较, 运算结果见表 1 . 表 2 展示了当 $n=6$ $\alpha=0.2$ $0.5$ $0.8 $ $m=10$ $15$ $20$ $25$ $30$ $m = 5 $ $\alpha = 0.5 $ $n=10$ $15$ $20$ $25$ $30$ 图 1 所示. ...
... 绝对误差与文献 [6 ] 的对比结果 ...
The Sinc-Legendre collocation method for a class of fractional convection-diffusion equations with variable coefficients
1
2012
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation
2
2017
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
... 引理2.1 [8 ] 对任意的 $0<\alpha<1$ $b_{j}$
A fourth-order extrapolated compact difference method for time-fractional convection-reaction-diffusion equations with spatially variable coefficients
1
2017
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
Collocation method for time fractional diffusion equation based on the Chebyshev polynomials of second kind
3
2020
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
... 精确解是 $u(x,t)=t^{2}\sin(2\pi x)$ $f(x,t)=\frac{2}{\Gamma(3-\alpha)}t^{2-\alpha}\sin(2\pi x)+4\pi^{2}t^{2}\sin(2 \pi x)$ . 当 $\alpha=0.7$ $t=0.1$ [10 ] 的对比情况如表 6 所示. 图 3 展示了真解 $u(x,t)$ $m=50$ $t=0.3$ $0.5$ $0.7$ $0.9$ $u^{n+1}_{50}(x)$ $(n=3$ $5$ $7$ $9)$ 图 4 所示. 通过观察发现, 当 $t$ $n$ $u^{n+1}_{50}(x)$
... 数值结果与文献 [10 ] 的对比 ...
The Chebyshev collocation method for a class of time fractional convection-diffusion equation with variable coefficients
1
2021
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
RBFs approximation method for time fractional partial differential equations
1
2011
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
An approximation scheme for the time fractional convection-diffusion equation
1
2018
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
1
2022
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
1
2019
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
带有 Caputo-Fabrizio 导数的分数阶微分方程的快速高阶算法的研究
1
2023
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
带有 Caputo-Fabrizio 导数的分数阶微分方程的快速高阶算法的研究
1
2023
... 分数阶偏微分方程在物理学中广泛应用, 它们是反常扩散、信号处理和控制、图像处理和地震分析的重要数学模型. 人们对分数阶微分方程的不同数学模型的数值解非常感兴趣[1 ⇓ ⇓ -4 ] . 与整数阶偏微分问题相比, 处理分数阶导数是相对复杂的问题, 部分算法还存在计算时间长, 存储空间大, 精度不够, 效率不高等问题. 因此对于分数阶偏微分问题的研究还处于发展阶段. 分数阶对流-扩散方程是分数阶偏微分方程重要的一支, 源自 Montroll 和 Weiss 于 1965 年提出的连续时间随机游走模型. 此类方程在化工, 物理, 生物和医疗等领域引起普遍关注, 是流体力学, 气体动力学等重要的数学模型, 具备广阔的应用前景. 由于解析法很难得到对流-扩散方程的解析解, 对流扩散问题的有效数值解总是计算数学中一个重要的研究内容. 林等人 [5 ] 应用了有限差分和谱近似方法来求解该方程. 陈等人[6 ] 提出了一种小波方法来研究变系数时间分数阶对流扩散模型. Saadatmandi 等人[7 ] 提出了 Sinc-Legendre 配置法来求解此类方程. Yaseen 等人 [8 ] 基于三次三角样条提出了有限差分方法来求解时间分数阶对流-扩散方程. 任等人[9 ] 提出了四阶外推紧致差分方法来求解带有空间变系数的时间分数阶对流扩散模型. 应用配置法求解变系数时间分数阶对流-扩散方程. 还有配置法 [10 ,11 ] , B-样条方法, 有限点等其他方法均用来求解此类方程[12 ⇓ ⇓ ⇓ -16 ] . ...
1
1988
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
The representation of the solution of a kind of operator equation Au=f
1
1995
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
Piecewise reproducing kernel method for linear impulsive delay differential equations with piecewise constant arguments
1
2019
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
A novel method for nonlinear impulsive differential equations in broken reproducing kernel space
1
2020
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
An efficient computational method for linear fifth-order two-point boundary value problems
1
2010
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
Solving system of second-order BVPs using a new algorithm based on reproducing kernel Hilbert space
1
2020
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
A reproducing kernel method for solving heat conduction equations with delay
1
2020
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
A new reproducing kernel method for Duffing equations
1
2021
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
Shifted-Legendre orthonormal method for high-dimensional heat conduction equations
1
2022
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
A pseudo-spectral method based on reproducing kernel for solving the time-fractional diffusion-wave equation
1
2022
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
Solving two-sided fractional super-diffusive partial differential equations with variable coefficients in a class of new reproducing kernel spaces
1
2022
... 崔明根教授和他的同事们[17 ] 从 1980 年成为利用再生核方法求解线性非线性问题的先导. 有许多研究者提出利用再生核方法求解各类模型. 李等人 [18 ] 通过分段再生核方法求解线性摄动延迟微分方程. 梅等人 [19 ] 结合再生核方法求解非线性微分方程. 吕等人 [20 ] 和 Sahihi 等人 [21 ] 运用再生核方法求解边值问题. 一些学者基于再生核方法求解热扩散方程[22 ,23 ] , 高阶扩散方程[24 ] , 分数阶扩散方程等 [25 ⇓ -27 ] .本文利用有限差分法逼近 Caputo 分数阶导数, 得到了该方程的半离散格式. 最后, 给出了再生核的方法. ...
Functions of positive and negative type and their connection with theory of integral equations
2
1909
... 这里 $r(x,t)=\frac{2t^{\alpha}}{\Gamma(3-\alpha)}+2x-2$ $u(x,t)=x^{2}+t^{2}$ $T=1$ $n=5$ 表 3 展示了我们的方法在 $\alpha=0.2$ $0.5$ $0.8$ $m=10$ $15$ $20$ $25$ $30$ $\alpha=0.7$ $m=20$ $n=5$ $10$ $15$ $20 $ $x=0.2$ $0.4$ $0.6$ $0.8$ 表 4 所示. 图 2 展示了当 $m=20$ $t=1$ $\alpha=0.25$ $0.5$ $0.75$ 表 5 展示了当 $T=2$ $\alpha=0.5$ 28 ] 的方法进行比较, 从而证得所提方法的有效性. ...
... 数值结果与文献 [28 ] 的比较 ...