1 引言
设 $H$ $\langle\cdot, \cdot\rangle$ $\|\cdot\|$ $C$ $H$ $F: H\to H$ $T: H\to H$ . 经典变分不等式问题 (VIP) 是指: 寻找 $x^*\in C$
(1.1) $\begin{equation}\label{eq1.1} \langle F(x^*), x - x^*\rangle \ge 0, \ \ \forall x\in C. \end{equation} $
$T$ $x^*\in H$
(1.2) $\begin{equation}\label{eq1.2} T(x^*) = x^*. \end{equation} $
映射 $T$ ${\rm Fix}(T)$ .
变分不等式问题与不动点问题的公共解是指: 寻找 $x^*\in H$
这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] .
2003 年, Takahashi 和 Toyoda[5 ] 基于求解变分不等式问题的投影梯度法[10 ] 和求解不动点问题的 Mann 迭代法[11 ] 提出了如下算法
(1.3) $\begin{equation}\label{GMT} \left\{ \begin{array}{lr} x^0 \in C,& \\ x^{n + 1} = (1 - \beta_n)x^n + \beta_nT(P_C(x^{n} - \lambda_nF(x^{n}))), \end{array} \right. \end{equation} $
其中 $\{\lambda_n\} \subset [a, b] \subset (0, 2\eta)$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $\eta$ - 余强制和映射 $T$ 5 ] 证明了算法(1.3) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解.
为了削弱映射 $F$ 4 ] 基于求解变分不等式问题的外梯度算法[12 ] 提出了如下算法
(1.4) $\begin{equation}\label{EGMT} \left\{ \begin{array}{lr} x^0 \in C, \\ y^n = P_C(x^n - \lambda_n F(x^n)), \\ x^{n + 1} = (1 - \beta_n)x^n + \beta_nT(P_C(x^n - \lambda_n F(y^n))), \end{array} \right. \end{equation} $
其中 $\{\lambda_n\} \subset [a, b] \subset (0, \frac{1}{L})$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ 4 ] 证明了算法 (1.4) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解.
为了减少向 $C$ [13 ] 将文献 [4 ] 中的算法第二次向 $C$
(1.5) $\begin{equation}\label{SEGMT} \left\{ \begin{array}{lr} x^0 \in H,& \\ y^n = P_C(x^n - \lambda F(x^n)),& \\ T_n = \{x \in H|\langle x^n - \lambda F(x^n) - y^n, x - y^n\rangle \leq 0\},& \\ x^{n + 1} = (1 - \beta_n)x^n + \beta_nT(P_{T_n}(x^n - \lambda F(y^n))), \end{array} \right. \end{equation} $
其中 $\lambda \in (0, \frac{1}{L})$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ 13 ]证明了算法 (1.5)所产生的序列弱收敛到变分不等式问题与不动点问题的公共解.
另一方面, 2018 年, Thong 和 Hieu[6 ] 基于求解变分不等式的 Tseng 型外梯度算法[14 ] , 提出以下算法
(1.6) $\begin{equation}\label{TEGMT} \begin{cases} x^0 \in H, \\ y^n = P_C(x^n - \lambda_n F(x^n)),\\ \text{其中} \lambda_n: = r\mathit{l}^{m_n}, m_n \text{是满足下式的最小非负整数}~m:\\ r\mathit{l}^m\|F(x^n) - F(P_C(x^n - r\mathit{l}^mF(x^n)))\| \leq \tau\|x^n - P_C(x^n - r\mathit{l}^mF(x^n)) \|, \\ z^n = y^n - \lambda_n (F(y^n) - F(x^n)),\\ x^{n + 1} = (1 - \beta_n)z^n + \beta_nT(z^n), \end{cases} \end{equation} $
其中 $r > 0$ $\mathit{l}\in (0, 1)$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ $I-T$ 6 ] 证明了算法 (1.6) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解.
为了进一步获得强收敛的结果, 2018 年 Thong 等[6 ] 基于 Halpern 迭代法[15 ] 提出如下算法
(1.7) $\begin{equation}\label{TEGMTS} \begin{cases} x^0, u^0 \in H, \\ y^n = P_C(x^n - \lambda_n F(x^n)),\\ \text{其中}~ \lambda_n: = r\mathit{l}^{m_n}, m_n ~\text{是满足下式的最小非负整数}~ m:\\ r\mathit{l}^m\|F(x^n) - F(P_C(x^n - r\mathit{l}^mF(x^n)))\| \leq \tau\|x^n - P_C(x^n - r\mathit{l}^mF(x^n)) \|, \\ z^n = y^n - \lambda_n (F(y^n) - F(x^n)),\\ q^n = \alpha_n u^0 + (1 - \alpha_n)z^n, \\ x^{n + 1} = (1 - \beta_n)q^n + \beta_nT(q^n), \end{cases} \end{equation} $
其中 $r > 0$ $\mathit{l}\in (0, 1)$ $\{\alpha_n\} \subset (0, 1)$ $\lim\limits_{n\to \infty}\alpha_n = 0$ $\sum\limits_{n = 1}^\infty\alpha_n = \infty$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ $I-T$ 6 ] 证明了算法 (1.7) 产生的序列强收敛到 $P_{{\rm Fix}(T) \cap S}(u^0)$ .
众所周知, 单调映射和伪单调映射一定是拟单调映射, 但反之不一定成立, 见文献[16 ]. 因此, 有必要将映射 $F$ 17 ]提出求解拟单调变分不等式问题与伪压缩映射不动点问题的公共解的如下算法
(1.8) $\begin{equation}\label{Yin} \begin{cases} x^0\in H, \lambda_0>0, 0<u<1,\\ w^n = (1 - \beta_n)x^n + \beta_nT[(1 - \alpha_n)x^n + \alpha_nT(x^n)], \\ y^n = P_C(w^n - \lambda_n F(w^n)),\\ z^n = y^n - \lambda_n (F(y^n) - F(w^n)),\\ x^{n + 1} = (1 - \gamma_n)w^n + \gamma_nz^n,\\ \lambda_{n+1} = \begin{cases} \min\Big\{\lambda_n, \frac{u\|w^n - y^n\|}{\|F(w^n) - F(y^n)\|}\Big\}, &\text{若 $\|F(w^n)-F(y^n)\|\ne0$},\\ \lambda_n, &\text{其它},\\ \end{cases} \end{cases} \end{equation} $
其中 $\{\alpha_n\}$ $\{\beta_n\}$ $\{\gamma_n\}$ $(0,1)$
假设映射 $T$ $F$ $x^n\rightharpoonup x$ $\liminf\limits_{n\to\infty}\|F(x^n)\|=0$ $\{x^n\}$ $F(x)=0$ $\{x\in C:F(x)=0\}\setminus S_D$ ${\rm Fix}(T)\cap S_D\ne\emptyset$ 17 ] 证明了算法 (1.8) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解.
一方面, 为了削弱文献 [6 ] 中映射 $F$ $T$ 17 ] 中映射 $F$ $F$ $T$ 6 ] 相比, 本文将映射 $F$ $F$ $T$ 17 ] 相比, 本文将映射 $F$
本文的内容安排如下: 在第 2 节中, 回顾一些定义和引理. 在第 3 节中, 提出算法并分析算法的收敛性. 最后, 在第 4 节中用几个数值例子说明算法的有效性.
2 预备知识
设 $H$ $\langle \cdot, \cdot\rangle$ $\|\cdot\|$ $C$ $H$ $x^n\to x$ $\{x^n\}$ $x$ $x^n\rightharpoonup x$ $\{x^n\}$ $x$ .
定义2.1 设映射 $F:H\rightarrow H$
(iv) $F$ $L > 0$
(v) $F$ $x^n \rightharpoonup x$ $\{x^n\}$ $F(x^n) \rightharpoonup F(x)$ .
定义2.2 [8 ] 设映射 $T:H\rightarrow H$
(iii) $T$ $\kappa$ - 半压缩映射, 若对任意 $z\in {\rm Fix}(T), x\in H$ $\kappa\in[0, 1)$
(2.1) $\begin{equation}\label{dif_k} \|T(x) - z\|^2 \le \|x - z\|^2 + \kappa\|(I - T)x\|^2; \end{equation} $
(iv) $I-T$ $\{x_n\}\subset H$ $x_n\rightharpoonup x$ $(I-T)x_n\to 0$ $x\in {\rm Fix}(T)$ .
注2.1 由定义 2.2 中映射 $T$ $\Rightarrow$ ( ii)$\Rightarrow$ ( iii), 但(i)$\nLeftarrow$ ( ii)$\nLeftarrow$ ( iii), 见文献[18 ,19 ]. 有 (i)$\Rightarrow$ ( iv), 但(ii)$\nRightarrow$ ( iv), 见文献 [20 ,21 ].
对任意的非空闭凸集 $C\subset H$ $x\in H$ $x$ $C$ $P_C(x)$ $P_C(x)$ $C$
显然, 若 $x\in C$ $x=P_C(x)$ . 下面给出投影的一些基本性质.
引理2.1 [22 ,23 ] 令 $C\subset H$ $x\in H$ $\alpha \ge \beta > 0$
(i) $\langle P_{C}(x) - x, y - P_{C}(x)\rangle \ge 0, \forall y\in C$
(ii) $\|y - P_{C}(x)\|^{2} \le \|y - x\|^{2} - \|P_{C}(x) - x\|^{2}, \forall y\in C$
(iii) $\frac{\|x - P_C(x - \alpha F(x))\|}{\alpha} \le \frac{\|x - P_C(x - \beta F(x))\|}{\beta}$
(iv) $\|x - P_C(x - \beta F(x))\| \le \|x - P_C(x - \alpha F(x))\|$ .
下面给出一些引理, 其对算法收敛性的证明至关重要.
引理2.2 [24 ] 设 $\{\Phi_n\}$ $\{s_n\}\subset(0,1)$ $\sum\limits_{n = 0}^\infty s_n = \infty$ $\{\Omega_n\}$
如果对满足 $\liminf\limits_{k\to\infty}(\Phi_{n_{k+1}} - \Phi_{n_k}) \ge 0$ $\{\Phi_n\}$ $\{\Phi_{n_k}\}$ $\{\Omega_{n_k}\}$ $\limsup\limits_{k\to\infty}\Omega_{n_k} \le 0$ $\lim\limits_{n\to\infty}\Phi_n = 0$ .
引理2.3 [3 ] 设 $T:H\rightarrow H$ $\kappa$ - 半压缩映射且 ${\rm Fix}(T)\neq \emptyset$ $T_\alpha = (1 - \alpha)I + \alpha T$ $\alpha \in (0, 1 - \kappa)$
(i) ${\rm Fix}(T) = {\rm Fix}(T_\alpha)$
(ii) $\|T_\alpha(x) - z\|^2 \le \|x - z\|^2 - \frac{1}{\alpha}(1 - \kappa -\alpha)\|(I - T_\alpha)x\|^2, \forall x\in H, z\in {\rm Fix}(T)$
(iii) ${\rm Fix}(T)$ $H$
本文将假设 ${\rm Fix}(T)\cap S_D\ne\emptyset$ $S_D$
定义2.3 [25 ,26 ] 问题 (1.1) 的对偶变分不等式是: 寻找 $x^* \in C$
(2.2) $\begin{equation}\label{sd} \langle F(y), y - x^*\rangle \ge 0, \ \ \forall y\in C. \end{equation} $
记对偶变分不等式的解集为 $S_D$ . 用 $S_T$ $S_N$
注2.3 由文献[25 ]可知, 当 $C$ $F$ $C$ $S_D\subset S$ . 进一步, 当 $F$ $C$ $S = S_D$ . 但当 $F$ $S_D \neq S$ 26 ,例 4.2].
其次给出 ${\rm Fix}(T)\cap S_D$
引理2.4 映射 $F:H\to H$
(a) $F$ $C$ ${\rm Fix}(T)\cap S\neq \emptyset$
(b) $F$ $C$ ${\rm Fix}(T)\cap S_N\neq \emptyset$
(c) $F$ $C$ $C$ $x^* \in {\rm Fix}(T)\cap S$ $F(x^*)\neq 0$
则 ${\rm Fix}(T)\cap S_D\ne\emptyset$ .
证 类似文献 [26 ]. 其中 (a) 是因为伪单调的定义和注2.3; (b) 是文献[26 ,引理 2.7] 的推论; (c) 是因为 (b) 和文献[26 ,定理 2.1].
3 算法及收敛性分析
条件 1 映射 $F:H\to H$ $H$ $C$ $x\in C$ $F(x)\neq 0$ .
条件 2 映射 $T:H\to H$ $\kappa$ - 半压缩的, 且 $I - T$
条件 3 ${\rm Fix}(T)\cap S_D\ne\emptyset$ .
算法1 ${\bf 初始}$ $r > 0, \mathit{l}\in (0,1), \tau\in (0,1)$ $\theta > 0$ . 选取正实数序列 $\{\alpha_n\}, \{\beta_n\}, \{\varepsilon_n\}$ $\{\alpha_n\}\subset(0,1)$ $\lim\limits_{n\to\infty}\alpha_n = 0$ $\sum\limits_{n = 1}^\infty \alpha_n = \infty$ $\lim\limits_{n\to\infty}\frac{\varepsilon_n}{\alpha_n} = 0$ $\{\beta_n\}\subset(a,b)\subset(0,1 - \kappa)$ $a$ $b$ $0 < a < b < 1$ . 任取 $ x^0, x^1, u^0\in H.$
${\bf 迭代}$ $x^{n - 1}$ $x^n(n \geq 1)$ . 计算
(3.1) $\begin{equation}\label{wn} w^n = x^n + \theta_n(x^n - x^{n - 1}), \end{equation} $
其中 $0 \le \theta_n \le \bar{\theta}_n,$
(3.2) $\begin{equation}\label{yn} y^n = P_C(w^{n} - \lambda_nF(w^{n})), \end{equation} $
其中 $\lambda_n: = r\mathit{l}^{m_n}$ $m_n$ $m$
(3.3) $\begin{equation}\label{linesearch} r\mathit{l}^m\|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| \le \tau\|w^n - P_C(w^n - r\mathit{l}^mF(w^n))\|. \end{equation} $
(3.4) $z^n = y^n - \lambda_n(F(y^n) - F(w^n)),$
(3.5) $q^n = \alpha_n u^0 + (1 - \alpha_n)z^n,$
(3.6) $x^{n + 1} = (1 - \beta_n)q^n + \beta_nT(q^n).$
首先, 根据算法 1 中参数的选取, 有以下结论成立.
注3.1 设 $\{x^n\}$ $\theta_n$
(i) $\{\theta_n\}\subset[\theta]$
(ii) $\lim\limits_{n\to\infty}\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| = 0$ $M_1 > 0$ $n\ge 1$ $\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| \le M_1$ .
其中 (i) 由 $\theta_n$ $\bar{\theta}_n$ $0 \le \frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| \le \frac{\bar{\theta}_n}{\alpha_n}\|x^n - x^{n - 1}\| \le \frac{\varepsilon_n}{\alpha_n}$ $\lim\limits_{n\to\infty}\frac{\varepsilon_n}{\alpha_n} = 0$ $\lim\limits_{n\to\infty}\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| = 0$ . 因此, 由极限的定义可知存在 $M_1 > 0$ $n\ge 1$ $\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| \le M_1$ .
引理3.1 假设条件1 成立, $w^n$ $n\ge1$ $m$
(3.7) $\begin{equation}\label{9} r\mathit{l}^m\|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| \le \tau\|w^n - P_C(w^n - r\mathit{l}^mF(w^n))\|. \end{equation} $
证 若 $w^n\in S$ $w^n = P_C(w^n - rF(w^n))$ $m = 0$
若 $w^n\notin S$ $m$
(3.8) $\begin{equation}\label{11} r\mathit{l}^m\|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| > \tau\|w^n - P_C(w^n - r\mathit{l}^mF(w^n)) \|, \end{equation} $
(3.9) $\begin{equation}\label{12} \|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| > \tau\frac{\|w^n - P_C(w^n - r\mathit{l}^mF(w^n)) \|}{r\mathit{l}^m}. \end{equation} $
${\bf 情形 1}$ $w^n\in C$ . 因为 $P_C$
(3.10) $\begin{equation}\label{13} \lim_{m\to\infty}\|w^n - P_C(w^n - r\mathit{l}^mF(w^n))\| = \|w^n - w^n\| = 0. \end{equation} $
再由条件 1知, 映射 $F$ $H$
(3.11) $\begin{equation}\label{14} \lim_{m\to\infty}\|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| = 0. \end{equation} $
(3.12) $\begin{equation}\label{15} \lim_{m\to\infty}\frac{\|w^n - P_C(w^n - r\mathit{l}^mF(w^n)) \|}{r\mathit{l}^m} = 0. \end{equation} $
令 $h^m = P_C(w^n - r\mathit{l}^mF(w^n))$
(3.13) $\begin{equation}\label{16} \langle\frac{h^m - w^n}{r\mathit{l}^m}, x - h^m\rangle + \langle F(w^n), x - w^n\rangle + \langle F(w^n), w^n - h^m\rangle \ge 0, \ \ \forall x\in C. \end{equation} $
对 (3.13) 式取极限 $m\to\infty$ $ \langle F(w^n), x - w^n\rangle \ge 0, \forall x\in C, $ $w^n\in S$ $w^n\notin S$ $m$
${\bf 情形 2}$ $w^n\notin C$ . 因为 $P_C$
(3.14) $\begin{equation}\label{17} \lim_{m\to\infty}\tau\|w^n - P_C(w^n - r\mathit{l}^mF(w^n))\| > 0. \end{equation} $
由条件 1 知, 映射 $F$ $H$ $P_C$
(3.15) $\begin{equation}\label{18} \lim_{m\to\infty}r\mathit{l}^m\|F(w^n) - F(P_C(w^n - r\mathit{l}^mF(w^n)))\| = 0, \end{equation} $
由 (3.14), (3.15) 式知这与 (3.8) 式矛盾, 从而存在非负整数 $m$
先给出以下引理, 这对证明算法的收敛性起着关键性的作用.
引理3.2 假设条件 1-3 成立, 若算法 1 生成的序列 $\{x^n\}$ $\lim\limits_{n\to\infty}\|w^n - y^n\| = 0$ $\lim\limits_{n\to\infty}\|w^n - x^n\| = 0$ $\lim\limits_{n\to\infty}\|q^n - x^n\| = 0$ $\lim\limits_{n\to\infty}\|T(q^n) - q^n\| = 0$ $\{x^{n_k}\}\subset\{x^n\}$ $x^{n_k}\rightharpoonup \hat{x}\in H$ $\hat{x}\in {\rm Fix}(T)\cap S_D$ .
证 由于 $x^{n_k}\rightharpoonup \hat{x}$ $\lim\limits_{k\to\infty}\|w^{n_k} - x^{n_k}\| = 0$ $w^{n_k}\rightharpoonup \hat{x}$ . 由于 $\lim\limits_{n\to\infty}\|w^n - y^n\| = 0$ $y^{n_k}\rightharpoonup \hat{x}$ . 又因为 $\{y^n\}\subset C$ $C$ $\hat{x}\in C$ . 由 $y^n$
(3.16) $\begin{equation}\label{19} \frac{1}{\lambda_{n_k}}\langle w^{n_k} - y^{n_k}, x - y^{n_k}\rangle + \langle F(w^{n_k}), y^{n_k} - w^{n_k}\rangle \le \langle F(w^{n_k}), x - w^{n_k}\rangle, \ \ \forall x\in C. \end{equation} $
(3.17) $\begin{equation}\label{infx} \liminf_{k\to\infty}\langle F(w^{n_k}), x - w^{n_k}\rangle \ge 0, \ \ \forall x\in C, \end{equation} $
(3.18) $\begin{equation}\label{infy} \liminf_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle \ge 0, \ \ \forall x\in C. \end{equation} $
(1) 当 $\displaystyle\liminf_{k\to\infty}\lambda_{n_k} > 0$ . 因为 $\{x^n\}$ $\displaystyle\lim_{n\to\infty}\|w^n - x^n\| = 0$ $\{w^{n_k}\}$ $F$ $H$ 27 ]可知, $\{F(w^{n_k})\}$ $\displaystyle\lim_{k\to\infty}\|w^{n_k} - y^{n_k}\| = 0$ $\{y^{n_k}\}$
(2) 当 $\displaystyle\liminf_{k\to\infty}\lambda_{n_k} = 0$ . 由于 $\mathit{l}\in (0, 1)$ $\lambda_{n_k}\mathit{l}^{-1} > \lambda_{n_k}$ . 由引理 2.1 得
为了方便表达, 令 $t^{n_k} := P_C(w^{n_k} - \lambda_{n_k}\mathit{l}^{-1}F(w^{n_k}))$ $ \|w^{n_k} - t^{n_k}\| \le \frac{1}{\mathit{l}}\|w^{n_k} - y^{n_k}\|. $ $\displaystyle\lim_{k\to\infty}\|w^{n_k} - t^{n_k}\| = 0$ . 因此 $t^{n_k}\rightharpoonup \hat{x} \in C$ $\{t^{n_k}\}$ $F$ $H$
(3.19) $\begin{equation}\label{21} \lim_{k\to\infty}\|F(w^{n_k}) - F(t^{n_k})\| = 0. \end{equation} $
(3.20) $\begin{equation}\label{22} \frac{1}{\tau}\|F(w^{n_k}) - F(t^{n_k})\| > \frac{\|w^{n_k} - t^{n_k}\|} {\lambda_{n_k}\mathit{l}^{-1}}. \end{equation} $
(3.21) $\begin{equation}\label{22.5} \lim_{k\to\infty}\frac{\|w^{n_k} - t^{n_k}\|} {\lambda_{n_k}\mathit{l}^{-1}} = 0. \end{equation} $
根据 $t^{n_k}$
(3.22) $\begin{equation}\label{23} \frac{1}{\lambda_{n_k}\mathit{l}^{-1}}\langle w^{n_k} - t^{n_k}, x - t^{n_k}\rangle + \langle F(w^{n_k}), t^{n_k} - w^{n_k}\rangle \le \langle F(w^{n_k}), x - w^{n_k}\rangle, \ \ \forall x\in C. \end{equation} $
对 (3.22) 式取下极限, 结合(3.21) 式有对任意 $x\in C$ $\displaystyle\liminf_{k\to\infty}\langle F(w^{n_k}), x - w^{n_k}\rangle \ge 0$
(3.23) $\begin{equation}\label{24} \begin{split} \langle F(y^{n_k}), x - y^{n_k}\rangle =& \langle F(y^{n_k}), x - w^{n_k}\rangle + \langle F(y^{n_k}), w^{n_k} - y^{n_k}\rangle\\ =& \langle F(y^{n_k}) - F(w^{n_k}), x - w^{n_k}\rangle + \langle F(w^{n_k}), x - w^{n_k}\rangle\\ &+ \langle F(y^{n_k}), w^{n_k} - y^{n_k}\rangle.\\ \end{split} \end{equation} $
由于 $F$ $H$ $\displaystyle\lim_{k\to\infty}\|w^{n_k} - y^{n_k}\| = 0$
然后证明 $\hat{x}\in S_D$ . 为了方便表达, 令 $V^{n_k} := \frac{F(y^{n_k})}{\|F(y^{n_k})\|^2}$ $k \ge 1$ $\langle F(y^{n_k}), V^{n_k}\rangle = 1$ . 取
(3.24) $\begin{equation}\label{xik} \xi_k = |\langle F(y^{n_k}), x - y^{n_k}\rangle| + \frac{1}{k}, \end{equation} $
(3.25) $\begin{equation}\label{25} \limsup_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle \ge \liminf_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle \ge 0. \end{equation} $
考虑以下两种情况: (1) 当对任意 $x\in C$ $\displaystyle\limsup_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle > 0$ . 由上极限定义知, 存在 $\{y^{n_{k_j}}\}\subset\{y^{n_k}\}$ $ \langle F(y^{n_{k_j}}), x - y^{n_{k_j}}\rangle > 0, \forall j \ge 1. $ $F$ $H$ $ \langle F(x), x - y^{n_{k_j}}\rangle \ge 0, ~ \forall j \ge 1. $ $j\to\infty$ $ \langle F(x), x - \hat{x}\rangle \ge 0,~ \forall x\in C, $ $\hat{x}\in S_D$ .
(2) 当对任意 $x \in C$ $\displaystyle\limsup_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 (3.25) 式知 $\displaystyle\lim_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 $\xi_k$ $\displaystyle\lim_{k\to\infty}\xi_k = 0$ . 由于 $y^{n_k}\rightharpoonup \hat{x}$ $F$ $C$ $F(y^{n_k})\rightharpoonup F(\hat{x})$ $F(\hat{x}) \neq 0$ . 注意范数映射是序列弱下半连续的[28 ,29 ] , 因此
由 $\displaystyle\lim_{k\to\infty}\xi_k = 0$
从而 $\displaystyle\lim_{k\to\infty}\|\xi_kV^{n_k}\| = 0$ $\displaystyle\lim_{k\to\infty}\xi_kV^{n_k} = 0$ . 由 $\xi_k$ $ \langle F(y^{n_k}), x - y^{n_k}\rangle + \xi_k > 0, \ \ \forall x\in C, $
(3.26) $\begin{equation}\label{26} \langle F(x + \xi_kV^{n_k}) - F(x), x + \xi_kV^{n_k} - y^{n_k}\rangle \ge - \langle F(x), x + \xi_kV^{n_k}-y^{n_k}\rangle, \ \ \forall x\in C. \end{equation} $
因为 $\displaystyle\lim_{k\to\infty}\xi_kV^{n_k} = 0$ $F$ $H$
(3.27) $\begin{equation}\label{27} \lim_{k\to\infty}\|F(x + \xi_kV^{n_k}) - F(x)\| = 0. \end{equation} $
在 (3.26) 式中令 $k\to\infty$ $ \langle F(x), x - \hat{x}\rangle \ge 0, \forall x\in C, $ $\hat{x}\in S_D$ .
最后证明 $\hat{x}\in {\rm Fix}(T)$ . 因为 $\displaystyle\lim_{n\to\infty}\|x^n - q^n\| = 0$ $x^{n_k}\rightharpoonup \hat{x}$ $q^{n_k}\rightharpoonup \hat{x}$ . 又因为 $\displaystyle\lim_{n\to\infty}\|T(q^n) - q^n\| = 0$ $I - T$ $\hat{x}\in {\rm Fix}(T)$ .
综上可得, $\hat{x}\in {\rm Fix}(T)\cap S_D$ .
下面证明算法 1 生成的序列 $\{x^n\}$
引理3.3 假设条件 1-3 成立, $\{w^n\}$ $\{x^n\}$ $\{y^n\}$ $\{q^n\}$ $\{z^n\}$ $x^*\in {\rm Fix}(T)\cap S_D$
(i) $\|x^{n + 1} - x^*\|^2 \le \|q^n - x^*\|^2 - \beta_n(1 - \kappa - \beta_n)\|T(q^n) - q^n\|^2$
(ii) $\|z^n - x^*\|^2 \le \|w^n - x^*\|^2 - (1 - \tau^2)\|w^n - y^n\|^2$
(iii) 存在 $M_1 > 0$ $n \ge 1$ $\|w^n - x^*\| \le (1 - \alpha_n)\|x^n - x^*\| + \alpha_nM_1$
证 (i) 由 $x^{n + 1}$
其中 (a) 成立是因为 $T$ $\kappa$ - 半压缩映射. 由定义 2.2 得
(ii) 由 $z^n$
(3.28) $ \begin{matrix}\label{29} \|z^n - x^*\|^2 = &\|y^n - \lambda_n(F(y^n) - F(w^n)) - x^*\|^2\\ = &\|y^n - x^*\|^2 + \lambda_n^2\|F(y^n) - F(w^n)\|^2 - 2\lambda_n\langle y^n - x^*, F(y^n) - F(w^n)\rangle\\ = &\|w^n - x^*\|^2 + \|w^n - y^n\|^2 + 2\langle y^n - w^n, w^n - x^*\rangle + \lambda_n^2\|F(y^n) - F(w^n)\|^2\\ & - 2\lambda_n\langle y^n - x^*, F(y^n) - F(w^n)\rangle\\ = &\|w^n - x^*\|^2 + \|w^n - y^n\|^2 - 2\langle y^n - w^n, y^n - w^n\rangle + 2\langle y^n - w^n, y^n - x^*\rangle\\ & + \lambda_n^2\|F(y^n) - F(w^n)\|^2 - 2\lambda_n\langle y^n - x^*, F(y^n) - F(w^n)\rangle\\ = &\|w^n - x^*\|^2 - \|w^n - y^n\|^2 + 2\langle y^n - w^n, y^n - x^*\rangle + \lambda_n^2\|F(y^n) - F(w^n)\|^2\\ & - 2\lambda_n\langle y^n - x^*, F(y^n) - F(w^n)\rangle\\ = &\|w^n - x^*\|^2 - \|w^n - y^n\|^2 + 2\langle y^n - w^n + \lambda_nF(w^n), y^n - x^*\rangle\\ &+ \lambda_n^2\|F(y^n) - F(w^n)\|^2 - 2\lambda_n\langle F(y^n), y^n - x^*\rangle. \end{matrix} $
一方面, 因为 $x^*\in {\rm Fix}(T)\cap S_D$ $y^n\in C$ $\langle F(y^n), F(y^n) - x^*\rangle \ge 0$ . 另一方面, 因为 $y^n = P_C(w^{n} - \lambda_nF(w^{n}))$ $\langle y^n - w^n + \lambda_n F(w^n), y^n - x^*\rangle \le 0$ . 将其代入 (3.28) 式有
(3.29) $\begin{equation}\label{30} \|z^n - x^*\|^2 \le \|w^n - x^*\|^2 - \|w^n - y^n\|^2 + \lambda_n^2\|F(y^n) - F(w^n)\|^2. \end{equation} $
根据 (3.3) 式有 $\lambda_n^2\|F(y^n) - F(w^n)\|^2 \le \tau^2\|y^n - w^n\|^2$
(iii) 由注 3.1 的 (ii) 可知, 存在正数 $M_1$ $n \ge 1$ $\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| \le M_1$ . 因此对 $\forall n \ge 1,$
(iv) 由 $\alpha_n$ $\beta_n$ $\{\alpha_n\} \subset (0, 1)$ $\{\beta_n\} \subset (a, b)\subset (0, 1-\kappa)$
其中 (a) 成立是因为由 (i) 可得 $\|x^{n + 1} - x^*\| \le \|q^n - x^*\|$ $q^n$ $\|z^n - x^*\| \le \|w^n - x^*\|$ $ \begin{equation*} \|x^{n + 1} - x^*\| \le \max\{\|x^n - x^*\|, \|u^0 - x^*\| + M_1\} \le \cdots \le \max\{\|x^1 - x^*\|, \|u^0 - x^*\| + M_1\}. \end{equation*} $ $\{x^n\}$
引理3.4 假设条件 1-3 成立, $\{w^n\}$ $\{x^n\}$ $\{y^n\}$ $\{q^n\}$ $\{z^n\}$ $x^*\in {\rm Fix}(T)\cap S_D$
其中 (a) 成立是因为 $q^n$ $\{\alpha_n\}\subset (0, 1)$
其中 (a) 成立是因为 $\{x^n\}$ $\{\alpha_n\}\subset (0, 1)$ $M_2 > 0$
(ii) 因为 $\{x^n\}$ $\theta_n \le \theta$ $M_3 > 0$
(3.30) $\begin{equation}\label{M3} 2\|x^n - x^*\| + \theta_n\|x^n - x^{n - 1}\| \le 2\|x^n - x^*\| + \theta\|x^n - x^{n - 1}\| \le M_3, \ \ \forall n \ge 1. \end{equation} $
其中 (a) 成立是因为 $q^n$ $\{\alpha_n\} \subset (0, 1)$ $w^n$
最后证明 $\{x^n\}$ $P_{S_D\cap {\rm Fix}(T)}(u^0)$ . 由 $S_D\cap {\rm Fix}(T)\neq \emptyset$ ${\rm Fix}(T)\neq \emptyset$ $T$ ${\rm Fix}(T)$ $S_D$ $S_D$ $S_D\cap {\rm Fix}(T)$ $P_{S_D\cap {\rm Fix}(T)}(u^0)$
定理3.1 假设条件 1-3 成立, $\{x^n\}$ $\{x^n\}$ $\widetilde{x} := P_{S_D\cap {\rm Fix}(T)}(u^0)$ .
证 记 $\Phi_n := \|x^n - \widetilde{x}\|^2$ $s_n := \alpha_n$ $\Omega_n := M_3\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| + 2\langle u^0 - \widetilde{x}, q^n - \widetilde{x}\rangle$ $ \Phi_{n + 1} \le (1 - s_n)\Phi_n + s_n \Omega_n, \forall n \ge 1, $ $\{s_n\} \subset (0, 1)$ $\sum\limits_{n=1}^{\infty}s_n = \infty$ . 由引理 2.2 知, 要证 $\Phi_n : \|x^n - \widetilde{x}\|^2\to 0(n\to\infty)$ $\displaystyle\liminf_{k\to\infty} (\Phi_{n_{k+1}} - \Phi_{n_k}) \ge 0$ $\{\Phi_n\}$ $\{\Phi_{n_k}\}$ $\{\Omega_{n_k}\}$ $\displaystyle\limsup_{k\to\infty}\Omega_{n_k} \le 0$ . 为此, 不妨假设存在 $\{\|x^n - \widetilde{x}\|^2\}$ $\{\|x^{n_k} - \widetilde{x}\|^2\}$
(3.31) $\begin{equation}\label{infxx1} \liminf_{k\to\infty}(\|x^{n_{k+1}} - \widetilde{x}\|^2- \|x^{n_k} - \widetilde{x}\|^2) \ge 0. \end{equation} $
其中 (a) 成立是因为 $\{\beta_n\}\subset(a,b)\subset(0,1 - \kappa)$ $\tau\in (0, 1)$
(3.32) $\lim_{k\to\infty}\|T(q^{n_k}) - q^{n_k}\| = 0, $
(3.33) $\lim_{k\to\infty}\|w^{n_k} - y^{n_k}\| = 0. $
其中 (a) 成立是因为 (3.3) 式. 根据 (3.33) 式可得
(3.34) $\begin{equation}\label{40} \lim_{k\to\infty}\|z^{n_k} - y^{n_k}\| = 0. \end{equation} $
由于 $\{\alpha_n\} \subset (0, 1)$
由注 3.1(ii) 知 $\lim\limits_{n\to\infty}\frac{\theta_n}{\alpha_n}\|x^n - x^{n - 1}\| = 0$
(3.35) $\begin{equation}\label{wnxn} \lim_{k\to\infty}\|w^{n_k} - x^{n_k}\| = 0. \end{equation} $
由 $\{\alpha_n\} \subset (0, 1)$
由于 $\{x^{n_k}\}$ $\alpha_n \to 0(n\to \infty)$
(3.36) $\begin{equation}\label{qnxn} \lim_{k\to\infty}\|q^{n_k} - x^{n_k}\| = 0. \end{equation} $
因为 $\{x^{n_k}\}$ $\{w^{n_k}\}$ $\{y^{n_k}\}$ $\{z^{n_k}\}$ $\{x^{n_{k_i}}\}$ $\{x^{n_k}\}$
记 $\bar{x}$ $\{x^{n_{k_i}}\}$ $\widetilde{x} = P_{{\rm Fix}(T)\cap S_D}(u^0)$
注意到 $x^{n_{k_i}}\rightharpoonup \bar{x}(i\to\infty)$ $\bar{x}\in S_D\cap {\rm Fix}(T)$ . 因此 $\langle u^0 - \widetilde{x}, \bar{x} - \widetilde{x}\rangle \le 0$ . 又因为 $x^{n_{k_i}}\rightharpoonup \bar{x}(i\to\infty)$
由引理 2.2 可得 $\displaystyle\lim_{n\to\infty}\|x^n - \widetilde{x}\|^2 = 0$ .
4 算法的计算机检验
本节将进行数值实验来说明算法 1 的有效性. 在 Windows 10, CPU AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx (2100 MHz) 的系统环境下使用版本为 R2016a 的 Matlab 进行计算. 用 iter 表示迭代的次数, time 表示运行所花费的时间 (以秒为单位), 当 $D_n = ||x^{n + 1} - x^n|| \le \varepsilon$
本文例 4.1 和例 4.2 中, 映射 $F$ $\mathbb{R}^k$ $H$ 31 ,算法 3.1], [7 ,算法 3.1,3.2] 比较. 例 4.3 中映射 $F$ 7 ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
例4.1 考虑映射 $F:\mathbb{R}^k\to\mathbb{R}^k$ $F(x) = (x_1 + \cos(x_1), x_2 + \cos(x_2),\cdots,x_k + \cos(x_k))$ . 定义映射 $T:\mathbb{R}^k\to\mathbb{R}^k$ $T(x) = -\frac{3}{2}x$ . 可行集 $C=\mathbb{R}^k_+$ .
由文献 [31 ] 可知, 映射 $F$ $L = 2$ . 事实上, 对任意的 $z\in\mathbb{R}$ $g(z):=z + \cos(z)$ $g'(z) = 1 - \sin(z)$ $z\in\mathbb{R}$ $0\leq g'(z)\leq 2$ . 进一步, 对任意的 $x, y \in\mathbb{R}^k$
其中 $z_i$ $x_i$ $y_i$ $F$
其中 $z_i$ $x_i$ $y_i$ $\|F(x)-F(y)\|\le 2\|x-y\|$ $F$ $L = 2$ .
由于映射 $F$ $F$ $x\in C$ $F(x)\neq 0$ $S = S_D$ . 容易验证 $0 \in S$ . 映射 $T$ $\frac{1}{5}$ - 半压缩映射且 $I - T$ ${\rm Fix}(T) = \{0\}$ 7 ]. 因此 ${\rm Fix}(T)\cap S_D = {\rm Fix}(T)\cap S = \{0\}\ne\emptyset$
比较算法 1, 文献 [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下
1. 文献 [算法 1]: $\tau = \frac{0.5}{L}, \theta = 0.1, \lambda_1 = 0.1, \alpha_n = \frac{1}{\sqrt{n+3}}, \varepsilon_n = \frac{100}{(n+1)^2}, \beta_n = \frac{1-\alpha_n}{2}, \xi_n = \frac{1}{(n + 1)^2}$ .
2. 文献 [算法 2]: $\tau=0.55, \theta=0.45, \lambda_1=0.43, \alpha_n = \frac{1}{3n+4}, \varepsilon_n=\frac{80}{(n+1)^2}, \beta_n=\frac{n}{2n+1}$ .
3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ .
4. 文献 [7 ,算法 3.1,3.2]: $\tau=0.5, \lambda_0=0.5, \alpha_n=\frac{1}{\sqrt{n+1}}, \beta_n=\frac{n}{2n+1}$ .
5. 算法 1: $r=0.1, \mathit{l}=0.1, \tau=0.7, \theta=0.1, \alpha_n=\frac{1}{\sqrt{n+1}}, \varepsilon_n=\frac{100}{(n+1)^2}, \beta_n=\frac{n}{2n+1}, u^0=0$ .
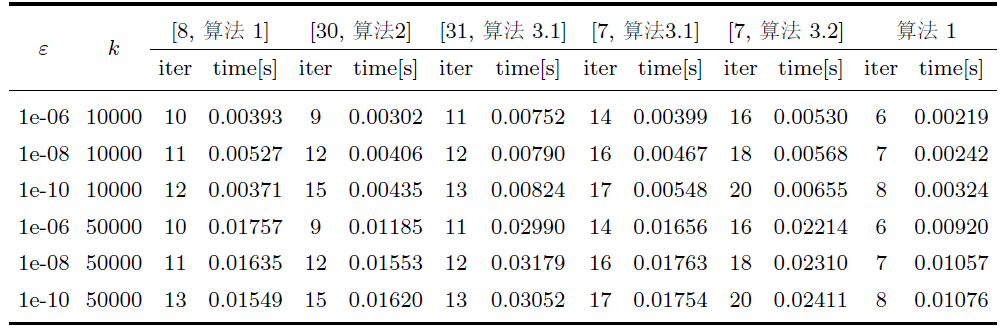
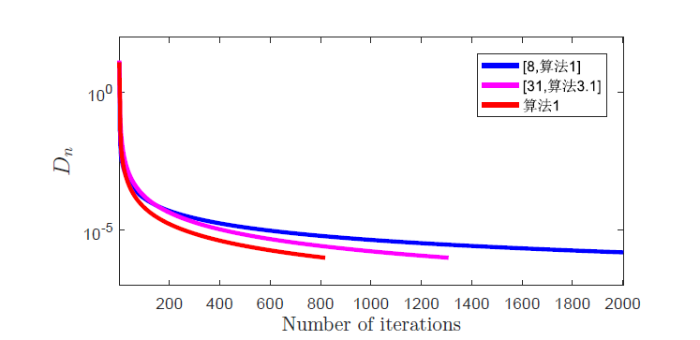
选取初始点为 $x^0=x^1=(1000,1000,\cdots,1000)^T$ 表 1 和图 1 .
图1
图1
例 4.1 中 $k=10000, \varepsilon=10^{-12}$
例4.2 设 $H=L^2([0,1])$ $x,y\in H$ $\langle x, y\rangle = \int_0^1x(t)y(t){\rm d}t$ $||x|| = (\int_0^1|x(t)|^2{\rm d}t)^\frac{1}{2}$ . 映射 $F: H\to H$
定义映射 $T: H\to H$ $(Tx)(t) = \int_0^1tx(s){\rm d}s, t\in[0,1]$ . 可行集 $C=\{x\in H:\int_0^1 x(t){\rm d}t \geq 0\}$ .
结合文献 [8 ] 不难发现, 映射 $F$ $H$ $L = 1$ $x\in C$ $F(x)\neq 0$ $0 \in S = S_D$ . 由于 $0 \in {\rm Fix}(T)$ ${\rm Fix}(T)\ne \emptyset$ . 由文献 [8 ] 可知映射 $T$ $T$ $0$ - 半压缩映射且 $I - T$ $0\in {\rm Fix}(T)\cap S = {\rm Fix}(T)\cap S_D \ne \emptyset$
比较算法 1, [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下
1. 文献 [算法 1]: $\tau = \frac{0.5}{L}, \theta = 0.1, \lambda_1 = 0.1, \alpha_n = \frac{1}{n+3}, \varepsilon_n = \frac{100}{(n+1)^2}, \beta_n = \frac{1-\alpha_n}{2}, \xi_n = \frac{1}{(n+1)^2}$ .
2. 文献 [算法 2]: $\tau=0.65, \theta=0.55, \lambda_1=0.22, \alpha_n = \frac{1}{5n+8}, \varepsilon_n=\frac{1}{(n+1)^2}, \beta_n=\frac{n}{5n+1}$ .
3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ .
4. 文献 [7 ,算法 3.1,3.2]: $\tau=0.5, \lambda_0=0.5, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}$ .
5. 算法 1: $r=1, \mathit{l}=0.3, \tau=0.5, \theta=0.2, \alpha_n=\frac{1}{\sqrt{n+1}}, \varepsilon_n=\frac{100}{(n+1)^2}, \beta_n=\frac{n}{2n+1}, u^0 = 0$ .
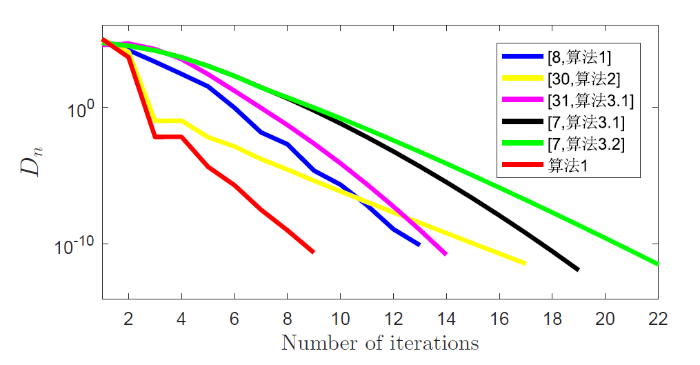
图2
图2
例 4.2 的初始点为 $x^0(t)=t+0.5 cost, \varepsilon=10^{-13}$
通过表 2 和图 2 可以发现: 算法 1 的迭代步数更少, 迭代时间更短.
例4.3 映射 $F:\mathbb{R}^2\to\mathbb{R}^2$
定义映射 $T:\mathbb{R}^2\to\mathbb{R}^2$ $T(x) = \frac{1}{2}(x + 2.707)$ . 可行集 $C=\{x\in \mathbb{R}^2: (x_1 - 2)^2 + (x_2 - 2)^2\leq 1\}$ .
由文献 [29 ] 可知, 映射 $F$ $L = 5$ $S = \{(2.707,2.707)^T\}$ . 结合注2.3 可知 $S_D = S =\{(2.707,2.707)^T\}$ $F$ $x\in C$ $F(x)\neq 0$ $T$ ${\rm Fix}(T) = \{(2.707,2.707)^T\}$ $T$ $0$ - 半压缩映射且 $I - T$ ${\rm Fix}(T)\cap S_D = {\rm Fix}(T)\cap S = \{(2.707,2.707)^T\}\ne \emptyset$
比较算法 1, 文献 [算法 1], [31 ,算法 3.1], 且其参数选取与原文一致并列举如下. 由于 $F$ 7 ,算法 3.1,3.2] 不适用于本例.
1. 文献 [算法 1]: $\tau \!=\! \frac{0.5}{L},\ \theta\! =\! 0.1,\ \lambda_1 \!= \!0.1,\ \alpha_n \!= \!\frac{1}{\sqrt{n+3}},\ \varepsilon_n \!= \!\frac{100}{(n+1)^2},\ \beta_n \!=\! \frac{1-\alpha_n}{2},$ $ \xi_n = \frac{1}{(n+1)^2}$ .
2. 文献 [31 ,算法 3.1]: $r\!=\!0.5,\ \mathit{l}\!=\!0.5,\ \tau\!=\!0.5,\ \alpha_1\!=\!\beta_1\!=\!0.1,\ \alpha_n\!=\!\frac{1}{n+1},\ \beta_n\!=\!\frac{n}{2n+3},$ $ f(x)=0.5x$ .
3. 算法 1: $r\!=\!1,\ \mathit{l}\!=\!0.5,\ \tau\!=\!0.5,\ \theta\!=\!0.5,\ \alpha_n\!=\!\frac{1}{n+1},\ \varepsilon_n\!=\!\frac{100}{(n+1)^2},\ \beta_n\!=\!\frac{n}{2n+1},\ u^0\! =\! (2,2)^T$ .
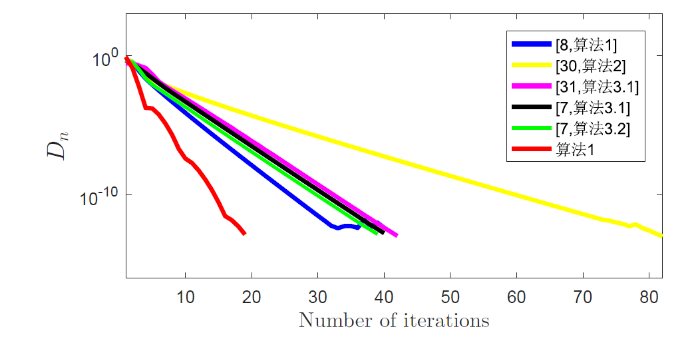
图3
图3
例 4.3的初始点为 $x^0=(-5,-5)^T, \varepsilon=10^{-6}$
通过表 3 和图 3 可以发现: 算法 1 的迭代步数更少, 迭代时间更短.
例4.4 令 $C=[-1,1]$ $F$
定义映射 $T(x) = \frac{1}{2}(x - 1)$ .
由文献 [16 ] 可知, 映射 $F$ $\mathbb{R}$ $x\in C$ $F(x)\neq 0$ $F$ $x = 2$ $y = -1$ $\langle F(x), y - x\rangle = 0$ $\langle F(y), y - x\rangle = 2*(-3) < 0$ . 因此映射 $F$ $\mathbb{R}$ $S = S_D = \{-1\}$ . 显然映射 $T$ $T$ $0$ - 半压缩映射且 $I - T$ ${\rm Fix}(T) = \{-1\}$ . ${\rm Fix}(T)\cap S_D = \{-1\}\neq \emptyset$ .
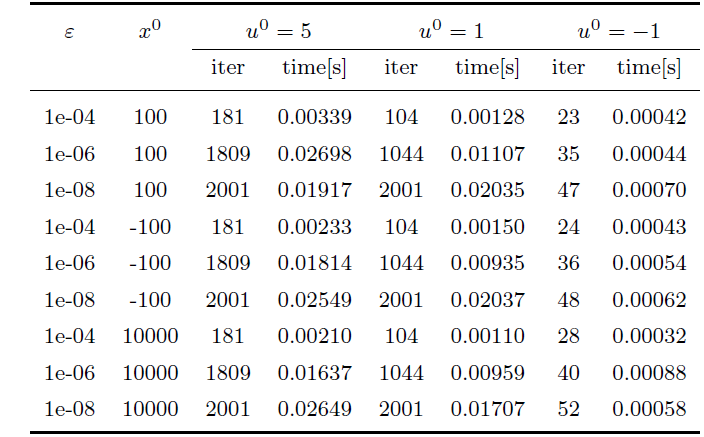
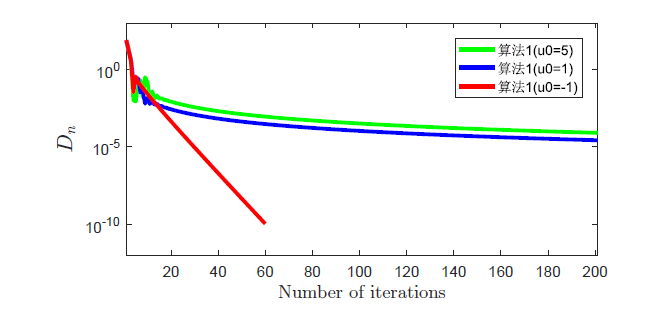
由于映射 $F$ $u^0$ $u^0 = 5$ $u^0$ $C$ $u^0 = 1$ $u^0$ $C$ $u^0 = -1$ $u^0$ $C$
1. 算法 1: $r=1, \mathit{l}=0.5, \tau=0.5, \theta=0.5, \alpha_n=\frac{1}{n+1}, \varepsilon_n=\frac{100}{(n+1)^2}, \beta_n=\frac{n}{2n+1}$ .
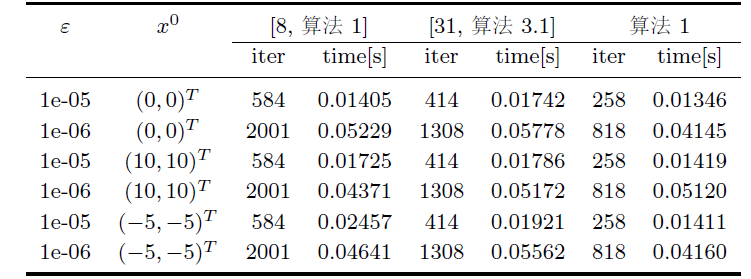
图4
图4
例 4.4 中初始点 $x^0=x^1=100, \varepsilon=10^{-10}$
通过表 4 和图 4 可以发现: 在其它参数相同的情况下, $u^0$
参考文献
View Option
[1]
Iiduka H . Acceleration method for convex optimization over the fixed point set of a nonexpansive mapping
Mathematical Programming , 2015 , 149 1 ): 131 -165
[本文引用: 1]
[2]
Maingé P E . A hybrid extragradient-viscosity method for monotone operators and fixed point problems
SIAM Journal on Control and Optimization , 2008 , 47 3 ): 1499 -1515
[本文引用: 1]
[3]
Thong D V Hieu D V . Modified subgradient extragradient algorithms for variational inequality problems and fixed point problems
Optimization , 2018 , 67 1 ): 83 -102
[本文引用: 2]
[4]
Nadezhkina N Takahashi W . Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings
Journal of Optimization Theory and Applications , 2006 , 128 191 -201
[本文引用: 4]
[5]
Takahashi W Toyoda M . Weak convergence theorems for nonexpansive mappings and monotone mappings
Journal of Optimization Theory and Applications , 2003 , 118 417 -428
[本文引用: 3]
[6]
Thong D V Hieu D V . New extragradient methods for solving variational inequality problems and fixed point problems
Journal of Fixed Point Theory and Applications , 2018 , 20 3 ): Article 129
[本文引用: 7]
[7]
Thong D V Hieu D V . Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems
Numerical Algorithms , 2019 , 82 3 ): 761 -789
[本文引用: 9]
[8]
Thong D V Liu L L Dong Q L , et al . Fast relaxed inertial Tseng's method-based algorithm for solving variational inequality and fixed point problems in Hilbert spaces
Journal of Computational and Applied Mathematics , 2023 , 418 114739
[本文引用: 4]
[9]
段洁 , 夏福全 . 求解变分不等式与不动点问题公共解的新 Tseng 型外梯度算法
数学物理学报 , 2023 , 43A 1 ): 274 -290
[本文引用: 1]
Duan J Xia F Q . A new Tseng-like extragradient algorithm for common solutions of variational inequalities and fixed point problems
Acta Math Sci , 2023 , 43A 1 ): 274 -290
[本文引用: 1]
[10]
Goldstein A A . Convex programming in Hilbert space
Bulletin of the American Mathematical Society , 1964 , 70 5 ): 109 -112
[本文引用: 1]
[11]
Mann W R . Mean value methods in iteration
Proceedings of the American Mathematical Society , 1953 , 4 3 ): 506 -510
[本文引用: 1]
[12]
Korpelevich G M . The extragradient method for finding saddle points and other problems
Matecon , 1976 , 12 747 -756
[本文引用: 1]
[13]
Censor Y Gibali A Reich S . The subgradient extragradient method for solving variational inequalities in Hilbert space
Journal of Optimization Theory and Applications , 2011 , 148 2 ): 318 -335
PMID:21490879
[本文引用: 2]
We present a subgradient extragradient method for solving variational inequalities in Hilbert space. In addition, we propose a modified version of our algorithm that finds a solution of a variational inequality which is also a fixed point of a given nonexpansive mapping. We establish weak convergence theorems for both algorithms.
[14]
Tseng P . A modified forward-backward splitting method for maximal monotone mappings
SIAM Journal on Control and Optimization , 2000 , 38 2 ): 431 -446
[本文引用: 1]
[15]
Halpern B . Fixed points of nonexansive maps
Bulletin of the American Mathematical Society , 1967 , 73 957 -961
[本文引用: 1]
[16]
Wang Z B Chen X Yi J Chen Z Y . Inertial projection and contraction algorithms with larger step sizes for solving quasimonotone variational inequalities
Journal of Global Optimization , 2022 , 82 3 ): 499 -522
[本文引用: 2]
[17]
Yin T C Wu Y K Wen C F . An iterative algorithm for solving fixed point problems and quasimonotone variational inequalities
Journal of Mathematics , 2022 , 2022 1 ): 8644675
[本文引用: 4]
[18]
Chidume C E Măuşter Ş . Iterative methods for the computation of fixed points of demicontractive mappings
Journal of Computational and Applied Mathematics , 2010 , 234 3 ): 861 -882
[本文引用: 1]
[19]
Mongkolkeha C Cho Y J Kumam P . Convergence theorems for k-dimeicontactive mappings in Hilbert spaces
Mathematical Inequalities & Applications , 2013 , 16 4 ): 1065 -1082
[本文引用: 1]
[20]
Kraikaew R Saejung S . Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces
Journal of Optimization Theory and Applications , 2014 , 163 399 -412
[本文引用: 1]
[21]
Tian M Xu G . Inertial modified Tseng's extragradient algorithms for solving monotone variational inequalities and fixed point problems
J Nonlinear Funct Anal , 2020 , 2020 35
[本文引用: 1]
[22]
Bauschke H H Combettes P L . Convex Analysis and Monotone Operator Theory in Hilbert Spaces . New York : Springer , 2011
[本文引用: 1]
[23]
Denisov S V Semenov V V Chabak L M . Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators
Cybernetics and Systems Analysis , 2015 , 51 757 -765
[本文引用: 1]
[24]
Saejung S Yotkaew P . Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Analysis: Theory
Methods & Applications , 2012 , 75 2 ): 742 -750
[本文引用: 1]
[25]
Ye M L . An infeasible projection type algorithm for nonmonotone variational inequalities
Numerical Algorithms , 2022 , 89 4 ): 1723 -1742
[本文引用: 2]
[26]
Ye M L He Y R . A double projection method for solving variational inequalities without monotonicity
Computational Optimization and Applications , 2015 , 60 1 ): 141 -150
[本文引用: 5]
[27]
Iusem A Otero R G . Inexact versions of proximal point and augmented Lagrangian algorithms in Banach spaces
Numerical Functional Analysis and Optimization , 2001 , 22 5/6 ): 609 -640
[本文引用: 1]
[28]
Cai G Dong Q L Peng Y . Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators
Journal of Optimization Theory and Applications , 2021 , 188 447 -472
[本文引用: 1]
[29]
Shehu Y Dong Q L Jiang D . Single projection method for pseudo-monotone variational inequality in Hilbert spaces
Optimization , 2019 , 68 1 ): 385 -409
[本文引用: 2]
[30]
Rehman H U Kumam P Kumam W Sombut K . A new class of inertial algorithms with monotonic step sizes for solving fixed point and variational inequalities
Mathematical Methods in the Applied Sciences , 2022 , 45 16 ): 9061 -9088
[31]
杨静 , 龙宪军 . 关于伪单调变分不等式与不动点问题的新投影算法
数学物理学报 , 2022 , 42A 3 ): 904 -919
[本文引用: 9]
Yang J Long X J . A new projection algorithm for solving pseudo-monotone variational inequality and fixed point problems
Acta Math Sci , 2022 , 42A 3 ): 904 -919
[本文引用: 9]
Acceleration method for convex optimization over the fixed point set of a nonexpansive mapping
1
2015
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
A hybrid extragradient-viscosity method for monotone operators and fixed point problems
1
2008
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
Modified subgradient extragradient algorithms for variational inequality problems and fixed point problems
2
2018
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 引理2.3 [3 ] 设 $T:H\rightarrow H$ $\kappa$ - 半压缩映射且 ${\rm Fix}(T)\neq \emptyset$ $T_\alpha = (1 - \alpha)I + \alpha T$ $\alpha \in (0, 1 - \kappa)$
Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings
4
2006
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 为了削弱映射 $F$ 4 ] 基于求解变分不等式问题的外梯度算法[12 ] 提出了如下算法 ...
... 其中 $\{\lambda_n\} \subset [a, b] \subset (0, \frac{1}{L})$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ 4 ] 证明了算法 (1.4) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解. ...
... 为了减少向 $C$ [13 ] 将文献 [4 ] 中的算法第二次向 $C$
Weak convergence theorems for nonexpansive mappings and monotone mappings
3
2003
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 2003 年, Takahashi 和 Toyoda[5 ] 基于求解变分不等式问题的投影梯度法[10 ] 和求解不动点问题的 Mann 迭代法[11 ] 提出了如下算法 ...
... 其中 $\{\lambda_n\} \subset [a, b] \subset (0, 2\eta)$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $\eta$ - 余强制和映射 $T$ 5 ] 证明了算法(1.3) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解. ...
New extragradient methods for solving variational inequality problems and fixed point problems
7
2018
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 另一方面, 2018 年, Thong 和 Hieu[6 ] 基于求解变分不等式的 Tseng 型外梯度算法[14 ] , 提出以下算法 ...
... 其中 $r > 0$ $\mathit{l}\in (0, 1)$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ $I-T$ 6 ] 证明了算法 (1.6) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解. ...
... 为了进一步获得强收敛的结果, 2018 年 Thong 等[6 ] 基于 Halpern 迭代法[15 ] 提出如下算法 ...
... 其中 $r > 0$ $\mathit{l}\in (0, 1)$ $\{\alpha_n\} \subset (0, 1)$ $\lim\limits_{n\to \infty}\alpha_n = 0$ $\sum\limits_{n = 1}^\infty\alpha_n = \infty$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ $I-T$ 6 ] 证明了算法 (1.7) 产生的序列强收敛到 $P_{{\rm Fix}(T) \cap S}(u^0)$ . ...
... 一方面, 为了削弱文献 [6 ] 中映射 $F$ $T$ 17 ] 中映射 $F$ $F$ $T$ 6 ] 相比, 本文将映射 $F$ $F$ $T$ 17 ] 相比, 本文将映射 $F$
... 是半压缩映射的条件下, 证明了算法所产生的序列强收敛到变分不等式问题与不动点问题的公共解. 与文献 [6 ] 相比, 本文将映射 $F$ $F$ $T$ 17 ] 相比, 本文将映射 $F$
Some extragradient-viscosity algorithms for solving variational inequality problems and fixed point problems
9
2019
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 本文例 4.1 和例 4.2 中, 映射 $F$ $\mathbb{R}^k$ $H$ 31 ,算法 3.1], [7 ,算法 3.1,3.2] 比较. 例 4.3 中映射 $F$ 7 ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... 是伪单调但不是单调的映射, 不适用于文献[算法 2], [7 ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... 由于映射 $F$ $F$ $x\in C$ $F(x)\neq 0$ $S = S_D$ . 容易验证 $0 \in S$ . 映射 $T$ $\frac{1}{5}$ - 半压缩映射且 $I - T$ ${\rm Fix}(T) = \{0\}$ 7 ]. 因此 ${\rm Fix}(T)\cap S_D = {\rm Fix}(T)\cap S = \{0\}\ne\emptyset$
... 比较算法 1, 文献 [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 4. 文献 [7 ,算法 3.1,3.2]: $\tau=0.5, \lambda_0=0.5, \alpha_n=\frac{1}{\sqrt{n+1}}, \beta_n=\frac{n}{2n+1}$ . ...
... 比较算法 1, [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 4. 文献 [7 ,算法 3.1,3.2]: $\tau=0.5, \lambda_0=0.5, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}$ . ...
... 比较算法 1, 文献 [算法 1], [31 ,算法 3.1], 且其参数选取与原文一致并列举如下. 由于 $F$ 7 ,算法 3.1,3.2] 不适用于本例. ...
Fast relaxed inertial Tseng's method-based algorithm for solving variational inequality and fixed point problems in Hilbert spaces
4
2023
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
... 定义2.2 [8 ] 设映射 $T:H\rightarrow H$
... 结合文献 [8 ] 不难发现, 映射 $F$ $H$ $L = 1$ $x\in C$ $F(x)\neq 0$ $0 \in S = S_D$ . 由于 $0 \in {\rm Fix}(T)$ ${\rm Fix}(T)\ne \emptyset$ . 由文献 [8 ] 可知映射 $T$ $T$ $0$ - 半压缩映射且 $I - T$ $0\in {\rm Fix}(T)\cap S = {\rm Fix}(T)\cap S_D \ne \emptyset$
... . 由文献 [8 ] 可知映射 $T$ $T$ $0$ - 半压缩映射且 $I - T$ $0\in {\rm Fix}(T)\cap S = {\rm Fix}(T)\cap S_D \ne \emptyset$
求解变分不等式与不动点问题公共解的新 Tseng 型外梯度算法
1
2023
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
求解变分不等式与不动点问题公共解的新 Tseng 型外梯度算法
1
2023
... 这一问题在许多领域都有应用, 如信号处理、图像恢复和网络资源分配[1 ⇓ -3 ] . 近年来, 求解 Hilbert 空间中变分不等式问题与不动点问题的公共解的投影算法受到众多学者关注[4 ⇓ ⇓ ⇓ ⇓ -9 ] . ...
Convex programming in Hilbert space
1
1964
... 2003 年, Takahashi 和 Toyoda[5 ] 基于求解变分不等式问题的投影梯度法[10 ] 和求解不动点问题的 Mann 迭代法[11 ] 提出了如下算法 ...
Mean value methods in iteration
1
1953
... 2003 年, Takahashi 和 Toyoda[5 ] 基于求解变分不等式问题的投影梯度法[10 ] 和求解不动点问题的 Mann 迭代法[11 ] 提出了如下算法 ...
The extragradient method for finding saddle points and other problems
1
1976
... 为了削弱映射 $F$ 4 ] 基于求解变分不等式问题的外梯度算法[12 ] 提出了如下算法 ...
The subgradient extragradient method for solving variational inequalities in Hilbert space
2
2011
... 为了减少向 $C$ [13 ] 将文献 [4 ] 中的算法第二次向 $C$
... 其中 $\lambda \in (0, \frac{1}{L})$ $\{\beta_n\} \subset [c, d] \subset (0, 1)$ . 在映射 $F$ $T$ 13 ]证明了算法 (1.5)所产生的序列弱收敛到变分不等式问题与不动点问题的公共解. ...
A modified forward-backward splitting method for maximal monotone mappings
1
2000
... 另一方面, 2018 年, Thong 和 Hieu[6 ] 基于求解变分不等式的 Tseng 型外梯度算法[14 ] , 提出以下算法 ...
Fixed points of nonexansive maps
1
1967
... 为了进一步获得强收敛的结果, 2018 年 Thong 等[6 ] 基于 Halpern 迭代法[15 ] 提出如下算法 ...
Inertial projection and contraction algorithms with larger step sizes for solving quasimonotone variational inequalities
2
2022
... 众所周知, 单调映射和伪单调映射一定是拟单调映射, 但反之不一定成立, 见文献[16 ]. 因此, 有必要将映射 $F$ 17 ]提出求解拟单调变分不等式问题与伪压缩映射不动点问题的公共解的如下算法 ...
... 由文献 [16 ] 可知, 映射 $F$ $\mathbb{R}$ $x\in C$ $F(x)\neq 0$ $F$ $x = 2$ $y = -1$ $\langle F(x), y - x\rangle = 0$ $\langle F(y), y - x\rangle = 2*(-3) < 0$ . 因此映射 $F$ $\mathbb{R}$ $S = S_D = \{-1\}$ . 显然映射 $T$ $T$ $0$ - 半压缩映射且 $I - T$ ${\rm Fix}(T) = \{-1\}$ . ${\rm Fix}(T)\cap S_D = \{-1\}\neq \emptyset$ . ...
An iterative algorithm for solving fixed point problems and quasimonotone variational inequalities
4
2022
... 众所周知, 单调映射和伪单调映射一定是拟单调映射, 但反之不一定成立, 见文献[16 ]. 因此, 有必要将映射 $F$ 17 ]提出求解拟单调变分不等式问题与伪压缩映射不动点问题的公共解的如下算法 ...
... 假设映射 $T$ $F$ $x^n\rightharpoonup x$ $\liminf\limits_{n\to\infty}\|F(x^n)\|=0$ $\{x^n\}$ $F(x)=0$ $\{x\in C:F(x)=0\}\setminus S_D$ ${\rm Fix}(T)\cap S_D\ne\emptyset$ 17 ] 证明了算法 (1.8) 所产生的序列弱收敛到变分不等式问题与不动点问题的公共解. ...
... 一方面, 为了削弱文献 [6 ] 中映射 $F$ $T$ 17 ] 中映射 $F$ $F$ $T$ 6 ] 相比, 本文将映射 $F$ $F$ $T$ 17 ] 相比, 本文将映射 $F$
... 的拟非扩张性削弱为半压缩. 与文献 [17 ] 相比, 本文将映射 $F$
Iterative methods for the computation of fixed points of demicontractive mappings
1
2010
... 注2.1 由定义 2.2 中映射 $T$ $\Rightarrow$ ( ii)$\Rightarrow$ ( iii), 但(i)$\nLeftarrow$ ( ii)$\nLeftarrow$ ( iii), 见文献[18 ,19 ]. 有 (i)$\Rightarrow$ ( iv), 但(ii)$\nRightarrow$ ( iv), 见文献 [20 ,21 ]. ...
Convergence theorems for k-dimeicontactive mappings in Hilbert spaces
1
2013
... 注2.1 由定义 2.2 中映射 $T$ $\Rightarrow$ ( ii)$\Rightarrow$ ( iii), 但(i)$\nLeftarrow$ ( ii)$\nLeftarrow$ ( iii), 见文献[18 ,19 ]. 有 (i)$\Rightarrow$ ( iv), 但(ii)$\nRightarrow$ ( iv), 见文献 [20 ,21 ]. ...
Strong convergence of the Halpern subgradient extragradient method for solving variational inequalities in Hilbert spaces
1
2014
... 注2.1 由定义 2.2 中映射 $T$ $\Rightarrow$ ( ii)$\Rightarrow$ ( iii), 但(i)$\nLeftarrow$ ( ii)$\nLeftarrow$ ( iii), 见文献[18 ,19 ]. 有 (i)$\Rightarrow$ ( iv), 但(ii)$\nRightarrow$ ( iv), 见文献 [20 ,21 ]. ...
Inertial modified Tseng's extragradient algorithms for solving monotone variational inequalities and fixed point problems
1
2020
... 注2.1 由定义 2.2 中映射 $T$ $\Rightarrow$ ( ii)$\Rightarrow$ ( iii), 但(i)$\nLeftarrow$ ( ii)$\nLeftarrow$ ( iii), 见文献[18 ,19 ]. 有 (i)$\Rightarrow$ ( iv), 但(ii)$\nRightarrow$ ( iv), 见文献 [20 ,21 ]. ...
1
2011
... 引理2.1 [22 ,23 ] 令 $C\subset H$ $x\in H$ $\alpha \ge \beta > 0$
Convergence of the modified extragradient method for variational inequalities with non-Lipschitz operators
1
2015
... 引理2.1 [22 ,23 ] 令 $C\subset H$ $x\in H$ $\alpha \ge \beta > 0$
Approximation of zeros of inverse strongly monotone operators in Banach spaces. Nonlinear Analysis: Theory
1
2012
... 引理2.2 [24 ] 设 $\{\Phi_n\}$ $\{s_n\}\subset(0,1)$ $\sum\limits_{n = 0}^\infty s_n = \infty$ $\{\Omega_n\}$
An infeasible projection type algorithm for nonmonotone variational inequalities
2
2022
... 定义2.3 [25 ,26 ] 问题 (1.1) 的对偶变分不等式是: 寻找 $x^* \in C$
... 注2.3 由文献[25 ]可知, 当 $C$ $F$ $C$ $S_D\subset S$ . 进一步, 当 $F$ $C$ $S = S_D$ . 但当 $F$ $S_D \neq S$ 26 ,例 4.2]. ...
A double projection method for solving variational inequalities without monotonicity
5
2015
... 定义2.3 [25 ,26 ] 问题 (1.1) 的对偶变分不等式是: 寻找 $x^* \in C$
... 注2.3 由文献[25 ]可知, 当 $C$ $F$ $C$ $S_D\subset S$ . 进一步, 当 $F$ $C$ $S = S_D$ . 但当 $F$ $S_D \neq S$ 26 ,例 4.2]. ...
... 证 类似文献 [26 ]. 其中 (a) 是因为伪单调的定义和注2.3; (b) 是文献[26 ,引理 2.7] 的推论; (c) 是因为 (b) 和文献[26 ,定理 2.1]. ...
... ]. 其中 (a) 是因为伪单调的定义和注2.3; (b) 是文献[26 ,引理 2.7] 的推论; (c) 是因为 (b) 和文献[26 ,定理 2.1]. ...
... ,引理 2.7] 的推论; (c) 是因为 (b) 和文献[26 ,定理 2.1]. ...
Inexact versions of proximal point and augmented Lagrangian algorithms in Banach spaces
1
2001
... (1) 当 $\displaystyle\liminf_{k\to\infty}\lambda_{n_k} > 0$ . 因为 $\{x^n\}$ $\displaystyle\lim_{n\to\infty}\|w^n - x^n\| = 0$ $\{w^{n_k}\}$ $F$ $H$ 27 ]可知, $\{F(w^{n_k})\}$ $\displaystyle\lim_{k\to\infty}\|w^{n_k} - y^{n_k}\| = 0$ $\{y^{n_k}\}$
Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators
1
2021
... (2) 当对任意 $x \in C$ $\displaystyle\limsup_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 (3.25) 式知 $\displaystyle\lim_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 $\xi_k$ $\displaystyle\lim_{k\to\infty}\xi_k = 0$ . 由于 $y^{n_k}\rightharpoonup \hat{x}$ $F$ $C$ $F(y^{n_k})\rightharpoonup F(\hat{x})$ $F(\hat{x}) \neq 0$ . 注意范数映射是序列弱下半连续的[28 ,29 ] , 因此 ...
Single projection method for pseudo-monotone variational inequality in Hilbert spaces
2
2019
... (2) 当对任意 $x \in C$ $\displaystyle\limsup_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 (3.25) 式知 $\displaystyle\lim_{k\to\infty}\langle F(y^{n_k}), x - y^{n_k}\rangle = 0$ . 由 $\xi_k$ $\displaystyle\lim_{k\to\infty}\xi_k = 0$ . 由于 $y^{n_k}\rightharpoonup \hat{x}$ $F$ $C$ $F(y^{n_k})\rightharpoonup F(\hat{x})$ $F(\hat{x}) \neq 0$ . 注意范数映射是序列弱下半连续的[28 ,29 ] , 因此 ...
... 由文献 [29 ] 可知, 映射 $F$ $L = 5$ $S = \{(2.707,2.707)^T\}$ . 结合注2.3 可知 $S_D = S =\{(2.707,2.707)^T\}$ $F$ $x\in C$ $F(x)\neq 0$ $T$ ${\rm Fix}(T) = \{(2.707,2.707)^T\}$ $T$ $0$ - 半压缩映射且 $I - T$ ${\rm Fix}(T)\cap S_D = {\rm Fix}(T)\cap S = \{(2.707,2.707)^T\}\ne \emptyset$
A new class of inertial algorithms with monotonic step sizes for solving fixed point and variational inequalities
2022
关于伪单调变分不等式与不动点问题的新投影算法
9
2022
... 本文例 4.1 和例 4.2 中, 映射 $F$ $\mathbb{R}^k$ $H$ 31 ,算法 3.1], [7 ,算法 3.1,3.2] 比较. 例 4.3 中映射 $F$ 7 ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... 由文献 [31 ] 可知, 映射 $F$ $L = 2$ . 事实上, 对任意的 $z\in\mathbb{R}$ $g(z):=z + \cos(z)$ $g'(z) = 1 - \sin(z)$ $z\in\mathbb{R}$ $0\leq g'(z)\leq 2$ . 进一步, 对任意的 $x, y \in\mathbb{R}^k$
... 比较算法 1, 文献 [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ . ...
... 比较算法 1, [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ . ...
... 比较算法 1, 文献 [算法 1], [31 ,算法 3.1], 且其参数选取与原文一致并列举如下. 由于 $F$ 7 ,算法 3.1,3.2] 不适用于本例. ...
... 2. 文献 [31 ,算法 3.1]: $r\!=\!0.5,\ \mathit{l}\!=\!0.5,\ \tau\!=\!0.5,\ \alpha_1\!=\!\beta_1\!=\!0.1,\ \alpha_n\!=\!\frac{1}{n+1},\ \beta_n\!=\!\frac{n}{2n+3},$ $ f(x)=0.5x$ . ...
关于伪单调变分不等式与不动点问题的新投影算法
9
2022
... 本文例 4.1 和例 4.2 中, 映射 $F$ $\mathbb{R}^k$ $H$ 31 ,算法 3.1], [7 ,算法 3.1,3.2] 比较. 例 4.3 中映射 $F$ 7 ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... ,算法 3.1,3.2], 因此只考虑将算法 1 与文献[算法 1], [31 ,算法 3.1] 比较. 例4.4中映射 $F$ $u^0$
... 由文献 [31 ] 可知, 映射 $F$ $L = 2$ . 事实上, 对任意的 $z\in\mathbb{R}$ $g(z):=z + \cos(z)$ $g'(z) = 1 - \sin(z)$ $z\in\mathbb{R}$ $0\leq g'(z)\leq 2$ . 进一步, 对任意的 $x, y \in\mathbb{R}^k$
... 比较算法 1, 文献 [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ . ...
... 比较算法 1, [算法 1], [算法 2], [31 ,算法 3.1], [7 ,算法 3.1,3.2], 且其参数选取与原文一致并列举如下 ...
... 3. 文献 [31 ,算法 3.1]: $r=1, \mathit{l}=0.5, \tau=0.2, \alpha_1=\beta_1=0.1, \alpha_n=\frac{1}{n+1}, \beta_n=\frac{n}{2n+1}, f(x)=0.5x$ . ...
... 比较算法 1, 文献 [算法 1], [31 ,算法 3.1], 且其参数选取与原文一致并列举如下. 由于 $F$ 7 ,算法 3.1,3.2] 不适用于本例. ...
... 2. 文献 [31 ,算法 3.1]: $r\!=\!0.5,\ \mathit{l}\!=\!0.5,\ \tau\!=\!0.5,\ \alpha_1\!=\!\beta_1\!=\!0.1,\ \alpha_n\!=\!\frac{1}{n+1},\ \beta_n\!=\!\frac{n}{2n+3},$ $ f(x)=0.5x$ . ...