1 引言
设 $H_1$ $H_2$ $\langle \cdot,\cdot\rangle $ $\cdot$ $C$ $Q$ $H_1$ $H_2$ $A:H_1\to H_2$ $A \neq 0$ .
1994 年, Censor 和 Elfving[1 ] 在研究 CT 扫描图像重建的过程中首次提出了有限维 Hilbert 空间中的分裂可行性问题. 分裂可行性问题为寻求一点 $q \in H_1$
(1.1) $ \begin{equation}\label{11} q\in C, Aq\in Q. \end{equation} $
用 SFP$(C,Q,A)$
分裂可行性问题是不动点理论和最优化理论中的一个重要组成部分, 近年来受到了广泛的关注, 它在信号处理、图像重建、模拟调强放射治疗等方面有着很多的应用.
2002 年, Byrne 等人[2 ] 提出了 CQ 算法求解分裂可行性问题 (1.1). 对于任意的 $q_1$ $\in$ $C$
(1.2) $ \begin{equation}\label{12} q_{n+1}=P_C(q_n-\tau_nA^*(I-P_Q)Aq_n), \forall n\geq 1, \end{equation} $
其中, $\tau_n\in(0,\frac{2}{\|A\|^2})$ $P_C$ $P_Q$ $C$ $Q$ $A^*$ $A$ $\langle Ax, y \rangle = \langle x, A^* y \rangle, \forall x \in H_1,y \in H_2 $ . 令
其中, $\nabla f$ $f$
由于步长的选取 $\tau_n$ [3 ] 在有限维 Hilbert 空间中提出了可变步长 $\tau_n$
其中, $\sum\limits_{n=1}^{\infty} \rho_n=\infty$ $\sum\limits_{n=1}^{\infty} \rho_n^2<\infty$ .
由于可变步长 $ \tau_n$ [4 ] 提出了自适应步长 $\tau_n$
其中, $\{\rho_n\}\subset(0,4)$ $\inf_n \rho_n(4-\rho_n)>0$ .
非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] .
2019 年, Qin 等人[5 ] 提出求解分裂可行性问题和不动点问题的公共解的迭代算法, 并证明了该算法的强收敛性. 具体算法如下
(1.3) $ \begin{equation}\label{13} q_{n+1}=P_C(\alpha_ng(q_n)+\beta_nSq_n+\gamma_n(q_n-\tau_nA^*(I-P_Q)Aq_n)), \end{equation} $
其中, $S:C\to C$ $g:C\to C$ $\kappa$ - 压缩映射, $\kappa \in (0,1)$ .
2024 年, 王元恒等人[6 ] 将算法 (1.3) 中的非扩张算子推广至拟非扩张算子, 并引入了自适应步长和惯性迭代步, 使算法的收敛速度更快. 具体算法如下
(1.4) $ \begin{equation}\label{14} \left\{ \begin{aligned} &\omega_n=q_n+\mu_n(q_n-q_{n-1}), \\ &q_{n+1}=P_C(\alpha_n\xi g(q_n)+\beta_nS\omega_n+((1-\beta_n)I-\alpha_nB)(\omega_n-\tau_n\nabla f(\omega_n))). \end{aligned} \right. \end{equation} $
他们证明了在适当条件下, 由算法 (1.4) 生成的序列 $\{q_n\}$ $q^*\in \text{Fix}(S)\cap \text{SFP}$ $(C,Q,A)$ .
受上述事实的启发, 本文将算法 (1.4) 中的一个拟非扩张算子推广到有限族拟非扩张算子, 这使得能解决的问题更加广阔, 并提出自适应惯性平行迭代算法, 证明了由该算法生成的序列强收敛到分裂可行性问题与有限族拟非扩张算子不动点问题的公共解, 通过数值实验验证了该算法的收敛速度比算法 (1.4) 的收敛速度更快.
2 预备知识
设 $H$ $\langle \cdot,\cdot\rangle $ $\cdot$ $D$ $H$ $x,y\in H$
定义2.1 [6 ] 设 $T:H \to H$ $\text{Fix}(T)$ $T$ $\text{Fix}(T)=\{x \in H:Tx=x\}$ .
(i) 称 $T$ $ x,y \in H$ $\|Tx-Ty\|\leq \|x-y\|$ .
(ii) 称 $T$ $\kappa$ - 压缩的, 如果存在常数 $\kappa \in (0,1)$ $x,y \in H$ $\|Tx-Ty\|\leq \kappa \|x-y\|$ .
(iii) 称 $T$ $\text{Fix}(T)\neq \emptyset$ $x \in H,u\in \text{Fix}(T)$ $\|Tx-u\|\leq \|x-u\|$ . 显然一个存在不动点的非扩张映射是拟非扩张的.
(iv) 称 $T$ $L$ - Lipschitz 的, 如果存在非负常数 $L >0 $ $x,y \in H$ $\|Tx-Ty\|\leq L \|x-y\|$ .
(v) 称 $T$ $\eta$ - 强单调的, 如果存在非负常数 $\eta >0$ $x,y \in H$ $\langle Tx-Ty,x-y\rangle\geq \eta \|x-y\|^2$ .
定义2.2 [6 ] 令 $B:H \to H$ $B$ $\eta$ - 强正的, $\eta >0$
引理2.1 [9 ] 对于任意的 $x_i\in H$ $\alpha_i\in [0,1](i=1,2,\cdots,n)$
其中, $\sum\limits_{i=1}^{n}\alpha_i=1$ .
引理2.2 [6 ] 对于 $x\in D,y\in H$
(i) $x=P_Dy\Leftrightarrow \langle x-y,z-x\rangle \geq0,\forall z \in D$ .
(ii) $\|x-P_Dy\|^2 \leq \|x-y\|^2 - \|y-P_Dy\|^2 $ .
(iii) $ \langle P_Dy-y,z-y\rangle \geq \|P_Dy-y\|^2,\forall z \in D$ .
引理2.3 [10 ] 令 ${q_n}$
其中 $\{\Gamma_n\}$ $(0,1)$ $\{\Psi_n\}$ $\{\Phi_n\}$ $\{\Lambda_n\}$
(i) $\sum\limits_{n=1}^{\infty} \Gamma_n=\infty$
(ii) $\lim\limits_{n \to \infty}\Phi_n=0$
(iii) 对 $\{n\}$ $\{n_k\}$ $\lim\limits_{k \to \infty}\Psi_{n_{k}}=0$ $\lim\limits_{k \to \infty} \sup \Lambda_n \leq 0$ .
则$\lim\limits_{n \to \infty}q_n=0$ .
引理2.4 [6 ] 令 $f(q):=\dfrac{1}{2}\|(I-P_Q)Aq\|^2$ $\nabla f$ $\|A\|^2$ - Lipschitz 连续的.
定义2.3 [11 ] 令 $T:H \to H$ $\text{Fix}(T)\neq\emptyset$ $I$ $\{q_n\} \subset H$
引理2.5 [12 ] 令 $g:H \to H$ $\kappa$ - 压缩映射, $\kappa \in (0,1)$ $B:H \to H$ $\eta$ - 强正有界线性算子, $\eta >0$ $0\leq \xi \kappa<\eta $ $\xi $ $B-\xi g $ $(\eta- \xi \kappa)$ - 强单调的.
引理2.6 [12 ] 令 $B:H \to H $ $\eta$ - 强正有界线性算子, $\eta >0$ $ 0< \lambda \leq \frac{1}{\|B\|}$ $\|I-\lambda B\|\leq 1-\lambda\eta$ .
变分不等式问题表述为: 寻求一点 $y \in D$
(2.1) $ \begin{equation}\label{21} \langle Fx,y-x\rangle \geq 0, \forall x \in D, \end{equation} $
其中, $F:H \to H $
引理2.7 [13 ] 令 $F:H \to H $
3 主要结果
(B$_1$ ) $T_i:H_1 \to H_1$ $I-T_i$ $i=1,2,\cdots,N$ .
(B$_2$ ) $g:C\to C$ $\kappa$ - 压缩映射, $\kappa \in (0,1)$ .
(B$_3$ ) $\{\alpha_{n}^{i}\}\subset (0,1)$ $ 0<\lim\limits_{n \to \infty} \inf \alpha_{n}^{i} < \lim\limits_{n \to \infty} \sup \alpha_{n}^{i} <1$ $i=1,2,\cdots,N$ .
(B$_4$ ) $\bigcap\limits_{i=1}^{N} \text{Fix}(T_i) \cap \text{SFP}(C,Q,A)\neq \emptyset$ .
(B$_5$ ) $B:H_1 \to H_1$ $\eta$ - 强正有界线性算子, $\eta >0$ .
(B$_6$ ) $\{\alpha_{n}^{0}\}\subset (0,1)$ $\lim\limits_{n \to \infty}\alpha_{n}^{0}=0$ $\sum\limits_{n=1}^{\infty} \alpha_{n}^{0}=\infty$ .
(B$_7$ ) $\epsilon_n>0$ $\lim\limits_{n \to \infty}\frac{\epsilon_n}{\alpha_{n}^{0}}=0$ .
(B$_8$ ) $\sum\limits_{i=0}^{N}\alpha_{n}^{i}< 1$ .
(B$_9$ ) $\{\rho_n\}\subset(0,4)$ $\inf_n \rho_n(4-\rho_n)>0$ .
定义泛函 $f:H_1\to \text{R}$
算法3.1 选取 $q_0,q_1 \in H_1$ $\mu \geq 0$ $\xi >0$ $0\leq \xi\kappa <\eta$ .
${\bf 步骤二}$ $ \nabla f(\omega_n)=0$
${\bf 步骤三}$ $n:=n+1$
引理3.1 假设条件 (B$_1)-$ ( B$_9$ ) 成立, 序列 $\{q_n\}$ $\{q_n\}$
证 首先, 令 $\lambda_n=\frac{\alpha_{n}^{0}}{1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}}$ $y_n=\lambda_n\xi g(q_n)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n))$ $q_{n+1}=P_C(\sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})y_n)$ . 由 $\{\alpha_{n}^{0}\}$ $\{\epsilon_n\}$ $\{\alpha_{n}^{i}\}(1\leq i \leq N)$ $\{\lambda_n\} \subset(0,1) $ $\lim\limits_{n \to \infty}\frac{\epsilon_n}{\lambda_n}=0$ .
任取 $p\in \bigcap\limits_{i=1}^{N} \text{Fix}(T_i) \cap \text{SFP}(C,Q,A)$ $y_n$
(3.1) $ \begin{equation}\label{31} \begin{aligned} \|y_n-p\| = & \|\lambda_n(\xi g(q_n)-Bp)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n)-p)\| \\ \leq &\lambda_n\|\xi g(q_n)-Bp\|+\|I-\lambda_nB\|\|\omega_n-\tau_n\nabla f(\omega_n)-p\| \\ \leq& \lambda_n\|\xi g(q_n)-\xi g(p)\|+\lambda_n\|\xi g(p)-Bp\|+(1-\lambda_n\eta )\|\omega_n-\tau_n\nabla f(\omega_n)-p\| \\ \leq& \lambda_n \xi \kappa \|q_n-p\|+\lambda_n\|\xi g(p)-Bp\|+(1-\lambda_n\eta )\|\omega_n-\tau_n\nabla f(\omega_n)-p\|. \end{aligned} \end{equation} $
根据共轭算子的性质和引理2.2, 由 $p\in \text{SFP}(C,Q,A)$
(3.2) $ \begin{equation}\label{32} \begin{aligned} \|\omega_n-\tau_n\nabla f(\omega_n)-p\|^2 =& \|\omega_n-p\|^2+{\tau_n}^2\|\nabla f(\omega_n)\|^2-2\tau_n \langle \nabla f(\omega_n),\omega_n-p\rangle \\ =&\|\omega_n-p\|^2+{\tau_n}^2\|\nabla f(\omega_n)\|^2\\ &-2\tau_n \langle (I-P_Q)A\omega_n-(I-P_Q)Ap,A\omega_n-Ap\rangle \\ \leq& \|\omega_n-p\|^2+{\tau_n}^2\|\nabla f(\omega_n)\|^2-2\tau_n\|(I-P_Q)A\omega_n\|^2 \\ =&\|\omega_n-p\|^2+{\tau_n}^2\|\nabla f(\omega_n)\|^2-4\tau_nf(\omega_n) \\ =&\|\omega_n-p\|^2+\frac{{\rho_n}^2 {f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}-4\frac{\rho_n {f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}\\ =&\|\omega_n-p\|^2-\rho_n(4-\rho_n)\frac{{f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}. \end{aligned} \end{equation} $
(3.3) $ \begin{equation}\label{33} \|\omega_n-\tau_n\nabla f(\omega_n)-p\|\leq \|\omega_n-p\|. \end{equation} $
由 (3.1), (3.3) 式和 $q_{n+1}$
(3.4) $ \begin{matrix}\label{34} \|q_{n+1}-p\| &= \|P_C(\alpha_{n}^{0}\xi g(q_n)+\sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+((1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})I-\alpha_{n}^{0}B)(\omega_n-\tau_n\nabla f(\omega_n)))-p\| \\ & \leq \|\alpha_{n}^{0}\xi g(q_n)+\sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+((1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})I-\alpha_{n}^{0}B)(\omega_n-\tau_n\nabla f(\omega_n))-p\| \\ & = \|\sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})(\lambda_n\xi g(q_n)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n)))-p\| \\ & \leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}\|T_i\omega_n-p\|+(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})\|\lambda_n\xi g(q_n)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n))-p\| \\ & \leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n\!-\!p\|\!+\!\alpha_{n}^{0}\xi \kappa \|q_n\!-\!p\|\!+\!\alpha_{n}^{0}\|\xi g(p)\!-\!Bp\|\!+\!(1- \sum\limits_{i=1}^{N}\alpha_{n}^{i}\!-\!\alpha_{n}^{0}\eta )\|\omega_n\!-\!p\|\\ &= (1-\alpha_{n}^{0}\eta)\|\omega_n-p\| + \alpha_{n}^{0}\xi \kappa \|q_n-p\| + \alpha_{n}^{0}\|\xi g(p)-Bp\|. \end{matrix} $
根据 $\omega_n$ $\mu_n$
(3.5) $ \begin{equation}\label{35} \|\omega_n-p\| \leq \|q_n-p\| +\mu_n\|q_n-q_{n-1}\| \leq \|q_n-p\| +\epsilon_n. \end{equation} $
由条件 (B$_7)$ $M$ $ \frac{\epsilon_n}{\alpha_{n}^{0}}\leq M$
定理3.1 假设条件 (B$_1)-$ ( B$_9$ ) 成立, 序列 $\{q_n\}$ $\{q_n\}$ $q^*\in \bigcap\limits_{i=1}^{N} \text{Fix}(T_i) \cap \text{SFP}(C,Q,A)$ $q^*$
(3.6) $ \begin{equation}\label{36} \langle q-q^*,\xi g(q^*)-Bq^*\rangle \leq 0, \forall q\in \bigcap\limits_{i=1}^{N} \text{Fix}(T_i) \cap \text{SFP}(C,Q,A). \end{equation} $
(3.7) $ \begin{equation}\label{37} \begin{aligned} \|\omega_n-q^*\|^2 & \leq \|q_n-q^*\|^2 + 2\mu_n\langle q_n-q_{n-1},\omega_n-q^*\rangle \\ & \leq \|q_n-q^*\|^2 + 2\mu_n\| q_n-q_{n-1}\|\|\omega_n-q^*\| \\ & \leq \|q_n-q^*\|^2 + 2\epsilon_n\|\omega_n-q^*\|. \\ \end{aligned} \end{equation} $
由引理 2.6, $y_n$
(3.8) $ \begin{matrix}\label{38} \|y_n-q^*\|^2 & = \|\lambda_n(\xi g(q_n)-Bq^*)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n)-q^*)\|^2 \\ & = \|(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n)-q^*)\|^2+{\lambda_n}^2\|\xi g(q_n)-Bq^*\|^2 \\ &~~~+2\lambda_n \langle (I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n)-q^*),\xi g(q_n)-Bq^* \rangle \\ &\leq (1-\lambda_n\eta)^2\|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2+{\lambda_n}^2\|\xi g(q_n)-Bq^*\|^2 \\ &~~~ +2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q_n)-\xi g(q^*)\rangle \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle \\ &~~~-2{\lambda_n}^2\langle B(\omega_n-\tau_n\nabla f(\omega_n)-q^*),\xi g(q_n)-Bq^*\rangle \\ &\leq (1-\lambda_n\eta )^2\|\omega_n-q^*\|^2+{\lambda_n}^2\|\xi g(q_n)-Bq^*\|^2 \\ &~~~+2\lambda_n\xi\kappa \|\omega_n-q^*\|\|q_n-q^*\| \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle \\ &~~~+2{\lambda_n}^2 \|B\| \|\omega_n-\tau_n\nabla f(\omega_n)-q^*\| \|\xi g(q_n)-Bq^*\| \\ &= (1-2\lambda_n\eta)\|\omega_n-q^*\|^2+2\lambda_n\xi\kappa \|\omega_n-q^*\|\|q_n-q^*\| \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle \\ &~~~+{\lambda_n}^2\left( {\eta}^2\|\omega_n-q^*\|^2+\|\xi g(q_n)-Bq^*\|^2+2\|B\|\|\omega_n-q^*\|\|\xi g(q_n)-Bq^*\|\right) \\ &\leq (1-2\lambda_n\eta)\|\omega_n-q^*\|^2+2\lambda_n\xi\kappa \|\omega_n-q^*\|\|q_n-q^*\| \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle + {\lambda_n}^2M_1. \end{matrix} $
其中 $M_1\geq \sup\limits_{n \in\mathbb{N}}\{ {\eta}^2\|\omega_n-q^{*}\|^2+\|\xi g(q_n)-Bq^{*}\|^2+2\|B\|\|\omega_n-q^{*}\|\|\xi g(q_n)-Bq^{*}\|\}$
(3.9) $ \begin{matrix}\label{39} \|y_n-q^{*}\|^2 &\leq (1-2\lambda_n\eta)(\|q_n-q^{*}\|^2+2\epsilon_n \|\omega_n-q^{*}\|)+2\lambda_n\xi\kappa(\|q_n-q^{*}\|+\epsilon_n)\|q_n-q^{*}\| \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^{*}, \xi g(q^*)-Bq^{*}\rangle + {\lambda_n}^2M_1\\ &\leq (1-2\lambda_n\eta)\|q_n-q^*\|^2+2\epsilon_n \|\omega_n-q^{*}\|+2\lambda_n\xi\kappa\|q_n-q^{*}\|^2+2\xi\kappa\epsilon_n\|q_n-q^{*}\| \\ &~~~+2\lambda_n \langle \omega_n-\tau_n\nabla f(\omega_n)-q^{*}, \xi g(q^*)-Bq^{*}\rangle + {\lambda_n}^2M_1\\ &=(1-2\lambda_n(\eta -\xi\kappa))\|q_n-q^{*}\|^2+2\lambda_n\bigg(\langle \omega_n-\tau_n\nabla f(\omega_n)-q^{*}, \xi g(q^{*})-Bq^{*}\rangle \\ &~~~+\frac{\epsilon_n\|\omega_n-q^{*}\|}{\lambda_n} + \frac{\epsilon_n\xi\kappa\|q_n-q^{*}\|}{\lambda_n} + \frac{1}{2}\lambda_nM_1\bigg). \end{matrix} $
(3.10) $ \begin{equation}\label{310} \begin{aligned} \|q_{n+1}-q^*\|^2 &= \bigg\|P_C\bigg( \sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})y_n \bigg)-q^* \bigg\|^2\\ &\leq\bigg\|\sum\limits_{i=1}^{N}\alpha_{n}^{i}T_i\omega_n+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)y_n -q^*\bigg\|^2 \\ &= \bigg\|\sum\limits_{i=1}^{N}\alpha_{n}^{i}(T_i\omega_n-q^*) +\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)(y_n-q^*)\bigg\|^2\\ &\leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n-q^*\|^2 + \bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|y_n-q^*\|^2 \\ &~~~-\alpha_{n}^{i}\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|T_i\omega_n-y_n\|^2(i=1,2,\cdots,N). \end{aligned} \end{equation} $
(3.11) $ \begin{equation}\label{311} \|q_{n+1}-q^*\|^2 \leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n-q^*\|^2+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|y_n-q^*\|^2. \end{equation} $
通过 (3.7), (3.9) 和 (3.11) 式, 可得
(3.12) $ \begin{matrix}\label{312} \|q_{n+1}-q^*\|^2 &\leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}(\|q_n-q^*\|^2+2\epsilon_n\|\omega_n-q^*\|)+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}-2\alpha_{n}^{0}(\eta-\xi\kappa)\bigg)\|q_n-q^*\|^2\\ &~~~+2\alpha_{n}^{0}(\langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle\\ &~~~ +\frac{\epsilon_n\|\omega_n-q^*\|}{\lambda_n} + \frac{\epsilon_n\xi\kappa\|q_n-q^*\|}{\lambda_n} +\frac{1}{2}\lambda_nM_1)\\ & \leq (1-2\alpha_{n}^{0}(\eta -\xi\kappa))\|q_n-q^*\|^2+2\alpha_{n}^{0}\bigg(\langle \omega_n-\tau_n\nabla f(\omega_n)-q^*, \xi g(q^*)-Bq^*\rangle\\ &~~~+\frac{\epsilon_n\|\omega_n-q^*\|}{\lambda_n} + \frac{\epsilon_n\xi\kappa\|q_n-q^*\|}{\lambda_n}+ \frac{\epsilon_n\|\omega_n-q^*\|}{\alpha_{n}^{0}}+ \frac{1}{2}\lambda_nM_1\bigg). \end{matrix} $
(3.13) $ \begin{equation}\label{313} \begin{aligned} \|y_n-q^*\|^2 &=\|\lambda_n\xi g(q_n)+(I-\lambda_nB)(\omega_n-\tau_n\nabla f(\omega_n))-q^*\|^2\\ &=\|(\omega_n-\tau_n\nabla f(\omega_n)-q^*)+\lambda_n(\xi g(q_n)-B(\omega_n-\tau_n\nabla f(\omega_n)))\|^2\\ &\leq \|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2+2\lambda_n\langle \xi g(q_n)-B(\omega_n-\tau_n\nabla f(\omega_n)), y_n-q^*\rangle\\ &\leq \|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2+2\lambda_n\|\xi g(q_n)-B(\omega_n-\tau_n\nabla f(\omega_n))\|\|y_n-q^*\|\\ &\leq \|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2 +\lambda_nM_2. \end{aligned} \end{equation} $
其中 $M_2\geq 2\sup\limits_{n \in \mathbb{N}} \{\|\xi g(q_n)-B(\omega_n-\tau_n\nabla f(\omega_n))\|\|y_n-q^*\|\}$
(3.14) $ \begin{equation}\label{314} \begin{aligned} \|q_{n+1}-q^*\|^2 &\leq \sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n-q^*\|^2+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)(\|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2 \\ &~~~+\lambda_nM_2)-\alpha_{n}^{i}(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i})\|T_i\omega_n-y_n\|^2\\ &=\sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n-q^*\|^2+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|\omega_n-\tau_n\nabla f(\omega_n)-q^*\|^2\\ &~~~+\alpha_{n}^{0}M_2-\alpha_{n}^{i}\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|T_i\omega_n-y_n\|^2(i=1,2,\cdots,N). \end{aligned} \end{equation} $
(3.15) $ \begin{matrix}\label{315} \|q_{n+1}-q^*\|^2 &\leq\sum\limits_{i=1}^{N}\alpha_{n}^{i}\|\omega_n-q^*\|^2+\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\bigg(\|\omega_n-q^*\|^2\\ &~~~-\rho_n(4-\rho_n)\frac{{f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}\bigg)+\alpha_{n}^{0}M_2-\alpha_{n}^{i}\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|T_i\omega_n-y_n\|^2\\ &=\|\omega_n-q^*\|^2-\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\rho_n(4-\rho_n)\frac{{f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}+\alpha_{n}^{0}M_2\\ &~~~-\alpha_{n}^{i}\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|T_i\omega_n-y_n\|^2(i=1,2,\cdots,N). \end{matrix} $
(3.16) $ \begin{equation}\label{316} \begin{aligned} \|q_{n+1}-q^*\|^2 &\leq \|q_n-q^*\|^2-\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\rho_n(4-\rho_n)\frac{{f(\omega_n)}^2}{\|\nabla f(\omega_n)\|^2}\\ &~~~-\alpha_{n}^{i}\bigg(1-\sum\limits_{i=1}^{N}\alpha_{n}^{i}\bigg)\|T_i\omega_n-y_n\|^2+2\epsilon_n\|\omega_n-q^*\|\\ &~~~+\alpha_{n}^{0}M_2 (i=1,2,\cdots,N). \end{aligned} \end{equation} $
令 $\Gamma_n =2\alpha_{n}^{0}(\eta -\xi\kappa)$
则 (3.12) 和 (3.16) 式可以被表示为
由条件 $\left( B_2\right) $ $\left( B_6\right) $ $\left( B_7\right) $ $\lim \limits_{n \to \infty}\Gamma_n =0$ $\sum\limits_{n=0}^{\infty}\Gamma_n=\infty$ $\lim \limits_{n \to \infty}\Phi_n = 0$ .
接下来证明对 $\{n\}$ $\{n_k\}$ $\lim \limits_{k \to \infty}\Psi_{n_k} =0$ $\lim \limits_{k \to \infty}\sup \Lambda_{n_k}\leq0$ . 假设子列 $\{n_k\} \subset \{n\} $ $\lim \limits_{k \to \infty}\Psi_{n_k} =0$ . 由 $\{\alpha_{n}^{0}\}$ $\{\rho_n\}$ $\{\alpha_{n}^{i}\}(1\leq i \leq N)$
(3.17) $\lim \limits_{k \to \infty} \frac{{f(\omega_{n_k})}}{\|\nabla f(\omega_{n_k})\|}=0,$
(3.18) $\lim \limits_{k \to \infty} \|T_i\omega_{n_k}-y_{n_k}\|=0 (i=1,2,3,\cdots,N). $
选取 $\{q_{n_k}\}$ $\{q_{n_{k_j}}\}$
由引理 3.1 知 $\{q_n\}$ $q_{n_{k_j}}\rightharpoonup z^{\prime} $ . 由 $\omega_n$
即 $\|q_{n_k}-\omega_{n_k}\| \rightarrow 0$ . 因此, $\omega_{n_{k_j}}\rightharpoonup z^{\prime} $ . 由 $\tau_n$
(3.19) $ \begin{equation}\label{319} \begin{aligned} \|\lambda_{n_k} \xi g(q_{n_k}) +(I-\lambda_{n_k}B)\omega_{n_k}-y_{n_k}\|&=\|(I-\lambda_{n_k}B)( \tau_{n_k} \nabla f(\omega_{n_k}))\| \\ &\leq (1-\lambda_{n_k}\eta) \tau_{n_k} \|\nabla f(\omega_{n_k})\| \\ & \leq \tau_{n_k} \|\nabla f(\omega_{n_k})\| \rightarrow 0(k\rightarrow \infty), \end{aligned} \end{equation} $
(3.20) $ \begin{equation}\label{320} \begin{aligned} \|\lambda_{n_k} \xi g(q_{n_k}) +(I-\lambda_{n_k}B)\omega_{n_k}-\omega_{n_k}\| &=\|\lambda_{n_k} \xi g(q_{n_k})-\lambda_{n_k}B\omega_{n_k}\| \\ &= \lambda_{n_k}\|\xi g(q_{n_k})-B\omega_{n_k}\|\rightarrow 0(k\rightarrow \infty). \end{aligned} \end{equation} $
结合 (3.18), (3.19) 和 (3.20) 式, 可得
通过上式, 结合 $I-T_i(i=1,2 \cdots N)$ $z^{\prime} \in \text{Fix}(T_i)(i=1,2,3,\cdots,N)$ . 因此, $z^{\prime} \in \bigcap\limits_{i=1}^{N}\text{Fix}(T_i)$ .
由引理 2.4知 $\{\|\nabla f(\omega_n)\|\}$ $f(\omega_{n_k})\rightarrow 0 (k\rightarrow \infty)$ . 利用 $\|\cdot\|^2$ $0\leq f(z^{\prime})\leq \lim \limits_{j \to \infty} \inf f(\omega_{n_{k_j}})=0$ $f(z^{\prime})=0 $ . 由 $f$ $Az^{\prime} \in Q$ $C$ $z^{\prime} \in C$ . 因此 $z^{\prime} \in \text{SFP}(C,Q,A) $ .
综上, $z^{\prime} \in \bigcap\limits_{i=1}^{N}\text{Fix}(T_i)\cap \text{SFP}(C,Q,A)$
(3.21) $ \begin{equation}\label{321} \begin{split} &\lim \limits_{k \to \infty} \sup \langle \omega_{n_k}-\tau_{n_k}\nabla f(\omega_{n_k})-q^*,\xi g(q^*)-Bq^* \rangle \\ = &\lim \limits_{k \to \infty} \sup \langle \omega_{n_k}-q^*,\xi g(q^*)-Bq^* \rangle \\ =& \lim \limits_{k \to \infty} \sup \langle q_{n_k}-q^*,\xi g(q^*)-Bq^* \rangle \\ =& \lim \limits_{j \to \infty} \langle q_{n_{k_j}}-q^*,\xi g(q^*)-Bq^* \rangle \\ =& \langle z^{\prime}-q^*,\xi g(q^*)-Bq^* \rangle \leq 0. \end{split} \end{equation} $
由 $\lim\limits_{n \to \infty}\frac{\epsilon_n}{\lambda_n}=0$ $(B_6)$ $(B_7)$
即通过 (3.21) 式可得 $\lim \limits_{k \to \infty} \sup \Lambda_{n_k} \leq 0 $ .
综上, 由引理 2.3 知 $\lim \limits_{n \to \infty} \|q_n-q^*\|=0 $ $\{q_n\}$ $q^*$ .
注3.1 本文所得的结果改进和推广了文献 [6 ] 的相关结论, 将文献 [6 ] 中关于一个拟非扩张算子的不动点问题推广到有限族拟非扩张算子的公共不动点问题. 当 $N=1$ 6 ] 中的算法 2.
4 数值实验
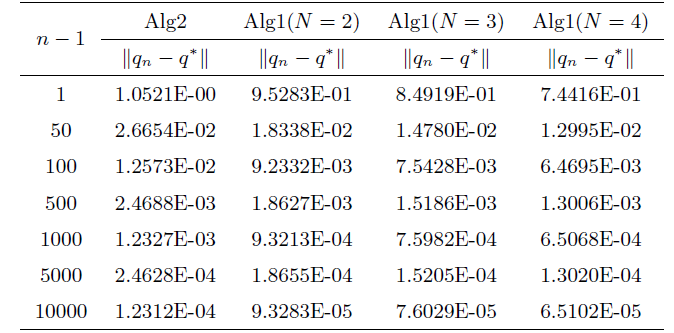
本节数值实验是在 MATLAB-R2022a 和 Windows11 中运行; 用 "Alg1" 表示本文的算法 3.1, 用 "Alg2" 表示文献 [6 ] 的算法 2, 用 "$n$ $\|q_n-q^*\|$ $n$ $N=1,2,3,4$ $N=1$ 6 ] 的 Alg2.
例4.1 令 $H_1=H_2=C=\mathbb{R}^5$ $Q=\{kb:k \in \mathbb{R}\}$ $b$ $ \mathbb{R}^5$
对任意的 $x \in \mathbb{R}^5$
易知, $T_i(i=1,2,3,4)$ $q^*=[\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2},1]^T$ $T_i(i=1,2,3,4)$ $q^* \in \bigcap\limits_{i=1}^{4}\text{Fix}(T_i)$ . 根据 $q^* \in C$ $Aq^*=[\frac{43}{16},2,\frac{19}{16}, \frac{51}{8},\frac{41}{8}]=b\in Q$ $q^* \in \text{SFP}(C,Q,A)$ . 综上, $q^* \in \bigcap\limits_{i=1}^{4}\text{Fix}(T_i)\cap \text{SFP}(C,Q,A)$ .
在 Alg1 和 Alg2 中, 取初始值 $q_0=q_1=[1,1,1,1,1]^T$, $g(x)=\frac{1}{5}x$ $\alpha_{n}^{0} =\frac{1}{10n}$ $B=I$ $\rho_n=3+\frac{1}{n+1}$ $\xi =1$ $\mu =1$ $\epsilon_n=\frac{1}{n^2}$ .
考虑 $N=1$ $S=T_1$ $\alpha_{n}^{1} =0.3$
考虑 $N=2$ $T_1$ $T_2$ $\alpha_{n}^{1} =0.3$ $\alpha_{n}^{2} =0.1$
考虑 $N=3$ $T_1$ $T_2$ $T_3$ $\alpha_{n}^{1} =0.3$ $\alpha_{n}^{2} =0.1$ $\alpha_{n}^{3} =0.1$
考虑 $N=4$ $T_1$ $T_2$ $T_3$ $T_4$ $\alpha_{n}^{1} =0.3$ $\alpha_{n}^{2} =0.1$ $\alpha_{n}^{3} =0.1$ $\alpha_{n}^{4} =0.1$
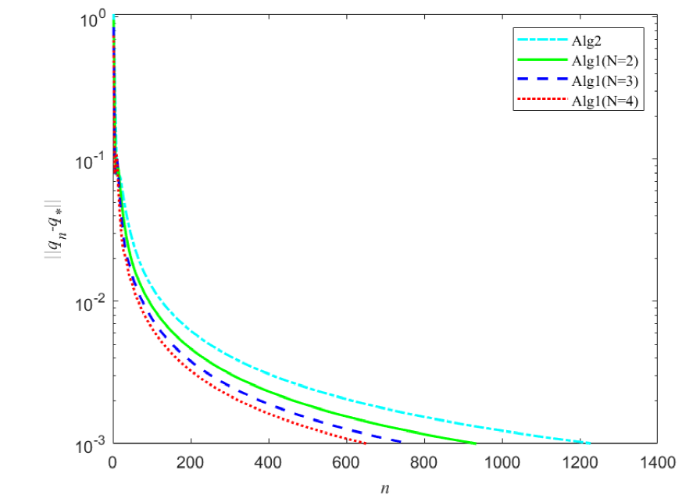
图1
图1
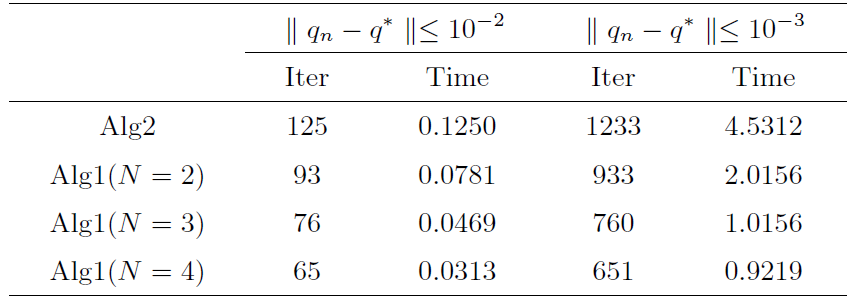
当$\parallel q_n-q^*\parallel\leq10^{-3}$
注4.1 从表 1 可以看出, 本文的 Alg1 随着迭代步数的增长, 序列 $\{q_n\}$ $q^*$ 图 1 和表 2 可以看出, 本文的 Alg1 比文献 [6 ] 中 Alg2 的收敛速度更快, 从而验证了本文所提出算法的优越性.
参考文献
View Option
[1]
Censor Y Elfving T . A multiprojection algorithm using Bregman projections in a product space
Numer Algorithms , 1994 , 8 2 ): 221 -239
[本文引用: 1]
[2]
Byrne C . Iterative oblique projection onto convex sets and the split feasibility problem
Inverse Problems , 2002 , 18 2 ): 441 -453
[本文引用: 1]
[3]
Yang Q . On variable-step relaxed projection algorithm for variational inequalities
J Math Anal Appl , 2005 , 302 1 ): 166 -179
[本文引用: 1]
[4]
López G Martín-Márquez V Wang F , et al . Solving the split feasibility problem without prior knowledge of matrix norms
Inverse Problems , 2012 , 28 8 ): 085004
[本文引用: 1]
[5]
Qin X Yao J . A viscosity iterative method for a split feasibility problem
J Nonlinear Convex Anal , 2019 , 20 8 ): 1497 -1506
[本文引用: 2]
[6]
王元恒 , 许甜甜 , 姚任之 , 等 . 两类问题公共解集上的变分不等式解的算法
数学学报 , 2024 , 67 4 ): 704 -718
DOI:10.12386/A20220171
[本文引用: 12]
We study a new algorithm to solve a common solution of the split feasibility problem and the fixed point problem involving quasi-nonexpansive mappings in Hilbert spaces. Based on the common solutions of these two classes of problems, we solve the variational inequality problem. Compared with the predecessors, the self-adaptive technique and the inertial iteration method are added, which can speed up the convergence rate of the iterative sequence generated by our algorithms. At the same time, we extend the involving previous nonexpansive mappings to extensive quasi-nonexpansive mappings. In addition, a strong positive bounded operator is added to the algorithm, which extends the original viscous iterative algorithm to a more general viscous iterative algorithm. The effectiveness of the algorithm is verified by numerical examples.
Wang Y H Xu T T Yao R Z et al. An algorithm to solve the variational inequality problem based on the common solutions of two classes of problems
Acta Mathematica Sinica , 2024 , 67 4 ): 704 -718
DOI:10.12386/A20220171
[本文引用: 12]
We study a new algorithm to solve a common solution of the split feasibility problem and the fixed point problem involving quasi-nonexpansive mappings in Hilbert spaces. Based on the common solutions of these two classes of problems, we solve the variational inequality problem. Compared with the predecessors, the self-adaptive technique and the inertial iteration method are added, which can speed up the convergence rate of the iterative sequence generated by our algorithms. At the same time, we extend the involving previous nonexpansive mappings to extensive quasi-nonexpansive mappings. In addition, a strong positive bounded operator is added to the algorithm, which extends the original viscous iterative algorithm to a more general viscous iterative algorithm. The effectiveness of the algorithm is verified by numerical examples.
[7]
Wang Y Xu T Yao J Jiang B . Self-Adaptive method and inertial modification for solving the split feasibility problem and fixed-point problem of quasi-nonexpansive mapping
Mathematics , 2022 , 10 9 ): 1612 -1626
[本文引用: 1]
[8]
Qin X Wang L . A fixed point method for solving a split feasibility problem in Hilbert spaces
Rev R Acad Cienc Exactas Fís Nat Ser A Mat RACSAM , 2019 , 113 315 -325
[本文引用: 1]
[9]
Zhou H Wang P . A new iteration method for variational inequalities on the set of common fixed points for a finite family of quasi-pseudocontractions in Hilbert spaces
J Inequal Appl , 2014 , 2014 1 -12
[本文引用: 1]
[10]
He S Yang C . Solving the variational inequality problem defined on intersection of finite level sets
Abstr Appl Anal , 2013 , 2013 1 ): 942315
[本文引用: 1]
[11]
刘丽平 , 彭建文 . 求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法
数学物理学报 , 2022 , 42A 5 ): 1517 -1536
[本文引用: 1]
Liu L P Peng J W . Modified Subgradient Extragradient Algorithms for Solving Common Elements of Variational Inequality and Fixed Point Problems
Acta Mathematica Scientia , 2022 , 42A 5 ): 1517 -1536
[本文引用: 1]
[12]
Marino G Xu H . A general iterative method for nonexpansive mappings in Hilbert space
J Math Anal Appl , 2006 , 318 1 ): 43 -52
[本文引用: 2]
[13]
Zhou H Zhou Y Feng G . Iterative methods for solving a class of monotone variational inequality problems with applications
J Inequal Appl , 2015 , 2015 1 -17
[本文引用: 1]
A multiprojection algorithm using Bregman projections in a product space
1
1994
... 1994 年, Censor 和 Elfving[1 ] 在研究 CT 扫描图像重建的过程中首次提出了有限维 Hilbert 空间中的分裂可行性问题. 分裂可行性问题为寻求一点 $q \in H_1$
Iterative oblique projection onto convex sets and the split feasibility problem
1
2002
... 2002 年, Byrne 等人[2 ] 提出了 CQ 算法求解分裂可行性问题 (1.1). 对于任意的 $q_1$ $\in$ $C$
On variable-step relaxed projection algorithm for variational inequalities
1
2005
... 由于步长的选取 $\tau_n$ [3 ] 在有限维 Hilbert 空间中提出了可变步长 $\tau_n$
Solving the split feasibility problem without prior knowledge of matrix norms
1
2012
... 由于可变步长 $ \tau_n$ [4 ] 提出了自适应步长 $\tau_n$
A viscosity iterative method for a split feasibility problem
2
2019
... 非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] . ...
... 2019 年, Qin 等人[5 ] 提出求解分裂可行性问题和不动点问题的公共解的迭代算法, 并证明了该算法的强收敛性. 具体算法如下 ...
两类问题公共解集上的变分不等式解的算法
12
2024
... 非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] . ...
... 2024 年, 王元恒等人[6 ] 将算法 (1.3) 中的非扩张算子推广至拟非扩张算子, 并引入了自适应步长和惯性迭代步, 使算法的收敛速度更快. 具体算法如下 ...
... 定义2.1 [6 ] 设 $T:H \to H$ $\text{Fix}(T)$ $T$ $\text{Fix}(T)=\{x \in H:Tx=x\}$ . ...
... 定义2.2 [6 ] 令 $B:H \to H$ $B$ $\eta$ - 强正的, $\eta >0$
... 引理2.2 [6 ] 对于 $x\in D,y\in H$
... 引理2.4 [6 ] 令 $f(q):=\dfrac{1}{2}\|(I-P_Q)Aq\|^2$ $\nabla f$ $\|A\|^2$ - Lipschitz 连续的. ...
... 注3.1 本文所得的结果改进和推广了文献 [6 ] 的相关结论, 将文献 [6 ] 中关于一个拟非扩张算子的不动点问题推广到有限族拟非扩张算子的公共不动点问题. 当 $N=1$ 6 ] 中的算法 2. ...
... ] 的相关结论, 将文献 [6 ] 中关于一个拟非扩张算子的不动点问题推广到有限族拟非扩张算子的公共不动点问题. 当 $N=1$ 6 ] 中的算法 2. ...
... 时, 本文的算法 3.1 可变成文献 [6 ] 中的算法 2. ...
... 本节数值实验是在 MATLAB-R2022a 和 Windows11 中运行; 用 "Alg1" 表示本文的算法 3.1, 用 "Alg2" 表示文献 [6 ] 的算法 2, 用 "$n$ $\|q_n-q^*\|$ $n$ $N=1,2,3,4$ $N=1$ 6 ] 的 Alg2. ...
... 时, 本文的 Alg1 可变成文献 [6 ] 的 Alg2. ...
... 注4.1 从表 1 可以看出, 本文的 Alg1 随着迭代步数的增长, 序列 $\{q_n\}$ $q^*$ 图 1 和表 2 可以看出, 本文的 Alg1 比文献 [6 ] 中 Alg2 的收敛速度更快, 从而验证了本文所提出算法的优越性. ...
两类问题公共解集上的变分不等式解的算法
12
2024
... 非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] . ...
... 2024 年, 王元恒等人[6 ] 将算法 (1.3) 中的非扩张算子推广至拟非扩张算子, 并引入了自适应步长和惯性迭代步, 使算法的收敛速度更快. 具体算法如下 ...
... 定义2.1 [6 ] 设 $T:H \to H$ $\text{Fix}(T)$ $T$ $\text{Fix}(T)=\{x \in H:Tx=x\}$ . ...
... 定义2.2 [6 ] 令 $B:H \to H$ $B$ $\eta$ - 强正的, $\eta >0$
... 引理2.2 [6 ] 对于 $x\in D,y\in H$
... 引理2.4 [6 ] 令 $f(q):=\dfrac{1}{2}\|(I-P_Q)Aq\|^2$ $\nabla f$ $\|A\|^2$ - Lipschitz 连续的. ...
... 注3.1 本文所得的结果改进和推广了文献 [6 ] 的相关结论, 将文献 [6 ] 中关于一个拟非扩张算子的不动点问题推广到有限族拟非扩张算子的公共不动点问题. 当 $N=1$ 6 ] 中的算法 2. ...
... ] 的相关结论, 将文献 [6 ] 中关于一个拟非扩张算子的不动点问题推广到有限族拟非扩张算子的公共不动点问题. 当 $N=1$ 6 ] 中的算法 2. ...
... 时, 本文的算法 3.1 可变成文献 [6 ] 中的算法 2. ...
... 本节数值实验是在 MATLAB-R2022a 和 Windows11 中运行; 用 "Alg1" 表示本文的算法 3.1, 用 "Alg2" 表示文献 [6 ] 的算法 2, 用 "$n$ $\|q_n-q^*\|$ $n$ $N=1,2,3,4$ $N=1$ 6 ] 的 Alg2. ...
... 时, 本文的 Alg1 可变成文献 [6 ] 的 Alg2. ...
... 注4.1 从表 1 可以看出, 本文的 Alg1 随着迭代步数的增长, 序列 $\{q_n\}$ $q^*$ 图 1 和表 2 可以看出, 本文的 Alg1 比文献 [6 ] 中 Alg2 的收敛速度更快, 从而验证了本文所提出算法的优越性. ...
Self-Adaptive method and inertial modification for solving the split feasibility problem and fixed-point problem of quasi-nonexpansive mapping
1
2022
... 非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] . ...
A fixed point method for solving a split feasibility problem in Hilbert spaces
1
2019
... 非线性算子的不动点问题和分裂可行性问题两者相互关联, 可以相互转化. 最近, 很多学者将不动点问题和分裂可行性问题结合起来, 提出了求其公共解的迭代算法并得到相应的收敛定理. 目前国内外许多学者对分裂可行性问题与不动点问题的公共元进行了深入研究[5 ⇓ ⇓ -8 ] . ...
A new iteration method for variational inequalities on the set of common fixed points for a finite family of quasi-pseudocontractions in Hilbert spaces
1
2014
... 引理2.1 [9 ] 对于任意的 $x_i\in H$ $\alpha_i\in [0,1](i=1,2,\cdots,n)$
Solving the variational inequality problem defined on intersection of finite level sets
1
2013
... 引理2.3 [10 ] 令 ${q_n}$
求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法
1
2022
... 定义2.3 [11 ] 令 $T:H \to H$ $\text{Fix}(T)\neq\emptyset$ $I$ $\{q_n\} \subset H$
求解变分不等式和不动点问题的公共元的修正次梯度外梯度算法
1
2022
... 定义2.3 [11 ] 令 $T:H \to H$ $\text{Fix}(T)\neq\emptyset$ $I$ $\{q_n\} \subset H$
A general iterative method for nonexpansive mappings in Hilbert space
2
2006
... 引理2.5 [12 ] 令 $g:H \to H$ $\kappa$ - 压缩映射, $\kappa \in (0,1)$ $B:H \to H$ $\eta$ - 强正有界线性算子, $\eta >0$ $0\leq \xi \kappa<\eta $ $\xi $ $B-\xi g $ $(\eta- \xi \kappa)$ - 强单调的. ...
... 引理2.6 [12 ] 令 $B:H \to H $ $\eta$ - 强正有界线性算子, $\eta >0$ $ 0< \lambda \leq \frac{1}{\|B\|}$ $\|I-\lambda B\|\leq 1-\lambda\eta$ . ...
Iterative methods for solving a class of monotone variational inequality problems with applications
1
2015
... 引理2.7 [13 ] 令 $F:H \to H $