1 引言
给定一个非空集合 $X$, $f:X\to X$ 是一个自映射, 记
其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容.
近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] .
本文研究了可分逐段严格单调的 Markov 映射的迭代, 即存在特殊的不动点将映射划分为在多个子区间上逐段严格单调的 Markov 自映射, 将整体的迭代简化为对局部的迭代, 并分别给出子区间上映射的迭代与具体表达式.
2 准备工作
给定映射 $f:I:=[a,b]\to I$, 如果 $f$ 在 $x_0\in I$ 的小邻域内严格单调, 则称 $x_0$ 为 $f$ 的 "单调点", 否则为 $f$ 的 "非单调点" (参见文献 [18 ]). 令集合 $PM(I,I)$ 表示定义在区间 $I$ 上的所有具有有限多非单调点的连续自映射, $S(f)$ 为 $f\in PM(I,I)$ 的所有非单调点集合. 下面给出可分映射与可拼接映射的定义.
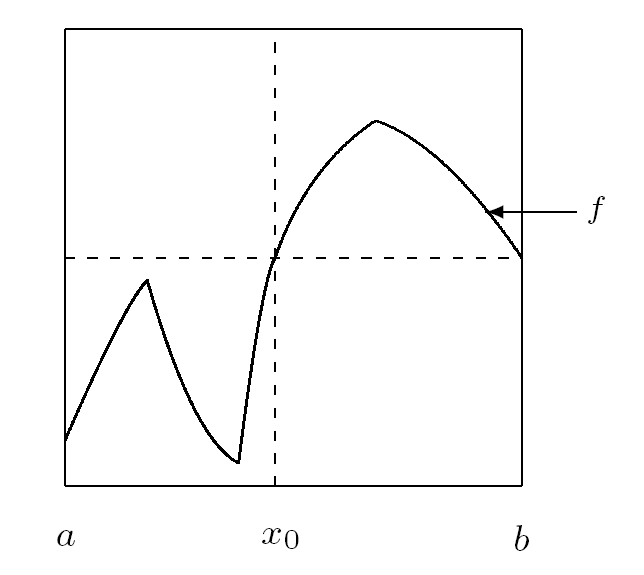
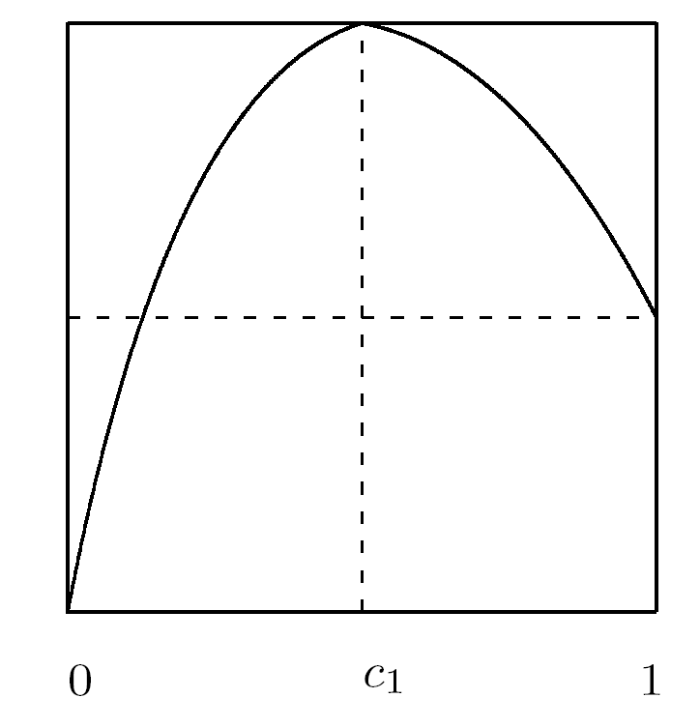
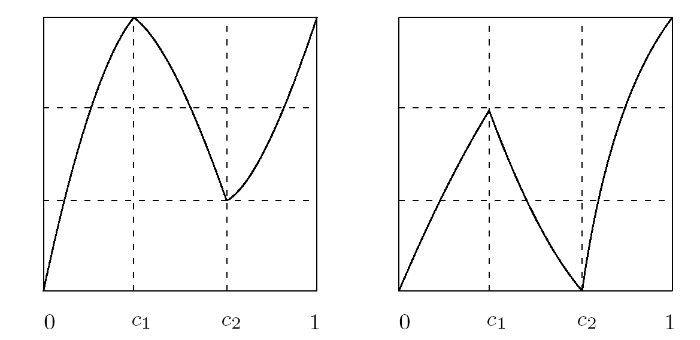
定义2.1 令 $f\in PM(I,I)$, 若存在不动点 $x_0$ 使得
其中 $f_1(I_1)\subset I_1$, $f_2(I_2)\subset I_2$, 则称 $f$ 为可分映射, $x_0$ 为 $f$ 的可分不动点 (如图 2.1 ). 令集合 $\mathcal{F}(f)$ 表示 $f$ 的所有可分不动点.
图 2.1
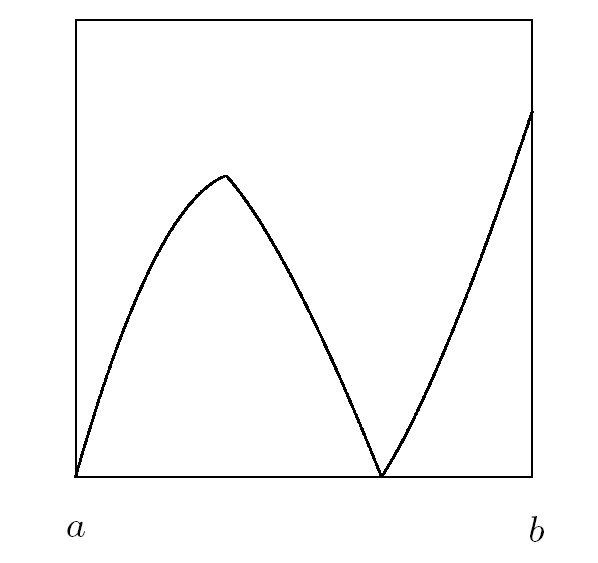
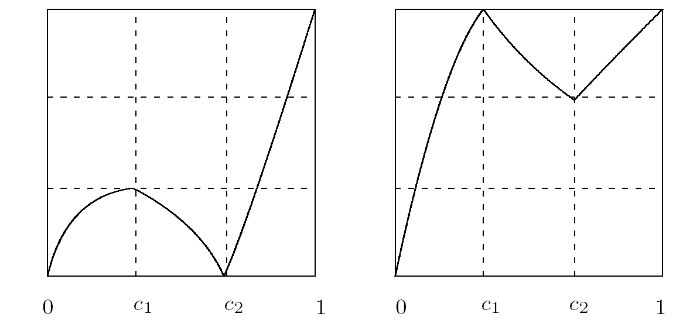
定义2.2 令 $f\in PM(I,I)$, $I=[a,b]$, 若 $f(a)=a$ 或 $f(b)=b$, 且区间 $I$ 内部无可分不动点, 则称 $f$ 为可拼接映射 (如图 2.2 ).
图 2.2
由定义 2.1 和定义 2.2 可知一个可分映射可以被可分不动点划分为一些可拼接映射, 从而可分映射的 $n$ 次迭代可以转化为这些可拼接自映射的 $n$ 次迭代. 特别地, 我们只考虑 $f$ 可分不动点有限的情形, 否则一定存在区间 $[a',b']\subset I$ 使得 $f$ 为恒等映射, 其任意次迭代仍为恒等映射, 从而
那么显然有 $I=\bigcup_{i=0}^{m} I_i:=\bigcup_{i=0}^{m} [x_i,x_{i+1}]$, 对 $f:I\to I$ 有
(2.1) $f=f_i, \mbox{其中} f_i:I_i\to I_i \mbox{为可拼接映射}, i=0,1,\cdots,m.$
接下来我们将给出可分映射与 Markov 映射之间的关系.
定义2.3 (参见文献 [13 ]) 设 $f\in PM(I,I)$, $S(f):=\{a_1,a_2,\cdots,a_m\}$ 且 $a_0=a, a_{m+1}=b$, 若 $E(f)=\{f^n(a_i)| n\in\mathbb{Z}^+, i=0,1,\cdots,m+1\}$ 是个有限集, 则称 $f$ 为 Markov 自映射.
接下来我们将给出可分映射与 Markov 映射之间的关系.
定理2.1 令 $f\in PM(I,I)$ 且定义在 (2.1) 式中, 则 $f$ 为 Markov 映射当且仅当对任意的 $i=0,1,\cdots,m$ 都有 $f_i$ 为 Markov 映射.
证 必要性. 由假设 $f$ 为 Markov 映射和定义 2.3 知 $E(f)$ 为有限集, 且对任意的 $i\in\{0,1,\cdots,m\}$ 都有 $x_i\in \mathcal{F}(f)$, 即 $\{f^n(x_i)| n\in\mathbb{Z}^+\}=\{x_i\}$, 故 $E(f_i)\subset E(f)\cup\{x_i,x_{i+1}\}$ 为有限集, 这意味着 $f_i:[x_i,x_{i+1}]\to[x_i,x_{i+1}]$ 为 Markov 映射.
充分性. 由假设对任意的 $i\in\{0,1,\cdots,m\}$ 都有 $f_i$ 为 Markov 映射, 可知 $E(f_i)$ 为有限集. 从而 $E(f)\subset\bigcup_{i=0}^{m}E(f_i)$ 为有限集. 即 $f$ 为 Markov 映射.
现令 $S^*(f):=S(f)\cup\{a, b\}$, 本文我们研究 $f(S^*(f))\subset S^*(f)$ 的可分映射的迭代, 显然 $f$ 也是 Markov 映射. 由定理 2.1 知可分 Markov 映射是由有限多个可拼接的 Markov 自映射构成, 而自映射的迭代仍在其定义的区间上, 故接下来我们只讨论这类自映射的迭代. 现令 $g\in PM(I,I)$ 为可拼接的 Markov 自映射, 其非单调点集
(2.2) $S(g)=\{c_1,c_2,\cdots,c_{N(g)}\} \mbox{满足} a=c_0<c_1<\cdots<c_{N(g)}<c_{N(g)+1}=b,$
其中 $N(g)$ 表示其非单调点的个数, 并不失一般性令 $I=[a,b]=[0,1]$. 那么显然 $g$ 由一系列分段单调映射组成, 即
(2.3) $g(x):=g_{i+1}(x), \forall x\in J_i:=[c_i,c_{i+1}], i=0,1,\cdots,N(g).$
$\mathcal{A}$ :=$\{g\in PM(I,I)|g \mbox{为 Markov 映射}, g(0)=0, g(1)\neq 1$ 或 $g(0)\neq 0, g(1)=1\}$,
$\mathcal{B}$ :=$\{g\in PM(I,I)|g \mbox{为 Markov 映射}, g(0)=0$ 且 $g(1)=1\}$.
3 $g\in\mathcal{A}$ 的情形
由于 $g\in\mathcal{A}$ 且 $g(0)=0$ 的情形与 $g\in\mathcal{A}$ 且 $g(1)=1$ 的情形可以通过一个反向同胚相互共轭, 因此我们首先考虑前一种情形并满足 $N(g)=1$. 令
(3.1) $\begin{matrix} g(x)= \begin{cases} g_1(x), & x\in J_0= [c_1], \\ g_2(x), & x\in J_1=[c_1,1]. \end{cases} \label{gA} \end{matrix}$
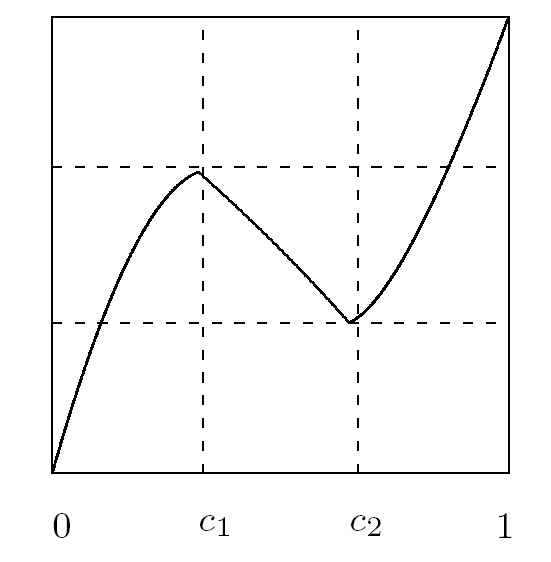
根据 $g$ 为 Markov 映射以及定义 2.3, $\mathcal{A}$ 中映射可以分为 (分别见图 3.1 -3.3 )
图3.1
图3.2
图3.3
下面我们将分别给出这 3 类映射的正整数 $n$ 次迭代的具体表达式.
定理3.1 若 $g\in\mathcal{A}_1$ 定义在 (3.1) 式中, 则对任意 $n\in\mathbb{Z}^+$ 有
(3.2) $\begin{matrix} g^n(x)= \begin{cases} {g_1}^n(x), & x\in J_0, \\ {g_1}^{n-1}\circ g_2(x), & x\in J_1. \end{cases} \label{gA1} \end{matrix}$
证 由假设 $g\in\mathcal{A}_1$ 知 $g_1(J_0)=J_0, g_2(J_1)=J_0$ 和 $g(c_1)=c_1$, 于是对任意 $n\in\mathbb{Z}^+$ 都有
从而 (3.2) 式为 $g\in\mathcal{A}_1$ 的 $n$ 次迭代.
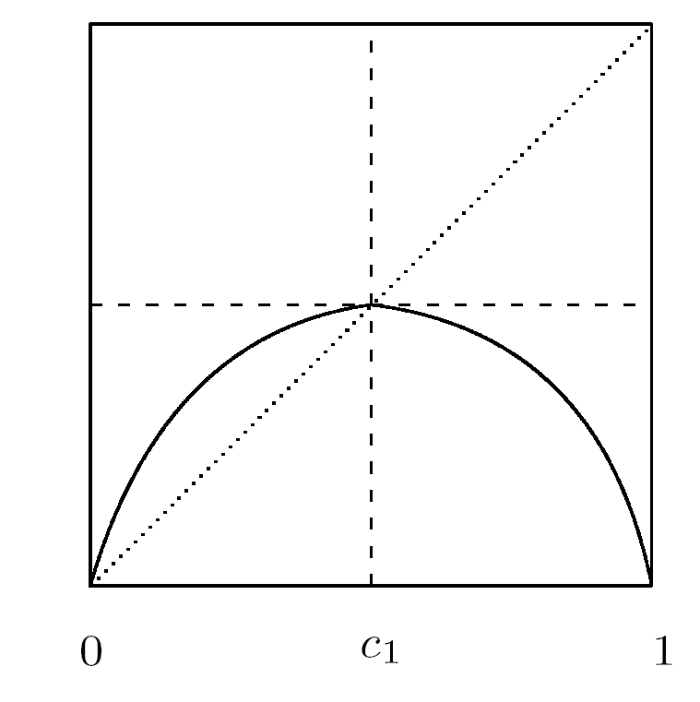
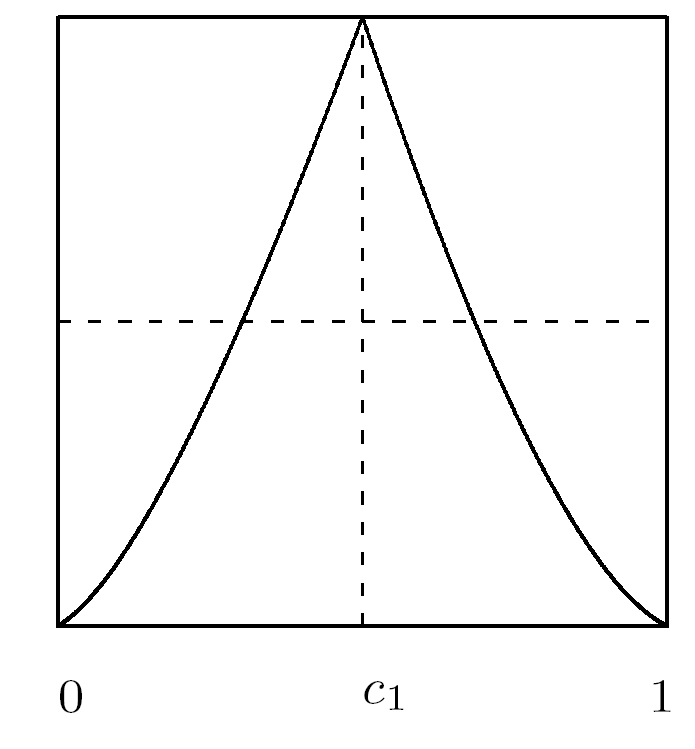
定理3.2 若 $g\in\mathcal{A}_2$ 定义在 (3.1) 式中, 且满足 $g_1,g_2$ 是 $C^1$ 和扩张的, 则对任意 $n\in\mathbb{Z}^+$ 有
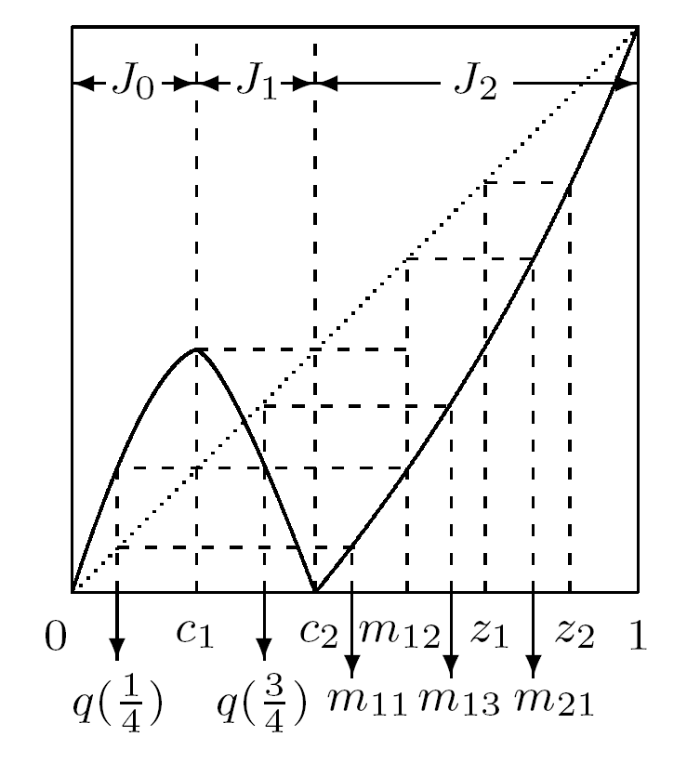
(3.3) $\begin{matrix} g^n(x)=q\big((-1)^i2^nq^{-1}(x)+(-1)^{i+1}2\big[\frac{i+1}{2}\big]\big), x\in [q(\frac{i}{2^n}), q(\frac{i+1}{2^n})], \label{gA2} \end{matrix}$
其中 $i=0,1,\cdots, 2^n-1$, $q$ 是满足共轭方程 $g\circ q=q\circ T$ 的保向同胚解以及
(3.4) $\begin{matrix} T(x)= \begin{cases} 2x, & x\in [\frac{1}{2}], \\ -2x+2, & x\in [\frac{1}{2},1]. \end{cases} \label{T} \end{matrix}$
证 由文献 [4 ,定理 2.7] 可知, 若 $g$ 满足假设条件, 则一定存在逐段线性映射 $T$ 与之拓扑共轭, 即共轭方程 $g\circ q=q\circ T$ 存在保向同胚解 $q:I\to I$, 其中 $T:I\to I$ 定义在 (3.4) 式中, 从而
(3.5) $\begin{matrix} g^n=q\circ T\circ q^{-1}\circ q\circ T\circ q^{-1}\circ\cdots\circ q\circ T\circ q^{-1}=q\circ T^n\circ q^{-1}. \label{gn} \end{matrix}$
至于映射 $T$ 的 $n$ 次迭代, 由文献 [7 ,引理 2.3] 有
(3.6) $\begin{matrix} S(T^n)=S(T)\cup\{x\in I| T(x)\in S(T^{n-1})\}. \label{STn} \end{matrix}$
特别地, 我们可以验证当 $n=2$ 时, $S(T^2)=\{\frac{1}{4},\frac{1}{2},\frac{3}{4}\}$, 于是归纳可得 $N(T^n)=2^n-1$ 以及 $S(T^n)=\{\frac{1}{2^n},\frac{2}{2^n},\cdots,\frac{2^n-1}{2^n}\}$, 并计算可得
其中 $\big[\frac{i+1}{2}\big]$ 表示对 $\frac{i+1}{2}$ 取整, 进一步将其代入 (3.5) 式即可得 (3.3) 式为 $g$ 的 $n$ 次迭代.
注3.1 若 $g\in\mathcal{A}_2$ 不满足在极大单调区间上扩张, 则其非单调点的原像在 $I$ 中未必稠密, 从而共轭方程 $g\circ q=q\circ T$ 的保向同胚解的存在性难以验证. 对于 $g\in\mathcal{A}_2$ 且 $g$ 更一般的情形, 其非单调点的存在情况在 $n$ 次迭代后就会变得非常复杂.
定理3.3 若 $g\in\mathcal{A}_3$ 且定义在 (3.1) 式中, 则对任意 $n\in\mathbb{Z}^+$ 有 $g^n(x)= {g_2}^{n-k}\circ {g_1}^k(x), x\in [\alpha_k,\alpha_{k-1}], k=0,1,\cdots,n,$ 其中 $\displaystyle \alpha_k=\begin{cases}g_1^{-k}(c_1), &k=0,1,\cdots n-1,\\ 0, &k=n.\end{cases}$
(3.7) $\begin{matrix} S(g^n)=\{\alpha_0,\alpha_1,\cdots,\alpha_{n-1}\}. \label{Sn} \end{matrix}$
由于 $g\in\mathcal{A}_3$, 故 $g(0)=0, g(c_1)=1, g(1)=c_1$, 从而可验证 $g(J_0)=I, g(J_1)=J_1$ 且 $g$ 分别在 $J_0$ 和 $J_1$ 上单调递增和递减. 故存在 $1\in J_1$ 和唯一 $\alpha_1=g_1^{-1}(c_1)\in J_0$ 使得 $g(1)=g(\alpha_1)=c_1$. 而 $1$ 是区间端点, 故由 (3.6) 式知
又因 $\alpha_1<c_1$ 且 $g$ 在 $J_0$ 上严格递增, 故存在唯一 $\alpha_2\in (0,\alpha_1)$ 使得 $g^2(\alpha_2)=g(\alpha_1)=c_1$, 即
从而利于归纳总结可证得断言成立. 特别地从证明过程中还有对任意 $k=1,2,\cdots,n-1$ 都有 $\alpha_k<\alpha_{k-1}$ 和 $g(\alpha_k)=\alpha_{k-1}$.
第二步: 利用 $S(g^n)$ 中的点划分区间并研究区间相关性质.
令 $J_{0_k}:=[\alpha_k,\alpha_{k-1}]$, 其中 $k=1,2,\cdots,n$, 则由 (3.7) 式和 $\alpha_n=0$ 知 $J_0=\bigcup_{k=1}^{n}J_{0_k}$. 当 $k=1$ 时, 由 $g(\alpha_1)=\alpha_0=c_1$ 和 $g(c_1)=1$ 知 $g(J_{0_1})=J_1$. 当 $k\in\{2,3,\cdots,n-1\}$ 时, 由 $g(\alpha_k)=\alpha_{k-1}$ 我们有
(3.8) $\begin{matrix} g(J_{0_k})=J_{0_{k-1}} \mbox{以及} g^k(J_{0_k})=\cdots=g(J_{0_{1}})=J_1. \label{J0k} \end{matrix}$
当 $k=n$ 时, 由 $g(0)=0$ 知 $g(J_{0_n})=g([\alpha_n,\alpha_{n-1}])=g([\alpha_{n-1}])=[\alpha_{n-2}]$, 进而
(3.9) $\begin{matrix} g^n(J_{0_n})=g^{n-1}([\alpha_{n-2}])=\cdots=g([\alpha_0])=g(J_0). \label{J0n} \end{matrix}$
首先由 $g(J_1)=J_1$ 知对任意 $x\in J_1$ 有 $g^n(x)= g_2^n(x)$. 当 $k=1$ 时, 由第二步中 $g(J_{0_1})=J_1$ 知对任意 $x\in J_{0_1}$ 有$g^n(x)=g^{n-1}\circ g(x)=g_2^{n-1}\circ g_1(x)$. 当 $k\in\{2,3,\cdots,n-1\}$ 时, 由 (3.8) 式可知对任意 $x\in J_{0_k}$ 有 $g^n(x)=g_2^{n-k}\circ g_1^k(x)$. 当 $k=n$ 时, 由 (3.9) 式可知对任意 $x\in J_{0_n}$ 有 $g^n(x)= g_1^n(x)$. 由上我们可归纳总结为
(3.10) $\begin{matrix} g^n(x)= {g_2}^{n-k}\circ {g_1}^k(x), \forall x\in [\alpha_k,\alpha_{k-1}], k=0,1,\cdots,n. \label{gnA3} \end{matrix}$
其次易验证 $ I=J_0\cup J_1=\textstyle\bigcup_{k=1}^nJ_{0_k}\cup J_1, $ 从而 (3.10) 式即为 $g\in\mathcal{A}_3$ 的 $n$ 次迭代.
定理 3.1-3.3 得到了当 $g\in\mathcal{A}$ 满足 $g(0)=0$ 且 $g(1)\ne 1$ 时 $g$ 的迭代的具体表达式. 接下来我们利用共轭的方法给出 $h\in\mathcal{A}$ 满足 $h(0)\ne 0$ 且 $h(1)=1$ 时 $h$ 的迭代.
注3.2 现给定任意映射 $h\in\mathcal{A}$ 且 $h(1)=1$, 其非单调点集为 $S(h)=\{d_1,d_2,\cdots,d_{N(h)}\}$ 以及 $d_0=0$, $d_{N(h)+1}=1$. 令 $ g(x):=\phi^{-1}\circ h\circ \phi(x), \forall x\in [0,1], $ 其中 $\phi(x)=1-x$, 即 $g(x)=1-h(1-x)$. 首先易验证 $g(0)=0$ 以及对任意 $i=0,1,\cdots,N(h)+1$ 都有 $c_i:=1-d_i$ 为 $g$ 的所有非单调点和端点. 其次由 $h$ 是 Markov 映射我们知道所有 $d_i$ 在 $h$ 作用下的正半轨是有限的, 那么由 $g(c_i)=1-h(d_i)$ 知 $c_i$ 在 $g$ 作用下的正半轨也是有限的, 即 $g\in\mathcal{A}$ 且满足定理 3.1-3.3, 进而
4 $g\in\mathcal{B}$ 的情形
接下来讨论 $g\in\mathcal{B}$ 的情形, 即 $g$ 是一个可拼接的 Markov 映射且满足 $g(0)=0$ 和 $g(1)=1$. 若 $g$ 定义在 (2.3) 式中, 则由 $g(0)=0$ 知 $g$ 在 $J_0=[c_1]=[c_0,c_1]$ 上单调递增. 又因为 $g(1)=1$, 所以 $g$ 在 $J_{N(g)}=[c_{N(g)},1]$ 上也单调递增, 这暗示了 $N(g)$ 为一个偶数. 因此我们讨论 $g\in\mathcal{B}$ 且 $N(g)=2$ 的情形, 即 $S(g):=\{c_1, c_2\}$. 令
(4.1) $\begin{matrix} g(x)= \begin{cases} g_1(x), & x\in J_0:=[c_1], \\ g_2(x), & x\in J_1:=[c_1,c_2], \\ g_3(x), & x\in J_2:=[c_2,1]. \end{cases} \label{gB} \end{matrix}$
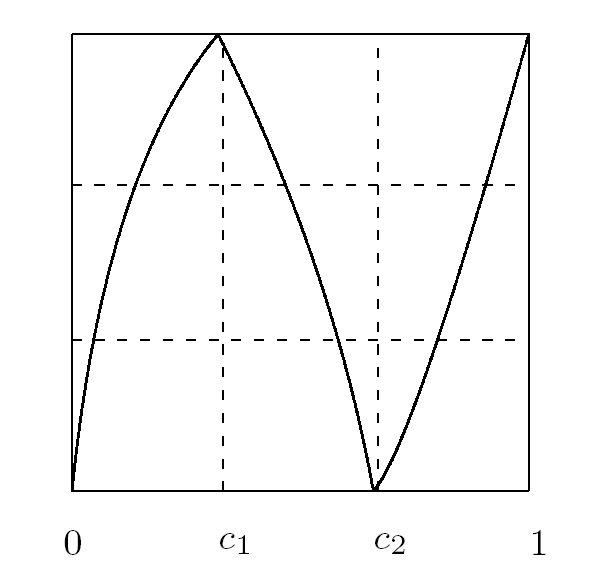
根据 $g$ 为 Markov 映射以及定义 2.3, $\mathcal{B}$ 中映射可以分为 (分别见图 4.1 -4.4 )
图4.1
图4.2
图4.3
图4.4
下面我们将分别给出这 4 类映射的正整数 $n$ 次迭代.
定理4.1 若 $g\in\mathcal{B}_1$ 定义在 (4.1) 式中且 $g(c_1)=c_1$, 则对任意 $n\in\mathbb{Z}^+$ 有
(4.2) $\begin{matrix} g^n(x)= \left\{ \begin{array}{ll} {g_1}^n(x), & x\in [c_1], \\ {g_1}^{n-1}\circ g_2(x), & x\in [c_1,c_2], \\ {g_1}^{n-k}\circ {g_3}^k (x),& x\in [\alpha_{2k-2},\alpha_{2k-1}], \\ {g_1}^{n-1-k}\circ g_{2}\circ {g_3}^k (x),\quad & x\in [\alpha_{2k-1},\alpha_{2k}], \\ {g_3}^n(x), & x\in [\alpha_{2n-2},1], \end{array}\right. \label{gnB1} \end{matrix}$
其中对所有 $k=0,1,\cdots n-1$ 有 $\alpha_{2k-1}={g_3}^{-k}(c_1)$ 和 $\alpha_{2k}={g_3}^{-k}(c_2)$.
(4.3) $\begin{matrix} S(g^n)=\{\alpha_{-1},\alpha_0,\alpha_1,\alpha_2,\cdots,\alpha_{2n-2}\}. \label{Sn1} \end{matrix}$
在假设 $g\in\mathcal{B}_1$ 下我们可验证
(4.4) $\begin{matrix} g(J_0)=J_0, g(J_1)=J_0, g(J_2)=I \label{gJ} \end{matrix}$
且 $g$ 在 $J_0$ 和 $J_2$ 上递增, 在 $J_1$ 上递减, 那么一定唯一存在 $\alpha_1=g_3^{-1}(c_1)\in J_2$ 和 $\alpha_2=g_3^{-1}(c_2)\in J_2$ 使得$g(\alpha_1)=c_1, g(\alpha_2)=c_2$. 此外由 $g$ 在 $J_2$ 上单调递增我们有 $\alpha_1<\alpha_2$, 从而由 (3.6) 式知
又因 $\alpha_{-1}<\alpha_0<\alpha_1<\alpha_2$ 且 $g([\alpha_1,\alpha_2])=[c_1,c_2]$, 故由 (4.4) 式知存在唯一 $\alpha_3, \alpha_4\in (\alpha_2, 1)\subset J_2$ 使得 $g^2(\alpha_3)=g(\alpha_1)=c_1, g^2(\alpha_4)=g(\alpha_2)=c_2$, 同样易验证 $\alpha_3<\alpha_4$ 以及
从而归纳可得断言成立. 此外从证明过程中还知对任意 $k=1,2,\cdots,2n-2$ 有
(4.5) $\begin{matrix} \alpha_{k-1}<\alpha_k \mbox{且} g(\alpha_k)=\alpha_{k-2}. \label{ga} \end{matrix}$
第二步: 利用 $S(g^n)$ 中的点划分区间并研究区间相关性质.
令 $J_{2_k}:=[\alpha_k,\alpha_{k+1}]$, 其中 $k=0,1,\cdots,2n-3$, 则由 (4.3) 式知 $J_2=\big(\bigcup_{k=0}^{n}J_{2_k}\big)\cup [\alpha_{2n-2},1]$. 当 $k=0$ 时, 由 $g(\alpha_0)=0$ 和 $g(\alpha_1)=c_1$ 可知 $g(J_{2_0})=J_0$. 当 $k=1$ 时, 由 $g(\alpha_1)=c_1$ 和 $g(\alpha_2)=c_2$ 知 $g(J_{2_1})=J_1$. 当 $k\in\{2,3,\cdots,2n-3\}$ 时, 由 (4.5) 式有 $g(J_{2_k})=J_{2_{k-2}}$ 以及
(4.6) $\begin{matrix} g^j(J_{2_{2j-2}})=\cdots=g(J_{2_0})=J_0, g^j(J_{2_{2j-1}})=\cdots=g(J_{2_1})=J_1. \label{J0k1} \end{matrix}$
其中 $j=1,2,\cdots,n-1$. 此外当 $x\in[\alpha_{2n-2},1]$ 时, 由 $g\in\mathcal{B}_1$ 知 $g(1)=1$, 从而
(4.7) $\begin{matrix} g^n([\alpha_{2n-2},1])=g^{n-1}([\alpha_{2n-4},1])=\cdots=g([\alpha_0,1])=g(J_2). \label{J0n1} \end{matrix}$
首先由 (4.4) 式有对任意 $x\in J_0$ 有 $g^n(x)= g_1^n(x)$; 对任意 $x\in J_1$ 有 $g^n(x)= g_1^{n-1}\circ g_2(x)$.
当 $k=0$ 时, 由 $g(J_{2_0})=J_0$ 知对任意 $x\in J_{2_0}$ 有 $g^n(x)=g^{n-1}\circ g(x)=g_1^{n-1}\circ g_3(x)$.
当 $k=1$ 时, 由 $g(J_{2_1})=J_1$ 知对任意 $x\in J_{2_1}$ 有 $g^n(x)=g^{n-1}\circ g(x)=g_1^{n-2}\circ g_2\circ g_3(x)$.
当 $k=2j-2, j\in\{1,2,\cdots,n-1\}$ 时, 由 (4.6) 式知对任意 $x\in J_{2_{2j-2}}$ 有 $g^n(x)=g_1^{n-j}\circ g_3^j(x)$.
当 $k=2j-1, j\in\{1,2,\cdots,n-1\}$ 时, 由 (4.6) 式知对任意 $x\in J_{2_{2j-1}}$ 有 $g^n(x)=g_1^{n-j-1}\circ g_2\circ g_3^j(x)$.
当 $x\in[\alpha_{2n-2},1]$ 时, 由 (4.7) 式知对任意 $x\in [\alpha_{2n-2},1]$ 有$g^n(x)= g_3^n(x)$.
从而 (4.2) 式就是 $g\in\mathcal{B}_1$ 时的 $n$ 次迭代.
类似于注记 3.2, $f\in\mathcal{B}_1$ 且 $f(c_2)=c_2$ 时的情形可通过共轭转化为 $g\in\mathcal{B}_1$且$g(c_1)=c_1$ 时的情形得到其整数次迭代.
定理4.2 若 $g\in\mathcal{B}_2$ 且定义在 (4.1) 式中, 则对任意 $n\in\mathbb{Z}^+$ 有
(4.8) $\begin{matrix} g^n(x)= \left\{ \begin{array}{ll} {g_2}^{n-k}\circ {g_1}^k(x),\quad & x\in [\alpha_{1_{k+1}},\alpha_{1_k}], \\ {g_2}^n(x), & x\in [c_1,c_2], \\ {g_2}^{n-k}\circ {g_3}^k(x), & x\in [\alpha_{2_k},\alpha_{2_{k+1}}], \end{array}\right. \label{4.2} \end{matrix}$
其中当 $k=0,1,\cdots, n-1$ 时 $\alpha_{1_k}={g_1}^{-k}(c_1)$, $\alpha_{2_k}={g_3}^{-k}(c_2)$, 当 $k=n$ 时 $\alpha_{1_n}=0, \alpha_{2_n}=1$.
由 $g\in\mathcal{B}_2$ 知 $g(J_1)=J_1$ 且 $g$ 在 $J_1$ 上单调递减, 故不存在 $x_0\in (c_1,c_2)$ 使得 $g(x_0)=c_1$ 或 $ c_2$. 此外还有 $g(J_0)=J_0\cup J_1$, $g(J_2)=J_1\cup J_2$, 则存在唯一 $\alpha_{1_1}\in J_0$ 使得 $g_1(\alpha_{1_1})=c_1$ 和唯一 $\alpha_{2_1}\in J_2$ 使得 $g_3(\alpha_{2_1})=c_2$, 进而类似于定理 3.3 证明过程第一步可得
(4.9) $\begin{matrix} S(g^n)=\{\alpha_{1_0},\alpha_{1_1},\cdots,\alpha_{1_{n-1}}, \alpha_{2_0},\alpha_{2_1},\cdots,\alpha_{2_{n-1}} \} \label{4.21} \end{matrix}$
满足 $0=\alpha_{1_n}<\alpha_{1_{n-1}}<\cdots<\alpha_{1_1}<\alpha_{1_0}=c_1<c_2=\alpha_{2_0}<\alpha_{2_1}<\cdots<\alpha_{2_{n-1}}<\alpha_{2_n}=1$ 以及当 $k=1,2\cdots,n-1$ 时有 $g_1(\alpha_{1_k})=\alpha_{1_{k-1}}$ 和 $g_3(\alpha_{2_k})=\alpha_{2_{k-1}}$.
第二步: 利用 $S(g^n)$ 中的点划分区间并研究区间相关性质.
令 $J_{0_k}:=[\alpha_{1_k},\alpha_{1_{k-1}}], J_{2_k}:=[\alpha_{2_{k-1}},\alpha_{2_k}]$, 其中 $k=1,2,\cdots,n$. 由 (4.9) 知 $J_0=\bigcup_{k=1}^{n}J_{0_k}$ 和 $J_2=\bigcup_{k=1}^{n}J_{2_k}$. 此外由 $g_1(\alpha_{1_k})=\alpha_{1_{k-1}}$ 和 $g_3(\alpha_{2_k})=\alpha_{2_{k-1}}$ 可得
(4.10) $g_1(J_{1_k})=J_{1_{k-1}} \mbox{以及} g_1^k(J_{0_k})=g_1^{k-1}(J_{0_{k-1}})=\cdots=J_1,$
(4.11) $g_3(J_{2_k})=J_{2_{k-1}} \mbox{以及} g_3^k(J_{2_k})=g_3^{k-1}(J_{2_{k-1}})=\cdots=J_1,$
其中 $k=1,2,\cdots,n-1$. 特别地, 当 $k=n$ 时,
(4.12) $g_1^n(J_{0_n})=g_1(J_0), g_3^n(J_{2_n})=g_3(J_2).$
类似于定理 3.3 证明过程第三步可得: 当 $x\in J_0$ 时, 由 (4.10) 和 (4.12) 知对任意 $x\in[\alpha_{1_{k}},\alpha_{1_{k-1}}]$ 和任意 $k=1,2,\cdots,n$ 有 $g^n(x)={g_2}^{n-k}\circ {g_1}^k(x)$. 当 $x\in J_1$ 时, 由 $g(J_1)=J_1$ 知对任意 $x\in J_1$ 有 $g^n(x)=g_2^n(x)$. 当 $x\in J_2$ 时, 由 (4.11) 和 (4.12) 式知对任意 $x\in[\alpha_{2_{k-1}},\alpha_{2_k}]$ 和任意 $k=1,2,\cdots,n$ 有 $g^n(x)={g_2}^{n-k}\circ {g_3}^k(x)$. 其次易验证
从而 (4.8) 式就是 $g\in\mathcal{B}_2$ 时的 $n$ 次迭代.
定理4.3 若 $g\in\mathcal{B}_3$ 定义在 (4.1) 式中满足 $g_1,g_2,g_3$ 是 $C^1$ 且扩张的, 则对任意 $n\in\mathbb{Z}^+$ 有
其中 $i=0,1,\cdots, 3^n-1$, $q$ 是满足共轭方程 $g\circ q=q\circ T$ 的保向同胚解以及
定理4.4 若 $g\in\mathcal{B}_4$ 定义在 (4.1) 式中满足 $g(c_1)=c_2, g(c_2)=0$ 且 $g_1,g_2$ 是 $C^1$ 并扩张的, 则对任意 $n\in\mathbb{Z}^+$ 有
其中 $k=0,1,\cdots, 2^n-1$, $q$ 定义在定理 $3.2$ 中并且 $m_{i_j}=g_3^{-i}\circ q(\frac{j}{2^{n-i}})$, $i=1,2,\cdots,n-1, j=0,1,\cdots, 2^{n-i}-1$.
证 令 $h:=g|_{J_0\cup J_1}$, 则易验证 $h$ 为自映射且满足定理 3.2, 从而可得其在 $J_0\cup J_1$ 上的 $n\in\mathbb{Z}^+$ 次迭代.
故接下来我们主要考虑 $g$ 在 $J_2$ 上的非单调点情况.
由于 $g(J_0\cup J_1)=J_0\cup J_1$, $g(J_2)=I$ 且 $g$ 在 $J_2$ 上单调递增, 故与定理 4.1 中证明的第一步 $\alpha_k$ 且 $k$ 为偶数时的生成方式一致 (如图 4.5 , $z_1$ 为 $c_2$ 的一个原像, $z_1$ 的原像只会在其右侧产生为 $z_2$), 存在点列
以及 $g^i([z_{i-1},z_i])=g^{i-1}([z_{i-2},z_{i-1}])=\cdots=[c_2]$. 于是可初步得到
然而与定理 4.1 不一致的是 $c_1$ 不仅会在 $J_2$ 产生原像, 还会在 $J_0$ 和 $J_1$ 上产生, 而 $J_0$ 和 $J_1$ 上的点在 $J_2$ 上亦有原像 (如图 4.5 , $c_2$ 的原像为 $c_1$ 和 $z_1$, 而 $c_1$ 的原像有 $q(\frac{1}{4}), q(\frac{3}{4})$ 和 $m_{12}$), 故增加了定理证明的困难. 接下来我们就考虑这些新产生的非单调点. 由定理 3.2 可知,
图4.5
图4.5
$z_i$ 与 $m_{ij}$ 的生成
其中 $j=0,1,\cdots,2^{n-i}-1$, 从而有 $S(g^{n-i})\cap(0,c_2)=\{q(\frac{j}{2^{n-i}})|j=1,2,\cdots,2^{n-i}-1\}$. 又因为对任意 $i=1,2,\cdots,n-1$ 都有 $g^i([z_{i-1},z_i])=g_3^i([z_{i-1},z_i])=[c_2]$, $g(J_2)=I$ 且 $g$ 在 $J_2$ 上单调递增, 故一定存在唯一 $m_{i_j}\in[z_{i-1},z_i]$ 使得 $g^i(m_{ij})=q(\frac{j}{2^{n-i}})$, 即 $m_{i_j}=g_3^{-i}\circ q(\frac{j}{2^{n-i}})$. 利用单调性易验证点列满足
且 $g^i([m_{i_j},m_{i_{j+1}}])=[q(\frac{j}{2^{n-i}}),q(\frac{j+1}{2^{n-i}})]$, 从而有
其中 $j=1,2,\cdots,2^{n-i}-1$. 此外类似于 (3.9) 式, 由 $g(1)=1$ 和当 $i=1,2,\cdots,n-1$ 时有 $g(z_i)=z_{i-1}$ 知当 $x\in[z_{n-1},1]$ 时, $g^n(x)=g_3^n(x)$. 得证.
类似于注记 3.2, $f\in\mathcal{B}_4$ 且 $f(c_1)=1,f(c_2)=c_1$ 的情形可通过共轭转化为 $g\in\mathcal{B}_4$ 且 $g(c_1)=c_2,\,g(c_2)=0$ 时的情形得到其整数次迭代.
5 可分映射的迭代及举例
由定义 2.1 可知, 可分映射可以划分为有限多个可拼接自映射, 从而其迭代可以转化这些自映射的迭代. 而一类特殊的 Markov 可拼接映射的迭代在第 3 节和第 4 节已经给出, 故接下来我们将用一个例子刻画可分映射的迭代.
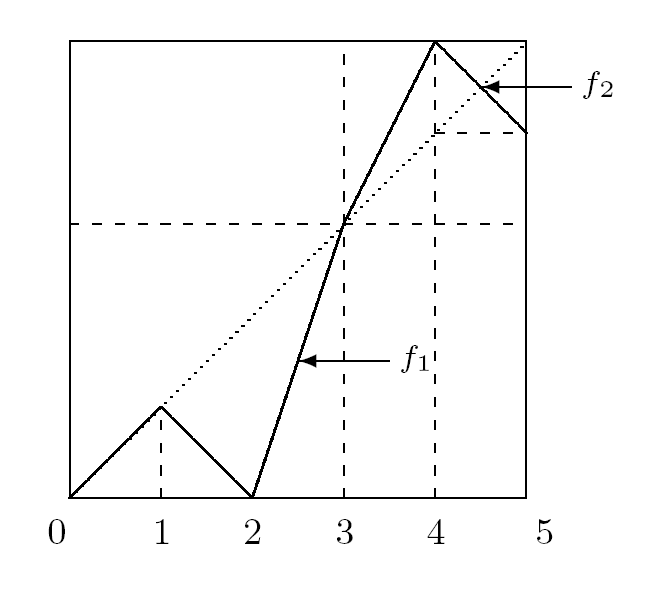
易验证 $f(3)=3$ 以及 $f([0,3])\subset[0,3]$ 和 $f([3,5])\subset[3,5]$. 则由定义 $2.1$ 可知 $f$ 为可分映射, $x=3$ 为其可分不动点且可分为可拼接自映射. 令 $f_1=f|_{[0,3]}$ 和 $f_2=f|_{[3,5]}$, 则 $f_1\in\mathcal{B}_1, f_2\in\mathcal{A}_3$ (见图 5.1 ). 接下来我们分别计算 $f_1$ 和 $f_2$ 的迭代. 首先易验证 $f_1\in\mathcal{B}_1$ 且 $S(f_1)=\{c_1:=1,c_2:=2\}$, 则由定理 $4.1$ 的断言 (4.3) 式可知 $S(f_1^3)=\{\alpha_{-1},\alpha_0, \alpha_1, \alpha_2, \alpha_3, \alpha_4\}$ 且满足
图5.1
于是利用定理 $4.1$ 可得其 $3$ 次迭代. 其次易验证 $f_2\in\mathcal{A}_3$ 且 $S(f_2)=\{4\}$, 类似利用定理 $3.3$ 有 $S(f_2^3)=\{\alpha_0=4, \alpha_1=\frac{7}{2}, \alpha_2=\frac{13}{4}\}$, 进而可得其 $3$ 次迭代. 综上可得 $f$ 的 $3$ 次迭代结果为
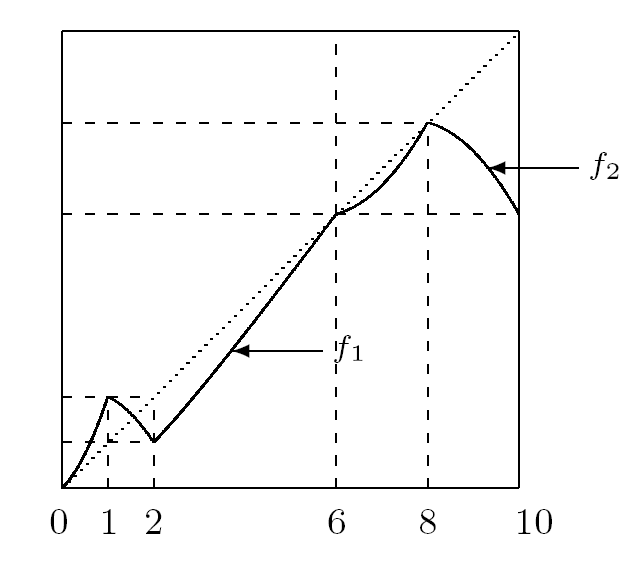
易验证 $f(6)=6$ 以及 $f([0,6])\subset[0,6]$ 和 $f([6,8])\subset[6,8]$. 则由定义 $2.1$ 可知 $f$ 为可分映射, $x=6$ 为其可分不动点且可分为可拼接自映射. 令 $f_1=f|_{[0,6]}$ 和 $f_2=f|_{[6,8]}$, 则 $f_1\in\mathcal{B}_2, f_2\in\mathcal{A}_1$ (见图 5.2 ). 接下来我们分别计算 $f_1$ 和 $f_2$ 的迭代. 首先易验证 $f_1\in\mathcal{B}_2$ 且 $S(f_1)=\{c_1:=1,c_2:=2\}$, 则由定理 4.2 的断言 (4.9) 式可知 $S(f_1^3)=\{\alpha_{1_0}, \alpha_{1_1}, \alpha_{1_2}, \alpha_{2_0}, \alpha_{2_1}, \alpha_{2_2}\}$ 且满足
图5.2
于是利用定理 4.2 可得其 $3$ 次迭代. 其次易验证 $f_2\in\mathcal{A}_1$ 且 $S(f_2)=\{8\}$, 利用定理 3.1 可得其 $3$ 次迭代. 综上可得 $f$ 的 $3$ 次迭代结果为
参考文献
View Option
[1]
Blokh L Coven E Topological conjugacy and transitivity for a class of piecewise monotone maps of the interval
Tran Am Math Soc , 1987 , 300 297 -306
[本文引用: 1]
[2]
Bugiel P A note on invariant measures for Markov maps of an interval
Z Wahrscheinlichkeitstheor Verw Geb , 1985 , 70 345 -349
[本文引用: 1]
[3]
Bugiel P Ergodic properties of Markov maps in $R^d$
Probab Th Rel , 1991 , 88 483 -496
[本文引用: 1]
[4]
Fotiades N Boudourides M Topological conjugacies of piecewise monotone interval maps
Int J Math Math Sci , 2001 , 25 119 -127
[本文引用: 1]
[5]
Galeeva R Martens M Tresser C Inducing, slopes, and conjugacy classes
Isr J Math , 1997 , 99 123 -147
[本文引用: 1]
[6]
Kuczma M Functional Equations in a Single Variable . Warsaw: Państwowe Wydawnictwo Naukowe , 1968
[本文引用: 1]
[7]
Liu L Jarczyk W Li L Zhang W Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2
Nonlinear Anal, 2012 , 75 1 ): 286 -303
[本文引用: 1]
[8]
Marčenko V Questions on mathematical physics and functional analysis . Kiev: Naukova Dumka , 1976
[本文引用: 1]
[9]
Milnor J Thurston W On iterated maps of the interval
Lecture Notes in Math , 1988 , 1342 465 -563
[本文引用: 1]
[10]
Reich L Smítal J Targoński G Iteration Theory . Graz: Karl-Franzens-Universität Graz , 1997
[本文引用: 1]
[11]
Rufus B Invariant measures for Markov maps of the interval
Commun Math Phys , 1979 , 69 1 -17
[本文引用: 1]
[12]
Shi Y Chen L Extension of iterative roots
Aequationes Math , 2015 , 89 3 ): 485 -495
[本文引用: 1]
[13]
孙太翔 . 区间上满的扩张 Markov 自映射的迭代根
纯粹数学与应用数学 , 2001 , 17 2 ): 99 -103
[本文引用: 2]
Sun T X Iterative roots of expanding Markov surjective self-maps on intervals
Pure Appl Math , 2001 , 17 2 ): 99 -103
[本文引用: 2]
[14]
Takano K On the iteration of holomorphic mappings
Funkcial Ekvac , 1974 , 17 107 -156
[本文引用: 1]
[15]
唐肖 , 李林 . 非特征端点条件下 PM 函数的迭代根
数学物理学报 , 2022 , 42A 2 ): 557 -569
[本文引用: 1]
Li L Characteristic endpoints question for piecewise monotone functions
Acta Math Sci , 2022 , 42A 2 ): 557 -569
[本文引用: 1]
[16]
Targoński G Progress of iteration theory since 1981
Aeq Math, 1995 , 50 50 -72
[本文引用: 1]
[17]
Yu Z Yang L Zhang W Discussion on polynomials having polynomial iterative roots
J Symbolic Comput , 2012 , 47 10 ): 1154 -1162
[本文引用: 1]
[18]
张景中 , 杨路 . 论逐段单调连续函数的迭代根
数学学报 , 1983 , 26 4 ): 398 -412
DOI:10.12386/A1983sxxb0043
[本文引用: 1]
设E是一个集,f和g是将E映射到自身的函数.f~og表示f和g的复合函数(f~og)(x)=f(g(x)),x∈E.f的迭代函数f~n的定义是 f~o(x)=x,f~(n+1)=fof~n,n=0,1,2,….如果对一个整数r≥2和一切x∈E成立着 f~r=g,我们就说f是g的一个r阶的迭代根. 关于迭代根的研究至少可以上溯到Abel,甚至更早的Babbage.多年以来这问题一直引起许多作者的注意.1950年R.Isaacs在一篇精辟的论文中完成了一个奠基
Zhang J Z Yang L Iterative roots of a piecewise monotone continuous self-mapping
Acta Math Sinica , 1983 , 26 4 ): 398 -412
DOI:10.12386/A1983sxxb0043
[本文引用: 1]
设E是一个集,f和g是将E映射到自身的函数.f~og表示f和g的复合函数(f~og)(x)=f(g(x)),x∈E.f的迭代函数f~n的定义是 f~o(x)=x,f~(n+1)=fof~n,n=0,1,2,….如果对一个整数r≥2和一切x∈E成立着 f~r=g,我们就说f是g的一个r阶的迭代根. 关于迭代根的研究至少可以上溯到Abel,甚至更早的Babbage.多年以来这问题一直引起许多作者的注意.1950年R.Isaacs在一篇精辟的论文中完成了一个奠基
[19]
张萍萍 , 李林 . 上半连续集值函数的区间迭代
数学物理学报 , 2016 , 36A 2 ): 231 -243
[本文引用: 1]
Li L Iteration of upper semi-continuous multifunctions on interval
Acta Math Sci , 2016 , 36A 2 ): 231 -243
[本文引用: 1]
Topological conjugacy and transitivity for a class of piecewise monotone maps of the interval
1
1987
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
A note on invariant measures for Markov maps of an interval
1
1985
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
Ergodic properties of Markov maps in $R^d$
1
1991
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
Topological conjugacies of piecewise monotone interval maps
1
2001
... 证 由文献 [4 ,定理 2.7] 可知, 若 $g$ 满足假设条件, 则一定存在逐段线性映射 $T$ 与之拓扑共轭, 即共轭方程 $g\circ q=q\circ T$ 存在保向同胚解 $q:I\to I$, 其中 $T:I\to I$ 定义在 (3.4) 式中, 从而 ...
Inducing, slopes, and conjugacy classes
1
1997
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
1
1968
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
Iterative roots of piecewise monotonic functions of nonmonotonicity height not less than 2
1
2012
... 至于映射 $T$ 的 $n$ 次迭代, 由文献 [7 ,引理 2.3] 有 ...
1
1976
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
On iterated maps of the interval
1
1988
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
1
1997
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
Invariant measures for Markov maps of the interval
1
1979
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
Extension of iterative roots
1
2015
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
区间上满的扩张 Markov 自映射的迭代根
2
2001
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
... 定义2.3 (参见文献 [13 ]) 设 $f\in PM(I,I)$, $S(f):=\{a_1,a_2,\cdots,a_m\}$ 且 $a_0=a, a_{m+1}=b$, 若 $E(f)=\{f^n(a_i)| n\in\mathbb{Z}^+, i=0,1,\cdots,m+1\}$ 是个有限集, 则称 $f$ 为 Markov 自映射. ...
区间上满的扩张 Markov 自映射的迭代根
2
2001
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
... 定义2.3 (参见文献 [13 ]) 设 $f\in PM(I,I)$, $S(f):=\{a_1,a_2,\cdots,a_m\}$ 且 $a_0=a, a_{m+1}=b$, 若 $E(f)=\{f^n(a_i)| n\in\mathbb{Z}^+, i=0,1,\cdots,m+1\}$ 是个有限集, 则称 $f$ 为 Markov 自映射. ...
On the iteration of holomorphic mappings
1
1974
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
非特征端点条件下 PM 函数的迭代根
1
2022
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
非特征端点条件下 PM 函数的迭代根
1
2022
... 近几十年来, 学者们围绕逐段单调映射展开了对其相关性质的大量研究, 其中满足所有非单调点和区间端点的走出的轨道是有限的 Markov 映射就是一类特殊的这样的映射. 1979 年 Rufus[11 ] 研究了 Markov 映射并给出了其严格定义. 随后在 1985 年, Bugiel[2 ] 给出了满足扩张条件的两个 Markov 映射的例子. 1987 年 Blokh[1 ] 进一步研究了线性 Markov 映射的共轭问题. 近些年来, 对于 Markov 映射可测性, 扩张性以及其迭代根的研究也取得一些进展[3 ],[5 ],[12 ],[13 ],[15 ] . ...
Progress of iteration theory since 1981
1
1995
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
Discussion on polynomials having polynomial iterative roots
1
2012
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
论逐段单调连续函数的迭代根
1
1983
... 给定映射 $f:I:=[a,b]\to I$, 如果 $f$ 在 $x_0\in I$ 的小邻域内严格单调, 则称 $x_0$ 为 $f$ 的 "单调点", 否则为 $f$ 的 "非单调点" (参见文献 [18 ]). 令集合 $PM(I,I)$ 表示定义在区间 $I$ 上的所有具有有限多非单调点的连续自映射, $S(f)$ 为 $f\in PM(I,I)$ 的所有非单调点集合. 下面给出可分映射与可拼接映射的定义. ...
论逐段单调连续函数的迭代根
1
1983
... 给定映射 $f:I:=[a,b]\to I$, 如果 $f$ 在 $x_0\in I$ 的小邻域内严格单调, 则称 $x_0$ 为 $f$ 的 "单调点", 否则为 $f$ 的 "非单调点" (参见文献 [18 ]). 令集合 $PM(I,I)$ 表示定义在区间 $I$ 上的所有具有有限多非单调点的连续自映射, $S(f)$ 为 $f\in PM(I,I)$ 的所有非单调点集合. 下面给出可分映射与可拼接映射的定义. ...
上半连续集值函数的区间迭代
1
2016
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...
上半连续集值函数的区间迭代
1
2016
... 其中 $n$ 为正整数, 称 $f^n$ 为 $f$ 的 $n$ 次迭代. 迭代是自然界和人类生活中的普遍现象. 许多物理, 力学, 生物学以及天文学问题的数学模型都是通过迭代描述, 因此研究迭代具有十分重要的意义, 迭代理论也日渐丰富[6 ],[16 ] . 近几十年来, 学者们关心特殊映射的迭代, 比如形式幂级数[8 ] , 全纯映射[14 ] , 多项式函数[17 ] , 集值函数[19 ] 等. 1988 年, Milnor[9 ] 提出了一种描述区间上分段单调映射连续迭代定性行为的演算方法. 此外 Reich 等[10 ] 总结了包括周期循环, 迭代映射的随机扰动等许多与迭代相关的内容. ...