在欧几里得空间 $\mathbb{R}^{3}$ 中, 本文研究带引力项的定常可压缩 Euler 方程组^[1],[6]

其中 $\rho,\ p,\ e$ 分别是流体的密度、压力和内能, $\textbf{u}=(u_{1},u_{2},u_{3})$ 为流体的速度向量, $\textbf{I}$ 为单位张量, $\textbf{F}$ 为单位质量流体所受引力. 对于多方理想气体, 状态方程为 $p(\rho,S)=A(S)\rho^{\gamma}$, $e=\frac{p}{(\gamma-1)\rho}$, $S$ 为熵, 绝热指数 $\gamma>1$. $A(S)=k\text{exp}(\frac{S}{c_{v}})$, $k$ 和 $c_{v}$ 为已知的正常数. 为便于计算, 令 $k=c_{v}=1$. 引力方向指向原点, 流体运动方向与引力方向相反, 于是 $\textbf{F}=-\frac{mG}{r^{3}}\textbf{r}=\nabla\frac{mG}{r}$, 其中 $\textbf{r}=(x,y,z)$, $r=|\textbf{r}|=\sqrt{x^{2}+y^{2}+z^{2}}$ 为流体到地心的距离, $m$ 为地球质量, $G$ 为万有引力常数 (为了方便, 记 $K=mG$). 于是 (1.1) 可改写为

这里 "$\text{div}$" 和 "$\nabla$" 是笛卡尔坐标系 $(x,y,z)$ 下的散度和梯度算子, 其中 $\textbf{u}\otimes\textbf{u}$ 为速度向量的张量积, Bernoulli 函数 $B=\frac{1}{2}|\textbf{u}|^{2}+\frac{\gamma}{\gamma-1}\frac{p}{\rho}$ ($|\textbf{u}|=\sqrt{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}}$). 为研究定常可压缩 Euler 方程组, 需要引入马赫数 $M=\frac{|\textbf{u}|}{c}$ ($c=\sqrt{\frac{\gamma p}{\rho}}$ 是音速) 来区分流体. 当 $M>1$ 时, 称流体为超音速流; 当 $M<1$ 时, 称流体为亚音速流. 本文考虑流体受引力影响充分小时的流动. 从物理角度来看, 当管道距离地心足够远时, 引力对流体的流动影响充分小. 在数学的设定上, 为便于后续计算工作的开展, 我们固定管道位置, 取 $K$ 值充分小, 以达到引力影响充分小的目的.

对于 Euler 方程组的研究有着非常重要的理论和实际意义, 此处仅介绍部分与本文相关的成果. 管道中跨音速激波问题的研究最早开始于 Chen 和 Feldman^[2]. 在文献 [2] 中, Chen 和 Feldman 将跨音速激波作为自由边界, 给出了确定自由边界的迭代方案. 在文献 [3] 中, Chen 和 Feldman 又讨论了半无限长管道内的跨音速激波问题, 根据来流确定了在无穷远处亚音速流的渐近性态. 随后, Chen-Chen-Feldman 在文献 [4] 中研究了半无限长管道中完全欧拉跨音速流的适定性问题. Yuan^[8] 在二维扩张管道 (角扇区部分) 和三维球对称扩张管道 (不包含顶点的圆锥部分) 中, 得出了跨音速激波位置和强度可以根据出口压力的大小自动调整的结论. 此外, Yuan 在文献 [9],[10] 中还研究了二维管道 (管壁几乎趋于直的) 流, 当管道出口处的压力允许一定自由度 (相差一个常数) 时, 证明了跨音速流的适定性. Chen^[5] 和 Li-Xin-Yin^[7] 研究了二维扩张管道流, 如果在管道入口处给定来流初值, 并在管道出口处给定合适的压力的情况下, 证明了跨音速激波解的适定性. 两篇文章的不同之处在于 Chen^[5] 研究的是完全欧拉流, 管道壁允许任意小扰动; Li-Xin-Yin^[7] 则研究的是等熵流, 而管道扩张部分的管道壁是直的.

大多数情况下, 由于空气引力对管道内的气动现象影响微小, 对跨音速激波问题的研究会忽略引力的影响. 然而在某些特殊的情况下需考虑引力的影响. 例如, 火山喷发时所产生的气流, 由于喷发时会夹杂火山灰等物质, 这时流体的密度大, 引力对流体的运动状态会产生不可忽略的影响. 本文考虑包含引力项的跨音速激波问题, 与文献 [8] 不同的是, 由于流体受引力影响, Bernoulli 函数 $B$ 沿流线不再是常数.

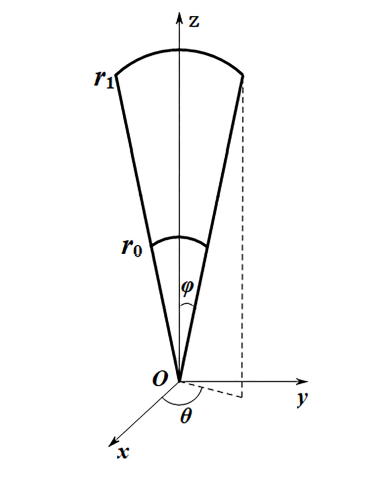
在笛卡尔坐标系 $(x,y,z)$ 下, 本文所考虑的三维直扩张喷管如图所示

定义1.1 如果在管道内存在一个激波面 $\Sigma$, 使得超音速来流 $U_{-}=(\textbf{u}_{-}, p_{-}, \rho_{-})$ 越过激波面后到了亚音速下游 $U_{+}=(\textbf{u}_{+}, p_{+}, \rho_{+})$, 在激波面上满足 Rankine-Hugoniot 激波跳跃条件 (简称 R-H 条件)

其中, $\textbf{n}$ 表示在激波面上由超音速区域指向亚音速区域的单位法向量, $[f]=f_{+}-f_{-}$ 为 $f$ 越过激波面的跃度. 并且若有熵条件 $[p]=p_{+}-p_{-}>0$, 那么 $U_{-}$ 与 $U_{+}$ 状态由激波面连接所形成的结构, 称为跨音速激波解.

方程组 (1.2) 表示流体在管道内满足的三大守恒律. 由 (1.2) 式中的第一个和第三个方程可知

这表明 $\frac{1}{2}|\textbf{u}|^{2}+\frac{\gamma p}{(\gamma-1)\rho}-\frac{K}{r}$ 沿着光滑的流线恒为常数, 不妨设该常数为 $a_{0}$, 即

由于管道具有球对称性, 引入球坐标变换

根据笛卡尔坐标系与球坐标系的关系

其中, $(\textbf{e}_{x},\textbf{e}_{y},\textbf{e}_{z})$ 与 $(\textbf{e}_{r},\textbf{e}_{\theta},\textbf{e}_{\varphi})$ 分别表示笛卡尔坐标系和球坐标系中的单位坐标向量. 于是

由 (1.2) 和 (1.4) 式, 有

由于管道具有球对称性, 即 $\textbf{u},\ p,\ \rho$ 仅依赖于 $r$, 所以 $\textbf{u},\ p,\ \rho$ 关于 $\theta$ 和 $\varphi$ 的偏导数都为 $0$. 于是对速度而言, 只需考虑径向分量 $u^{r}$. 由 (1.5) 式可得到 $u^{r}$ 满足的常微分方程组 (在下文中, 我们将 $u^{r}$ 简记为 $u$)

由 (1.6) 式的第一个方程可知 $r^{2}\rho u$ 恒为常数, 于是 $r^{2}\rho u=r_{0}^{2}\rho_{0} u_{0}$. 记 $b_{0}:=r_{0}^{2}\rho_{0} u_{0}$.

现将本文所研究的问题陈述如下

喷管在球坐标系下可被描述为区域 $\Omega=\{(r,\theta,\varphi)|0<r_{0}\leq r\leq r_{1},\ 0\leq\varphi\leq\alpha,\ 0\leq\theta\leq 2\pi\}$. 给定 $U_{0}=(u_{0},p_{0},\rho_{0})$ 为入口 $r=r_{0}$ 处的超音速初始状态, 其中 $\rho_{0}>0$. $U_{-}=(u_{-}, p_{-}, \rho_{-})$ 和 $U_{+}=(u_{+}, p_{+}, \rho_{+})$ 分别是位于激波两侧的超音速状态和亚音速状态. $p_{\ast}$ 为出口 $r=r_{1}$ 处给定的适当大的压力, 下面给出跨音速激波球对称解的定义.

定义1.2 我们称 $(U_{-},U_{+},\tau)$ 为 (1.6) 式的一个跨音速激波球对称解, 其中 $\tau\in[r_{0},\ r_{1}]$. 如果下述条件成立

1) $U_{-}\in\big(C^{1}(r_{0},\tau)\big)^{3}\bigcap\big(C[r_{0},\tau]\big)^{3},\ U_{+}\in(C^{1}\big(\tau,r_{1})\big)^{3}\bigcap\big(C[\tau,r_{1}]\big)^{3}$, 且分别在 $(r_{0},\tau)$ 和 $(\tau,r_{1})$ 上满足 (1.6) 式.

2)

3) 在 $r=\tau$ 上满足 R-H 条件

4) 在 $r=\tau$ 上满足熵条件: $[p]=p_{+}(\tau)-p_{-}(\tau)>0$.

注1.1 对于在出口处给定的适当大的压力 $p_{\ast}$, 对 (1.6) 式直接求解是相对困难的. 我们转而考虑出口压力与激波位置 $\tau$ 的关系, 分析管道内各物理量在超音速区域与亚音速区域的单调性, 从而来确定超音速流和亚音速流关于激波强度的变化规律.

由初始条件 $U_{0}=(u_{0},p_{0},\rho_{0})$ 可知, $a_{0}=\frac{1}{2}u_{0}^{2}+\frac{c_{0}^{2}}{\gamma-1}-\frac{K}{r_{0}}$. 利用 $c^{2}=\frac{{\rm d}p}{{\rm d}\rho}=\gamma A(S)\rho^{\gamma-1}=\frac{\gamma p}{\rho}$, (1.6) 式的第一个和第二个方程可改写为

对上述方程组可看成是 $\frac{{\rm d}u}{{\rm d}r}$ 和 $\frac{{\rm d}\rho}{{\rm d}r}$ 的线性方程组, 求解可得

对于入口处给定超音速初始状态 $U_{0}$, 方程组 (1.11)-(1.13) 在超音速区域解的曲线, 称为超音速曲线, 而在亚音速区域解的曲线称为亚音速曲线.

将 $M=\frac{u}{c}$ 和 $\frac{1}{2}u^{2}+\frac{c^{2}}{\gamma-1}-\frac{K}{r}=a_{0}$ 关于 $r$ 求导有

和

利用 (1.12) 式, 有

入口处给定超音速初始状态 $U_{0}$, 对任意的 $\tau\in[r_{0},r_{1}]$, 由超音速曲线可以得到激波前的状态 $U_{-}(\tau)$. 再由 $\big(u_{+}(\tau),p_{+}(\tau),\rho_{+}(\tau)\big)$ 与 $\big(u_{-}(\tau),p_{-}(\tau),\rho_{-}(\tau)\big)$ 之间的关系式可以得到激波后的状态 $U_{+}(\tau)$, 本文将描述 $U_{+}(\tau)$ 与 $\tau$ 关系的曲线称为 R-H 曲线, 记作 $U_{R}(\tau)$.

注1.2 对于给定的 $\tau$, 可以得到以 $U_{+}(\tau)=\big(u_{+}(\tau),p_{+}(\tau),\rho_{+}(\tau)\big)$ 为初值的亚音速曲线 $U_{T}(\tau,r):=\big(u_{T}(\tau,r),p_{T}(\tau,r),\rho_{T}(\tau,r)\big)$. 显然亚音速曲线有两个变量 $\tau$ 和 $r$, 但本文只涉及到对 $r$ 的导数, 而未涉及到对 $\tau$ 的偏导数. 为了与前文常微分方程组的符号保持一致, 因此对 $r$ 的导数记为 $\frac{{\rm d}U_{T}}{{\rm d}r}$. 特别地, $M_{T}(\tau,r)=u_{T}(\tau,r)\big/\sqrt{\gamma A_{\ast}(\tau)\rho_{T}^{\gamma-1}(\tau,r)}$, 其中 $A_{\ast}(\tau)=e^{S(\tau)}=p_{+}(\tau)/\rho_{+}^{\gamma}(\tau)$.

对于跨音速激波问题, 下面两个定理是本文的主要结论.

定理1.1 入口处给定超音速初始状态 $U_{0}$, 当 $K$ (依赖于 $r_{0},\ r_{1}$ 和 $U_{0}$) 充分小, 在出口处, $u_{T}(\tau,r_{1}),\ M_{T}(\tau,r_{1})$ 为 $\tau\in[r_{0},r_{1}]$ 的严格单调递增连续函数; $\rho_{T}(\tau,r_{1}),\ p_{T}(\tau,r_{1})$ 为 $\tau\in[r_{0},r_{1}]$ 的严格单调递减连续函数.

定理1.2 (引力作用下跨音速激波的存在唯一性) 入口处给定超音速初始状态 $U_{0}$, 当 $K$ (依赖于 $r_{0},\ r_{1}$ 和 $U_{0}$) 充分小, 存在 $p_{max}>p_{min}>0$ (依赖于 $r_{0},\ r_{1},\ U_{0}$ 和 $K$), 使得当 $p_{\ast}\in[p_{min},p_{max}]$ 时, (1.6) 式存在唯一的跨音速激波解.

命题2.1 已知 $U_{-}(\tau)=\big(u_{-}(\tau),p_{-}(\tau),\rho_{-}(\tau)\big)$ 是超音速的, 通过激波条件可以解出唯一的亚音速 $U_{+}(\tau)=\big(u_{+}(\tau),p_{+}(\tau),\rho_{+}(\tau)\big)$.

证 我们只需证明 $U_{+}$ 是亚音速的, 并验证在激波面上, R-H 条件 (1.7)-(1.9) 和熵条件 $p_{-}(\tau)<p_{+}(\tau)$ 成立.

第 1 步 我们求解出 $u_{+},\ p_{+},\ \rho_{+}$ 与 $u_{-},\ p_{-}, \ \rho_{-}$ 之间的关系式. 由 (1.7) 和 (1.9) 式,

将 (1.8) 式两端乘上 $\frac{\gamma}{\gamma-1}u_{+}$, 有

将 (2.2) 式减去 (2.1) 式, 再利用 (1.7) 式, 可得关于 $u_{+}$ 的一元二次方程

显然 $u_{+}=u_{-}$ 是 (2.3) 式的其中一个解, 并且 $u_{-}>0$ 是超音速的. 注意到 $\rho\equiv0$ 是 (1.11) 式的一个解，而 $\rho_{-}$ 也满足 (1.11) 式, 由已知条件知 $r^{2}\rho u=r_{0}^{2}\rho_{0}u_{0}>0$, 进而常微分方程 (1.11) 不存在零解, 否则这将与常微分方程解的唯一性矛盾. 根据韦达定理, (2.3) 式的另一个解为

利用 (1.9) 式,

类似地, $u_{+}>0$ 满足 (1.12) 式, 常微分方程 (1.12) 也不存在零解. 记 $a_{\ast}:=\frac{2(\gamma-1)(a_{0}+\frac{K}{\tau})}{\gamma+1}$, 于是

第 2 步 下证 $U_{+}=(u_{+},p_{+},\rho_{+})$ 是亚音速的. 根据 (1.9) 式, 有

即

所以 $U_{+}$ 是亚音速的.

第 3 步 验证熵条件. 联立 (2.6) 和 (2.9) 式, 可得

命题2.2 对入口给定的超音速初值 $U_{0}=(u_{0},p_{0},\rho_{0})$, $M_{0}=\frac{u_{0}}{c_{0}}>1$, $K$ (依赖于 $r_{0},\ r_{1}$ 和 $U_{0}$) 充分小, 那么当 $r$ 增大时, 有以下结论:

1) 在超音速区域 $[r_{0},\tau]$, $M_{-}, u_{-}$ 单调递增, $\rho_{-},\ p_{-}$ 单调递减.

2) 在亚音速区域 $[\tau,r_{1}]$, $M_{T}, u_{T}$ 单调递减, $\rho_{T}, \ p_{T}$ 单调递增.

证 由于流体受到引力影响, 由 (1.11)-(1.14) 式不易直接得到各物理量的单调性. 我们下面分四步确定 $K$ 的取值范围, 以保证各物理量的单调性.

第 1 步 设 $K<2r_{0}c_{0}^{2}$. 于是在 $r_{0}$ 处, 有

由 $u_{-},\ M_{-}$ 和 $\rho_{-}$ 导数的连续性, 可知它们在 $r_{0}$ 处的局部单调性成立, 且 $M_{-}>1$.

根据 (1.14) 式, 我们有 $\frac{{\rm d}M_{-}}{{\rm d}r}\leq\frac{M_{-}}{r}\Big(\frac{2+(\gamma-1)M_{-}^{2}}{M_{-}^{2}-1}\Big)$, 分离变量

在 $[r_0,r]$ 上, 对上述不等式两端积分,

即

于是

由于 $\big(2+(\gamma-1)M_{-}^{2}\big)^{\frac{\gamma+1}{4(\gamma-1)}} \geq\left((\gamma-1)M_{-}^{2}\right)^{\frac{\gamma+1}{4(\gamma-1)}}$, 因此

记 $C_{1}:=\Big(2+(\gamma-1)M_{0}^{2}\Big)^{\frac{\gamma+1}{4}}\Big/\Big((\gamma-1)^{\frac{\gamma+1}{4(\gamma-1)}}r_{0}M_{0}^{\frac{1}{2}}\Big)^{\gamma-1}$, $C_1$ 是仅与初值有关的常数. 于是

由 (2.11) 式可知, $c_{-}\geq (C_{1}r^{\gamma-1})^{-1}u_{-} \geq(C_{1}r_{1}^{\gamma-1})^{-1}u_{0}.$ 记 $c_{\ast}:=(C_{1}r_{1}^{\gamma-1})^{-1}u_{0}$, 同时令 $K_{\ast}:=2r_{0}c_{\ast}^{2}$ (这里 $c_{\ast}\leq c_{0}$), 使得 $K<K_{\ast}$ 成立, 即在 $r_{0}$ 局部满足 $K<2rc_{-}^{2}$.

第 2 步 验证在超音速区域内, $K<2rc_{-}^{2}$ 始终成立.

入口处给定超音速初始状态 $U_{0}$, 对任意的 $r=r_{0}+L$, $L\in(0,r_{1}-r_{0}]$, 存在 $\delta>0$, 使得超音速曲线的解区间可以延拓到 $[r,r+\delta)$. 从而在整个超音速区域内 $K$ 都满足 $K<2rc_{-}^{2}$. 因此,

即 $u_{-},\ M_{-}$ 关于 $r$ 单调递增, $\rho_{-},\ p_{-}$ 关于 $r$ 单调递减.

第 3 步 对于 $u_{-}$, 由 (2.11) 式可知, $u_{-}\leq C_{1}r_{1}^{\gamma-1}c_{0}$. 令 $K<\frac{1}{2}r_{0}u_{0}^{2}$, 在亚音速区域入口 $r=\tau$ 处, 联立 (2.6) 和 (2.7) 式,

其中 $a_{0}=\frac{1}{2}u_{0}^{2}+\frac{c_{0}^{2}}{\gamma-1}-\frac{K}{r_{0}}$, 且

因此 $c_{+}(\tau)>a_{\ast}>\sqrt{\frac{2}{\gamma+1}}c_{0}$.

根据 (2.11) 式, 易知 $C_{1}r_{1}^{\gamma-1}>1$, 所以 $\frac{2}{\gamma+1}\frac{c_{0}}{C_{1}r_{1}^{\gamma-1}}>\sqrt{\frac{2}{\gamma+1}}\frac{c_{0}}{C_{1}r_{1}^{\gamma-1}}$, 且 $\sqrt{\frac{2}{\gamma+1}}c_{0}>$ $\sqrt{\frac{2}{\gamma+1}}\frac{c_{0}}{C_{1}r_{1}^{\gamma-1}}$. 记 $u_{\ast}:=\sqrt{\frac{2}{\gamma+1}}\frac{c_{0}}{C_{1}r_{1}^{\gamma-1}}$, 设 $K<2r_{0}u_{\ast}^{2}$, 有 $K<2\tau u_{+}^{2}(\tau)$, 且 $K<2\tau c_{+}^{2}(\tau)$. 于是, 在 $\tau$ 处有

由 $u_{T},\ M_{T}$ 和 $\rho_{T}$ 导数的连续性, 可知它们在 $\tau$ 处的局部单调性成立. 由命题 (2.1), 易知 $0<M_{T}<1$.

类似地, 由 (1.14) 式, 有 $-\frac{M_{T}}{r}\Big(\frac{2+(\gamma-1)M_{T}^{2}}{1-M_{T}^{2}}\Big)\leq\frac{{\rm d}M_{T}}{{\rm d}r}$. 分离变量, 得到

在 $[\tau,r]$ 上, 对上述不等式两端积分,

即

于是

由于 $\big(1+\frac{\gamma-1}{2}M_{T}^{2}\big)^{\frac{\gamma+1}{2(\gamma-1)}}\geq1$, 因此

与第 1 步不同的是, 这里 $M_{+}(\tau)=\frac{u_{+}(\tau)}{c_{+}(\tau)}$ 依赖于 $\tau$. 已知 $u_{+}(\tau)>\frac{2}{\gamma+1}\frac{c_{0}}{C_{1}r_{1}^{\gamma-1}}$, 利用 (2.7) 式,

易知上式中第二个不等号的右端是正常数. 于是

记上述不等式右端的常数为 $C_{2}$, 即有 $\tau^{2}M_{+}(\tau)>C_{2}r_{0}^{2}$. 由于

不妨令 $C_{3}:=C_{2}r_{0}^{2}/(\frac{\gamma+1}{2})^{\frac{\gamma+1}{\gamma-1}}$, 于是

由 (2.12) 式可知, $u_{T}\geq C_{3}r^{-2}c_{T}\geq C_{3}r^{-2}c_{+}(\tau)\geq C_{3}r_{1}^{-2}u_{\ast}$. 记 $u_{\ast\ast}:=C_{3}r_{1}^{-2}u_{\ast}$, 同时令 $K_{\ast\ast}:=2r_{0}u_{\ast\ast}^{2}$, 使得 $K<K_{\ast\ast}$ 成立, 即在 $\tau$ 局部满足 $K<2ru_{T}^{2}$.

在亚音速区域内, 对解的曲线类似可以延拓, 即在整个亚音速区域内, $K<2ru_{T}^{2}$. 因此,

即 $c_{T},\ \rho_{T}$ 关于 $r$ 单调递增, $u_{T},\ M_{T}$ 关于 $r$ 单调递减.

第 4 步 令 $K<\min(K_{\ast},K_{\ast\ast}$), 则在超音速区域内 $K<2rc_{-}^{2}$, 在亚音速区域内 $K<2ru_{T}^{2}$, 进而上述单调性均成立.

注2.1 命题 2.2 中的 $C_{1},\ C_{2},\ C_{3},\ c_{\ast},\ u_{\ast},\ u_{\ast\ast},\ K_{\ast}$ 和 $K_{\ast\ast}$ 都是仅与 $r_{0},\ r_{1}$ 及 $U_{0}$ 有关的常数.

证 本节分四步证明定理的结论.

第 1 步 我们先证明 $U_{T}(\tau,r_{1})$ 关于 $\tau$ 的连续性.

$U_{-}(\tau)$ 是常微分方程组 (1.11)-(1.13) 在 $\tau$ 处的解, 因此 $U_{-}(\tau)$ 关于 $\tau$ 是 $C^{1}$ 函数. $U_{+}(\tau)$ 是由 $U_{-}(\tau)$ 和 R-H 条件解出来的, 所以 $U_{+}(\tau)$ 关于 $U_{-}(\tau)$ 连续. 又由常微分方程解对初值的连续依赖性可知, $U_{T}(\tau,r_{1})$ 是 $U_{+}(\tau)$ 的连续函数. 从而 $U_{T}(\tau,r_{1})$ 是 $\tau$ 的 $C^{1}$ 连续函数.

第 2 步 证明 $u_{T}(\tau,r_{1})$ 关于 $\tau$ 是严格单调递增的.

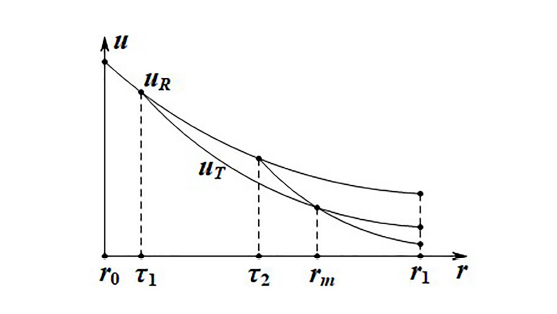
直接证明 $u_{T}(\tau,r_{1})$ 关于 $\tau$ 单调递增是相对困难的, 我们转而证明经过点 $\big(\tau,u_{+}(\tau)\big)$ 的 $u_{T}$ 曲线在 $u_{R}$ 曲线的下方.

对任意的 $\tau\in[r_{0},r_{1}]$, 由 (1.12) 和 (2.6) 式, 可得到 $u_{R}$ 满足的常微分方程

以及 $u_{T}$ 满足的常微分方程

于是, 在 $r=\tau$ 处有

由命题 2.2 和 (1.14) 式可知

也就是说, $\frac{{\rm d}u_{R}}{{\rm d}\tau}-\frac{{\rm d}u_{T}}{{\rm d}r}\Big|_{r=\tau}>0$. 这表明 $u_{R}$ 曲线在 $\tau$ 处的切线斜率比 $u_{T}$ 曲线在此处的斜率大, 即经过点 $\big(\tau,u_{+}(\tau)\big)$ 的 $u_{T}$ 曲线在 $u_{R}$ 曲线的下方.

接下来, 我们用反证法证明严格单调性. 由 (1.6) 式的第三个方程和 (1.12) 式可得

假设存在 $\tau_{1},\ \tau_{2}\in(r_{0},r_{1})$, $\tau_{1}<\tau_{2}$, 且 $u(\tau_{1},r_{1})\geq u(\tau_{2},r_{1})$. 由连续函数的介值定理, 存在一点 $r_{m}\in[\tau_{2},r_{1}]$, 使得分别过 $u_{R}$ 曲线上两点 $\big(\tau_{1},u_{+}(\tau_{1})\big)$ 与 $\big(\tau_{2},u_{+}(\tau_{2})\big)$ 的两条 $u_{T}$ 曲线在 $r=r_{m}$ 处相交(如图 2). 这表明以 $u_+(r_{m})$ 为初值的亚音速曲线有两个解, 这与常微分方程解的局部唯一性矛盾. 因此, $u_{T}(r_{0},r_{1})<u_{+}(r_{1})=u_{T}(r_{1},r_{1})$, 即 $u_{T}(\tau,r_{1})$ 是 $\tau$ 的严格单调递增函数.

第 3 步 由 (1.6) 式, 有

由上式右端可知，$\frac{1}{M_{T}^{2}(\tau,r_{1})}$ 是关于 $\tau$ 的严格单调递减连续函数, 即 $M_{T}(\tau,r_{1})$ 是 $\tau$ 的严格单调递增函数.

第 4 步 证明 $\rho_{T}(\tau,r_{1})$ 和 $p_{T}(\tau,r_{1})$ 是 $\tau$ 的严格单调递减函数.

由质量守恒公式 $r_{1}^{2}\rho_{T}(\tau,r_{1})u_{T}(\tau,r_{1})=r_{0}^{2}\rho_{0}u_{0}=b_{0}$, 再结合第 2 步中的证明可知, $\rho_{T}(\tau,r_{1})$ $=\frac{b_{0}}{r_{1}^{2}}\frac{1}{u_{T}(\tau,r_{1})}$ 是关于 $\tau$ 严格单调递减的函数. 对于 $p_{T}(\tau,r_{1})$, 有

显然 $p_{T}(\tau,r_{1})$ 是关于 $\tau$ 的严格单调递减函数.

推论2.1 当 $\tau\in[r_{0},r_{1}]$ 时, $A_{\ast}(\tau)=e^{S(\tau)}$ 是关于 $\tau$ 的严格单调递增函数.

证 流体在 $r_{1}$ 处的状态方程为

再利用 $r_{1}^{2}\rho_{T}(\tau,r_{1})u_{T}(\tau,r_{1})=r_{0}^{2}\rho_{0}u_{0}=b_{0}$, (2.16) 式可改写为

对 (2.17) 和 (2.18) 式关于 $\tau$ 求导有

进一步

即得

由定理 1.1 中 $p_{T}(\tau,r_{1})$ 的单调性, $A_{\ast}(\tau)=e^{S(\tau)}$ 是 $\tau\in[r_{0},r_{1}]$ 的严格单调递增函数.

证 根据定理 1.1 的证明, 易知 $p_{max}=p_{T}(r_{0},r_{1}),\ p_{min}=p_{+}(r_{1})=p_{T}(r_{1},r_{1})$. 利用 $p_{T}(\tau,r_{1})$ 的严格单调性, 可知存在唯一的 $\tau\in[r_{0},r_{1}]$, 使得 $p_{T}(\tau,r_{1})=p_{\ast}\in[p_{min},p_{max}]$.