数学物理学报, 2025, 45(2): 389-407

强耦合变系数波动方程的间接边界镇定

崔佳楠,1,2, 柴树根,1,*

1山西大学数学科学学院 太原 030006

2晋中学院数学系 山西晋中 030619

Indirect Boundary Stabilization of Strongly Coupled Variable Coefficient Wave Equations

Cui Jianan,1,2, Chai Shugen,1,*

1School of Mathematical Sciences, Shanxi University, Taiyuan 030006

2Department of Mathematics, Jinzhong University, Shanxi Jinzhong 030619

通讯作者: * 柴树根，E-mail: sgchai@sxu.edu.cn

收稿日期: 2024-05-28   修回日期: 2024-10-30  

基金资助: 国家自然科学基金(12271316)
晋中学院博士专项基金(23E00611)

Received: 2024-05-28   Revised: 2024-10-30  

Fund supported: NSFC(12271316)
Jinzhong University Research Funds for Doctor(23E00611)

作者简介 About authors

崔佳楠，E-mail:1391958885@qq.com

摘要

该文旨在研究带变系数和边界阻尼的强耦合波动方程的间接镇定. 值得注意的是, 系统中只有一个方程直接受到边界阻尼的影响. 利用黎曼几何方法和高阶能量方法, 证明了全局耦合系统的衰减速率受边界条件类型的影响. 研究结果表明, 当无阻尼方程具有 Dirichlet 边界条件时, 系统表现出指数稳定性, 而当无阻尼方程具有 Neumann 边界条件时, 系统仅有多项式稳定性. 最后, 在 Dirichlet 和 Neumann 边界条件下建立了局部耦合系统的指数稳定性.

关键词： 间接镇定; 强耦合; 非均匀介质; 边界反馈

Abstract

In this paper, the indirect stabilization of strongly coupled wave equations with variable coefficients and boundary damping is studied. It is important to note that only one equation in the system is directly affected by boundary damping. By using Riemannian geometry method and higher order energy method, it is proved that the decay rate of the globally coupled system is affected by the type of boundary conditions. The results show that when the undamped equations have Dirichlet boundary conditions, the system exhibits exponential stability, while when the undamped equations have Neumann boundary conditions, the system has only polynomial stability. Finally, the exponential stability of the locally coupled system is established under Dirichlet and Neumann boundary conditions.

Keywords： indirect stabilization; strong coupling; inhomogeneous media; boundary feedback

PDF (641KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

崔佳楠, 柴树根. 强耦合变系数波动方程的间接边界镇定[J]. 数学物理学报, 2025, 45(2): 389-407

Cui Jianan, Chai Shugen. Indirect Boundary Stabilization of Strongly Coupled Variable Coefficient Wave Equations[J]. Acta Mathematica Scientia, 2025, 45(2): 389-407

1 引言

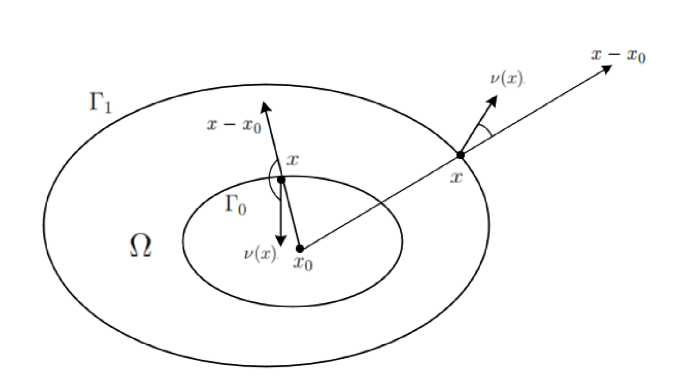
令 $ \Omega \subset \mathbb{R}^n(n\geq2) $ 为一个有界开的星形区域 (参见图 1), 带有 $ C^{\infty} $ 边界 $ \Gamma=\Gamma_0 \cup \Gamma_1 $, 其中 $ \Gamma_0, \Gamma_1 $ 是非空的, 闭的且互不相交. 考虑下面的仅带边界阻尼的强耦合系统

$\begin{cases}y_{tt}-\Delta_gy-b(x)\Delta_gu= 0, \ &(x,t)\in\Omega\times(0,\infty),\\u_{tt}-\Delta_gu+b(x)y=0, \ &(x,t)\in\Omega\times(0,\infty),\\y=u=0, \ &(x,t)\in\Gamma_0\times(0,\infty),\\y=0, \ \partial_{\mu}u+u_t=0, \ &(x,t)\in\Gamma_1\times(0,\infty)\end{cases}$

和

$\begin{cases}y_{tt}-\Delta_gy-b(x)\Delta_gu=0, \ &(x,t)\in \Omega\times(0,\infty),\\u_{tt}-\Delta_gu+b(x)y=0, \ &(x,t)\in \Omega\times(0,\infty),\\y=u=0, \ &(x,t)\in\Gamma_0\times(0,\infty),\\\partial_{\mu}y=0, \ \partial_{\mu}u+u_t=0, \ &(x,t)\in \Gamma_1\times(0,\infty).\end{cases}$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   在 $ \Gamma_0 $ 上, $ (x-x_0)\cdot \nu(x)\leq 0. \ \Gamma_0 $ 被称为边界 $ \Gamma $ 上的不可控部分, 而在 $ \Gamma_1 $ 上满足$ (x-x_0)\cdot \nu(x)>0 $. 这种区域称为星形域.


初值条件为

$y(x,0)=y_0(x),\ y_t(x,0)=y_1(x), \ u(x,0)=u_0(x), \ u_t(x,0)=u_1(x), \ \ x\in\Omega.$

其中 $ \Delta_gy=\text{div}(A(x)\nabla y) $, $ A(x)=(a_{ij}(x)) $ 是一个对称正定的矩阵且 $ a_{ij}:\Omega\rightarrow \mathbb{R},$ $ 1\leq i,$ $j\leq n $ 为光滑函数, 对所有的 $ x\in \Omega $ 满足 $ a_{ij}(x)=a_{ji}(x) $. $ \text{div} X $ 表示向量场 $ X $ 在欧氏度量下的散度. $ \nu=(\nu_1,\nu_2,\cdots,\nu_n) $ 为边界上的单位外法向量, $ \mu=A\nu $ 且

$\begin{align*} \partial_{\mu} u=\sum_{i,j=1}^{n} a_{ij}\nu_i\frac{\partial u}{\partial x_j}=\langle A(x)\nabla u,\nu\rangle. \end{align*}$

$ y_0,y_1,u_0,u_1 $ 是给定的实值函数, $ b: \Omega\rightarrow \mathbb{R} $ 是一个非负函数且 $ b\in L^{\infty}(\Omega) $.

对系统 (1.1) 和 (1.2) 的间接镇定的研究既有趣又极具挑战性. 这主要是由于阻尼只应用于边界 $ \Gamma_1 $, 且系统带有变系数波动方程主部和非恒定耦合系数. 当 $ A(x)=I $ 且 $ b(x)=b $, $ b $ 是一个正的常数时, Rao[1] 考虑了全局耦合波动方程系统的间接镇定问题. 利用频域方法, 他证明了系统在 Dirichlet 条件下呈指数衰减, 而在 Neumann 边界下则呈多项式衰减. 然而, 到目前为止变系数的情形还没有人研究过.

变系数的存在在数学模型中代表振动介质是非均匀的. 人们已经对带变系数的波动方程的稳定性和精确能控性进行了广泛的研究 (参见文献 [2],[3],[4],[5],[6],[7],[8],[9] 及其参考文献). 这些论文一致表明, 与常系数波动方程相比, 变系数波动方程表现出更大的复杂性, 并且在研究中存在更多的挑战. 然而, 变系数的情形在实际应用比如物理和工程模型中更接近于材料的真实性质. 带变系数的波动方程系统的边界镇定问题也已经被许多人研究过, 相关研究可以参见文献 [2],[3],[4],[7],[8],[10]. 值得注意的是, 上述所有提到的变系数工作都用到了黎曼几何方法. Yao[11] 引入的这一方法最初是用来推导受特定几何条件约束的变系数波动方程系统的能观性不等式. 在此基础上, Yao[12] 进一步发展了该方法, 并利用它证明了二阶变系数双曲方程系统的精确可控性. 随后, 用此方法建立了文献 [13] 中变系数双曲方程的能观性不等式.

间接镇定是 Russell[14] 在 1993 年提出的一个概念, 它描述了耗散只直接存在于一个方程, 但对整个系统的稳定性有级联效应的情况. 这个概念特别适用于在所有组件上施加阻尼不切实际或成本高昂的情况, 因此探索具有有限反馈的耦合系统的间接稳定至关重要. 间接阻尼系统的研究与各种工程和机械应用相关, 例如分析弹性结构 (地震和地震波) 中的振动或设计机器人系统. 相关的研究可以参见文献 [15],[16],[17],[18],[19].

Alabau-Boussouira[15] 研究了包括波动方程和 Kirchhoff 板在内的各种耦合系统的边界间接镇定. 并研究了传播速度对波动方程系统的影响. 在文献 [16] 中, 作者研究了由弱耦合双曲型方程组成的抽象系统的间接镇定问题. 通过建立一个广义的积分不等式, 推导出了多项式衰减率. 之后, 广义积分不等式在文献 [4],[19],[18],[15] 中得到了应用. 值得注意的是, 以上的研究主要是关于常系数情形. 据我们所知, 关于变系数耦合系统的研究很少, 特别是关于间接镇定的研究. Cavalcanti 等[20]研究了非均匀介质 $ \Omega $ 中的耦合 Klein-Gordon 系统, 其中在光滑边界 $ \partial\Omega $ 附近的邻域 $ \omega $ 内存在局部阻尼项. 在考虑阻尼只存在于一个方程的情况下, 得到了局部耦合系统的一致稳定性. 在文献 [21] 中, 研究了一类具有两个局部非线性阻尼项的半线性非齐次 Timoshenko 系统. 他们通过微局部分析技术证明了系统的均匀稳定性.

本研究的主要目标是分析系统 (1.1) 和 (1.2) 在两种情形下的间接镇定: (1) 耦合系数 $ b(x)=b $ 是一个正的常数; (1.2) $ \mathrm{supp} b(x)=O\subset \Omega $, $ \overline{O}\cap \Gamma_0\neq \emptyset $. 我们发现从常系数到变系数的推广并不是一个直接的过程, 原因是系统的耦合项 $ b(x)\Delta_gu, b(x)y $ 带有不同的阶数. 此时需要对逃逸向量场施加额外的几何假设. 对于系统 (1.2), 隐性正则性不成立, 这就使得几何乘子方法不再适用. 为了克服这一困难, 用到了文献 [16] 中提出并用于文献 [15],[18] 的广义积分不等式. 通过反证法, 对局部耦合系统在两种情形下都证明了指数稳定性.

本文的其余部分组织如下. 第 2 节给出了一些符号以及本文的主要结果, 并给出了一些初步的技术引理. 第 3 节介绍了系统 (1.1), (1.2) 的适定性. 第 4 节研究了全局耦合系统. 其中第 4.1 小节建立了系统 (1.1) 的一致指数稳定性, 第 4.2 小节给出了系统 (1.2) 的多项式稳定性的证明. 第 5 节建立了局部耦合系统的指数稳定性.

2 一些符号和主要结果

2.1 黎曼几何中的一些符号

这一节将引入一些之后会用到的符号. 文章中用到的所有符号都是标准的, 参考了文献 [22].

令 $ a_{ij} $ 作为 $ \mathbb{R}^n $ 中的光滑函数, 满足

$\begin{align*} \begin{split} &a_{ij}(x)=a_{ji}(x),\ \ \lambda |\xi|^2\leq \sum_{i,j=1}^na_{ij}(x)\xi_i\xi_j\leq\Lambda |\xi|^2,\\ &\forall x\in \mathbb{R}^n, \ \xi=(\xi_1,\cdots,\xi_n)\in\mathbb{R}^n, \end{split} \end{align*}$

其中 $ \lambda, \Lambda $ 为正的常数.

令

$\begin{align*} \begin{split} &A(x)=(a_{ij}(x)), \\ &G(x)=(A(x))^{-1}=(g_{ij}(x)). \end{split} \end{align*}$

对每个 $ x\in \mathbb{R}^n $, 在 $ \mathbb{R}^n_{x} $ 将内积 $ g(\cdot, \cdot)=\langle\cdot, \cdot\rangle $ 和范数 $ |\cdot| $ 定义为

$\begin{align*} \begin{split} &g(X,Y)=\langle X,Y\rangle_g=\sum_{i,j=1}^ng_{ij}(x)\alpha_i\beta_j,\ \ |X|_g=\langle X,X\rangle_g^{\frac{1}{2}}, \\ & \forall X=\sum_{i=1}^n\alpha_i\frac{\partial}{\partial x_i}, \ \ Y=\sum_{i=1}^n\beta_i\frac{\partial}{\partial x_i}\in \mathbb{R}^n_{x}. \end{split} \end{align*}$

那么 $ (\mathbb{R}^n, g) $ 为带度量 $ g $ 的一个黎曼流形.

令 $ D $ 作为一个 Levi-Civita 联络, 且 $ H $ 为 $ (\mathbb{R}^n, g) $ 上的一个向量场, 那么 $ H $ 的协变微分 $ DH $ 在 $ \mathbb{R}^n_{x}\times \mathbb{R}^n_{x} $ 上决定了一个如下的双线性形式, 对每个 $ x\in \mathbb{R}^n $,

$\begin{align*} DH(X,Y)=\langle D_{Y}H,X\rangle_{g}, \ \ \forall X,Y\in \mathbb{R}^n_{x}, \end{align*}$

其中 $ D_{Y}H $ 表示 $ H $ 关于 $ Y $ 的协变导数.

令 $ \nabla_g $ 为黎曼流形 $ (\mathbb{R}^n, g) $ 上的梯度算子. 根据文献 [11,引理 2.1] 以及文献 [23] 可得

$\begin{align*} \begin{split} &\nabla_gu=\sum_{i=1}^n(\sum_{j=1}^na_{ij}\frac{\partial u}{\partial x_j})\frac{\partial}{\partial x_i}, \\ &|\nabla_gu|_{g}^2=\sum_{i,j=1}^na_{ij}\frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_j}. \end{split} \end{align*}$

黎曼流形 $ (\mathbb{R}^n, g) $ 上的 Beltrami-Laplace 算子定义为

$\begin{matrix}\label{Delta g u} \Delta_gu=\frac{1}{\sqrt{|G|}}\sum_{i,j=1}^n\frac{\partial}{\partial x_i}(\sqrt{|G|}a_{ij}\frac{\partial u}{\partial x_j})=\text{div}(A(x)\nabla u), \end{matrix}$

其中 $ |G|=\det(G) $.

下面的引理给出了一些有用的关系式 (参见文献 [11,引理 2.1]).

引理2.1 令 $ u,v\in C^1(\overline{\Omega}) $, $ H $ 为 $ (\mathbb{R}^n, g) $ 上的向量场, 且 $ \mu $ 为 $ \Gamma $ 上在黎曼度量 $ g $ 下的单位法向量场. 那么有

(a) 散度定理

$\text{div}(uH)=u\text{div} H+H(u), \ \ \int_{\Omega}\text{div} H{\rm d}x=\int_{\Gamma}\langle H, \mu\rangle_{g}{\rm d}\Gamma.$

(b) 格林公式

$\int_{\Omega}v \Delta_{g}u{\rm d}x=\int_{\Gamma}v\partial_{\mu}u{\rm d}\Gamma-\int_{\Omega}\langle \nabla_gu, \nabla_gv\rangle_{g}{\rm d}x,$

其中 $ {\rm d}x $ 和 $ {\rm d}\Gamma $ 分别代表 $ \Omega $ 和 $ \Gamma $ 的体积元.

(c)

$\langle\nabla_g u,\nabla_g(H(u))\rangle_{g}=DH(\nabla_g u, \nabla_g u)+\frac{1}{2}\text{div} (|\nabla_g u|_g^2H)-\frac{1}{2}|\nabla_g u|_g^2\text{div} H.$

符号

$F\sim G$

表示 $ F $ 等价于 $ G $. $ \|\cdot\| $ 表示 $ L^2(\Omega) $ 范数.

因为 $ a_{ij}(x), i,j=1,\cdots,n $ 是 $ C^{\infty} $ 函数, 可得

$\begin{align*} &\int_{\Omega}\langle\nabla_g u,\nabla_g v\rangle_g{\rm d}x\sim \int_{\Omega}\langle\nabla u,\nabla v\rangle {\rm d}x, \ \ \forall u,v\in H^1(\Omega),\\ &\||\nabla_g u|_g\|^2\sim \|\nabla u\|^2, \ \ \forall u\in H^1(\Omega). \end{align*}$

令

$H_{\Gamma_0}^1(\Omega)=\{u\in H^1(\Omega)| u|_{\Gamma_0}=0\},$

则存在最小的常数 $ \tau_0, \tau_1 $ 使得

$\begin{matrix}\label{trace} \|u\|_{L^2(\Gamma)}^2\leq \tau_0\||\nabla_g u|_g\|^2, \ \ \forall u \in H_{\Gamma_0}^1(\Omega), \end{matrix}$
$\begin{matrix}\label{poincare} \|u\|^{2}\leq \tau_1\||\nabla_g u|_g\|^2, \ \ \forall u\in H_{\Gamma_0}^1(\Omega). \end{matrix}$

下文中, 用 $ C $ 表示正的常数, 它在每一项和每一行之间都可能会发生变化. 并记

$\begin{align*} \begin{split} &Q=\Omega\times (0,T), \ \ \Sigma=\Gamma\times (0,T),\\ &\Sigma_0=\Gamma_0\times (0,T), \ \ \Sigma_1=\Gamma_1\times (0,T). \end{split} \end{align*}$

2.2 主要结果

为了得到我们的主要结果, 需要作出以下假设.

假设2.1 存在一个在黎曼流形 $ (\mathbb{R}^n, g) $ 上的向量场 $ H $, 以及正的常数 $ \rho,q_1,q_2 $ 使得

$DH(X,X)\geq \rho|X|_g^2, \ \ \forall x\in \overline{\Omega}, \ X\in\mathbb{R}^n_x$

和

$q_1\leq \text{div} H\leq q_2<q_1+2\rho$

成立. 此外, 存在常数 $ \delta $ 满足

$\Gamma_0\text{上}H\cdot \nu\leq0, \ \ \Gamma_1\text{上} H\cdot \nu\geq\delta>0.$

注2.1 在常系数情形, 条件 (2.4) 对于固定点 $ x_0\in \mathbb{R}^n $ 取 $ H=x-x_0 $ 与 $ \rho=1 $ 是自动满足的. 对于变系数情形, 我们在 $ \mathbb{R}^2 $ 中找到了一个满足条件 (2.4)-(2.6) 的例子, 见下面的命题 2.1 和例 2.1.

命题2.1[pp390] 假设存在一个度量 $ \hat{g} $ 可以使得 $ (\mathbb{R}^n,\hat{g}) $ 的曲率为零, 并且在 $ \mathbb{R}^n $ 上存在函数 $ u $ 满足以下关系

$ g={\rm e}^{2u}\hat{g}, \ \ \forall x \in \mathbb{R}^n. $

给定 $ x\in \mathbb{R}^n $, 用 $ \hat{\rho}(x) $ 表示在度量 $ \hat{g} $ 下从 $ x_0 $ 到 $ x $ 的距离函数. 设

$H=\hat{\rho}\hat{D}\hat{\rho},$

其中 $ \hat{D} $ 是在 $ (\mathbb{R}^n,\hat{g}) $ 上的 Levi-Civita 联络. 那么

$ \hat{D}H(X,X)=\langle(1+H(u))X,X\rangle_g, \ \ \forall X \in \mathbb{R}^n_x, \ x\in \mathbb{R}^n. $

例2.1[pp390] 令 $ (\mathbb{R}^2,g) $ 作为一个带以下度量的黎曼流形

$ g=\frac{1}{1+ax_1^2+bx_2^2}(dx_1^2+dx_2^2), $

其中 $ a $ 和 $ b $ 是正的常数. 对任意的 $ (x_1,x_2)\in \mathbb{R}^2 $, 高斯曲率为

$ k(x_1,x_2)=\frac{a+b+a(b-a)x_1^2+b(a-b)x_2^2}{(1+ax_1^2+bx_2^2)^3}. $

根据 (2.7) 式我们有 $ g={\rm e}^{2u}\hat{g} $, 其中 $ u=-\frac{1}{2}\log(1+x_1^2+x_2^2) $ 且 $ \hat{g}=dx_1^2+dx_2^2 $. $ (\mathbb{R}^2,g) $ 是零曲率的. 取 $ \hat{\rho}=\sqrt{x_1^2+x_2^2} $, 那么 $ H=x_1\frac{\partial}{\partial x_1}+x_2\frac{\partial}{\partial x_2} $ 且

$ 1+H(u)=\frac{1}{1+ax_1^2+bx_2^2}>0, \ \ \forall (x_1,x_2)\in \mathbb{R}^2. $

因此, 可以在 $ \rho=1 $ 时找到合适的常数 $ a $ 和 $ b $. 此时, 向量场 $ H $ 满足 (2.6) 式且有 $ \text{div} H=2 $. 进一步, 可以找到合适的常数 $ q_1,q_2 $ 满足 (2.5) 式. 综上, 假设 2.1 是合理的.

假设2.2 假设 $ b(\cdot)\in L^{\infty}(\Omega) $ 是一个非负函数, 存在一个正的常数 $ b_0 $, 满足

$b(x)\leq\|b\|_{\infty}<\min\{\frac{1}{2(1+\tau_0+\tau_1)}, \frac{q_1-\beta}{(2q_2-\frac{\beta}{2})(1+\tau_1)+2M}, \frac{1}{4C}\},$
$b(x)>b_0, \ \ \forall x\in \mathrm{supp} b(x),$

其中常数 $ \beta, M, C $ 的值将在之后具体给定.

引入系统 (1.1) 的能量

$E(t)=\frac{1}{2}\int_{\Omega}|\nabla_g y|_g^2+|y_t|^2+|\Delta_gu|^2+|\nabla_g u_t|_g^2+\langle\nabla_g (b(x)y), \nabla_g u\rangle_g{\rm d}x,$

定义关于系统 (1.2) 能量的相关泛函如下

$\begin{matrix}\label{Ej(t)} &\widetilde{E}_0(t;u,y)=\frac{1}{2}\int_{\Omega}|\nabla_g y|_g^2+|y_t|^2+|\Delta_g u|^2+|\nabla u_t|_g^2+2\langle\nabla_g (b(x)y), \nabla_g u\rangle_g +\int_{\Gamma_1}b(x)yu_t{\rm d}\Gamma,\notag\\ &\widetilde{E}(t)=\widetilde{E}_0(t;u,y),\notag\\ &\widetilde{E}_j(t)=\widetilde{E}_j(t;u,y)=\widetilde{E}_0(t;\partial_t^ju,\partial_t^jy), \ \ j=1,2,\cdots. \end{matrix}$

下面先给出一个能量等价关系.

引理2.2 令 $ (y,u) $ 作为系统 (1.1) 或 (1.2) 的解, 设

$\begin{align*} L_j(t)=\int_{\Omega}(|\nabla_g (\partial_t^j y)|_g^2+|\partial_t^{j+1} y|^2+|\Delta_g (\partial_t^j u)|^2+|\nabla_g (\partial_t^{j+1} u)|_g^2){\rm d}x, j=0,1,2,\cdots. \end{align*}$

此外, 我们假定 (2.8) 式的约束条件成立. 则如下等价关系

$\begin{matrix}\label{L} \frac{1}{4}L_0(t)<E(t)<L_0(t), \end{matrix}$
$\begin{matrix}\label{Lj} \frac{1}{4}L_j(t)< \widetilde{E}_j(t)<L_j(t), \ \ \ j=0,1,2,\cdots \end{matrix}$

成立.

证 利用 Hölder 不等式和 Green 公式可得

$\begin{align*} &|\int_{\Omega}\langle\nabla_g (b(x)y), \nabla_g u\rangle_g| =|\int_{\Omega}b(x)y\Delta_gu| \leq \frac{(1+\tau_1)\|b\|_{\infty}}{2}L_0(t) \end{align*}$

和

$\begin{align*} &|\int_{\Omega}\langle\nabla_g (b(x)\partial_t^j y), \nabla_g (\partial_t^j u)\rangle_g{\rm d}x+\int_{\Gamma_1}b(x)\partial_t^j y\partial_t^{j+1} u{\rm d}\Gamma|\\ =&|\int_{\Omega}b(x)\partial_t^j y \Delta_gu{\rm d}x| \leq\frac{(1+\tau_1)\|b\|_{\infty}}{2}L_j(t), \ j=0,1,2,\cdots, \end{align*}$

此处用到了 (2.3) 式和边界条件. 根据 $ E, \widetilde{E}_j, L_j $ 的定义有

$\begin{align*} \frac{1-\|b\|_{\infty}(1+\tau_1)}{2}L_0(t)\leq E(t)\leq \frac{1+\|b\|_{\infty}(1+\tau_1)}{2}L_0(t) \end{align*}$

和

$\begin{align*} \frac{1-\|b\|_{\infty}(1+\tau_1)}{2}L_j(t) \leq \widetilde{E}_j(t) \leq \frac{1+\|b\|_{\infty}(1+\tau_1)}{2}L_j(t), \ j=0,1,2,\cdots. \end{align*}$

再利用条件 (2.8), 可得

$\begin{align*} \frac{\|b\|_{\infty}(1+\tau_1)}{2}<\frac{1}{4}. \end{align*}$

由此可以得到 (2.12) 和 (2.13) 式成立.

本节的主要结果如下

定理2.1 令 $ b(x)=b>0 $, 条件 (2.8) 和假设 2.1 成立. 那么系统 (1.1) 的能量指数地衰减到 $ 0 $, 即存在与初始数据无关的正的常数 $ N_1 $ 和 $ k_1 $, 对所有光滑初始数据 $ (y_0,y_1,u_0,u_1) $ 满足

$E(t)\leq N_1{\rm e}^{-k_1 t}E(0), \ \ \forall t\geq0. $

定理2.2 令 $ b(x)=b>0 $, 条件 (2.8) 和假设 2.1 成立. 对所有光滑初始数据 $ (y_0,y_1,u_0,u_1) $ 以及 $ k\geq 0 $, 满足

$\begin{align*} \sum_{j=0}^{k+1}\widetilde{E}_{j}(0)<\infty. \end{align*}$

那么系统 (1.2) 的能量直至前 $ k $ 阶项的和 $ \sum_{j=0}^{k}\widetilde{E}_{j}(t) $ 多项式地衰减. 更精确地说, 存在一个正的常数 $ \widehat{C} $ 使得

$\begin{align*} \sum_{j=0}^{k}\widetilde{E}_{j}(t)\leq \frac{\widehat{C}}{t}\sum_{j=0}^{k+1}\widetilde{E}_{j}(0), \ \ \ \forall t>T, \end{align*}$

其中 $ T $ 可以充分的大.

定理2.3 假设 $ \mathrm{supp}b=O\subset\Omega, \ \overline{O}\cap \Gamma_0\neq \emptyset $. 令条件 (2.8), (2.9) 和假设 2.1 成立. 那么, 我们可以得到系统 (1.1) 和 (1.2) 的能量都是指数衰减的, 这表明存在两个独立于初始数据的正的常数 $ N_2, k_2 $, 对所有的光滑初始数据 $ (y_0,y_1,u_0,u_1) $ 满足

$\begin{align*} F(t)\leq N_2{\rm e}^{-k_2 t}F(0), \ \ \forall t\geq 0, \end{align*}$

其中 $ F=E, \widetilde{E} $.

为了证明以上结果, 引用如下技术性引理

引理2.3[25,26] (积分不等式) 令$ \varphi: [0, \infty)\rightarrow [0, \infty) $ 是一个 $ C^1 $ 类严格递增的函数, 满足

$\varphi(0)=0 \text{且} \lim_{t\rightarrow \infty}\varphi(t)=\infty.$

令 $ E:[0, \infty)\rightarrow [0, \infty) $ 是一个递减的局部绝对连续函数, 且存在常数 $ \theta\geq 0 $ 和 $ \Theta>0 $ 使得

$\int_{S}^{\infty}E(t)^{\theta+1}\varphi'(t){\rm d}t\leq C^{-1}E(0)^{\theta}E(S), \ \ \forall S\geq0.$

那么, 对任意的 $ t\geq0 $ 有

$\begin{eqnarray*} E(t)\leq \begin{cases} E(0){\rm e}^{1-\Theta\varphi(t)}, &\text{当} \theta=0,\\ E(0)(\frac{1+\theta}{1+\Theta\theta \varphi(t)})^{\frac{1}{\theta}}, &\text{当} \theta>0. \end{cases} \end{eqnarray*}$

3 适定性

本节将分别给出系统 (1.1), (1.2) 的适定性结果.

3.1 系统 (1.1) 的适定性

定义能量空间

$ \mathcal{H}=\left\{ \begin{split}&(y,z,u,v)\in H_{0}^1(\Omega)\times L^2(\Omega)\times H^2(\Omega)\times H_{\Gamma_0}^1(\Omega)\\& \ \text{在} \Gamma_1 \text{上满足} \partial_{\mu}u+v=0 \end{split} \right\}, $
$ \|(y,z,u,v)\|_{\mathcal{H}}^2=\int_{\Omega}(|\Delta_g u|^2+|\nabla _gv|_g^2+|\nabla_g y|_g^2+|z|^2+2\langle\nabla_g u, \nabla_g (b(x)y)\rangle_g){\rm d}x, $

易知 $ \mathcal{H} $ 是一个 Hilbert 空间. 定义线性无界算子

$\begin{align*} \mathcal{B}_b= \left( \begin{matrix} 0 &Id &0 &0\\ \Delta_g &0 &b(x)\Delta_g &0\\ 0 &0 &0 &Id\\ -b(x) &0 &\Delta_g &0 \end{matrix} \right) \end{align*}$

带有定义域

$ D(\mathcal{B}_b)=\left\{ \begin{split} &(y,z,u,v)\in \mathcal{H} \ \text{且} \ y\in H^2(\Omega)\cap H_{0}^1(\Omega), \ z\in H_{0}^1(\Omega)\\ &u\in H^3(\Omega)\cap H_{\Gamma_0}^1(\Omega), \ v\in H^2(\Omega)\cap H_{\Gamma_0}^1(\Omega)\\ &\Gamma_0 \text{上} \Delta_gu=0, \ \Gamma_1 \text{上} \partial_{\mu}u+v=0 \text{且} \partial_{\mu}v+\Delta_gu=0 \end{split} \right\}. $

令 $ U=(y,y_t,u,u_t) $ 作为一个状态变量, 可以将系统 (1.1) 重写为如下的 Cauchy 问题

$ \begin{cases} U_t=\mathcal{B}_bU,\\ U(0)=U_0\in \mathcal{H}. \end{cases} $

直接计算可得出

$ \mathrm{Re}\langle\mathcal{B}_bU, U\rangle_{\mathcal{H}}=-\int_{\Gamma_1}|\partial_{\mu}u_t|^2{\rm d}\Gamma. $

由此可知 $ \mathcal{B}_b $ 是耗散的. 再利用线性半群理论, $ \mathcal{B}_b $ 在 $ \mathcal{H} $ 上生成一个 $ C_0 $-压缩半群 $ S_b(t) $. 此外, 可得下面的能量等式

$E(t)-E(0)=-\int_0^t\int_{\Gamma_1}|u_{tt}|^2{\rm d}\Gamma {\rm d}\tau, \ \ \forall t>0.$

3.2 系统 (1.2) 的适定性

令 $ \widetilde{\mathcal{H}} $ 是一个能量空间, 定义为

$ \widetilde{\mathcal{H}}=\left\{ \begin{split}&(y,z,u,v)\in H_{\Gamma_0}^1(\Omega)\times L^2(\Omega)\times (H^2(\Omega)\cap H_{\Gamma_0}^1(\Omega))\times H_{\Gamma_0}^1(\Omega)\\ &\text{在} \Gamma_1 \text{上满足} \partial_{\mu}u+v=0\end{split}\right\} $
$\begin{align*} \|(y,z,u,v)\|_{\widetilde{\mathcal{H}}}^2\!=\!& \int_{\Omega}(|\nabla_g y|_g^2\!+\!|z|^2\!+\!|\Delta_g u|^2\!+\!|\nabla _gv|_g^2\!+\!2\langle\nabla_g u, \nabla_g (b(x)y)\rangle_g){\rm d}x\!+\!2\int_{\Gamma_1}b(x)yv{\rm d}\Gamma. \end{align*}$

易证明 $ \widetilde{\mathcal{H}} $ 是一个 Hilbert 空间. 在 $ \widetilde{\mathcal{H}} $ 上定义一个线性无界算子

$\begin{align*} \widetilde{\mathcal{B}}_b= \left( \begin{matrix} 0 &Id &0 &0\\ \Delta_g &0 &b(x)\Delta_g &0\\ 0 &0 &0 &Id\\ -b(x) &0 &\Delta_g &0 \end{matrix} \right) \end{align*}$
$ D(\widetilde{\mathcal{B}}_b)=\left\{ \begin{split} &(y,z,u,v)\in \widetilde{\mathcal{H}} \ \text{且} \ y\in H^2(\Omega)\cap H_{\Gamma_0}^1(\Omega), \ z\in H_{\Gamma_0}^1(\Omega)\\ &u\in H^3(\Omega)\cap H_{\Gamma_0}^1(\Omega), \ v\in H^2(\Omega)\cap H_{\Gamma_0}^1(\Omega)\\ &\Gamma_1 \text{上满足} \partial_{\mu}y=0, \partial_{\mu}u+v=0, \partial_{\mu}v+\Delta_gu-b(x)y=0 \end{split} \right\}. $

设 $ U=(y,y_t,u,u_t) $ 为状态变量, 可以把系统 (1.2) 写成下面的 Cauchy 问题

$ \begin{cases} U_t=\widetilde{\mathcal{B}}_bU,\\ U(0)=U_0. \end{cases} $

直接计算即可得出

$ \mathrm{Re}\langle\widetilde{\mathcal{B}}_bU, U\rangle_{\mathcal{\widetilde{H}}}=-\int_{\Gamma_1}|\partial_{\mu}u_t|^2{\rm d}\Gamma. $

由此可知算子 $ \widetilde{\mathcal{B}}_b $ 是耗散的. 然后, 利用线性半群理论, $ \widetilde{\mathcal{B}}_b $ 在 $ \widetilde{\mathcal{H}} $ 上可以生成一个 $ C_0 $-压缩半群 $ \widetilde{S}_b(t) $. 此外, 可得以下能量等式

$\begin{matrix}\label{Ej(t)-Ej(0)} \widetilde{E}_j(t)-\widetilde{E}_j(0)=-\int_0^t\int_{\Gamma_1}|\partial_{\tau}^{j+2}u|^2{\rm d}\Gamma {\rm d}\tau, \ \ \forall t>0, \ j=1,2,\cdots. \end{matrix}$

4 全局耦合系统的稳定性

在本部分, 我们将研究在适当的几何假设 2.1 和耦合系数的有界性条件 (2.8) 下, 全局耦合系统 (1.1), (1.2) 的镇定. 为简单起见, 我们假设 $ b(x)=b $ 是一个正的常数.

4.1 系统 (1.1) 的指数稳定性

在这里, 我们将利用一些几何乘子来证明系统 (1.1) 的指数衰减率. 为此, 首先给出如下关于隐性正则性的引理.

引理4.1 令 $ \Omega\subset \mathbb{R}^n $ 是一个边界为 $ \Gamma $ 的 $ C^{\infty} $ 紧连通的黎曼流形. 那么, 存在 $ C_{\widehat{H}}>0 $, 使得

$\begin{matrix}\label{L4} \int_{\Sigma_1}|\partial_{\mu}y|^2 \leq &C_{\widehat{H}}E(0)+C_{\widehat{H}}\int_0^TE(t){\rm d}t, \end{matrix}$

其中 $ C_{\widehat{H}} $ 是一个与向量场 $ \widehat{H} $ 有关的常数.

证 令 $ \widehat{H} $ 为 $ \overline{\Omega} $ 上的向量场, 满足

$\Gamma_0 \text{上} \widehat{H}=0, \ \ \ \ \Gamma_1 \text{上} \widehat{H}=\mu.$

用 $ 2\widehat{H}(y) $ 去乘以 (1.1) 式的第一个方程, 并在 $ Q $ 上积分可得

$0=\int_Q2y_{tt}\widehat{H}(y)-2\Delta_gy\widehat{H}(y)-2b\Delta_gu\widehat{H}(y).$

首先, 对 (4.2) 式右边的各项进行计算. 利用引理 2.1 以及 $ y|_{\Gamma}=0 $ 可得

$\begin{matrix}\label{L4-2} 2\int_Qy_{tt}\widehat{H}(y) =&\int_Q\text{div}_g \widehat{H} |y_t|^2+2\bigg[\int_{\Omega}y_t\widehat{H}(y){\rm d}x\bigg]_0^T, \end{matrix}$
$\begin{matrix}\label{L4-3} -2\int_Q\Delta_gy\widehat{H}(y) =&\int_Q2D\widehat{H}(\nabla_g y, \nabla_g y)-\text{div} \widehat{H} |\nabla_g y|_g^2 +\int_{\Sigma}\langle \widehat{H},\mu\rangle_g|\nabla_g y|_g^2-2\partial_{\mu}y\widehat{H}(y). \end{matrix}$

接下来, 结合 (4.2)-(4.4) 式可得下面估计

$\begin{matrix}\label{L4-4} \int_{\Sigma_1}|\partial_{\mu} y|^2 \leq &C_{\widehat{H}}E(0)+C_{\widehat{H}}\int_0^TE(t){\rm d}t, \end{matrix}$

其中 $ y|_{\Gamma}=0 $ 表明 $ \Gamma $ 上满足

$ \nabla_g y=\langle\nabla_g y, \mu\rangle_g\mu=\partial_{\mu}y \cdot\mu $

和

$ \partial_{\mu}y\widehat{H}(y)=\partial_{\mu}y\langle \widehat{H}, \nabla_gy\rangle_g=|\partial_{\mu}y|^2\langle \widehat{H},\mu\rangle_g. $

为了清楚起见, 在定理证明之前先用黎曼几何方法建立一些估计值.

引理4.2 令 $ (y,u) $ 是系统 (1.1) 的弱解, 那么

$\begin{matrix}\label{E1-2} \int_Q|y_t|^2{\rm d}x{\rm d}t \leq 2(1+\tau_1)E(0)+\int_Q\Big(1+\frac{b\tau_1}{2}\Big)|\nabla_g y|_g^2+\frac{b}{2}|\Delta_gu|^2, \end{matrix}$
$\begin{matrix}\label{E2-2} &\beta\int_Q|\nabla_g u_t|_g^2-|\Delta_gu|^2 =\beta\bigg[\int_{\Omega}\langle\nabla_g u, \nabla_g u_{t}\rangle_g{\rm d}x\bigg]_{0}^T-\beta\int_{\Sigma_1}u_{tt}\partial_{\mu}u-b\beta\int_Q \Delta_gu y, \end{matrix}$
$\begin{matrix}\label{E3-5} \int_Q|\nabla_g y|_g^2 \leq &\int_Q|\Delta_gu|^2+\frac{2+C_\epsilon+\epsilon C_{\widehat{H}}}{b}E(0)+\frac{\epsilon C_{\widehat{H}}}{b} \int_0^TE(t){\rm d}t, \end{matrix}$

其中 $ \beta $ 是一个正的常数, $ \epsilon>0 $ 可以取任意小.

证 用 $ y $ 去乘以 (1.1) 式的第一个方程并在 $ Q $ 上进行积分, 可得

$\begin{matrix}\label{E1-1} 0 =\int_Q|y_t|^2-|\nabla_g y|_g^2+by\Delta_gu-\bigg[\int_{\Omega}yy_t{\rm d}x\bigg]_0^T, \end{matrix}$

此处用到了 $ y|_{\Gamma}=0 $. 利用 Young 不等式可以建立估计 (4.6) 式.

令 $ \beta $ 是一个正的常数. 将 (1.1) 式中的第二个方程乘以 $ \beta \Delta_gu $, 并在 $ Q $ 上进行积分可得

$\begin{matrix}\label{E2-1} 0=&\beta\int_Q |\nabla_g u_t|_g^2-|\Delta_gu|^2+b\Delta_gu y-\beta\bigg[\int_{\Omega}\langle\nabla_g u, \nabla_g u_{t}\rangle_g{\rm d}x\bigg]_{0}^T+\beta\int_{\Sigma_1}u_{tt}\partial_{\mu}u, \end{matrix}$

此处用到了 Green 公式, 分部积分公式以及 $ u|_{\Gamma_0}=0 $. 由此可得等式 (4.7) 成立.

下证 (4.8) 式, 它是主要结果证明中的重要成分.

用 $ \Delta_gy $ 去乘以 (1.1) 式的第二个方程, 在 $ Q $ 上进行积分, 并利用引理 2.1 可得

$\begin{matrix}\label{E3-1} 0=&-\int_Q\langle\nabla_g u_{tt}, \nabla_g y\rangle_g-\Delta_gu\Delta_gy-b|\nabla_g y|_g^2+\int_{\Sigma_1}u_{tt}\partial_{\mu}y, \end{matrix}$

此处用到了 $ y|_{\Gamma}=0, u|_{\Gamma_0}=0 $ 以及 Green 公式. 类似的, 再用 $ \Delta_gu $ 去乘以 (1.1) 式的第一个方程并在 $ Q $ 上进行积分可得

$\begin{matrix}\label{E3-2} 0 =&-\int_Q\langle\nabla_g y, \nabla_g u_{tt}\rangle_g+\Delta_gy\Delta_gu+b|\Delta_gu|^2-\bigg[\int_{\Omega}y\Delta_gu_t-y_t\Delta_gu{\rm d}x\bigg]_0^T. \end{matrix}$

从 (4.11) 和 (4.12) 式可以得出, 对于 $ \forall \epsilon>0 $

$\begin{matrix}\label{E3-3} \int_Q|\nabla_g y|_g^2 \leq &\int_Q|\Delta_gu|^2+\frac{2+C_{\epsilon}}{b}E(0)+\frac{\epsilon }{b}\int_{\Sigma_1}|\partial_{\mu}y|^2. \end{matrix}$

最后, 将 (4.1) 式代入 (4.13) 式可得 (4.8) 式.

引理4.3 令 $ (y,u) $ 是系统 (1.1) 的弱解, 那么

$\int_Q|\Delta_gu|^2+|\nabla_g u_t|_g^2\leq \frac{C_0}{\alpha}E(0)+\epsilon \frac{C_1}{\alpha}\int_0^TE(t){\rm d}t,$

其中 $ \epsilon>0 $ 可以取任意小, $ \alpha, C_0, C_1 $ 将在之后给定.

证 用 $ 2H(\Delta_gu)+(\text{div}_{g}H-\rho)\Delta_gu $ 去乘以 (1.1) 的第二个方程, 在 $ Q $ 上积分可得

$\begin{matrix}\label{E4-1} 0=&\int_Q(u_{tt}-\Delta_gu+by)[2H(\Delta_gu)+(\text{div}_{g}H-\rho)\Delta_gu]. \end{matrix}$

下面去估计 (4.15) 式右边各项. 首先, 利用引理 2.1 可得

$\begin{matrix}\label{E4-2} &\int_Q-\Delta_gu[2H(\Delta_gu) +(\text{div}_{g}H-\rho)\Delta_gu]\notag\\ =&-\int_QH(|\Delta_gu|^2)-(\text{div}_{g}H-\rho)|\Delta_gu|^2 =\rho\int_Q|\Delta_gu|^2-\int_{\Sigma_1}\langle H, \mu\rangle_g|\Delta_gu|^2 \end{matrix}$

和

$\begin{matrix}\label{E4-3} &\int_Qu_{tt}[2H(\Delta_gu) +(\text{div}_{g}H-\rho)\Delta_gu]\notag\\ =&\int_Q2H(u_{t})\Delta_gu_t+(\text{div}_gH+\rho)(b\Delta_guy-|\Delta_gu|^2) -2\bigg[\int_{\Omega}H(u_{t})\Delta_gu{\rm d}x\bigg]_0^T\notag\\ &+2\int_{\Sigma_1}\langle H, \mu\rangle_g\Delta_guu_{tt}, \end{matrix}$

此处用到了 $ \Gamma_0 $ 上 $ \Delta_gu=0 $. 接下来, 对 (4.17) 式右边的第一项应用引理 2.1 可得

$\begin{matrix}\label{E4-4} &\int_Q2H(u_t)\Delta_gu_t\notag\\ =&-\int_Q2DH(\nabla_g u_t, \nabla_g u_t)+\text{div}_gH|\nabla_g u_t|_g^2-\int_{\Sigma}\langle H, \mu\rangle_g|\nabla_g u_t|_g^2\notag\\ \leq&\int_Q(-2\rho+\text{div}_gH)|\nabla_g u_t|_g^2+\int_{\Sigma_0}\langle H, \mu\rangle_g|\nabla_g u_t|_g^2+\int_{\Sigma_1}2\partial_{\mu}u_{t}H(u_t)-\langle H, \mu\rangle_g|\nabla_g u_t|_g^2, \end{matrix}$

其中, 最后一步是根据 $ \Gamma_0 $ 上 $ u=0 $ 这一事实得出的, 由此可得 $ \Gamma_0 $ 上满足

$\begin{align*} & u_t=0, \ \nabla_gu_t=\langle\nabla_gu_t, \mu\rangle_g\mu=\partial_{\mu}u_t\mu, \\ &\partial_{\mu}u_tH(u_t)= \partial_{\mu}u_t\langle H, \nabla_g u_t\rangle_g=|\nabla_gu_t|_g^2\langle H, \mu\rangle_g. \end{align*}$

将 (4.16)-(4.18) 式代入 (4.15) 式可得

$\begin{matrix}\label{E4-6} &-\int_Q(\text{div}_gH-2\rho)|\nabla_g u_t|_g^2+\text{div}_gH|\Delta_gu|^2\notag\\ \leq &\int_{Q}2b[H(\Delta_gu)+\text{div}_gH\Delta_gu]y-\bigg[\int_{\Omega}2H(u_t) \Delta_gu{\rm d}x\bigg]_0^T+\int_{\Sigma_1}2H(u_t)\partial_{\mu}u_{t} \notag\\&+\int_{\Sigma_1}\langle H, \mu\rangle_g(2\Delta_gu u_{tt}-|\nabla_g u_t|_g^2), \end{matrix}$

此处用到了 $ \Gamma_1 $ 上 $ \langle H, \mu\rangle_g>0 $, $ \Gamma_0 $ 上 $ \langle H, \mu\rangle_g\leq0 $.

结合 (4.19) 和 (4.7) 式, 由假设 2.1 以及 (2.5) 式可得

$\begin{matrix}\label{E4-7} &\int_Q(q_1-\beta)|\Delta_gu|^2+(\beta+2\rho-q_2)|\nabla_g u_t|_g^2\notag\\ \leq &2b\int_{Q}[H(\Delta_gu)+(\text{div}_gH-\frac{\beta}{2})\Delta_gu]y -\bigg[\int_{\Omega}2H(u_t)\Delta_gu-\beta\langle\nabla_g u, \nabla_g u_t\rangle_g{\rm d}x\bigg]_0^T\notag\\ &+\int_{\Sigma_1}\langle H, \mu\rangle_g(2\Delta_gu u_{tt}-|\nabla_g u_t|_g^2)+2H(u_t)\partial_{\mu}u_t-\beta u_{tt}\partial_{\mu}u, \end{matrix}$

其中 $ \beta $ 是一个满足 $-2\rho+q_2<\beta<q_1 $ 的正的常数. 下面, 再去估计 (4.20) 式的右边各项. 记 $ M=\max_{\overline{\Omega}}|H|_g $, 根据边界 $ \Gamma $ 上 $ y=0 $ 以及 (2.5) 式可得

$\begin{matrix}\label{E4-8} 2b\int_{Q}H(\Delta_gu)y \leq b\int_Q(q_2+M)|\Delta_gu|^2+(q_2\tau_1+M) |\nabla_g y|_g^2. \end{matrix}$

根据 Hölder 不等式, (2.5) 和 (2.3) 式, 有

$\begin{matrix}\label{E4-9} 2b|\int_Q \Big(\text{div}_gH-\frac{\beta}{2}\Big)\Delta_guy| \leq b\int_Q\Big(q_2-\frac{\beta}{2}\Big) |\Delta_gu|^2+\tau_1\Big(q_2-\frac{\beta}{2}\Big) |\nabla_g y|_g^2. \end{matrix}$

接下来, 利用 Hölder 不等式和 (2.12) 式, 可得

$\begin{matrix}\label{E4-14} \bigg|\bigg[\int_{\Omega}2H(u_{t})\Delta_gu\bigg]_0^T\bigg|\leq 4ME(0). \end{matrix}$

再利用引理 2.1, Hölder 不等式, (2.2) 和 (2.12) 式可得

$\begin{matrix}\label{E4-13} \bigg|\beta\bigg[\int_{\Omega}\langle\nabla_g u, \nabla_g u_{t}\rangle_g\bigg]_{0}^T\bigg| \leq 2\beta(1+\tau_0+2\tau_1)E(0). \end{matrix}$

利用 $ \Gamma_1 $ 上 $ \partial_{\mu}u_t=-u_{tt} $ 以及 (3.1) 式可得

$\begin{align*} \bigg|2\int_{\Sigma_1}H(u_t)\partial_{\mu}u_t\bigg|\leq &2\int_{\Sigma_1}|H|_g |\nabla_g u_t|_g |\partial_{\mu}u_t| \leq \int_{\Sigma_1}\frac{\delta}{\Lambda}|\nabla_g u_t|_g^2+\frac{\Lambda}{\delta}M^2E(0). \end{align*}$

因此,

$\begin{matrix}\label{E4-10} \int_{\Sigma_1}2H(u_t)\partial_{\mu}u_t-\langle H, \mu\rangle_g|\nabla_g u_t|_g^2\leq \frac{\Lambda}{\delta}M^2E(0), \end{matrix}$

此处用到了 $ \Gamma_1 $ 上 $ \langle H, \mu\rangle_g=\frac{1}{|\nu_{A}|_g}H\cdot\nu>\frac{\delta}{\Lambda} $. 再利用 $ \Gamma_1 $ 上 $ \Delta_gu=u_{tt} $ 可得

$\begin{matrix}\label{E4-11} \bigg|\int_{\Sigma_1}2\langle H, \mu\rangle_g\Delta_gu\cdot u_{tt}\bigg|\leq 2ME(0). \end{matrix}$

之后, 注意到在 $ \Gamma_1 $ 上 $ \partial_{\mu}u=-u_{t} $, 再利用 (2.2) 和 (2.12) 式, 可得以下估计

$\begin{matrix}\label{E4-12} \bigg|-\int_{\Sigma_1}\beta u_{tt}\partial_{\mu}u\bigg| =&\frac{\beta}{2}\bigg|\bigg[\int_{\Gamma_1}u_{t}^2\bigg]_0^T\bigg| \leq2\beta\tau_0E(0). \end{matrix}$

将 (4.21)-(4.27) 式代入 (4.20) 式可得

$\begin{matrix}\label{E4-15} &\int_Q(q_1-\beta)|\Delta_gu|^2+(\beta+2\rho-q_2)|\nabla_g u_t|_g^2\notag\\ \leq&\bigg[6M+\frac{\Lambda}{\delta}M^2+2\beta(1+2\tau_0+2\tau_1)\bigg]E(0) +b\bigg(2q_2+M-\frac{\beta}{2}\bigg)\int_Q |\Delta_gu|^2\notag\\ &+b\bigg[\tau_1\bigg(2q_2-\frac{\beta}{2}\bigg)+M\bigg]\int_Q |\nabla_g y|_g^2. \end{matrix}$

为了完成 $ \int_Q|\Delta_gu|^2+|\nabla_g u_t|_g^2 $ 的估计, 还需要去吸收 (4.28) 式右边的积分项 $ \int_Q|\nabla_g y|_g^2 $ 和 $ \int_Q|\Delta_gu|^2 $. 利用 (4.8) 式中对 $ \int_Q|\nabla_gy|_g^2{\rm d}x{\rm d}t $ 的估计, 并结合 (4.28) 式可得

$\begin{matrix}\label{E4-16} &\int_Q(q_1-\beta)|\Delta_gu|^2+(\beta+2\rho-q_2)|\nabla_g u_t|_g^2\notag\\ \leq&C_0E(0)+b\bigg[\bigg(2q_2-\frac{\beta}{2}\bigg)(1+\tau_1)+2M\bigg]\int_Q |\Delta_gu|^2+\epsilon C_1\int_0^TE(t){\rm d}t, \end{matrix}$

其中

$\begin{align*} &C_0=6M+\frac{\Lambda}{\delta}M^2+2\beta(1+2\tau_0+2\tau_1)+(2+C_{\epsilon}+\epsilon C_{\widehat{H}})\bigg[M+\tau_1\bigg(2q_2-\frac{\beta}{2}\bigg)\bigg],\\ &C_1=C_{\widehat{H}}\bigg[\tau_1(2q_2-\frac{\beta}{2})+M\bigg]. \end{align*}$

接下来, 通过回顾条件 (2.8) 可得

$\begin{matrix}\label{E4-17} l:=(q_1-\beta)-b[(2q_2-\frac{\beta}{2})(1+\tau_1)+2M]>0. \end{matrix}$

记 $ \alpha:=\min \{l, \beta+2\rho-q_2\}>0, $ 易得 (4.14) 式成立.

定理 2.1 的证明 利用 (4.6)-(4.8), (4.14) 式和 (2.12) 式可得

$\begin{align*} \int_0^TE(t){\rm d}t< &\int_Q|\nabla_g y|_g^2+|y_t|^2+|\Delta_gu|^2+|\nabla_g u_t|_g^2 \leq C_{2}E(0)+\epsilon C_{3}\int_{0}^TE(t){\rm d}t, \end{align*}$

其中

$\begin{align*} &C_{2}=2(1+\tau_1)+\frac{2+C_{\epsilon}+\epsilon C_{\widehat{H}}}{b}\bigg(2+\frac{b\tau_1}{2}\bigg)+\frac{C_0}{\alpha}\bigg[3+\frac{b(1+\tau_1)}{2}\bigg],\\ &C_{3}=\frac{C_{\widehat{H}}}{b}\bigg(2+\frac{b\tau_1}{2}\bigg)+\frac{C_1}{\alpha}\bigg[3+\frac{b(1+\tau_1)}{2}\bigg]. \end{align*}$

令 $ T\rightarrow \infty $, 取 $ \epsilon $ 使得 $ 1-\epsilon C_{3}>\frac{1}{2} $ 可得

$\begin{align*} \int_0^\infty E(t){\rm d}t\leq 2C_{2}E(0). \end{align*}$

因此, 利用引理 2.3 并取 $ \varphi(t)=t $, 就能得到均匀指数衰减率.

4.2 系统 (1.2) 的多项式稳定性

由于缺乏隐性正则性, 为了吸收边界积分项 $ \int_{\Sigma_1}\partial_t^{j+1}y\partial_t^{j+2}u $, 用到了高阶能量法. 在证明定理 2.2 之前, 我们首先建立如下估计.

引理4.4 令 $ (y,u) $ 是系统 (1.2) 的弱解, 那么

$\begin{matrix}\label{E1'} \int_Q|\partial_t^{j+1}y|^2\leq C\widetilde{E}_j(0)+\int_{Q}\bigg(1+\frac{b\tau_1}{2}\bigg)|\nabla_g(\partial_t^{j}y)|^2 +\frac{b}{2}|\Delta_g (\partial_t^{j}u)|^2, \end{matrix}$
$\begin{matrix}\label{E2'} \beta\int_Q|\nabla_g (\partial_t^{j+1}u)|_g^2-|\Delta_g(\partial_t^{j}u)|^2\notag =&-\beta\bigg\{b\int_Q \Delta_g(\partial_t^{j}u) \partial_t^{j}y+\int_{\Sigma_1}\partial_t^{j+2}u\partial_{\mu}(\partial_t^{j}u) \\&-\bigg[\int_{\Omega}\langle\nabla_g (\partial_t^{j}u), \nabla_g (\partial_t^{j+1}u)\rangle_g\bigg]_{0}^T\bigg\}, \end{matrix}$
$\begin{matrix}\label{E3'} \int_{Q}|\nabla_g(\partial_t^jy)|_g^2\leq &\int_{Q}|\Delta_g (\partial_t^ju)|^2+\frac{C_{\epsilon}+2(\tau_0+1)}{b} [\widetilde{E}_j(0)+\widetilde{E}_{j+1}(0)]+\frac{4\epsilon \tau_0}{b} \int_0^T\widetilde{E}_j(\tau){\rm d}\tau, \end{matrix}$
$\begin{matrix}\label{E4'} \int_{Q}|\Delta_g (\partial_t^{j}u)|^2{\rm d}x{\rm d}t+\int_{Q}|\nabla_g(\partial_t^{j+1}u)|_g^2{\rm d}x{\rm d}t \leq C\widetilde{E}_j(0)+\epsilon C\int_0^T\widetilde{E}_j(t){\rm d}t, \end{matrix}$

其中 $ \epsilon>0 $ 可以取任意小, $ \beta $ 是一个正的常数.

证 注意到 $ \Gamma_0 $ 上 $ y=0 $ 以及 $ \Gamma_1 $ 上 $ \partial_{\mu}y=0 $, 用 $ \partial_t^{j}y $ 去乘以

$\partial_t^{j+2}y-\Delta_g(\partial_t^{j}y)-b\Delta_g(\partial_t^{j}u)=0$

并在 $ Q $ 上进行积分, 可得 (4.31) 式. 这一过程与 $ \int_{Q}|y_t|^2 $ 的估计类似.

用 $ \beta\Delta_g(\partial_t^{j}u) $ 去乘以

$\partial_t^{j+2}u-\Delta_g(\partial_t^{j}u)+b\partial_t^{j}y=0,$

并在 $ Q $ 上进行积分可得 (4.32) 式. 这个过程与前一部分 $ \int_Q|\nabla_g u_t|_g^2-|\Delta_gu|^2 $ 的估计相似.

下面, 我们将建立估计 (4.33) 式. 与 Dirichlet 问题 (1.1) 不同, 这里的 Neumann 问题在迹 $ y_t|_{\Gamma_1} $ 上没有隐性正则性. 为了吸收边界积分项 $ \int_{\Sigma_1}\partial_t^{j+1}y\partial_t^{j+2}u $, 我们将使用比 $ \widetilde{E}_j(0) $ 更高阶的能量.

用 $ \Delta_g (\partial_t^ju) $ 去乘以 (4.35) 式并在 $ Q $ 上进行积分, 可得

$\begin{matrix}\label{E3'-1} 0=&\int_{Q}\langle\nabla_g(\partial_t^{j+1}y), \nabla_g(\partial_t^{j+1}u)\rangle_{g}-\Delta_g(\partial_t^jy) \Delta_g (\partial_t^ju)-b|\Delta_g(\partial_t^ju)|^2\notag\\ &-\bigg[\int_{\Omega}\langle\nabla_g(\partial_t^{j+1}y), \nabla_g(\partial_t^ju)\rangle_{g}{\rm d}x\bigg]_0^T-\bigg[\int_{\Gamma_1}\partial_t^{j+1} y\partial_t^{j+1}u{\rm d}\Gamma\bigg]_0^T+\int_{\Sigma_1}\partial_t^{j+1}y \partial_t^{j+2}u, \end{matrix}$

此处用到了 $ \Gamma_0 $ 上 $ \partial_t^j y=0 $ 以及 $ \Gamma_1 $ 上 $ \partial_{\mu}(\partial_t^ju)=-\partial_t^{j+1}u $. 再用 $ \Delta_g(\partial_t^jy) $ 去乘以 (4.36) 式并在 $ Q $ 上进行积分, 可得

$\begin{matrix}\label{E3'-2} 0=&\int_{Q}\langle\nabla_g(\partial_t^{j+1}u), \nabla_g(\partial_t^{j+1}y)\rangle_{g}-\Delta_g(\partial_t^ju)\Delta_g (\partial_t^jy) -b|\nabla_g(\partial_t^jy)|_g^2\notag\\&-[\int_{\Omega}\langle\nabla_g (\partial_t^{j+1}u), \nabla_g(\partial_t^jy)\rangle_{g}{\rm d}x]_0^T, \end{matrix}$

此处用到了边界条件 $ \Gamma_0 $ 上 $ \partial_t^jy=\partial_t^ju=0 $ 以及在 $ \Gamma_1 $ 上满足 $ \partial_{\mu}(\partial_t^jy)=0 $. 从 (4.37) 和 (4.38) 式可以得出, 对 $ \forall \epsilon>0 $ 有

$\begin{align*} b\int_Q|\nabla_g(\partial_t^jy)|_g^2 \leq&b\int_Q|\Delta_g(\partial_t^{j}u)|^2+[C_\epsilon+2(\tau_0+1)] [\widetilde{E}_j(0)+\widetilde{E}_{j+1}(0)] +4\epsilon \tau_0\int_0^T\widetilde{E}_j(t){\rm d}t, \end{align*}$

此处用到了 (2.13) 式. 由此可得 (4.33) 式成立.

估计 (4.34) 式的建立与上一节估计 $ \int_{Q}|\Delta_g u|^2+ |\nabla_gu_t|_g^2 $ 的过程类似, 此处就不再赘述.

定理 2.2 的证明 回顾 $ \widetilde{E}_j(t) $ 的定义, 然后利用 (4.31)-(4.34) 式可以得到对 $ \forall t\geq T $,

$\begin{align*} \int_0^t\sum_{j=0}^{k}\widetilde{E}_j(\tau){\rm d}\tau \leq &C\sum_{j=0}^{k+1}\widetilde{E}_j(0)+(bC+\epsilon C)\int_0^t\sum_{j=0}^{k}\widetilde{E}_j(\tau){\rm d}\tau. \end{align*}$

回顾 (2.8) 式, 并取足够小的 $ \epsilon $, 有

$ 1-(bC+\epsilon C)>\frac{1}{2}, $

由此可以推断出

$\begin{matrix}\label{P3.2-1} \int_0^t\sum_{j=0}^k\widetilde{E}_j(\tau){\rm d}\tau\leq C\sum_{j=0}^{k+1}\widetilde{E}_j(0)<\infty. \end{matrix}$

再根据 $ \widetilde{E}_j(t) $ 的耗散性, 易得

$\begin{align*} \frac{\rm d}{{\rm d}t}[t\sum_{j=0}^k\widetilde{E}_j(t)]=\sum_{j=0}^k\widetilde{E}_j(t) +t\sum_{j=0}^k\frac{\rm d}{{\rm d}t}\widetilde{E}_j(t)\leq\sum_{j=0}^k\widetilde{E}_j(t), \end{align*}$

与 (4.39) 式结合可得

$\begin{align*} \sum_{j=0}^k\widetilde{E}_j(t)\leq \frac{C}{t}\sum_{j=0}^{k+1}\widetilde{E}_j(0). \end{align*}$

5 局部耦合系统的指数稳定性

这部分, 假设 $ b(\cdot)\in L^{\infty}(\Omega) $ 且

$\begin{matrix}\label{b0} \left\{ \begin{array}{ll} \|b\|_{\infty}\geq b(x)>b_0>0, & 当 x ∈ O 时, \\ b(x)=0, & 当 x ∈ \Omega \setminus O 时, \end{array} \right. \end{matrix}$

其中 $ O $ 是 $ \Omega $ 的一个子集, $ \overline{O}\cap \Gamma_0\neq \emptyset $. 注意 $ b $ 依然满足条件 (2.8) 和 (2.9). 下面, 我们将证明定理 2.3. 进一步可以得出边界条件的类型 (Dirichlet 或 Neumann) 对局部耦合系统的衰减率没有影响. 为简单起见, 记 $ F=E, \widetilde{E}. $

根据引理 2.2, 有

$\begin{matrix}\label{6-1} \int_{Q}|y_t|^2\leq 2(1+\tau_1)F(0)+\bigg(1+\frac{\tau_1\|b\|_{\infty}}{2}\bigg)\int_Q|\nabla_g y|_g^2+\frac{\|b\|_{\infty}}{2}\int_Q|\Delta_g u|^2, \end{matrix}$
$\begin{matrix}\label{6-2} \int_{Q}|\nabla_g u_t|_g^2\leq2(1+\tau_0+\tau_1)F(0)+\bigg(1+\frac{\|b\|_{\infty}}{2}\bigg)\int_Q|\Delta_g u|^2 +\frac{\tau_1\|b\|_{\infty}}{2}\int_Q|\nabla_g y|_g^2. \end{matrix}$

下面, 在引理 5.1 中先建立一个关键性的估计.

引理5.1 当 $ b(x) $ 在 $ \Omega $ 的子区域 $ O $ 内为正且 $ O\neq\Omega $, 系统 (1.1), (1.2) 的解都满足下面的不等式

$\begin{matrix}\label{L6-y u} \int_Q|\nabla_g y|_g^2+|\Delta_g u|^2 \leq C\bigg[\int_{\Sigma_1}|u_{tt}|^2+\int_{Q}b(x)(|\nabla_g y|_g^2+|\Delta_gu|^2)\bigg]. \end{matrix}$

证 为了证明估计 (5.4) 式, 采用反证法. 假设存在一个子序列

$ U_{k}(t)=(y_{k}(t), y_{kt}(t), u_{k}(t), u_{kt}(t)) $

为系统 (1.1) (或者系统 (1.2)) 在初始条件 $ U_{k0}\in \mathcal{H} $ (或者 $ U_{k0}\in \mathcal{\widetilde{H}} $) 下的解, 那么

$\begin{matrix}\label{6-4} & \int_Q|\nabla_g y_{k}|_g^2{\rm d}x{\rm d}t+\int_Q|\Delta_gu_{k}|^2{\rm d}x{\rm d}t\notag\\ &>k\bigg[\int_{\Sigma_1}|u_{k tt}|^2{\rm d}\Gamma {\rm d}t+\int_{Q}b(x)(|\nabla_g y_{k}|_g^2+|\Delta_gu_{k}|^2){\rm d}x{\rm d}t\bigg], \ \ \forall k \in \mathbb{N}. \end{matrix}$

定义

$\begin{align*} &\lambda_{k}^2:=\int_Q|\nabla_g y_{k}|_g^2{\rm d}x{\rm d}t+\int_Q|\Delta_gu_{k}|^2{\rm d}x{\rm d}t,\\ &\hat{U}_{k}(t)=(\hat{y}_{kn}(t), \hat{y}_{kt}(t), \hat{u}_k(t), \hat{u}_{knt}(t)):=\frac{U_{k}(t)}{\lambda_k}. \end{align*}$

由 (5.5) 式, 通过一个直接的计算可得

$\int_Q|\nabla_g \hat{y}_k|_g^2{\rm d}x{\rm d}t+\int_Q|\Delta_g \hat{u}_k|^2{\rm d}x{\rm d}t=1,$
$\int_{\Sigma_1}|\hat{u}_{ktt}|^2{\rm d}\Gamma {\rm d}t\leq\frac{1}{k}$

和

$\int_{Q}b(x)(|\nabla_g \hat{y}_k|_g^2+|\Delta_g \hat{u}_k|^2){\rm d}x{\rm d}t\leq\frac{1}{k}.$

根据引理 2.2, 易得

$ \int_0^TF_{\hat{y}_k, \hat{u}_k}(t){\rm d}t\leq \int_Q|\hat{y}_{kt}|^2+|\nabla_g\hat{y}_k|_g^2+|\nabla _g\hat{u}_{kt}|_g^2+|\Delta_g \hat{u}_k|^2{\rm d}x{\rm d}t. $

从 (5.2), (5.3) 和 (5.6) 式可以推导出, 存在 $ C>0 $ 使得

$\begin{matrix}\label{bounded} \int_0^TF_{\hat{y}_k, \hat{u}_k}(t){\rm d}t\leq C. \end{matrix}$

令 $ k\rightarrow \infty $, 根据 (5.8) 和 (5.7) 式可得 $ \int_Qb(x)(|\nabla_g \hat{y}_k|_g^2+|\Delta_g\hat{u}_k|^2){\rm d}x{\rm d}t \rightarrow 0 $ 以及 $ \int_{\Sigma_1}|\hat{u}_{ktt}|^2{\rm d}\Gamma{\rm d}t $ $ \rightarrow 0 $. 因此,

$\hat{u}_{ktt} \text{在空间} L^{2}(\Sigma_{1}) \text{强收敛到 0},$
$b(x)\nabla_g \hat{y}_k, b(x)\Delta_g \hat{u}_k \text{在空间} L^{2}(Q) \text{强收敛到 0}.$

结合 (2.3) 和 (5.1) 式的定义可得

$\begin{matrix}\label{limit 1-1} &b(x) \hat{y}_k \text{在空间} L^{2}(Q) \text{强收敛到 0}. \end{matrix}$

利用 (5.9) 式可知

$\hat{y}_{k} \text{在空间} H^{1}(Q) \text{弱收敛到} \hat{y},\ \ \text{在空间} L^{\infty}(0,T;H^{1}(\Omega))\text{* 弱收敛到} \hat{y},$
$\hat{y}_{kt} \text{在空间} L^{2}(Q) \text{弱收敛到} \hat{y}_{t},$
$\hat{u}_{k} \text{在空间} H^{2}(Q) \text{弱收敛到} \hat{u},\ \ \text{在空间} L^{\infty}(0,T;H^{2}(\Omega))\text{* 弱收敛到} \hat{u},$
$\hat{u}_{kt} \text{在空间} H^{1}(Q) \text{弱收敛到} \hat{u}_{t}. $

更多的, 利用 Aubin 类型紧性结果, 可以推出

$\hat{y}_{k} \text{在空间} L^{\infty}(0,T;L^2(\Omega)) \text{强收敛到} \ hat{y},$
$\hat{u}_{k} \text{在空间} L^{\infty}(0,T;H^1(\Omega)) \text{强收敛到} \ hat{u}.$

令 $ k\rightarrow \infty $, 根据 (5.10)-(5.17) 式可得在分布意义下有

$\begin{matrix}\label{zv} \begin{cases} \hat{y}_{tt}-\Delta_g \hat{y}=0 \ &\text{于} Q \text{内},\\ \hat{u}_{tt}-\Delta_g \hat{u}=0 \ &\text{于} Q \text{内},\\ \hat{y}=\hat{u}=0 \ &\text{于} \Sigma_{0} \text{上},\\ \hat{y}=0 \ \text{或者} \ \partial_{\mu} \hat{y}=0, \ \partial_{\mu} \hat{u}+\hat{u}_t=0 \ &\text{于} \Sigma_{1} \text{上} \end{cases} \end{matrix}$

和

$\int_Q|\nabla_g \hat{y}|_g^2{\rm d}x{\rm d}t+\int_Q|\Delta_g \hat{u}|^2{\rm d}x{\rm d}t=1.$

因此, $ \hat{u} $ 满足下面的系统

$\begin{matrix}\label{v system} \begin{cases} \hat{u}_{tt}-\Delta_g \hat{u}=0 \ &\text{于} Q \text{内},\\ \hat{u}=0 \ &\text{于} \Sigma_{0} \text{上},\\ \partial_{\mu} \hat{u}+\hat{u}_t=0 \ &\text{于} \Sigma_{1} \text{上}. \end{cases} \end{matrix}$

对 (5.21) 式关于时间 $ t $ 进行二阶导可得

$\begin{matrix}\label{utt system} \begin{cases} (\hat{u}_{tt})_{tt}-\Delta_g \hat{ u}_{tt}=0 \ &\text{于} Q \text{内},\\ \hat{u}_{tt}=0 \ &\text{于} \Sigma_{0} \text{上},\\ \hat{u}_{tt}=\partial_{\mu} \hat{u}_{tt}=0 \ &\text{于} \Sigma_{1} \text{上}. \end{cases} \end{matrix}$

因此, 根据波方程的解的唯一延拓性结果, 可得系统 (5.22) 只有一个唯一的零解, 即 $ \hat{u}_{tt}\equiv0 \text{于} Q \text{内}. $ 类似的, 我们可得 $ \hat{y} $ 满足下面的系统

$\begin{matrix}\label{y system} \begin{cases} \hat{y}_{tt}-\Delta_g \hat{y}=0 \ &\text{于} Q \text{内},\\ \hat{y}=0 \ \text{或者} \ \partial_{\mu} \hat{y}=0 \ &\text{于} O\times(0,T) \text{内}. \end{cases} \end{matrix}$

对 (5.23) 式关于时间进行二阶导, 可得

$\begin{align*} \begin{cases} (\hat{y}_{tt})_{tt}-\Delta_g \hat{y}_{tt}=0 \ &\text{于} Q \text{内},\\ \hat{y}_{tt}=0 \ &\text{于} O\times(0,T) \text{内}. \end{cases} \end{align*}$

再利用波动方程的唯一延拓性定理, 我们有 $ \hat{y}_{tt}\equiv0 \text{于} Q \text{内}. $ 回到 (5.19) 式,

$\begin{matrix}\label{zv2} \begin{cases} -\Delta_g \hat{y}=0 \ &\text{于} Q \text{内},\\ -\Delta_g \hat{u}=0 \ &\text{于} Q \text{内},\\ \hat{y}=\hat{u}=0 \ &\text{于} \Sigma_{0} \text{上},\\ \hat{y}=0 \ \text{或者} \ \partial_{\mu} \hat{y}=0, \ \partial_{\mu} \hat{u}+\hat{u}_t=0 \ &\text{于} \Sigma_{1} \text{上}. \end{cases} \end{matrix}$

用 $ \hat{y} $ 和 $ \Delta_g \hat{u} $ 分别去乘以 (5.24)$_1$ 和 (5.24)$_2$, 再在 $ Q $ 上进行积分可得

$0=\int_{Q}|\nabla_g \hat{y}|_{g}^2+|\Delta_g \hat{u}|^2,$

这与 (5.20) 式相矛盾.

定理 2.3 的证明 回顾条件 (2.8) 可知 $ C\|b\|_{\infty}<\frac{1}{2}. $ 再利用引理 5.1 的结果可得

$\int_{Q}|\nabla_g y|_{g}^2+|\Delta_gu|^2\leq C\int_{\Sigma_1}|u_{tt}|^2=-C\int_0^TF'(t){\rm d}t\leq CF(0).$

回顾引理 2.2, 利用 (5.2), (5.3) 和 (5.26) 式, 有以下估计

$\begin{split}\int_0^TF(t){\rm d}t&\leq \int_Q|y_{t}|^2+|\nabla_gy|_g^2+|\nabla_gu_t|_g^2+|\Delta_g u|^2\leq CF(0),\end{split}$

其中 $ F=E, \widetilde{E} $. 令 $ T\rightarrow \infty $, 有

$\int_0^{\infty}F(t){\rm d}t\leq CF(0).$

因此, 利用引理 2.3 并取 $ \varphi(t)=t $, 指数衰减率得证.

参考文献

Rao B P.

On the sensitivity of the transmission of boundary dissipation for strongly coupled and indirectly damped systems of wave equations

Z Angew Math Phys, 2019, 70(3): 1-25

[本文引用: 1]

Chai S G, Liu K S.

Boundary stabilization of the transmission of wave equations with variable coefficients

Chinese Ann Math A, 2005, 26(5): 605-612

[本文引用: 2]

Chai S G, Guo Y X.

Boundary stabilization of wave equations with variable coefficients and memory

Differ Integral Equ, 2004, 17(5/6): 669-680

[本文引用: 2]

Liu Y X.

Polynomial decay of a variable coefficient wave equation with an acoustic undamped boundary condition

J Math Anal Appl, 2019, 479(2): 1641-1652

[本文引用: 3]

Ning Z H.

Asymptotic behavior of the nonlinear Schrödinger equation on exterior domain

Math Re Lett, 2020, 27(1): 1825-1866

[本文引用: 1]

Zhao X P, Ning Z H, Shen S X.

Stabilization of the wave equation with variable coefficients and a delay in dissipative internal feedback

J Math Anal Appl, 2013, 405(1): 148-155

[本文引用: 1]

Guo B Z, Shao Z C.

On exponential stability of a semilinear wave equation with variable coefficients under the nonlinear boundary feedback

Nonlinear Anal-Theor, 2009, 71(12): 5961-5978

[本文引用: 2]

Ning Z H, Yan Q X.

Stabilization of the wave equation with variable coefficients and a delay in dissipative boundary feedback

J Math Anal Appl, 2010, 367(1): 167-173

[本文引用: 2]

Guo Z L, Chai S G.

Stabilization of the transmission wave equation with variable coefficients and interior delay

J Geom Anal, 2022, 2: 33-53

[本文引用: 1]

Feng S J, Feng D X.

Nonlinear boundary stabilization of wave equations with variable coefficients

Chinese Ann Math, 2003, 24(2): 239-248

[本文引用: 1]

Yao P F.

On the observability inequalities for exact controllability of wave equations with variable coefficients

SIAM J Control Optim, 1999, 37(5): 1568-1599

[本文引用: 3]

Lasiecka I, Triggiani R, Yao P F.

Exact controllability for second-order hyperbolic equations with variable coefficients-principal part and first-order term

Nonlinear Anal-Theor, 1997, 30(1): 111-122

[本文引用: 1]

Lasiecka I, Triggiani R, Yao P F.

Inverse/observability estimates for second-order hyperbolic equations with variable coefficients

J Math Anal Appl, 1999, 235(1): 13-57

[本文引用: 1]

Russell D L.

A general framework for the study of indirect damping mechanisms in elastic systems

J Math Anal Appl, 1993, 173(2): 339-358

[本文引用: 1]

Alabau-Boussouira F.

Stabilisation frontiere indirecte de systemes faiblement couplés

Compt Rendus Acad Sci Math, 1999, 328(11): 1015-1020

[本文引用: 4]

Alabau-Boussouira F, Cannarsa P, Komornik V.

Indirect internal stabilization of weakly coupled evolution equations

J Evol Equ, 2002, 2(2): 127-150

[本文引用: 3]

Alabau-Boussouira F, Cannarsa P, Guglielmi R.

Indirect stabilization of weakly coupled systems with hybrid boundary conditions

Math Control Relat F, 2011, 1: 413-436

[本文引用: 1]

Alabau-Boussouira F, Léautaud M.

Indirect stabilization of locally coupled wave-type systems

ESAIM Contr Optim Ca, 2012, 18(2): 548-582

[本文引用: 3]

Alabau-Boussouira F, Wang Z Q, Yu L X.

A one-step optimal energy decay formula for indirectly nonlinearly damped hyperbolic systems coupled by velocities

ESAIM Contr Optim Ca, 2017, 23(2): 721-749

[本文引用: 2]

Cavalcanti M M, Domingos Cavalcanti V N, Mansouri S, et al.

Asymptotic stability for a strongly coupled Klein-Gordon system in an inhomogeneous medium with locally distributed damping

J Differ Equ, 2020, 268(2): 447-489

[本文引用: 1]

Cavalcanti M M, Corrêa W J, Domingos Cavalcanti V N, et al.

Uniform stability for a semilinear non-homogeneous Timoshenko system with localized nonlinear damping

Z Angew Math Phys, 2021, 72: 1-20

[本文引用: 1]

Wu H, Shen C L, Yu Y L. An Introduction to Riemannian Geometry. Beijing: Peking University Press, 1989

[本文引用: 1]

Yao P F. Modeling and Control in Vibrational and Structural Dynamics:A Differential Geometric Approach. Boca Raton: CRC Press, 2011

[本文引用: 1]

Yao P F.

Observability inequalities for the Euler-Bernoulli plate with variable coefficients

Contemp Math-Singap, 2000, 268: 383-406

Martinez P.

Stabilisation de systèmes distribués semilinéaires: domaines presque étoilés et inégalités intégrales généralisées

France: University of Strasbourg, 1998

[本文引用: 1]

Martinez P.

A new method to obtain decay rate estimates for dissipative systems

ESAIM Contr Optim Ca, 1999, 4: 419-444

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发