数学物理学报, 2025, 45(2): 604-618

一类近-Hamilton 多项式系统的极限环分支问题

顾栒,, 熊艳琴,*

南京信息工程大学数学与统计学院 南京 210044

Bifurcations of Limit Cycles in a Class of Near-Hamiltonian Polynomial Systems

Gu Xun,, Xiong Yanqin,*

School of Mathematics and Statistics, Nanjing university of information science & technology, Nanjing 210044

通讯作者: * 熊艳琴，E-mail: yqxiong@nuist.edu.cn

收稿日期: 2023-12-24   修回日期: 2024-12-20  

基金资助: 国家自然科学基金(12371171)
江苏省自然科学基金面上项目(BK20221339)

Received: 2023-12-24   Revised: 2024-12-20  

Fund supported: NSFC(12371171)
Natural Science Foundation of Jiangsu Province(BK20221339)

作者简介 About authors

顾栒，E-mail:372099143@qq.com

摘要

该文主要借助 Abel 积分来研究一类近-Hamilton 多项式系统的极限环分支问题. 首先, 借助分析的技巧分别推出 Abel 积分在中心奇点处及异宿环附近的近似展开式并给出系数的计算表达式; 这些结果可以用来研究扰动系统的 Hopf 分支及异宿分支问题. 具体而言, 所讨论的近-Hamilton 多项式系统在中心奇点附近可产生 $[\frac{n+1}{4}]+[\frac{n-1}{4}]+1$ 个极限环及在异宿环附近可分支出 $2[\frac{n+1}{4}]+[\frac{n-1}{4}]$ 个极限环.

关键词： 近-Hamilton 系统; 极限环; Abel 积分; 异宿分支

Abstract

This article primarily focuses on the study of the limit cycle bifurcation problem of a class of near-Hamiltonian polynomial systems using Abel integral. First, by utilizing analytical techniques, approximate expansions of Abel integral are derived around the central singularity and in the vicinity of the heteroclinic loop, along with the calculated expressions for the coefficients. These results can be utilized to analyze the Hopf bifurcation or heteroclinic bifurcation of the perturbed system. Specifically, it is shown that the discussed near-Hamiltonian polynomial system can produce $[\frac{n+1}{4}]+[\frac{n-1}{4}]+1$ limit cycles near the central singularity and branch out $2[\frac{n+1}{4}]+[\frac{n-1}{4}]$ limit cycles near the heteroclinic loop.

Keywords： Near-Hamiltonian system; Limit cycle; Abel integral; Heteroclinic loop bicurcation

PDF (687KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

顾栒, 熊艳琴. 一类近-Hamilton 多项式系统的极限环分支问题[J]. 数学物理学报, 2025, 45(2): 604-618

Gu Xun, Xiong Yanqin. Bifurcations of Limit Cycles in a Class of Near-Hamiltonian Polynomial Systems[J]. Acta Mathematica Scientia, 2025, 45(2): 604-618

1 引言和主要结果

总所周知, 在 1900 年, 著名的德国数学家 Hilbert 在巴黎国际数学会议上提出了 23 个问题, 这些问题引起了许多数学工作者的关注, 其中第 16 个问题的后半部分是关于寻找平面 $n$ 次多项式系统的极限环个数及其分布的问题[5]. 至提出以后, 引起大量的数学学者钻研此问题, 并且获得了一系列优秀的结果, 可参考文献 [7],[6],[9],[10] 及其参考文献. 虽然提出了很多优秀的方法, 至今为止对于二次多项式拥有的极限环的最大个数依然尚待商榷. 通过具体的例子见文献 [2],[8], 我们可以知道二次多项式系统至少可以出现 4 个极限环.

为了简化此问题, 在 1977 年, Arnold[1] 提出弱化的 Hilbert 第 16 问题: 找出如下 Abel 积分

$\begin{matrix}\label{tu12a5} I(h)=\oint_{H(x,y)=h}q(x,y){\rm d}x-p(x,y){\rm d}y \end{matrix}$

最大简单零点的个数, 其中 $H$ 是关于 $x, y$ 的 $m+1$ 次多项式, $p$ 和 $q$ 是关于 $x, y$ 的 $n$ 次多项式; 此外 $H(x,y)=h$ 是代表一簇闭轨中一闭轨线. 实际上, $I(h)$ 也是近 Hamilton 系统

$\begin{matrix}\label{xj25} \dot{x}=H_y+\varepsilon p(x,y),\ \ \dot{y}=-H_x+\varepsilon q(x,y) \end{matrix}$

的首阶 Melnikov 函数. 根据文献 [3] 的第三章可知, 我们可以借助 Abel 积分 $I(h)$ 来研究近-Hamilton 系统 (1.2) 的极限环分支问题, 可参考文献 [4],[6] 等. 不难发现借助此方法来研究含幂零奇点异宿环的文章颇为少见, 本文将借助 Abel 积分来探究含幂零奇点异宿环的极限环分支问题.

主要考虑如下近-Hamilton 多项式系统

$\dot{x}=y-4y^3+\epsilon\sum_{i+j=0}^{n}a_{ij}x^iy^j,\ \\dot{y}=-4x^3+\epsilon\sum_{i+j=0}^{n}b_{ij}x^iy^j,$

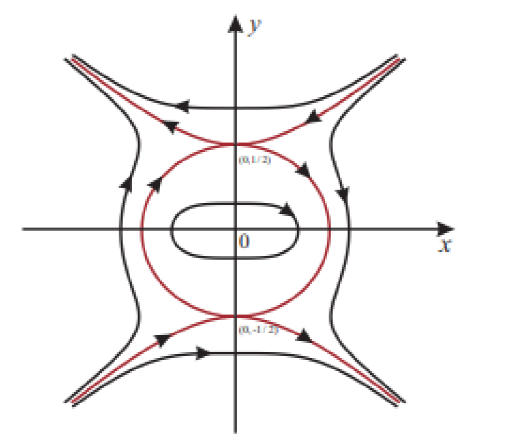
这里 $\epsilon>0$ 是小参数, $(a_{ij},b_{ij})\in\mathcal{D}\subset\mathbb{R}^{(n+1)(n+2)}$ 且 $\mathcal{D}$ 是一个有界闭集. 当 $\epsilon=0$ 时, 不难发现未扰动系统 (1)$|_{\epsilon=0}$ 有一个一阶幂零中心 $(0,0)$ 和两个一阶幂零鞍点 $(0,\pm\frac{1}{2})$ 且是一个 Hamilton 系统, 其相应的 Hamilton 函数为

$H(x,y)=\frac{1}{2}y^2-y^4+x^4.$

围绕原点有如下一簇闭轨族

$L_h:H(x,y)=h,\ \ h\in(0,\frac{1}{16})$

并以连接两个幂零鞍点 $(0,\pm\frac{1}{2})$ 的异宿环 $\mathbf{L}$ 为外边界线. 图 1 展示了系统 (1)$|_{\epsilon=0}$ 在有限平面上的相图.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   系统 $(2.1)$ 在 $\epsilon=0$ 的相图


对应于周期闭轨族 $\{ L_h | h\in(0,\frac{1}{16}) \}$, 由 (1.1) 式所定义的 Abel 积分变为

$I(h)=\oint_{L_h}\sum_{i+j=0}^{n}b_{ij}x^iy^j{\rm d}x-\sum_{i+j=0}^{n}a_{ij}x^iy^j{\rm d}y,\ \ h\in\Big(0,\frac{1}{16}\Big).$

借助 (1.6) 式, 本文的主要定理可以陈述如下.

定理1.1 对于系统 (1.3) 来说, 有如下结论成立

(i) 令 $L(n)$ 表示系统 (1.3) 在原点处的 Hopf 环性数, 则

$ L(h)=\left\{\begin{array}{l} 2([\frac{n+1}{4}]+[\frac{n-1}{4}]),\ \ 1\leq n\leq 16,\\ [2mm] [\frac{n+1}{4}]+[\frac{n-1}{4}]+1,\ \ n\geq17. \end{array}\right. $

(ii) 系统 (1.3) 在异宿环 $\mathbf{L}$ 附近可出现 $2[\frac{n+1}{4}]+[\frac{n-1}{4}],n\geq1$ 个极限环.

本文接下来安排如下: 第二部分主要给出 Abel 积分 $I(h)$ 的代数结构; 第三部分利用所得到的代数结构给出定理 1.1 的证明.

2 Abel 积分的代数结构

首先, 借助文献 [11,引理 3.1], 我们直接有

引理2.1 假设 (1.4) 和 (1.5) 式都成立, 则由 (1.6) 式定义的 $I(h)$ 可以表达成

$I(h)=\sum_{i+j=0}^{[\frac{n-1}{2}]}A_{ij}I_{ij}(h),\ \ h\in\Big(0,\frac{1}{16}\Big),$

其中

$\begin{aligned}A_{ij}=b_{2i,2j+1}+\frac{2i+1}{2j+1}a_{2i+1,2j},\quad I_{ij}(h)=\oint_{L_h}x^{2i}y^{2j+1}{\rm d}x,\end{aligned}$

且系数 $A_{ij}$ 彼此之间相互独立.

通过上述引理 2.1, 要获得 Abel 积分 $I(h)$ 的代数结构, 我们需要得到曲线积分 $I_{ij}(h)$ 的信息. 为此, 我们有如下两个引理来展示它们彼此之间的相互关系.

引理2.2 如果 (1.4) 和 (1.5) 式都成立, 那么对于 (2.2) 式所定义的函数 $I_{ij}(h)$ 我们有

$\begin{aligned}I_{ij}(h)&=\frac{2j+1}{8(i+j+1)}\Big(\frac{2i+4j-1}{2j-1}I_{i,j-1}(h)-4hI_{i,j-2}(h)\Big),\ \ i \geq0, j \geq2,\\I_{i1}(h)&=\frac{3(2i+3)}{8(i+2)}I_{i,0}(h)-\frac{3(2i-3)}{8(i+2)}hI_{i-2,0}(h)+\frac{2i-3}{2(i+2)}hI_{i-2,1}(h),\ \ i \geq2,\\I_{i0}(h)&=-\frac{2i-3}{24(i+1)}I_{i-2,1}(h)+\frac{2i-3}{2(i+1)}hI_{i-2,0}(h),\ \ i \geq2.\end{aligned}$

证 首先对 (1.4) 式中的等式两边进行微分, 可得 $ y{\rm d}y-4y^3{\rm d}y+4x^3{\rm d}x=0. $ 对上式两边同乘以因子 $x^{2i+1}y^{2j-3}$, 再把所得到的结果沿着闭轨线 $L_h$ 进行积分, 便得

$ \oint_{L_h}x^{2i+1}y^{2j-2}{\rm d}y-4\oint_{L_h}x^{2i+1}y^{2j}{\rm d}y+4\oint_{L_h}x^{2i+4}y^{2j-3}=0. $

又因为

$ -\oint_{L_h}x^{2i+1}y^{2j-2}{\rm d}y=\frac{2i+1}{2j-1}\oint_{L_h}x^{2i}y^{2j-1}{\rm d}x,\quad -\oint_{L_h}x^{2i+1}y^{2j}{\rm d}y=\frac{2i+1}{2j+1}\oint_{L_h}x^{2i}y^{2j+1}{\rm d}x, $

再根据 (2.2) 式, 则有

$-\frac{2i+1}{2j-1}I_{i,j-1}(h)+\frac{4(2i+1)}{2j+1}I_{ij}(h)+4I_{i+2,j-2}(h)=0,\quad i \geq0,\quad j \geq2.$

此外, 对 (1.4) 式中的等式两边同时乘以因子 $x^{2i}y^{2j-3}$ 并沿着闭轨线 $L_h$ 积分, 获得

$\frac{1}{2}I_{i,j-1}(h)-I_{i,j}(h)+I_{i+2,j-2}(h)=hI_{i,j-2}(h),\quad i \geq0,\quad j \geq2.$

把 (2.4) 和 (2.5) 式相结合并消去这一项 $I_{i+2,j-2}$, 得到

$8\frac{i+j+1}{2j+1}I_{i,j}(h)=\frac{2i+4j-1}{2j-1}I_{i,j-1}(h)-4hI_{i,j-2}(h),\ \ i \geq0,\quad j \geq2.$

因此, 我们获得了 (2.3) 式中的第一个表达式.

在 (2.4) 式中令 $i\rightarrow i-2$

$ 4I_{i,j-2}(h)=\frac{2i-3}{2j-1}I_{i-2,j-1}(h)-\frac{4(2i-3)}{2j+1}I_{i-2,j}(h). $

将上式代入 (2.6) 式可得

$\begin{aligned}8\frac{i+j+1}{2j+1}I_{ij}(h)\!=\! \frac{2i+4j-1}{2j-1}I_{i,j-1}(h)\!-\!\frac{2i-3}{2j-1}hI_{i-2,j-1}(h)\!+\!\frac{4(2i-3)}{2j+1}hI_{i-2,j}(h),i \geq2,j \geq1.\end{aligned}$

令 $j=1$, 我们便得到了 (2.3) 式中的第二个恒等式.

同样的, 在 (2.4) 和 (2.5) 式中令 $j=2$, 分别得到如下

$\begin{align*} -\frac{2i+1}{3}I_{i1}(h)+\frac{4(2i+1)}{5}I_{i2}(h)+4I_{i+2,0}(h)=0,\quad \frac{1}{2}I_{i1}(h)-I_{i2}(h)+I_{i+2,0}(h)=hI_{i0}(h). \end{align*}$

消去 $I_{i2}(h)$, 得

$ \frac{8}{5}(i+3)I_{i+2,0}(h)=-\frac{2i+1}{15}I_{i1}(h)+\frac{4}{5}(2i+1)hI_{i0}(h) $

并令 $i\rightarrow i-2$, 便可得到 (2.3) 式中的最后一个恒等式.

引理2.3 关于函数 $I_{2i,0}(h)$, $I_{2i+1,0}(h)$, $I_{2i,1}(h)$ 及 $I_{2i+1,1}(h)$, 当 $h\in(0,\frac{1}{16})$ 时

$\begin{aligned}&I_{2i,0}(h)=\sum_{l=1}^{i}\alpha_{2i,l}h^lI_{00}(h)+\sum_{l=0}^{i-1}\overline{\alpha}_{2i,l}h^lI_{01}(h),\\&I_{2i+1,0}(h)=\sum_{l=1}^{i}\alpha_{2i+1,l}h^lI_{10}(h)+\sum_{l=0}^{i-1}\overline{\alpha}_{2i+1,l}h^lI_{11}(h),\\&I_{2i,1}(h)=\sum_{l=0}^{i}\beta_{2i,l}h^lI_{01}(h)+\sum_{l=1}^{i}\overline{\beta}_{2i,l}h^lI_{00}(h),\\&I_{2i+1,1}(h)=\sum_{l=0}^{i}\beta_{2i+1,l}h^lI_{11}(h)+\sum_{l=1}^{i}\overline{\beta}_{2i+1,l}h^lI_{10}(h),\end{aligned}$

这里的 $\alpha_{ij},\overline{\alpha}_{ij},\beta_{ij},\overline{\beta}_{ij}$ 是常数且满足 $\alpha_{2i,i}\neq0,\alpha_{2i+1,i}\neq0,\beta_{2i,i}\neq0,\beta_{2i+1,i}\neq0,i \geq1$.

证 首先, 根据 (2.3) 式中的第二、第三式易得

$\begin{align*} I_{20}(h)=-\frac{1}{72}I_{01}(h)+\frac{1}{6}hI_{00}(h),\ \ I_{21}(h)=-\frac{7}{768}I_{01}(h)+\frac{1}{8}hI_{01}(h)+\frac{1}{64}hI_{00}(h), \end{align*}$

这意味着 (2.7) 式中的表达式 $I_{2i,0}(h)$、$I_{2i,1}(h)$ 对 $i=1$ 成立. 这里,

$\alpha_{21}=\frac{1}{6}\neq0,\ \ \beta_{2i,i}=\frac{1}{8}\neq0.$

现在, 我们假设这两式对 $i$ 成立, $i\geq1$. 则, 当 $i\rightarrow i+1$ 时, 再次利用 (2.3) 式中的第三式得

$ I_{2i+2,0}(h)=-\frac{4i+1}{24(2i+3)}I_{2i,1}(h)+\frac{4i+1}{2(2i+3)}hI_{2i,0}(h). $

根据数学归纳法

$\begin{align*} I_{2i+2,0}(h)&=-\frac{4i+1}{24(2i+3)}\Big(\sum_{l=0}^{i}\beta_{2i,l}h^lI_{01}(h)+\sum_{l=1}^{i}\overline{\beta}_{2i,l}h^lI_{00}(h)\Big)\\ &\ \ \ +\frac{4i+1}{2(2i+3)}h\bigg(\sum_{l=1}^{i}\alpha_{2i,l}h^lI_{00}(h)+\sum_{l=0}^{i-1}\overline{\alpha}_{2i,l}h^lI_{01}(h)\bigg)\\ &=\sum_{l=1}^{i+1}\alpha_{2i+2,l}h^lI_{00}(h)+\sum_{l=0}^{i}\overline{\alpha}_{2i+2,l}h^lI_{01}(h), \end{align*}$

这里

$\begin{align*} &\alpha_{2i+2,1} =-\frac{4i+1}{24(2i+3)}\overline{\beta}_{2i,1},\\ &\alpha_{2i+2,l}=-\frac{4i+1}{24(2i+3)}\overline{\beta}_{2i,l}+\frac{4i+1}{2(2i+3)}\alpha_{2i,l-1},\ \ l=2,3,\cdots,i, \\ &\alpha_{2i+2,i+1}=\frac{4i+1}{2(2i+3)}\alpha_{2i,i},\quad \overline{\alpha}_{2i+2,0}=-\frac{4i+1}{24(2i+3)}\beta_{2i,0},\\ &\overline{\alpha}_{2i+2,l}=-\frac{4i+1}{24(2i+3)}\beta_{2i,l}+\frac{4i+1}{2(2i+3)}\overline{\alpha}_{2i,l-1},\ \ l=1,2,\cdots,i. \end{align*}$

这说明 (2.7) 式中的表达式 $I_{2i,0}(h)$ 对 $i+1$ 成立. 同时, 将上述式子与 (2.8) 式相结合, 易得

$ \alpha_{2i,i}=\frac{\prod_{l=1}^{i}(4l-3)}{2^i(2i+1)!!}\neq0. $

类似地

$\begin{align*} I_{2i+2,1}(h)&=\frac{3(4i+7)}{8(2i+4)}I_{2i+2,0}(h)-\frac{3(2i+1)}{8(2i+4)}hI_{2i,0}(h)+\frac{4i+1}{2(2i+4)}hI_{2i,1}(h)\\ &=\frac{3(4i+7)}{8(2i+4)}\Big(\sum_{l=1}^{i+1}\alpha_{2i+2,l}h^lI_{00}(h)+\sum_{l=0}^{i}\overline{\alpha}_{2i+2,l}h^lI_{01}(h)\Big)\\ &\ \ \ -\frac{3(2i+1)}{8(2i+4)}h\Big(\sum_{l=1}^{i}\alpha_{2i,l}h^lI_{00}(h)+\sum_{l=0}^{i-1}\overline{\alpha}_{2i,l}h^lI_{01}(h)\Big)\\ &\ \ \ +\frac{4i+1}{2(2i+4)}h\Big(\sum_{l=0}^{i}\beta_{2i,l}h^lI_{01}(h)+\sum_{l=1}^{i}\overline{\beta}_{2i,l}h^lI_{00}(h)\Big)\\ &=\sum_{l=0}^{i+1}\beta_{2i+2,l}h^lI_{01}(h)+\sum_{l=1}^{i+1}\overline{\beta}_{2i+2,l}h^lI_{00}(h), \end{align*}$

这里

$\begin{align*} &\beta_{2i+2,0} =\frac{3(4i+7)}{8(2i+4)}{\alpha}_{2i+2,0},\\ &\beta_{2i+2,l}=\frac{3(4i+7)}{8(2i+4)}{\alpha}_{2i+2,l}-\frac{3(2i+1)}{8(2i+4)}\overline{\alpha}_{2i,l-1}+\frac{4i+1}{2(2i+4)}\beta_{2i,l-1},\ \ l=1,2,\cdots,i, \\ &\beta_{2i+2,i+1}=\frac{4i+1}{2(2i+4)}\beta_{2i,i},\quad \overline{\beta}_{2i+2,0}=\frac{3(4i+7)}{8(2i+4)}\alpha_{2i+2,1},\\ &\overline{\beta}_{2i+2,l}=\frac{3(4i+7)}{8(2i+4)}{\alpha}_{2i+2,l}-\frac{3(2i+1)}{8(2i+4)}\alpha_{2i,l-1}+\frac{4i+1}{2(2i+4)}\overline{\beta}_{2i,l-1},\ \ l=2,3,\cdots,i+1. \end{align*}$

显然, $I_{2i,1}(h)$的表达式对 $i+1$ 也成立并且

$ \beta_{2i,i}=\frac{\prod_{l=1}^{i}(4l-3)}{4^i(i+1)!}\neq0. $

同样, 我们可以运用数学归纳法来证明 (2.7) 式中的表达式 $I_{2i+1,0}(h)$、$I_{2i+1,1}(h)$ 也成立并且

$ \alpha_{2i+1,i}=\frac{\prod_{l=1}^{i}(4l-1)}{4^i(i+1)!}\neq0,\ \ \beta_{2i+1,i}=\frac{\prod_{l=1}^{i}(4l-1)}{2^i\prod_{l=1}^{i}(2l+3)}\neq0. $

根据上面的三个引理, 我们可以获得 Abel 积分 $I(h)$ 的代数结构.

命理2.1 假设 (1.4) 和 (1.5) 式都成立. 则由 (1.6) 定义的 $I(h)$ 在 $h\in(0,\frac{1}{16})$ 且 $n\geq5$ 时具有如下表达式

$I(h)=\sum_{i=0}^{[\frac{n-1}{4}]}B_{0i}h^iI_{00}(h)+\sum_{i=0}^{[\frac{n-3}{4}]}B_{1i}h^iI_{10}(h)+\sum_{i=0}^{[\frac{n-3}{4}]}B_{2i}h^iI_{01}(h)+\sum_{i=0}^{[\frac{n-5}{4}]}B_{3i}h^iI_{11}(h),$

其中 $B_{ij}$ 是关于 $A_{ij}$ 的线性函数且彼此之间相互独立并且 $A_{ij}$ 由 (2.2) 式所定义.

证 在 (2.1) 式中取 $n=5,6$, 可得

$ I(h)=A_{00}I_{00}(h)+A_{10}I_{10}(h)+A_{01}I_{01}(h)+A_{20}I_{20}(h)+A_{11}I_{11}(h)+A_{02}I_{02}(h). $

借助 (2.3) 式中的第一式 $(i=0,j=2)$ 和最后一式 $(i=2)$, 上式可重新整理成如下

$\begin{align*} I_(h)&=A_{00}I_{00}(h)+A_{10}I_{10}(h)+A_{01}I_{01}(h)+A_{11}I_{11}(h)+A_{20}\Big(-\frac{1}{72}I_{01}(h)+\frac{1}{6}hI_{00}(h)\Big)\\ &\ \ \ +A_{02}\Big(\frac{35}{72}I_{01}(h)-\frac{5}{6}hI_{00}(h)\Big)\\ &=\big(A_{00}+\frac{1}{6}(A_{20}-5A_{11})h\big)I_{00}(h)+A_{10}I_{10}(h)\\ & +\Big(A_{01}-\frac{1}{72}A_{20}+\frac{35}{72}A_{02}\Big)I_{01}(h)+A_{11}I_{11}(h), \end{align*}$

这便是 (2.9) 式中的表达式. 这里

$\begin{aligned}&B_{00}=A_{00},\ \ B_{01}=\frac{1}{6}(A_{20}-5A_{11})h,\\&B_{10}=A_{10},\ \ B_{20}=A_{01}-\frac{1}{72}A_{20}+\frac{35}{72}A_{02},\ \ B_{30}=A_{11}.\end{aligned}$

用类似的方法可推导 $n=7,8$, 有

$\begin{align*} I(h)&=A_{00}I_{00}(h)+A_{10}I_{10}(h)+A_{01}I_{01}(h)+A_{20}I_{20}(h)+A_{11}I_{11}(h)+A_{02}I_{02}(h)\\ &\ \ \ +A_{30}I_{30}(h)+A_{21}I_{21}(h)+A_{12}I_{12}(h)+A_{03}I_{03}(h)\\ &=A_{00}I_{00}(h)+A_{10}I_{10}(h)+A_{01}I_{01}(h)+A_{11}I_{11}(h)+A_{20}\Big(-\frac{1}{72}I_{01}(h)+\frac{1}{6}hI_{00}(h)\Big)\\ &\ \ \ +A_{02}\Big(\frac{35}{72}I_{01}(h)-\frac{5}{6}hI_{00}(h)\Big)+A_{30}\Big(-\frac{1}{32}I_{11}(h)+\frac{3}{8}hI_{10}(h)\Big)\\ &\ \ \ +A_{21}\Big(-\frac{7}{768}I_{01}(h)+\frac{1}{64}hI_{00}(h)+\frac{1}{8}hI_{01}(h)\Big)+A_{12}\Big(\frac{15}{32}I_{11}(h)-\frac{5}{8}hI_{10}(h)\Big)\\ &\ \ \ +A_{03}\Big(\frac{539}{2304}I_{01}(h)-\frac{77}{192}hI_{00}(h)-\frac{7}{8}hI_{01}(h)\Big). \end{align*}$

易知 (2.9) 式对 $n=7,8$, 且

$\begin{aligned}&B_{00}=A_{00},\ \ B_{01}=\frac{1}{6}A_{20}-\frac{5}{6}A_{11}+\frac{1}{64}A_{21}-\frac{77}{192}A_{03},\\&B_{10}=A_{10},\ \ B_{11}=\frac{3}{8}A_{30}-\frac{5}{8}A_{12},\\&B_{20}=A_{01}-\frac{1}{72}A_{20}+\frac{35}{72}A_{02}-\frac{7}{768}A_{21}+\frac{539}{2304}A_{03},\\&B_{21}=\frac{1}{8}A_{21}-\frac{7}{8}A_{03},\\&B_{30}=A_{11}-\frac{1}{32}A_{30}+\frac{15}{32}A_{12}.\end{aligned}$

假设 (2.9) 式对 $n=4k-3,4k-2,4k-1,4k,k\geq2$ 成立. 那么, 当 $n=4k+1,4k+2$ 时, 一方面根据 (2.1) 式可得

$I(h)=\sum_{i+j=0}^{2k}A_{ij}I_{ij}(h)=\sum_{i+j=0}^{2k-1}A_{ij}I_{ij}(h)+\sum_{i+j=2k}A_{ij}I_{ij}(h).$

另一方面, 借助 (2.3) 中的第一式, 可得出

$\begin{align*} &\ \ \ \sum_{i+j=2k}A_{ij}I_{ij}(h)\\ &=\sum_{i+j=2k,j\geq2}A_{ij}I_{ij}(h)+A_{2k,0}I_{2k,0}(h)+A_{2k-1,1}I_{2k-1,1}(h)\\ &=\sum_{i+j=2k,j\geq2}\frac{2j+1}{8(i+j+1)}A_{ij}\Big(\frac{2i+4j-1}{2j-1}I_{i,j-1}(h)\!-\!4hI_{i,j-2}(h)\Big)\!+\!A_{2k,0}I_{2k,0}(h)\!+\!A_{2k,1}I_{2k,1}(h)\\ &=\sum_{i+j=2k-1}\frac{2j+3}{8(i+j+2)}\frac{2i+4j+3}{2j+1}A_{i,j+1}I_{ij}(h)-h\sum_{i+j=2k-2}\frac{2j+3}{2(i+j+3)}A_{i,j+2}I_{ij}(h)\\ &\ \ \ +A_{2k,0}I_{2k,0}(h)+A_{2k-1,1}I_{2k-1,1}(h). \end{align*}$

因此, 由引理 2.3, (2.12) 式可以重新整理得

$\begin{align*} I(h)&=\sum_{i+j=0}^{2k-1}A_{ij}^{*}I_{ij}(h)+h\sum_{i+j=[\frac{4k-4}{2}] or [\frac{4k-3}{2}]}\overline{A}_{ij}I_{ij}(h)\\ & +A_{2k,0}\Big(\sum_{l=1}^{k}\alpha_{2k,l}h^lI_{00}(h)+\sum_{l=0}^{k-1}\overline{\alpha}_{2k,l}h^lI_{01}(h)\Big)\\ &\ \ \ +A_{2k-1,1}\Big(\sum_{l=0}^{k-1}\beta_{2k-1,l}h^lI_{11}(h)+\sum_{l=1}^{k-1}\overline{\beta}_{2k-1,l}h^lI_{10}(h)\Big), \end{align*}$

这就意味着 (2.9) 式对 $n=4k+1,4k+2$ 也是成立的. 用相似的方法, 不难证明该结论对 $n=4k+3,4k+4$ 也成立.

接下来, 对 $n=4k-3,4k-2$ 和 $n=4k-1,4k,k\geq2$, 我们分别标记行列式如下

$\begin{aligned}&\ \ \ \frac{\partial(B_{00},B_{10},B_{20},B_{30};B_{01},B_{11},B_{21},B_{31};B_{02},B_{12},B_{22},B_{32};\cdots;B_{0,k-2},B_{1,k-2},B_{2,k-2},B_{3,k-2},B_{0,k-1})}{\partial(A_{00},A_{10},A_{01},A_{11},A_{20},A_{30},A_{21},A_{40},A_{31},A_{50},A_{41},\cdots,A_{2k-2,0},A_{2k-3,1})}\\&\triangleq\left| \mathcal{A}_{4k-2} \right|=\left| \mathcal{A}_{2[\frac{n+1}{2}]} \right|,\\&\ \ \ \frac{\partial(B_{00},B_{10},B_{20},B_{30};B_{01},B_{11},B_{21},B_{31};\cdots;B_{0,k-2},B_{1,k-2},B_{2,k-2},B_{3,k-2},B_{0,k-1},B_{1,k-1},B_{2,k-1})}{\partial(A_{00},A_{10},A_{01},A_{11},A_{20},A_{30},A_{21},A_{40},A_{31},A_{50},A_{41},\cdots,A_{2k-2,0},A_{2k-3,1},A_{2k-1,0},A_{2k-2,1})}\\&\triangleq\left| \mathcal{A}_{4k} \right|=\left |\mathcal{A}_{2[\frac{n+1}{2}]} \right|.\end{aligned}$

借助 (2.10) 和 (2.11) 式, 我们再根据根据引理 2.3, 不难得到

$\begin{align*} &\left| \mathcal{A}_6 \right| = \begin{vmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & -\frac{1}{72} \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -\frac{5}{6} & \frac{1}{6} \\ \end{vmatrix} =\frac{1}{6}=\alpha_{21}\neq0,\\ &\left| \mathcal{A}_8 \right| = \begin{vmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & -\frac{1}{72} & 0 & -\frac{7}{768} \\ 0 & 0 & 0 & 1 & 0 & -\frac{1}{32} & 0 \\ 0 & 0 & 0 & -\frac{5}{6} & \frac{1}{6} & 0 & \frac{1}{64} \\ 0 & 0 & 0 & 0 & 0 & \frac{3}{8} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{8} \\ \end{vmatrix} =\frac{3}{64}\left| \mathcal{A}_6 \right|=\alpha_{21}\beta_{21}\alpha_{31}\neq0. \end{align*}$

另一方面, 根据上面的讨论, 易得

$\begin{align*} &\left| \mathcal{A}_{4k-2} \right|=\beta_{2k-3,k-2}\alpha_{2k-2,k-1}\left| \mathcal{A}_{4k-4} \right|,k\geq3, &\left| \mathcal{A}_{4k} \right|=\beta_{2k-2,k-1}\alpha_{2k-1,k-1}\left| \mathcal{A}_{4k-2} \right|,k\geq2. \end{align*}$

从而,

$ \left| \mathcal{A}_{2[\frac{n+1}{2}]} \right|=\alpha_{21}\sum_{i=2}^{[\frac{n-3}{2}]}\beta_{i,[\frac{i}{2}]}\alpha_{i+1,[\frac{i+1}{2}]}\neq0,n\geq5. $

这就意味着 (2.9) 式中的系数是相互之间彼此独立的.

根据引理 2.1, 不难得到如下两个推论.

推论2.1 假设 (1.4) 和 (1.5) 式都成立. 当 $n=1,2,3,4$ 时, $I(h)$ 可以表示为

$ I(h)= \begin{cases} A_{00}I_{00}(h), & n=1,2,\\ A_{00}I_{00}(h)+A_{10}I_{10}(h)+A_{01}I_{01}(h), & n=3,4. \end{cases} \ \ h \in \left(0, \frac{1}{16}\right). $

推论2.2 假设 (1.4) 和 (1.5) 式都成立. 当 $n\geq5$ 时, 由 (2.9) 式所定义的函数 $I(h)$ 在 $h\in(0,\frac{1}{16})$ 可以被改写为

$\begin{aligned}I(h)&=\sum_{i=0}^{[\frac{n-1}{4}]}D_{0i}(\frac{1}{16}-h)^iI_{00}(h)+\sum_{i=0}^{[\frac{n-3}{4}]}D_{1i}(\frac{1}{16}-h)^iI_{10}(h)\\&\ \ \ +\sum_{i=0}^{[\frac{n-3}{4}]}D_{2i}(\frac{1}{16}-h)^iI_{01}(h)+\sum_{i=0}^{[\frac{n-5}{4}]}D_{3i}(\frac{1}{16}-h)^iI_{11}(h),\end{aligned}$

这里的所有的参数 $D_{ij}$ 彼此之间也是相互独立的.

3 定理 1.1 的证明

关于函数 $I_{00}(h),I_{10}(h),I_{01}(h),I_{11}(h)$, 我们首先有

引理3.1 由 (2.9) 式中所给出的函数 $I_{00}(h),I_{10}(h),I_{01}(h),I_{11}(h)$, 在 $h \in \left(0, \frac{1}{16}\right)$ 时, 满足

$I'_{01}(h)=12hI'_{00}(h)-6I_{00}(h),\ I'_{11}(h)=12hI'_{10}(h)-12I_{10}(h).$

证 运用文献 [3,引理 3.1.2], 可以得到

$ I'_{ij}(h)=(2j+1)\oint_{L_h}x^{2i}y^{2j}{\rm d}t. $

再沿着曲线 $L_h:{\rm d}t=\frac{{\rm d}x}{y-4y^3}$ 进行积分得到

$I'_{ij}(h)=(2j+1)\oint_{L_h}\frac{x^{2i}y^{2j-1}}{1-4y^2}{\rm d}x.$

可以推出

$\begin{aligned}I_{ij}(h)&=\frac{1}{2j+3}I'_{i,j+1}(h)-\frac{4}{2j+5}I'_{i,j+2}(h),\\hI'_{ij}(h)&=(2j+1)\oint_{L_h}\frac{x^{2i}y^{2j-1}(\frac{1}{2}y^2-y^4+x^4)}{1-4y^2}{\rm d}x\\&=\frac{2j+1}{2(2j+3)}I'_{i,j+1}(h)-\frac{2j+1}{2j+5}I'_{i,j+2}(h)+I'_{i+2,j}(h).\end{aligned}$

从另一个角度来看, 根据 ${\rm d}y=\frac{-4x^3}{y-4y^3}{\rm d}x$, 我们可以推出

$I_{ij}(h)=-\frac{2j+1}{2i+1}\oint_{L_h}x^{2i+1}y^{2j}{\rm d}y=\frac{4(2j+1)}{2i+1}\oint_{L_h}\frac{x^{2i+4}y^{2j-1}}{1-4y^2}{\rm d}x=\frac{4}{2i+1}I'_{i+2,j}(h).$

因此, 把 (3.2)、 (3.3) 和 (3.4) 三式相结合, 不难发现

$ hI'_{ij}(h)=\frac{2j+1}{4(2j+3)}I'_{i,j+1}(h)+\frac{1}{2}(i+j+1)I_{ij}(h). $

通过取 $(i,j)=(0,0), (1,0)$, 这便是我们的结论.

在引理 3.1 的帮助下, 可以给出函数 $I_{00}(h),I_{10}(h),I_{01}(h),I_{11}(h)$ 在 $h=0$ 和 $h=\frac{1}{16}$ 处的近似展开式.

引理3.2 由 (2.9) 式中所给出的函数 $I_{00}(h),I_{10}(h),I_{01}(h),I_{11}(h)$ 在 $0<h\ll1$ 时分别可以展开为

$\begin{aligned}I_{00}(h)&=h^{\frac{3}{4}}\sum_{l\geq0}\varrho_{0l}h^l,\ \ \ \ \ \ \ \ \ \ \ \ I_{10}(h)=h^{\frac{5}{4}}\sum_{l\geq0}\varrho_{1l}h^l,\\I_{01}(h)&=h^{\frac{7}{4}}\sum_{l\geq0}\frac{48l+12}{4l+7}\varrho_{0l}h^l,\ I_{11}(h)=h^{\frac{9}{4}}\sum_{l\geq0}\frac{48l+12}{4l+9}\varrho_{1l}h^l,\end{aligned}$

这里的所有 $\varrho_{il},i=1,0,l\geq0$ 都是常数且满足

$\begin{aligned}&\varrho_{i0}=\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{3}{2}),\ \ \ \ \ \ \ \ \varrho_{i1}=2\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{5}{2}),\\&\varrho_{i2}=14\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{7}{2}),\ \ \ \ \ \\varrho_{i3}=132\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{9}{2}),\\&\varrho_{i4}=1430\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{11}{2}),\ \ \varrho_{i5}=16796\sqrt{2}\mathbf{B}(\frac{2i+1}{4},\frac{13}{2}).\end{aligned}$

这里 $\mathbf{B}$ 是指 Beta 函数.

证 通过 (1.4)、 (1.5) 和 (2.2) 式, 我们易推导出

$\begin{aligned}I_{i0}(h)&=2\int_{0}^{h^{\frac{1}{4}}}x^{2i}(1-\sqrt{1-16(h-x^4)})^{\frac{1}{2}}{\rm d}x\ \ (\mbox{令} x=h^{\frac{1}{4}}t)\\&=2h^{\frac{2i+1}{4}}\int_{0}^{1}t^{2i}(1-\sqrt{1-16h(1-t^4)})^{\frac{1}{2}}{\rm d}t.\end{aligned}$

注意到 $t\in[0,1]$, 则对于足够小的正数 $h$, 有 $16(1-t^4)\in[0,1]$. 从而,

$\begin{align*} 1-\sqrt{1-16h(1-t^4)}&=8h(1-t^4)+\sum_{k\geq2}\frac{(2k-3)!!}{(2k)!!}16^kh^k(1-t^4)^k\\ &=8h(1-t^4)\Big(1+\sum_{k\geq1}\frac{(2k-1)!!}{(2k+2)!!}16^kh^k(1-t^4)^k\Big). \end{align*}$

进而可以推出

$\begin{align*} (1-\sqrt{1-16h(1-t^4)})^{\frac{1}{2}} &=2\sqrt{2}h^{\frac{1}{2}}(1-t^4)^{\frac{1}{2}}\Big(1+\sum_{k\geq1}\frac{(2k-1)!!}{(2k+2)!!}16^kh^k(1-t^4)^k\Big)^{\frac{1}{2}}\\ &=2\sqrt{2}h^{\frac{1}{2}}(1-t^4)^{\frac{1}{2}}\Big(1+\frac{1}{2}\sum_{k\geq1}\frac{(2k-1)!!}{(2k+2)!!}16^kh^k(1-t^4)^k\\ &\ \ \ -\sum_{l\geq2}(-1)^l\frac{(2l-3)!!}{(2l)!!}\big(\sum_{k\geq1}\frac{(2k-1)!!}{(2k+2)!!}16^kh^k(1-t^4)^k\big)^l\Big)\\ &=2\sqrt{2}h^{\frac{1}{2}}(1-t^4)^{\frac{1}{2}}\sum_{l\geq0}\overline{\varrho}_lh^l(1-t^4)^l, \end{align*}$

这里 $\overline{\varrho}_l$ 都是常数并满足

$ \overline{\varrho}_0=1,\ \ \overline{\varrho}_1=2,\ \ \overline{\varrho}_2=14,\ \ \overline{\varrho}_3=132,\ \ \overline{\varrho}_4=1430,\ \ \overline{\varrho}_5=16796. $

因此, (3.7) 式可重新改写成如下

$ I_{i0}=4\sqrt{2}h^{\frac{2i+3}{4}}\sum_{l\geq0}\overline{\varrho}_lh^l\int_{0}^{1}t^{2i}(1-t^4)^{l+\frac{1}{2}}{\rm d}t. $

这就给出了 (3.5) 式中函数 $I_{00}(h)$ 和 $I_{10}(h)$ 的表达式并满足

$ \varrho_{il}=4\sqrt{2}\overline{\varrho}_l\int_{0}^{1}t^{2i}(1-t^4)^{l+\frac{1}{2}}{\rm d}t,\ \ i=0,1. $

通过直接计算便可得 (3.6) 式.

此外, 借助引理 3.1 易得函数 $I_{01}(h)$ 和 $I_{11}(h)$ 在 $h=0$ 处的近似展开式.

引理3.3 由 (2.9) 式中所给出的函数 $I_{00}(h),I_{10}(h),I_{01}(h),I_{11}(h)$ 在 $0<\frac{1}{16}-h\ll1$ 时分别可展开为

$\small\begin{aligned}I_{00}(h)&=\eta_{000}+\eta^{*}_{000}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}+\sum_{l\geq1}\Big(\eta_{00l}+\tilde{\eta}_{00l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta^{*}_{00l}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l,\\I_{10}(h)&=\eta_{100}+\sum_{l\geq1}\Big(\eta_{10l}+\tilde{\eta}_{10l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta^{*}_{10l}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l,\\I_{01}(h)&=\eta_{010}+\eta^{*}_{010}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}+\sum_{l\geq1}\Big(\eta_{01l}+\tilde{\eta}_{01l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta^{*}_{01l}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l,\\I_{11}(h)&=\eta_{110}+\sum_{l\geq1}\Big(\eta_{11l}+\tilde{\eta}_{11l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta^{*}_{11l}\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l,\end{aligned}$

这里的所有系数 $\eta_{ijl}, \eta_{ijl}^*$ 是常数并满足

$\begin{aligned}\eta_{000}&=\frac{\pi}{4},\ \ \ \ \eta_{100}=\frac{\pi}{64},\ \ \ \ \eta_{010}=\frac{3\pi}{16},\ \ \eta_{110}=\frac{\pi}{128},\\\eta^{*}_{000}&=4\overline{A}_0,\ \ \eta^{*}_{010}=3\overline{A}_0,\ \ \tilde{\eta}_{101}=8\overline{A}_1,\ \ \tilde{\eta}_{111}=6\overline{A}_1\end{aligned}$

且 $\overline{A}_0>0,\overline{A}_1<0$.

证 借助文献 [3,注 3.1.4], 对 (2.9) 式中的曲线积分 $I_{00},I_{10}$ 做变量替换 $\mu=x,\nu=y-\frac{1}{2},\tau=-2t$ 得

$\begin{align*} I_{00}(h)=2\oint_{\frac{1}{2}\nu^2-\nu^3+\frac{1}{2}\nu^4-\frac{1}{2}\mu^4=-\frac{1}{2}h+\frac{1}{32}}\nu {\rm d}\mu,\ \ \ I_{10}(h)=2\oint_{\frac{1}{2}\nu^2-\nu^3+\frac{1}{2}\nu^4-\frac{1}{2}\mu^4=-\frac{1}{2}h+\frac{1}{32}}\mu^2\nu {\rm d}\mu. \end{align*}$

再借助文献 [3,定理 3.6.5], 当 $0<-\frac{1}{2}h+\frac{1}{32}\ll1$ 时, 我们有

$\begin{align*} I_{00}(h)&=\eta_{00}+\eta^{*}_{00}\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^{\frac{3}{4}}+\sum_{l\geq1}\Big(\eta_{0l}+\tilde{\eta}_{0l}\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^{\frac{1}{4}}+\eta^{*}_{0l}\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^{\frac{3}{4}}\Big)\\ &\ \ \ \times \Big(-\frac{1}{2}h+\frac{1}{32}\Big)^l,\\ I_{10}(h)&=\eta_{10}+\sum_{l\geq1}\Big(\eta_{1l}+\tilde{\eta}_{1l}\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^{\frac{1}{4}}+\eta^{*}_{1l}\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^{\frac{3}{4}}\Big)\Big(-\frac{1}{2}h+\frac{1}{32}\Big)^l, \end{align*}$

其中的所有系数都是常数且满足

$\begin{align*} \eta_{00}&=\oint_{L_{\frac{1}{16}}}y{\rm d}x=\frac{\pi}{4},\ \ \eta_{10}=\oint_{L_{\frac{1}{16}}}x^2y{\rm d}x=\frac{\pi}{64},\ \ \tilde{\eta}_{00}=2^{\frac{11}{4}}\overline{A}_0,\ \ \tilde{\eta}_{11}=2^{\frac{13}{4}}\overline{A}_1, \end{align*}$

这里 $\overline{A}_0>0,\overline{A}_1<0$. 因此, 再借助引理 3.1, 易得该结论成立.

现在, 我们提供定理的证明.

证 (定理 1.1 的证明) 当 $n=4k+1,4k+2,k\geq1$ 时, 借助 (3.5) 式, (2.9) 式在 $h=0$ 处可以被展开成如下

$\begin{align*} I_(h)&=\sum_{i=0}^{k}B_{0i}h^iI_{00}(h)+\sum_{i=0}^{k-1}B_{1i}h^iI_{10}(h)+\sum_{i=0}^{k-1}B_{2i}h^iI_{01}(h)+\sum_{i=0}^{k-1}B_{3i}h^iI_{11}(h)\\ &=h^{\frac{3}{4}}\sum_{i=0}^{k}B_{0i}h^{i}\sum_{l\geq0}\varrho_{0l}h^l+h^{\frac{5}{4}}\sum_{i=0}^{k-1}B_{1i}h^i\sum_{l\geq0}\varrho_{1l}h^l\\ &\ \ \ +h^{\frac{7}{4}}\sum_{i=0}^{k-1}B_{2i}h^{i}\sum_{l\geq0}\frac{48l+12}{4l+7}\varrho_{0l}h^l+h^{\frac{9}{4}}\sum_{i=0}^{k-1}B_{3i}h^i\sum_{l\geq0}\frac{48l+12}{4l+9}\varrho_{1l}h^l. \end{align*}$

进而推出

$I(h)=h^{\frac{3}{4}}\sum_{i\geq0}(c_i+\overline{c}_ih^{\frac{1}{2}})h^{i},$

其中

$\begin{align*} c_0&=\varrho_{00}B_{00},\quad \overline{c}_0=\varrho_{10}B_{10},\\ c_1&=\varrho_{00}B_{01}+\frac{12}{7}\varrho_{00}B_{20}+\mathbf{L}(B_{00}),\quad \overline{c}_1=\varrho_{10}B_{11}+\frac{4}{3}\varrho_{10}B_{30}+\mathbf{L}(B_{10}),\\ c_i&=\varrho_{00}B_{0i}+\frac{12}{7}\varrho_{00}B_{2,i-1}+\mathbf{L}(B_{00},B_{01},\cdots,B_{0,i-1},B_{20},B_{21},\cdots,B_{2,i-2}),i=2,3,\cdots,k,\\ \overline{c}_i&=\varrho_{10}B_{1i}+\frac{4}{3}\varrho_{10}B_{3,i-1}+\mathbf{L}(B_{10},B_{11},\cdots,B_{1,i-1},B_{30},B_{31},\cdots,B_{3,i-2}),i=2,3,\cdots,k-1,\\ \overline{c}_k&=\frac{4}{3}\varrho_{10}B_{3,k-1}+\mathbf{L}(B_{10},B_{11},\cdots,B_{1,k-1},B_{30},B_{31},\cdots,B_{3,k-2}),\\ c_i&=\mathbf{L}(B_{00},B_{01},\cdots,B_{0,k},B_{20},B_{21},\cdots,B_{2,k-1}),i\geq k+1,\\ \overline{c}_i&=\mathbf{L}(B_{10},B_{11},\cdots,B_{1,k-1},B_{30},B_{31},\cdots,B_{3,k-1}),i\geq k+1, \end{align*}$

这里 $\mathbf{L}(\cdot)$ 是一个线性组合. 不难发现, $c_i,\overline{c}_i,i=0,1,2,\cdots,k$ 彼此之间相互独立. 因此, 我们可以自由选择它们使它们满足

$ 0<-c_0\ll\overline{c}_0\ll-c_1\ll\overline{c}_1\ll-c_2\ll\overline{c}_2\ll\cdots\ll-c_k\ll\overline{c}_k\ll1, $

这便意味着 (3.10) 式中的函数 $I(h)$ 的符号被改变了 $2k+1$ 次. 因此, 我们可以在原点附近找到 $2k+1=[\frac{n+1}{4}]+[\frac{n-1}{4}]+1$ 个极限环. 实际上, 当 $k=3$ 时,

$\begin{align*} c_0&=\varrho_{00}B_{00},\\ c_1&=\varrho_{00}B_{01}+\varrho_{01}B_{00}+\frac{12}{7}\varrho_{00}B_{20},\\ c_2&=\varrho_{00}B_{02}+\varrho_{01}B_{01}+\varrho_{02}B_{00}+\frac{60}{11}\varrho_{01}B_{20}+\frac{12}{7}\varrho_{00}B_{21},\\ c_3&=\varrho_{00}B_{03}+\varrho_{01}B_{02}+\varrho_{02}B_{01}+\varrho_{03}B_{00}+\frac{36}{5}\varrho_{02}B_{20}+\frac{60}{11}\varrho_{01}B_{21}+\frac{12}{7}\varrho_{00}B_{22},\\ c_4&=\varrho_{01}B_{03}+\varrho_{02}B_{02}+\varrho_{03}B_{01}+\varrho_{04}B_{00}+\frac{156}{19}\varrho_{03}B_{20}+\frac{36}{5}\varrho_{02}B_{21}+\frac{60}{11}\varrho_{01}B_{22},\\ c_5&=\varrho_{05}B_{00}+\varrho_{04}B_{01}+\varrho_{03}B_{02}+\varrho_{02}B_{03}+\frac{204}{23}\varrho_{04}B_{20}+\frac{156}{19}\varrho_{03}B_{21}+\frac{36}{5}\varrho_{02}B_{22},\\ c_6&=\varrho_{06}B_{00}+\varrho_{05}B_{01}+\varrho_{04}B_{02}+\varrho_{03}B_{03}+\frac{28}{3}\varrho_{05}B_{20}+\frac{204}{23}\varrho_{04}B_{21}+\frac{156}{19}\varrho_{03}B_{22},\\ \overline{c}_0&=\varrho_{10}B_{10},\\ \overline{c}_1&=\varrho_{10}B_{11}+\varrho_{11}B_{10}+\frac{4}{3}\varrho_{10}B_{30},\\ \overline{c}_2&=\varrho_{10}B_{12}+\varrho_{11}B_{11}+\varrho_{12}B_{10}+\frac{60}{13}\varrho_{11}B_{30}+\frac{4}{3}\varrho_{10}B_{31},\\ \overline{c}_3&=\varrho_{11}B_{12}+\varrho_{12}B_{11}+\varrho_{13}B_{10}+\frac{108}{17}\varrho_{12}B_{30}+\frac{60}{13}\varrho_{11}B_{31}+\frac{4}{3}\varrho_{10}B_{32},\\ \overline{c}_4&=\varrho_{12}B_{12}+\varrho_{13}B_{11}+\varrho_{14}B_{10}+\frac{52}{7}\varrho_{13}B_{30}+\frac{108}{17}\varrho_{12}B_{31}+\frac{60}{13}\varrho_{11}B_{32},\\ \overline{c}_5&=\varrho_{13}B_{12}+\varrho_{14}B_{11}+\varrho_{15}B_{10}+\frac{204}{25}\varrho_{14}B_{30}+\frac{52}{7}\varrho_{13}B_{31}+\frac{108}{17}\varrho_{12}B_{32}. \end{align*}$

利用 Maple 18 计算得

$ \det\frac{\partial(c_0,c_1,\cdots,c_6,\overline{c}_0,\overline{c}_1,\cdots,\overline{c}_5)}{\partial(B_{00},B_{01},B_{02},B_{03},B_{20},B_{21},B_{22},B_{10},B_{11},B_{12},B_{30},B_{31},B_{32})}=2.082652755\times10^{15}\neq0. $

这就意味着 $c_0,c_1,\cdots,c_6,\overline{c}_0,\overline{c}_1,\cdots,\overline{c}_5$ 是相互独立. 类似于上述过程, 在这种情况下我们能在原点附近找到 $12=4k=2([\frac{n+1}{4}]+[\frac{n-1}{4}])$ 个极限环.

对于 $n=4k+3,4k+4,k\geq1$ 和 $n=1,2,3,4$, 我们可类似的证明. 因此, 定理 1.1(i) 的结论得证.

当 $n=4k+1,4k+2,k\geq1$ 时, 根据 (3.8) 和 (3.13) 式在 $\frac{1}{16}-h>0$ 充分小时有

$\begin{align*} \begin{split} I(h)&=\sum\limits_{i=0}^{k}D_{0i}\Big(\frac{1}{16}-h\Big)^i\\ &\ \ \ \times\Big(\eta_{000}+\eta_{000}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}} +\sum\limits_{l\geq1}\Big(\eta_{00l}+\tilde{\eta}_{00l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta_{00l}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l\Big)\\ &\ \ \ +\sum\limits_{i=0}^{k-1}D_{1i}\Big(\frac{1}{16}-h\Big)^i\Big(\eta_{100}+\sum\limits_{l\geq1}\Big(\eta_{10l}+\tilde{\eta}_{10l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta_{10l}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l\Big)\\ &\ \ \ +\sum\limits_{i=0}^{k-1}D_{2i}\Big(\frac{1}{16}-h\Big)^i\\ &\ \ \ \times\Big(\eta_{010}+\eta_{010}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}} +\sum\limits_{l\geq1}\Big(\eta_{01l}+\tilde{\eta}_{01l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta_{01l}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l\Big)\\ &\ \ \ +\sum\limits_{i=0}^{k-1}D_{3i}\Big(\frac{1}{16}-h\Big)^i\Big(\eta_{110}+\sum\limits_{l\geq1}\Big(\eta_{11l}+\tilde{\eta}_{11l}\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+\eta_{11l}^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^l\Big). \end{split} \end{align*}$

重新整理上式易得

$\begin{matrix}\label{tu12b24} I(h)=b_0+b_0^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}+\sum\limits_{l\geq1}\Big(b_l+\tilde{b}_l\Big|h-\frac{1}{16}\Big|^{\frac{1}{4}}+b_l^*\Big|h-\frac{1}{16}\Big|^{\frac{3}{4}}\Big)\Big|h-\frac{1}{16}\Big|^{l}, \end{matrix}$

其中

$\begin{align*} b_0&=\eta_{000}D_{00}+\eta_{100}D_{10}+\eta_{010}D_{20}+\eta_{110}D_{30},\\ b_0^*&=\eta_{000}^*D_{00}+\eta_{010}^*D_{20},\\ \tilde{b}_1&=\tilde{\eta}_{101}D_{10}+\tilde{\eta}_{111}D_{30},\\ b_1&=\eta_{000}D_{01}+\eta_{100}D_{11}+\eta_{010}D_{21}+\eta_{110}D_{31}+\mathbf{L}(D_{00},D_{10},D_{20},D_{30}),\\ b_1^*&=\eta_{000}^*D_{01}+\eta_{010}^*D_{21}+\mathbf{L}(D_{00},D_{10},D_{20},D_{30}),\\ \tilde{b}_2&=\tilde{\eta}_{101}D_{11}+\tilde{\eta}_{111}D_{31}+\mathbf{L}(D_{00},D_{10},D_{20},D_{30},D_{01},D_{21}),\\ b_l&=\eta_{000}D_{0l}+\eta_{100}D_{1l}+\eta_{010}D_{2l}+\eta_{110}D_{3l}\\ &\ \ +\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,l-1},D_{1,l-1},D_{2,l-1},D_{3,l-1}), l=2,3,\cdots,k-1,\\ b_l^*&=\eta_{000}^*D_{0l}+\eta_{010}^*D_{2l}\\ &\ \ +\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,l-1},D_{1,l-1},D_{2,l-1},D_{3,l-1}), l=2,3,\cdots,k-1,\\ \tilde{b}_{l+1}&=\tilde{\eta}_{101}D_{1l}+\tilde{\eta}_{111}D_{3l}\\ &\ \ +\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,l-1},D_{1,l-1},D_{2,l-1},D_{3,l-1},D_{0l},D_{2l}), l=2,3,\cdots,k-1,\\ b_k&=\eta_{000}D_{0k}+\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,k-1},D_{1,k-1},D_{2,k-1},D_{3,k-1}),\\ b_l&=\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,k-1},D_{1,k-1},D_{2,k-1},D_{3,k-1},D_{0k}), l\geq k+1,\\ b_l^*&=\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,k-1},D_{1,k-1},D_{2,k-1},D_{3,k-1},D_{0k}), l\geq k,\\ \tilde{b}_l&=\mathbf{L}(D_{00},D_{10},D_{20},D_{30},\cdots,D_{0,k-1},D_{1,k-1},D_{2,k-1},D_{3,k-1},D_{0k}), l\geq k+1. \end{align*}$

从而,

$\begin{align*} &\det\frac{\partial(b_0,b_0^*,\tilde{b}_1,b_1,b_1^*,\tilde{b}_2,\cdots,b_{k-1},b_{k-1}^*,\tilde{b}_k,b_k)}{\partial(D_{00},D_{10},D_{30},D_{11},D_{11},D_{31},\cdots,D_{0,k-1},D_{1,k-1},D_{3,k-1},D_{0,k})}\\ =&\left|\begin{array}{ccccccc} \mathbf{A}_{3\times3}&\mathbf{0}_{3\times3}&\mathbf{0}_{3\times3}&\cdots&\mathbf{0}_{3\times3}&\mathbf{0}_{3\times3}&0\\ \mathbf{A}_{21}&\mathbf{A}_{3\times3}&\mathbf{0}_{3\times3}&\cdots&\mathbf{0}_{3\times3}&\mathbf{0}_{3\times3}&0\\ \mathbf{A}_{31}&\mathbf{A}_{32}&\mathbf{A}_{3\times3}&\cdots&\mathbf{0}_{3\times3}&\mathbf{0}_{3\times3}&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\ \mathbf{A}_{k-1,1}&\mathbf{A}_{k-1,2}&\mathbf{A}_{k-1,3}&\cdots&\mathbf{A}_{3\times3}&\mathbf{0}_{3\times3}&0\\ \mathbf{A}_{k,1}&\mathbf{A}_{k,2}&\mathbf{A}_{k,3}&\cdots&\mathbf{A}_{k,k-1}&\mathbf{A}_{3\times3}&0\\ \mathbf{A}_{k+1,1}&\mathbf{A}_{k+1,2}&\mathbf{A}_{k+1,3}&\cdots&\mathbf{A}_{k+1,k-1}&\mathbf{A}_{k+1,k}&\eta_{000} \end{array}\right|:=|\mathbf{A}_{(3k+1)\times(3k+1)}|, \end{align*}$

这里的 $\mathbf{0}_{3\times3}$ 是一个 3 阶零矩阵, $A_{ij},j=1,2,\cdots,i-1,i=2,3,\cdots,k$ 是 $3\times3$ 矩阵, $A_{k+1,j},j=1,2,\cdots,k$ 是$1\times3$ 矩阵且

$ \mathbf{A}_{3\times3}=\left(\begin{array}{ccc} \eta_{000}&\eta_{100}&\eta_{110}\\ \eta_{000}^*&0&0\\ 0&\tilde{\eta}_{101}&\tilde{\eta}_{111} \end{array}\right). $

此时根据 (3.9) 式, 不难计算

$\begin{align*} |\mathbf{A}_{(3k+1)\times(3k+1)}|&=\eta_{000}|\mathbf{A}_{3\times3}|^k=(-1)^k\eta_{000}(\eta_{000}^*)^k(\eta_{100}\tilde{\eta}_{111}-\eta_{110}\tilde{\eta}_{101})^k\\ &=2\eta_{000}(\tilde{\eta}_{101})^k\Big(\frac{\pi}{64}\Big)^k(\bar{A}_1)^k\neq0. \end{align*}$

这意味系数 $b_0,b_0^*,\tilde{b}_1,b_1,b_1^*,\tilde{b}_2,\cdots,b_{k-1},b_{k-1}^*,\tilde{b}_k,b_k$ 可视为自由参数. 我们可以自由选择它们使它们满足

$\begin{align*} &0<b_0\ll-b_0^*\ll b_1\ll-\tilde{b}_1\ll b_1^*\ll-b_2\ll \tilde{b}_2\ll -b_2^*\ll b_3\ll-\tilde{b}_3\ll b_3^*\ll-b_4\\ &\ll\tilde{b}_4\ll-b_4^*\ll\cdots\ll (-1)^{k-1}b_{k-2}\ll(-1)^{k-2}\tilde{b}_{k-2}\ll(-1)^{k-1}b_{k-2}^*\\ &\ll (-1)^kb_{k-1}\ll(-1)^{k-1}\tilde{b}_{k-1}\ll (-1)^kb_{k-1}^*\ll (-1)^{k+1}b_k\ll(-1)^k\tilde{b}_k\ll1. \end{align*}$

这样 (3.11) 式中的函数 $I(h)$ 的符号便被改变了 $3k=2[\frac{n-1}{4}]+[\frac{n+1}{4}]$ 次. 因此, 可在异宿环附近找到 $2[\frac{n-1}{4}]+[\frac{n+1}{4}]$ 个极限环.

对于 $n=4k+3,4k+4,k\geq1$ 和 $n=1,2,3,4$, 我们可作类似的讨论. 至此, 定理 2.1 证毕.

参考文献

Arnold V I.

Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields

Funct Anal Appl, 1977, 11(2): 85-92

[本文引用: 1]

Chen L, Wang M S.

The relative position and number of limit cycles of a quadratic differential system

Acta Math Sinica (Chin Ser), 1979, 22(6): 751-758

[本文引用: 1]

Han M. Bifurcation Theory of Limit Cycles. Beijing: Science Press, 2013

[本文引用: 4]

Han M, Yang J, Tarta A, Yang G.

Limit cycles near homoclinic and heteroclinic loops

J Dynam Differential Equations, 2008, 20: 923-944

[本文引用: 1]

Hilbert D.

Mathematical problems

Transl Bull Amer Math Soc, 1902, 8: 437-479

[本文引用: 1]

Li W, Llibre J, Zhang X.

Melnikov functions for period annulus, nondegenerate centers, heteroclinic and homoclinic cycles

Pacific J Math, 2004, 213(1): 49-77

[本文引用: 2]

Liu C, Xiao D.

The smallest upper bound on the number of zeros of Abelian integrals

J Differential Equations, 2020, 269: 3816-3852

[本文引用: 1]

Shi S.

A concrete example of the existence of four limit cycles for plane quadratic systems

Sci Sinica, 1980, 23: 153-158

[本文引用: 1]

Tian Y, Han M, Xu F.

Bifurcations of small limit cycles in Liénard systems with cubic restoring terms

J Differential Equations, 2019, 267: 1561-1580

[本文引用: 1]

Xiong Y, Han M.

New lower bounds for the Hilbert number of polynomial systems of Liénard type

J Differential Equations, 2014, 257: 2565-2590

[本文引用: 1]

Xiong Y, Hu J.

Double homoclinic bifurcations by perturbing a class of cubic Z$_2$-equivariant polynomial systems with nilpotent singular points

Bull Sci Math, 2024, 190: 103377

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发