数学物理学报, 2025, 45(3): 767-775

非局域反时空高阶非线性薛定谔方程的达布变换及其精确解

鹿高杰1, 韩众1, 刘露,2,*

1浙江金融职业学院信息技术学院 杭州 310000

2山东科技大学经济管理学院 山东青岛 266590

Darboux Transformation and Exact Solutions of the Nonlocal Reverse Space-Time Higher-Order Nonlinear Schrödinger Equation

Lu Gaojie1, Han Zhong1, Liu Lu,2,*

1Institute of Information Technology, Zhejiang Financial College, Hangzhou 310000

2School of Economics and Management, Shandong University of Science and Technology, Shandong Qingdao 266590

通讯作者: *E-mail:Magic_Liu@sdust.edu.cn

收稿日期: 2024-07-8   修回日期: 2024-11-14  

基金资助: 国家自然科学基金(72272089)
国家自然科学基金(71902105)
泰山学者工程专项经费(tsqn202312191)

Received: 2024-07-8   Revised: 2024-11-14  

Fund supported: NSFC(72272089)
NSFC(71902105)
Special Fund of Taishan Scholars Project(tsqn202312191)

摘要

该文研究了由 Ablowitz-Kaup-Newell-Segur 线性散射问题导出的非局部反时空高阶非线性薛定谔方程. Darboux 变换是以行列式的形式提供的. 通过应用达布变换, 得到了非局部反时空高阶非线性薛定谔方程的精确解, 包括孤子解、复子解和怪波解. 最后, 解的动力学行为通过图解进行讨论. 这些结果可用于理解非线性光学和相关领域中的相关物理现象.

关键词： 非局域反时空高阶非线性薛定谔方程; 达布变换; 孤子; 复子解; 怪波

Abstract

Under investigation in this paper is the nonlocal reverse space-time higher-order nonlinear Schrödinger (HNLS) equation which can be derived from the Ablowitz-Kaup-Newell-Segur linear scattering problem. The Darboux transformation is provided in the form of determinants. By applying the Darboux transformation, we arrive at exact solutions of the nonlocal reverse space-time HNLS equation, including soliton, complextion and rogue wave solutions. Finally, the dynamical behaviors of solutions are elucidated graphically. These results could be used to understand related physical phenomena in nonlinear optics and relevant fields.

Keywords： the nonlocal reverse space-time higher-order nonlinear Schröodinger equation; Darboux transformation; soliton; complexiton solution; Rogue wave

PDF (919KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

鹿高杰, 韩众, 刘露. 非局域反时空高阶非线性薛定谔方程的达布变换及其精确解[J]. 数学物理学报, 2025, 45(3): 767-775

Lu Gaojie, Han Zhong, Liu Lu. Darboux Transformation and Exact Solutions of the Nonlocal Reverse Space-Time Higher-Order Nonlinear Schrödinger Equation[J]. Acta Mathematica Scientia, 2025, 45(3): 767-775

1 引言

非局域可积方程一直以来都是非常受欢迎的研究领域. 1998 年, Bender 和Boettcher 指出非埃尔米特哈密尔顿量只要满足对称性和时间反转对称性的组合, 就可以具有正实特征值 (通常称为 $\mathcal{PT}$-对称)[1]. 他们的研究结果吸引了众多学者探究非局域非线性可积系统. Ablowitz 和 Musslimani 首先提出了一个反空间非局域非线性薛定谔方程[2]. 由于散射对称性的差异, 反时空非局域可积系统在数学物理上越来越受到重视[3,4]. 在此之后, 大量的非局域反时间、反时空非线性可积系统得到了广泛的研究, 如非局域导数非线性薛定谔方程, 非局域 Sasa-Satsuma 方程, 非局域复 mKdV 方程, 等等[5-8]. 为了获得 (非局域) 可积系统更多复杂而有趣的解, 多种求解方法被提出, 如 Hirota 双线性导数法[9,10], 达布变换[11-14], 黎曼-希尔伯特方法[15,16].

本文基于非局域非线性薛定谔方程, 研究了以下非局域反时空高阶非线性薛定谔方程

$\begin{equation}\label{hnls} \begin{split} &{\rm i}q_{x}+\frac{1}{2}(q_{tt}+2q^2r)+\delta(q_{tttttt}+q^2(60q_tr_tr+50r^2q_{tt}+2r_{tttt})\\ &+q(12rq_{tttt}+8q_tr_{ttt}+22q_{tt}r_{tt}+18q_{ttt}r_t+70r^2q_t^2)+20(q_t^2r_{tt}+rq_{tt}^2)\\ &+10q_t(5q_{tt}r_t+3rq_{ttt})+10q^3(r_t^2+2rr_{tt})+20q^4r^3)=0, \end{split} \end{equation}$

其中, $q=q(x,t)$ 是具有时间坐标 $x$ 和空间坐标 $t$ 的复函数, $r=-q(-x,-t)$. 当 $r=q^*(x,t)$ 时, 方程 (1.1) 转变为局域高阶非线性薛定谔方程[17]. 高以天教授导出了局域高阶非线性薛定谔方程的呼吸子到孤子的跃迁和非线性波[18,19]. 陈勇课题组研究了局域高阶非线性薛定谔方程的调制不稳定性以及怪波解[20]. 张翼教授给出了呼吸子与怪波的碰撞解[21]. 然而, 据我们所知, 目前该非局域反时空高阶非线性薛定谔方程的相关解并未被探究. 因此, 本文旨在通过达布变换, 得到了非局域反时空高阶非线性薛定谔方程的精确解, 包括孤子、复子解以及怪波解. 此外, 通过三维图像详细分析这些解的动力学行为.

2 非局域反时空高阶非线性薛定谔方程的达布变换

方程 (1.1) 的 Lax 对可以表示为

$\begin{equation} \Psi_t=U\Psi,\quad \Psi_x=V\Psi, \end{equation}$

其中 $\Psi=(\Psi_1(x,t),\Psi_2(x,t))^T$ 是特征函数, $\lambda$ 是特征值, $T$ 表示向量转置. $U$ 和 $V$ 分别表示为以下形式

$\begin{equation} U={\rm i} \begin{pmatrix} \lambda & r(x,t)\\ q(x,t) & -\lambda \end{pmatrix},\quad V={\rm i} \begin{pmatrix} V_1(x,t) & V_2(x,t)\\ V_3(x,t) & -V_1(x,t) \end{pmatrix}, \end{equation}$
$\begin{equation}\nonumber \begin{split} V_1=&-\frac{1}{2}qr-10\delta q^3r^3-5\delta q^2_tr^2+r^2_tq^2-10\delta qr(q_{tt}r+r_{tt}q)-\delta q_{tt}r_{tt}+\delta(q_tr_{ttt}+r_tq_{ttt}\\ &-rq_{tttt}-qr_{tttt})+\lambda(12{\rm i}\delta qr(q_tr-r_tq)+2{\rm i}\delta(q_tr_{tt}-r_tq_{tt}+rq_{ttt}-qr_{ttt}))+\lambda^2(1\\ &+12\delta q^2r^2+4\delta(qr_{tt}+q_{tt}r-q_tr_t))+8{\rm i}\lambda^3\delta(qr_t-q_tr)-16\lambda^4\delta qr+32\lambda^6\delta,\\ V_2=&-\frac{\rm i}{2}r_t-{\rm i}\delta r_{tttt}-10{\rm i}\delta(rq_tr_{tt}+rq_{tt}r_t+qrr_{ttt}+3q^2r^2r_t+q_tr^2_t+2qr_tr_{tt})+\lambda(r\\ &+12\delta qr^2_t+16\delta qrr_{tt}+4\delta r^2q_{tt}+2\delta r_{tttt}+12\delta q^2r^3+8\delta rq_tr_t)+\lambda^2(24{\rm i}\delta qrr_t\\ &+4{\rm i}\delta r_{ttt})+\lambda^3(-16\delta qr^2-8\delta r_{tt})-16{\rm i}\delta\lambda^4r_t+32\delta \lambda^5r,\\ V_3=&\frac{\rm i}{2}q_t+{\rm i}\delta q_{tttt}+10{\rm i}\delta(qr_tq_{tt}+qr_{tt}q_t+qrq_{ttt}+3q^2r^2q_t+q_t^2r_t+2rq_tq_{tt})+\lambda(q\\ &+12\delta rq^2_t+16\delta qrq_{tt}+4\delta q^2r_{tt}+2\delta q_{tttt}+12\delta q^3r^w+8\delta qq_tr_t)+\lambda^2(-24{\rm i}\delta qrq_t\\ &-4{\rm i}\delta q_{ttt})+\lambda^3(-16\delta rq^2-8\delta q_{tt})+16{\rm i}\delta\lambda^4q_t+32\delta \lambda^5q.\\ \end{split} \end{equation}$

基于 Lax 对, 方程 (1.1) 的达布变换可以被构造. 首先, 引入规范变换

$\begin{equation} \Psi[1]=T[1]\Psi. \end{equation}$

在此规范变换下, 新的 Lax 对可以表示为

$\begin{equation} \begin{split} &\Psi[1]_t=(T[1]_t+T[1]U(T[1])^{-1})\Psi[1]\triangleq U[1]\Psi[1],\\ &\Psi[1]_x=(T[1]_x+T[1]V(T[1])^{-1})\Psi[1]\triangleq V[1]\Psi[1], \end{split} \end{equation}$

达布矩阵 $T$ 可以建立为

$\begin{equation} T[1]=\lambda I+S[1]= \begin{pmatrix} \lambda+s_{11}[1] & s_{12}[1]\\ s_{21}[1] & \lambda+s_{22}[1] \end{pmatrix}, \end{equation}$

这里的 $s_{ij}[1](i,j=1,2)$ 是关于 $x$ 和 $t$ 的函数. 将 $T[1]$ 代入 Lax 对中, 新函数可以写为

$\begin{equation} \begin{split} &q[1]=q+2s_{21}[1],\\ &r[1]=r-2s_{12}[1]. \end{split} \end{equation}$

为了确保达布变换适用于非局域反时空高阶非线性薛定谔方程 (1.1), 对称约化 $r[1](x,t)=-q[1](-x,-t)$ 也应该在条件 $r(x,t)=-q(-x,-t)$ 下满足, 由此可以导出规范变换 $T[1]$ 的约束条件为

$\begin{equation} s_{21}[1](x,t)=s_{12}[1](-x,-t). \end{equation}$

此外, 可以发现 $T(\lambda)\Psi(\lambda_i)(i=1,2)$ 是特征值 $\lambda=\lambda_i$ 处的退化变换, 其中 $\Psi(\lambda_i)$ 是相应的特征函数. 因此, 存在常数 $\gamma_j(j=1,2)$ 使得 Lax 对的两个基解 $\psi(\lambda_j)=(\psi_1(\lambda_j),\psi_2(\lambda_j))^T$ 和 $\phi(\lambda_j)=(\phi_1(\lambda_j),\phi_2(\lambda_j))^T$ 满足

$\begin{equation} \begin{split} &\lambda_j+s_{11}[1]+\sigma_j s_{12}[1]=0,\\ &s_{21}[1]+\sigma_j(\lambda_j+s_{22}[1])=0, \end{split} \end{equation}$

其中

$\begin{equation}\label{sig} \sigma_j=\frac{\psi_2(\lambda_j)+\gamma_j\phi_2(\lambda_j)}{\psi_1(\lambda_j)+\gamma_j\phi_1(\lambda_j)},\quad j=1,2. \end{equation}$

基于上述讨论并经过复杂的计算, $T[1]$ 可以通过克拉默法则获得

$\begin{equation} T[1]= \begin{pmatrix} \lambda & 0\\ 0 & \lambda \end{pmatrix} +\frac{1}{\sigma_2-\sigma_1} \begin{pmatrix} \lambda_2\sigma_1-\lambda_1\sigma_2 & \lambda_1-\lambda_2\\ \sigma_1\sigma_2(\lambda_2-\lambda_1) & \lambda_1\sigma_1-\lambda_2\sigma_2 \end{pmatrix}, \end{equation}$

并且, 根据 $(T[1])^{-1}=\frac{(T[1])^*}{{\rm det}(T[1])}$ 以及 $(T[1]_t+T[1]U)(T[1])^*$ 中的元素为关于 $\lambda$ 的二次或三次多项式, 可以证明 $\lambda_j$ 是 ${\rm det}(T[1])$ 的根. 由此可得

$\begin{equation}\nonumber \begin{split} &(T[1]_t+T[1]U)(T[1])^*={\rm det}(T[1])\phi(\lambda),\\ &\phi(\lambda)= \begin{pmatrix} \phi_{11}^{(1)}\lambda+\phi_{11}^{(0)} & \phi_{12}^{(0)}\\ \phi_{21}^{(0)} & \phi_{22}^{(1)}\lambda+\phi_{22}^{(0)} \end{pmatrix}, \end{split} \end{equation}$

这里的 $\phi_{ij}^{(k)}(i,j=1,2,k=0,1)$ 是有待确定的函数. 另一方面, $\phi(\lambda)$ 也拥有以下形式

$\begin{equation} T[1]_t+T[1]U=\phi(\lambda)T[1]. \end{equation}$

通过比较 $\lambda$ 的系数, 得到

$\begin{equation}\nonumber \begin{split} \lambda^2: &\quad {\rm i}-\phi_{11}^{(1)}=0,\\ &-{\rm i}-\phi_{22}^{(1)}=0,\\ \lambda: &\quad {\rm i}s_{11}[1]-\phi_{11}^{(1)}s_{11}[1]-\phi_{11}^{(0)}=0,\\ &\quad {\rm i}r-{\rm i}s_{12}[1]-\phi_{11}^{(1)}s_{12}[1]-\phi_{12}^{(0)}=0,\\ &\quad {\rm i}q+{\rm i}s_{21}[1]-\phi_{22}^{(1)}s_{21}[1]-\phi_{21}^{(0)}=0,\\ &\quad -{\rm i}s_{22}[1]-\phi_{22}^{(1)}s_{22}[1]-\phi_{22}^{(0)}=0,\\ \lambda^0: &\quad {\rm i}qs_{12}[1]-\phi_{11}^{(0)}s_{11}[1]-\phi_{12}^{(0)}s_{21}[1]+s_{11}[1]_t=0,\\ &\quad {\rm i}rs_{11}[1]-\phi_{11}^{(0)}s_{12}[1]-\phi_{12}^{(0)}s_{22}[1]+s_{12}[1]_t=0,\\ &\quad {\rm i}qs_{22}[1]-\phi_{22}^{(0)}s_{21}[1]-\phi_{21}^{(0)}s_{11}[1]+s_{21}[1]_t=0,\\ &\quad {\rm i}rs_{21}[1]-\phi_{22}^{(0)}s_{22}[1]-\phi_{21}^{(0)}s_{12}[1]+s_{22}[1]_t=0. \end{split} \end{equation}$

解上述方程组, 有

$\begin{equation} \phi_{11}^{(1)}={\rm i},\ \phi_{22}^{(1)}=-{\rm i},\ \phi_{11}^{(0)}=0,\ \phi_{22}^{(0)}=0,\ \phi_{12}^{(0)}={\rm i}r-2{\rm i}s_{12}[1],\ \phi_{21}^{(0)}= {\rm i}q+2{\rm i}s_{21}[1]. \end{equation}$

显而易见, $U[1]=\phi(\lambda)$ 与 $U$ 有相同的形式. 同理可证, $V[1]$ 与 $V$ 有相同的形式.

基于上述讨论, 通过迭代就可以得到 $N$-重达布变换, 即

$\begin{equation} \Psi[N]=T[N]\Psi, \end{equation}$

其中

$\begin{equation}\nonumber \begin{split} T[N]&=T[1]T[2]\cdots T[N]\\ &= \begin{pmatrix} \lambda+s_{11}[1] & s_{12}[1]\\ s_{21}[1] & \lambda+s_{22}[1] \end{pmatrix} \begin{pmatrix} \lambda+s_{11}[2] & s_{12}[2]\\ s_{21}[2] & \lambda+s_{22}[2] \end{pmatrix} \cdots \begin{pmatrix} \lambda+s_{11}[N] & s_{12}[N]\\ s_{21}[N] & \lambda+s_{22}[N] \end{pmatrix}\\ &= \begin{pmatrix} \lambda^N & 0\\ 0 & \lambda^N \end{pmatrix} +\sum_{k=0}^{N-1}\lambda^k \begin{pmatrix} \widetilde{s}_{11}[k] & \widetilde{s}_{12}[k]\\ \widetilde{s}_{21}[k] & \widetilde{s}_{22}[k] \end{pmatrix}, \end{split} \end{equation}$

$\widetilde{s}_{ij}[k](i,j=1,2,k=1,2,\cdots,N)$ 是 $s_{ij}[k]$ 的函数. 由此得到

$\begin{equation} \begin{split} &q[N]=q+2\widetilde{s}_{21}[N-1],\\ &r[N]=r-2\widetilde{s}_{12}[N-1], \end{split} \end{equation}$

并且 $r[N](x,t)=-q[N](-x,-t)$ 和 $\widetilde{s}_{12}[N-1](x,t)=\widetilde{s}_{21}[N-1](-x,-t)$ 都应该被满足. 所以, 存在常数 $\gamma_j(j=1,2,\cdots,2N)$ 使得

$\begin{equation} \begin{split} &((T[N])_{11}+\sigma_j(T[N])_{12})|_{\lambda=\lambda_j}=0,\\ &((T[N])_{21}+\sigma_j(T[N])_{22})|_{\lambda=\lambda_j}=0, \end{split} \end{equation}$

其中

$\begin{equation} \sigma_j=\frac{\psi_2(\lambda_j)+\gamma_j\phi_2(\lambda_j)}{\psi_1(\lambda_j)+\gamma_j\phi_1(\lambda_j)},\quad j=1,2,\cdots,2N. \end{equation}$

随后, 利用如下行列式表示 $N$-重达布变换

$\begin{equation}\label{qr} \begin{split} &q[N]=q+2\frac{\delta_{11}}{\delta_{12}},\\ &r[N]=r-2\frac{\delta_{21}}{\delta_{12}}, \end{split} \end{equation}$

其中

$\begin{equation}\nonumber \delta_{11}=\left| \begin{matrix} 1 & \lambda_1 & \cdots & \lambda_1^{N-2} & -\lambda_1^{N}\sigma_1 & \sigma_1 & \lambda_1\sigma_1 & \cdots & \lambda_1^{N-2}\sigma_1 & \lambda_1^{N-1}\sigma_1\\ 1 & \lambda_2 & \cdots & \lambda_2^{N-2} & -\lambda_2^{N}\sigma_2 & \sigma_2 & \lambda_2\sigma_2 & \cdots & \lambda_2^{N-2}\sigma_2 & \lambda_2^{N-1}\sigma_2\\ \vdots & \vdots & \vdots &\vdots & \vdots & \vdots\\ 1 & \lambda_{2N} & \cdots & \lambda_{2N}^{N-2} & -\lambda_{2N}^{N}\sigma_{2N} & \sigma_{2N} & \lambda_{2N}\sigma_{2N} & \cdots & \lambda_{2N}^{N-2}\sigma_{2N} & \lambda_{2N}^{N-1}\sigma_{2N} \end{matrix} \right|, \end{equation}$
$\begin{equation}\nonumber \delta_{12}=\left| \begin{matrix} 1 & \lambda_1 & \cdots & \lambda_1^{N-2} & \lambda_1^{N-1} & \sigma_1 & \lambda_1\sigma_1 & \cdots & \lambda_1^{N-2}\sigma_1 & \lambda_1^{N-1}\sigma_1\\ 1 & \lambda_2 & \cdots & \lambda_2^{N-2} & \lambda_2^{N-1} & \sigma_2 & \lambda_2\sigma_2 & \cdots & \lambda_2^{N-2}\sigma_2 & \lambda_2^{N-1}\sigma_2\\ \vdots & \vdots & \vdots &\vdots & \vdots & \vdots\\ 1 & \lambda_{2N} & \cdots & \lambda_{2N}^{N-2} & \lambda_{2N}^{N-1} & \sigma_{2N} & \lambda_{2N}\sigma_{2N} & \cdots & \lambda_{2N}^{N-2}\sigma_{2N} & \lambda_{2N}^{N-1}\sigma_{2N} \end{matrix} \right|, \end{equation}$
$\begin{equation}\nonumber \delta_{21}=\left| \begin{matrix} 1 & \lambda_1 & \cdots & \lambda_1^{N-2} & \lambda_1^{N-1} & \sigma_1 & \lambda_1\sigma_1 & \cdots & \lambda_1^{N-2}\sigma_1 & -\lambda_1^{N}\\ 1 & \lambda_2 & \cdots & \lambda_2^{N-2} & \lambda_2^{N-1} & \sigma_2 & \lambda_2\sigma_2 & \cdots & \lambda_2^{N-2}\sigma_2 & -\lambda_2^{N}\\ \vdots & \vdots & \vdots &\vdots & \vdots & \vdots\\ 1 & \lambda_{2N} & \cdots & \lambda_{2N}^{N-2} & \lambda_{2N}^{N-1} & \sigma_{2N} & \lambda_{2N}\sigma_{2N} & \cdots & \lambda_{2N}^{N-2}\sigma_{2N} & \lambda_{2N}^{N} \end{matrix} \right|, \end{equation}$

值得注意的是, 在考虑非局域方程时, 应该更多注意不同约化的影响.

3 非局域反时空高阶非线性薛定谔方程的精确解

这一节, 利用上面给出的达布变换并选取零种子解和非零种子解来构造非局域反时空高阶非线性薛定谔方程的精确解.

3.1 零种子解下的孤子解和复子解

首先, 考虑零种子解 $q(x,t)=-r(-x,-t)=0$, 非局域方程 (1.1) 的相应的特征函数为

$\begin{equation} \psi[1]=\left( \begin{array}{c} {\rm e}^{{\rm i}\lambda t+{\rm i}(32\delta\lambda^6+\lambda^2)x}\\ 0 \end{array} \right),\; \phi[1]=\left( \begin{array}{c} 0\\ {\rm e}^{-{\rm i}\lambda t-{\rm i}(32\delta\lambda^6+\lambda^2)x} \end{array} \right). \end{equation}$

随后, 将其代入表达式 (2.9), 可得

$\begin{equation} \begin{split} &\sigma_j=\gamma_j{\rm e}^{\theta_j}\quad (j=1,2),\\ &s_{12}[1]=\frac{\lambda_1-\lambda_2}{\gamma_2{\rm e}^{\theta_2}-\gamma_1{\rm e}^{\theta_1}},\quad s_{21}[1]=\frac{(\lambda_2-\lambda_1)\gamma_1\gamma_2{\rm e}^{\theta_1+\theta_2}}{\gamma_2{\rm e}^{\theta_2}-\gamma_1{\rm e}^{\theta_1}},\\ &\theta_j=-2{\rm i}\lambda_j(t+32\delta\lambda_j^5x+\lambda_jt). \end{split} \end{equation}$

同时, 由条件 $s_{21}[1](x,t)=s_{12}[1](-x,-t)$ 可知

$\begin{equation} \gamma_1(\gamma_2^2-1)=0, \gamma_2(1-\gamma_1^2)=0. \end{equation}$

不失一般性, 取 $\gamma_1=-1, \gamma_2=1$. 在此之下, 有

$\begin{equation}\label{q1} q[1]=\frac{-2(\lambda_2-\lambda_1){\rm e}^{\theta_1+\theta_2}}{{\rm e}^{\theta_2}+{\rm e}^{\theta_1}}, \end{equation}$

并且

$\begin{equation}\nonumber \begin{split} &|{\rm e}^{\theta_1}+{\rm e}^{\theta_2}|^2=2{\rm e}^{\Re(\theta_1)+\Re(\theta_2)}(\cosh(\Re(\theta_1)-\Re(\theta_2))+\cos(\Im(\theta_1)+\Im(\theta_2))),\\ &\Re(\theta_j)=2\Im(\lambda_j)t+(-64\delta\Re(\lambda_j)^3\Im(\lambda_j)+4\Re(\lambda_j)\Im(\lambda_j)+64\delta\Re(\lambda_j)\Im(\lambda_j)^3)x,\\ &\Im(\theta_j)=-2\Re(\lambda_j)t+(16\delta\Re(\lambda_j)^4-96\delta\Re(\lambda_j)^2\Im(\lambda_j)^2+16\delta\Im(\lambda_j)^4-2\Re(\lambda_j)^2+2\Im(\lambda_j))x. \end{split} \end{equation}$

值得注意的是,

$\Im(\lambda_1)=\Im(\lambda_2),$
$\quad\,-64\delta\Re(\lambda_1)^3\Im(\lambda_1)+4\Re(\lambda_1)\Im(\lambda_1)+64\delta\Re(\lambda_1)\Im(\lambda_1)^3$
$=-64\delta\Re(\lambda_2)^3\Im(\lambda_2)+4\Re(\lambda_2)\Im(\lambda_2)+64\delta\Re(\lambda_2)\Im(\lambda_2)^3$

不能同时满足. 因此, 解 (3.4) 是非奇异的.

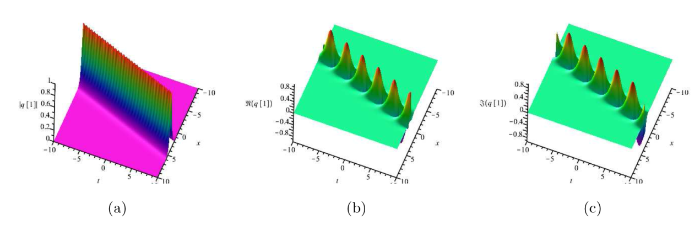
当 $\Re(\theta_1)+\Re(\theta_2)=0,\Im(\theta_1)-\Im(\theta_2)=0$ 时, 我们就能导出一孤子解, 见图1. 从图中可以看到, 一孤子解的实部和虚部均为一阶呼吸子. 此外, 我们发现孤子的波速取决于 $-\delta\Re(\lambda_1)^3+\frac{1}{16}\Re(\lambda_1)+\delta\Re(\lambda_1)\Im(\lambda_1)^2$ 的绝对值, 而孤子的传播方向取决于 $-\delta\Re(\lambda_1)^3+\frac{1}{16}\Re(\lambda_1)+\delta\Re(\lambda_1)\Im(\lambda_1)^2$ 的符号.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   (a) 孤子解, 参数为 $\delta=\frac{1}{2},\lambda_1=\frac{1}{2}-\frac{i}{2},\lambda_2=\frac{1}{2}+\frac{i}{2}$.


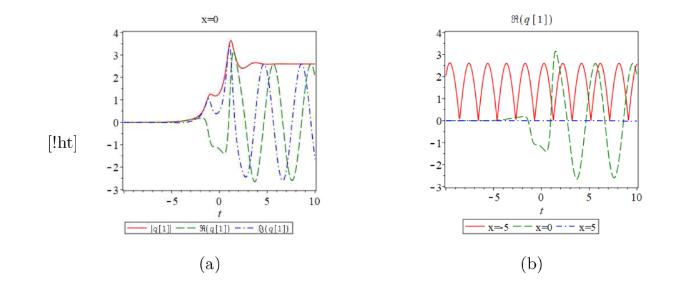
当 $\Re(\theta_2)=0, \Re(\lambda_2)=-2\Re(\lambda_1)$ 时, 那么我们便可以得到复子解, 见图2-3. 从复子解的实部情况可以看到, 随着时间的推移, 呼吸子逐渐消失, 见图3(b).

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   复子解, 参数为 $\delta=1,\lambda_1=\frac{2}{5}-\frac{1}{2},\lambda_2=-\frac{4}{5}.$


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   复子解的平面演化图.


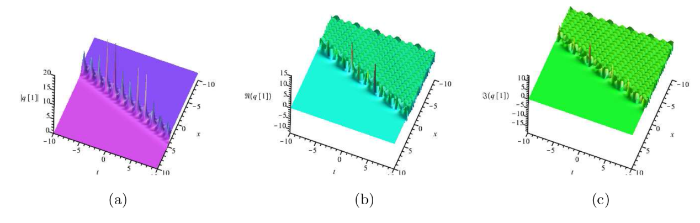
接下来, 我们使用2重达布变换, 即在公式 (2.17) 中取 $N=2$. 另一方面, 约束条件 $\widetilde{s}_{21}[N-1](x,t)=\widetilde{s}_{12}[N-1](-x,-t)$ 可推出 $\gamma_j^2=1(j=1,2,3,4)$, 就可以获得二孤子解, 见图4-5. 与一孤子解的情形相似, 二孤子解的实部和虚部均为二呼吸子解.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   二孤子解, 参数为 $\delta=1,\gamma_1=\gamma_3=-1,\gamma_2=\gamma_4=1,\lambda_1=\lambda_2^*=-\frac{1}{5}-\frac{i}{5},\lambda_3=\lambda_4^*=\frac{2}{5}+\frac{2i}{5}.$


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   二孤子解平面演化图.


3.2 非零种子解下的怪波

为了获得非局域方程 (1.1) 更多有趣的精确解, 这一部分我们将考虑非零种子解 $q(x,t)={\rm e}^{{\rm i}(kt+\omega x)}$, 其中 $\omega=-k^6\delta+30k^4\delta-90k^2\delta-\frac{1}{2}k^2+20\delta+1$ 将此非零种子解代入 Lax 对, $\lambda_j$ 对应的解可推导为

$\begin{equation} \Psi(\lambda_j)=\left( \begin{array}{c} i(C_{1,j}{\rm e}^{\eta}-C_{2,j}{\rm e}^{-\eta}){\rm e}^{-\frac{\rm i}{2}(kt+\omega x)}\\ (C_{2,j}{\rm e}^{\eta}-C_{1,j}{\rm e}^{-\eta}){\rm e}^{\frac{\rm i}{2}(kt+\omega x)} \end{array} \right) \end{equation}$
$\begin{equation}\nonumber \begin{split} C_{1,j}&=\frac{\sqrt{k+2\lambda_j+\sqrt{(k+2\lambda_j)^2+4}}}{\sqrt{(k+2\lambda_j)^2+4}},\ C_{2,j}=\frac{\sqrt{k+2\lambda_j-\sqrt{(k+2\lambda_j)^2+4}}}{\sqrt{(k+2\lambda_j)^2+4}},\\ \eta&=\frac{1}{4}\sqrt{(k+2\lambda_j)^2+4}(2{\rm i}t+({\rm i}(-2k^5+4k^4\lambda_j-8k^3\lambda_j^2+16k^2\lambda_j^3-32k\lambda_j^4\\ &+64\lambda_j^5+40k^3-48k^2\lambda_j+48k\lambda_j-32\lambda_j^3-60k+24\lambda_j)\delta+{\rm i}(-k+2\lambda_j))x), \end{split} \end{equation}$

我们取一对共轭特征值 $\lambda_1=\lambda_2^*=-\frac{k}{2}+i$, 并通过取极限, 我们就能得到怪波解

$\begin{equation} q[1]=(1+\frac{W_1}{W_2}){\rm e}^{{\rm i}(kt+\omega x)}, \end{equation}$
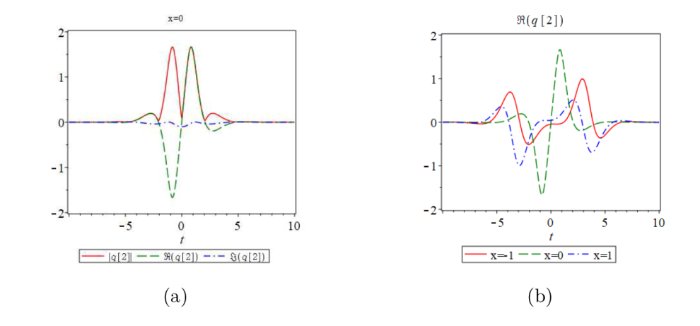
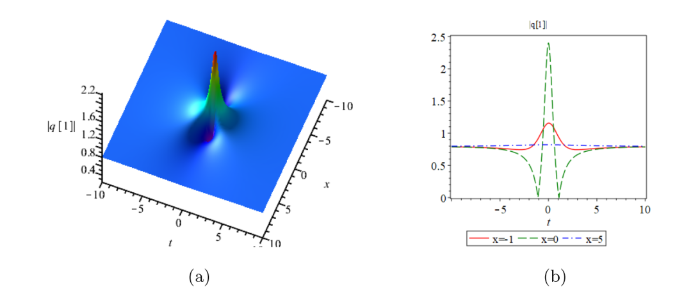
$\begin{equation} \begin{split} W_1&=-288(k^{10}-15k^8+160k^6-200k^4+300k^2+100)\delta^2x^2-96(k^6-15k^4+10)\delta x^2\\ &+96(k^4-20k^2+30)k\delta xt+240{\rm i}(k^4-6k^2+2)\delta x-8(k^2+1)x^2+16kxr+8{\rm i}x-8t^2+2,\\ W_2&=144(k^{10}-15k^8+160k^6-200k^4+300k^2+100)\delta^2 x^2+48(k^6-15k^4+10)\delta x^2\\ &-48(k^4-20k^2+30)k\delta xt+4(k^2+1)x^2-8kxt+4t^2+1. \end{split} \end{equation}$

从图6 可知, 怪波解拥有一个峰两个谷, 有趣的是此怪波的振幅并没有达到平面波振幅的三倍.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   (a) 怪波解, 参数为 $\delta=1,k=2$; (b) 怪波的平面演化图


4 结论

本文主要研究了非局域反时空高阶非线性薛定谔方程的精确解. 首先以行列式的形式构造该非局域方程的 $N$-重达布变换. 通过选择零种子解和非零种子解, 呈现了不同种类的解, 包括孤子解、复子解、怪波解. 然后借助于Maple软件进行了数值模拟, 通过三维图像和平面演化图观察这些解的丰富的动力学行为. 希望文中所得到的结果能对解释物理学中的某些非线性现象有所帮助. 在之后的研究中, 我们将考虑利用达布变换求得其他非局域可积方程更多有趣的精确解, 比如孤子、呼吸子、怪波等的互相作用解.

参考文献

Bender C M, Boettcher S.

Real spectra in non-Hermitian Hamiltonians having PT symmetry

Phys Rev Lett, 1998, 80(24): 5243-5246

[本文引用: 1]

Ablowitz M J, Musslimani Z H.

Integrable nonlocal nonlinear Schrödinger equation

Phys Rev Lett, 2013, 110( 6): 064105

[本文引用: 1]

Ablowitz M J, Musslimani Z H.

Integrable nonlocal nonlinear equations

Stud Appl Math, 2017, 139(1): 7-59

[本文引用: 1]

Ablowitz M J, Feng B F, Luo X D, Musslimani Z H.

Reverse space-time nonlocal sine-Gordon/sinh-Gordon equations with nonzero boundary conditions

Stud Appl Math, 2018, 141(3): 267-307

[本文引用: 1]

Zhou Z X.

Darboux transformations and global solutions for a nonlocal derivative nonlinear Schrödinger equation

Commun Nonlinear Sci Numer Simulat, 2018, 62: 480-488

[本文引用: 1]

Song C Q, Xiao D M, Zhu Z N.

Reverse space-time nonlocal Sasa-Satsuma equation and its solutions

J Phys Soc Jpn, 2017, 86( 5): 054001

Ma L Y, Shen S F, Zhu Z N.

Soliton solution and gauge equivalence for an integrable nonlocal complex modified Korteweg-de Vries equation

J Math Phys, 2017, 58( 10): 103501

Wang X, Kang J F, et al.

Darboux transformation and loop soliton solutions for the complex space-time-shifted nonlocal short pulse equation

Nonlinear Dynam, 2023, 111(14): 13375-13390

[本文引用: 1]

Rao J G, Cheng Y, He J S.

Rational and semi-rational solutions of the nonlocal Davey-Stewartson equations

Stud Appl Math, 2017, 13(4): 568-598

[本文引用: 1]

房春梅, 田守富.

约化的 (3+1) 维 Hirota 方程的呼吸波解、lump 解和半有理解

数学物理学报, 2022, 42A(3): 775—783

[本文引用: 1]

Fang C M, Tian S F.

Breather Wave Solutions, Lump solutions and semi-rational solutions of a reduced (3+1) dimensional Hirota equation

Acta Math Sci, 2022, 42A(3): 775-783

[本文引用: 1]

Feng B F, Ling L M, Takahashi D A.

Multi-breather and high-order rogue waves for the nonlinear Schrödinger equation on the elliotic function background

Stud Appl Math, 2020, 144(1): 46-101

[本文引用: 1]

Zhai Y Y, Ji T, Geng X G.

Coupled derivative nonlinear Schrödinger III equation: Darboux transformation and higher-order rogue waves in a two-mode nonlinear fiber

Appl Math Comput, 2021, 411: 126551

Niu J X, Guo R, Zhang J W.

Solutions on the periodic background and transition state mechanisms for the higher-order Chen-Lee-Liu equation

Wave Motion, 2023, 123: 103233

Shi X R, Yang Y Q.

Exact solutions and Darboux transformation for the reverse space-time nonlocal Lakshmanan-Porsezian-Daniel equation

Wave Motion, 2023, 119: 103141

[本文引用: 1]

Ma W X.

Riemann-Hilbert problems and $N$-soliton solutions for a coupled mKdV system

J Geom Phys, 2018, 132: 45-54

[本文引用: 1]

刘甲玉, 魏含玉, 张燕, 夏铁成, 王惠.

阿尔法螺旋蛋白中三分量四阶非线性 Schrödinger 系统孤子解及其非线性动力行为研究

数学物理学报, 2022, 42A(6): 1873—1885

[本文引用: 1]

Liu J Y, Wei H Y, Zhang Y, Xia T C, Wang H.

Soliton solutions and its nonlinear dynamics behavior research of the three-component four-order nonlinear Schrödinger system in alpha helical protein

Acta Math Sci, 2022, 42A(6): 1873-1885

[本文引用: 1]

Ankiewicz A, Kedziora D J, Chowdury A, Bandelow U, Akhmediev N.

Infinite hierarchy of nonlinear Schrödinger equations and their solutions

Phys Rev E, 2016, 93( 1): 012206

[本文引用: 1]

Huang Q M, Gao Y T, Hu L.

Breather-to-soliton transition for a sixth-order nonlinear Schrödinger equation in an optical fiber

Appl Math Lett, 2017, 75: 135-140

[本文引用: 1]

Jiang X H, Gao Y T, Huang Q M.

Nonlinear wave solutions for an integrable sixth-order nonlinear Schrödinger equation in an optical fiber

Opt, 2017, 144: 685-697

[本文引用: 1]

Yue Y F, Huang L L, Chen Y.

Modulation instability, rogue waves and spectral analysis for the sixth-order nonlinear Schrödinger equation

Commun Nonlinear Sci Numer Simulat, 2020, 89: 105284

[本文引用: 1]

Lou Y, Zhang Y, Ye R S.

Interactional solutions of the extended nonlinear Schrödinger equation with higher-order operators

Int J Comput Math, 2022: 99(10): 1989-2000

[本文引用: 1]

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发