1 引言和模型
2015 年, Berestycki 等[1 ] 提出用于描述社会张力-动荡演化的常微分方程模型,
这里$u(\tau)$ $v(\tau)$ $G(u)=u(1-u)$ $r(v)=\frac{1}{1+{\rm e}^{-\beta(v-\alpha)}}$ $v$
$h(u)=\theta(1+u)^{-p}$ $u$ $v$ $h(u)$ $h(u)$ $p$ $\theta$ $\sum_{i=1}^{n}A_{i}\delta_{x=x_{i},t=t_{i}}$
基于上述 Berestycki 等提出的常微分系统, Bakhshi 等[2 ] 考虑了扩散效应, 提出了如下用于描述社会张力-动荡演化的反应-扩散系统
(1.1) $\left\{\begin{array}{l} u_{\tau}=d_{1} \Delta u+r(v) G(u)-\omega u, \\ v_{\tau}=d_{2} \Delta v+1-h(u) v, \end{array}\right.$
这里$u=u(\tau,x)$ $v=v(\tau,x)$ $G, r, h$ $0<d_i\ll1, i=1,2$ $0<d_1=O(1), 0<d_2\ll1$ [2 ] 利用几何奇异摄动理论, 证明系统 (1.1) 存在连接两个稳态解的波前解.
基于 Bakhshi 等[2 ] 提出的反应-扩散系统, 本文引入 Allee 效应, 即考虑如下反应-扩散系统,
(1.2) $\left\{\begin{array}{l}u_{\tau}=d_{1} \Delta u+\frac{\Gamma}{1+\mathrm{e}^{-\beta(v-1)}} u(1-u)(u-a)-\omega u, \\v_{\tau}=d_{2} \Delta v+1-(1+u)^{p} v,\end{array}\right.$
这里 $a\in(0,1)$ $p>0$ . 一方面, 从数学建模的角度看, 相比于 logistic 增长, Allee 效应作为生态学中的一个重要概念, 它可用于 “阈值” 问题的建模, 对于刻画 “社会张力” 的爆发阈值有一定意义, 因此模型的建立应该是更为合理; 另一方面, 从数学理论的角度看, Allee 效应的引入, 使得 (1.2) 式的稳态解的个数比模型 (1.1) 更多且类型难以判断, 这导致模型 (1.2) 波前解的产生更为复杂. 那么, 相比于模型 (1.1), 模型 (1.2) 是否有新的波前解的产生, 是本文研究的主要内容. 模型 (1.2) 的异宿连接, 代表着从不同的稳态之间的迁移.
本文结构安排如下: 第 2 节分析了 (1.2) 式稳态解的个数及其类型; 第 3 节在扩散系数 $d_i, i=1,2$ $0<d_1=O(1), 0<d_2\ll1$
2 方程 (1.2) 稳态解的个数和类型
令$\Gamma/\omega=\gamma$
(2.1) $\begin{equation} \label{a3} \left\{\begin{aligned} u_\tau&=d_1u_{xx}+\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}u(1-u)(u-a)-u),\\ v_\tau&=d_2v_{xx}+1-(1+u)^pv. \end{aligned}\right. \end{equation}$
显然, 系统 (2.1) (等价于系统 (1.2)) 的稳态解为如下非线性代数方程组的根,
(2.2) $\begin{equation} \label{a5} \left\{\begin{aligned} \frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}u(1-u)(u-a)-u&=0,\\ 1-(1+u)^pv&=0. \end{aligned}\right. \end{equation}$
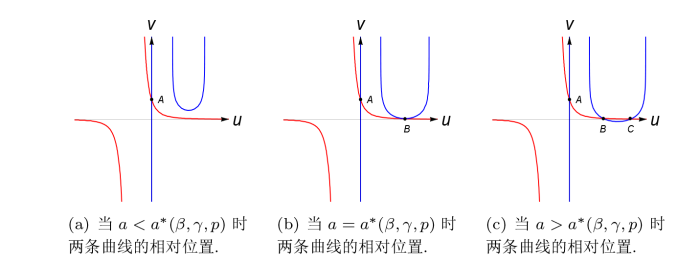
引理 2.1 方程组 (2.2) 最多有三个根, 即系统 (1.2) 最多有三个稳态解, 即存在临界参数 $a^{*}(\beta,\gamma,p)$
(1) 当 $a<a^{*}(\beta,\gamma,p)$ $A(0,1)$ 图1(a) ;
图1
(2) 当 $a=a^{*}(\beta,\gamma,p)$ $A(0,1)$ $B(\overline{u},\overline{v})$ $B(\overline{u},\overline{v})$ 图1(b) ;
(3) 当 $a>a^{*}(\beta,\gamma,p)$ $A(0,1)$ $B(\overline{u},\overline{v})$ $C(u^*,v^*)$ 图1(c) , 其中 $(\overline{u},\overline{v})$ $(u^*,v^*)$ $a$
(2.3) $\begin{equation}\label{a6} \frac{\gamma}{1+{\rm e}^{-\beta((1+u)^{-p}-1)}}(1-u)(u-a)-1=0, \end{equation}$
见图-1 , 而 $a^{*}(\beta,\gamma,p)$ $u$
(2.4) $\begin{equation} \label{a7} \left\{\begin{aligned} &-\frac{1}{\beta}\ln[\gamma(1-u)(u-a)-1]+1=(1+u)^{-p},\\ &\frac{\gamma(2u-a-1)}{\beta[\gamma(1-u)(u-a)-1]}=-p(1+u)^{-p-1}. \end{aligned}\right. \end{equation}$
(2.5) $\begin{equation} \label{a500} \left\{\begin{aligned} u&=0,\\ v&=(1+u)^{-p} \end{aligned}\right. \end{equation}$
(2.6) $\begin{equation} \label{a501} \left\{\begin{aligned} &\frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}(1-u)(u-a)=1,\\ &v=(1+u)^{-p} \end{aligned}\right. \end{equation}$
的根. 由方程 (2.5) 可得稳态解 $A(0,1)$ . 对于方程组 (2.6) 的根, 可将第一个方程的 $v$ $u$ $u$ $v$ $u$ $u$ $u$ $a$ $a^{*}(\beta,\gamma,p)$
注 2.1 由于临界参数 $a^{*}(\beta,\gamma,p)$ $\beta, \gamma,p$ $a$
本文考虑系统 (1.2)) 有三个稳常态解 $A(0,1)$ $B(\overline{u}_{1},\overline{v}_{1})$ $C(u_{1}^*,v_{1}^*)$ $a>a^{*}(\beta,\gamma,p)$ .
记$f_1(u_1,v_1)=-(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1), f_2(u_1,v_1)=-(1-(1+u_1)^pv_1).$
(2.7) $\begin{equation} \label{a20} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&=\frac{\omega}{c}f_1(u_1,v_1),\\ \frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}f_2(u_1,v_1). \end{aligned}\right. \end{equation}$
引理 2.2 若系统 (2.7) 有三个平衡点 $A(0, 1)$ $B(\overline{u}_{1}, \overline{v}_{1})$ $C(u_{1}^*, v_{1}^*)$ $A(0, 1)$ $B(\overline{u}_{1}, \overline{v}_{1})$ $u_{1}^*\geq\frac{a+1}{2}$ $C(u_{1}^*, v_{1}^*)$ $u_{1}^*<\frac{a+1}{2}$ $C(u_{1}^*, v_{1}^*)$
(2.8) $\begin{equation} \label{a22} \left\{\begin{aligned} f_{1u_{1}}&=-(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}(1-u_1)(u_1-a)-1)+\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}[u_1(u_1-a)-(1-u_1)u_1],\\ f_{1v_{1}}&=-\frac{\gamma\beta {\rm e}^{-\beta(v_1-1)}}{(1+{\rm e}^{-\beta(v_1-1)})^{2}}u_1(1-u_1)(u_1-a),\\ f_{2u_{1}}&=p(1+u_1)^{p-1}v_1,\\ f_{2v_{1}}&=(1+u_1)^p, \end{aligned}\right. \end{equation}$
(2.9) $\begin{equation}\label{a21} \lambda_{1,2}=\frac{1}{2c}(f_{2v_{1}}+\omega f_{1u_{1}}\pm\sqrt{(f_{2v_{1}}-\omega f_{1u_{1}})^{2}+4\omega f_{1v_{1}}f_{2u_{1}}}). \end{equation}$
因此, 系统 (2.7) 在点 $A(0,1)$ $\lambda_{1}(A)=\frac{1}{c}, \lambda_{2}(A)=\frac{\omega(a\gamma+2)}{2c}$ $A(0,1)$
根据引理 2.1, $B(\overline{u}_{1},\overline{v}_{1})$ $C(u_{1}^*,v_{1}^*)$
(2.10) $\begin{equation} \label{a23} \left\{\begin{aligned} \frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}(1-u_{1})(u_{1}-a)-1&=0,\\ 1-(1+u_{1})^pv_{1}&=0. \end{aligned}\right. \end{equation}$
从引理 2.1 中的图1 , 比较两曲线在 $B(\overline{u}_{1},\overline{v}_{1})$ $C(u_{1}^*,v_{1}^*)$
(2.11) $\frac{\gamma\left(2 \bar{u}_{1}-a-1\right)}{\beta\left[\gamma\left(1-\bar{u}_{1}\right)\left(\bar{u}_{1}-a\right)-1\right]}<-p\left(1+\bar{u}_{1}\right)^{-p-1}$
(2.12) $\frac{\gamma\left(2 u_{1}^{*}-a-1\right)}{\beta\left[\gamma\left(1-u_{1}^{*}\right)\left(u_{1}^{*}-a\right)-1\right]}>-p\left(1+u_{1}^{*}\right)^{-p-1}.$
因此, 对于点 $B(\overline{u}_{1},\overline{v}_{1})$
(2.13) $\begin{equation} \label{a26} \left\{\begin{aligned} f_{1u_{1}}(B)&=\frac{\gamma}{1+{\rm e}^{-\beta(\overline{v}_1-1)}}\overline{u}_1(2\overline{u}_1-a-1),\\ f_{1v_{1}}(B)&=-\frac{\overline{u}_1\beta {\rm e}^{-\beta(\overline{v}_1-1)}}{1+{\rm e}^{-\beta(\overline{v}_1-1)}},\\ f_{2u_{1}}(B)&=p(1+\overline{u}_1)^{p-1}\overline{v}_1,\\ f_{2v_{1}}(B)&=(1+\overline{u}_1)^p, \end{aligned}\right. \end{equation}$
(2.14) $\begin{aligned}f_{1 u_{1}}(B) f_{2 v_{1}}(B)-f_{1 v_{1}}(B) f_{2 u_{1}}(B) &=\frac{\bar{u}_{1}\left(1+\bar{u}_{1}\right)^{p-1}}{1+\mathrm{e}^{-\beta\left(\bar{v}_{1}-1\right)}}\left[\gamma\left(2 \bar{u}_{1}-a-1\right)\left(1+\bar{u}_{1}\right)+\beta \mathrm{e}^{-\beta\left(\bar{v}_{1}-1\right)} p \bar{v}_{1}\right] \\&<0\end{aligned}$
因此, 点$B(\overline{u}_{1},\overline{v}_{1})$
对于点 $C(u_{1}^*,v_{1}^*)$ $f_{1u_{1}}(C)f_{2v_{1}}(C)-f_{1v_{1}}(C)f_{2u_{1}}(C)>0$ $C(u_{1}^*,v_{1}^*)$
此时, 需要再判断 $\omega f_{1u_{1}}(C)+f_{2v_{1}}(C)$
(1) 若 $u_{1}^*\geq\frac{a+1}{2}$ $\omega f_{1u_{1}}(C)+f_{2v_{1}}(C)>0$ $C(u_{1}^*,v_{1}^*)$
(2) 若 $u_{1}^*<\frac{a+1}{2}$ $\omega f_{1u_{1}}(C)+f_{2v_{1}}(C)$ $\omega$ $C(u_{1}^*,v_{1}^*)$
3 当 $0<d_1, d_2\ll1$
引入行波坐标 $\xi=x-c\tau$ $c$
(3.1) $\begin{equation} \label{a10} \left\{\begin{aligned} 0&=d_1u_{\xi\xi}+cu_\xi+\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}u(1-u)(u-a)-u),\\ 0&=d_2v_{\xi\xi}+cv_\xi+1-(1+u)^pv. \end{aligned}\right. \end{equation}$
因 $0<d_1, d_2\ll1$ $d_1=\epsilon$ $d_2=\mu d_1$ $0<\mu=O(1)$ $0<\epsilon\ll 1$
(3.2) $\begin{equation} \label{a12} \left\{\begin{aligned} 0&=\epsilon u_{\xi\xi}+cu_\xi+\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}u(1-u)(u-a)-u),\\ 0&=\mu \epsilon v_{\xi\xi}+cv_\xi+1-(1+u)^pv. \end{aligned}\right. \end{equation}$
(3.3) $\begin{equation} \label{a13} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&=u_2,\\ \epsilon\frac{\text{d}u_2}{\text{d}\xi}&=-cu_2-\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \frac{\text{d}v_1}{\text{d}\xi}&=v_2,\\ \mu\epsilon\frac{\text{d}v_2}{\text{d}\xi}&=-cv_2-1+(1+u_1)^pv_1. \end{aligned}\right. \end{equation}$
我们称系统 (3.3) 为慢系统. 引入快变量 $\zeta=\xi/\epsilon$
(3.4) $\begin{equation} \label{a14} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\zeta}&=\epsilon u_2,\\ \frac{\text{d}u_2}{\text{d}\zeta}&=-cu_2-\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \frac{\text{d}v_1}{\text{d}\zeta}&=\epsilon v_2,\\ \mu\frac{\text{d}v_2}{\text{d}\zeta}&=-cv_2-1+(1+u_1)^pv_1. \end{aligned}\right. \end{equation}$
在快系统 (3.4) 令 $\epsilon=0$
(3.5) $\begin{equation} \label{a17} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\zeta}&=0,\\ \frac{\text{d}u_2}{\text{d}\zeta}&=-cu_2-\omega(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \frac{\text{d}v_1}{\text{d}\zeta}&=0,\\ \mu\frac{\text{d}v_2}{\text{d}\zeta}&=-cv_2-1+(1+u_1)^pv_1, \end{aligned}\right. \end{equation}$
(3.6) $\begin{equation}\label{a15} M_0=\{(u_1,u_2,v_1,v_2)|u_2=-\frac{\omega}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),v_2=\frac{1}{c}(-1+(1+u_1)^pv_1)\}, \end{equation}$
系统 (3.5) 在 $M_0$ $0$ $-c$ $M_0$
在临界流形 $M_0$
(3.7) $\begin{equation} \label{a16} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&=-\frac{\omega}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}(-1+(1+u_1)^pv_1). \end{aligned}\right. \end{equation}$
根据 Fenichel's 不变流形定理[3 ,4 ] , 存在 $M_0$ $\epsilon-$ $M_\epsilon$ $M_\epsilon$
上的慢流是 $M_0$ $\epsilon$ - 阶扰动.
根据引理 2.2, 我们只考虑 $u_{1}^*\geq\frac{a+1}{2}$ $\omega\ll 1$ $\omega\gg1$
对系统 (3.7), 令 $\eta=\omega\xi$
(3.8) $\begin{equation} \label{a28} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\eta}&=-\frac{1}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \omega\frac{\text{d}v_1}{\text{d}\eta}&=\frac{1}{c}(-1+(1+u_1)^pv_1), \end{aligned}\right. \end{equation}$
这里 $v_1$ $u_1$ $\omega=0$
(3.9) $\begin{equation} \label{a29} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&=0,\\ \frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}(-1+(1+u_1)^pv_1) \end{aligned}\right. \end{equation}$
(3.10) $\begin{equation} \label{a30} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\eta}&=-\frac{1}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ 0&=\frac{1}{c}(-1+(1+u_1)^pv_1). \end{aligned}\right. \end{equation}$
(3.11) $\begin{equation}\label{a31} \{(u_1,v_1)|v_1=\frac{1}{(1+u_1)^p}\}, \end{equation}$
(3.12) $\frac{\mathrm{d} u_{1}}{\mathrm{~d} \eta}=-\frac{1}{c} u_{1}\left(\frac{\gamma}{1+\mathrm{e}^{-\beta\left(\frac{1}{\left(1+u_{1}\right)^{p}}-1\right)}}\left(1-u_{1}\right)\left(u_{1}-a\right)-1\right),$
它有三个平衡点, 分别为 $\overline{A}=0$ $\overline{B}=\overline{u}_1$ $\overline{C}=u_{1}^*$ .
系统 (3.12) 在点 $\overline{A}$ $\frac{\gamma a+2}{2c}$ $\overline{B}$ $\overline{C}$ $\overline{A}$ $\overline{C}$ $\overline{B}$ $\overline{A}$ $\overline{B}$ $\overline{C}$ $\overline{B}$
对于系统 (3.9), 它关于 (3.11) 式任意一点 $(u_1,v_1)$ $\frac{1}{c}(1+u_1)^p$ $0$ [3 ,4 ] , 当 $\omega$ $\omega-$
(3.13) $\begin{equation}\label{a33} \ v_{1}=\frac{1}{(1+u_1)^p}+O(\omega). \end{equation}$
其上的流由 (3.12) 式的 $\omega-$
(3.14) $\frac{\mathrm{d} u_{1}}{\mathrm{~d} \eta}=-\frac{1}{c} u_{1}\left(\frac{\gamma}{1+\mathrm{e}^{-\beta\left(\frac{1}{\left(1+u_{1}\right)^{p}}-1\right)}}\left(1-u_{1}\right)\left(u_{1}-a\right)-1\right)+O(\omega).$
显然, 当 $\omega$ $\overline{A}, \overline{C}$ $\overline{B}$
进一步地, 根据 Fenichel 不变流形理论[3 ,4 ] ,当 $\epsilon$ $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
定理 3.1 设 $\gamma, c, \beta, p, a>0$ $a>a^{*}(\beta,\gamma,p)$ $0<\epsilon\ll\omega\ll1$ $(0,0,1,0)$ $(\overline{u},0,\overline{v},0)$ $(u^{*},0,v^{*},0)$ $(\overline{u},0,\overline{v},0)$ $A(0,1)$ $B(\overline{u},\overline{v})$ $C(u^{*},v^{*})$ $B(\overline{u},\overline{v})$
令 $\delta=\frac{1}{\omega}$ $0<\delta\ll1$
(3.15) $\begin{equation} \label{a35} \left\{\begin{aligned} \delta\frac{\text{d}u_1}{\text{d}\xi}&=-\frac{1}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ \frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}(-1+(1+u_1)^pv_1), \end{aligned}\right. \end{equation}$
此时 $u_1$ $v_1$
令 $z=\xi/\delta$
(3.16) $\begin{equation} \label{a36} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}z}&=-\frac{1}{c}u_1(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}(1-u_1)(u_1-a)-1),\\ \frac{\text{d}v_1}{\text{d}z}&=\frac{\delta}{c}(-1+(1+u_1)^pv_1). \end{aligned}\right. \end{equation}$
在系统 (3.16) 和 (3.15) 中分别令 $\delta=0$
(3.17) $\begin{equation} \label{a37} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}z}&=-\frac{1}{c}u_1(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}(1-u_1)(u_1-a)-1),\\ \frac{\text{d}v_1}{\text{d}z}&=0 \end{aligned}\right. \end{equation}$
(3.18) $\begin{equation} \label{a150} \left\{\begin{aligned} &0=-\frac{1}{c}(\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}u_1(1-u_1)(u_1-a)-u_1),\\ &\frac{\text{d}v_1}{\text{d}\xi}=\frac{1}{c}(-1+(1+u_1)^pv_1). \end{aligned}\right. \end{equation}$
此时的临界曲线由直线 $S^{1}_{0}=\{(u_1,v_1):u_1=0\}$ $S^{2}_{0}=\{(u_1,v_1):\frac{\gamma}{1+{\rm e}^{-\beta(v_1-1)}}(1-u_1)(u_1-a)-1=0\}$ $S^{1}_{0}$ $S^{2}_{0}$ $u_{1}<\frac{a+1}{2}$ $u_{1}>\frac{a+1}{2}$ $S^{1}_{0}$ $S^{2}_{0}$
(3.19) $\frac{\mathrm{d} v_{1}}{\mathrm{~d} z}=-\frac{\delta}{c}\left(1-v_{1}\right)$
(3.20) $\frac{\mathrm{d} v_{1}}{\mathrm{~d} z}=\frac{\delta}{c}\left(-1+\left(1+u_{1}\left(v_{1}\right)\right)^{p} v_{1}\right).$
对于系统 (3.19), 其平衡点 $v_1=1$ $\delta$ $S^{1}_{0}$ $(0,1)$ $v_1=\overline{v_1}$ $v_1=v^{*}_1$ $\delta$ $u_{1}<\frac{a+1}{2}$ $S^{2}_{0}$ $(\overline{u_1},\overline{v_1})$ $S^{2}_{0}$ $u_{1}>\frac{a+1}{2}$ $(u^{*}_1,v^{*}_1)$ $\delta$ $(\overline{u_1},\overline{v_1})$ $(0,1)$ $(u^{*}_1,v^{*}_1)$ $(\overline{u_1},\overline{v_1})$ [3 ,4 ] , 四维相空间中存在连接平衡点 $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
定理 3.2 设 $\gamma, c, \beta, p, a>0$ $a>a^{*}(\beta,\gamma,p)$ $0<\epsilon\ll\frac{1}{\omega}\ll1$ $(0,0,1,0)$ $(\overline{u},0,\overline{v},0)$ $(u^{*},0,v^{*},0)$ $(\overline{u},0,\overline{v},0)$ $A(0,1)$ $B(\overline{u},\overline{v})$ $C(u^{*},v^{*})$ $B(\overline{u},\overline{v})$
总结起来, 当 $a>a^{*}(\beta,\gamma,p)$ $0<\epsilon\ll\omega\ll1$ $0<\epsilon\ll\frac{1}{\omega}\ll1$ $A(0,1)$ $B(\overline{u},\overline{v})$ $C(u^{*},v^{*})$ $B(\overline{u},\overline{v})$
4 当 $0<d_1=O(1)$ $0<d_2\ll1$
因 $0<d_1=O(1)$ $0<d_2\ll1$ $d_1=1,d_2=\epsilon \ll 1$
(4.1) $\begin{equation} \label{a41} \left\{\begin{aligned} 0&=u_{\xi\xi}+cu_{\xi}+\frac{\gamma}{1+{\rm e}^{-\beta(v-1)}}u(1-u)(u-a)-u,\\ 0&=\epsilon v_{\xi\xi}+cv_{\xi}+\frac{1}{\omega}(1-(1+u)^{p}v). \end{aligned}\right. \end{equation}$
(4.2) $\begin{equation} \label{a42} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&=u_{2},\\ \frac{\text{d}u_2}{\text{d}\xi}&=u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a),\\ \frac{\text{d}v_1}{\text{d}\xi}&=v_{2},\\ \epsilon \frac{\text{d}v_2}{\text{d}\xi}&=-cv_{2}+\frac{1}{\omega}((1+u_{1})^{p}v_{1}-1). \end{aligned}\right. \end{equation}$
称系统 (4.2) 为慢系统, 令 $\zeta=\xi/\epsilon$
(4.3) $\begin{equation} \label{a43} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\zeta}&=\epsilon u_{2},\\ \frac{\text{d}u_2}{\text{d}\zeta}&=\epsilon (u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a)),\\ \frac{\text{d}v_1}{\text{d}\zeta}&=\epsilon v_{2},\\ \frac{\text{d}v_2}{\text{d}\zeta}&=-cv_{2}+\frac{1}{\omega}((1+u_{1})^{p}v_{1}-1). \end{aligned}\right. \end{equation}$
不同于第三节, 本节的系统 (4.2) 和 (4.3) 的快慢变量的维数分别为 1 维和 3 维.
对于快慢系统 (4.2) 和 (4.3), 其三维的临界流形为
(4.4) $\begin{equation}\label{a44} M_{\epsilon=0,\omega}=\{(u_1,u_2,v_1,v_2)| v_2=\frac{1}{\omega c}(-1+(1+u_1)^pv_1)\}, \end{equation}$
(4.5) $\begin{equation} \label{a47} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\zeta}&=0,\\ \frac{\text{d}u_2}{\text{d}\zeta}&=0,\\ \frac{\text{d}v_1}{\text{d}\zeta}&=0,\\ \frac{\text{d}v_2}{\text{d}\zeta}&=-cv_2+\frac{1}{\omega}((1+u_1)^pv_1-1). \end{aligned}\right. \end{equation}$
系统 (4.5) 在 $M_{\epsilon=0,\omega}$ $0$ $-c$ $M_{\epsilon=0,\omega}$ [3 ,4 ] , 对于足够小的 $\epsilon>0$ $M_{\epsilon,\omega}$ $M_{\epsilon=0,\omega}$ $O(\epsilon)$ - 阶扰动
(4.6) $M_{\epsilon, \omega}=\left\{\left(u_{1}, u_{2}, v_{1}, v_{2}\right) \left\lvert\, v_{2}=\frac{1}{\omega c}\left(-1+\left(1+u_{1}\right)^{p} v_{1}\right)+O(\epsilon)\right.\right\}$
在不变流形 $M_{\epsilon,\omega}$
(4.7) $\begin{equation} \label{a49} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&= u_{2}\\ \frac{\text{d}u_2}{\text{d}\xi}&= u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a)\\ \omega\frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}((1+u_{1})^{p}v_{1}-1)+O(\epsilon). \end{aligned}\right. \end{equation}$
(4.8) $\begin{equation} \label{a45} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&= u_{2},\\ \frac{\text{d}u_2}{\text{d}\xi}&= u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a),\\ \omega\frac{\text{d}v_1}{\text{d}\xi}&=\frac{1}{c}((1+u_{1})^{p}v_{1}-1). \end{aligned}\right. \end{equation}$
显然, 若 $0<\omega\ll1$ $\epsilon\ll\omega$ ) , 那么 (4.8) 式亦为快慢系统. 这意味着 (4.3) 和 (4.2) 式为三尺度系统.
令 $z=\xi/\omega$
(4.9) $\begin{equation} \label{a46} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}z}&=\omega u_{2},\\ \frac{\text{d}u_2}{\text{d}z}&=\omega(u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a)),\\ \frac{\text{d}v_1}{\text{d}z}&=\frac{1}{c}((1+u_{1})^{p}v_{1}-1). \end{aligned}\right. \end{equation}$
对于系统 (4.9), 令 $\omega=0$
(4.10) $\begin{equation} \label{a51} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}z}&=0,\\ \frac{\text{d}u_2}{\text{d}z}&=0,\\ \frac{\text{d}v_1}{\text{d}z}&=\frac{1}{c}((1+u_{1})^{p}v_{1}-1), \end{aligned}\right. \end{equation}$
(4.11) $\begin{equation}\label{a50} M_{\epsilon=0,\omega=0}=\{(u_1,u_2,v_1)| v_1=\frac{1}{(1+u_1)^p)}\} \end{equation}$
系统 (4.10) 在 $M_{\epsilon=0,\omega=0}$ $(\widetilde{u_1},\widetilde{v_1})$ $0$ $\frac{1}{c}(1+\widetilde{u_1})^p$ $M_{\epsilon=0,\omega=0}$
$M_{\epsilon=0,\omega=0}$
(4.12) $\begin{equation} \label{a52} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&= u_{2},\\ \frac{\text{d}u_2}{\text{d}\xi}&= u_{1}-cu_{2}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a), \end{aligned}\right. \end{equation}$
(4.13) $\begin{equation}\label{a53} 0=\frac{\text{d}^{2}u_1}{\text{d}\xi^{2}}+c\frac{\text{d}u_1}{\text{d}\xi}-u_{1}+\frac{\gamma}{1+{\rm e}^{-\beta(\frac{1}{(1+u_1)^{p}}-1)}}u_1(1-u_1)(u_1-a). \end{equation}$
显然, 系统 (4.13) 为如下反应-扩散方程对应的行波方程
(4.14) $\begin{equation}\label{a54} u_t=u_{xx}-u+\frac{\gamma}{1+{\rm e}^{-\beta(\frac{1}{(1+u)^{p}}-1)}}u(1-u)(u-a). \end{equation}$
引理 4.1 [7 ] 考虑方程 $u_t=u_{xx}+f(u)$ $t, x\in R$ $f\in C^{1}[0,1],$ $f(0)=f(1)=0,f'(0)<0,f'(1)<0$ $f$ $(0, 1)$ $u=q(x-ct)$ $c$
推论 4.1 对于方程 $u_t=u_{xx}+f(u),x, u\in R$ $f\in C^{1}[L], l\in R^{+},f(0)=f(L)=0,f'(0)<0, f'(L)<0$ $f$ $(0, L)$ $u=q(x-ct)$ $c$
显然, $f(0)=f(u^*)=0$ . 同时, 经过计算可得
另由不等式 (2.12) 及 $u_1=u$
即可得 $f'(0)<0,f'(u^{*})<0$ . 则由推论 4.1 可知方程 (4.14) 存在唯一一个波前解 $u=q(x-ct)$ $c$ $q(-\infty)=0, q(\infty)=u^{*}.$
另一方面, 当 $c=0$
(4.15) $\begin{equation} \label{a55} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}\xi}&= u_{2},\\ \frac{\text{d}u_2}{\text{d}\xi}&= u_{1}-\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a), \end{aligned}\right. \end{equation}$
它有三个平衡点, 其中 $(0, 0)$ $(u_1^*, 0)$ $(\bar{u}_1,0)$
(4.15) $H(u_1, u_2)=\frac{u_2^2}{2}+G(u),$
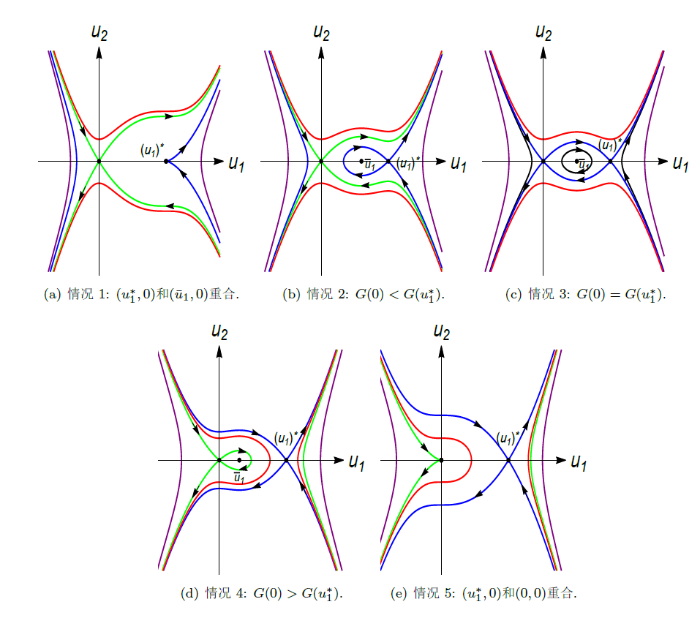
其中 $G(u_1)$ $g(u_1)=-u_{1}+\frac{\gamma}{1+{\rm e}^{-\beta(v_{1}-1)}}u_1(1-u_1)(u_1-a)$ $G(0)$ $G(u_1^*)$ $a$ 图2 所示, 这里我们总假定 $a>a^{*}(\beta,\gamma,p)$ .
图2
图2
层系统 (55) 在不同的参数条件下的全局相图.
然而, 如果 $c$ $c=0$ $-cu_{2}$
命题 4.1 层系统 (4.12) 对应的向量场关于 $c$ $c$
这说明系统 (4.15) 对应的向量场除了在有限条直线 (这些直线不是系统的轨道) 外, 向量场严格旋转. 因此, 对应的向量场形成一个广义旋转向量场. 系统 (4.15) 的任何轨道的切向量除了可能在有限个数的点外, 都随 $c$
针对图-2(b), 我们定义系统 (4.12) 平衡点 $(0,0)$ $\Gamma_{0}^{u}$ $(u^{*},0)$ $\Gamma_{u^{*}}^{s}$
(4.16) $\begin{equation}\label{a56} d(c,a)=h_{1}(c,a)-h_{2}(c,a), \end{equation}$
其中 $h_{i}(c,a), i=1,2$ $\Gamma_{0}^{u}$ $\Gamma_{u^{*}}^{s}$ $d(0,a)>0$ . 又根据命题 1, 系统 (4.12) 对应的向量场 形成广义旋转向量场, 其轨道随 $c$ $d(c,a)$ $c$
(4.17) $\begin{equation}\label{a57} \frac{\partial d(c,a)}{\partial c}<0, (c>0). \end{equation}$
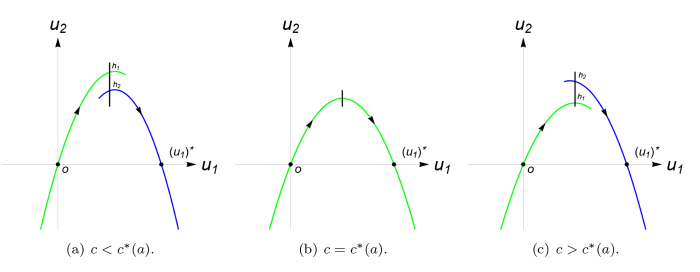
因此, 从几何上讲, $(0,0)$ $\Gamma_{0}^{u}$ $(u^{*},0)$ $\Gamma_{u^{*}}^{s}$ $c=c^{*}(a)$ $\Gamma_{0}^{u}$ $\Gamma_{u^{*}}^{s}$ $(0,0)$ $(u^{*},0)$
图3
图3
平衡点 $(0,0)$ $(u^{*},0)$ $u_1$ - $u_2$
将系统 (4.9) 在点 $(0,0,1)$
(4.18) $\begin{equation} \label{a58} \left\{\begin{aligned} \frac{\text{d}u_1}{\text{d}z}&=\omega u_{2}\\ \frac{\text{d}u_2}{\text{d}z}&=\omega(1+\frac{a\gamma}{2})u_{1}-\omega cu_{2}\\ \frac{\text{d}v_1}{\text{d}z}&=\frac{p}{c}u_{1}+\frac{1}{c}v_{1}. \end{aligned}\right. \end{equation}$
直接计算可知: 系统 (4.9) 在点 $(0,0,1)$ $\frac{1}{c}$ $\frac{-\omega c+\sqrt{\omega^{2}c^{2}+\omega^{2}(4+2a\gamma)}}{2}$ $\frac{-\omega c-\sqrt{\omega^{2}c^{2}+\omega^{2}(4+2a\gamma)}}{2}$ $(u^{*},0,v^{*})$ $(u^{*},0,v^{*})$ $(0,0,1)$ $(u^{*},0,v^{*})$ $(0,0,1)$ $(u^{*},0,v^{*})$ $\epsilon$
定理 4.1 设 $\gamma, c, \beta, p, a>0$ $a>a^{*}(\beta,\gamma,p)$ $0<\epsilon\ll\omega\ll1$ $c^{*}(a)$ $A(0,1)$ $C(u^{*},v^{*})$
值得指出的是: 定理 1-3 的波前解的连接机制均是不一样的.
参考文献
View Option
[1]
Berestycki H Nadal J P Rodíguez N A model of riots dynamics: shocks, diffusion and thresholds
Networks Heterogeneous Media , 2017 , 10 3 ): 443 -475
[本文引用: 1]
[2]
Bakhshi M Ghazaryan A Manukian V Rodriguez N Traveling wave solutions in a model for social outbursts in a tension-inhibitive regime
Studies in Applied Mathematics , 2021 , 147 2 ): 650 -674
[本文引用: 3]
[3]
Fenichel N Geometric singular perturbation theory for ordinary differential equations
J Differential Equations , 1979 , 31 1 ): 53 -98
[本文引用: 5]
[4]
Jones C Geontetric singular perturbation theory//Dynamical systems (Montecatini Terme, 1994), volume 1609 of Lecture Notes in Math
Berlin: Springer , 1995 : 44 -118
[本文引用: 5]
[5]
Perko L M Rotated vector fields
J Differential Equations , 1993 , 103 1 ): 127 -145
[6]
Shen J H Zhang X Traveling pulses in a coupled FitzHugh-Nagumo equation
Physica D: Nonlinear Phenomena , 2021 , 418 1 ): 1 -11
[7]
叶其孝 , 李正元 , 王明新 , 吴雅萍 . 反应扩散方程引论 (第二版) . 北京 : 科学出版社 , 2011
[本文引用: 1]
Ye Q X Li Z Y Wang M X Wu Y P Introduction to Reaction Diffusion Equations (Second edition) . Beijing : Science Press , 2011
[本文引用: 1]
[8]
Zhang X Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems
Science China Mathematics , 2019 , 62 1687 -1704
[9]
Berestycki H Rossi L Rodríguez N Periodic cycles of social outbursts of activity
J Differential Equations , 2018 , 264 163 -196
[10]
Kuehn C Multiple Time Scale Dynamics . Austria: Applied Mathematical Sciences , 2015
A model of riots dynamics: shocks, diffusion and thresholds
1
2017
... 2015 年, Berestycki 等[1 ] 提出用于描述社会张力-动荡演化的常微分方程模型, ...
Traveling wave solutions in a model for social outbursts in a tension-inhibitive regime
3
2021
... 基于上述 Berestycki 等提出的常微分系统, Bakhshi 等[2 ] 考虑了扩散效应, 提出了如下用于描述社会张力-动荡演化的反应-扩散系统 ...
... 这里$u=u(\tau,x)$ $v=v(\tau,x)$ $G, r, h$ $0<d_i\ll1, i=1,2$ $0<d_1=O(1), 0<d_2\ll1$ [2 ] 利用几何奇异摄动理论, 证明系统 (1.1) 存在连接两个稳态解的波前解. ...
... 基于 Bakhshi 等[2 ] 提出的反应-扩散系统, 本文引入 Allee 效应, 即考虑如下反应-扩散系统, ...
Geometric singular perturbation theory for ordinary differential equations
5
1979
... 根据 Fenichel's 不变流形定理[3 ,4 ] , 存在 $M_0$ $\epsilon-$ $M_\epsilon$ $M_\epsilon$
... 对于系统 (3.9), 它关于 (3.11) 式任意一点 $(u_1,v_1)$ $\frac{1}{c}(1+u_1)^p$ $0$ [3 ,4 ] , 当 $\omega$ $\omega-$
... 进一步地, 根据 Fenichel 不变流形理论[3 ,4 ] ,当 $\epsilon$ $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
... 对于系统 (3.19), 其平衡点 $v_1=1$ $\delta$ $S^{1}_{0}$ $(0,1)$ $v_1=\overline{v_1}$ $v_1=v^{*}_1$ $\delta$ $u_{1}<\frac{a+1}{2}$ $S^{2}_{0}$ $(\overline{u_1},\overline{v_1})$ $S^{2}_{0}$ $u_{1}>\frac{a+1}{2}$ $(u^{*}_1,v^{*}_1)$ $\delta$ $(\overline{u_1},\overline{v_1})$ $(0,1)$ $(u^{*}_1,v^{*}_1)$ $(\overline{u_1},\overline{v_1})$ [3 ,4 ] , 四维相空间中存在连接平衡点 $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
... 系统 (4.5) 在 $M_{\epsilon=0,\omega}$ $0$ $-c$ $M_{\epsilon=0,\omega}$ [3 ,4 ] , 对于足够小的 $\epsilon>0$ $M_{\epsilon,\omega}$ $M_{\epsilon=0,\omega}$ $O(\epsilon)$ - 阶扰动 ...
Geontetric singular perturbation theory//Dynamical systems (Montecatini Terme, 1994), volume 1609 of Lecture Notes in Math
5
1995
... 根据 Fenichel's 不变流形定理[3 ,4 ] , 存在 $M_0$ $\epsilon-$ $M_\epsilon$ $M_\epsilon$
... 对于系统 (3.9), 它关于 (3.11) 式任意一点 $(u_1,v_1)$ $\frac{1}{c}(1+u_1)^p$ $0$ [3 ,4 ] , 当 $\omega$ $\omega-$
... 进一步地, 根据 Fenichel 不变流形理论[3 ,4 ] ,当 $\epsilon$ $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
... 对于系统 (3.19), 其平衡点 $v_1=1$ $\delta$ $S^{1}_{0}$ $(0,1)$ $v_1=\overline{v_1}$ $v_1=v^{*}_1$ $\delta$ $u_{1}<\frac{a+1}{2}$ $S^{2}_{0}$ $(\overline{u_1},\overline{v_1})$ $S^{2}_{0}$ $u_{1}>\frac{a+1}{2}$ $(u^{*}_1,v^{*}_1)$ $\delta$ $(\overline{u_1},\overline{v_1})$ $(0,1)$ $(u^{*}_1,v^{*}_1)$ $(\overline{u_1},\overline{v_1})$ [3 ,4 ] , 四维相空间中存在连接平衡点 $(0,0,1,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$ $(u^*,0,v^*,0)$ $(\overline{u}_{1},0,\overline{v}_{1},0)$
... 系统 (4.5) 在 $M_{\epsilon=0,\omega}$ $0$ $-c$ $M_{\epsilon=0,\omega}$ [3 ,4 ] , 对于足够小的 $\epsilon>0$ $M_{\epsilon,\omega}$ $M_{\epsilon=0,\omega}$ $O(\epsilon)$ - 阶扰动 ...
Rotated vector fields
1993
Traveling pulses in a coupled FitzHugh-Nagumo equation
2021
1
2011
... 引理 4.1 [7 ] 考虑方程 $u_t=u_{xx}+f(u)$ $t, x\in R$ $f\in C^{1}[0,1],$ $f(0)=f(1)=0,f'(0)<0,f'(1)<0$ $f$ $(0, 1)$ $u=q(x-ct)$ $c$
1
2011
... 引理 4.1 [7 ] 考虑方程 $u_t=u_{xx}+f(u)$ $t, x\in R$ $f\in C^{1}[0,1],$ $f(0)=f(1)=0,f'(0)<0,f'(1)<0$ $f$ $(0, 1)$ $u=q(x-ct)$ $c$
Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems
2019
Periodic cycles of social outbursts of activity
2018