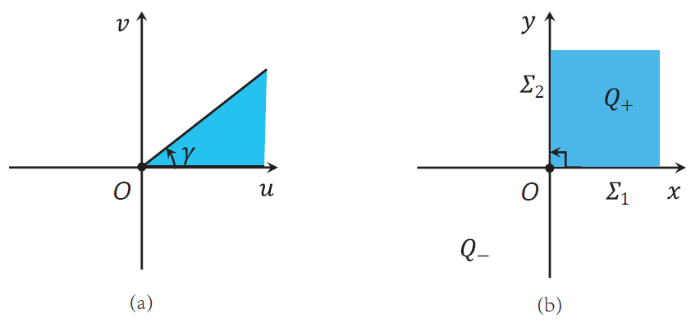1 引言与主要结论
极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义.
根据平面分段光滑系统边界的连续性, Bernardo 等[9 ] 将其分为连续平面分段光滑系统 (向量场连续, Jacobi 矩阵不连续) 和不连续平面分段光滑系统 (向量场与 Jacobi 矩阵都不连续). 其中, 最简单的不连续平面分段光滑系统是具有一条直线边界且子系统均为平面线性系统的不连续平面分段线性系统
(1.1) $\begin{aligned} \dot{x}&=F_{+}(x,y)=cx+dy+f,&\dot{y}&=G_{+}(x,y)=ax+by+e,&\text{在}&~R_{+}~\text{区域内},\\ \dot{x}&=F_{-}(x,y)=\theta x+\delta y+\phi,&\dot{y}&=G_{-}(x,y)=\alpha x+\beta y+\epsilon,&\text{在}&~R_{-}~\text{区域内}. \end{aligned}$
整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ .
然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响.
近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ].
其中, Cardin 和 Torregrosa[7 ] 考虑了具有不规则折线边界 $\Sigma_{\gamma}$ $\Sigma_{\gamma}$
如图1 所示, 其中 $\Sigma_{\gamma}$ $(0,0)$
图 1
图 1
系统具有不规则折线边界的示意图. (a) 折线夹角为 $\gamma\in (0,\pi)$ $\gamma\neq\frac{\pi}{2}$ . (b) 折线夹角 $\gamma=\frac{\pi}{2}$ .
由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
根据 Filippov[10 ,15 ] 理论, 定义不连续边界 $\Sigma$ $\Sigma_{1,2}$ $\Sigma_{1,2}^{s}$ $\Sigma_{1,2}^{c}$
(1.2) $\begin{aligned} &\Sigma_{1}^{s}=\{(x,0):G_{+}(x,0)G_{-}(x,0)\leq0\}, ~\text{在} ~\Sigma_{1}~\text{上},\\ &\Sigma_{1}^{c}=\{(x,0):G_{+}(x,0)G_{-}(x,0)>0\}, ~\text{在} ~\Sigma_{1}~\text{上}, \\ &\Sigma_{2}^{s}=\{(0,y):F_{+}(0,y)F_{-}(0,y)\leq0\},~ ~\text{在} ~\Sigma_{2}~\text{上},\\ &\Sigma_{2}^{c}=\{(0,y):F_{+}(0,y)F_{-}(0,y)>0\}, ~ ~\text{在} ~\Sigma_{2}~\text{上}, \end{aligned}$
并称滑动 (穿越) 区域中的点为滑动 (穿越) 点. 显然, 穿越区域 $\Sigma_{1,2}^{c}$ $\Sigma_{1,2}^{s}$ $\Sigma_{1,2}$
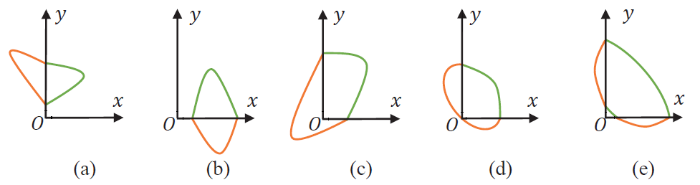
针对具有折线边界 $\Sigma=\Sigma_{1}\cup\Sigma_{2}$ 图1 所示. 其中三点极限环为第二类两点极限环与四点极限环的过渡形式, 可以将其视为其中一种, 本文不做详细研究.
图2
图2
(a) 和 (b) 第一类两点极限环. (c) 第二类两点极限环. (d) 三点极限环. (e) 四点极限环.
特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2.
根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的.
因此, 本文假设区域 $Q_{+,-}$ $Q_{-,+}$
为了方便起见, 将上述两类不连续平面分段线性系统简写为: PLH+PWLC 系统和 PWLC+PLH 系统 (PLH 和 PWLC 分别为 piecewise linear Hamiltonian 和 piecewise linear center 的英文缩写). PLH+PWLC 系统和 PWLC+PLH 系统中的极限环分别称为 Hamiltonian-中心和中心-Hamiltonian 型极限环.
基于上述假设, 第一类两点极限环即为仅具有一条直线边界的不连续平面分段线性系统 (1.1) 中的两点极限环, 利用首次积分方法, 可以得到关于第一类两点极限环的结论
引理 1.1 PLH+PWLC 系统和 PWLC+PLH 系统中不存在仅与 $\Sigma_{1}$ $\Sigma_{2}$
由于 PLH+PWLC 系统和 PWLC+PLH 系统中不存在第一类两点极限环, 因此, 下文如无特别说明, 简称第二类两点极限环为两点极限环. 关于第二类两点极限环和四点极限环的主要结论如下
定理 1.1 在 PLH+PWLC 系统中以下结论成立
(a) Hamiltonian-中心型两点极限环的最大个数为 2;
(b) Hamiltonian-中心型四点极限环的最大个数为 1;
(c) 在 1 个 Hamiltonian-中心型四点极限环存在的前提下, 最多具有 1 个 Hamiltonian- 中心型两点极限环与其共存.
定理 1.2 在PWLC+PLH 系统中以下结论成立
(a) 中心-Hamiltonian 型两点极限环的最大个数为 2;
(b) 中心-Hamiltonian 型四点极限环的最大个数为 1;
(c) 在 1 个中心-Hamiltonian 型四点极限环存在的前提下, 最多具有 1 个中心-Hamiltonian 型两点极限环与其共存.
命题 1.1 和 1.2分别提供了具有 2 个 Hamiltonian-中心型两点极限环、 1 个 Hamiltonian-中心型两点极限环与 1 个 Hamiltonian-中心型四点极限环共存的数值例子.
命题 1.1 考虑具有边界 $\Sigma$
(1.3) $\begin{aligned} &\dot{x}=2x-2y+\frac{9}{10},&&\dot{y}=2x-2y+1,&&\text{在}~Q_{+}~\text{区域内},\\ &\dot{x}=-y+\frac{ 49}{100},&&\dot{y}=5x-\frac{1}{10},&&\text{在}~Q_{-}~\text{区域内}. \end{aligned}$
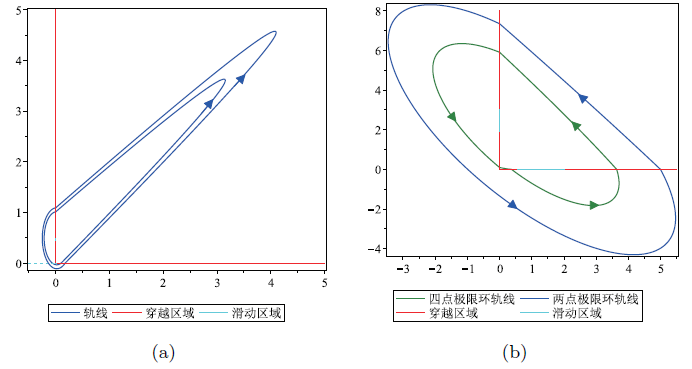
$Q_{+}$ $Q_{-}$ $(\frac{1}{50},\frac{49}{100})$ $\Sigma_{1}^{s}=\{(x,0):x\in[\frac{1}{50}]\}$ $\Sigma_{2}^{s}=\{(0,y):y\in[\frac{9}{20},\frac{49}{100}]\}$ $\Sigma$ $(0.1023675152\cdots,0)$ $(0.1763529866\cdots,0)$ $(0,1.011557320\cdots)$ $(0,1.090276005\cdots)$ 图 3(a) 所示.
图3
图3
(a) 2 个 Hamiltonian-中心型两点极限环. (b) 1 个 Hamiltonian-中心型四点极限环和唯一的 Hamiltonian- 中心型两点极限环.
命题 1.2 考虑具有边界 $\Sigma$
(1.4) $\begin{aligned} &\dot{x}=-\frac{23}{40}x-\frac{1}{2}y+\frac{24}{25},&&\dot{y}=\frac{529}{800}x+\frac{23}{40}y-\frac{9}{25},&&&&\text{在}~Q_{+}~\text{区域内},\\ &\dot{x}=-x-y+3,&&\dot{y}=2x+y-4,&&&&\text{在}~Q_{-}~\text{区域内}. \end{aligned}$
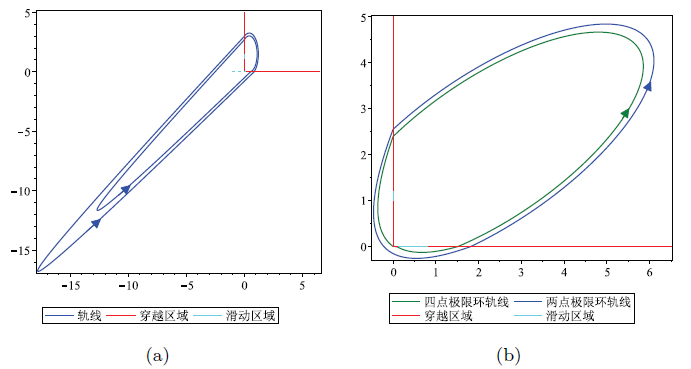
$Q_{+}$ $Q_{-}$ $\Sigma_{1}^{s}=\{(x,0):x\in[\frac{288}{529},2]\}$ $\Sigma_{2}^{s}=\{(0,y):y\in[\frac{48}{25},3]\}$ $\Sigma$ $(2\pm\frac{108\sqrt{1066389073}}{2163061},0)$ $(0,3\pm\frac{385\sqrt{1066389073}}{4326122} )$ $\Sigma$ $(4.989713352\cdots,0)$ $(0,7.344740712\cdots)$ 图 3(b) 所示.
命题 1.3 和 1.4} 分别提供了具有 2 个中心-Hamiltonian 型两点极限环、1 个中心-Hamiltonian 型两点极限环与 1 个中心-Hamiltonian 型四点极限环共存的数值例子.
命题 1.3 考虑具有边界 $\Sigma$
(1.5) $\begin{aligned} &\dot{x}=-y+\frac{3}{2},&&\dot{y}=5x-\frac{21}{10},&&\text{在}~Q_{+}~\text{区域内},\\ &\dot{x}=x-y+\frac{11}{10},&&\dot{y}=x-y+1,&&\text{在}~Q_{-}~\text{区域内}. \end{aligned}$
$Q_{+}$ $(\frac{21}{50},\frac{3}{2})$ $Q_{-}$ $\Sigma_{1}^{s}=\{(x,0):x\in[\frac{21}{50}]\}$ $\Sigma_{2}^{s}=\{(0,y):y\in[\frac{11}{10},\frac{3}{2}]\}$ $\Sigma$ $(0.5261320950\cdots,0)$ $(0.8309805435\cdots,0)$ $(0,2.693448829\cdots)$ $(0,2.987455894\cdots)$ 图 4(a) 所示.
图4
图4
(a) 2 个中心-Hamiltonian 型两点极限环. (b) 1 个中心-Hamiltonian 型四点极限环和唯一的中心-Hamiltonian 型两点极限环.
命题 1.4 考虑具有边界 $\Sigma$
(1.6) $\begin{aligned} &\dot{x}=x-2y+2,&&\dot{y}=x-y-\frac{13}{100},&&\text{在}~Q_{+}~\text{区域内},\\ &\dot{x}=\frac{1}{2}x-\frac{1}{2}y+\frac{3}{5},&&\dot{y}=\frac{1}{2}x- \frac{1}{2}y-\frac{2}{5},&&\text{在}~Q_{-}~\text{区域内}. \end{aligned}$
$Q_{+}$ $(\frac{113}{50},\frac{213}{100})$ $Q_{-}$ $\Sigma_{1}^{s}=\{(x,0):x\in[\frac{13}{100},\frac{4}{5}]\}$ $\Sigma_{2}^{s}=\{(0,y):y\in[\frac{6}{5}]\}$ $\Sigma$ $(\frac{4}{5}\pm\frac{8\sqrt{55335}}{2635},0)$ $(0,\frac{6}{5}\pm\frac{67\sqrt{55335}}{13175})$ $\Sigma$ $(1.814680995\cdots,0)$ $(0,2.552618764\cdots)$ 图 4(b) 所示.
2 主要结论的证明
本节首先提供无平衡点的线性 Hamiltonian 系统的规范型 (参见文献 [11 ,22 ,29 ])
引理 2.1 无平衡点的线性 Hamiltonian 系统的规范型为
(2.1) $\begin{aligned} \dot{x}=-\frac{\partial H(x,y)}{\partial y}=-\lambda dx+dy+f,\quad \dot{y}=\frac{\partial H(x,y)}{\partial x}=-\lambda^{2} dx+\lambda dy+e, \end{aligned}$
其中 $\lambda f\neq e$ $d\neq0$
(2.2) $H_{H}(x,y)=-\lambda^{2}dx^{2}+2\lambda dxy-dy^{2}+2ex-2fy.$
下面提供具有中心型平衡点线性系统的规范型 (参见文献 [21 ,23 ,30 ,31 ])
(2.3) $\dot{x}=-\beta x-\frac{\beta^{2}+M^{2}}{\alpha}y+\phi,~~\dot{y}=\alpha x+\beta y+\epsilon,$
其中 $\alpha\neq0$ $M>0$
(2.4) $H_{C}(x,y)=(\alpha x+ \beta y)^{2}+2\alpha (\epsilon x- \phi y)+M^{2}y^{2}.$
注意到引理 2.1 和 2.2 中的规范型与坐标变换无关, 所以可以在 $Q_{+}$ $Q_{-}$
2.1 引理 1.1 的证明
证 假设系统 (2.1), (2.3) 具有一个第一类两点极限环, 且仅与边界 $\Sigma_{2}$ $(0,Y_{1})$ $(0,Y_{2})$ $0<Y_{1}<Y_{2}$ . 则首次积分 $H_{H}$ $H_{C}$ $Q_{+}$ $Q_{-}$
(2.5) $\begin{aligned} &H_{H}(Y_{1},0)=H_{H}(Y_{2},0),\\ &H_{C}(Y_{2},0)=H_{C}(Y_{1},0), \end{aligned}$
(2.6) $\begin{aligned} &-(Y_{1}-Y_{2})\left(d(Y_{1}+Y_{2})+2f\right)=0,\\ &(Y_{2}-Y_{1})\left((\beta^2+M^2)(Y_{1}+Y_{2})-2\alpha\phi\right)=0, \end{aligned}$
由于 $0<Y_{1}<Y_{2}$
(2.7) $\begin{aligned} &\Upsilon_{1}:~Y_{1}=-Y_{2}-\frac{2f}{d},\\ &\Upsilon_{2}:~Y_{1}=-Y_{2}+\frac{2\alpha\phi}{\beta^2+M^2}, \end{aligned}$
显然, 直线 $\Upsilon_{1}$ $\Upsilon_{2}$ $-\frac{f}{d}=\frac{\alpha\phi}{\beta^2+M^2}$ $\Sigma_{2}$ $-\frac{f}{d}\neq\frac{\alpha\phi}{\beta^2+M^2}$ $\Sigma_{2}$ $\Sigma_{2}$
类似地, 可以证明系统 (2.1)+(2.3) 不存在仅与 $\Sigma_{1}$
2.2 定理 1.1(a) 的证明
证 假设系统 (2.1)+(2.3) 具有一个第二类两点极限环, 与边界 $\Sigma$ $(x_{+},0)$ $(0,y_{+})$ $x_{+}>0$ $y_{+}>0$ . $Q_{+}$ 22 ] 可知, 令 $H_{H}(x, y)=h,(h \in \mathbb{R})$
利用线性变换 $Y=\lambda x-y$
其中 $d(e-\lambda f) \neq 0$ $y=\lambda x-\frac{f}{d}$
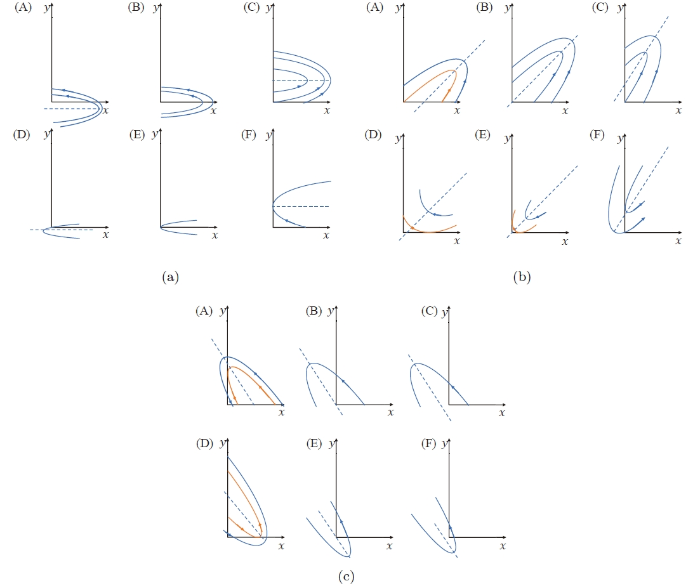
(a) 当 $\lambda=0$ $e \neq 0$ $y=-\frac{f}{d}$ $x$ - 轴, 若同时满足 $de<0$ 图 5(a)(A-C) ; 若同时满足 $de>0$ 图 5(a)(D-F) ;
图5
图5
$Q_{+}$ $\lambda=0$ $y$ - 轴. (b) $\lambda>0$ $\lambda<0$
(b) 当 $\lambda>0$ $e \neq 0$ $y=\lambda x-\frac{f}{d}$ $d(e-\lambda f)<0$ 图 5(b)(A-C) ; 若同时满足 $d(e-\lambda f)>0$ 图 5(b)(D-F) ;
(c) 当 $\lambda<0$ $e \neq 0$ $y=\lambda x-\frac{f}{d}$ $d(e-\lambda f)<0$ 图 5(c)(A-C) ; 若同时满足 $d(e-\lambda f)>0$ 图 5(c)(D-F) .
以对称轴的斜率和抛物线的开口方向为分类标准, $Q_{+}$ 图 5 所示. 显然, 除了图 5(a)(D、E) (对称轴 $y=-\frac{f}{d}\leq0$ ) 和图 5(b)(F) (对称轴 $y=\lambda x-\frac{f}{d}$ $x$ - 轴交点的横坐标小于 0) 的轨线结构, 其余的轨线结构类型在 $Q_{+}$ $(x_{+},0)$ $(0,y_{+})$ 图 5(b)(A) 中, 点 $(x_{+},0)$ $x$ - 轴的交点 $(\frac{2e}{d\lambda^{2}},0)$ 图 5(b)(D、E) 中, 点 $(x_{+},0)$ $x$ - 轴的切点 $(\frac{e}{d\lambda^{2}},0)$ 图 5(c)(A) 中, 点 $(x_{+},0)$ $x$ - 轴的右端交点的右侧; 在图 5(c)(D) 中, 点 $(x_{+},0)$ $x$ - 轴的切点 $(\frac{e}{d\lambda^{2}},0)$
此时, 若系统 (2.1)+(2.3) 存在两点极限环, 首次积分 $H_{H}$ $H_{C}$ $Q_{+}$ $Q_{-}$
(2.8) $\begin{aligned} &H_{H}(x_{+},0)=H_{H}(0,y_{+}),\\ &H_{C}(0,y_{+})=H_{C}(x_{+},0), \end{aligned}$
(2.9) $\begin{aligned} \lambda^{2}d x_{+}^{2}-d y_{+}^{2}-2e x_{+}-2f y_{+}&=0,\\ \alpha^{2}x_{+}^{2}-(\beta^{2}+M^{2})y_{+}^{2}+2\alpha \epsilon x_{+}+2\alpha \phi y_{+}&=0, \end{aligned}$
根据 Bezout 定理, 最高次数分别为 2 和 2 的两个多项式方程 (2.9) 最多具有 4 个实数解 $(x_{+}, y_{+})$ $(0,0)$ $(x_{+k}, y_{+k}),k=1,2,3$
(2.10) $0<x_{+1}<x_{+2}<x_{+3} \quad\text{且}\quad 0<y_{+1}<y_{+2}<y_{+3},$
否则, 在 $Q_{+}$ $(x_{+k}, 0)$ $(0, y_{+k})$
与此同时, 系统 (2.9) 可以转化为两个多项式方程
(2.11) $\begin{aligned} d \left(\alpha^{2}-\lambda^{2}(\beta^{2}+M^{2})\right)x_{+}^{2} +2\left(\alpha \epsilon d +e (\beta^{2}+M^{2})\right)x_{+} +2\left(\alpha \phi d +f (\beta^{2}+M^{2})\right)y_{+}&=0,\\ d \left(\alpha^{2}-\lambda^{2}(\beta^{2}+M^{2})\right) y_{+}^{2} +2\alpha(\epsilon\lambda^{2}d +\alpha e )x_{+} +2\alpha(\phi\lambda^{2}d +\alpha f )y_{+}&=0. \end{aligned}$
如果 $\alpha^{2}=\lambda^{2}(\beta^{2}+M^{2})$
如果 $\alpha^{2}\neq\lambda^{2}(\beta^{2}+M^{2})$ $\alpha \phi d +f (\beta^{2}+M^{2})=0$ $\alpha(\epsilon\lambda^{2}d +\alpha e )=0$ $\alpha \phi d +f (\beta^{2}+M^{2})\neq0$ $\alpha(\epsilon\lambda^{2}d +\alpha e )\neq0$
(2.12) $\begin{aligned} \mathcal{M}_{1}:y_{+}=&k_{1}\left(x_{+} -b_{1}\right)x_{+},\\ \mathcal{M}_{2}:x_{+}=&k_{2} \left(y_{+} - b_{2}\right)y_{+}, \end{aligned}$
针对这种情形, 极限环的个数可以转化为两个抛物线方程满足条件 (2.10) 的交点的最大个数. 在 $(x_{+},y_{+})$ $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ $\mathcal{M}_{1}$ $x$ - 轴具有两个交点, 分别为 $(0,0)$ $(b_{1},0)$ . 类似地, 抛物线 $\mathcal{M}_{2}$ $y$ - 轴具有两个交点, 分别为 $(0,0)$ $(0,b_{2})$ . 因此, $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ 22 ], 系统 (2.12) 的剩余三个解中满足条件 (2.10) 的最大个数为 2, 相应地, 系统 (2.1)+(2.3) 最多具有 2 个第二类两点极限环.
综上所述, 系统 (2.1)+(2.3) 最多具有 2 个第二类两点极限环, 结合命题 1.1 的数值结果, 定理 1.1(a) 的证明完毕.
2.3 定理 1.1(b) 的证明
证 假设系统 (2.1)+(2.3) 具有一个四点极限环, 与边界 $\Sigma$ $(x_{1}, 0)$ $(x_{2}, 0)$ $(0, y_{1})$ $(0, y_{2})$ $0 < x_{1} < x_{2}$ $0 < y_{1} < y_{2}$ $Q_{+}$ 图 5(c)(A、D) . 则首次积分 $H_{H}$ $H_{C}$ $Q_{+}$ $Q_{-}$
(2.13) $\begin{aligned} H_{H}(x_{2},0)=H_{H}(0,y_{2}),\\ H_{C}(0,y_{2})=H_{C}(0,y_{1}),\\ H_{H}(0,y_{1})=H_{H}(x_{1},0),\\ H_{C}(x_{1},0)=H_{C}(x_{2},0), \end{aligned}$
(2.14) $\begin{aligned} &e_{1} =\frac{\lambda^{2} d }{2} x_{2}^{2}-\frac{d }{2} y_{2}^{2}-e x_{2}-fy_{2}=0,\\ &e_{2}=(y_{2}-y_{1})((\beta^{2}+M^{2})(y_{1}+y_{2})-2\alpha \phi)=0,\\ &e_{3}=-\frac{\lambda^{2} d }{2} x_{1}^{2}+\frac{d }{2} y_{1}^{2}+e x_{1}+fy_{1}=0, \\ &e_{4}=\alpha(x_{1}-x_{2})(\alpha(x_{1}+x_{2})+2 \epsilon)=0. \end{aligned}$
根据系统 (2.14) 容易得到: 如果 $(x_{1}, x_{2}, y_{1}, y_{2})$ $(x_{2}, x_{1}, y_{2}, y_{1})$ $x_{1}<x_{2}$ $y_{1}<y_{2}$
因为 $\beta^{2}+M^{2}>0$ $\alpha\neq0$ $e_{2}=0$ $e_{4}=0$
(2.15) $\begin{aligned} &y_{2}=-y_{1}+w_{1},~ &x_{2}=-x_{1}-w_{2}, \end{aligned}$
其中 $w_{1}=\frac{2\alpha \phi}{\beta^{2}+M^{2}}$ $w_{2}=\frac{2\epsilon}{\alpha}$ . 为了保证 $x_{1}<x_{2}$ $y_{1}<y_{2}$
将 (2.15) 代入 $e_{1}=0$ $e_{3}=0$
(2.16) $\begin{aligned} m_{1}\left(x_{1}+\frac{w_{2}}{2}\right)+m_{2}\left(y_{1}-\frac{w_{1}}{2}\right)=0, \\ -\frac{\lambda^{2} d }{2} x_{1}^{2}+\frac{d }{2} y_{1}^{2}+e x_{1}+fy_{1}=0, \end{aligned}$
其中 $m_{1}=2 e +\lambda^{2} d w_{2}$ $m_{2}=2 f +d w_{1}$ . 系统 (2.16) 的第二个方程同样可以写作
(2.17) $\begin{aligned} \lambda^{2}\left(x_{1}-W_{1}\right)^{2}-\left(y_{1}+W_{2}\right)^{2}=\frac{e ^{2}-\lambda^{2}f ^{2}}{\lambda^{2}d ^{2}}, \end{aligned}$
其中 $W_{1}=\frac{e }{\lambda^{2}d }$ $W_{2}=\frac{f }{d }$ .
如果 $m_{1}=m_{2}=0$
如果 $m_{1}=0$ $m_{2}=0$ $(x_{1}, y_{1})$ . 更详细地, 如果 $m_{1}=0$ $m_{2}\neq0$ $y_{1}=\frac{w_{1}}{2}$ $y_{1}<\frac{w_{1}}{2}<y_{2}$ $m_{1}=0$ $m_{2}\neq0$ $x_{1}=-\frac{w_{2}}{2}$ $x_{1}<-\frac{w_{2}}{2}<x_{2}$
如果 $m_{1}m_{2}\neq0$ $y_{1}$
(2.18) $\begin{aligned} &y_{1}=Kx_{1}+\gamma,\\ &a_{0}x_{1}^{2}+a_{1}x_{1}+a_{2}=0, \end{aligned}$
根据 Bezout 定理, 系统 (2.18) 最多具有两个解. 由系统 (2.18) 的两个解, 可以得到系统 (2.14) 的解 $(x_{1}, x_{2}, y_{1}, y_{2})$ $x_{1}<x_{2}$ $y_{1}< y_{2}$ . 引入系统 (2.18) 的第二个方程根的判别式 $\bigtriangleup_{1}=a_{1}^{2}-4a_{0}a_{2}$ . 如果 $\bigtriangleup_{1}<0$ $\bigtriangleup_{1}=0$ $x_{1} = x_{2}$ $\bigtriangleup_{1}>0$ $(x_{11}, y_{11})$ $(x_{12}, y_{12})$ $0<x_{11}<x_{12}$ . 根据前文分析可知
(2.19) $\begin{aligned} x_{21}=x_{12},~~ x_{22}=x_{11},~~ y_{21}=y_{12},~~ y_{22}=y_{11}, \end{aligned}$
则可以使用记号 $x_{1i}$ $y_{1i}$ $i=1,2$ . 若系统存在极限环, 极限环的轨线与边界的四个交点为 $(x_{11}, 0)$ $(x_{12}, 0)$ $(0, y_{11})$ $(0, y_{12})$ $x$ - 轴和 $y$ - 轴的正半轴. 若满足条件 $0 < y_{11} < y_{12}$
综上所述, 系统 (2.1)+(2.3) 最多具有 1 个四点极限环, 结合命题 1.2 的数值结果, 定理 1.1(b) 的证明完毕.
2.4 定理 1.1(c) 的证明
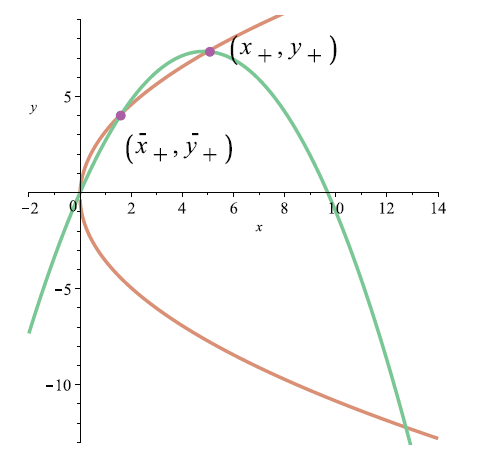
证 首先假设系统 (2.1)+(2.3) 具有一个四点极限环与边界 $\Sigma$
假设系统存在四点极限环, 系统 (2.16) 可以重新写作
(2.20) $\begin{aligned}&\mathcal{L}:m_{1}\left(x_{1}+\frac{w_{2}}{2}\right)+m_{2}\left(y_{1}-\frac{w_{1}}{2}\right)=0,\\&\mathcal{S}_{1}:\lambda^{2}\left(x_{1}-W_{1}\right)^{2}-\left(y_{1}+W_{2}\right)^{2}=\frac{e ^{2}-\lambda^{2}f ^{2}}{\lambda^{2}d ^{2}},\end{aligned}$
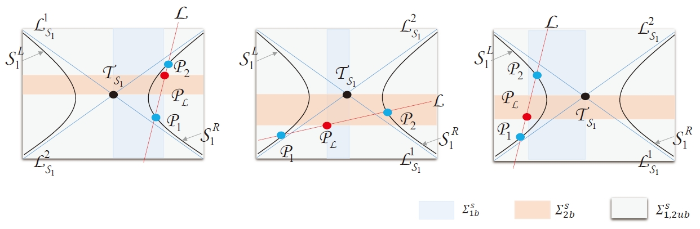
其中 $W_{1}=\frac{e }{\lambda^{2}d }$ $W_{2}=\frac{f}{d }$ . 显然, 系统 (2.20) 的第一个方程在 $(x_{1},y_{1})$ $\mathcal{L}$ $\mathcal{P}_{\mathcal{L}}=(-\frac{w_{2}}{2},\frac{w_{1}}{2})$ $\mathcal{L}$ $\mathcal{S}_{1}$ . 如果 $e^{2}=\lambda^{2}f ^{2}$ $\mathcal{S}_{1}$ $e^{2}\neq\lambda^{2}f^{2}$ $\mathcal{S}_{1}$ $\mathcal{T}_{\mathcal{S}_{1}}=\left(W_{1},-W_{2} \right)$ . 显然, 直线 $\mathcal{L}$ $\mathcal{S}_{1}$ $\mathcal{L}$ $\mathcal{S}_{1}$ $\mathcal{S}_{1}$ $\mathcal{S}_{1}^{L}$ $\mathcal{S}_{1}^{R}$ . 正如前文所言, 令 $(x_{1}, 0)$ $(x_{2}, 0)$ $(0, y_{2})$ $(0, y_{1})$ $x$ - 轴和 $y$ - 轴正半轴的四个连续交点, 此外, 其坐标需要满足 $0 < x_{1} < x_{2}$ $0 < y_{1} < y_{2}$ . 为了满足这两个条件, 直线 $\mathcal{L}$ $y_{1}<\frac{w_{1}}{2}<y_{2}$ $x_{1}<-\frac{w_{2}}{2}<x_{2}$ $\mathcal{L}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{P}_{1}(x_{1},y_{1})$ $\mathcal{P}_{2}(x_{2},y_{2})$
(A) $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $\mathcal{S}_{1}$ $\mathcal{S}_{1}^{R}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{S}_{1}^{R}$ $\mathcal{L}$ $\mathcal{L}_{\mathcal{S}_{1}}^{2}$
(B) $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $\mathcal{S}_{1}$ $\mathcal{S}_{1}^{L}$ $\mathcal{S}_{1}^{R}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{S}_{1}^{L}$ $\mathcal{S}_{1}^{R}$ $\mathcal{L}$ $\mathcal{L}_{\mathcal{S}_{1}}^{2}$
(C) $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $\mathcal{S}_{1}$ $\mathcal{S}_{1}^{L}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{S}_{1}^{L}$ $\mathcal{L}$ $\mathcal{L}_{\mathcal{S}_{1}}^{2}$ 图 6 所示.
图6
图6
直线 $\mathcal{L}$ $\mathcal{S}_{1}$
下面计算边界上的滑动区域, 用以排除不满足极限环存在性条件的无效解. 如果 $\lambda\alpha>0$ $(<0)$
(2.21) $\begin{aligned} &\Sigma_{1b}^{s}=\{(x,0):x\in[\min\bar{X},\max\bar{X}]\} \cap \{x\in \mathbb{R}^{+}\},\quad \text{其中}~\bar{X}\in\left\{-\frac{w_{2}}{2},W_{1}\right\}\\ &\Sigma_{2b}^{s}=\{(0,y):y\in[\min\bar{Y},\max\bar{Y}]\} \cap \{y\in \mathbb{R}^{+}\},\quad \text{其中}~\bar{Y}\in\left\{\frac{w_{1}}{2},-W_{2}\right\} \end{aligned}$
(2.22) $\begin{aligned} &\Sigma_{1ub}^{s}=\{(x,0):x\in(-\infty,\min\bar{X}]\cup[\max\bar{X},+\infty]\} \cap \{x\in \mathbb{R}^{+}\},\\ &\Sigma_{2ub}^{s}=\{(0,y):y\in(-\infty,\min\bar{Y}]\cup[\max\bar{Y},+\infty]\} \cap \{y\in \mathbb{R}^{+}\}. \end{aligned}$
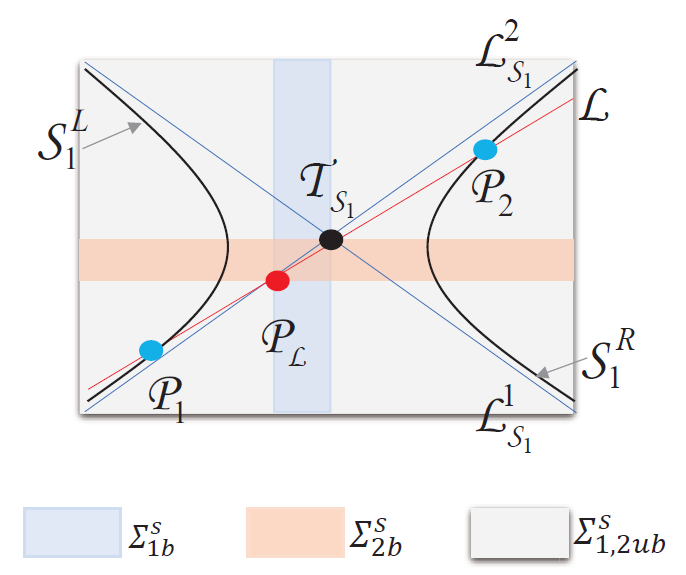
显然, 对于图 6 中的第一种和第三种相交情况, 由于直线 $\mathcal{L}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $Q_{\pm}$ $\Sigma_{1b}^{s}$ $\Sigma_{2b}^{s}$ $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ 图 6 中的第一种和第三种相交情形, 总是不存在四点极限环. 在图 6 中的第二种相交情形, 如果点 $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $y$ - 坐标均大于或小于 $\mathcal{T}_{\mathcal{S}_{1}}$ $y$ - 坐标, 总是存在一个点 $\mathcal{P}_{1}$ $\mathcal{P}_{2}$
通过调整图 6 中第二种相交状态下直线 $\mathcal{L}$ $\mathcal{P}_{1}$ $y$ - 坐标小于点 $\mathcal{T}_{\mathcal{S}_{1}}$ $y$ - 坐标, 且点 $\mathcal{P}_{2}$ $y$ - 坐标大于点 $\mathcal{T}_{\mathcal{S}_{1}}$ $y$ - 坐标, 则如果滑动区域有界, 点 $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ 图 7 所示.
图7
图7
直线 $\mathcal{L}$ $\mathcal{S}_{1}$
基于上述分析, 已经保证了四点极限环的存在性, 下面将证明系统 (2.1)+(2.3) 最多具有 1 个两点极限环与其共存, 其中两点极限环与边界 $\Sigma$ $(x_{+},0)$ $(0,y_{+})$ . 显然, 系统 (2.9) 的第一个方程与系统 (2.20) 的第二个方程相同, 系统 (2.9) 的第二个方程还可写作
(2.23) $\mathcal{S}_{2}:\left(\alpha x_{+}+\epsilon\right)^{2}-\left(\sqrt{\beta^{2}+M^{2}}y_{+}-\frac{\alpha \phi}{\sqrt{\beta^{2}+M^{2}}}\right)^{2}= \epsilon^{2}-\frac{\alpha^{2}\phi^{2}}{\beta^{2}+M^{2}},$
系统 (2.23) 为 $(x_{+},y_{+})$ $\mathcal{S}_{2}$ $\mathcal{S}_{2}$
如果 $\epsilon^{2}=\frac{\alpha^{2}\phi^{2}}{\beta^{2}+M^{2}}$ $\mathcal{S}_{2}$ $\mathcal{L}_{\mathcal{S}_{2}}^{1}$ $\mathcal{L}_{\mathcal{S}_{2}}^{2}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{L}$ $\mathcal{S}_{1}$ $\mathcal{S}_{2}$
(2.24) $\begin{aligned} 0<x_{1}<x_{2}<x_{+i} \quad\text{且}\quad 0<y_{1}<y_{2}<y_{+i},\quad~i=1,2. \end{aligned}$
值得注意的是, 如果系统 (2.1)+(2.3) 同时存在四点极限环和两点极限环, 这些极限环一定是套索结构, 因为中心型系统或无平衡点 Hamiltonian 系统的轨线必然相互嵌套形成椭圆, 这意味着四点极限环一定位于由两点极限环包围的内部区域.
下面基于图7 中四点极限环的存在性考虑两点极限环的最大共存个数. 双曲线 $\mathcal{S}_{1}$ $\mathcal{S}_{2}$ $\mathcal{P}_{2}$ $\mathcal{S}_{1}^{R}$ $\mathcal{S}_{2}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{P}_{2}$ $\mathcal{S}_{2}$ $\mathcal{S}_{1}$ $\mathcal{S}_{2}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{P}_{1}$ $\mathcal{P}_{2}$ $\mathcal{P}_{\mathcal{L}}$ $\mathcal{P}_{2}$ $\mathcal{S}_{2}$ $\mathcal{S}_{2}$ $\mathcal{S}_{1}$ $\mathcal{S}_{2}$
综上所述, 系统 (2.1)+(2.3) 最多具有一个两点极限环与四点极限环共存. 结合命题 1.2 的数值结果, 定理1.1(c) 的证明完毕.
3 命题 1.1-1.2 的证明
3.1 命题 1.1 的证明
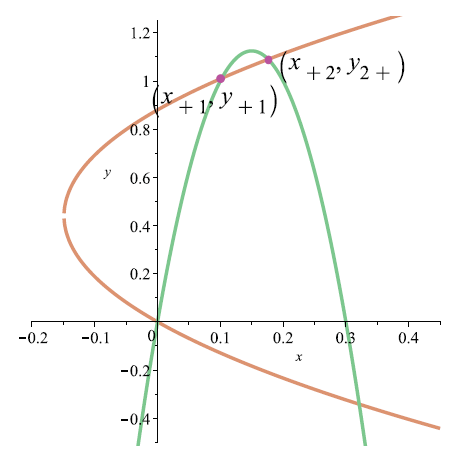
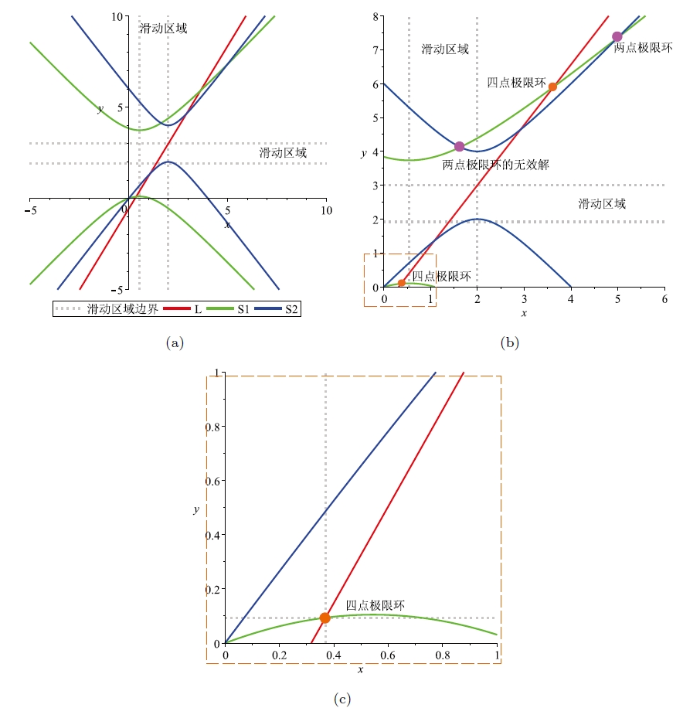
证 不连续平面分段线性系统 (1.3) 在 $Q_{+}$ $Q_{-}$ $(\frac{1}{50},\frac{49}{100})$
上述两个方程的几何结构如图 8 所示, 考虑限制条件 (2.10), 上述系统的两个有效解为
图8
图8
抛物线 $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ .
则在 $Q_{+}$ $(x(0),y(0))=(x_{+i},0)$
两条轨线的运行时间分别 $t_{+1}=11.13924835\cdots$ $t_{+2}=12.66628991\cdots$ . 在 $Q_{-}$ $(x(0),y(0))=(0,y_{+i})$
两个轨线的运行时间分别 $t_{-1}=1.527500398\cdots$ $t_{-2}=1.648858170\cdots$ . 最后, 利用数值模拟, 得到两个轨线为逆时针旋转的两点极限环, 如图 3(a) 所示.
3.2 命题 1.2 的证明
证 不连续平面分段线性系统 (1.4) 在 $Q_{+}$ $Q_{-}$ $(1,2)$
系统的第二个方程根的判别函数为 $\Delta = \frac{1066389073}{116640000}>0$
则在 $Q_{+}$ $(x(0),y(0))=(x_{2},0)$
轨线的运行时间为 $t=\frac{25}{589062}\sqrt{1066389073}+\frac{175}{186}$ . $Q_{-}$ $(x(0),y(0))=(0,y_{2})$
轨线的运行时间为 $t=\pi-\arctan\left(\frac{1540}{64422681}\sqrt{1066389073}\right)$ .
在 $Q_{+}$ $(x(0),y(0))=(0,y_{1})$
轨线的运行时间为 $t=\frac{25}{589062} \sqrt{1066389073}-\frac{175}{186}$ . $Q_{-}$ $(x(0),y(0))=(x_{1},0)$
轨线的运行时间为 $t=\pi-\arctan\left(\frac{216}{3587291}\sqrt{1066389073}\right)$ . 利用数值模拟, 得到轨线为逆时针旋转的四点极限环, 如图 3(b) 所示.
下面考虑两点极限环与四点极限环的共存性. 在保证四点极限环的存在性前提下, 系统 (2.20) 中直线
的几何结构如图 9(a) 所示, 满足定理 1.1(c) 证明中图 7 的几何结构. 与此同时, 保证两点极限环存在性的双曲线
(3.1) $\begin{aligned} \Sigma_{1b}^{s}=\left\{(x,0):x\in\left[\frac{288}{529},2\right]\right\},\quad \Sigma_{2b}^{s}=\left\{(0,y):y\in\left[\frac{48}{25},3\right]\right\}, \end{aligned}$
图9
图9
直线 $\mathcal{L}$ $\mathcal{M}_{1}$ $\mathcal{M}_{2}$
显然, 直线 $\mathcal{L}$ $\mathcal{S}_{1}$ 图 9(b) 和 9(c) 所示. 双曲线 $\mathcal{S}_{1}$ $\mathcal{S}_{2}$ 图 9(b) 所示.
下面提供两点极限环的详细计算过程, 利用两个子系统的首次积分, 对应系统 (2.9) 为
考虑限制条件 (2.10), 可以得到系统的两个解
又因为点 $(\bar{x}_{+},0)\in\Sigma_{1b}^{s}$ $(x_{+},y_{+})$ 图 10 所示. 因此, 系统 (1.4) 仅存在唯一的两点极限环与四点极限环共存.
图10
图10
抛物线 $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ .
在 $Q_{+}$ $(x(0),0)=(x_{+},0)$
轨线的运行时间为 $t_{+}=2.159368760\cdots $ . 在 $Q_{-}$ $(0,y(0))=(0,y_{+})$
轨线的运行时间分别 $t_{-}=4.948781233\cdots$ . 最后, 利用数值模拟, 得到轨线为逆时针旋转的两点极限环, 如图 3(b) 所示.
注 3.1 类似于引理 1.1、定理 1.1、命题 1.1 和命题 1.2 的证明, 利用引理 2.1 和 2.2 中的两个首次积分, 可以讨论定理 1.2、 命题 1.3} 和命题 1.4 的中心-Hamiltonian 型极限环的存在性和最大个数. 由于证明过程类似, 本文不再赘述.
参考文献
View Option
[1]
Alves A M Euzéebio R D Periodic trajectories in planar discontinuous piecewise linear systems with only centers and with a nonregular switching line
Nonlinearity , 2023 , 36 12 ): 6747 -6776
[本文引用: 5]
[2]
Anacleto M E Llibre J Valls C Vidal C Limit cycles of discontinuous piecewise differential systems formed by linear centers in $R^2$
Nonlin Anal: Real World Appl , 2021 , 60 103281
[本文引用: 1]
[3]
Andrade K S Cespedes O A R Cruz D R Novaes D D Higher order Melnikov analysis for planar piecewise linear vector flelds with nonlinear switching curve
J Differ Equ , 2021 , 287 1 -36
[本文引用: 1]
[4]
Barkat M Benterki R Llibre J The extended 16th Hilbert problem for a class of discontinuous piecewise differential systems
Nonlinear Dyn , 2023 , 111 2 ): 1475 -1484
[本文引用: 2]
[5]
Baymout L Benterki R Llibre J Limit cycles of the discontinuous piecewise differential systems separated by a nonregular line and formed by a linear center and a quadratic one
Int J Bifurcation and Chaos , 2024 , 34 5 ): 2450058
[本文引用: 2]
[6]
Braun F da Cruz L P C Torregrosa J On the number of limit cycles in piecewise planar quadratic differential systems
Nonlinear Anal Real World Appl , 2024 , 79 104124
[本文引用: 2]
[7]
Cardin P T Torregrosa J Limit cycles in planar piecewise linear differential systems with nonregular separation line
Physica D: Nonlinear Phenomena , 2016 , 337 67 -82
[本文引用: 3]
[8]
de Carvalho Braga D Mello L F More than three limit cycles in discontinuous piecewise linear differential systems with two zones in the plane
Int J Bifurcation and Chaos , 2014 , 24 4 ): 1450056
[本文引用: 1]
[9]
di Bernardo M Budd C J Champneys A R Kowalczyk P Piecewise Smooth Dynamical Systems, Theory and Applications . London : Springer-Verlag , 2008
[本文引用: 4]
[10]
Filippov A F Differential Equations with Discontionuous Righthand Sides
Netherlands: Kluwer Academic , 1988
[本文引用: 1]
[11]
Fonseca A Llibre J Mello L F Limit cycles in planar piecewise linear hamiltonian systems with three zones without equilibrium points
Int J Bifurcation and Chaos , 2023 , 30 11 ): 2050157
[本文引用: 2]
[12]
Gasull A Some open problems in low dimensional dynamical systems
SeMA J , 2021 , 78 3 ): 233 -269
[本文引用: 1]
[13]
Han M Zhang W On Hopf bifurcation in non-smooth planar systems
J Differ Equ , 2010 , 248 2399 -2416
[本文引用: 2]
[14]
He D Llibre J Limit cycles in a class of planar discontinuous piecewise quadratic differential systems with a non-regular line of discontinuity (II)
Mediterr J Math , 2024 , 21 6 ): Article 174
[本文引用: 2]
[15]
Hilbert D Mathematical problems
Bull Amer Math , 1902 , 8 437 -479
[本文引用: 3]
[16]
Huan S Yang X On the number of limit cycles in general planar piecewise linear systems
Discrete Con- tinuous Dyn Syst , 2012 , 32 6 ): 2147 -2164
[本文引用: 1]
[17]
姜雪丽 , 邓璇 , 文邱浩 , 熊艳琴 . 带两条平行切换直线多项式微分系统的极限环分支
数学物理学报 , 2022 , 42A 2 ): 353 -364
[本文引用: 1]
Jiang X L Deng X Wen Q H Xiong Y Q Limit circle bifurcations of polynomial differential system with two parallel switch straight lines
Acta Math Sci , 2022 , 42A 2 ): 353 -364
[本文引用: 1]
[18]
Leine R I Nijmeijer H Dynamics and Bifurcations of Nonsmooth Mechanical Systems. Lecture Notes in Applied and Computational Mechanics
Berlin:Springer-Verlag , 2004
[本文引用: 2]
[19]
李时敏 , 陈挺 , 刘玉记 , 黎小丽 . 平面折射系统极限环的存在和唯一性
中国科学: 数学 , 2021 , 51 4 ): 605 -614
[本文引用: 3]
Li S Chen T Liu Y Li X On the existence and uniqueness of limit cycles in planar refracted systems
Sci China: Math , 2021 , 51 4 ): 605 -614
[本文引用: 3]
[20]
Li T Llibre J Limit cycles in piecewise polynomial systems allowing a non-regular switching boundary
Physica D , 2021 , 419 132855
[本文引用: 3]
[21]
Li Z Liu X Limit cycles in the discontinuous planar piecewise linear systems with three zones
Qual Theory Dyn Syst , 2021 , 20 1 -22
[本文引用: 1]
[22]
Li Z Liu X Limit cycles in discontinuous piecewise linear planar Hamiltonian systems without equilibrium points
Int J Bifurcation and Chaos , 2022 , 32 10 ): 2250153
[本文引用: 8]
[23]
Li Z Liu X Impact limit cycles in the planar piecewise linear hybrid systems
Commun Nonlinear Sci Numer Simul , 2023 , 119 107074
[本文引用: 1]
[24]
Liang F Romanovski V G Zhang D Limit cycles in small perturbations of a planar piecewise linear Hamiltonian system with a non-regular separation line
Chaos Solit Fract , 2018 , 111 18 -34
[本文引用: 1]
[25]
Liu H Wei Z Moroz I Limit cycles and bifurcations in a class of planar piecewise linear systems with a nonregular separation line
J Math Anal Appl , 2023 , 526 2 ): 127318
[本文引用: 3]
[26]
Llibre J Mereu A C Limit cycles for discontinuous quadratic differential systems with two zones
J Math Anal Appl , 2014 , 413 2 ): 763 -775
[本文引用: 2]
[27]
Llibre J Ponce E Three nested limit cycles in discontinuous piecewise linear differential systems with two zones
Dyn Contin Discrete Impuls Syst Ser B Appl Algorithms , 2012 , 19 3 ): 325 -335
[本文引用: 2]
[28]
Llibre J Tang Y Limit cycles of discontinuous piecewise quadratic and cubic polynomial perturbations of a linear center
Discrete Contin Dyn Syst Ser B , 2019 , 24 4 ): 1769 -1784
[本文引用: 2]
[29]
Llibre J Teixeira M A Piecewise linear differential systems without equilibria produce limit cycles?
Non- linear Dyn , 2017 , 88 157 -164
[本文引用: 2]
[30]
Llibre J Teixeira M A Piecewise linear differential systems with only centers can create limit cycles?
Nonlinear Dyn , 2018 , 91 249 -255
[本文引用: 2]
[31]
Llibre J Zhang X Limit cycles created by piecewise linear centers
Chaos , 2019 , 29 053116
[本文引用: 1]
[32]
Llibre J Valls C The extended 16th Hilbert problem for discontinuous piecewise systems formed by linear centers and linear Hamiltonian saddles separated by a nonregular line
Int J Bifurcation and Chaos , 2023 , 33 16 ): 2350196
[本文引用: 3]
[33]
Novaes D D On the Hilbert number for piecewise linear vector flelds with algebraic discontinuity set
Physica D , 2022 , 441 133523
[本文引用: 1]
[34]
Sun L Du Z Crossing limit cycles in planar piecewise linear systems separated by a nonregular line with node-node type critical points
Int J Bifurcation and Chaos , 2024 , 34 4 ): 2450049
[本文引用: 3]
[35]
杨纪华 , 马亮 . 具有尖点环的非光滑微分系统的极限环分支
数学物理学报 , 2023 , 43A 6 ): 1667 -1680
[本文引用: 1]
Yang J Ma L Limit cycle bifurcations of a non-smooth differential system with a cuspidal loop
Acta Math Sci , 2023 , 43A 6 ): 1667 -1680
[本文引用: 1]
[36]
Zhao Q Wang C Yu J Limit cycles in discontinuous planar piecewise linear systems separated by a nonregular line of center-center type
Int J Bifurcation and Chaos , 2021 , 31 2150136
[本文引用: 4]
Periodic trajectories in planar discontinuous piecewise linear systems with only centers and with a nonregular switching line
5
2023
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. ...
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
... [1 ]、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
Limit cycles of discontinuous piecewise differential systems formed by linear centers in $R^2$ and separated by two circles
1
2021
... 然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响. ...
Higher order Melnikov analysis for planar piecewise linear vector flelds with nonlinear switching curve
1
2021
... 然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响. ...
The extended 16th Hilbert problem for a class of discontinuous piecewise differential systems
2
2023
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [4 ]研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Limit cycles of the discontinuous piecewise differential systems separated by a nonregular line and formed by a linear center and a quadratic one
2
2024
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
On the number of limit cycles in piecewise planar quadratic differential systems
2
2024
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [6 ]通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Limit cycles in planar piecewise linear differential systems with nonregular separation line
3
2016
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 其中, Cardin 和 Torregrosa[7 ] 考虑了具有不规则折线边界 $\Sigma_{\gamma}$ $\Sigma_{\gamma}$
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
More than three limit cycles in discontinuous piecewise linear differential systems with two zones in the plane
1
2014
... 然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响. ...
4
2008
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... 根据平面分段光滑系统边界的连续性, Bernardo 等[9 ] 将其分为连续平面分段光滑系统 (向量场连续, Jacobi 矩阵不连续) 和不连续平面分段光滑系统 (向量场与 Jacobi 矩阵都不连续). 其中, 最简单的不连续平面分段光滑系统是具有一条直线边界且子系统均为平面线性系统的不连续平面分段线性系统 ...
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
... [9 ]、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
Differential Equations with Discontionuous Righthand Sides
1
1988
... 根据 Filippov[10 ,15 ] 理论, 定义不连续边界 $\Sigma$ $\Sigma_{1,2}$ $\Sigma_{1,2}^{s}$ $\Sigma_{1,2}^{c}$
Limit cycles in planar piecewise linear hamiltonian systems with three zones without equilibrium points
2
2023
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... 本节首先提供无平衡点的线性 Hamiltonian 系统的规范型 (参见文献 [11 ,22 ,29 ]) ...
Some open problems in low dimensional dynamical systems
1
2021
... 然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响. ...
On Hopf bifurcation in non-smooth planar systems
2
2010
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Limit cycles in a class of planar discontinuous piecewise quadratic differential systems with a non-regular line of discontinuity (II)
2
2024
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
Mathematical problems
3
1902
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... 根据 Filippov[10 ,15 ] 理论, 定义不连续边界 $\Sigma$ $\Sigma_{1,2}$ $\Sigma_{1,2}^{s}$ $\Sigma_{1,2}^{c}$
On the number of limit cycles in general planar piecewise linear systems
1
2012
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
带两条平行切换直线多项式微分系统的极限环分支
1
2022
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
带两条平行切换直线多项式微分系统的极限环分支
1
2022
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
Dynamics and Bifurcations of Nonsmooth Mechanical Systems. Lecture Notes in Applied and Computational Mechanics
2
2004
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
... [18 ]等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
平面折射系统极限环的存在和唯一性
3
2021
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [19 ]总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
平面折射系统极限环的存在和唯一性
3
2021
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [19 ]总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Limit cycles in piecewise polynomial systems allowing a non-regular switching boundary
3
2021
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
Limit cycles in the discontinuous planar piecewise linear systems with three zones
1
2021
... 下面提供具有中心型平衡点线性系统的规范型 (参见文献 [21 ,23 ,30 ,31 ]) ...
Limit cycles in discontinuous piecewise linear planar Hamiltonian systems without equilibrium points
8
2022
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. ...
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
... 本节首先提供无平衡点的线性 Hamiltonian 系统的规范型 (参见文献 [11 ,22 ,29 ]) ...
... 证 假设系统 (2.1)+(2.3) 具有一个第二类两点极限环, 与边界 $\Sigma$ $(x_{+},0)$ $(0,y_{+})$ $x_{+}>0$ $y_{+}>0$ . $Q_{+}$ 22 ] 可知, 令 $H_{H}(x, y)=h,(h \in \mathbb{R})$
... 针对这种情形, 极限环的个数可以转化为两个抛物线方程满足条件 (2.10) 的交点的最大个数. 在 $(x_{+},y_{+})$ $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ $\mathcal{M}_{1}$ $x$ - 轴具有两个交点, 分别为 $(0,0)$ $(b_{1},0)$ . 类似地, 抛物线 $\mathcal{M}_{2}$ $y$ - 轴具有两个交点, 分别为 $(0,0)$ $(0,b_{2})$ . 因此, $\mathcal{M}_{1}$ $\mathcal{M}_{2}$ 22 ], 系统 (2.12) 的剩余三个解中满足条件 (2.10) 的最大个数为 2, 相应地, 系统 (2.1)+(2.3) 最多具有 2 个第二类两点极限环. ...
Impact limit cycles in the planar piecewise linear hybrid systems
1
2023
... 下面提供具有中心型平衡点线性系统的规范型 (参见文献 [21 ,23 ,30 ,31 ]) ...
Limit cycles in small perturbations of a planar piecewise linear Hamiltonian system with a non-regular separation line
1
2018
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
Limit cycles and bifurcations in a class of planar piecewise linear systems with a nonregular separation line
3
2023
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
Limit cycles for discontinuous quadratic differential systems with two zones
2
2014
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Three nested limit cycles in discontinuous piecewise linear differential systems with two zones
2
2012
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Limit cycles of discontinuous piecewise quadratic and cubic polynomial perturbations of a linear center
2
2019
... 整个相平面由直线边界 $\Lambda=\{(x,y)\in\mathbb{R}^{2}:x=s_{1},~s_{1}=\text{常数}\}$ $R_{+}$ $R_{-}$ . 因此, 整个相平面为 $\mathbb{R}^{2}=R_{+}\cup R_{-}\cup \Lambda$ $R_{+}$ $R_{-}$ $\Lambda$ 13 ,19 ,22 ,27 ]. Han 和 Zhang[13 ] 证明了系统 (1.1) 可以存在 2 个极限环. 随后, Huan 和 Yang[16 ] 利用数值模拟得到了 3 个极限环的存在性, Llibre 和 Ponce[27 ] 提供了这一数值例子的严格解析证明. 此后, 系统 (1.1) 中极限环的最大个数问题成为了一个悬而未决的公开问题. 国内外学者利用不同方法, 提供了包含焦点 (F)、 鞍点 (S) 和结点 (N) 的系统 (1.1) 中穿越极限环的最大个数下界估计, 李时敏、陈挺和刘玉记等[19 ] 总结了在 F-F、F-S、F-N 型系统 (1.1) 中穿越极限环的最大个数为 3, S-S、S-N、N-N 型系统 (1.1) 中穿越极限环的最大个数为 2, 并证明了向量场在边界上具有相同方向的平面分段线性折射系统中对应穿越极限环的最大个数为 1. 然而, 系统 (1.1) 中穿越极限环的个数大于 3 的例子尚未被发现. 此外, 针对具有一条直线边界的不连续平面分段光滑系统[4 ,6 ,26 ,28 ] , Llibre 和 Mereu[26 ] 利用一阶平均法证明了由两个二次等时中心构造的周期轨在二次多项式扰动下, 系统至少存在 5 个穿越极限环. Llibre 和 Tang[28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
... [28 ] 利用 5 阶平均法证明了线性中心在二次和三次多项式扰动下分别可以分支出 8 和 13 个穿越极限环. 为了避免求解平均法中的复杂积分, Braun 等[6 ] 通过展开位移映射, 分别证明了在特定斜直线上 Loud 族中的四个等时中心在多项式扰动下穿越极限环的最佳个数下界为 12. Barkat 等[4 ] 研究了由线性中心和 $n$ $n=1,2,3,4,5$ $n \geq6$ $0, 1, 2, 3, 4, 5$ . ...
Piecewise linear differential systems without equilibria produce limit cycles?
2
2017
... 特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. ...
... 本节首先提供无平衡点的线性 Hamiltonian 系统的规范型 (参见文献 [11 ,22 ,29 ]) ...
Piecewise linear differential systems with only centers can create limit cycles?
2
2018
... 特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. ...
... 下面提供具有中心型平衡点线性系统的规范型 (参见文献 [21 ,23 ,30 ,31 ]) ...
Limit cycles created by piecewise linear centers
1
2019
... 下面提供具有中心型平衡点线性系统的规范型 (参见文献 [21 ,23 ,30 ,31 ]) ...
The extended 16th Hilbert problem for discontinuous piecewise systems formed by linear centers and linear Hamiltonian saddles separated by a nonregular line
3
2023
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
On the Hilbert number for piecewise linear vector flelds with algebraic discontinuity set
1
2022
... 然而, 在众多描述实际问题的应用模型中, 边界并不总是一条规则的直线, 也可能为折线、非线性曲线等不规则形式. 文献 [8 ] 研究了具有多夹角折线边界的两区域不连续平面分段线性系统, 并推测存在具有 $n\in\mathbb{N}$ 3 ] 研究了具有非线性曲线边界 $y=x^{n}$ $\mathcal{L}(n)$ $\mathcal{L}(2)\geq4$ $\mathcal{L}(3)\geq8$ $n\geq4$ $\mathcal{L}(n)\geq7$ $n\geq5$ $\mathcal{L}(n)\geq9$ . 在此基础上, 文献 [12 ] 中的公开问题 18 提出要进一步提升极限环最大个数 $\mathcal{L}(n)$ 33 ] 证明了当 $k\geq1$ $\mathcal{L}(2k)\geq k^{2}+2k+1$ $\mathcal{L}(2k+1)\geq k^{2}+2k+3$ . 此外, 文献 [2 ] 研究了边界由具有相同中心的两个圆环构成的三区域不连续平面分段线性系统, 证明了系统最多具有 3 个穿越极限环. 因此, 边界的几何结构对于不连续平面分段线性系统中极限环的最大个数具有重要影响. ...
Crossing limit cycles in planar piecewise linear systems separated by a nonregular line with node-node type critical points
3
2024
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...
具有尖点环的非光滑微分系统的极限环分支
1
2023
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
具有尖点环的非光滑微分系统的极限环分支
1
2023
... 极限环是平面微分动力系统所有周期轨道集合中的一个孤立周期轨道. 平面分段光滑系统极限环的最大个数与相对位置问题与 Hilbert[15 ] 第 16 问题紧密相关, 参见文献 [9 11 ,15 ,17 ,19 ,35 ]. 近年来, 随着动力系统理论的发展及计算机技术的进步, 越来越多的实际问题可以通过平面分段光滑系统进行描述, 如: 食饵-捕食者模型、 动植物疾病预防模型、 药物动力学胶囊模型等. 周期运动现象广泛存在于这些实际应用模型中, 因此, 研究与之对应的平面分段光滑系统极限环理论具有重要意义. ...
Limit cycles in discontinuous planar piecewise linear systems separated by a nonregular line of center-center type
4
2021
... 近年来, 具有不规则折线边界的不连续平面分段线性系统引起了国内外学者的广泛关注, 参见文献 [1 ,5 ,7 ,14 ,20 ,22 ,25 ,32 ,34 ,36 ]. ...
... 由于不规则折线边界夹角大小的不确定性, 系统极限环的个数与相对位置问题是十分复杂的. 文献 [14 ,24 ] 分别研究了不规则折线边界夹角 $\gamma=\frac{\pi}{2}$ $\gamma\neq\frac{\pi}{2}$ $\gamma\in (0,\pi)$ 7 ,20 ] 主要研究了 $\gamma\neq\frac{\pi}{2}$ 1 ,5 ,22 ,25 ,32 ,34 ,36 ] 主要研究了 $\gamma=\frac{\pi}{2}$ $\gamma=\frac{\pi}{2}$
... 特别地, 文献 [29 ,30 ] 分别提出了两个公开问题: 无平衡点或仅具有中心型平衡点的平面分段线性系统是否存在极限环? 针对具有折线边界的不连续平面分段线性系统, 文献 [1 ,36 ] 证明了仅具有中心型平衡点的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. 文献 [22 ] 证明了仅具有无平衡点 Hamiltonian 向量场的不连续平面分段线性系统中不存在第一类两点极限环, 第二类两点极限环和四点极限环的最大个数分别为 2 和 1, 两类极限环的最大共存个数为 2. ...
... 根据已有文献 [1 ,9 ,18 ,20 ,22 ,25 ,32 ,34 ,36 ] 可知, 许多实际应用模型均可利用具有折线边界的不连续平面分段线性系统进行表示, 诸如:非线性振子[1 ] 、拐角碰撞模型[9 ] 、 不连续支撑的质量弹簧模型[18 ] 等, 并且在具有折线边界的不连续平面分段线性系统中, 极限环的 Poincaré 映射构造相对复杂, 研究难度更大. 因此, 从应用和理论的角度来看, 进一步研究这类不连续平面分段线性系统的极限环问题具有重要意义. 与此同时, 在这些实际应用模型中, 两个不同的子系统可能为无平衡点的 Hamiltonian 线性系统或具有中心型平衡点的线性系统, 然而, 在这种情况下各类极限环的存在性、共存性及最大共存个数仍然是未知的. ...