1 引言
本文主要应用Abelian 积分的相关理论来研究一类单摆方程的Poincaré 分支. 考虑如下类单摆方程的扰动方程
(1.1) $\begin{array}{ll} \ddot{x}+\sin(x)=\epsilon\sum_{m=0}^{n}Q_{n,m}(x)\dot{x}^m, \end{array}$
其中$\epsilon$ $Q_{n,m}(x)$
即$Q_{n,m}(x)$ $n$
系统(1.1)可以看作如下平面哈密顿系统的扰动系统
(1.2) $\begin{array}{ll} \dot{x}=y,\dot{y}=-\sin(x), \end{array}$
(1.3) $H(x,y)=\frac{y^2}{2}+1-\cos(x).$
系统(1.1)的Poincaré 分支问题可以看作弱化 Hilbert $16$
由于$\sin(ix),\cos(ix)$ $2\pi$ $[-\pi,\pi]\times\mathbb{R}$
注意到, 当 $h\in(0,2)$ $\{\gamma_h\}=\{(x,y):H(x,y)=h\}$ $h\in(2,+\infty)$ $y>0$ $\gamma^+_h$ $y<0$ $\gamma^-_h$ . 对于 $h\in(0,2)$
通常称为振荡区域, 我们将用 $R^0$ $h\in(2,+\infty)$ $\pm y>0$ $\mathrm{R}^{\pm}$
2016 年 Gasull 等人在文献 [3 ] 中的考虑了如下类单摆方程
(1.4) $\ddot{x}+\sin(x)=\epsilon\sum_{m=m_1}^{m_2}Q_{n,m}(x)\dot{x}^m,$
其中$Q_{n,m}(x)$ $n(n\geq 1)$
在$(0,2)$ $\mathbf{B}(b)$
定理 1.1 当$m_1=m_2$ $M^0(h)$ $n$
注 1.1 注意到, 当$m_1=m_2=2k$ $y^{2k}=(h-1+\cos(x))^k$ . 容易验证
Gasull 等人在其文章第三部分的引理3.6 中应用到了如下积分
其中$P$ $d$ $p,v\in \mathbb{N}_+$ $\gamma_h\subseteq \{y^2/2+1-\cos(x)=h,h\in (0,2)\}$ . 容易验证该积分发散, 因而引理 3.6 后续部分的证明是无效的.事实上
其中$\mu(h)$ $1-\cos(\mu(h))=h$ . 而当 $x\rightarrow 0$
根据以上讨论, 我们期望能给定理1.1 一个正确的证明. 因为, 对一般情形的处理尚没有有效的处理方法, 对此我们将问题锁定在一些特殊的情形, 如
$n=2,m=2s+1$
(1.5) $\ddot{x}+\sin(x)=\epsilon\sum_{i=0}^{2}\left(a_i\cos(ix)+b_i\sin(ix)\right)\dot{x}^m,$
$M^0(h)$
由$y=\sqrt{h-1+\cos(x)}=\sqrt{h-1+\cos(-x)}$
定理 1.2 $M^0(h)$ $(0,2)$ $2$
注 1.2 根据定理 [4 ,定理 2.2 或定理 2.3]知, 定理1.2 意味着系统 (1.5) 至多可从振荡区域 $R^0$
文中主要结构安排如下: 第一章我们主要介绍问题的研究背景以及主要定理; 第二章介绍了相关的概念以及基本引理;
第三部分是利用第二部分的基本引理来证明我们的主要定理.
2 准备工作
(2.1) $\dot{x}=2y,\dot{y}=-\Psi'(x),$
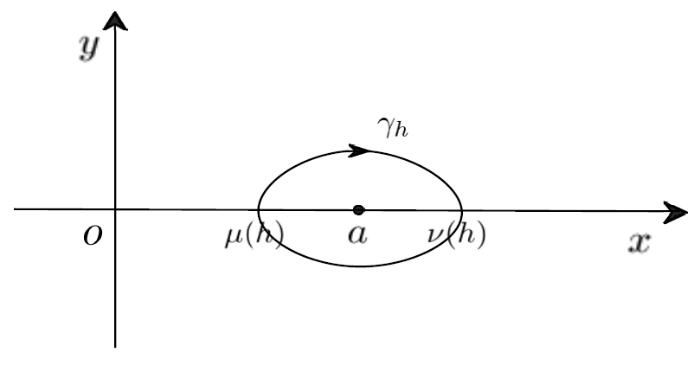
其相应的首次积分为$H(x,y)=y^2+\Psi(x)$ $\Psi(x)$ $(\mu,\nu)$ $a\in (\mu,\nu)$
在条件$({\rm H}_1)$ $(a,0)$ $h_{a}=H(a,0)$ $\Psi(\mu)=\Psi(\nu)=h_{s}$ . 由$({\rm H}_1)$ $h_{s}>h_{a}$ . 记$\{\gamma_h\}$ $\{(x,y)| H(x,y)=h,h_{a}<h<h_{s}\}$ .
图1
对任意的 $h\in(h_{a},h_{s})$ $\mu(h),\nu(h)$ $\gamma_{h}$ $x$ $\mu<\mu(h)<a<\nu(h)<\nu$ 图 1 ).此外, 根据条件$({\rm H}_1)$ $x\in (a,\nu(h))$ $x\mapsto \sigma(x)\in (\mu(h),a)$ $\Psi(x)=\Psi(\sigma(x))$ .
(2.2) $I(h)=\alpha I_1(h)+\beta I_2(h)=\alpha \oint_{\gamma_h}f_1(x)y\mathrm{d}x+\beta \oint_{\gamma_h}f_2(x)y\mathrm{d}x,$
其中 $ \gamma_h(h_a<h<h_s)$ $(a,0)$ $ f_1(x)$ $ f_2(x)$ $(\mu, \nu)$ $\alpha,\beta\in \mathbb{R}$ .
(2.3) $F_k(x)=\frac{f_k(x)}{\Psi'(x)}-\frac{f_k(\sigma(x))}{\Psi'(\sigma(x))},\quad x\in (a,\nu), \quad k=1, 2.$
值得指出, 这些$F_k$
(2.4) $\xi(x)=\frac{F_2(x)}{F_1(x)}=\frac{f_2(x)\Psi'(\sigma(x))-f_2(\sigma(x))\Psi'(x)}{f_1(x)\Psi'(\sigma(x))-f_1(\sigma(x))\Psi'(x)},$
1996 年, 李承治和张芷芬基于判别函数$\xi(x)$ $\frac{I_2(h)}{I_1(h)}$ 6 , 定理 1]).此后, 在文献 [2 ] 中, Grau 等人将文献[6 ] 中的结果一般化, 给出判别$n$ $f_1, f_2, \cdots, f_{n}$ $n$ $f_1, f_2, \cdots, f_{n}$ $n-1$
本文主要考虑的是具有三个生成元的Abelian 积分. 为此, 考虑如下具有三个生成元的 Abelian 积分
(2.5) $I(h)=\alpha \oint_{\gamma_h}f_1(x)y\mathrm{d}x+\beta \oint_{\gamma_h}f_2(x)y\mathrm{d}x+\gamma \oint_{\gamma_h}f_3(x)y\mathrm{d}x,$
其中$\gamma_h(h_a<h<h_s)$ $(a,0)$ $f_i(x)$ $i=1,2,3$ $(\mu, \nu)$ $\alpha,\beta$ $\gamma$
(2.6) $\xi(x)=\frac{F_2(x)}{F_1(x)}, \quad \eta(x)=\frac{F_3(x)}{F_1(x)}.$
对上述判别函数, 刘长剑和肖冬梅在文献[7 ] 给出如下$\mathrm{Abelian}$
引理 2.1 假设$({\rm H}_1)$ $({\rm H}_2)$
$({\bf H_3})$ $x\in (a, \nu)$ $F_1'(x)>0$
$({\bf H_4})$ $\xi'(x)$ $\left(\frac{\eta'(x)}{\xi'(x)}\right)'$ $x\in (a, \nu)$
则对任意的$\alpha,\beta$ $\gamma$ $\mathrm{Abelian}$ $(h_a, h_s)$
下面我们将说明引理2.1 的方法不能有效的解决主要定理. 事实上当系统(1.5) 中的$m=1$
其中$\{\gamma_h\}=\{(x,y):H(x,y)=y^2/2+1-\cos(x)=h,h\in(0,2)\}$ $1,\cos(x)$ $\cos(2x)$ $f_1(x)$ $F_1(x)$ $F_1'(x)$ $(0,\pi)$ 1 ,性质 2.8]知对具有三个生成元的Abelian 积分Chebyshev 性质判别法,引理2.1 的判别法是优于 Grau 等人的判别法. 因此, 有必要尝试用新的方法来处理该问题.
在$\xi(x)$ $(a,\nu)$ 8 ]).
引理 2.2 假设条件$({\rm H}_1)$ $({\rm H}_2)$
$({\bf H_5})$ $\xi'(x)$ $(a, \nu)$ $x^*$
$({\bf H_6})$ $x\in (x^*, \nu)$ $(\Psi(x)F_1(x))'>0$ .
则对任意的$\alpha,\beta\in \mathbb{R}$ $\mathrm{Abelian}$ $(h_a,\ h_s)$
基于刘长剑和肖冬梅在文献[7 ] 中的想法结合引理2.2, 对于Abelian 积分(2.5) 我们有如下结果.
定理 2.1 假设$({\rm H_1})$ $({\rm H}_2)$
$(\bar{\bf H_3})$ $x\in (a, \nu)$ $(\Psi(x)F_1(x))'>0$
$({\bf H_4})$ $\xi'(x)$ $\left(\frac{\eta'(x)}{\xi'(x)}\right)'$ $x\in (a, \nu)$
则对任意的$\alpha,\beta$ $\gamma$ $\mathrm{Abelian}$ $(h_a,\ h_s)$
如果$\zeta'(x)$ $(a, \nu)$ $I(h)$ $(h_a,\ h_s)$ $\zeta'(x)$ $(a, \nu)$
由$\xi'(x)\neq 0$ $\left(\frac{\eta'(x)}{\xi'(x)}\right)'\neq 0$ $\beta\in \mathbb{R}$ $\zeta'(x)$ $(a, \nu)$ $\zeta'(x)$ $(a, \nu)$ $\zeta'(x)$ $(a, \nu)$ $x^*(\beta)$ $({\rm H}_5)$ $x\in (x^*(\beta),\nu)$ $(\Psi(x)F_1(x))'>0$ . 根据引理 2.2, 可得$I(h)=\alpha I_1(h)+I_2(h)$ $(h_a,\ h_s)$
注 2.1 由$\Psi'(x)>0$ $\Psi(a)=0$ $(\bar{\rm H}_3)$ $({\rm H}_3)$ . 这意味着定理2.1 要优于引理2.1.
3 主要定理的证明
本章主要任务是借助定理2.1 对定理1.2 给出一个完整的证明.
引理 3.1 若$\mathrm{Abelian}$
在开区间$(h_a,\ h_s)$ $k$ $\gamma_h(h_a<h<h_s)$ $(a,0)$ $f_i(x)$ $i=1,2,\cdot\cdot\cdot,n$ $(\mu, \nu)$ $\alpha_i\in \mathbb{R}$ . 则对任意的正奇数$m$ $\mathrm{Abelian}$
在开区间$(h_a,\ h_s)$ $k$
当$m=2q-1(q\geq 1)$
则当$m=2q+1$ $y^2/2+\Psi(x)=h$ $\frac{\partial y}{\partial h}=\frac{1}{y}$
在开区间$(h_a,\ h_s)$ $k+1$
下证$I(h)$ $k$ $I(h)$ $(h_a,\ h_s)$ $k+1$
由文献 [4 ,引理2.3]证明知, 函数$I'(h)$ $(h_1,h_{k+1})$ $k$ $\lim_{h\rightarrow h_a}I(h)=0$ $I'(h)$ $(h_a,\ h_1)$ $1$ $(h_a,\ h_s)$ $k+1$
综上可知, 对任意的正奇数 $m$
在开区间$(h_a,\ h_s)$ $k$
我们采用第二章的记号,$\Psi(x)=1-\cos(x)$ $a=0,\mu=-\pi,\nu=\pi,\sigma(x)=-x,f_1(x)=1,f_2(x)=\cos(x),h\in(0,2)$ $\mu(h)=\arccos(1-h)$ .
证 由引理 3.1 可知我们只要证明$m=1$ $({\rm H}_2),({\rm H}_3),({\rm H}_4)$
$\bullet \textbf{(1)}$ $({\rm H}_2)$ .
易得当$x\in (0,\pi)$ $F_1(x)=\frac{2}{\sin(x)}>0$
$\bullet \textbf{(2)}$ $({\rm H}_3)$ .
$\bullet \textbf{(3)}$ $({\rm H}_4)$ .
易知 $F_1(x)=\frac{2}{\sin(x)}>0$ $F_2(x)=2\frac{\cos(x)}{\sin(x)}$ $F_3(x)=2\frac{\cos(2x)}{\sin(x)}$ . 由 $\xi(x)=\frac{F_2(x)}{F_1(x)}$ $x\in (0,\pi)$ $\xi'(x)=-\sin(x)\neq 0$ . 又因$\eta'(x)=-2\sin(2x)$ $x\in (0,\pi)$
综合以上讨论结合定理2.1 可知$M^0(h)$ $(0,2)$ $2$
4 总结和讨论
本文主要讨论的是二次三角多项式的情形, 并没有对三次及以上的三角多项式给出相关结果. 这里有必要说明是采取的方法有所限制,我们的方法只能处理具有三个生成元的情形. 事实上具有三个以上生成元的Abelian 积分Chebyshev 性质判别法我们已经建立 (已投稿), 但用该方法处理Gasull 的这个问题的可行性和 Grau 等人的判别法是一样的. 这表明, 对该问题的完整解决需要用到其它方法. 本文主要结果与文献[9 ,定理5.1]的结论$(3)$
参考文献
View Option
[1]
Cen X Liu C Sun Y Wang J Cyclicity of period annulus for a class of quadratic reversible systems with a non-rational first integral
Proceedings of the Royal Society of Edinburgh . 2023 , 153 5 ): 1706 -1728
[本文引用: 1]
[2]
Grau M Mañosas F Villadelpart J A Chebychev criterion for Abelian integral
Trans Amer Math Soc , 2011 , 363 109 -129
[本文引用: 1]
[3]
Gasull A Geyer A Mañosas F On the number of limit cycles for perturbed pendulum equations
J Differ Equ , 2016 , 261 3 ): 2141 -2167
[本文引用: 1]
[4]
Han M Yang J The maximum number of zeros of functions with parameters and application to differential equations
Journal of Nonlinear Modeling and Analysis , 2021 , 1 13 -34
[本文引用: 3]
[5]
Karlin S Studden W Tchebycheff System:With Applications in Analysis and Statistic . New York : Interscience Publishers , 1966
[6]
Li C Zhang Z A criterion for determining the monotonocity of the ratio of two Abelian integrals
J Diff Eqns , 1996 , 124 407 -424
[本文引用: 2]
[7]
Liu C Xiao D The smallest upper bound on the number of zeros of Abelian integrals
J Differ Equ , 2020 , 269 4 ): 3816 -3852
[本文引用: 2]
[8]
Sun Y Liu C The Poincaré bifurcation of a SD oscillator
Discrete Contin Dyn Syst Ser B , 2021 , 26 3 ): 1565 -1577
[本文引用: 1]
[9]
Shi Y Han M Zhang L Homoclinic bifurcationof limit cycles innear Hamiltoniansystems on the cylinder
J Differ Equ , 2021 , 304 1 -28
[本文引用: 1]
Cyclicity of period annulus for a class of quadratic reversible systems with a non-rational first integral
1
2023
... 其中$\{\gamma_h\}=\{(x,y):H(x,y)=y^2/2+1-\cos(x)=h,h\in(0,2)\}$ $1,\cos(x)$ $\cos(2x)$ $f_1(x)$ $F_1(x)$ $F_1'(x)$ $(0,\pi)$ 1 ,性质 2.8]知对具有三个生成元的Abelian 积分Chebyshev 性质判别法,引理2.1 的判别法是优于 Grau 等人的判别法. 因此, 有必要尝试用新的方法来处理该问题. ...
A Chebychev criterion for Abelian integral
1
2011
... 1996 年, 李承治和张芷芬基于判别函数$\xi(x)$ $\frac{I_2(h)}{I_1(h)}$ 6 , 定理 1]).此后, 在文献 [2 ] 中, Grau 等人将文献[6 ] 中的结果一般化, 给出判别$n$ $f_1, f_2, \cdots, f_{n}$ $n$ $f_1, f_2, \cdots, f_{n}$ $n-1$
On the number of limit cycles for perturbed pendulum equations
1
2016
... 2016 年 Gasull 等人在文献 [3 ] 中的考虑了如下类单摆方程 ...
The maximum number of zeros of functions with parameters and application to differential equations
3
2021
... 注 1.2 根据定理 [4 ,定理 2.2 或定理 2.3]知, 定理1.2 意味着系统 (1.5) 至多可从振荡区域 $R^0$
... 从而, 根据文献 [4 ,引理2.3] 知 ...
... 由文献 [4 ,引理2.3]证明知, 函数$I'(h)$ $(h_1,h_{k+1})$ $k$ $\lim_{h\rightarrow h_a}I(h)=0$ $I'(h)$ $(h_a,\ h_1)$ $1$ $(h_a,\ h_s)$ $k+1$
A criterion for determining the monotonocity of the ratio of two Abelian integrals
2
1996
... 1996 年, 李承治和张芷芬基于判别函数$\xi(x)$ $\frac{I_2(h)}{I_1(h)}$ 6 , 定理 1]).此后, 在文献 [2 ] 中, Grau 等人将文献[6 ] 中的结果一般化, 给出判别$n$ $f_1, f_2, \cdots, f_{n}$ $n$ $f_1, f_2, \cdots, f_{n}$ $n-1$
... ] 中, Grau 等人将文献[6 ] 中的结果一般化, 给出判别$n$ $f_1, f_2, \cdots, f_{n}$ $n$ $f_1, f_2, \cdots, f_{n}$ $n-1$
The smallest upper bound on the number of zeros of Abelian integrals
2
2020
... 对上述判别函数, 刘长剑和肖冬梅在文献[7 ] 给出如下$\mathrm{Abelian}$
... 基于刘长剑和肖冬梅在文献[7 ] 中的想法结合引理2.2, 对于Abelian 积分(2.5) 我们有如下结果. ...
The Poincaré bifurcation of a SD oscillator
1
2021
... 在$\xi(x)$ $(a,\nu)$ 8 ]). ...
Homoclinic bifurcationof limit cycles innear Hamiltoniansystems on the cylinder
1
2021
... 本文主要讨论的是二次三角多项式的情形, 并没有对三次及以上的三角多项式给出相关结果. 这里有必要说明是采取的方法有所限制,我们的方法只能处理具有三个生成元的情形. 事实上具有三个以上生成元的Abelian 积分Chebyshev 性质判别法我们已经建立 (已投稿), 但用该方法处理Gasull 的这个问题的可行性和 Grau 等人的判别法是一样的. 这表明, 对该问题的完整解决需要用到其它方法. 本文主要结果与文献[9 ,定理5.1]的结论$(3)$