在干旱半干旱地区, 水分是制约植被生长的重要的因素之一. 目前已有很多学者建立了关于植被-水动力学反应扩散方程, 进而从理论和数值上研究了植被斑图的形成^[1-3]. 植被斑图可以表征植被在时间和空间上的分布特征. 1999 年, Klausmeier^[4] 首次应用反应扩散方程建立了一个二变量的植被-水模型

这里$P$ 表示植被密度,$W$ 表示水的密度,$R$ 表示植被吸收水分的速率,$J$ 为植被将吸收的水分转化为自身生长的转化率,$M$ 为植被的死亡率,$A$ 为降水速率,$L$ 为因蒸发引起的水分流失的速率,$V\nabla W$ 表示因坡度引起的水径流量,$D_P$ 为植被的扩散系数. Klausmeier 模型主要研究了山坡上的条状斑图的形成原因, 结果表明: 在半干旱生态系统中, 山坡上的条状斑图是由于行波失稳导致的; 平地上的不规则植被分布结构是由空间异质性引起的. HilleRisLambers 等人^[5]在模型(1.1) 的基础上将水分为地下水和地表水, 建立了三变量反应扩散系统并研究了植被斑图的形成机制. 事实上, 遮阳效应对减少水分的蒸发起到了很大的作用^[6]. 因此研究遮阳效应对干旱半干旱地区植被的影响是一项有意义的工作. 但是, 目前关于带有遮阳效应的植被模型的研究工作较少. 为此, 基于模型(1.1), 我们构建了一类具有遮阳效应的植被-水模型

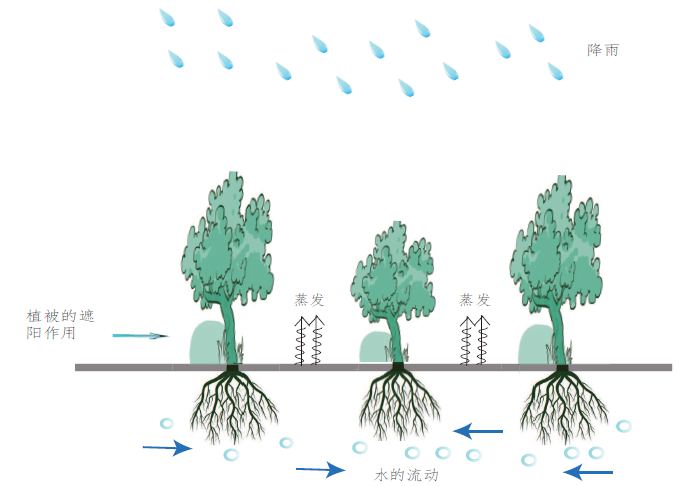
其中, $\Omega\subset\mathbb{R} $, $\alpha$ 为因遮阳作用减少的水分蒸发的速率, $D_W$ 表示水的扩散系数, 这里假设植被生长在平坦的环境下. 该模型的边界条件为零流边界. 图1 展示了植被的遮阳效应以及植被和水之间相互作用的示意图

目前, 有很多研究是基于图灵理论研究图灵斑图的演化过程^[3,5]. 事实上, 图灵斑图是图灵分支的产物, 而图灵分支是一种特殊的稳态分支. 迄今为止, 一些学者对反应扩散模型的稳态分支问题进行了研究^[7-10]. 例如, Wang 等人^[7]运用Crandall-Rabinowitz 分歧定理得到了非常数稳态解的结构. Yi 等人^[8]研究了Hopf 分支和稳态分支问题. 但以上研究都只考虑了单特征值情形下的稳态分支问题. 为了进一步分析和完善稳态分支理论, 本文选取$\alpha$ 作为分支参数, 研究了模型(1.2) 的稳态分支问题.

与文献 [7-10] 相比, 本文的主要工作和贡献在于从正常数解出发, 研究了模型 (1.2) 在单特征值和双特征值情形下非常数稳态解的解析结构. 需要指出的是, 由于经典的 Crandall-Rabinowitz 分歧定理不能适用于双特征值情形, 因此需要提出一种有效的方法解决这一问题. 这里, 我们应用隐函数定理和空间分解方法对双特征值情形进行理论分析.

本文的主要内容安排如下: 第2 节, 建立了一类具有遮阳效应的植被-水模型, 给出了稳态分支产生的条件. 第3 节, 分别分析了在单特征值和双特征值情形下非常数解的解析结构. 第4 节, 通过数值模拟验证了非常数解的存在性. 第5 节为本文的结论.

对(1.2) 式进行无量纲化

得到如下模型

下面将$\rho$ 作为分支参数, 研究模型(2.1) 的稳态分支问题.模型(2.1) 有三个平衡点: 一个裸地平衡点$E_0=(0, a)$ 和两个正平衡点

当且仅当$a+\rho m>2m$.

下面对这三个常数解进行稳定性分析. 所研究的空间区域为$\Omega=(0, l\pi)$. 首先给出了系统(2.1) 对应的稳态问题

考虑如下特征值问题

(2.3) 式对应的特征值为 $\lambda _k=(\frac{k}{l})^2, \ k\in \{0,1,2,\cdot\cdot\cdot\},$ 其对应的归一化特征向量为

方程(2.2) 的线性化系统为

其中

这里$p^*,w^*$为常数平衡点.

记线性化算子

该算子的特征方程为:$L(\rho)(\phi,\psi)^\mathrm{T}=\mu(\phi,\psi)^\mathrm{T}$,其中,$\phi=\sum\limits_{k=0}^{\infty}a_k\phi_k(x), \psi=\sum\limits_{k=0}^{\infty}b_k\phi_k(x), a_k,$$ b_k\in \mathbb{R}$. 进一步可得

其中

因此可得特征方程

其中$k$ 为非负整数,$T_k(\lambda _k,\rho)=-(1+d)\lambda _k+a_{11}+a_{22}$, $D_k(\lambda _k,\rho)=d\lambda _k^2-(a_{11}d+a_{22})\lambda _k+a_{11}a_{22}-a_{12}a_{21}$.

下面分别对三个常数解进行稳定性分析.

定理 2.1 当$a+\rho m>2m$ 时, 对于任意的非负整数$k$, 裸地平衡点$E_0=(0,a)$ 是渐近稳定的; 正平衡点$E_1=(p_1,w_1)$ 是不稳定的.

证 对于平衡点$E_0$, 有

则对于任意的非负整数$k$, 有

因此$E_0$ 始终是渐近稳定的.

对于平衡点$E_1$, 有

通过计算可得

因此$E_1$ 是不稳定的.

定理 2.2 当$a+\rho m>2m$ 且$a>m^2-\frac{a\sqrt{(a+\rho m)^2-4m^2}}{2m}$时, 定义

则有当$\rho>\rho_{\rm max}$ 时, 对所有的$k\geq1$, 平衡点$E_2$ 是渐近稳定的; 当$\rho<\rho_{k}$时, 对某些$k\geq1$, 平衡点$E_2$ 是不稳定的.

证 当$a>m^2-\frac{a\sqrt{(a+\rho m)^2-4m^2}}{2m}$, 有$T_k(\lambda _k,\rho)<0$. 因此平衡点$E_2$ 的稳定性主要取决于$D_k(\lambda _k,\rho)$. 又因为有$D_0=\frac{(a+\rho m)^2-4m^2+(a+\rho m)\sqrt{(a+\rho m)^2-4m^2}}{2m}>0$, 因此下面主要考虑$D_k, k\geq1$ 的符号. 当$\rho>\rho_{\rm max}$ 时, 对所有的$k\geq1$, 有$D_k>0$, $E_2$ 是渐近稳定的; 当$\rho<\rho_{k}$ 时, 对某些$k\geq1$, 有$D_k<0$, 则$E_2$ 是不稳定的.

定理 2.3 设$\Gamma=\{k\mid k\geq1, D_k(\lambda _k,0)>0\}$ 且有$a+\rho m>2m$ 和$a>m^2-\frac{a\sqrt{(a+\rho m)^2-4m^2}}{2m}$ 成立时, 则对于任意的$k\in \Gamma$, 系统(2.1) 在$(\rho_k,(p_2, w_2))$ 处发生稳态分支.

证明 任意的$k\in \Gamma$ 时,$\rho_k$ 满足(这里$\rho_k$ 在(2.4) 式中已经给出)$D_k(\lambda_k,\rho_k)=0$ 且关于$\rho$ 求导有$D_k^\prime(\lambda_k,\rho_k)=p_2\lambda_k\neq0$, 因此系统(2.1) 在$(\rho_k,(p_2, w_2))$ 处发生稳态分支.

下面分析从$(n_2,w_2)$ 产生的稳态分支以及非常数稳态解的存在性和解析结构,$(n_1,w_1)$ 的情况类似. 从$\rho_k$ 的表达式可以看出, 当$k\neq n$ 时, 可能存在两种情形:$\rho_k\neq\rho_n$(单特征值情形) 或$\rho_k=\rho_n$(双特征值情形). 接下来我们分别从这两种情形来讨论稳态解的解析结构.

首先, 令$X=\{(p,w)\in W^{2,2}(0,l\pi)\times W^{2,2}(0,l\pi), p'=w'=0,x=0,l\pi\}$, $Y=L^2(0, l\pi)\times L^2(0, l\pi)$. 定义如下映射$I:\mathbb{R}^+\times X\rightarrow Y$

则有$I$ 的零解是系统(2.1) 的稳态解. 容易看出$I(\rho,(p_2,w_2))=0$ 且$I$ 在$(p_2,w_2)$ 处的Fréchet 导数为

首先分析单特征值的情形, 给出如下定理.

定理 3.1 假设对任意的$n,k\in \Gamma$, 当$k\neq n$, 有$\rho_k\neq \rho_n$, 则$(\rho_k,(p_2, w_2)$ 是$I(\rho, (p, w))=0$ 的分支点. 另外, 对于充分小的$|s|$, 存在一非常数解曲线$\Gamma_k(s)=(\rho(s),(p(s), w(s)))$ 满足$\rho(0)=\rho_k$, $(p(0), w(0))=(p_2, w_2)$, $p(s)=p_2+s\phi_k+o(s^2)$, $w(s)=w_2+sb_k\phi_k+o(s^2)$, 其中$b_k=\frac{\lambda_k-m}{p_2^2}$.

证 利用Crandall -Rabinowitz 分歧定理来分析稳态问题(2.2)的非常数稳态解的解析结构^[11]. 要证明$(\rho_k, U^\ast)$ 是$I(\rho,U)=0$ (这里$U=(p_2, w_2)$) 的一个分支点需同时满足如下条件^[12]

(1) $I_{\rho}, I_U$, $I_{\rho U}$ 存在且连续;

(2) dimker$ I_U(\rho_k,U^\ast)={\rm codim} R(I_U(\rho_k,U^\ast))=1$;

(3) $I_{\rho U}(\rho_k,U^\ast)\Psi\notin R(I_U(\rho_k,U^\ast))$, 其中 $\Phi\in {\rm ker} I_U(\rho_k,U^\ast)$.

通过 (3.1) 式可以看出$I_{\rho}, I_U$, $I_{\rho U}$ 存在且连续. 当$\rho=\rho_k$ 时, 有

记$F(\rho_k)$ 的$0$ 特征值对应的特征函数为$(a_k\phi_k,b_k\phi_k)^\mathrm{T}$. 令$a_k=1$, 可以得到$b_k=\frac{\lambda_k-m}{p_2^2}$.

因此, ker$ F(\rho_k)={\rm span} \{\Phi_k\}$,$\Phi_k=\begin{pmatrix} 1\\ b_k\\ \end{pmatrix}\phi_k.$则有dimker$ F(\rho_k)=1.$$F(\rho_k)$ 的伴随算子为

类似地, 可以得到$kerF^\ast(\rho_k)={\rm span} \{\Phi_k^\ast\}$, 这里$\Phi_k^\ast=\begin{pmatrix} 1\\ b_k^\ast\\ \end{pmatrix}\phi_p,$$b_k^\ast=\frac{m-\lambda_k}{p_2^2}$. 又因为 $R(F(\rho_k))=({\rm ker} F^\ast(\rho_k))^\bot,$ 有codim$R(F(\rho_k))=1={\rm dim\,(ker} F(\rho_k))$.

因为

可得

因此, $I(\rho,U)=0$ 在$(\rho_k, U^*)$ 附近的解集由曲线$U=U^\ast$ 和$\{(\rho(s),U(s)):s\in (-\epsilon,\epsilon)\}$ 构成, 其中$U(s)=U^\ast+s\Phi+o(s^2), \rho(0)=\rho_k$.

下面考虑双特征值的情形.

定理 3.2 假设存在一非负整数$n \ (\neq k)$, $n, k \in \Gamma$ 使得$\rho_n=\rho_k=\hat{\rho}$.令

其中$b_n=\frac{\lambda_n-m}{p_2^2}$, $b_n^\ast=\frac{m-\lambda_n}{p_2^2}$.此外, 令

若$1+b_nb_n^\ast\neq0, 1+b_kb_k^\ast\neq0$ 且$n=2k$ (或 $k=2n)$, 则$(\hat{\rho},(p_2, w_2))$ 是$I(\rho,(p, w))=0$ 的分支点. 此外, 对于充分小的$|\omega-\omega_0|$, 存在一非常数解曲线$(\rho(\omega),U+s(\omega)(\cos\omega\Phi_n+\sin\omega\Phi_k+W(\omega)))$, $\rho(\omega_0)=\hat{\rho}, s(\omega_0)=0, W(\omega_0)=0$, 这里, $\omega_0$ 满足

这里, $U=(p_2, w_2)$, $\rho(\omega),s(\omega),W(\omega)\in X_2$ 是关于$\omega$ 的连续可微函数.

证 假设存在非负整数$n \ (\neq k)$, $n, k \in \Lambda$ 使得$\rho_n=\rho_k=\hat{\rho}$, 因此有

则有dimker$ F(\hat{\rho})={\rm codim} R(\hat{\rho})=2$, 因此Crandall-Rabinowitz 分歧定理不适用于此情形. 下面采用隐函数定理和空间分解方法来分析双分支点的情形^[13-15].

步骤 1 将变量平移到原点: $(u,v)=(p,w)-(p_2,w_2)$, 给出新的映射:$\widetilde{I}:=\mathbb{R}^+\times X\rightarrow Y$

这里$f_1=u^2v+2p_2uv+w_2u^2,$$g_1=\rho uv-f_1$.容易得到,$\widetilde{I}(\hat{\rho},(0,0))=0, \widetilde{I}_{(u,v)}(\hat{\rho},(0,0))=F(\hat{\rho})$, $(p,w)$ 是(2.2) 式的解当且仅当$(u,v)$ 满足$\widetilde{I}(\rho,(u,v))=0$.

步骤 2 将空间$X$ 进行如下分解

其中$X_1={\rm span}\{\Phi_n,\Phi_k\}$, $X_2$ 为

接下来寻找$\widetilde{I}(\rho,(u,v))=0$ 的解, 该解具有如下形式

这里$s,\omega\in \mathbb{R}$.为了分解$Y$, 定义映射$P$

有$R(P)={\rm span}\{\Phi_n,\Phi_k\}=X_1$, $P^2=P$. 所以$P$ 是一个正交投影算子. 对$Y$ 进行分解: $Y=Y_1\oplus Y_2$, 其中$Y_1=R(P)=X_1$, $Y_2={\rm ker}(P)=R(F(\hat{\rho}))=X_2$.

步骤 3 通过隐函数定理寻找满足$\widetilde{I}(\rho,(u,v))=0$ 的非常数解$(u,v)$. 固定$\omega_0\in\mathbb{R}$, 定义映射:$K(\rho,s,W;\omega):\mathbb{R}^+\times \mathbb{R}\times X_2\times (\omega_0-\epsilon,\omega_0+\epsilon)\rightarrow Y$

这里$\widetilde{f_1}=W_2(\phi_n\cos\omega+\phi_k\sin\omega+W_1)^2+2p_2 (\phi_n\cos\omega+\phi_k\sin\omega+W_1)(b_n\phi_n\cos\omega+b_k\phi_k\sin\omega+W_2)+\mathcal{O}(\vert s\vert)$, $\widetilde{g_1}=\rho(\phi_n\cos\omega+\phi_k\sin\omega+W_1)(b_n\phi_n\cos\omega+b_k\phi_k\sin\omega+W_2)-\widetilde{f_1}$.

$K(\rho,s,W;\omega)$ 关于$(\rho,s,W)$ 在$(\hat{\rho},0,0;\omega_0)$ 的Fréchet 导数为

这里,$A_1=w_2+p_2b_k, A_2=w_2+p_2b_n, A_3=w_2+2p_2b_n, A_4=w_2+2p_2b_k, A_5=w_2, A_6=b_k+b_n$.

接下来证明$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0):\mathbb{R}\times \mathbb{R}\times X_2\rightarrow Y$ 是一同构映射. 为此, 将$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0)(\rho,s,W)$ 写为

这里$\mathrm{y_1}\in Y_1, \mathrm{y_2}\in Y_2$. 我们做如下分解

其中

接下来讨论两种情形:$n=2k$ 和$k=2n$.

情形 1$n=2k$

此时有,$\int_0^{l\pi}\phi_n^2\phi_k{\rm d}x=\int_0^{l\pi}\phi_n^3{\rm d}x=0$, 则$\begin{pmatrix} \phi_n^2\\ -\phi_n^2\\ \end{pmatrix}\in Y_2$, $\begin{pmatrix} 0\\ \phi_n^2\\ \end{pmatrix}\in Y_2$. 分解

其中,

通过上述分解, 有

令$K_{(\rho,s,W))}(\hat{\rho},0,0;\omega_0)(\rho,s,W)=0$, 则有$\mathrm{y_1}=0, \mathrm{y_2}=0$. $\mathrm{y_1}=0$ 等价于

假设$\sin\omega_0\neq0\,$ 且$2c_4A_5\cos\omega_0(c_1A_2\cos\omega_0+c_6b_k\sin^2\omega_0)\neq c_3A_4\sin^2\omega_0(c_2A_1+c_5A_6\cos\omega_0)$, 可得$s=0, \rho=0$. 将它们带入$\mathrm{y_2}=0$, 有$W=0$. 根据以上推导, 我们有$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0)$ 是单射.

下面验证$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0)$ 是满射, 即对于任意的$(u,v)\in Y$, 需要找到$(\rho,s,W)\in\mathbb{R}^+\times \mathbb{R}\times X_2$ 满足

根据$Y$ 的空间分解, 存在$\eta,\gamma\in \mathbb{R}$ 和$(u_0,v_0)\in Y_2$ 使得

将上式带入到(3.4) 式, 得到

通过计算可得$\rho=\tilde{\rho}, s=\tilde{s}$, 其中

接下来将$\tilde{\rho},\tilde{s}$ 带入到(3.5) 的第三个等式, 得到:$W=F^{-1}(\hat{\rho})\begin{pmatrix} \tilde{u}\\ \tilde{v}\\ \end{pmatrix},$这里

则$(\rho,s,W)=\left(\tilde{\rho},\tilde{s},F^{-1}(\hat{\rho})\begin{pmatrix} \tilde{u}\\ \tilde{v}\\ \end{pmatrix}\right)$是(3.4) 式的解, 进而可以推得$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0)$ 是满射.

因此, 根据隐函数定理, 对于充分小的$|\omega-\omega_0|$, 存在非常数稳态解$(\rho(\omega),s(\omega), W(\omega))$ 使得$\rho(\omega_0)=\hat{\rho}, s(\omega_0)=0, W(\omega_0)=0$. 所以$(\rho(\omega),U+s(\omega)(\cos\omega\Phi_n+\sin\omega\Phi_k+W(\omega)))$ 是$F(\rho,(p,w))=0$ 的非常数稳态解.

情形 2$k=2n$

此时有$\int_0^{l\pi}\phi_k^2\phi_n{\rm d}x=\int_0^{l\pi}\phi_k^3{\rm d}x=0$, 则$\begin{pmatrix} \phi_k^2\\ -\phi_k^2\\ \end{pmatrix}\in Y_2$, $\begin{pmatrix} 0\\ \phi_k^2\\ \end{pmatrix}\in Y_2$. 分解

其中,

通过上述分解, 有

类似于情形 1 的方法, 可以证明当$\omega_0$ 满足$\cos\omega_0\neq0\,$ 且 $2c_8A_5\sin\omega_0(c_2A_1\sin\omega_0+c_{10}b_n$$\cos^2\omega_0)\neq c_7A_3\cos^2\omega_0(c_1A_2+c_9A_6\sin\omega_0)$ 时,$K_{(\rho,s,W)}(\hat{\rho},0,0;\omega_0)$ 是一个从$\mathbb{R}^+\times \mathbb{R}\times X_2$ 到空间$Y$ 的同构映射.

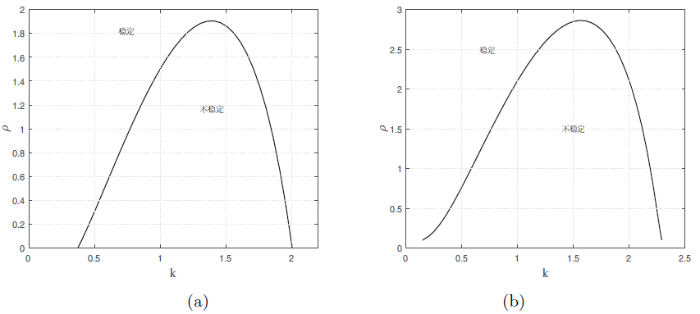
下面将通过数值模拟来验证前面得到的理论结果. 选取参数$a=10.4, m=4.4, d=17.85,$ 由 (2.4) 式可以得到图2, 该图展示了分支参数$\rho_k$ 和波数$k$ 之间的关系. 可以看出, 图2(a) 有一个单分支点$(\rho_{1}, (p_2, w_2))$, 且在曲线$\rho_k$ 的下方, 常数稳态解$(p_2, w_2)$ 是不稳定的, 在曲线$\rho_k$ 的上方, 常数稳态解$(p_2, w_2)$ 稳定. 在分支线上, 当$k=1$ 时, $\rho_{1}=1.5021$. 选取参数$a=10.4, m=5.4, d=17.85$, 可以得到双分支点$(\hat{\rho}, (p_2, w_2))$, 此时有$\rho_1=\rho_2=\hat{\rho}=2.1078$, 如图2(b) 所示.

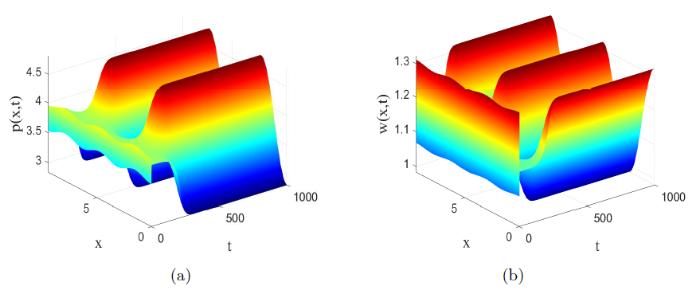
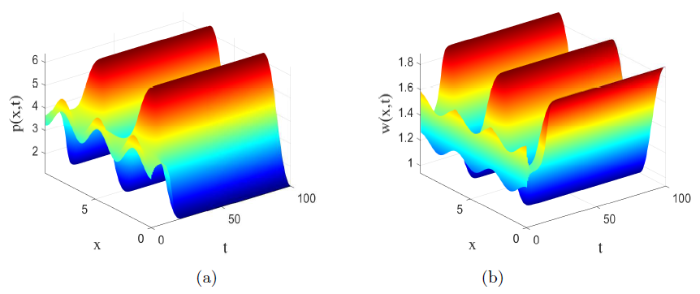
令$l=3$, 当参数$a=10.4, m=4.4, d=17.85, \rho=1.5\approx \rho_1(=1.5021)$ 时, 系统(2.1) 在单分支点$(\rho_1, (p_2, w_2))$ 附近会出现非常数正稳态解, 如图3 所示, 这与定理3.1 的结果一致. 此外, 当$a=10.4, m=5.4, d=17.85, \rho=2.1\approx \hat{\rho}$ 时, 系统(2.1) 在双分支点$(\hat{\rho}, (p_2, w_2))$ 附近会出现非常数正稳态解, 如图4 所示, 这与定理3.2 的结果一致.

本文研究了一类空间植被模型的稳态分支问题, 从分支的角度研究了稳态斑图的出现. 首先通过数学分析研究了常数稳态解的稳定性, 并证明了稳态分支的存在性, 得到了稳态分支产生的条件, 进而验证了在单特征值情形和双特征值情形下非常数解的解析结构. 具体来讲, 通过Crandall-Rabinowitz 分歧定理分析了单特征值情形, 利用隐函数定理和空间分解方法研究了双特征值情形. 最后进行了数值实验, 分别模拟了单特征值和双特征值两种情形下的非常数解的结构. 结果表明在分支点附近会出现一条非常数解曲线, 进而验证了理论结果. 本文为双特征情形下的稳态分支问题提供了新的思路.