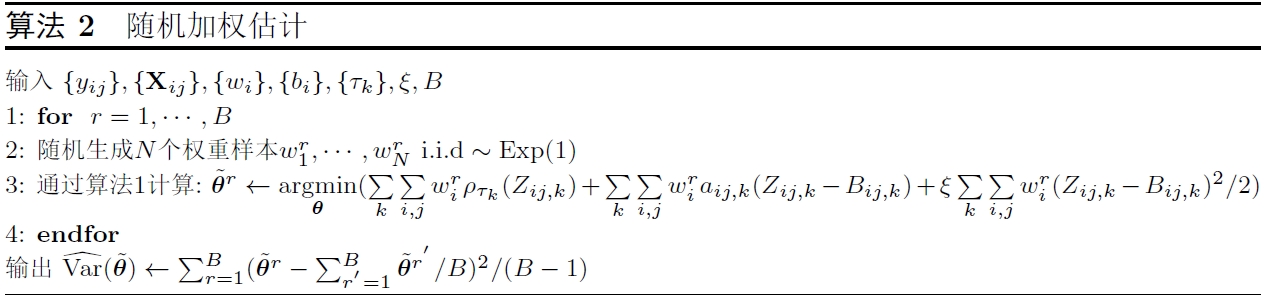1 引言
在临床医学领域, 如何识别出治疗敏感亚组患者, 并在相同治疗条件下去判断这些治疗敏感亚组患者是否比其他患者具有更好的治疗效果, 是亚组分析中备受关注的重要问题. 由于患者的基线特征 (比如年龄、性别、疾病严重程度等) 不同, 治疗效果通常具有异质性. 将患者根据基线特征分为不同亚组, 探索不同患者亚组之间的疗效差异, 对于确定最佳获益人群及设计个性化治疗方案具有重要意义. 近年来, 患者报告结果 (patient reported outcome, PRO) 被广泛运用于临床研究中, 它提供患者对自身健康状态的主观评价, 与客观临床指标互为补充, 有助于更好地评估治疗效果. PRO 主要通过量表进行测量, 由于量表存在天花板效应和地板效应, 即观测数据可能受到上、下限的限制, 这导致测量数据具有双删失的特征. 在实际应用中, 患者通常会在一段研究期间中被反复测量, 这样, 试验记录到的数据是具有双删失特征的纵向数据. 一个具有双删失特征纵向数据的实例是, 为研究癌症药物西妥昔单抗 (cetuximab) 在晚期结直肠癌治疗中的效果, 加拿大癌症试验组进行一项随机临床试验 CO.17, 其中有一项关于患者生活质量 (quality of life, QoL) 的数据, 该数据由欧洲癌症研究治疗组织生活质量问卷 C30 (European organization for the research and treatment of cancer quality of life questionnaire C30, EORTC QLQ-C30) 评估得到. 在 CO.17 试验中, 572 名患者被随机分为以下两组
$ \bullet $
$ \bullet $
要求患者在试验开始后的第 0 周 (基线)、第 4 周、第 8 周、第 16 周和第 24 周完成问卷量表 C30. 在该量表中, 前五个问题构成一个子量表, 用于评估患者躯体功能, 每个问题的分数被限制在下限 1 和上限 4 之间. 这样, 该试验所得到的观测数据是双删失纵向数据.
众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据.
关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题.
最近, 文献 [25 ] 研究阈值 Tobit 分位数回归模型, 它基于区间有界的纵向观测和一个连续生物标志物协变量来识别治疗敏感亚组. 该模型只考虑单个分位点, 参数估计效率不高. 参数估计效率是影响亚组识别的重要因素之一, 研究如何在保持稳健性的基础上提升参数估计效率, 对于增强亚组识别效果而言具有实际意义. 据笔者所知, 鲜有研究将复合分位数回归方法应用于研究治疗敏感亚组的识别问题. 据此, 本文研究复合 Tobit 分位数亚组分析回归方法, 基于双删失纵向数据和一个连续协变量来识别治疗敏感亚组. 与单分位数回归相比, 复合分位数回归提高了参数估计的效率, 增强了治疗敏感亚组的识别效果. 在参数估计部分, 由于待优化的目标函数是非光滑的, 我们采用两步光滑化处理.
$ \bullet $ 26 ] 的方法将其光滑化;
$ \bullet $ 27 ] 的方法将其光滑化.
对光滑后的目标函数, 利用交替乘子算法 (alternating direction method of multipliers, ADMM)[28 ] 数值地求解优化问题, 得到参数估计量. 在估计方差时, 应用随机加权方法[29 ] 计算方差, 该方法避开了对冗余参数的估计, 易于执行. 为了研究方法的效果, 在不同的误差分布和删失比例下进行模拟实验. 结果表明该方法相较于单分位数回归方法具有更高的参数估计效率, 并且说明用随机加权方法估计参数估计量方差是可行的. 最后, 分析直肠癌患者生活质量数据 CO.17, 识别出根据年龄划分的西妥昔单抗药物治疗敏感亚组.
本文的内容安排如下. 第 2 节介绍复合分位数回归模型及其参数统计推断方法. 第 3 节研究参数估计量的相合性. 第 4 节是数值模拟研究. 第 5 节将方法应用于直肠癌试验组 CO.17 数据分析.
2 复合分位数回归模型及其统计推断
2.1 模型介绍
假设被观测的个体数为 $ N $ $ i $ $ n_{i} $ $ n=\sum_{i=1}^N n_{i} $ . 又设 $ y_{ij} $ $ i $ $ j $ $ t_{ij} $ $ \textbf{X}_{ij}\in\mathbb{R}^p $ $ y_{ij} $ $ y_{ij} $
(2.1) $y_{ij}=\alpha+\textbf{X}_{ij}^\top\boldsymbol{\beta}+\eta_{1}I(w_{i}>c)+\eta_{2}b_{i}I(w_{i}>c)+\epsilon_{ij},$
其中, $ \alpha $ $ \boldsymbol{\beta} $ $ \eta_{1} $ $ \eta_{2} $ $ c $ $ b_{i} $ $ b_{i}=1 $ $ i $ $ b_{i}=0 $ $ i $ $ w_{i} $ $ i $ $ \epsilon_{ij} $ $ \epsilon_{ij} $ $ i $ $ j $ $ j $ $ \epsilon_{1j},\cdots,\epsilon_{Nj} $ $ i $ $ \epsilon_{i1},\cdots,\epsilon_{in_{i}} $ $ \{\textbf{X}_{ij}\} $ $ \{w_{i}\} $ $ \{b_{i}\} $ 30 ] 以发达国家直肠癌诊断年龄中位数 70 岁为切点, 将患者分为两个年龄亚组, 研究西妥昔单抗在这两个年龄亚组之间的疗效差异. 实际上, 70 岁是否为一个合适的年龄切点其实是尚不清楚的, 需要用数据去估计, 即需要估计模型 (2.1) 中的未知参数 $ c $ . 此外, $ b_{i}=1 $ $ i $ $ + $ $ b_{i}=0 $ $ i $ $ w_{i} $ $ i $ $ I(w_{i}>c) $
在很多现实场景下, 由于量表等测量仪器受到上、下限的限制, 响应变量 $ y_{ij} $ $ [l,u] $ $ l $ $ u $ $ l<u $ . 为表达简洁, 对 $ y_{ij} $
基于双删失响应变量 $ y_{ij}^{*} $
(2.2) $y_{ij}^{*}=\left(\alpha+\textbf{X}_{ij}^\top\boldsymbol{\beta}+\eta_{1}I(w_{i}>c)+\eta_{2}b_{i}I(w_{i}>c)+\epsilon_{ij}\right)^{*},$
其中, (2.2) 式中的符号含义与 (2.1) 式中的符号含义相同.
2.2 参数估计
如果数据 $ y_{ij}^{*} $
全文假设误差 $ \big\{\epsilon_{ij}\big\} $ $ F $ $ F $ $ f $ $ \epsilon_{ij} $ $ \tau $ $ \alpha_{\tau} $ $ \tau\in(0,1) $ . 对于固定的 $ \tau $ 25 ] 考虑了单分位数回归模型
(2.3) $Q_{y_{ij}^{*}}(\tau|\textbf{X}_{ij},w_{i},b_{i})=\big(\alpha+\textbf{X}_{ij}^\top\boldsymbol{\beta}+\eta_{1}I(w_{i}>c)+\eta_{2}b_{i}I(w_{i}>c)+\alpha_{\tau}\big)^{*},$
其中, $ Q_{y_{ij}^{*}}(\tau|\textbf{X}_{ij},w_{i},b_{i}) $ $ \textbf{X}_{ij},w_{i},b_{i} $ $ y_{ij}^{*} $ $ \tau $
注 2.1 文献 [25 ] 中未直接出现 (2.3) 式, 下面通过简单推导说明该式正确性. 记 $ y_{ij} $ $ y_{ij}^{*} $ $ F_{y_{ij}} $ $ F_{y_{ij}^{*}} $ . 由 $ y_{ij}^{*} $
即$ Q_{y_{ij}^{*}}(\tau|\textbf{X}_{ij},w_{i},b_{i})=\big(Q_{y_{ij}}(\tau|\textbf{X}_{ij},w_{i},b_{i})\big)^{*} $ . 由于
由于单分位数回归估计会降低估计的效率, 并且在实际应用中, 如果没有足够多的有效信息, 挑选出一个恰当的分位数绝非易事. 为此, 本文采用复合分位数回归 (composite quantile regression, CQR) 方法, 即同时使用若干个不同的分位数来构造参数估计. 需要注意的是, 在 (2.3) 式中, 对于不同的分位点 $ \tau $ $ \alpha=0 $ . 现考虑 $ K $ $ 0<\tau_1<\cdots<\tau_K<1 $ $ \boldsymbol{\theta}=(\alpha_{1},\cdots,\alpha_{K},\boldsymbol{\beta}^\top,\eta_{1},\eta_{2},c)^\top $ $ \alpha_{k}=\alpha_{\tau_{k}},1\leq k\leq K $ . 记$ \boldsymbol{\theta}_{0}=(\alpha_{10},\cdots,\alpha_{K0},\boldsymbol{\beta}_{0}^\top,\eta_{10},\eta_{20},c_{0})^\top $ $ \boldsymbol{\theta} $ $ \boldsymbol{\theta} $
其中, $ \rho_{\tau_{k}}(u)=\{\tau_{k}-I(u<0)\}u $ $ \tau_{k} $ $ \sum_{k}\sum_{i,j}=\sum_{k=1}^K\sum_{i=1}^N \sum_{j=1}^{n_{i}} $ .
由于示性函数 $ I(w_{i}>c) $ $ 0 $ $ 1 $ $ c $ $ c $ 13 ] 的方法, 采用 $ \Phi({(w_{i}-c)}/{h_{n}}) $ $ I(w_{i}>c) $ $ \Phi(\cdot) $ $ h_{n} $ $ \lim\limits_{n\rightarrow\infty}h_{n}=0 $ . 易知函数 $ \Phi(\cdot) $
这样, $ \boldsymbol{\theta} $
(2.4) $\tilde{\boldsymbol{\theta}}=\operatorname*{argmin}\limits_{\boldsymbol{\theta}}\sum_{k}\sum_{i,j}\rho_{\tau_{k}}\left\{y_{ij}^{*}-\big(\alpha_{k}+\textbf{X}_{ij}^\top\boldsymbol{\beta}+\eta_{1}\Phi((w_{i}-c)/h_{n})+\eta_{2}b_{i}\Phi((w_{i}-c)/h_{n})\big)^{*}\right\}.$
下面, 将光滑近似的思想和牛顿迭代法的思想相结合, 应用交替乘子算法对参数估计进行数值求解. 将 (2.4) 式写成等价形式
(2.5) $\begin{aligned} &\operatorname*{min}\limits_{\boldsymbol{\theta}}\sum_{k}\sum_{i,j}\rho_{\tau_{k}}(Z_{ij,k})\\ & s.t. Z_{ij,k} = y_{ij}^{*}-\big(\alpha_{k}+\textbf{X}_{ij}^\top\boldsymbol{\beta}+\eta_{1}\Phi((w_{i}-c)/h_{n})+\eta_{2}b_{i}\Phi((w_{i}-c)/h_{n})\big)^{*}. \end{aligned}$
由于 $ y_{ij}^{*} $ $ \boldsymbol{\theta} $
此表明, 当 $ h $ $ K_{h}(x) $ $ x^{*} $ . 令
(2.5) 式中优化问题则可转化为如下的渐近等价形式
(2.6) $\begin{aligned} &\operatorname*{min}\limits_{\boldsymbol{\theta}}\sum_{k}\sum_{i,j}\rho_{\tau_{k}}(Z_{ij,k})\\ & s.t. Z_{ij,k}-B_{ij,k}=0. \end{aligned}$
(2.7) $\begin{equation} \begin{aligned} & \operatorname*{min}\limits_{\boldsymbol{\theta}}l_s(\boldsymbol{\theta};\{Z_{ij,k}\},\{a_{ij,k}\})\\ & s.t. Z_{ij,k}-B_{ij,k}=0. \end{aligned} \end{equation}$
其中, $ \{a_{ij,k}\} $ $ \xi $
记得分函数 $ S_{\boldsymbol{\theta}}(g)=(\partial g)/(\partial\boldsymbol{\theta}) $ $ H_{\boldsymbol{\theta}}(g)=(\partial^{2}g)/ (\partial\boldsymbol{\theta}{\partial\boldsymbol{\theta}}^{\top}) $ . 利用交替乘子算法求解 $ \boldsymbol{\theta} $
2.3 随机加权估计
从 2.2 节可以看出 $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ f $ [31 ] . 为了避免估计冗余参数, 本文使用随机加权方法来估计 $ \tilde{\boldsymbol{\theta}} $ $ \text{Var}(\tilde{\boldsymbol{\theta}}) $ . 关于随机加权方法的进一步讨论可参见文献 [24 ].
在第 $ r $ $ w_1^{r},\cdots,w_N^{r} $ $ N $ $ r=1,\cdots,B $ . 将这 $ N $ $ l_s $ $ \boldsymbol{\theta} $
将上述过程重复 $ B $ $ B $ $ \tilde{\boldsymbol{\theta}}^{1},\cdots,\tilde{\boldsymbol{\theta}}^{B} $ . 用这 $ B $ $ \text{Var}(\tilde{\boldsymbol{\theta}}) $ $ {\rm Exp}(1) $ $ \text{Var}(\tilde{\boldsymbol{\theta}}) $
3 相合性
本节证明估计量 $ \tilde{\boldsymbol{\theta}} $ $ \boldsymbol{\theta}_{0} $
记 $ \textbf{H}_{ij,1}=(1,0,\cdots,0,\textbf{X}_{ij}^{\top},I(w_{i}>c_{0}),b_{i}I(w_{i}>c_{0}))^{\top} $ $ \cdots $ $ \textbf{H}_{ij,K}=(0,\cdots,0,1,\textbf{X}_{ij}^{\top},I(w_{i}>c_{0}),b_{i}I(w_{i}>c_{0}))^{\top} $ $ \mu_{ij}=\textbf{X}_{ij}^{\top}\boldsymbol{\beta}_{0}+\eta_{10}I(w_{i}>c_{0})+\eta_{20}b_{i}I(w_{i}>c_{0}) $ $ \mu_{ij,k}=\alpha_{k0}+\textbf{X}_{ij}^{\top}\boldsymbol{\beta}_{0}+\eta_{10}I(w_{i}>c_{0})+\eta_{20}b_{i}I(w_{i}>c_{0}),1\leq k\leq K $ . 其中, $ \boldsymbol{\theta}_{0}=(\alpha_{10},\cdots,\alpha_{K0},\boldsymbol{\beta}_{0}^{\top},\eta_{10},\eta_{20},c_{0})^{\top} $ $ \alpha_{k0}=Q_{\epsilon_{ij}}(\tau_{k}) $ $ \epsilon_{ij} $ $ \tau_{k} $
(A1 ) 真实参数 $ \boldsymbol{\theta}_{0} $ $ \Theta $
(A2 ) $ \lbrace\epsilon_{ij}\rbrace $ $ F $ $ f $
(A3 ) $ \{n_{i}\} $
(A4 ) $ \lim\limits_{\upsilon\rightarrow0}\lim\limits_{n\rightarrow\infty}\sup\limits_{c}n^{-1}\sum_{i}I(|w_{i}-c|<\upsilon)=0 $ .
(A5 ) $ n^{-1}\sum_{k}\sum_{i,j}I(l<\mu_{ij,k}<u)\textbf{H}_{ij,k}\textbf{H}_{ij,k}^{\top} $
注 3.1 条件 (A1) 和条件 (A2) 与文献 [第 11 章] 中的条件类似. 条件 (A3) 表明总样本数 $ n $ $ N $ 33 ]. 条件 (A3) 与条件 (A4) 共同保证中心化后的目标函数 $ \Psi_{n}(\boldsymbol{\theta}) $ $ \Psi_{n}(\boldsymbol{\theta};h_{n}) $ 32 ].
定理 3.1 假设正则条件 (A1)-(A5) 成立. 那么, 当 $ n\rightarrow\infty $
定理 3.1 的证明需要利用下面的引理 3.1, 引理 3.2 和引理 3.3.
引理 3.1 当 $ n\rightarrow\infty $
证 记 $ \textbf{b}_{i}=(1,b_{i})^{\top}, \boldsymbol{\eta}=(\eta_{1},\eta_{2})^{\top} $ . 易有
这里 $ C>0 $ $ C $
(3.1) $\begin{matrix} &\quad\sup_{\boldsymbol{\theta}\in\Theta}\frac{C}{n}\sum_{i}\big|I(w_{i}>c)-\Phi((w_{i}-c)/h_{n})\big|\nonumber\\&\leq\sup_{\boldsymbol{\theta}\in\Theta}\frac{C}{n}\sum_{i}\big|I(w_{i}>c)-\Phi((w_{i}-c)/h_{n})\big|I(|w_{i}-c|\geq\upsilon)\\ &\quad+\sup_{\boldsymbol{\theta}\in\Theta}\frac{C}{n}\sum_{i}\big|I(w_{i}>c)-\Phi((w_{i}-c)/h_{n})\big|I(|w_{i}-c|<\upsilon).\nonumber \end{matrix}$
显然, 当 $ n\rightarrow\infty $ $ h_{n}\rightarrow0 $
(3.2) $\begin{matrix} \lim\limits_{\upsilon\rightarrow0}\lim\limits_{n\rightarrow\infty}\sup_{\boldsymbol{\theta}\in\Theta}\frac{C}{n}\sum_{i}|I(w_{i}>c)-\Phi((w_{i}-c)/h_{n})|I(|w_{i}-c|\geq\upsilon)=0. \end{matrix}$
处理 (3.1) 式右端的第二项, 利用 $ 0\leq\Phi(\cdot)\leq1 $
(3.3) $\begin{matrix} &\quad \lim\limits_{\upsilon\rightarrow0}\lim\limits_{n\rightarrow\infty}\sup_{\boldsymbol{\theta}\in\Theta}\frac{C}{n}\sum_{i}\big|I(w_{i}>c)-\Phi((w_{i}-c)/h_{n})\big|I(|w_{i}-c|<\upsilon)\nonumber\\&\leq \lim\limits_{\upsilon\rightarrow0}\lim\limits_{n\rightarrow\infty}\sup_{c}\frac{C}{n}\sum_{i}I(|w_{i}-c|<\upsilon)=0. \end{matrix}$
综合 (3.2) 和 (3.3) 式, 当 $ n\rightarrow\infty $
引理 3.2 记 $ \Psi(\boldsymbol{\theta})=\mathbb{E}[\Psi_{n}(\boldsymbol{\theta})] $ . 当 $ n\rightarrow\infty $
证 记 $ M=\max\{n_{1},\cdots,n_{N}\} $ . 为叙述方便, 定义 $ \psi_{ij,k}(\boldsymbol{\theta})=0,1\leq i\leq N, n_{i}<j\leq M, 1\leq k\leq K $
注意到对任意 $ 1\leq j\leq M $ $ \sum\limits_{k}\psi_{1j,k}(\boldsymbol{\theta}),\cdots,\sum\limits_{k}\psi_{Nj,k}(\boldsymbol{\theta}) $ $ \mathcal{G}_{N,j} $
显然, $ \big(K(u-l),\cdots,K(u-l)\big)_{N\times1} $ $ \mathcal{G}_{N,j} $ 32 , 第 7 章] 的计算, 有
根据 $ \text{C}_{r} $
引理3 3. 对任意 $ \boldsymbol{\theta}\in\Theta $
等号成立当且仅当 $ \boldsymbol{\theta}=\boldsymbol{\theta}_{0} $ .
证 根据 $ \Psi_{n}(\boldsymbol{\theta}) $
由于 $ F(\alpha_{k0})=\tau_{k} $ $ i,j,k $
等号在 $ \boldsymbol{\theta}=\boldsymbol{\theta}_{0} $ $ \Psi(\boldsymbol{\theta}) $ $ \Psi(\boldsymbol{\theta_{0}})=0 $ .
当 $ \boldsymbol{\theta}\neq\boldsymbol{\theta}_{0} $
若存在 $ k^{'} $ $ i^{'} $ $ j^{'} $ $ \alpha_{k^{'}}+\textbf{X}_{i^{'}j^{'}}^{\top}\boldsymbol{\beta}+\eta_{1}I(w_{i^{'}}>c)+\eta_{2}b_{i^{'}}I(w_{i^{'}}>c)\leq l $ $ \alpha_{k^{'}}+\textbf{X}_{i^{'}j^{'}}^{\top}\boldsymbol{\beta}+\eta_{1}I(w_{i^{'}}>c)+\eta_{2}b_{i^{'}}I(w_{i^{'}}>c)\geq u $ $ g_{i^{'}j^{'},k^{'}}>0 $ $ \Psi(\boldsymbol{\theta})>0 $ . 若对任意 $ 1\leq k\leq K, 1\leq i\leq N, n_{i}<j\leq M $
现仅对 $ c\neq c_{0},\alpha_{k}\neq\alpha_{k0},\boldsymbol{\beta}^{\top}\neq\boldsymbol{\beta}_{0}^{\top},\boldsymbol{\eta}^{\top}\neq\boldsymbol{\eta}_{0}^{\top} $ $ c\neq c_{0},\alpha_{k}\neq\alpha_{k0},\boldsymbol{\beta}^{\top}\neq\boldsymbol{\beta}_{0}^{\top},\boldsymbol{\eta}^{\top}\neq\boldsymbol{\eta}_{0}^{\top} $
此时, $ \Psi(\boldsymbol{\theta})>0 $ .
证 (A1) 假设 $ \boldsymbol{\theta}_{0} $ $ \Theta $ $ a_{0}>0 $
引理 3.3 证明 $ \boldsymbol{\theta}=\boldsymbol{\theta}_{0} $ $ \Psi(\boldsymbol{\theta}) $ $ 0<a<a_{0} $ $ n_{a} $
结合引理 3.1 和引理 3.2 知, 当 $ n\rightarrow\infty $ $ \tilde{\boldsymbol{\theta}}\stackrel{\text{p}}{\rightarrow}\boldsymbol{\theta}_{0} $ .
4 数值模拟
4.1 平衡数据情形
(4.1) $\begin{matrix} y_{i j}^{*} =&\big( \beta_{0}+\beta_{1} t_{i j}+\beta_{2} b_{i}+\eta_{1} I(w_{i}>c) +\eta_{2} b_{i} I(w_{i}>c)+\varepsilon_{i j}\big)^{*}, \end{matrix}$
其中, $ (\beta_{0},\beta_{1},\beta_{2},\eta_{1},\eta_{2},c)^\top=(2,1.5,-1.5,1,0.5,0.5)^\top $ $ \{b_{i}\} $ $ B(1,0.5) $ $ \{w_{i}\} $ $ U[0,1] $ $ \{\varepsilon_{i j}\} $ $ \epsilon_i=(\epsilon_{i1},\cdots,\epsilon_{in_{i}})^{\top} $ $ n_{i}\times n_{i} $ $ \Sigma_{n_{i}} $ $ (k,l) $ $ \sigma_{kl}=0.4^{|k-l|} $ . 取个体总数 $ N=200 $ $ i $ $ n_{i}=5 $ $ t_{i j} $
模拟将误差项分布设置为标准正态分布 $ N(0,1) $ $ t $ $ t(3) $ $ l $ $ u $ $ y_{ij} $ $ \epsilon_{i} \sim N(0,\Sigma_{n_{i}}) $ $ l $ $ u $
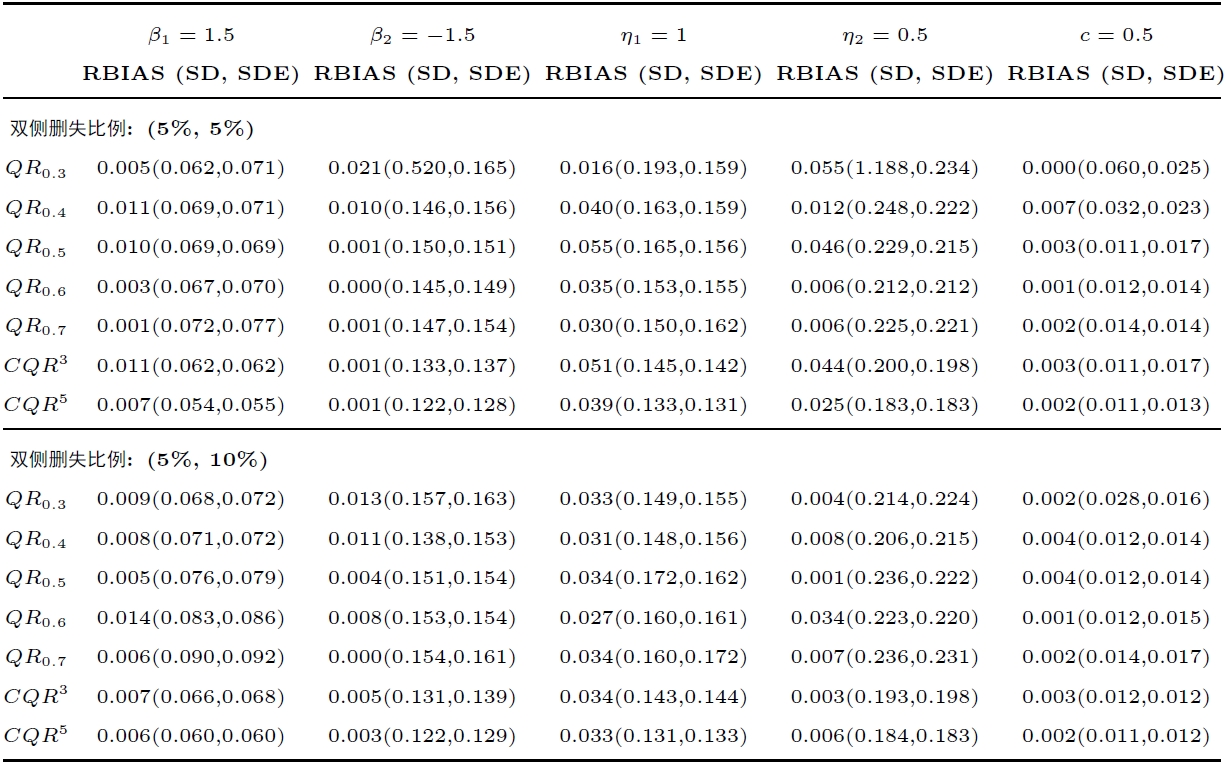
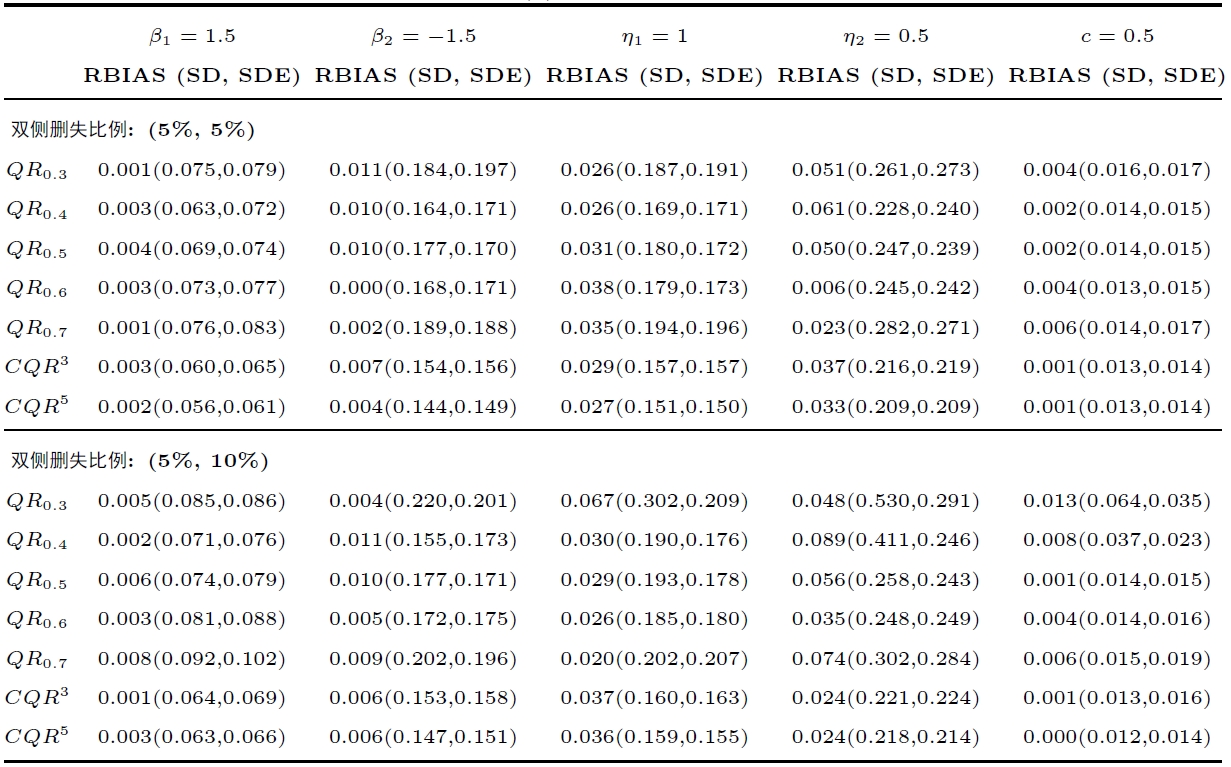
为展示方法的效果, 模拟与文献 [25 ] 的单分位数回归方法进行比较. 为方便叙述, 记 $ \tau $ $ QR_{\tau} $ . 对于本文所提的 CQR 方法, 取分位数 $ \{0.4,0.5,0.6\} $ $ \{0.3,0.4,0.5,0.6,0.7\} $ $ CQR^{3} $ $ CQR^{5} $ . 重复实验 200 次, 计算估计值与真实值的相对偏差, 平均值记为 RBIAS; 估计值的经验标准差记为 SD; 随机加权标准差估计值记为 SDE. 模拟选用文献 [10 ] 中的设置方法, 带宽 $ h_{n} $ $ \hat{\rho}n^{-1/3} $ $ \hat{\rho} $ $ n $ $ w_{i} $
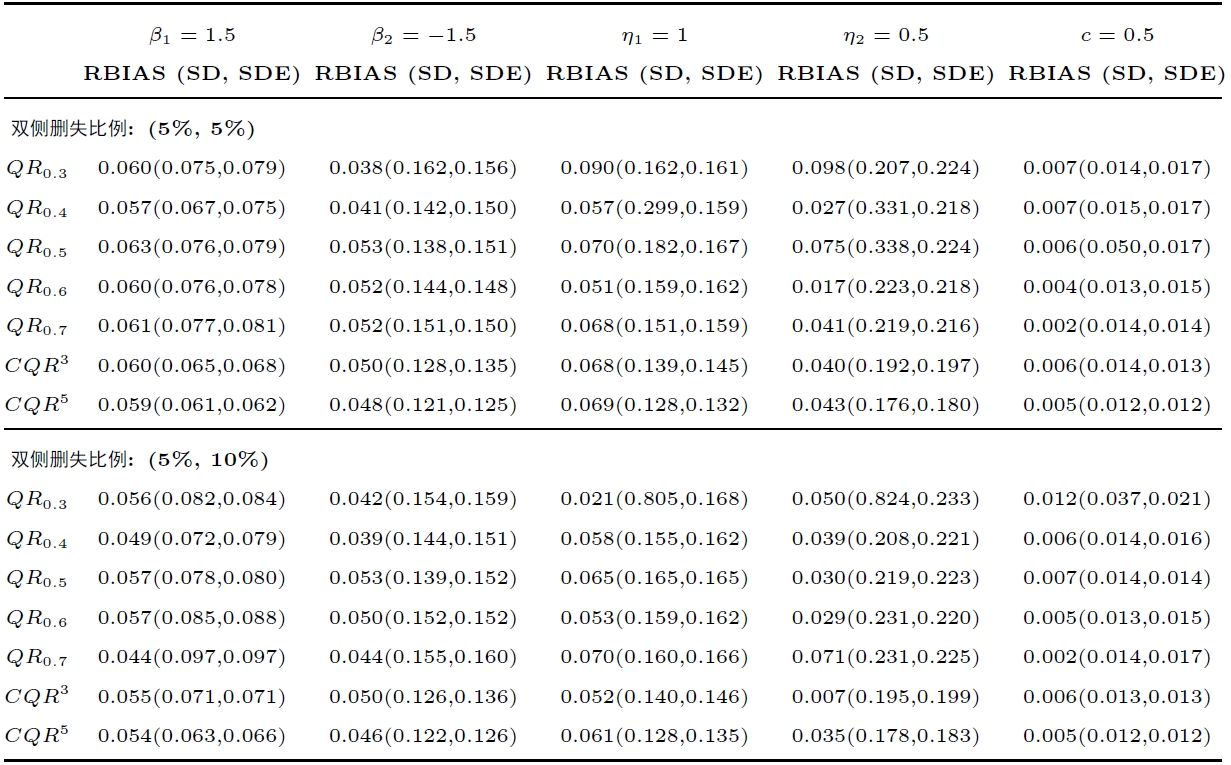
表1 和表2 分别是误差项 $ \epsilon_{ij} $ $ N(0,1) $ $ t(3) $ $ t(3) $ $ QR_{0.4} $ $ N(0,1) $ $ CQR^{3} $ $ CQR^{5} $ $ CQR^{5} $ $ CQR^{3} $ $ CQR^{5} $
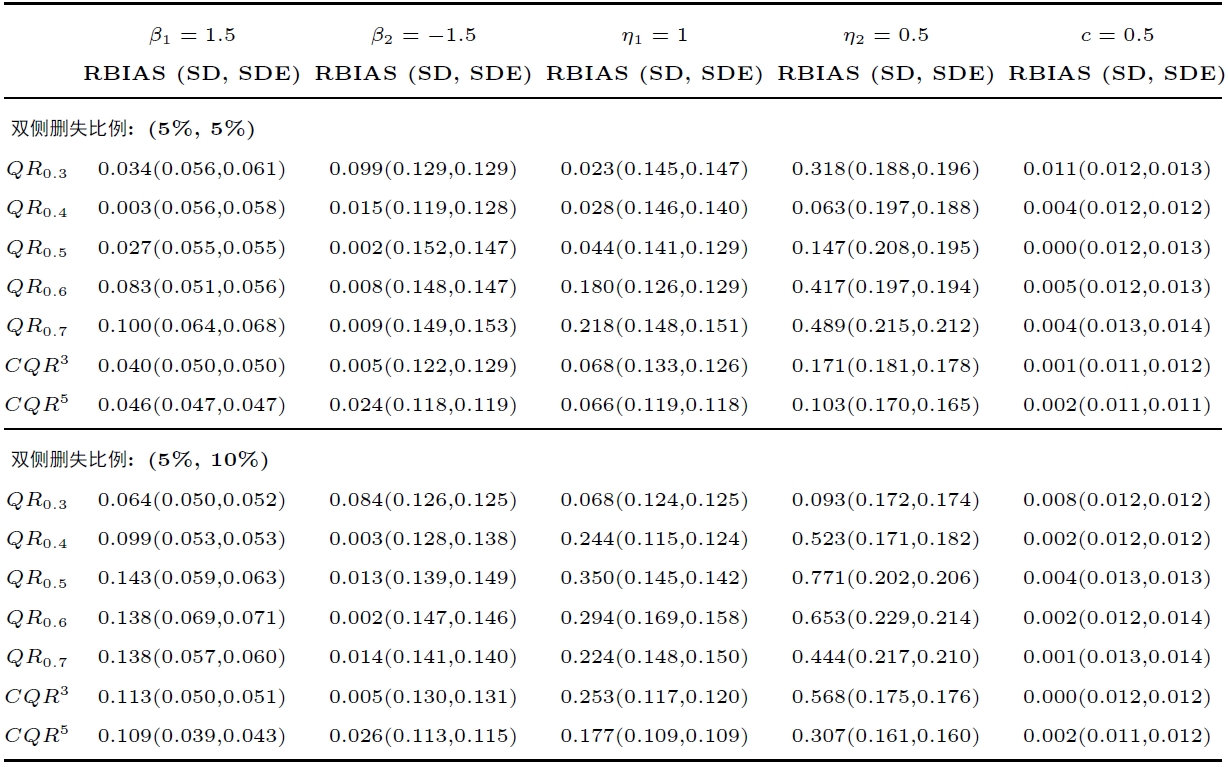
此外, 对于双删失数据, 为了验证利用到数据的上、下限信息可以提升拟合效果, 本文考虑正态误差情形: ( $ \epsilon_{i}\sim N(0,\Sigma_{n_{i}}), \sigma_{ij}=0.4^{|i-j|} $ $ y_{ij}^{*} $ 表 3 中.
对比表3 与表1 可以发现, 在绝大多数情形下, 表1 中参数估计的RBIAS远大于它在表1 中对应的 RBIAS. 以参数 $ \eta_{2} $ $ (5\%,10\%) $ 表1 中的 RBIAS 几乎都不超过 0.01, 而表3 中的 RBIAS 几乎都不低于 0.3. 因此, 本文所提方法考虑到数据的上、下限效应, 极大地降低了该参数的估计偏差, 有助于增强亚组识别效果. 并且, 注意到, 在数据删失比例更大时, 相较于未考虑删失的方法, 本文所提方法在估计偏差方面具有更明显的优势.
4.2 非平衡数据情形
在实际试验中, 有患者在某些时间点可能缺席试验, 这会导致观测区间内也出现部分数据删失. 因此, 模拟也考虑由这样的删失产生的非平衡数据. 模拟使用下面的 logit 回归模型[34 ] 生成数据,
(4.2) $\begin{equation} \text{logit}\lbrace P_{ik}(y_{i1},\cdots,y_{ik};\mathbf{\gamma})\rbrace = \gamma_{0} + \gamma_{1}y_{ik} + \sum_{j=2}^{k} \gamma_{j}y_{i,k+1-j},\text{ } k=2,\cdots,n_{i}, \text{ }i=1,\cdots,N, \end{equation}$
其中, $ P_{ik} $ $ i $ $ k $ $ \gamma_{1}=\gamma_{3}=\cdots=\gamma_{k}=0 $
(4.3) $\begin{equation} \text{log}\left(P_{ik}/(1-P_{ik})\right)=\gamma_{0}+\gamma_{2}y_{i,k-1}, \text{ }i=1,\cdots,N;\text{ } k=2,\cdots,n_{i}. \end{equation}$
对于个体 $ i $ $ P_{ik} $ $ 0.5 $ $ k $ $ \epsilon_{i}\sim N(0,\Sigma_{n_{i}}), \sigma_{ij}=0.4^{|i-j|} $ ) 观测区间 $ [l,u] $ $ 15\% $ $ \gamma_{0} $ $ \gamma_{2} $ $ -0.38 $ $ 0.1 $ .
表4 是误差项服从正态分布 ($ \epsilon_{i}\sim N(0,\Sigma_{n_{i}}), \sigma_{ij}=0.4^{|i-j|} $ ) 且观测区间内数据删失比例约为 $ 15\% $ 表4 可以得到与 4.1 节类似的结论: 在估计偏差方面, 复合分位数方法与单分位数方法表现比较接近; 但是, 在估计效率方面, 复合分位数方法相较于单分位数方法有明显提升. 并且, 与表1 相比, 表4 中的 RBIAS 与 SD 整体略有增大. 由于观测样本因数据删失而减少, 这一现象是合理的.
5 直肠癌患者生活质量数据分析
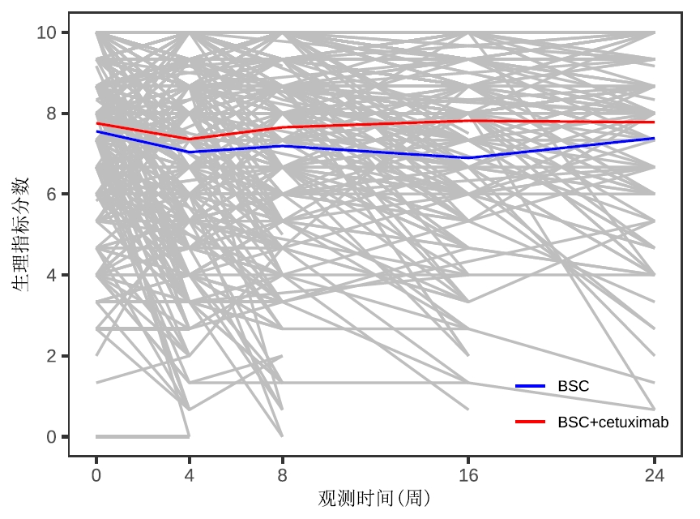
在 CO.17 数据中, 躯体功能子量表由五个问卷问题组成, 它们的得分均值记为生理指标. 为方便数据分析, 我们将生理指标值转化为分数 0 至 10, 即将分数映射到区间 [0,10] 中, 分数数值越高代表患者生活质量越好. 图 1 展示了最佳支持治疗组 (BSC) 与癌症药物西妥昔单抗 + BSC 治疗组 (BSC+cetuximab) 的生理指标样本平均值随时间变化的情况. 从图1 可以看出, 生理指标分数被限制在区间 $ [l,u]=[0,10] $ $ y_{ij}^{*} $
(5.1) $ \begin{matrix} y_{i j}^{*} =& \left(\beta_{0}+\beta_{1} b_{i}+\beta_{2} t_{i j}+\beta_{3}\left(t_{i j}-8\right)_{+}+\beta_{4}\left(t_{i j}-16\right)_{+}+\eta_{1} I(w_{i}>c) +\eta_{2} b_{i} I(w_{i}>c)+\varepsilon_{i j}\right)^{*}, \end{matrix} $
其中, $ b_{i} $ $ b_{i}=1 $ $ i $ $ b_{i}=0 $ $ i $ $ w_{i} $ $ i $ $ (s)_{+}=\max\{s,0\} $ .
图1
图1
两组治疗组的生理指标样本平均值随时间变化折线图
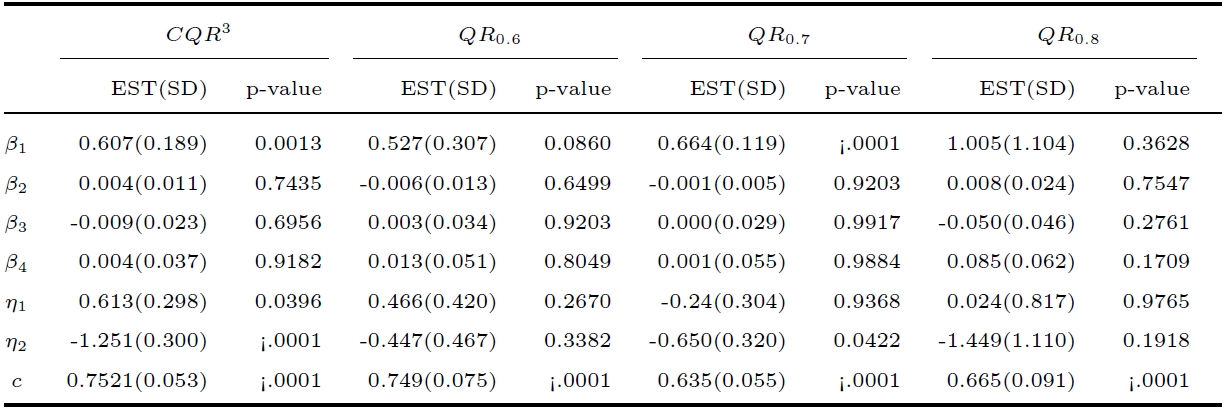
分别采用分位数 {0.6,0.7,0.8} 的复合分位数方法 $ CQR^{3} $ $ QR_{0.6} $ $ QR_{0.7} $ $ QR_{0.8} $ $ p $
表 5 展示四种不同方法 $ CQR^{3} $ $ QR_{0.6} $ $ QR_{0.7} $ $ QR_{0.8} $ 表 5 中的阈值 $ c $ $ \tau=0.7 $ $ \eta_2 $ $ p $ $ p $ $ QR_{0.8} $ $ \beta_{1} $ $ \eta_{2} $ 表 5 看出, 利用复合分位数方法 $ CQR^{3} $ $ \eta_{2} $ $ CQR^{3} $ $ \eta_{2} $ $ p $ $ c=0.7521 $ $ CQR^{3} $ $ \eta_{1} $ $ p $ $ \eta_{1} $ .
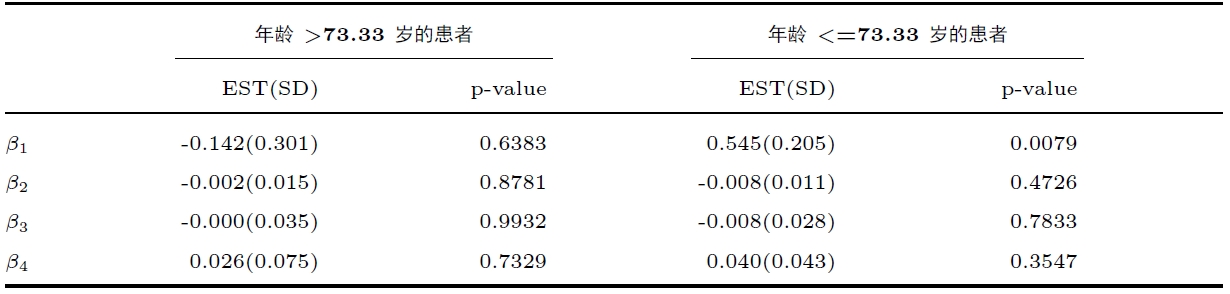
进一步, 本例研究以 73.33 岁为切点划分的两个年龄亚组之间的治疗效果差异. 利用 73.33 岁为切点将数据划分为两个数据集, 分别研究方法 BSC+cetuximab 的治疗效果. 在模型 (5.1) 中去除与年龄亚组有关的项, 仅用其余变量在这两个年龄亚组中分别做回归, 即
(5.2) $\begin{matrix} y_{i j}^{*} =& \left(\beta_{0}+\beta_{1} b_{i}+\beta_{2} t_{i j}+\beta_{3}\left(t_{i j}-8\right)_{+}+\beta_{4}\left(t_{i j}-16\right)_{+}+\varepsilon_{i j}\right)^{*}. \end{matrix}$
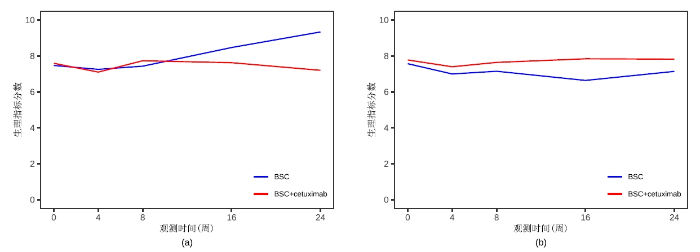
表 6 给出了复合分位数回归方法 $ CQR^{3} $ $ \beta_{1} $ $ p $ $ \beta_{1} $ $ p $ 图2 中分别绘制了治疗组 BSC 与 BSC+cetuximab 的生理指标样本平均值随时间变化的折线图. 从图 2 也可以看出, 对于年龄小于 73.33 岁的患者, 治疗组 BSC+cetuximab 的生活质量明显优于最佳支持治疗组 BSC, 而对于年龄大于 73.33 岁的患者则并不存在这一现象.
图2
图2
两组治疗组的生理指标样本平均值数据. (a) 年龄 >73.33 岁的患者生理指标样本平均值随时间变化折线图; (b) 年龄 <=73.33 岁的患者生理指标样本平均值随时间变化折线图
致谢
本文投稿前, 合作者吴耀华教授不幸离世, 谨以此文深切纪念吴耀华教授.
参考文献
View Option
[1]
Tobin J Estimation of relationships for limited dependent variables
Econometrica , 1958 , 26 1 ): 24 -36
[本文引用: 1]
[2]
Bauer T K Sinning M Blinder-oaxaca decomposition for tobit models
Applied Economics , 2010 , 42 12 ): 1569 -1575
[本文引用: 1]
[3]
Anastasopoulos P C Shankar V N Haddock J E et al. A multivariate tobit analysis of highway accident-injuryseverity rates
Accident Analysis & Prevention , 2012 , 45 1 ): 110 -119
[本文引用: 1]
[4]
Amore M D Murtinu S Tobit models in strategy research: Critical issues and applications
Global Strategy Journal , 2021 , 11 3 ): 331 -355
[本文引用: 1]
[5]
Twisk J Rijmen F Longitudinal tobit regression: a new approach to analyze outcome variables with floor or ceiling effects
Journal of Clinical Epidemiology , 2009 , 62 9 ): 953 -958
DOI:10.1016/j.jclinepi.2008.10.003
PMID:19211221
[本文引用: 1]
In many epidemiologic longitudinal studies, the outcome variable has floor or ceiling effects. Although it is not correct, these variables are often treated as normally distributed continuous variables.In this article, the performance of a relatively new statistical technique, longitudinal tobit analysis, is compared with a classical longitudinal data analysis technique (i.e., linear mixed models).The analyses are performed on an example data set from rehabilitation research in which the outcome variable of interest (the Barthel index measured at on average 16.3 times) has typical floor and ceiling effects. For both the longitudinal tobit analysis and the linear mixed models an analysis with both a random intercept and a random slope were performed.Based on model fit parameters, plots of the residuals and the mean of the squared residuals, the longitudinal tobit analysis with both a random intercept and a random slope performed best. In the tobit models, the estimation of the development over time revealed a steeper development compared with the linear mixed models.Although there are some computational difficulties, longitudinal tobit analysis provides a very nice solution for the longitudinal analysis of outcome variables with floor or ceiling effects.
[6]
Laird N M Ware J H Random-effects models for longitudinal data
Biometrics , 1982 , 38 4 ): 963 -974
PMID:7168798
[本文引用: 1]
Models for the analysis of longitudinal data must recognize the relationship between serial observations on the same unit. Multivariate models with general covariance structure are often difficult to apply to highly unbalanced data, whereas two-stage random-effects models can be used easily. In two-stage models, the probability distributions for the response vectors of different individuals belong to a single family, but some random-effects parameters vary across individuals, with a distribution specified at the second stage. A general family of models is discussed, which includes both growth models and repeated-measures models as special cases. A unified approach to fitting these models, based on a combination of empirical Bayes and maximum likelihood estimation of model parameters and using the EM algorithm, is discussed. Two examples are taken from a current epidemiological study of the health effects of air pollution.
[7]
Sattar A Weissfeld L A Molenberghs G Analysis of non-ignorable missing and left-censored longitudinal data using a weighted random effects tobit model
Statistics in Medicine , 2011 , 30 27 ): 3167 -3180
[本文引用: 1]
[8]
Jiang W Y Freidlin B Simon R Biomarker-adaptive threshold design: a procedure for evaluating treatment with possible biomarker-defined subset effect
Journal of the National Cancer Institute , 2007 , 99 13 ): 1036 -1043
[本文引用: 2]
[9]
Chen B E Jiang W Y Tu D S A hierarchical bayes model for biomarker subset effects in clinical trials
Computational Statistics & Data Analysis , 2014 , 71 19 ): 324 -334
[本文引用: 1]
[10]
He Y Lin H Z Tu D S A single-index threshold cox proportional hazard model for identifying a treatment-sensitive subset based on multiple biomarkers
Statistics in Medicine , 2018 , 37 23 ): 3267 -3279
[本文引用: 2]
[11]
Moineddin R Butt D A Tomlinson G et al. Identifying subpopulations for subgroup analysis in a longitudinal clinical trial
Contemporary Clinical Trials , 2008 , 29 6 ): 817 -822
DOI:10.1016/j.cct.2008.07.002
PMID:18718556
[本文引用: 1]
In a typical clinical trial treatment effects will not be expected to be the same on all of the study participants. As a result, investigators are often tempted to look at the effects of a given treatment in subgroups of patients in order to determine who will benefit the most or the least, especially when the treatment effect in the total sample is insignificant or borderline. This paper aims at demonstrating the application of random effect models as one approach to identify subpopulations suitable for subgroup analysis in a longitudinal study.Data collected from a double-blind randomized controlled trial were used to demonstrate how multilevel modeling using random effects can be used to identify subgroups of postmenopausal women who benefit the most from nonhormonal treatment (gabapentin) of their hot flashes.We estimated subject-specific treatment effects and correlated these effects with patient characteristics at baseline. We found that women with a higher severity of hot flashes score at baseline were more likely to have the greatest reduction in hot flashes score from the treatment. Also, women who had a serum creatinine level higher than the median level at baseline demonstrated a greater response to gabapentin compared to the placebo group.Our proposed method can help researchers identify patient factors that are associated with differential effect. Those factors are potential areas for further clinical investigation or for constructing subgroups for sub-analysis.
[12]
Shen J Qu A Subgroup analysis based on structured mixed-effects models for longitudinal data
Journal of Biopharmaceutical Statistics , 2020 , 30 4 ): 607 -622
DOI:10.1080/10543406.2020.1730867
PMID:32126871
[本文引用: 1]
In recent years, subgroup analysis has emerged as an important tool to identify unknown subgroup memberships. However, subgroup analysis is still under-studied for longitudinal data. In this paper, we propose a structured mixed-effects approach for longitudinal data to model subgroup distribution and identify subgroup membership simultaneously. In the proposed structured mixed-effects model, the heterogeneous treatment effect is modeled as a random effect from a two-component mixture model, while the membership of the mixture model is incorporated using a logistic model with respect to some covariates. One advantage of our approach is that we are able to derive the estimation of the treatment effects through an EM-type algorithm which keeps the subgroup membership unchanged over time. Our numerical studies and real data example demonstrate that the proposed model outperforms other competing methods.
[13]
Ge X Y Peng Y W Tu D S A threshold linear mixed model for identification of treatment-sensitive subsets in a clinical trial based on longitudinal outcomes and a continuous covariate
Statistics Methods in Medical Research , 2020 , 29 10 ): 2919 -2931
[本文引用: 3]
[14]
Koenker R Bassett G Regression quantiles
Econometrica , 1978 , 46 1 ): 33 -50
[本文引用: 1]
[15]
Zou H Yuan M Composite quantile regression and the oracle model selection theory
Annals of Statistics , 2008 , 36 3 ): 1008 -1126
[本文引用: 2]
[16]
Guo J Tang M L Tian M Z et al. Variable selection in high-dimensional partially linear additive models for composite quantile regression
Computational Statistics & Data Analysis , 2013 , 65 56 -67
[本文引用: 1]
[17]
Jiang R Qian W M Li J R Testing in linear composite quantile regression models
Computational Statistics , 2014 , 29 5 ): 1381 -1402
[本文引用: 1]
[18]
Huang H W Chen Z X Bayesian composite quantile regression
Journal of Statistical Computation and Simulation , 2015 , 85 18 ): 3744 -3754
[本文引用: 1]
[19]
Tang Y L Song X Y Zhu Z Y Variable selection via composite quantile regression with dependent errors
Statistica Neerlandica , 2015 , 69 1 ): 1 -20
[本文引用: 1]
[20]
Xu Q F Deng K Jiang C X et al. Composite quantile regression neural network with applications
Expert Systems with Applications , 2017 , 76 9 ): 129 -139
[本文引用: 1]
[21]
Jiang X J Jiang J C Song X Y Oracle model selection for nonlinear models based on weighted composite quantile regression
Statistica Sinica , 2012 , 22 4 ): 1479 -1506
[本文引用: 1]
[22]
Zhao W H Lian H Song X Y Composite quantile regression for correlated data
Computational Statistics & Data Analysis , 2017 , 109 15 -33
[本文引用: 1]
[23]
Tang L J Zhou Z G Wu C C Weighted composite quantile estimation and variable selection method for censored regression model
Statistics & Probability Letters , 2012 , 82 3 ): 653 -663
[本文引用: 1]
[24]
Xiao L Q Wang Z F Wu Y H Composite quantile regression estimation for left censored response longitudinal data
Acta Mathematicae Applicatae Sinica, English Series , 2018 , 34 4 ): 730 -741
[本文引用: 2]
[25]
Wang Z F Li T Xiao L Q et al. A threshold longitudinal tobit quantile regression model for identification of treatment-sensitive subgroups based on interval-bounded longitudinal measurements and a continuous covariate
Statistics in Medicine , 2023 , 42 25 ): 4618 -4631
[本文引用: 4]
[26]
Brown B M Wang Y G Induced smoothing for rank regression with censored survival times
Statistics in Medicine , 2007 , 26 4 ): 828 -836
[本文引用: 1]
[27]
Wang Z F Ding J L Sun L Q et al. Tobit quantile regression of left-censored longitudinal data with informative observation times
Statistica Sinica , 2018 , 28 1 ): 527 -548
[本文引用: 2]
[28]
Boyd S Parikh N Chu E et al. Distributed optimization and statistical learning via the alternating direction method of multipliers
Foundations and Trends® in Machine Learning , 2011 , 3 1 ): 1 -122
[本文引用: 1]
[29]
Wang Z F Wu Y H Zhao L C Approximation by randomly weighting method in censored regression model
Science in China Series A: Mathematics , 2009 , 52 3 ): 561 -576
[本文引用: 1]
[30]
Wells J C Tu D S Siu L L et al. Outcomes of older patients (≥70 years) treated with targeted therapy in metastatic chemorefractory colorectal cancer: Retrospective analysis of NCIC CTG CO.17 and CO.20
Clinical Colorectal Cancer , 2019 , 18 1 ): e140-e149
[本文引用: 1]
[31]
Xiao L Q Hou B Wang Z F et al. Random weighting approximation for tobit regression models with longitudinal data
Computational Statistics & Data Analysis , 2014 , 79 3 ): 235 -247
[本文引用: 1]
[32]
Pollard D Empirical Processes: Theory and Applications. NSF-CBMS Regional Conference Series in Probability and Statistics 2
Institute of Mathematical Statistics , 1990
[本文引用: 2]
[33]
Wang H Fygenson M Inference for censored quantile regression models in longitudinal studies
The Annals of Statistics , 2009 , 37 2 ): 756 -781
[本文引用: 1]
[34]
Diggle P Kenward M G Informative drop-out in longitudinal data analysis
Journal of the Royal Statistical Society , 1994 , 43 1 ): 49 -73
[本文引用: 1]
Estimation of relationships for limited dependent variables
1
1958
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Blinder-oaxaca decomposition for tobit models
1
2010
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
A multivariate tobit analysis of highway accident-injuryseverity rates
1
2012
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Tobit models in strategy research: Critical issues and applications
1
2021
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Longitudinal tobit regression: a new approach to analyze outcome variables with floor or ceiling effects
1
2009
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Random-effects models for longitudinal data
1
1982
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Analysis of non-ignorable missing and left-censored longitudinal data using a weighted random effects tobit model
1
2011
... 众所周知, Tobit 回归模型是被用于处理删失数据的常用模型之一, 该模型由文献 [1 ] 提出, 在经济学、心理学、生物医学等领域得到广泛应用, 见文献[2 ,3 ,4 ]. 文献 [5 ] 将 Tobit 模型应用到纵向流行病学研究中, 分析具有上、下限效应的纵向数据, 模拟结果表明, 纵向 Tobit模型比线性混合模型[6 ] 具有更好的拟合效果. 为分析不可忽略缺失的左删失数据, 文献 [7 ] 提出加权随机效应 Tobit 模型, 并分析白细胞介素-6 生物标志物数据. 然而, 这些模型和方法都没有考虑亚组问题和模型稳健问题. 为此, 本文提出一个同时考虑亚组问题和模型稳健的方法-复合 Tobit 分位数亚组分析回归方法, 用以分析双删失纵向数据. ...
Biomarker-adaptive threshold design: a procedure for evaluating treatment with possible biomarker-defined subset effect
2
2007
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
A hierarchical bayes model for biomarker subset effects in clinical trials
1
2014
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
A single-index threshold cox proportional hazard model for identifying a treatment-sensitive subset based on multiple biomarkers
2
2018
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... 为展示方法的效果, 模拟与文献 [25 ] 的单分位数回归方法进行比较. 为方便叙述, 记 $ \tau $ $ QR_{\tau} $ . 对于本文所提的 CQR 方法, 取分位数 $ \{0.4,0.5,0.6\} $ $ \{0.3,0.4,0.5,0.6,0.7\} $ $ CQR^{3} $ $ CQR^{5} $ . 重复实验 200 次, 计算估计值与真实值的相对偏差, 平均值记为 RBIAS; 估计值的经验标准差记为 SD; 随机加权标准差估计值记为 SDE. 模拟选用文献 [10 ] 中的设置方法, 带宽 $ h_{n} $ $ \hat{\rho}n^{-1/3} $ $ \hat{\rho} $ $ n $ $ w_{i} $
Identifying subpopulations for subgroup analysis in a longitudinal clinical trial
1
2008
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Subgroup analysis based on structured mixed-effects models for longitudinal data
1
2020
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
A threshold linear mixed model for identification of treatment-sensitive subsets in a clinical trial based on longitudinal outcomes and a continuous covariate
3
2020
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... 由于示性函数 $ I(w_{i}>c) $ $ 0 $ $ 1 $ $ c $ $ c $ 13 ] 的方法, 采用 $ \Phi({(w_{i}-c)}/{h_{n}}) $ $ I(w_{i}>c) $ $ \Phi(\cdot) $ $ h_{n} $ $ \lim\limits_{n\rightarrow\infty}h_{n}=0 $ . 易知函数 $ \Phi(\cdot) $
Regression quantiles
1
1978
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Composite quantile regression and the oracle model selection theory
2
2008
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Variable selection in high-dimensional partially linear additive models for composite quantile regression
1
2013
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Testing in linear composite quantile regression models
1
2014
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Bayesian composite quantile regression
1
2015
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Variable selection via composite quantile regression with dependent errors
1
2015
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Composite quantile regression neural network with applications
1
2017
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Oracle model selection for nonlinear models based on weighted composite quantile regression
1
2012
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Composite quantile regression for correlated data
1
2017
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Weighted composite quantile estimation and variable selection method for censored regression model
1
2012
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
Composite quantile regression estimation for left censored response longitudinal data
2
2018
... 关于治疗敏感亚组识别问题, 现有的方法较为丰富, 如文献[8 ,9 ,10 ,11 ,12 ,13 ], 其中阈值回归方法使用较为广泛. 文献 [8 ] 提出生物标志物自适应阈值模型, 基于生存数据, 将整体治疗效果的检验与生物标志物切点的建立相结合, 通过切点来划分治疗敏感亚组. 文献 [13 ] 对纵向数据提出阈值线性混合模型, 在确定生物标志物切点的同时, 评估治疗和亚组指标对纵向结果的交互作用. 需要说明的是, 该模型依赖数据服从正态分布的假设, 这对于删失数据而言, 通常难以满足. 分位数回归方法是解决上述问题的方法之一, 它根据响应变量的条件分位点对自变量进行回归, 不依赖数据服从某个特定分布, 且对异常值不敏感, 具有稳健性. 分位数回归最早由文献 [14 ] 提出, 因其宽松的假设条件得到了学者们的广泛关注. 与均值回归相比, 分位数回归可以从数据中挖掘出更为丰富的信息. 但是, 分位数回归的估计效率较低, 文献 [15 ] 指出, 分位数回归估计相对于最小二乘估计的相对效率可以任意小. 为克服这一缺陷, 文献 [15 ] 采用复合分位数回归方法, 在保持稳健性的基础上显著地提高了估计效率. 复合分位数回归更为深入的研究, 见文献 [16 ,17 ,18 ,19 ,20 ,21 ,22 ,23 ,24 ]. 通过梳理现有的复合分位数回归文献, 尚未发现文献考虑删失数据的亚组识别问题. ...
... 从 2.2 节可以看出 $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ f $ [31 ] . 为了避免估计冗余参数, 本文使用随机加权方法来估计 $ \tilde{\boldsymbol{\theta}} $ $ \text{Var}(\tilde{\boldsymbol{\theta}}) $ . 关于随机加权方法的进一步讨论可参见文献 [24 ]. ...
A threshold longitudinal tobit quantile regression model for identification of treatment-sensitive subgroups based on interval-bounded longitudinal measurements and a continuous covariate
4
2023
... 最近, 文献 [25 ] 研究阈值 Tobit 分位数回归模型, 它基于区间有界的纵向观测和一个连续生物标志物协变量来识别治疗敏感亚组. 该模型只考虑单个分位点, 参数估计效率不高. 参数估计效率是影响亚组识别的重要因素之一, 研究如何在保持稳健性的基础上提升参数估计效率, 对于增强亚组识别效果而言具有实际意义. 据笔者所知, 鲜有研究将复合分位数回归方法应用于研究治疗敏感亚组的识别问题. 据此, 本文研究复合 Tobit 分位数亚组分析回归方法, 基于双删失纵向数据和一个连续协变量来识别治疗敏感亚组. 与单分位数回归相比, 复合分位数回归提高了参数估计的效率, 增强了治疗敏感亚组的识别效果. 在参数估计部分, 由于待优化的目标函数是非光滑的, 我们采用两步光滑化处理. ...
... 全文假设误差 $ \big\{\epsilon_{ij}\big\} $ $ F $ $ F $ $ f $ $ \epsilon_{ij} $ $ \tau $ $ \alpha_{\tau} $ $ \tau\in(0,1) $ . 对于固定的 $ \tau $ 25 ] 考虑了单分位数回归模型 ...
... 注 2.1 文献 [25 ] 中未直接出现 (2.3) 式, 下面通过简单推导说明该式正确性. 记 $ y_{ij} $ $ y_{ij}^{*} $ $ F_{y_{ij}} $ $ F_{y_{ij}^{*}} $ . 由 $ y_{ij}^{*} $
... 为展示方法的效果, 模拟与文献 [25 ] 的单分位数回归方法进行比较. 为方便叙述, 记 $ \tau $ $ QR_{\tau} $ . 对于本文所提的 CQR 方法, 取分位数 $ \{0.4,0.5,0.6\} $ $ \{0.3,0.4,0.5,0.6,0.7\} $ $ CQR^{3} $ $ CQR^{5} $ . 重复实验 200 次, 计算估计值与真实值的相对偏差, 平均值记为 RBIAS; 估计值的经验标准差记为 SD; 随机加权标准差估计值记为 SDE. 模拟选用文献 [10 ] 中的设置方法, 带宽 $ h_{n} $ $ \hat{\rho}n^{-1/3} $ $ \hat{\rho} $ $ n $ $ w_{i} $
Induced smoothing for rank regression with censored survival times
1
2007
... $ \bullet $ 26 ] 的方法将其光滑化; ...
Tobit quantile regression of left-censored longitudinal data with informative observation times
2
2018
... $ \bullet $ 27 ] 的方法将其光滑化. ...
... [27 ] 的相同技巧, 考虑函数 ...
Distributed optimization and statistical learning via the alternating direction method of multipliers
1
2011
... 对光滑后的目标函数, 利用交替乘子算法 (alternating direction method of multipliers, ADMM)[28 ] 数值地求解优化问题, 得到参数估计量. 在估计方差时, 应用随机加权方法[29 ] 计算方差, 该方法避开了对冗余参数的估计, 易于执行. 为了研究方法的效果, 在不同的误差分布和删失比例下进行模拟实验. 结果表明该方法相较于单分位数回归方法具有更高的参数估计效率, 并且说明用随机加权方法估计参数估计量方差是可行的. 最后, 分析直肠癌患者生活质量数据 CO.17, 识别出根据年龄划分的西妥昔单抗药物治疗敏感亚组. ...
Approximation by randomly weighting method in censored regression model
1
2009
... 对光滑后的目标函数, 利用交替乘子算法 (alternating direction method of multipliers, ADMM)[28 ] 数值地求解优化问题, 得到参数估计量. 在估计方差时, 应用随机加权方法[29 ] 计算方差, 该方法避开了对冗余参数的估计, 易于执行. 为了研究方法的效果, 在不同的误差分布和删失比例下进行模拟实验. 结果表明该方法相较于单分位数回归方法具有更高的参数估计效率, 并且说明用随机加权方法估计参数估计量方差是可行的. 最后, 分析直肠癌患者生活质量数据 CO.17, 识别出根据年龄划分的西妥昔单抗药物治疗敏感亚组. ...
Outcomes of older patients (≥70 years) treated with targeted therapy in metastatic chemorefractory colorectal cancer: Retrospective analysis of NCIC CTG CO.17 and CO.20
1
2019
... 其中, $ \alpha $ $ \boldsymbol{\beta} $ $ \eta_{1} $ $ \eta_{2} $ $ c $ $ b_{i} $ $ b_{i}=1 $ $ i $ $ b_{i}=0 $ $ i $ $ w_{i} $ $ i $ $ \epsilon_{ij} $ $ \epsilon_{ij} $ $ i $ $ j $ $ j $ $ \epsilon_{1j},\cdots,\epsilon_{Nj} $ $ i $ $ \epsilon_{i1},\cdots,\epsilon_{in_{i}} $ $ \{\textbf{X}_{ij}\} $ $ \{w_{i}\} $ $ \{b_{i}\} $ 30 ] 以发达国家直肠癌诊断年龄中位数 70 岁为切点, 将患者分为两个年龄亚组, 研究西妥昔单抗在这两个年龄亚组之间的疗效差异. 实际上, 70 岁是否为一个合适的年龄切点其实是尚不清楚的, 需要用数据去估计, 即需要估计模型 (2.1) 中的未知参数 $ c $ . 此外, $ b_{i}=1 $ $ i $ $ + $ $ b_{i}=0 $ $ i $ $ w_{i} $ $ i $ $ I(w_{i}>c) $
Random weighting approximation for tobit regression models with longitudinal data
1
2014
... 从 2.2 节可以看出 $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ \tilde{\boldsymbol{\theta}} $ $ f $ [31 ] . 为了避免估计冗余参数, 本文使用随机加权方法来估计 $ \tilde{\boldsymbol{\theta}} $ $ \text{Var}(\tilde{\boldsymbol{\theta}}) $ . 关于随机加权方法的进一步讨论可参见文献 [24 ]. ...
Empirical Processes: Theory and Applications. NSF-CBMS Regional Conference Series in Probability and Statistics 2
2
1990
... 注 3.1 条件 (A1) 和条件 (A2) 与文献 [第 11 章] 中的条件类似. 条件 (A3) 表明总样本数 $ n $ $ N $ 33 ]. 条件 (A3) 与条件 (A4) 共同保证中心化后的目标函数 $ \Psi_{n}(\boldsymbol{\theta}) $ $ \Psi_{n}(\boldsymbol{\theta};h_{n}) $ 32 ]. ...
... 显然, $ \big(K(u-l),\cdots,K(u-l)\big)_{N\times1} $ $ \mathcal{G}_{N,j} $ 32 , 第 7 章] 的计算, 有 ...
Inference for censored quantile regression models in longitudinal studies
1
2009
... 注 3.1 条件 (A1) 和条件 (A2) 与文献 [第 11 章] 中的条件类似. 条件 (A3) 表明总样本数 $ n $ $ N $ 33 ]. 条件 (A3) 与条件 (A4) 共同保证中心化后的目标函数 $ \Psi_{n}(\boldsymbol{\theta}) $ $ \Psi_{n}(\boldsymbol{\theta};h_{n}) $ 32 ]. ...
Informative drop-out in longitudinal data analysis
1
1994
... 在实际试验中, 有患者在某些时间点可能缺席试验, 这会导致观测区间内也出现部分数据删失. 因此, 模拟也考虑由这样的删失产生的非平衡数据. 模拟使用下面的 logit 回归模型[34 ] 生成数据, ...