种间竞争是不同物种之间为争夺资源而进行的一类竞争现象, 这类现象在现实世界中十分常见, 对它的研究, 在生态学和经济学等诸多领域内都具有重要的理论和实际意义. 自从美国生物数学家 Lotka 和意大利数学家 Volterra 提出著名的 Lotka-Volterra模型^[1,2]以来, 常微分模型便被学者们广泛用于种群问题的研究.

由于季节更替和资源枯竭, 迁徙和扩散已经成为许多种群的常态, 因此在模型中有必要考虑扩散因素的影响, 对具有扩散项的种间竞争偏微分模型的研究具有重要的理论和实际意义. 当前, 反应扩散方程组在生态学等领域应用广泛, 通常用抛物型偏微分方程来研究反应扩散问题. 在过去的数十年内, 种群动力学模型一直是生态学研究的热门主题之一, 而反应扩散方程组的正平衡解及其长期行为是种群动力学模型所研究的主要内容^[3-7].

在现实世界中, 由于种群的生存与繁殖以及物种之间的竞争能力等, 都与其所处空间有密切的关联, 因此物种与环境以及其他物种的相互作用都与空间变量有关, 并呈现出空间非均匀性. 与空间均匀假设下的自治模型相比, 空间非均匀反应扩散方程组构成的非自治模型包含与空间变量有关的反应函数, 更能反映空间变量对种群的影响, 从而对后者的研究受到了学者们的重视.

现有的对空间非均匀反应扩散方程组的研究多是针对具有特殊性质的反应函数展开的^[8-18].例如, Lou 等^[15]是针对变量分离型反应函数进行了研究, Hutson 等^[18]是针对单调反应函数进行了研究. 2023 年 Lou 等^[19]针对一般的反应函数, 仅分析了单种群空间非均匀反应扩散模型, 未考虑种群之间的相互作用和竞争. 根据以上分析所发现的问题, 本文将针对一般的反应函数, 考虑如下的两种群空间非均匀反应扩散竞争模型

其中 $u$ 和 $v$ 分别表示两个种群的密度, 它们是关于 $(t,x)$ 的未知函数; $\mu>0$ 和 $\nu>0$ 分别代表二者的扩散系数; $f(u,v,x)$ 和 $g(u,v,x)$ 是反应率系数函数; $u_0$ 和 $v_0$ 分别表示两个种群的初始密度, 它们是关于 $x$ 的已知函数; $\Omega\subseteq\Bbb{R}^2$ 是一个具有光滑边界 $\partial\Omega$ 的有界域;$n$ 表示边界 $\partial\Omega$ 的单位外法向量; $\Delta$ 表示拉普拉斯算子.

与反应扩散方程组 $(1.1)$ 相应的反应方程组为

种群的反应函数依赖于种群密度、竞争种群密度以及空间变量. 在之前的研究中, 学者们会假设反应函数关于密度单调递减. 但是在实际的生态系统中, 当种群密度较小时, 资源相对丰富, 反应函数关于种群密度呈现单调递增趋势; 而随着种群密度增加, 资源不再充足, 出现种内竞争, 从而导致反应函数关于种群密度呈现单调递减趋势. 因此, 需要考虑反应函数关于种群密度不再单调的情况, 比如下面例 1.1 中所给出的反应函数.

例 1.1 考虑 $19$ 世纪欧洲野兔引入澳洲并与澳洲本地的袋鼠等生物种群竞争的例子. 野兔作为外来物种, 初入澳洲时, 种群密度较小, 反应函数随其种群密度增大而增大; 随着其种群密度增大, 资源变得不再充足, 出现种内竞争, 导致其反应函数随其种群密度增大而减小. 而本地的袋鼠种群密度已达饱和, 存在种内竞争, 导致其反应函数关于其种群密度呈现单调递减趋势. 用 $u$ 和 $v$ 分别表示野兔和袋鼠种群的密度, 则可用下面的两种群反应扩散方程组表示野兔和袋鼠之间的竞争过程

其中 $x=(x_1,x_2)$, $\Omega\subseteq\Bbb{R}^2$ 是有界的.

可以看出, 反应函数

在 $u\in (-\infty,\frac{1}{2})$ 上关于 $u$ 单调递增, 而在 $u\in (\frac{1}{2},+\infty)$ 上关于 $u$ 单调递减, 不再是关于 $u$ 的单调函数.

本文的结构如下: 在第 2 节给出本文的主要结论; 在第 3 节介绍一些预备知识; 在第 4 节证明本文的主要结论; 在第 5 节通过满足相应假设的一个例子的数值结果验证定理结论的正确性; 最后在第 6 节总结全文, 并给出将来的工作展望.

为了方便理解本文的主要结论, 现将参考文献[第 11 章]中的相关基本定义给出

定义2.1 对给定的 $\mu,\nu$, 若 $(\tilde{u} (x;\mu,\nu),\tilde{v}(x;\mu,\nu))\ (\forall x\in\bar\Omega)$ (下文中简记为$(\tilde{u}(x),\tilde{v}(x))$)满足方程组(1.1), 则称 $(\tilde{u}(x),\tilde{v}(x))$ 是方程组(1.1) 的平衡解.

定义2.2 设 $(\tilde{u}(x),\tilde{v}(x))\ (\forall x\in\bar\Omega)$ 为方程组(1.1) 的平衡解. 若对任意非负的 $(u_0(x),v_0(x))$, 方程组(1.1) 以 $(u_0(x),v_0(x))$ 为初值的解$(u(t,x),v(t,x))$ 满足

则称平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 是全局吸引的. 若平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 既是稳定的, 又是全局吸引的, 则称 $(\tilde{u}(x),\tilde{v}(x))$ 是全局渐近稳定的.

定义2.3 若 $(u^\star(x),v^\star(x))\ (\forall x\in\bar\Omega)$ 满足方程组(1.2), 则称它是方程组 (1.2) 的平衡解.

定义2.4 设 $(u^\star(x),v^\star(x))\ (\forall x\in\bar\Omega)$ 为方程组 (1.2) 的平衡解. 若对任意非负的 $(u_0(x),$$v_0(x))$, 方程组(1.2) 以 $(u_0(x),v_0(x))$ 为初值的解$(u(t,x),v(t,x))$满足

则称平衡解 $(u^\star(x),v^\star(x))$ 是全局吸引的. 若平衡解 $(u^\star(x),v^\star(x))$ 既是稳定的, 又是全局吸引的, 则称 $(u^\star(x),v^\star(x))$ 是全局渐近稳定的.

当反应函数与空间变量无关时, 即 $f(u,v,x)=\bar{f}(u,v),\ g(u,v,x)=\bar{g}(u,v)$ 时, 反应方程组 $(1.2)$ 的平衡解的全局稳定性意味着反应扩散方程组 $(1.1)$ 的全局稳定性^[18], 这是自治模型的特有结论. 而对于空间非均匀的非自治模型, 相应的结论是需要验证的, 即反应方程组 $(1.2)$ 对空间域的每个点 $x$ 都有一个全局渐近稳定的平衡解时, 相应的反应扩散方程组 $(1.1)$ 是否具有相同的结论?

一般来说, 任意给定一个反应扩散方程组, 相应的反应方程组的渐近行为对其渐近性研究帮助不大. 而对于较大扩散系数 $\mu$, $\nu$ 的反应扩散方程组, Conway 等^[8]给出了以下结论: 若其有一个 $L^{\infty}$ 有界正不变集, 则对该不变集中的初值, 对应的解才会逐渐接近于相应反应方程组的空间平衡解, 难以得出全局渐近稳定的结论. 而当扩散系数 $\mu$, $\nu$ 较小时, 具有非单调反应函数的反应扩散方程组是否具有全局渐近稳定性, 目前对这一问题未见公开发表的成果, 而这正是本文所要研究的问题.

根据种群竞争特点, 本文对方程组 $(1.1)$ 的反应函数做以下合理性假设

(H1) $f,g:C^1\times C^1\times \Omega\rightarrow\Bbb{R}$;

(H2) 对$\forall x\in\bar\Omega$, 存在一个正值函数$\bar u(x)>0$, 使得$\forall v(x)\ge 0$,

同时, 对$\forall x\in\bar\Omega$, 有$f_v(u,v,x)<0$;

(H3) 对$\forall x\in\bar\Omega$, 有$g_u(u,v,x)<0$, $g_v(u,v,x)<0$;

(H4) 存在一个正常数$M>0$, 使得$\forall x\in\bar\Omega$, 有

(H5) 对$\forall x\in\bar\Omega$, $f(u,v,x)=0$和$g(u,v,x)=0$有唯一解$(u^\star(x),v^\star(x))$, 满足

(H6) 对$\forall x\in\bar\Omega$,$(f_ug_v-f_vg_u)|_{(u,v,x)=(u^\star (x),v^\star(x),x)}>0$.

注2.1 满足假设(H1)-(H6) 的反应函数是存在的, 现说明如下.

如例 1.1 中的反应函数

和

显然满足 (H1) 和 (H4), 其中可取正常数 $M\ge \frac{9}{2}$.

对于 (H2) 和 (H3), $\forall x\in\bar\Omega$, $\forall u(x)\ge 0, v(x)\ge 0$, 有

此外, 对 $\forall x\in\bar\Omega$, 存在一个正函数 $\bar u(x)=\frac{1}{2}$, 使得 $\forall v(x)\ge 0$,

因此 (H2) 和 (H3) 成立.

对于 (H5) 和 (H6), 对 $\forall x\in\bar\Omega$, 方程组

有唯一解, 记作

且$(f_ug_v-f_vg_u)|_{(u^\star (x),v^\star(x),x)}=\frac{\sqrt{21-8\sqrt{2}\sin{(x_1+x_2-1-\frac{\pi}{4})}}}{2}>0.$

所以在例 1.1 中, 关于反应函数的假设 (H5) 和 (H6) 也成立.

注2.2

由文献[20]和[21]中的稳定性定理可知, 若假设 (H1)-(H6) 成立, 则反应方程组 (1.2) 有唯一的正平衡解 $(u^\star (x),v^\star(x))$, 它是双曲型的全局渐近稳定解.

在上述假设下, 可以得到本文的主要结论如下

定理2.1 在假设 (H1)-(H6) 下, 存在一个足够小的正数 $\delta>0$, 当max$\{\mu,\nu\}\le\delta$ 时, 方程组 (1.1) 有唯一的正平衡解 $(\tilde{u}(x),\tilde{v}(x))$, 且该正平衡解关于非负非平凡初值 $(u_0(x),v_0(x))$ 是全局渐近稳定的. 同时, 当扩散系数 $(\mu,\nu)$ 趋近于 $(0,0)$ 时, 该正平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 收敛到相应的反应方程组 (1.2) 的正平衡解 $(u^\star (x),v^\star(x))$, 即

且在 $\bar\Omega$ 内是一致收敛的.

为了证明定理 2.1, 我们先在这一部分中讨论反应函数 $f(u,v,x)$ 和 $g(u,v,x)$ 的一些性质.

引理3.1 若 (H2), (H3) 和 (H5) 成立, 则 $\forall x\in\bar\Omega$, $f(\bar u(x),0,x)>0$ 且 $g(0,0,x)>0$.

证 由 (H5) 知, $u^\star(x)$, $v^\star(x)$ 满足: $u^\star(x)>0$, $v^\star(x)>0$,

$f(u^\star(x),v^\star(x),x)=0,\ g(u^\star(x),v^\star(x),x)=0$,

而由 (H2) 和 (H3) 可知, 对 $\forall x\in\bar\Omega$, $f$, $g$ 关于 $v$ 单调递减, 故有

另一方面, 对 $\forall x\in\bar\Omega$, 有$u^\star(x)\ge\bar u(x)>0$, 且当 $\forall u(x)>\bar u(x)$ 时, 有 $f_u(u,v,x)<0$, $g_u(u,v,x)<0.$所以有

因此, 引理 3.1 证毕.

引理3.2 若 (H1)-(H5) 成立, 则

(i) 存在唯一的连续可微函数 $\alpha(x)$, $\beta(x)$, 满足 $\forall x\in\bar\Omega, $

(ii) 对 $\forall x\in\bar\Omega$, 存在唯一的函数 $v_f=v_f(u,x),$ 使得

此外, 对 $\forall x\in\bar\Omega$, $v_f(u,x)$ 在 $u\in [\bar u(x)]$ 上关于 $u$ 单调递增, 且在$u\ge \bar u(x)$ 时关于 $u$ 单调递减.

(iii) 对 $\forall x\in\bar\Omega$, 存在唯一的函数$v_g=v_g(u,x), $ 使得

此外, $v_g(u,x)$ 关于 $u$ 单调递减.

证 (i) 对 $\forall x\in\bar\Omega$, 由引理 3.1 和 (H4) 可知, 有

根据零点存在性定理及 (H2) 和 (H3), 可知必定存在唯一的函数 $\alpha(x)$, $\beta(x)$, 满足: $\forall x\in\bar\Omega, $$\alpha(x)>\bar u(x),\ \beta(x)>0, $且$f(\alpha(x),0,x)=0,\ g(0,\beta(x),x)=0.$再根据 (H1) 和隐函数定理, 可得 $\alpha(x)>\bar u(x)$ 和$\beta(x)>0$ 是连续可微的.

(ii) 由 (H1) 和 (H2) 及隐函数定理可知, 从 $f(u,v,x)=0$ 可求解出唯一的函数 $v_f=v_f(u,x)$, 使得 $f(u,v_f(u,x),x)\equiv 0. $

再由 (i) 中的结论 $f(\alpha(x),0,x)=0$, 结合唯一性可知, $v_f(\alpha(x),x)=0.$

由隐函数求导法则可得

再由 (H2) 可知 $\frac{\partial{f}}{\partial{v}}<0$, 从而 $\frac{\partial{v_f}}{\partial{u}}$ 与 $\frac{\partial{f}}{\partial{u}}$ 同号, 即得 $v_f(u,x)$ 在 $u\in [\bar u(x)]$ 上关于 $u$ 单调递增, 且在 $u\ge \bar u(x)$ 时关于 $u$ 单调递减.

类似于对 (ii) 的证明, 可证得 (iii).

因此, 引理 3.2 证毕.

引理3.3 若 (H1)-(H6) 成立, 则对 $\forall x\in\bar\Omega$, 有

进一步可得, $f(\bar u(x),\beta(x),x)>0,\ g(\alpha(x),0,x)>0$.

证 构造辅助函数 $G(u,x)=v_f(u(x),x)-v_g(u(x),x)$. 由 (H5) 以及引理 3.2 中 $v_f(u(x),x)$ 和$v_g(u(x),x)$ 的定义可知, $\forall x\in\bar\Omega$,

所以 $G(u^\star(x),x)=0$.

而由 (H1) 和隐函数求导法则可知

由 (H2), (H3) 和 (H6) 可得

即 $G(u,x)$ 在 $(u^\star(x),v^\star(x))$ 的邻域内关于 $u$ 单调递减.因此, 存在一个正常数 $\epsilon>0$, 使得

根据 (H5) 可知 $u^\star(x)$是 $G(u(x),x)=0$ 的唯一解, 故 $G(u,x)$ 在 $u^\star(x)$ 左右两侧分别定号. 再由 $(3.1)$ 式可知

故引理 3.3 的第一部分证毕.

对 $u>0$, 由引理 3.3 的第一部分, 可得

再由 $f_v(u,v,x)<0$, 可得

由 (H2) 和 (H3) 可知$f(u,v,x)$ 在 $u\in[\bar u(x)]$ 内关于 $u$ 单调递增, 因此

类似可得 $g(\alpha(x),0,x)>0. $ 故引理 3.3 证毕.

首先, 利用文献[18]中的证明, 我们可以得到方程组 (1.1) 的边界状态的不稳定性.

引理4.1 在定理 1.1 的假设下,存在一个足够小的正数 $\delta_1>0$, 满足若$ \mu,\nu \le\delta_1$, 则 $(u,0)$ 和 $(0,v)$ 都是不稳定的.

接下来, 利用上下解方法, 我们讨论方程组 $(1.1)$ 的正平衡解的一致收敛性.

引理4.2 在定理 1.1 的假设下, 令$(\tilde{u}(x),\tilde{v}(x))$ 表示方程组 (1.1) 的任意一个正平衡解, 其中 $\tilde{u}(x)>\bar u(x)$$(\forall x\in\bar\Omega)$,则当 $(\mu,\nu)\rightarrow(0,0)$ 时, $(\tilde{u}(x),\tilde{v}(x))$ 在 $\bar\Omega$ 上一致收敛到 $(u^\star(x),v^\star(x))$.

证 令 $\underline{v_0}=0$, 它显然满足

利用 (H2)-(H4), 易知 $\tilde{u}(x)$ 和 $M$ 分别是以下边值问题的下解和上解

由上下解方法可知, 边值问题 $(4.2)$ 有一个解, 记作 $\bar u_0(x)$, 满足

利用上下解方法和 $(4.3)$ 式, 可得边值问题

有一个解, 记作 $\underline{ v_1}(x)$, 且它是 (4.1) 式的一个上解, 所以有

最后, 可得两个单调序列 $\{\bar u_k\}|_0^\infty$ 和$\{\underline{v_k}\}|_0^\infty$, 它们分别满足 $({k\ge 1})$

和

此外, 对 $\forall x\in\bar\Omega$, 有

和$ \tilde v(x)\ge\cdots\ge \underline{v_k}(x)\ge \underline{v_{k-1}}(x)\ge\cdots\ge\ \underline{v_1}(x)\ge \underline{v_0}(x). $

令 $\bar v_0(x)$ 是$ \left\{\begin{array} & \nu\Delta v+vg(0,v,x)=0,\\ \frac{\partial v}{\partial n}|_{\partial\Omega}=0 \end{array}\right. $ 的解. 类似地, 可得另外两个单调序列 $\{\bar v_k\}|_0^\infty$ 和 $\{\underline{u_k}\}|_1^\infty$, 它们分别满足 $({k\ge 1})$

和

此外, 对 $\forall x\in\bar\Omega$, 有

和$ \tilde v(x)\le\cdots\le\bar v_k(x)\le\bar v_{k-1}(x)\le\cdots\le\bar v_1(x)\le\bar v_0(x)\le M. $

因此, 有

另一方面, 由零点存在性定理, 我们可以构造出四个单调序列 $\{\bar U_k(x)\}|_0^\infty$, $\{\bar V_k(x)\}|_0^\infty$, $\{ \underline{U_k}(x)\}|_1^\infty$ 和 $\{ \underline{V_k}(x)\}|_1^\infty$, 它们满足:$(1)\ \bar U_0(x)=\alpha(x)$; $(2)\ \bar V_0(x)=\beta(x)$; $(3)\ g(\bar U_{k-1},\underline{V_k},x)=0$; $(4)\ f(\bar U_{k},\underline{V_k},x)=0$;$(5)\ f(\underline{U_k},\bar V_{k-1},x)=0$; $(6)\ g(\underline{U_{k}},\bar V_k,x)=0\ (k\ge 1).$

此外, 对 $\forall x\in\bar\Omega$, 由引理 3.3 和(H2)-(H4), 得

由序列的一致收敛定理可得, 在$x\in\bar\Omega$上,

同时, 容易看出, 当 $(\mu,\nu)\rightarrow(0,0)$ 时, 有 $(\bar u_k,\underline{v_k})\rightarrow(\bar U_k,\underline{V_k})$ 和 $(\underline{u_k},\bar v_k)\rightarrow(\underline{U_k},\bar V_k), $且在 $\bar\Omega$ 内均是一致收敛的. 所以由$(4.6)$-$(4.7)$, 可得当 $(\mu,\nu)\rightarrow(0,0)$ 时, $(\tilde{u}(x),\tilde{v}(x))$ 在 $\bar\Omega$ 上一致收敛到 $(u^\star(x),v^\star(x))$.

因此, 引理 4.2 证毕.

定义4.1 令 $(u(x),v(x))$ 为方程组 (1.1) 的平衡解, 令 $(\xi(x,t),\eta(x,t))$ 为方程组 (1.1) 在 $(u(x), v(x))$ 处线性化后所得的方程组的解. 当 $t\rightarrow \infty$ 时, 若 $(\xi(x,t),\eta(x,t))$ 指数衰减到零平衡解, 则称 $(u(x),v(x))$ 是线性稳定的^[3].

由文献[3]中的稳定性定理, 有下述引理

引理4.3 若 $(u(x),v(x))$ 是方程组 (1.1) 的一个线性稳定的解, 则 $(u(x),v(x))$ 必定是渐近稳定的.

因此, 由引理 4.3, 只需证明方程组 $(1.1)$ 的正平衡解 $(\tilde{u}(x),\tilde{v}(x))\ (\tilde{u}(x)>\bar u(x), \forall x\in\bar\Omega)$是线性稳定的.

令 $\xi(x,t)=u(x,t)-\tilde{u}(x)$, $\eta(x,t)=v(x,t)-\tilde{v}(x)$, 其中 $u(x,t)$, $v(x,t)$ 为方程组 $(1.1)$ 的解.

将 $u(x,t)=\xi(x,t)+\tilde{u}(x)$, $v(x,t)=\eta(x,t)+\tilde{v}(x)$ 代入 $(1.1)$ 式, 整理可得正平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 处的线性化方程组

其中 $\xi(x,t)$, $\eta(x,t)$ 为线性化方程组 $(4.8)$ 的解.

为考虑该线性化方程组 $(4.8)$ 的指数衰减性, 令 $\xi(x,t)=\phi(x,t){\rm e}^{\lambda t}$, $\eta(x,t)=\psi(x,t){\rm e}^{\lambda t}$, 整理可得如下线性椭圆型偏微分方程组的特征问题

由假设 (H2), (H3) 和 (H6) 可知方程组 $(1.1)$ 为分段单调系统, 根据线性算子的 Krein-Rutman 定理, 借助椭圆方程的极大值原理, 运用反证法, 假设当扩散系数足够小时, 正平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 都不线性稳定. 由此可知线性椭圆方程组特征问题的特征值是非负的, 在反应函数逐段单调的区间上利用参考文献[18]中的方法和结论可得出矛盾, 从而可以得到如下引理

引理4.4 在定理 1.1 的假设下,存在一个足够小的正数 $\delta_2>0$, 满足若$\mu,\nu\le\delta_2$, 则方程组 (1.1) 的任一正平衡解 $(\tilde{u}(x),\tilde{v}(x))\ (\tilde{u}(x)>\bar u(x), \forall x\in\bar\Omega)$ 是线性稳定的.

最后来证明定理 2.1.

证 考虑如下椭圆型方程组

由 (H2) 和 (H3) 可知, 方程组 $(4.10)$ 的反应函数分段单调, 利用上下解方法容易得到该方程组在 $u(x)>\bar u(x)$ 时有唯一正解, 即反应扩散方程组 $(1.1)$ 对 $u(x)>\bar u(x)$ 有唯一的正平衡解 $(\tilde{u}(x),\tilde{v}(x))$.

由引理 4.1, 引理 4.3 和引理 4.4 可知, 存在一个足够小的正数$\delta=\min\{\delta_1,\delta_2\}>0, $ 如果 $\mu,\nu\le\delta$, 则方程组 $(1.1)$ 的唯一的正平衡解 $(\tilde{u}(x),\tilde{v}(x))$$(\tilde{u}(x)>\bar u(x), \forall x\in\bar\Omega)$ 是渐近稳定的.

又由引理 4.2 可知, 当 $(\mu,\nu)\rightarrow (0,0)$ 时, 方程组 $(1.1)$ 的唯一的渐近稳定的正平衡解$(\tilde{u}(x),\tilde{v}(x))$$(\tilde{u}(x)>\bar u(x), \forall x\in\bar\Omega)$ 一致收敛到 $(u^\star(x),v^\star(x))$.

因此, 定理 2.1 证毕.

在第 2 节中已经证明, 例 1.1 中的反应函数满足假设(H1)-(H6). 下面通过此例的数值解验证定理 2.1 结论的正确性.

反应扩散方程组 $(1.3)$ 对应的反应方程组为

其中$x=(x_1,x_2)$.

方程组 (5.1) 的正平衡解 $(u^\star(x),v^\star(x))$ 满足

解得

为保证 $u^\star(x)$ 和 $v^\star(x)$ 的非负性, 考虑到三角函数的周期性, 这里取 $\Omega=[\frac{1}{2}+\frac{\pi}{76},\frac{1}{2}+\frac{13\pi}{24}]^2$.

由定理 2.1 可知, 当 $\mu$ 和 $\nu$ 都足够小时, 反应扩散方程组 $(1.3)$ 的唯一正平衡解 $(\tilde{u}(x),\tilde{v}(x))$ 对非负非平凡初值 $(u_0(x),v_0(x))$ 是全局渐近稳定的, 且当 $(\mu,\nu)\rightarrow(0,0)$ 时, $(\tilde{u}(x),\tilde{v}(x))$ 在 $\Omega$ 上一致收敛到反应方程组 $(4.1)$ 的正平衡解 $(u^\star(x),v^\star(x))$.

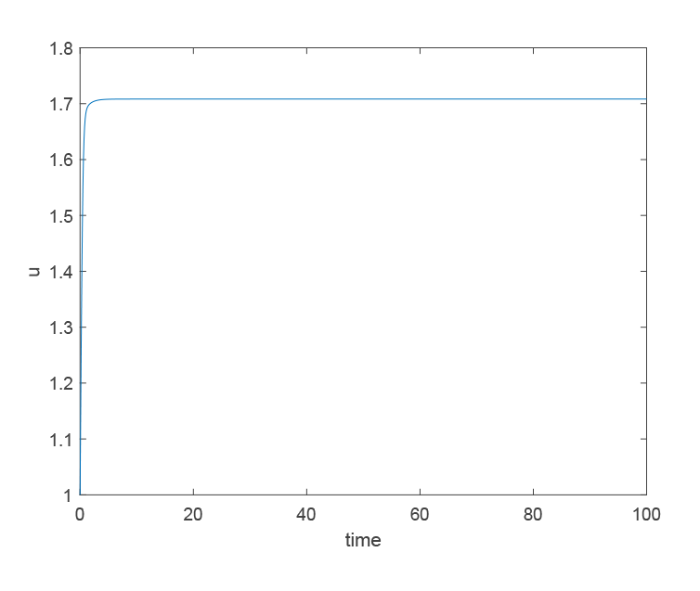
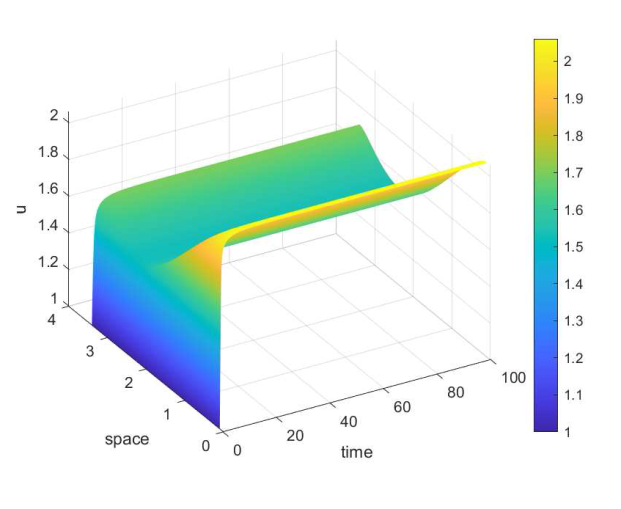
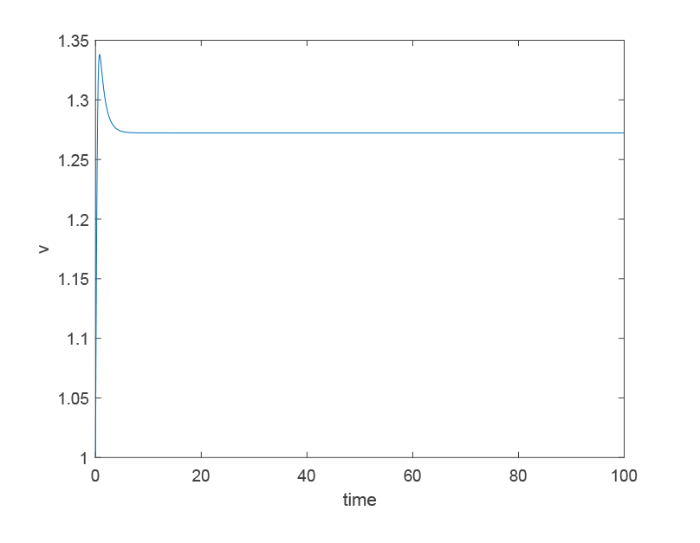
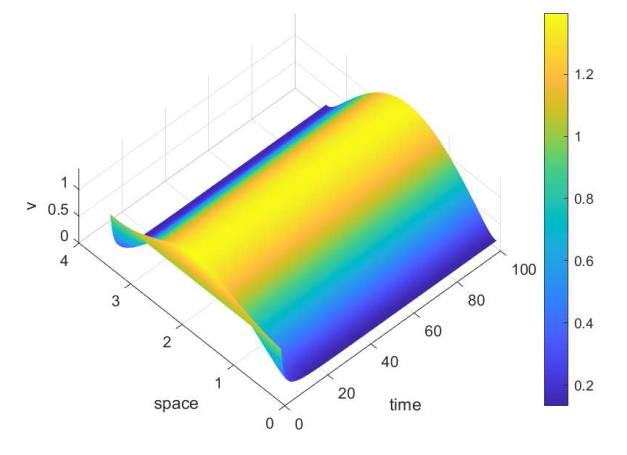
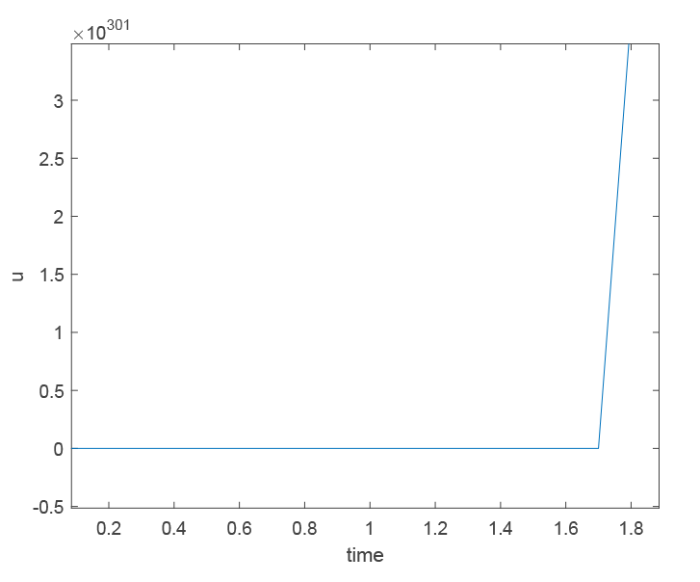
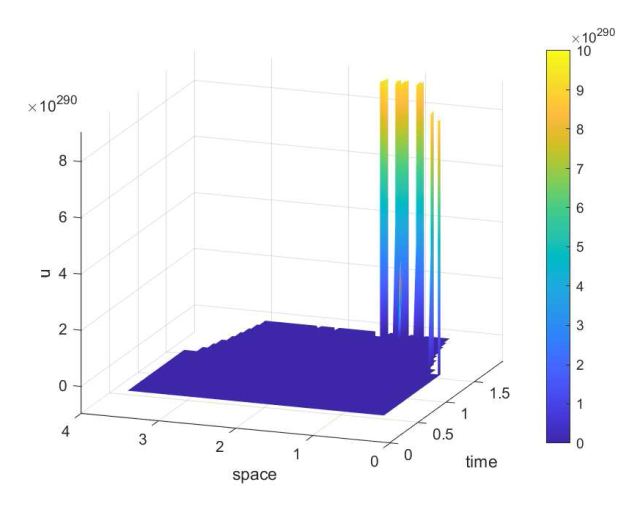
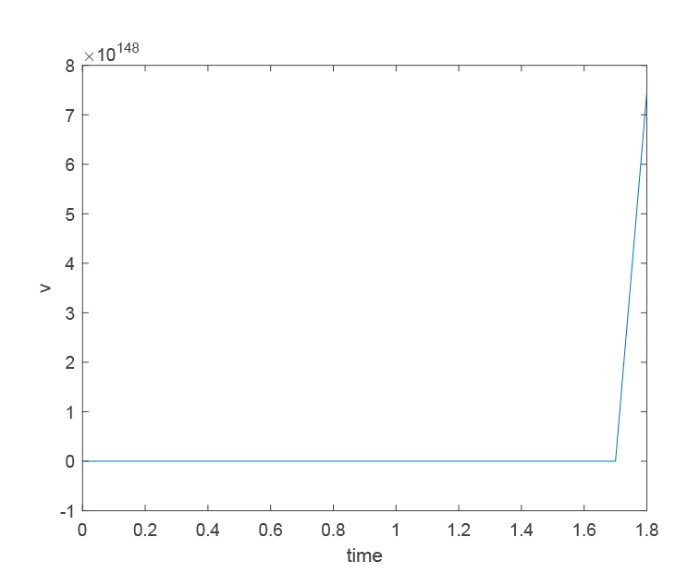
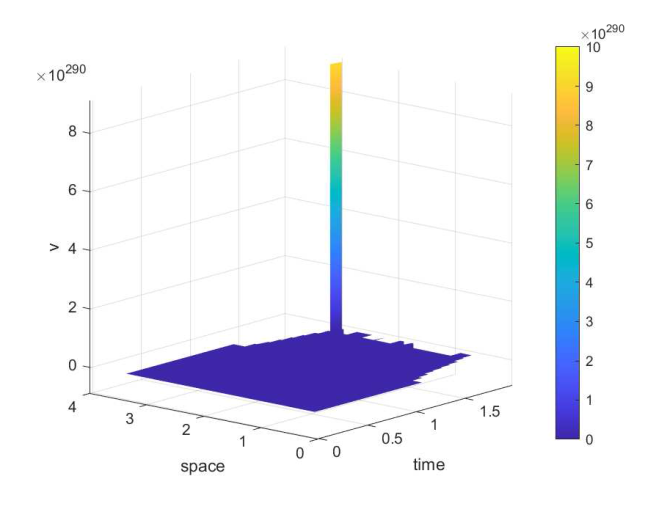
取 $\mu=0.002$, $\nu=0.001$. 图 1 和图 3 分别是将 $x=(x_1,x_2)$ 固定于定点 $(1.378,1)$ 处时, $u$ 和 $v$ 关于时间 $t$ 的变化趋势; 而图 2 和图 4 分别是将 $x_2$ 固定于定值 $1$ 处而 $x_1$ 变动时, $u$ 和 $v$ 关于时间 $t$ 的变化趋势.

但是, 当扩散系数 $\mu$ 或 $\nu$ 不足够小时, 反应扩散方程组 $(1.1)$ 的正平衡解可能不收敛到相应的反应方程组 $(1.2)$ 的正平衡解. 例如, 图 5-8 展示了$\mu=0.09$, $\nu=0.08$ 时 $u$ 和 $v$ 关于时间 t 的变化趋势, 可以很明显看出它们都是发散的. 由此可以看出扩散系数对反应扩散方程组 $(1.1)$ 正平衡解的影响.

本文考虑了两种群竞争的空间非均匀反应扩散方程组构成的非自治模型, 将种群反应函数推广到更一般的非单调形式, 在合理性假设下证明了反应扩散方程组唯一正平衡解的存在性及其全局渐近稳定性, 由此得到了小扩散系数下, 非单调反应函数的空间非均匀反应扩散方程组的正平衡解全局收敛到相应反应方程组的正平衡解. 因此, 可以看出较小的扩散系数不影响种群的最终分布和竞争关系, 而且它们是由种群的反应方程组所决定的. 从种群可持续发展的角度看, 种群适当范围的扩散最终不会对生态平衡造成影响. 基于此, 我们可以构建预测具有竞争关系的两种群的竞争发展轨迹的理论, 将之用于研究物种的扩散或小范围入侵, 以及市场竞争等实际问题, 为生态学和经济学等相关领域的研究提供方法借鉴和理论依据.

对于空间非均匀反应扩散方程组, 后续还有许多工作值得进一步探索, 例如三种及以上种群竞争问题; 此外, 在研究中还可以加入时滞对反应函数的影响, 使相关理论更加完善.