由于在生物学、生态学、工程技术等方面的重要应用, 带 Markov 切换的随机泛函微分方程 (SFDEwMS) 越来越受到研究者的关注, 特别是它的解的存在唯一性和稳定性问题更是关注的焦点. 一般来说, 这类方程具有如下形式

其中, $ x_t=\{x(t+\theta):-\tau\leq\theta\leq 0\}, \tau>0 $ 是常数. 这类方程的解的未来状态依赖于它在区间 $ [t-\tau, t] $ 上的状态. 方程 (1.1)的解的存在唯一性和稳定性问题已有较为深入的研究, 并出现了很多好的成果^[1-9], 但方程 (1.1) 不是 SFDEwMS 的唯一形式, 带 Markov 切换的随机比例泛函微分方程 (PSFDEwMS) 就具有另外的形式

其中, $ x_t=\{x(\theta t):\underline{\theta}\leq\theta\leq 1\}, 0<\underline{\theta}<1 $ 是常数. 这类方程的解的未来状态依赖于它在区间 $ [\underline{\theta}t, t] $ 上的状态. 和方程 (1.1) 不同, 目前对方程 (1.2) 的解的存在唯一性和稳定性的研究成果甚少^[10]. 基于这一原因, 本文考虑方程 (1.2), 着重研究它的全局解的存在唯一性和稳定性. Lyapunov 函数方法是研究这类问题的重要方法, 但这一方法一般是针对标量 Lyapunov 函数 (SLF) 而言, SLF 方法中给出的微分算子不等式往往过于保守. 相比之下, 向量 Lyapunov 函数 (VLF) 方法给出的各个分量满足的条件更加宽泛. 关于 SFDEwMS 的稳定性问题, 我们不仅关心它是否稳定, 而且关心方程的解以何种方式衰减至平衡态, 衰减的速率如何? 稳定性的种类可由常见的指数稳定、多项式稳定、对数稳定推广到 $ \lambda $ 稳定^[11]. 另外, SFDEwMS 不免受到现实生活中的各种干扰, 脉冲就是其中之一, 它是自然界普遍存在的现象, 其影响不可忽视. 因此, 本文把脉冲效应引入 PSFDEwMS, 得到以下形式的方程

并着重研究方程 (1.3) 的全局解的存在唯一性和稳定性.和文献[10]相比, 本文的创新之处在于: 1) 文献[10]中采用的是 SLF 方法, 而本文采用 VLF 方法, 本文的Lyapunov 函数满足的条件更弱; 2) 在研究方程 (1.2) 和 (1.3) 的稳定性时, 把文献[10]中的方程的稳定性种类由指数稳定和多项式稳定推广到 $ \lambda $ 稳定, 涵盖了文献[10]中的结果; 3) 本文第 4 节在模型和方程 (1.2) 完全相同的前提下引入脉冲效应, 得到方程 (1.3), 使系统更加复杂和完备, 给出了方程 (1.3) 的全局解的存在唯一性的判定定理, 并且在保留甚至弱化方程 (1.2) 的全局解的 $ \lambda $ 稳定性条件的基础上充分考虑脉冲的影响, 证明了在脉冲点满足一定条件时, 方程 (1.3) 的全局解仍然是矩 $ \lambda $ 稳定和几乎必然 $ \lambda $ 稳定的, 从而有效地补充了第 3 节的结果, 推广了文献[10]中的结果; 4) 脉冲可以是频繁发生的, 也可以是发生较为稀少的, 这里频繁的概念可用相邻脉冲点之间的距离的上确界的大小来刻画, 不同的 $ \lambda $ 类函数可使方程的全局解衰减的速率不同, 针对脉冲的这两种不同特点以及 $ \lambda $ 类函数衰减速率的不同, 定理 4.2 和定理 4.3 给出了方程 (1.3) 的全局解的矩 $ \lambda $ 稳定的判定条件; 五、由于脉冲的干扰, 方程 (1.3) 的全局解 $ x(t) $ 在 $ [0, +\infty) $ 上未必是连续的, 这使得文中的 $ U_{i0}(x(t), t) $ 在 $ [0, +\infty) $ 上也未必是连续的, 因而在证明 $ x(t), t\geq t_0 $ 几乎必然 $ \lambda $ 稳定时不能简单套用定理 3.2 中的半鞅收敛定理, 定理 4.4 采用 BDG 不等式、Chebyshev 不等式和 Borel-Cantelli 引理克服了这一困难, 在适当的条件下证明了 $ x(t), t\geq t_0 $ 的几乎必然 $ \lambda $ 稳定性.

设 $ (\Omega, \mathcal{F}, \{\mathcal{F}_t\}_{t\geq 0}, P) $ 是一个完备的带流的概率空间且满足通常条件, $ B(t) $ 是定义在此空间上的一个 $ d $ 维布朗运动, 对 $ x, y\in \mathbb{R}^{n_1} $, 用 $ |x| $ 表示欧氏范数, 用 $ x^Ty $ 表示欧氏空间 $ \mathbb{R}^{n_1} $ 中两个向量的内积. $ A^T $ 表示矩阵 $ A $ 的转置, $ |A| $ 表示 $ \sqrt{{\rm Tr}(AA^T)} $. $ \underline{\theta} $ 是常数, 且 $ 0<\underline{\theta}<1 $. $ C([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $ 表示所有定义在 $ [\underline{\theta}, 1] $ 上的取值于 $ \mathbb{R}^{n_1} $ 中的所有连续函数构成的族, $ PC([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $ 表示所有定义在 $ [\underline{\theta}, 1] $ 上的取值于 $ \mathbb{R}^{n_1} $ 中的所有右连续有左极限的函数构成的族, 对 $ \varphi\in C([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $, 或者 $ \varphi\in PC([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $, $ \|\varphi\|:=\sup\limits_{\underline{\theta}\leq t\leq 1}|\varphi(t)| $. 设 $ r(t) $ 是一个连续时间的取值于 $ S=\{1, 2, \cdots, N\} $ 中的马氏链, 它的生成元 $ \Gamma=(\gamma_{ij})_{N\times N} $ 满足条件

其中, $ \triangle>0, \gamma_{ij} $ 是从 $ i $ 到 $ j $ 的转移率.当 $ i\neq j $ 时, $ \gamma_{ij}\geq 0, \gamma_{ii}=-\sum\limits_{j\neq i}\gamma_{ij} $. $ r(t) $ 的样本轨道是一个右连续的阶梯函数, 在 $ [0, +\infty) $ 的任何有限子区间上只有有限多个跳跃点.假设马氏链 $ r(t) $ 和 布朗运动 $ B(t) $ 相互独立.用 $ C^{1, 2}(\mathbb{R}^{n_1}\times [0, +\infty)\times S; [0, +\infty)) $ 表示所有定义在 $ \mathbb{R}^{n_1}\times [0, +\infty)\times S $ 上的所有非负连续函数 $ V(x, t, i_1) $ 构成的族, 且对任意 $ i_1\in S $, $ V(x, t, i_1) $ 关于 $ t $ 一阶连续可微, 关于 $ x $ 二阶连续可微. 用 $ C^{1, 2}(\mathbb{R}^{n_1}\times [0, +\infty); [0, +\infty)) $ 表示所有定义在 $ \mathbb{R}^{n_1}\times [0, +\infty) $ 上的所有非负连续函数 $ U(x, t) $ 构成的族, 且 $ U(x, t) $ 关于 $ t $ 一阶连续可微, 关于 $ x $ 二阶连续可微.

定义2.1^[11] 如果函数 $ \lambda:[0, +\infty)\rightarrow (0, +\infty) $ 满足以下三个条件

(1) $ \lambda(\cdot) $ 在 $ [0, +\infty) $ 上单调递增且可微;

(2) $ \lambda(0)=1, \quad \lim\limits_{t\rightarrow+\infty}\lambda(t)=+\infty, \quad J:=\sup\limits_{t>0}\frac{\lambda'(t)}{\lambda(t)}<+\infty $;

(3)对任意的 $ t\geq 0, \quad s\geq 0 $, 有 $ \lambda(t+s)\leq \lambda(t)\lambda(s) $.

则称 $ \lambda(\cdot) $ 为 $ \lambda $ 类函数.

在以上定义中, 当 $ t<0 $ 时, 补充定义 $ \lambda(t):=1 $, 则对任意的 $ s, t\geq 0 $ 都有 $ \lambda(t)\leq\lambda(t-s)\lambda(s) $.

在这一节, 考虑方程 (1.2). 对任意的 $ V_i\in C^{1, 2}(\mathbb{R}^{n_1}\times [0, +\infty)\times S; [0, +\infty)) $, $ 1\leq i\leq m $, $ \varphi\in C([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $, 以及 $ i_1\in S $, 定义算子 $ L $ 如下

其中

且以下的关于方程 (1.2) 的 Itô 公式成立

这里, $ i=1, 2, \cdots, m $.对于给定的函数 $ \Lambda:[0, +\infty)\rightarrow [0, +\infty), D^+\Lambda(t):=\limsup\limits_{h\rightarrow 0^+}\frac{\Lambda(t+h)-\Lambda(t)}{h} $ 是函数 $ \Lambda(\cdot) $ 的右上 Dini 导数. 先做如下假设

(A1) (局部 Lipschitz 条件) 对任意的 $ R>0, \varphi, \varphi'\in C([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $ 且 $ \|\varphi\|\vee\|\varphi'\| \leq R $, 存在正的常数 $ C_R $, 使得

(A2) 存在函数 $ V_i\in C^{1, 2}(\mathbb{R}^{n_1}\times [0, +\infty)\times S; [0, +\infty)) $, $ U_{i0}, U_{ik}\in C^{1, 2}(\mathbb{R}^{n_1}\times [0, +\infty); $$[0,+\infty)) $, $ [\underline{\theta}, 1] $ 上的概率测度 $ \nu_k $, 非负常数 $ a_{i0}, a_{ik}, b_{kl}, w_{ijk} $, 正的常数 $ u, u' $ 及常数 $ \alpha_{kl} $, 满足 $ \frac{1}{u}+\frac{1}{u'}=1, $$ 0\leq \alpha_{kl}\leq 1 $, $ l=1, 2, \cdots, l_k. k=1, 2, \cdots, M. i=1, 2, \cdots, m. $ 使得以下条件成立

假设 (A1) 成立, 和文献[12]中同样的方法或直接由文献[10]可知, 方程 (1.2) 存在唯一的局部解 $ x(t) $, $ t\in [t_0, \rho] $. 其中, $ \rho $ 是爆破时. 下面给出方程(1.2) 存在唯一全局解的定理.

定理3.1 假设 (A1)-(A2) 成立, 且

则方程 (1.2) 存在唯一全局解.

证 设 $ x(t), t\in [t_0, \rho) $ 是方程 (1.2) 的唯一的局部解, 定义 $ \sigma_a:=\inf\{t\geq t_0:|x(t)|\geq a\} $, 利用 Itô 公式并取期望, 当 $ t\geq t_0 $ 时, 有

注意到

把 (3.6) 式代入 (3.5) 式, 得

其中, $ N_k=\max\limits_{1\leq i\leq m}\bigg[-(a_{ik}+w_{iik})+\frac{1}{u'}\sum\limits_{j=1}^m w_{ijk}+\sum\limits_{l=1}^{l_k}b_{kl}\alpha_{kl}+\sum\limits_{l=1}^{l_k}b_{kl}(1-\alpha_{kl})\frac{1}{\underline{\theta}}\bigg] $.所以

注意到

把 (3.9) 式代入 (3.8) 式, 并用 (3.2), (3.4) 式, 得

其中, $ c_0=\sum\limits_{i=1}^m EV_i(x(t_0), t_0, r(t_0))+\sum\limits_{i=1}^m \sum\limits_{k=1}^M \sum\limits_{l=1}^{l_k} b_{kl}(1-\alpha_{kl})\frac{1}{\underline{\theta}}\int_{\underline{\theta}t_0}^{t_0}EU_{ik}(\xi(s), s){\rm d}s. $

接下来类似文献[10,定理 3.1] 的证明方法可得 $ \rho>t, $ a.s. $ t $ 的任意性证明了 $ \rho=+\infty $ a.s. 故方程 (1.2) 存在唯一的全局解$ x(t), t\in [t_0, +\infty). $

注3.1 在定理 3.1 中, 如果 $ m>1 $, 那么 (3.3) 式的 $ m $ 个不等式条件中每一个都比文献[10,(3.5) 式] 弱. 如果令 $ m=1 $, 则假设 (A2) 变为文献 [假设 (H2')], 且条件 (3.4) 式变为文献[10]中的条件 (3.6) 式. 所以定理 3.1 的条件弱于文献[10,定理 3.1] 的条件, 本文的定理 3.1 涵盖了文献[10,定理 3.1].

做如下假设

(A3) 让假设 (A2) 成立, 但 (3.3) 式被以下的 (3.11) 式取代.

其中, $ \overline{\lambda}(\cdot, \cdot):[\underline{\theta}, 1]\times [0, +\infty)\rightarrow[0, +\infty) $ 满足 $ \inf\limits_{0\leq s<+\infty}\overline{\lambda}(\theta, s)\geq \beta(1-\theta) $, $ \beta $ 是常数,且 $ 0<\beta<\frac{a_{i1}}{J}, 1\leq i\leq m. $

定理3.2 假设 (A1) 成立, 且 $ a_{i0}=0, i=1, 2, \cdots, m $,

以下两个条件有且只有一个成立

1) 假设 (A2) 成立, $ \lambda(\cdot) $ 在 $ [0, +\infty) $ 上是凹函数;

2) 假设 (A3) 成立.

则: 1) 方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 几乎必然 $ \lambda $ 稳定;

2) 方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

证 第一部分 假设条件 1) 成立.

1) 定义 $ F_1(s):=\frac{\lambda(s)}{\underline{\theta}}-\lambda(\frac{s}{\underline{\theta}}), s\geq 0 $, 则 $ F_1(0)>0. $由于 $ \lambda(\cdot) $ 在 $ [0, +\infty) $ 上是凹函数, 所以 $ F_1'(s)=\frac{\lambda'(s)}{\underline{\theta}}-\frac{\lambda'(\frac{s}{\underline{\theta}})}{\underline{\theta}}\geq 0, s\geq0. $ 故有$ \frac{\lambda(s)}{\underline{\theta}}\geq\lambda(\frac{s}{\underline{\theta}}), s\geq 0. $ 取 $ \varepsilon>0 $, 定义

利用 Itô 公式, 当 $ t>t_0 $ 时, 有

所以

由 (3.12) 式可知, 当正数 $ \varepsilon $ 充分小时

所以

其中

根据半鞅收敛定理^[13]

即方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 几乎必然 $ \lambda $ 稳定;

2) 在 (3.17) 式两边取期望, 并注意到 $ \sum\limits_{i=1}^m M_i(t) $ 是局部鞅, 得到

即方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

第二部分 假设条件 2) 成立.

1) 取正数 $ \varepsilon' $ 充分小, 使得 $ 0<\varepsilon'\leq \beta $ 且 $ \varepsilon'=\frac{1}{p}, \quad p\in\mathbb{Z}^+ $ 且

利用 Itô 公式, 当 $ t>t_0 $ 时, 有

而

根据 $ \lambda $ 类函数的性质, 对任意的 $ s_1\geq 0, \quad \lambda(s_1)=\lambda(p\cdot\frac{s_1}{p})\leq\lambda^p(\frac{s_1}{p}) $,即 $ \lambda^{\varepsilon'}(s_1)\leq\lambda(\varepsilon's_1) $, 所以

把上式代入 (3.21) 式, 得到

类似第一部分的证明

其中

根据半鞅收敛定理^[13]

即方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 几乎必然 $ \lambda $ 稳定.

2) 在 (3.24) 式两边取期望, 并注意到 $ \sum\limits_{i=1}^m \overline{M}_i(t) $ 是局部鞅, 得到

即方程 (1.2) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

注3.2 在假设 (A2) 中, 如果 $ m>1 $, 那么 (3.3) 式的 $ m $ 个不等式条件中每一个都比文献[10,(3.5) 式] 弱. 令 $ m=1 $, 则假设 (A2) 变为文献 [假设 (H2')], (3.12) 式变为文献[10]中的

如果令 $ \lambda(t)=1+t, t\geq 0 $. 则 $ \lambda(t) $ 在 $ [0, +\infty) $ 上是凹函数, 定理 3.2 的第 1) 个结论涵盖了文献[10,定理 3.5]. 如果令 $ \lambda(t)=e^t, t\geq 0 $, 则 $ J=1 $, 在假设 (A3) 中, 如果 $ m>1 $, 那么 (3.11) 式的 $ m $ 个不等式条件中每一个都比文献[10,(3.4) 式] 弱. 如果 $ m=1 $, 则假设 (A3) 变为文献[假设 (H2)], 定理 3.2 的第 1) 个结论涵盖了文献[10]的定理 3.2 中 (iii) 的 (3.10) 式, 定理 3.2 的第 2) 个结论涵盖了文献[10]的定理 3.2 中 (iii) 的 (3.9) 式.

在这一节, 考虑方程 (1.3). 其中, $ \{t_k\} $ 是脉冲序列, $ t_0<t_1<t_2<\cdots<t_k<\cdots $ 且 $ \lim\limits_{k\rightarrow+\infty}t_k=+\infty $. $ I_k:\mathbb{R}^{n_1}\times S\rightarrow \mathbb{R}^{n_1}, k\in\mathbb{Z}^+ $.

先做如下假设

(A1') (局部 Lipschitz 条件) 对任意 $ R>0, \quad \varphi, \varphi'\in PC([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $ 且 $ \|\varphi\|\vee\|\varphi'\| \leq R $, 存在正常数 $ C_R $, 使得

算子 $ L $ 依第 3 节中定义, 但 $ \varphi $ 的范围改为 $ PC([\underline{\theta}, 1]; \mathbb{R}^{n_1}) $.

首先给出方程 (1.3) 的全局解的存在唯一性定理.

定理4.1 假设 (A1')、(A2) 成立, (3.4) 式成立, 且存在正常数 $ \underline{K}_k, k\in\mathbb{Z}^+ $, 使得

则方程 (1.3) 存在唯一的全局解 $ x(t), t\geq t_0 $, 且 $ x(t) $ 在 $ t\neq t_k $ 处连续, 在 $ t=t_k $ 处右连续有左极限, $ k\in \mathbb{Z}^+ $.

证 考虑以下方程

类似定理 3.1 可证明, 方程 (4.2) 有唯一的全局解 $ y(t), t\geq t_0 $, 所以, 当 $ t\in[t_0, t_1) $ 时, $ x(t)=y(t) $. a.s. 而 $ x(t_1)=I_1(x(t_1^-), r(t_1^-)) $, 且 $ |x(t_1)|\leq \underline{K}_1 |x(t_1^-)|<+\infty, $ a.s.再考虑以下方程

这里, $ z_{t_1}=x_{t_1} $ 指对任意的 $ \theta\in[\underline{\theta}, 1] $, 有$ z(\theta t_1)=x(\theta t_1) $.

类似定理 3.1 的证明过程, 方程 (4.3) 有唯一的全局解 $ z(t), t\geq t_1 $.

当 $ t\in [t_1, t_2) $ 时, $ x(t)=z(t) $a.s.. 而 $ x(t_2)=I_2(x(t_2^-), r(t_2^-)) $, 且 $ |x(t_2)|\leq \underline{K}_2 |x(t_2^-)|<+\infty, $ a.s..重复以上过程得到方程 (1.3) 的唯一的全局解 $ x(t), t\geq t_0, $ 且 $ x(t) $ 在 $ t\neq t_k $ 处连续, 在 $ t=t_k $ 处右连续有左极限, $ k\in \mathbb{Z}^+ $.

定义

这里, $ \inf\phi=+\infty $. 假设 $ \alpha^* $ 是常数, 且$ 0\leq\alpha_\lambda<\alpha^*<+\infty $.做如下假设

(A4) 令假设 (A2) 成立, 但 (3.3) 式被以下的 (4.4) 式取代

记

接下来给出方程 (1.3) 的全局解的矩 $ \lambda $ 稳定的判定定理

定理4.2 假设 (A1')、(A4) 成立, $ a_{i0}=0, \quad 1\leq i\leq m $ 且 (3.4)、(4.1) 式以及以下两个条件满足

则方程 (1.3) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

证 易见方程 (1.3) 有唯一全局解 $ x(t), t\geq t_0 $.

记 $ \varepsilon_1=\alpha^*, \varepsilon_2=\min\limits_{1\leq i\leq m}\frac{1}{Jr}[(a_{i1}+w_{ii1})-\frac{r}{u'}\sum\limits_{k=1}^M\sum\limits_{j=1}^m w_{ijk}]. $

取 $ \varepsilon^*\in(0, \varepsilon_1\wedge \varepsilon_2) $, $ n\in\mathbb{Z}^+\bigcup\{0\} $, 对 $ \lambda^{\varepsilon^*}(t)V_i (x(t), t, r(t)) $ 用 Itô 公式, 当 $ t\in [t_n, t_{n+1}) $ 时,

而

把 (4.9) 式代入 (4.8) 式, 并利用条件 1), 得

定义 $ Z(t):=\sum\limits_{i=1}^m\lambda^{\varepsilon^*}(t)EU_{i0}(x(t), t) $, 则

在 (4.11) 式中令 $ n=0 $, 得到当 $ t_0\leq t<t_1 $ 时, $ Z(t)\leq A+B\int_{t_0}^tZ(s){\rm d}s. $ 其中

利用 Gronwall 不等式, 当 $ t_0\leq t<t_1 $ 时

由条件 2)

所以

所以, $ Z(t_1)\leq \overline{q}Z(t_1^-) $, 在 (4.11) 式中令 $ n=1 $, 得到当 $ t_1\leq t<t_2 $ 时,

利用 Gronwall 不等式, 当 $ t_1\leq t<t_2 $ 时

多次重复以上过程, 得到

即方程 (1.3) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

注4.1 在定理 4.2 中, 令 $ \lambda(t)={\rm e}^t, \quad t\geq 0. $ 则 $ \alpha_\lambda=0. $ 令$ m=1 $, 则 (4.4) 式变为

取正数 $ \alpha^* $ 充分小时, 该条件弱于文献[10,(3.4) 式], 另外, 本文的 (3.4) 式变为

该条件弱于文献[10,定理 3.2] 的条件

因此, 如果没有脉冲的影响, 在定理 4.2 的条件下, 方程 (1.3) 的全局解未必是矩 $ \lambda $ 稳定的, 但无论稳定与否, 在有脉冲的影响且满足定理 4.2 的条件时, 方程 (1.3) 的全局解一定是矩 $ \lambda $ 稳定的. 因此, 在定理 4.2 的条件下, 脉冲可使不稳定的系统变为稳定的.

引理4.1 设 $ \zeta_i $ 是常数, 且 $ \zeta_i\geq 1, 1\leq i\leq m $, 且以下条件同时成立

1) $ -(a_{i1}+w_{ii1})+\sum\limits_{k=1}^M\sum\limits_{j=1}^m w_{ijk}r\zeta_i^{-1}\zeta_j+\sum\limits_{k=1}^M\sum\limits_{l=1}^{l_k}b_{kl}r<0, \quad 1\leq i\leq m; $

2) $ \lim\limits_{t\rightarrow +\infty}\frac{\lambda(\underline{\theta}t-t_0)}{\lambda(t-t_0)}=b $, 且 $ 0<b<1. $

则存在常数 $ \delta^*>0 $, 当 $ 0<\delta<\delta^* $ 时

证 当 $ t<0 $ 时, 补充定义 $ \lambda(t):=1 $.记

因为 $ G(t_0)=1, \lim\limits_{t\rightarrow+\infty}G(t)=b, 0<b<1, $且对任意的 $ t\geq t_0, $ 都有 $ G(t)>0 $, $ G(t) $ 在 $ [t_0, +\infty) $ 上连续, 所以 $ \inf\limits_{t_0\leq t<+\infty}G(t)>0. $ 另一方面

所以, 存在 $ \delta_i\in (0, -\frac{B_{1i}+B_2}{uJ}) $, 当 $ 0<\delta\leq \delta_i $ 时

即$ \frac{\lambda^{u\delta}(\underline{\theta}t-t_0)}{\lambda^{u\delta}(t-t_0)}>\frac{B_2}{-(u\delta J +B_{1i})}. $

故有 (4.17) 式成立, 取 $ \delta^*=\min\limits_{1\leq i\leq m}\{\delta_i\} $ 即可.

定理4.3 假设 (A1')、(A2) 和引理 4.1 的条件成立, $ a_{i0}=0, 1\leq i\leq m. $(3.4)、(4.1)、(4.6) 式以及下面的条件成立

其中, $ \delta_* $ 是常数, 且 $ 0<\delta_*<\delta^* $, $ \delta^* $ 由引理 4.1 中定义.则方程 (1.3) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

证 易见在本定理的条件下, 方程 (1.3) 存在唯一的全局解 $ x(t), t\geq t_0 $.

记 $ \overline{C}=\max\limits_{1\leq i\leq m}\sup\limits_{\underline{\theta}t_0\leq t\leq t_0}EU_{i1}(\xi(t), t) $, 取 $ \delta\in (\delta_*, \delta^*) $, 则

类似于文献[14,定理 2.1] 的证明过程, 或者文献 [定理 1] 的证明过程, 或者文献 [定理 1] 的证明过程, $ EV_i(x(t), t, r(t)) $ 在 $ (t_{k-1}, t_k) $ 内连续, 在 $ t_k $ 处右连续有左极限, $ k\in\mathbb{Z}^+ $.首先证明 (4.19) 式对 $ t\in[t_0, t_1) $ 成立. 用反证法, 假设存在 $ t^*\in[t_0, t_1) $, $ 1\leq i^* \leq m $, 使得以下三个结论成立

注意到 $ a_{i0}=0, 1\leq i\leq m $, 用 Hölder 不等式, 得到

根据 Itô 公式, 有

所以

由引理 4.1 可知这是一个矛盾! 所以 (4.19) 式对 $ t\in[t_0, t_1) $ 成立.我们断言

并且用数学归纳法证明. 当 $ n=1 $ 时已证, 假设 $ n=z $ 时, (4.22) 式成立, 则

接下来用反证法证明

如果 (4.24) 式不成立, 则存在 $ t_*\in[t_z, t_{z+1}), \quad 1\leq i_*\leq m, $ 使得以下三个结论成立

结合引理 4.1, 用类似 (4.21) 式的方法可得出矛盾, 所以 (4.24) 式成立. 即当 $ n=z+1 $ 时, (4.22) 式成立. 由归纳法原理可知断言成立.

对任意的 $ t\geq t_0 $, 必存在 $ n_0\in\mathbb{Z}^+ $, 使得 $ t_{n_0-1}\leq t<t_{n_0} $, 所以

方程 (1.3) 的全局解 $ x(t), t\geq t_0 $ 的矩 $ \lambda $ 稳定.

注4.2 在定理 4.2 中, $ \triangle_{max} $ 必须满足 (4.7) 式, 亦即 $ \triangle_{max} $ 必须有正的上界, 这适合于脉冲发生相对频繁的系统, 但在定理 4.3中对 $ \triangle_{max} $ 无此限制. 因此, 定理 4.3 对脉冲发生较为稀少的情形也适用.

注4.3 在定理 4.2 中, 要求 $ 0\leq\alpha_\lambda<\alpha^*<+\infty $, 这限定了衰减速率不能太慢, 比如: 不能取 $ \lambda(t)=\ln({\rm e}+t), \quad t\geq 0 $.在定理 4.3 中, 要求 $ \lim\limits_{t\rightarrow +\infty}\frac{\lambda(\underline{\theta}t-t_0)}{\lambda(t-t_0)}=b $, 且 $ 0<b<1. $,这限定了衰减速率不能太快, 比如: 不能取 $ \lambda(t)={\rm e}^t, t\geq 0 $. 可见, 定理 4.2 适用于衰减速率较快的情形, 定理 4.3 适用于衰减速率较慢的情形.

注4.4 定理 4.2 要求 (4.6) 式和 (4.7) 式成立, 而且 $ u', u, r, \underline{\theta}, B, \triangle_{max} $ 都是正数, $ b_{kl} $ 和 $ 1-\alpha_{kl} $ 是非负数,且 $ \int_{\underline{\theta}t_0}^{+\infty}\lambda^{-\alpha^*}(s){\rm d}s>0 $, 这限制了 (4.7) 式中的正数 $ \overline{q} $ 不能太大, 从而(4.6) 式中的正数 $ q_i $ 和 $ q_{ij} $也不能太大. 定理 4.3 要求 (4.18) 式成立, $ u, \delta_* $ 是正数且 $ \lim\limits_{t\rightarrow+\infty}\lambda(t)=+\infty $, 故当 $ t_n-t_0 $ 逐渐变大时, $ \widetilde{q} $可取较大的正数. $ \zeta_i $ 是不小于 1 的数, 因而正数 $ q_i $ 和 $ q_{ij} $ 的取值范围更宽. 定理 4.3 说明当脉冲点之间的间隔变大时,在脉冲点处需要满足的条件 (4.6) 可以放宽.

下面给出方程 (1.3) 的全局解几乎必然 $ \lambda $ 稳定的判定定理

定理4.4 假设定理 4.2 的条件成立, $ \triangle_{min}>0 $,

且存在常数 $ \widetilde{d}>0 $, 使得

则方程 (1.3) 的全局解几乎必然 $ \lambda $ 稳定.

证 因为假设 (A4) 成立, 所以假设 (A2) 成立, 利用 Itô 公式, 当 $ t_n\leq t<t_{n+1} $ 时

所以

利用 BDG 不等式和 (4.26) 式, 得到

其中, $ 0<\varepsilon_3<\frac{\sqrt{2}}{4\widetilde{d}} $, 把 (4.29) 式代入 (4.28) 式, 并注意到

所以

这里

限制 $ \varepsilon^*\in(\alpha_\lambda, \varepsilon_1\wedge\varepsilon_2) $, 取 $ \varepsilon_4\in(\alpha_\lambda, \varepsilon^*) $,根据 Chebyshev 不等式

而

利用 Borel-Cantelli 引理, 当 $ n $ 充分大时

而当 $ t_n\leq t<t_{n+1} $ 时

所以, 当 $ t $ 充分大时

即方程 (1.3) 的全局解几乎必然 $ \lambda $ 稳定.

在这一节, 考虑方程 (1.3), 我们通过一个例子验证结论的有效性.

令 $ n_1=1, \underline{\theta}=0.2, M=1, l_1=2, m=2, S=\{1, 2\}, t_0=0.1, r=1.2.$

定义 $ \lambda(t):=(1+t)^{10}, t\geq 0 $, 则 $ J=10, \alpha_\lambda=0.1 $. 取 $ \alpha^*=0.12 $.

容易验证

取$ a_{11}=8, a_{21}=7.8, b_{11}=0.002, b_{12}=0.003, w_{111}=0.1, w_{121}=10, w_{211}=10, w_{221}=0.03. $

则 $ w=10, \quad B=12.18. $取

则 $ \overline{q}=0.05 $, 再取 $ \widetilde{d}=4.8 $容易验证, 定理 4.2 和定理 4.4 的条件成立, 所以方程 (1.3) 的全局解的矩 $ \lambda $ 稳定且几乎必然 $ \lambda $ 稳定.

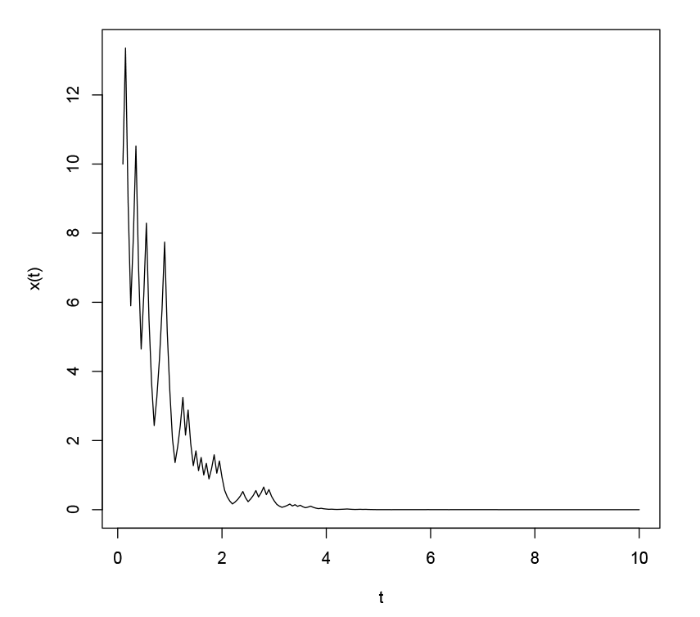
在这一节, 考虑方程 (1.3), 方程的相关参数由第 5 节中所定义, 图 1 是方程 (1.3) 的解$ x(t), t\geq t_0 $ 的计算机模拟.

本文采用 Lyapunov 函数方法证明了带 Markov 切换的随机比例泛函微分方程全局解的存在唯一性和 $ \lambda $ 稳定性. 其中, Lyapunov 函数是向量的形式, 这使得给出的条件更加宽松. $ \lambda $ 稳定性的种类包括指数稳定、多项式稳定和对数稳定等等, 因而更具有一般性. 而且, 本文把脉冲引入系统, 针对脉冲的不同特点以及 $ \lambda $ 类函数不同的衰减速率, 证明了在适当的条件下方程的全局解仍然具有上述性质, 从而补充并推广了文献[10]中的结果. 最后, 通过举例和数值模拟说明了结果的有效性.