PageRank 算法被广泛用于确定网页的重要性, 是 Web 搜索中最重要的问题之一, 最早由谷歌的创始人 Larry Page 和 Sergey Brin 在一系列论文^[1-4]中提出. 该模型的核心思想是通过网页之间的链接关系来评估网页的重要性. 随着时间的推移, PageRank 模型已经被广泛应用于各种科学问题的分析, 包括计算化学^[5],生物信息学^[6], 软件调试^[7]等领域.

PageRank 问题的数学表述可以归结为计算 Google 矩阵的主特征向量. Google 矩阵是一个维度超过数十亿的大型稀疏马尔可夫矩阵, 其主特征向量被称为 PageRank 向量. PageRank 问题可以用以下方程表示

其中, Google 矩阵 $G=\alpha P+(1-\alpha) ve^{\top}$, 其中 $\alpha\in (0,1)$ 是阻尼因子, 用于确定给予 Web 链接图的权重, $P\in\mathbb{R}^{n\times n}$ 是一个列随机矩阵, 其所有列的和为 $1$, $e$ 是一个全 $1$ 的列向量, $v=\frac{e}{n}$ 表示个性化或传送向量.

PageRank 问题 (1.1) 可以重构为以下线性系统

其中 $I\in\mathbb{R}^{n\times n}$ 是一个单位矩阵.

在过去十年左右的时间里, 研究人员针对这个线性系统进行了大量的研究, 特别是在处理大规模 (即 $n$ 非常大) 的情况下. 对于阻尼因子的中等值, 例如 Google 最初建议的搜索引擎排名的 $\alpha=0.85$, 基于简单幂法^[1]的解决策略已被证明是非常有效的. 然而, 当 $\alpha$ 接近 1 时, 包括幂法在内的经典平稳迭代方法开始出现显著的性能下降. 具体表现为迭代次数的急剧增加以及收敛速度的显著减缓. 因此研究人员提出了许多高效的求解方法, 例如使用基于 Arnoldi 分解^[8]的 Krylov 子空间方法进行大型 PageRank 计算, 主要是由于它们的内存效率和固有的并行性. Golub 和 Greif 将改进后的 Arnoldi 过程扩展到 PageRank 上, 强制相关位移为 1, 有效规避了算法复杂性的缺陷, 从而显著提升了算法效率^[9]. 此外, 许多技术试图将传统的 Arnoldi 方法与幂算法相结合, 以产生更快的求解器, 例如 Power-Arnoldi^[10]和 Arnoldi-inout^[11]方法. 在 Power-Arnoldi 算法中, 首先使用 Arnoldi 方法进行一定次数的迭代, 得到一个近似解. 如果这个近似解不满足要求, 就使用 Power 方法来进一步改进近似解. 这样反复迭代, 直到达到所需的精度. 在文献[12]中提出的技术中, 加权最小二乘问题根据残差的分量自适应地改变. 然后, 使用广义 Arnoldi 方法计算近似 PageRank 向量.

然而, 当 Krylov 子空间的维数增大时, 基于 Arnoldi 的求解器在内存和计算成本方面会显著增加. 相反, 如果维数过低, 这些方法有时可能无法有效加速基本的幂法, 特别是在阻尼系数较高时, 甚至可能出现停滞不前的情况. 为攻克这一难题, Hessenberg 于 1940 年引入海森伯格约简过程^[13], 并由于其较低的算术和存储需求, 该过程最近被重新启用, 以建立许多针对稀疏矩阵系统的具有成本效益的 Krylov 子空间求解器. 在此基础之上, 顾等人在 2019 年将 Hessenberg 过程与重新启动的技术相结合, 提出了 Hessenberg-type算法^[14]以用于计算 PageRank 向量. 胡等人在 2024 年将外推过程引入到 Hessenberg 型算法中, 得到了新的 Hessenberg-extrapolation^[15]算法. 本文尝试使用 Chebyshev 多项式来加速 Hessenberg 算法, 从而提出了一种新的 Hessenberg-Chebyshev 算法并详细探讨了该算法的构造和收敛性. 数值结果表明, 当阻尼因子 $\alpha$ 接近 1 时, Hessenberg-Chebyshev 算法的性能优于现有方法.

本文的其余部分组织如下. 在第 2 节中, 我们介绍了用于计算 PageRank 的 Hessenberg-type 算法; 在第 3 节中, 我们提出了计算 PageRank 的 Hessenberg-Chebyshev 算法, 在第 4 节中对该算法的收敛性进行分析; 数值实验和对比结果在第 5 节; 最后, 在第 6 节给出结论.

在本节中, 将对用于计算 PageRank 的 Hessenberg-type 算法^[14]进行介绍. Hessenberg-type 算法和 Arnoldi-type算法是相似的, Hessenberg-type 算法也产生 Krylov 子空间的一组基, 但这组基不是正交的. 下面给出了计算 PageRank 的 Hessenberg-type 算法.

注2.1 算法 1 的第 22 行的 $\sigma _{m}$ 是指 $H_{m+1,m}-[I_{m};0]$ 的最小奇异值, 第 $20$ 行的 $v_{m}$ 是对应的右奇异向量, $L_{m}$ 是由第 $7$ 步到第 $19$ 步中的 $l_{j}$ 构成的; 第 $22$ 行 $u_{m}$ 是对应的左奇异向量.

Hessenberg 过程是一种斜投影技术, 它将给定的非对称矩阵 $A\in\mathbb{R}^{n\times n}$ 简化为 Hessenberg 形式. 我们不从 $H_{m}$ 的特征向量中近似 $A$ 的特征向量 (所谓的 Ritz-like 向量). 相反, 我们计算改进的 Ritz-like 向量, 即与 $A-\lambda_{i}I$ 的最小奇异值相关的奇异向量, 其中 $\{\lambda_{i}\}_{i=1}^m $ 被命名为 Ritz-like 值. Hessenberg 过程可以很好地估计外部 Ritz 值, 在某些情况下甚至比 Arnoldi 更准确. Krylov 基矩阵 $L_m$ 的条件数是确定所采用方法精度的有效指标, 对于 Hessenberg 过程, 当 Krylov子空间的维数增加时, 条件数不会显著增长且 Hessenberg 分解的数值误差往往很小. 基于 Hessenberg与 Arnold 的变体具有相似的数值性质, 确保了特征向量的有效分离, 通过使用等于 1 的移位避免了复杂的算法, 最小的奇异值比最大的 Ritz 值更平滑地收敛于零.

表1 中显示了执行 Hessenberg-type 算法和 Arnoldi-type 算法一个周期所需的计算工作量. 这里 $N_z$ 表示的是矩阵 $A$ 每一行非零元素的平均个数.

在本节中, 我们尝试用 Chebyshev 加速 Hessenberg-type 算法用于计算 PageRank, 从而开发了 Hessenberg-Chebyshev 新算法. 我们使用 Chebyshev 多项式^[16]来改进 Hessenberg-type 算法以计算 PageRank. 假设 Google 矩阵 $A$ 的特征值按降序排列为 $1 = |\lambda_1| > |\lambda_2| \geq \cdots \geq |\lambda_n|$. 令 $P_{l}$ 表示度数不超过 $l$ 的多项式集合, 并且 $(\lambda_{i},\mu_i), i = 1, 2, \cdots, n$ 是 $A$ 的特征对. Chebyshev 过程的思想可以描述如下

构建一个多项式迭代模型

其中 $z_0$ 是初始向量, $p_l$ 是次数为 $l$ 的多项式. 我们希望找到一个多项式 $p_l$, 使得得到的向量 $z_l$ 迅速收敛到 $\lambda_1 = 1$ 时 $A$ 的特征向量 $\mu_1$. 在特征分解下 $z_0 = \sum_{i=1}^{n} y_i\mu_i$, 其中 $\|\mu_i\|_2 = 1$ 且 $y_i \neq 0, i = 1, 2, \cdots, n$, $z_l$ 可以表示为

因此, 我们希望多项式 $p_l$ 使得每个 $p_l(\lambda_i), i = 2, 3, \cdots, n$ 尽可能小, 并且 $p_l(\lambda_1) = 1$. 然而, 在没有获得 $A$ 的所有特征值的情况下, 找到这样的多项式是不可能的. 使用包含 $A$ 的所有特征值但排除 $\lambda_1$ 的连续域 $\Omega$, 我们转而寻找一个满足条件的多项式

设 $\Omega(d, c, \alpha)$ 是一个以实数中心 $d$, 焦距 $c$ 和长半轴 $\alpha$ 的椭圆, 然后用多项式求最小值

其中

是第一类 $l$ 次 Chebyshev 多项式, 更多详情请参阅文献[16].

实际上, 计算 $z_l = p_l(A)z_0$ 可以从以下三项递推关系中得出

设 $ \rho_{l}=T_{l}\left[\left(\lambda_{1}-d\right) / c\right](l=0,1, \cdots) $, 结合 (3.2) 和 (3.4) 式, 得到

此外, 令 $ \sigma_{l+1}=\rho_{l} / \rho_{l+1} $, (3.5) 式可以重写为

其中 $\sigma_i$ 可以通过递推计算得出

最后, 根据 (3.6) 和 (3.7) 式, 得到向量 $z_l= p_l(A)z_0$. 现在我们应用 Chebyshev 多项式来加速 Hessenberg 算法以计算 PageRank, 具体的算法如下所示

现在我们关注算法 2 的计算成本并与 Hessenberg-type 算法进行比较. 在每次迭代中, 算法 2 基本运算是矩阵向量积, 在 $m$ 步 Hessenberg 过程中应用了 $m$ 次且在 Chebyshev 过程中应用了 $l$ 次, 总共应用了 $2n(m+l+3)N_z$ 次, 每次迭代中还有其他操作, 如表2 所示.

虽然算法 2 的每次迭代要进行的计算成本比 Hessenberg-type 算法高, 但是算法 2 所需迭代次数远小于 Hessenberg-type 算法, 这在第五部分数值实验中我们进行了验证.

引理4.1^[17] 设 $P$ 是 $n\times n$ 列随机矩阵, 设 $\alpha$ 是 $0<\alpha<1$ 的实数. 设 $E$ 是 $n\times n$ 秩一列随机矩阵 $E=ve^\top $, 其中 $e$ 是元素均为 $1$ 的 $n$ 维向量, $v$ 是元素均非负且和为 $1$ 的 $n$ 维向量. 令 $A=\alpha P+(1-\alpha)E$, 则 $A$ 的最大特征值 $\lambda_1=1$, 第二大特征值 $|\lambda_2|\le\alpha $.

定理4.1 假设 $x^{(k)}$ 是通过算法 1 得到的所需 $\mathrm{PageRank}$ 向量的第 $k$ 次迭代近似, 在特征分解下

其中 $\theta_{i}\ne0$, $i=1, 2, 3\cdots, n$.在迭代过程中进一步假设椭圆为 $E(d, c, a)$, 即以 $d$ 为中心, 焦距为 $c$, 长半轴为 $a$ 的椭圆. 那么, 当 $c$ 趋于零时, 那么有

其中 $d_{*}$ 是使得函数 $\Phi(d) = \max _{i \neq 1}\left(\frac{\left|\lambda_{i}-d\right|}{1-d}\right)$ 在区间 $[-\alpha, \alpha]$ 内达到最小的值, 而 $\epsilon_{0} = \min _{q \in P_{m-1}, \left(\lambda_{1}\right)=1} \max _{\lambda \in\Lambda / \lambda_{1}}|q(\lambda)|$.

证 根据算法 2 的迭代过程, 我们首先通过 $m$ 步 Hessenberg 迭代得到一个近似值 $x^{\left(k+\frac{1}{2}\right)}$, 它位于 Krylov 子空间 $\mathcal{K}_{m}\left(A, x^{(k)}\right)$ 中, 并且可以表示为 $x^{\left(k+\frac{1}{2}\right)}=q_{m-1}(A) x^{(k)}$, 其中 $q_{m-1}(\lambda)$ 是一个次数不超过 $m-1$ 的多项式, 满足 $\min _{\varphi \in P_{m-1}, q\left(\lambda_{1}\right)=1} \max _{\lambda \in \Lambda / \lambda_{1}}|q(\lambda)|$.

另一方面, 通过 $x^{(k)}$ 的特征分解, $x^{\left(k+\frac{1}{2}\right)}$ 可以重写为

因此, 第 $(k+1)$ 次迭代近似 $x^{(k+1)}=p_{l}(A) x^{\left(k+\frac{1}{2}\right)}$, 通过 (3.2) 式中的 Chebyshev 多项式 $p_{l}(\lambda)$ 进行加速, 可以表达为

根据基本几何知识,

现在估计

的值. 根据 (3.2) 式中 Chebyshev 多项式的定义, 可知道

已知 $\omega_{i}=\omega_{i}^{ \pm}=\frac{\lambda_{i}-d}{c} \pm \sqrt{\left(\frac{\lambda_{i}-d}{c}\right)^{2}-1}, i=2,3, \cdots, n$, 以及 $\omega_{1}=\omega_{1}^{ \pm}=\frac{1-d}{c} \pm \sqrt{\left(\frac{1-d}{c}\right)^{2}-1}$. 在后续的讨论中, 取 $\omega_{i}=\omega_{i}^{+}, i=1,2, \cdots, n$, 因为 $\omega_{i}=\omega_{i}^{-}$ 会得到与 $\omega_{i}=\omega_{i}^{+}$ 相同的 $p_{l}\left(\lambda_{i}\right)$ 值. 在这里, 我们可以假设 $\left|\omega_{i}\right| \geq 1$, 否则 $\left|\omega_{i}\right|^{-1}>1$, 这对估计 $\left|p_{\mathrm{l}}\left(\lambda_{i}\right)\right|$ 没有影响.

注意, $\kappa(c)$ 在区间 $(0,1-d)$ 上是一个单调递增函数. 因此, $\lim _{c \rightarrow 0} \kappa(c) = \left(\frac{|\lambda_{i}-d|}{1-d}\right)^{l}$.

在本节中, 我们首先讨论重启数 $m$ 和 Chebyshev 步长 $l$ 的合适选择. 随后, 为了验证本文所提出的 Hessenberg-Chebyshev (HC) 算法的有效性, 我们将其与其他迭代法进行比较, 诸如 Hessenberg-type (HP) 算法, Arnoldi-type (AP) 算法以及文献[18]中的 Arnoldi-Chebyshev (AC) 算法. 针对表3 中的矩阵进行测试, 这些矩阵可以在 https://sparse.tamu.edu/ 上下载获得, 同时也列出了这些矩阵的一些性质, 其中 $n$ 表示矩阵的大小, $nnz$ 表示矩阵中非零元的数目, den 表示的是矩阵的稀疏程度其定义为 $\text{den}=\frac{nnz}{n\times n}\times 100\% $.

为了公平起见, 本节中所有算法都以相同的初始向量 $v_{0}=e/n,e=[\cdots,1]^{\top}$ 开始. 阻尼因子分别设为 $\alpha=0.9,0.95,0.99,0.995$. 在 Hessenberg-Chebyshev 算法中, 我们每个周期运行 Hessenberg 过程两次, 所有算法的容差为 $tol=10^{-8}$. 在数值实验中, 为了简单起见我们将 $\mathrm{Hessenberg}$-$\mathrm{Chebyshev}$ 算法的焦距 $c$ 设为 $0.01$, 中心点 $d$ 设为 $0$.

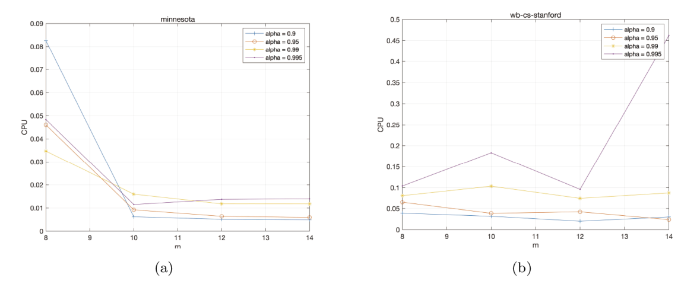
例 5.1 在本例中, 我们通过分析 $\mathrm{Minnesota}$ 矩阵和 $\mathrm{wb}$-$\mathrm{cs}$-$\mathrm{stanford}$ 矩阵来讨论 $\mathrm{Hessenberg}$-$\mathrm{Chebyshev}$ 算法重启数 $m$ 的选择. 图1 显示了当 $\alpha=0.9,0.95,0.99,0.995$, 重启次数 $m=8,10,12,14,16$ 时, $\mathrm{Hessenberg}$-$\mathrm{Chebyshev}$ 算法的迭代时间随重启次数 $m$ 的变化曲线.

经过对实验数据的深入分析, 我们观察到重启次数 $m$ 对迭代时间具有显著的影响, 对于 $\mathrm{Minnesota}$ 矩阵而言, 不同阻尼因子 $\alpha$ 对应的迭代时间与 $m$ 的相关曲线具有相似性. 当 $m = 8$ 时, 所需的迭代时间达到最长. 然而, 当 $m = 10$ 时, 所需迭代时间急剧下降, 在 $m$ 大于 10 之后, 其对迭代时间的影响不大. 对于 $\mathrm{wb}$-$\mathrm{cs}$-$\mathrm{stanford}$ 矩阵 $\alpha$ 小于 $0.995$ 时对应的迭代时间与 $m$ 的相关曲线是相似的, $m$ 的变化对于迭代时间的影响不大, 当 $\alpha$ 为 $0.995$ 时, $m$ 为 12 时所需迭代时间最短, $m$ 大于 12 时所需迭代时间急剧增加. 具体而言, 随着重启次数 $m$ 的增加, 迭代时间的变化呈现出一种非线性的趋势. 在多次实验和对比中, 发现当重启次数设置为 10 时, 迭代时间达到了一个明显的最低点. 这一观察结果意味着, 在这些条件下, 迭代算法的性能达到了一个最优点, 进一步增加了重启次数将不再显著提升性能, 反而可能导致计算资源的浪费. 基于上述分析, 我们决定在后续的实验中, 将重启次数 $m$ 设定为 10.

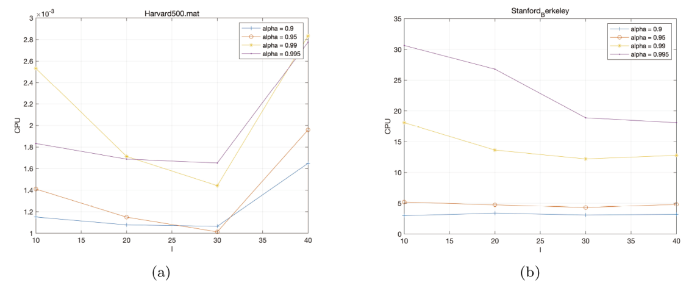
例 5.2 在本例中, 我们取 $m=10$, 讨论 $\mathrm{Chebyshev}$ 步长 $l$ 的合适选择. 在图2 中绘制了阻尼因子 $\alpha=0.9, 0.95, 0.99, 0.995$, $\mathrm{Chebyshev}$ 步长 $l=10, 20, 30, 40$ 时, $\mathrm{Harvard500}$ 矩阵和 $\mathrm{Stanford}$-$\mathrm{Berkeley }$ 矩阵的 $\mathrm{Hessenberg}$-$\mathrm{Chebyshev}$ 算法的时间和 $\mathrm{Chebyshev}$ 步长 $l$ 的关系曲线.

从上图的数据分析中, 我们可以清晰地观察到, $\mathrm{Chebyshev}$ 算法的最优步长 $l$ 在选择上受到不同谷歌矩阵和阻尼因子 $\alpha$ 的显著影响. 具体地说, 对于不同的矩阵结构和阻尼因子, $\mathrm{Chebyshev}$ 算法的收敛速度和稳定性会呈现出不同的表现, 因此最优步长的选取也会有所不同. 在多次实验和对比中, 我们发现当 $\mathrm{Chebyshev}$ 算法的步长设置为 $30$ 时, 其在多种条件下的性能均达到了一个显著的拐点. 这意味着, 在 $l=30$ 时, 算法能够在保证收敛速度的同时, 也具备良好的稳定性, 从而实现了性能和效率的平衡. 基于上述分析, 我们决定在后续的实验中, 将 $\mathrm{Chebyshev}$ 算法的步长 $l$ 统一设定为 $30$.

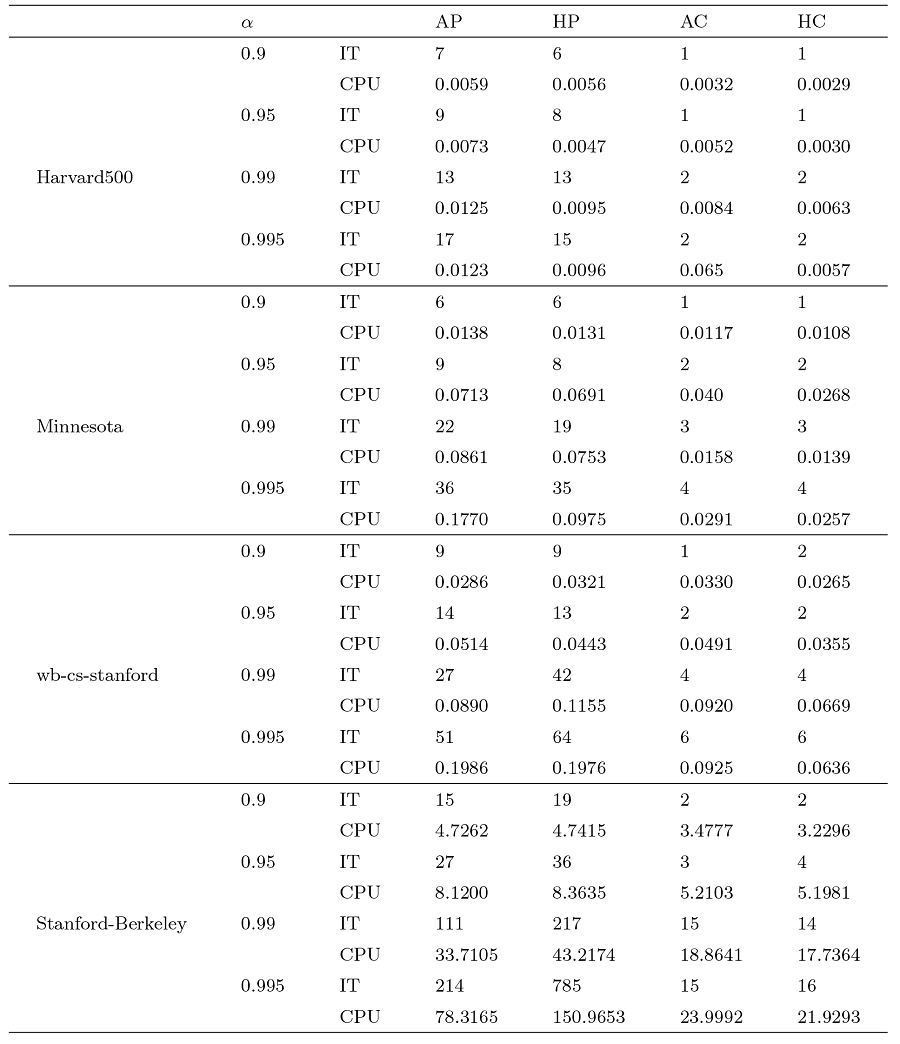
例 5.3 在本例中, 我们针对 $\mathrm{Harvard500}$, $\mathrm{Minnesota}$, $\mathrm{wb}$-$\mathrm{cs}$-$\mathrm{stanford}$ 和 $\mathrm{Stanford}$-$\mathrm{Berkeley }$ 矩阵在固定 $m=10$ 和 $l=30$ 的条件下, 对四种算法 $\mathrm{AP}$, $\mathrm{HP}$, $\mathrm{AC}$ 和 $\mathrm{HC}$ 进行了迭代次数 $\mathrm{IT}$ 和迭代时间 $\mathrm{CPU}$ 的实验对比. 实验通过调整不同的阻尼因子 $\alpha$ 值, 以评估不同算法在不同参数下的性能表现. 实验结果如下

从表4数据中可见, $\mathrm{HC}$ 算法在四个矩阵的实验中均表现出显著优势. 在不同的矩阵中, 如 $\mathrm{Harvard500}$, $\mathrm{Minnesota}$, $\mathrm{wb}$-$\mathrm{cs}$-$\mathrm{stanford}$ 和 $\mathrm{Stanford}$-$\mathrm{Berkeley}$ 矩阵, 随着参数的变化, $\mathrm{HC}$ 算法的 $\mathrm{CPU}$ 时间增长相对平缓. 对于 $\mathrm{Harvard500}$ 矩阵, 从参数 $0.9$ 到 $0.995$, $\mathrm{CPU}$ 时间虽有增加但幅度较小, 且结果稳定在 $1$ 或 $2$. 类似地, 在其他矩阵中, $\mathrm{HC}$ 算法也表现出稳定的输出结果. 这表明它对不同规模和复杂度的矩阵具有良好的适应性. 同时, 其稳定性使得在实际应用中能提供可靠的计算结果. 无论是面对小型矩阵还是复杂的大型矩阵, $\mathrm{HC}$ 算法都能发挥作用.

综上所述, $\mathrm{HC}$ 算法在处理这四个矩阵时, 无论是从迭代次数还是迭代时间来看, 均表现出更高的收敛性和计算效率, 是一个值得优先考虑的高效算法. 实际应用中, 可以根据具体的需求和参数条件选择更合适的算法如果更注重计算效率和迭代时间, 算法 $\mathrm{HC}$ 可能是较好的选择; 而如果对迭代次数有特定要求, 或者在某些特定的参数组合下, 可能需要综合考虑两种算法的性能表现.

本文提出了用于计算 Google 矩阵 PageRank 向量的 Hessenberg-Chebyshev 方法, 并着重探讨了该方法的收敛性. 切比雪夫加速技术促使 Hessenberg 过程在极为宽泛的阻尼系数范围内均能出色运作, 尤其是在处理具有高阻尼系数 (尤其是接近 1 的数值) 的场景下, 展现出了显著的优势. 通过数值算例彰显了新方法相较于现有算法所具备的优越性. 此外, 我们需要着重指出的是, 这两个参数 $l$ 和 $m$ 对于 Hessenberg-Chebyshev 方法的收敛性有着极为关键的影响. 然而, 如何精准地选取这两个参数以达到最优性能还值得深入研究.