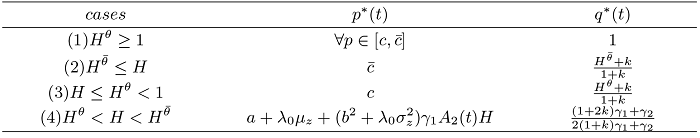1 引言
近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3] 和最大化终端财富期望效用[4 7] 以及均值-方差准则[8 10] .
在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略.
另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略.
在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产.
综上所述, 保险公司的最优投资再保险策略在国内外已经有了全面的研究, 但仍有一些可以完善的地方. 大多数的文章中没有考虑再保险公司的利益, 没有将保险公司和再保险公司的共同优化问题反映在模型中. 在本文中我们同时考虑了保险公司和再保险公司的利益, 在 Stackelberg 随机微分博弈下研究了保险公司和再保险公司的最优策略. 不同于以往大多数文章的是在本文中我们引入了突发事件对于保险公司的影响, 在保险公司的索赔过程中引入泊松跳, 以此来描述生活中突发事件对保险公司的影响. 同时, 对风险资产的模型由传统的 Black-Scholes 模型拓宽到 Heston 随机波动率模型, 此模型更能符合现实生活中风险资产的波动情形, 使模型更加贴切现实. 之后文章在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 随机微分博弈, 在此博弈中依次求解保险公司和再保险公司的优化问题, 从而得到保险公司和再保险公司的均衡策略.
2 模型构造
在本章, 我们假设 $(\Omega,\mathcal{F},P)$ $\sigma$ - 代数 $\mathcal{F}_{t}$ $t$ $T>0$ $P$ $\{\mathcal{F}_{t}\}_{t\in [T]}$ .
在本节中, 我们考虑保险市场包含一个保险公司和一个再保险公司. 考虑到突发事件发生的随机性, 我们假设保险公司的索赔满足跳扩散过程
(2.1) $\begin{equation} {\rm d} C( t ) = a{\rm d} t-b{\rm d}W_{0}(t) + d \Bigg(\sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Bigg), \end{equation}$
其中 $a$ $b$ $W_{0}(t)$ $\{N(t)\}_{t\geq 0}$ $\lambda_{0}>0$ $N(t)$ $[t]$ $Z_{i}$ $i$ $Z_{i},i=1,2,\cdots$ $\mu_{z}=E[Z_{i}]$ $\sigma_{z}^{2}=E[Z_{i}^{2}]$ . 进一步, 假设保险公司根据期望值保费原则收取保费, 其安全载荷因子 $\theta>0$ $c=({1+\theta})a$
(2.2) $\begin{equation} {\rm d} R ( t ) = \theta a {\rm d} t + b {\rm d} W _ { 0 } ( t ) - d\Bigg( \sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Bigg), \end{equation}$
(2.3) $\begin{equation} \theta a = ( 1 + \theta )\lambda_{0}\mu_{z}. \end{equation}$
对于每一个 $t\in[T]$ $Z_{i}$ $(1-q(t))\in[0, 1]$ $q(t)$ $q(t)=0$ $q(t)=1$ $t$ $p(t)\in[c,\bar{c}]$ $\bar{c}=(1+\bar{\theta})a$ . 这里 $p(t)\geq c$ $\bar{\theta}\geq \theta$
(2.4) $\begin{equation} {\rm d} X_{I}(t)=(1+\theta)a{\rm d}t-q(t)\Big(a{\rm d}t-b{\rm d}W_{0}(t)+d \sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Big)-\Big(1-q(t)\Big)p(t){\rm d}t \end{equation}$
(2.5) $\begin{equation} {\rm d} X_{R}(t)=(1-q(t))p(t){\rm d}t-(1-q(t))\Big(a{\rm d}t-b{\rm d}W_{0}(t)+d \sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Big). \end{equation}$
假定金融市场由一个无风险资产和一个风险资产组成. 此外, 我们假设交易可以在金融市场上在没有交易成本或税收的情况下持续进行, 并且所有的金融资产都是无限可分割的. 无风险资产 $S_{0}(t)$ ${\rm d}S_{0}(t)=rS_{0}(t){\rm d}t,\, S_{0}(0)=1,$ $r$ $S(t)$ $S(t)$
(2.6) $\begin{equation} \begin{cases} {\rm d}S(t)=S(t)[(r+\alpha L(t)){\rm d}t+\sqrt{L(t)}{\rm d}W_{S}(t)],\quad S(0)=s_{0}>0,\\ {\rm d}L(t)=\beta(\delta-L(t)){\rm d}t+\sigma \sqrt{L(t)}{\rm d}W_{L}(t),\quad L(0)=l_{0}>0, \end{cases} \end{equation}$
其中, $\alpha, \beta, \delta, \sigma$ $\alpha$ $\beta$ $L(t)$ $\delta$ $L(t)$ $\sigma$ $L(t)$ $L(t)$ $W_{S}(t)$ $W_{L}(t)$ $E[W_{S}(t)W_{L}(t)]=\rho t$ . 此外, 假设 $W_{0}(t)$ $W_{S}(t)$ $W_{L}(t)$ $2\beta \delta>\sigma^{2}$ $L(t)$
保险公司和再保险公司可以投资于风险资产, 用 $\pi_{I}(t)$ $\pi_{R}(t)$ $t$ $(q(t),\ \pi_{I}(t))$
(2.7) $\begin{equation} \begin{aligned} {\rm d}X(t)&=(1+\theta)a{\rm d}t-q(t)\Big(a{\rm d}t-b{\rm d}W_{0}(t)+d \sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Big)-(1-q(t))p(t){\rm d}t\\ & +\pi_{I}(t)\Big[(r+\alpha L(t)){\rm d}t+\sqrt{L(t)}{\rm d}W_{S}(t)\Big]+r\Big(X(t)-\pi_{I}(t)\Big){\rm d}t. \end{aligned} \end{equation}$
同时, 再保险公司在策略 $(p(t), \pi_{R}(t))$
(2.8) $\begin{equation} \begin{aligned} {\rm d}Y(t)&=(1-q(t))p(t) {\rm d}t-(1-q(t))\Big(a{\rm d}t-b{\rm d}W_{0}(t)+d \sum _ { i = 1 } ^ { N ( t ) } Z _ { i }\Big)\\ & +\pi_{R}(t)\Big[(r+\alpha L(t)){\rm d}t+\sqrt{L(t)}{\rm d}W_{S}(t)\Big]+r\Big(Y(t)-\pi_{R}(t)\Big){\rm d}t. \end{aligned} \end{equation}$
目前, 保险公司和再保险公司在保险市场上的地位并不平等, 因为在保险市场上保险公司的数量很多, 保险公司之间竞争很激烈, 而再保险公司的数量却很少, 再保险业务被少量再保险公司所垄断. 因此, 在保险市场中有一个领导者. 在下面, 我们将再保险公司和保险公司分别作为博弈的领导者和追随者. 根据文献[20 ]和[23 ], 我们的目标是依次求解优化问题. 更具体地来说, 我们可以将求解 Stackelberg 随机微分优化问题分为以下三个步骤
步骤一 再保险公司作为领导者, 首先给定任意的策略 $(p(\cdot),\ \pi_{R}(\cdot))$
步骤二 在了解到再保险公司的策略后, 保险公司根据再保险公司的策略解决其优化问题, 找到最优的策略 $q^{\ast}(\cdot)=f^{\ast}(\cdot,\ p(\cdot),\ \pi_{R}(\cdot)), \pi^{\ast}_{I}(\cdot)=g^{\ast}(\cdot,\ p(\cdot),\ \pi_{R}(\cdot))$
步骤三 知道保险公司的执行策略 $f^{\ast}(\cdot,\ p(\cdot),\ \pi_{R}(\cdot))$ $g^{\ast}(\cdot,\ p(\cdot),\ \pi_{R}(\cdot))$ $(p^{\ast}(\cdot),\ \pi_{R}^{\ast}(\cdot)).$
注2.1 博弈的双方 $($ $)$ $(p(\cdot),\ \pi_{R}(\cdot))$ $(q(\cdot),\ \pi_{I}(\cdot))$
定义2.1 策略 $u_{I}(\cdot)=(q(\cdot),\ \pi_{I}(\cdot))$ $u_{R}(\cdot)=(p(\cdot),\ \pi_{R}(\cdot))$
(1) $u_{I}(\cdot)$ $u_{R}(\cdot)$ $\mathcal F_{t} \}_{t\in [T]}$
(2) 对于任意的 $t\in[T],\ q(t)\in[0, 1],\ p(t)\in[c,\bar{c}];$
(3) 对于任意的 $t\in[T],$ $E_{t,x,l}\left[\int_{t}^{T}(q^{4}(s)+\pi_{I}^{4}(s)){\rm d}s\right]<+\infty,$ $E_{t,y,l}\left[\int_{t}^{T}(p^{4}(s)+\pi_{R}^{4}(s)){\rm d}s\right]<+\infty;$
(4) 对于任意的 $(t,x)\in[T]\times R,\ (t,y)\in[T]\times R$
令 $U:=U_{I}\times U_{R}$ $U_{I}$ $U_{R}$
类似文献[23 ], 作为 Stackelberg 博弈中的追随者, 保险公司的财富远低于再保险公司. 由于比较心理, 保险公司既关心自己的最终财富, 也关心自己与再保险公司之间的财富差距, 即保险人的目标是寻找一种再保险投资策略, 使下面定义的均值-方差成本函数在其相对绩效下最大化. 这里我们将保险公司的相对绩效定义为 $ \widehat{X}(t):=(1-k)X(t)+k(X(t)-Y(t))=X(t)-kY(t),$ $k\in[0, 1]$ $k$ $k=0$
保险公司在策略 $(q(t),\ \pi_{I}(t))$
(2.9) $\begin{equation} \begin{aligned} d\widehat{X}(t)&=\Big[r\widehat{X}(t)+\alpha L(t)(\pi_{I}(t)-k\pi_{R}(t))+\theta a-(1+k)(1-q(t))(p(t)-a)\Big]{\rm d}t\\ & +b\Big(q(t)-k+kq(t)\Big){\rm d}W_{0}(t)+\Big[\pi_{I}(t)-k\pi_{R}(t)\Big]{\rm d}W_{S}(t)\\ & -\Big[kq(t)+q(t)-k\Big]d\sum_{i=1}^{N(t)}Z_{i}, \end{aligned} \end{equation}$
初始条件 $ \widehat{X}(0)= \widehat{x}_{0}=x_{0}-ky_{0}.$
在本文, 我们假定保险公司和再保险公司的目标是最大化终端财富效用, 其中效用函数均为均值- 方差准则. 记 $E_{t,\widehat{x},l}[\cdot]=E[\cdot|\widehat{X}(t)=\widehat{x}, L(t)=l]$ $Var_{t,\widehat{x},l}[\cdot]=Var[\cdot|\widehat{X}(t)=\widehat{x}, L(t)=l]$ . 那么在均值-方差框架下, 保险公司和再保险公司的 Stackelberg 微分博弈有以下表述.
(2.10) $\begin{equation} \begin{cases} \underset{u_{I}(\cdot)\in U_{I}}{\rm{sup}}J_{I}(t,\widehat{x},l ;u_{I}(\cdot),u_{R}(\cdot)):=\underset{u_{I}(\cdot)\in U_{I}}{\rm{sup}}\Big\{E_{t,\widehat{x},l}[\widehat{X}(T)]-\frac{\gamma_{1}}{2}Var_{t,\widehat{x},l}[\widehat{X}(T)]\Big\}\\ \mbox{对于任意的} u_{R}(\cdot)\in U_{R},\quad(\widehat{x},l;\ u_{I}(\cdot),\ u_{R}(\cdot)) \mbox{满足} (2.9)\mbox{式}, \end{cases} \end{equation}$
(2.11) $\begin{equation} \begin{cases} \underset{u_{R}(\cdot)\in U_{R}}{\rm{sup}}J_{R}(t,y,l ;u_{I}^{\ast}(\cdot,u_{R}(\cdot)),u_{R}(\cdot)):=\underset{u_{R}(\cdot)\in U_{R}}{\rm{sup}}\Big\{E_{t,y,l}[Y(T)]-\frac{\gamma_{2}}{2}Var_{t,y,l}[Y(T)]\Big\}\\ \mbox{对于任意的} u_{I}^{\ast}(\cdot,u_{R}(\cdot)),\quad (y,l;\ u_{I}^{\ast}(\cdot,\ u_{R}(\cdot)),\ u_{R}(\cdot)) \mbox{满足} (2.8) \mbox{式}, \end{cases} \end{equation}$
其中正常数 $\gamma_{1}$ $\gamma_{2}$ $u_{I}^{\ast}(\cdot,u_{R}(\cdot))$
众所周知, 均值-方差准则下的再保险投资问题是时间不一致的. 按照文献[29 ]的方法, 我们寻求问题 (2.10) 和 (2.11) 的均衡策略和均衡值函数, 定义如下
定义2.3 对任意的再保险公司的策略 $u_{R}(\cdot)\in U_{R}$ $u^{\ast}_{I}(\cdot,\ u_{R}(\cdot))\in U_{I}$ $\widehat{u}_{I}(\cdot, u_{R}(\cdot))\in U_{I}$ $\epsilon$ $(t,\ \widehat{x},\ l)\in [T]\times R\times R^{+}$ $u^{\epsilon}_{I}(\cdot, u_{R}(\cdot))$
对任意的 $\widehat{u}_{I}(\cdot, u_{R}(\cdot))\in U_{I}$ $u _ { I } ^ { * } ( \cdot, \ u_ { R }(\cdot))$ $V_{I}(t,\widehat{x},l)$ $V_{I}(t,\widehat{x},l;u_{R}(\cdot)):=J_{I}(t,\widehat{x},l;u_{I}^{*}(\cdot,u_{R}(\cdot)),u_{R}(\cdot)).$
令 $u^{*}_{R}(\cdot)\in U_{R}$ $u^{*}_{I}(\cdot,\ u_{R}(\cdot))\in U_{I}$ $\widehat{u}_{R}(\cdot)\in U_{R}$ $\epsilon$ $(t,y,l)\in [T]\times R\times R^{+}$ $u^{\epsilon}_{R}(\cdot)$
对任意的 $\widehat{u}_{R}(\cdot)\in U_{R}$ $u^{*}_{R}(\cdot)$ $V_{R}(t,y,l)$ $V_{R}(t,y,l):=J_{R}(t,y,l;u_{I}^{*}(\cdot,u^{*}_{R}(\cdot)),u^{*}_{R}(\cdot)).$
根据定义2.3, 上述均衡策略是时间一致的. 我们的目的是寻求均衡策略 $u^{*}_{I}\times u^{*}_{R}$
命题2.1 均值-方差问题 (2.10) 和 (2.11) 的值函数对于他们自己的盈余 (即 $\widehat{x}$ $y$ ) 是可分离的,并且独立于对手的盈余. 此外, 保险公司和再保险公司的均衡策略都不依赖于状态变量.
根据命题2.1, 我们将保险公司和再保险公司的值函数简化为 $V_{I}(t,\widehat{x},l)$ $V_{R}(x,y,l)$ . 令 $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $t$ $x$ $l$ $\psi(t,x,l)$ $\psi(t,x,l)$ $\psi_{t}(t,x,l),\psi_{x}(t,x,l),\ \psi_{xx}(t,x,l),\ \psi_{l}(t,x,l),\ \psi_{ll}(t,x,l),\ \psi_{xl}(t,x,l)$ $[T]\times R \times R^{+}$ $D_{p}^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $x$ $l$ $\psi(t,x,l)$ 30 ]和[31 ]). 对于任意的函数 $\psi(t,\widehat{x},l)\in C^{1,2,2}$ $\mathcal{L}^{u_{I},u_{R}}_{1}$
(2.12) $\begin{align*} \mathcal{L}^{u_{I},u_{R}}_{1} \psi(t,\widehat{x},l) =\,&\frac{\partial \psi}{\partial t}+\Big[r\widehat{x}+\alpha l (\pi_{I}(t)-k\pi_{R}(t))+\theta a -(1+k)(1-q(t))(p(t)-a)\Big]\frac{\partial \psi}{\partial \widehat{x}} \\[2mm] &+\frac{1}{2}\Big[(bq(t)-kb+kbq(t))^{2}+(\pi_{I}(t)-k\pi_{R}(t))^{2}l\Big]\frac{\partial ^{2}\psi}{\partial \widehat{x}^{2}} \\[2mm] &+\beta (\delta -l)\frac{\partial \psi}{\partial l}+\frac{1}{2}\sigma^{2}l\frac{\partial ^{2}\psi}{\partial l^{2}}+(\pi_{I}(t)-k\pi_{R}(t))\sigma l \rho \frac{\partial ^{2}\psi}{\partial \widehat{x} \partial l} \\[2mm] &+\lambda_{0}E\Big[\psi(t,\widehat{x}-Z(kq(t)+q(t)-k),l)-\psi(t,\widehat{x},l)\Big]. \end{align*}$
对于任意的函数 $\phi(t,y,l)\in C^{1,2,2}$ $\mathcal{L}^{u_{I},u_{R}}_{2}$
(2.13) $\begin{align*} \mathcal{L}^{u_{I},u_{R}}_{2} \phi(t,y,l) =\,&\frac{\partial \phi}{\partial t}+\Big[ry+\alpha l \pi_{R}(t)+(1-q(t))(p(t)-a)\Big]\frac{\partial \phi}{\partial y} \\ &+\frac{1}{2}\Big[(1-q(t))^{2}b^{2}+l\pi_{R}^{2}(t)\Big]\frac{\partial ^{2}\phi}{\partial {y}^{2}}+\beta (\delta-l)\frac{\partial \phi}{\partial l} \\ &+\frac{1}{2}\sigma^{2}l \frac{\partial^{2} \phi}{\partial {l}^{2}}+\sigma l \rho \pi_{R}(t)\frac{\partial^{2}\phi}{\partial y \partial l}+\lambda_{0}E\Big[\phi(t,y-Z(1-q(t)),l)-\phi(t,y,l)\Big]. \end{align*}$
假设2.1 给定多项式增长条件中的常数 $p\geq 1$ $(u_{I}, u_{R})$ $(t, \widehat{x})\in [T]\times R$ $(t, y)\in [T]\times R$
下面的定理提供了与均值-方差问题 (2.10) 和 (2.11) 相关的扩展HJB方程的验证定理.
(2.15) 定理2.1 [验证定理]对于问题 (2.10), 我们假设存在实值函数 $W_{I}(t,\widehat{x},l), g_{I}(t,\widehat{x},l) \in D_{p}^{1,2,2}([T]\times R \times R^{+})$ 分别满足下面扩展的 HJB 方程 (2.14) 和
(2.14) $\begin{align*} & \underset{u_{I}\in U_{I}}{\rm{max}}\Big\{\mathcal{L}_{1}^{u_{I},u_{R}}W_{I}(t, \widehat{x},l)-\mathcal{L}_{1}^{u_{I},u_{R}}\frac{\gamma_{1}}{2}g_{I}^{2}(t, \widehat{x},l) \\ & +\gamma_{1}g_{I}(t, \widehat{x},l)\times \mathcal{L}_{1}^{u_{I},u_{R}}g_{I}(t, \widehat{x},l) \Big\}=0,\,\,\,0\leq t\leq T, \end{align*}$
(2.15) $\begin{equation} \mathcal{L}_{1}^{u^{*}_{I},u_{R}}g_{I}(t, \widehat{x},l)=0,\ W_{I}(T,\widehat{x},l)=\widehat{x},\ g_{I}(T,\widehat{x},l)=\widehat{x}, \,\,\, 0\leq t\leq T,\end{equation}$
那么 $W_{I}(t, \widehat{x},l)=V_{I}(t, \widehat{x},l),\ E_{t, \widehat{x},l}\left[ \widehat{X}^{u_{I}^{*},u_{R}}(T)\right] =g_{I}(t, \widehat{x},l),$ $u^{*}_{I}$
(2.17) (验证定理) 对于问题 $(2.11)$, 我们假设存在实值函数 $ W_{R}(t,y,l),\ g_{R}(t,y,l)\in D_{p}^{1,2,2}([T]\times R \times R^{+})$ 满足下面扩展的 HJB 方程 (2.16) 和
(2.16) $\begin{equation} \begin{aligned} &\underset{u_{R}\in U_{R}}{\rm{max}}\Big\{\mathcal{L}_{2}^{u^{*}_{I},u_{R}}W_{R}(t, y,l)-\mathcal{L}_{2}^{u^{*}_{I},u_{R}}\frac{\gamma_{2}}{2}g_{R}^{2}(t, y,l) \\ &+\gamma_{2}g_{R}(t, y,l)\times \mathcal{L}_{2}^{u^{*}_{I},u_{R}}g_{R}(t, y,l) \Big\}=0,\,\,\, 0\leq t\leq T, \end{aligned} \end{equation}$
(2.17) $\begin{equation} \mathcal{L}_{2}^{u^{*}_{I},u^{*}_{R}}g_{R}(t, y,l)=0,\ W_{R}(T,y,l)=y,\ g_{R}(T,y,l)=y,\,\,\, 0\leq t\leq T, \end{equation}$
那么 $W_{R}(t, y,l)=V_{R}(t, y,l),\ E_{t, y,l}\left[ Y^{u_{I}^{*},u^{*}_{R}}(T)\right] =g_{R}(t,y,l),$ $u^{*}_{R}$
证 因为定理的两部分的证明相似, 下面仅证明第一部分. 假设 $W_{I}(t,\widehat{x},l)$ $g_{I}(t,\widehat{x},l)$ $u^{*}_{I}$
(2.18) $\begin{equation} g_{I}(t,\widehat{x},l)=E_{t,\widehat{x},l}\left[ \widehat{X}^{u^{*}_{I},u_{R}}(T)\right],\\ \ W_{I}(t,\widehat{x},l)=V_{I}(t,\widehat{x},l). \end{equation}$
为鞅, 其中 $\widetilde{N}({\rm d}s, {\rm d}z)=N({\rm d}s, {\rm d}z)-\nu({\rm d}z){\rm d}s$ $N({\rm d}s, {\rm d}z)$
(2.19) $\begin{equation} g_{I}(t,\widehat{x},l)=E_{t,\widehat{x},l}\left[ g_{I}(T,\widehat{X}^{u_{I}^{*},u_{R}}(T),l(T))\right] =E_{t,\widehat{x},l}\left[ \widehat{X}^{u^{*}_{I},u_{R}}(T)\right]. \end{equation}$
接下来, 证明 $W_{I}(t,\widehat{x},l)=V_{I}(t,\widehat{x},l)$ . 最优策略在 (2.14) 式左侧取得, 同时与 (2.15) 式结合起来可得
(2.20) $\begin{equation} \mathcal{L}_{1}^{u_{I}^{*},u_{R}}W_{I}(t, \widehat{x},l)-\mathcal{L}_{1}^{u_{I}^{*},u_{R}}\frac{\gamma_{1}}{2}g_{I}^{2}(t, \widehat{x},l)=0. \end{equation}$
根据条件 $W_{I}(T,\widehat{x},l)=\widehat{x}$
(2.21) $\begin{equation} \begin{aligned} E_{t, \widehat{x},l}\left[\widehat{X}^{u^{*}_{I},u_{R}}(T)\right] &=E_{t,\widehat{x},l}\left[ W_{I}(T, \widehat{X}^{u_{I}^{*},u_{R}}(T),l(T))\right] \\ &=W_{I}(t, \widehat{x},l)+E_{t,\widehat{x},l}\left[ \int _{t}^{T}\mathcal{L}_{1}^{u^{*}_{I},u_{R}}W_{I}(s, \widehat{X}^{u^{*}_{I}}(s),l(s)){\rm d}s \right]. \end{aligned} \end{equation}$
(2.22) $\begin{equation} W_{I}(t, \widehat{x},l)=E_{t, \widehat{x},l}\left[\widehat{X}^{u^{*}_{I},u_{R}}(T)\right]- \frac{\gamma_{1}}{2}E_{t,\widehat{x},l}\left[\int_{t}^{T}\mathcal{L}_{1}^{u^{*}_{I},u_{R}}g^{2}_{I}(s,\widehat{X}^{u^{*},u_{R}}(s),l(s)){\rm d}s\right]. \end{equation}$
此外, 根据终端条件, Ito 公式和 (2.19) 式, 可得
(2.23) $\begin{align*} & E_{t, \widehat{x},l}\left[(\widehat{X}^{u_{I}^{*},u_{R}}(T))^{2}\right] =E_{t,\widehat{x},l}\left[ g_{I}^{2}(T, \widehat{X}^{u_{I}^{*},u_{R}}(T),l(T))\right] \\ &=g_{I}^{2}(t, \widehat{x},l)+E_{t,\widehat{x},l}\left[ \int _{t}^{T}\mathcal{L}_{1}^{u_{I}^{*},u_{R}}g_{I}^{2}(s, \widehat{X}^{u_{I}^{*},u_{R}}(s),l(s)){\rm d}s\right] \\ &=\left(E_{t, \widehat{x},l}\left[ \widehat{X}^{u_{I}^{*},u_{R}}(T)\right]\right)^{2}+E_{t, \widehat{x},l}\left[ \int _{t}^{T}\mathcal{L}_{1}^{u_{I}^{*},u_{R}}g_{I}^{2}(s, \widehat{X}^{u^{*}_{I},u_{R}},l(s)){\rm d}s \right]. \end{align*}$
(2.24) $\begin{equation} Var_{t,\widehat{x},l} \left[ \widehat{X}^{u_{I}^{*},u_{R}}(T)\right]=E_{t,\widehat{x},l}\left[ \int _{t}^{T}\mathcal{L}_{1}^{u^{*}_{I},u_{R}}g^{2}_{I}(s, \widehat{X}^{u_{I}^{*},u_{R}}(s),l(s)){\rm d}s\right]. \end{equation}$
最后, 把 (2.24) 式代入到 (2.22) 式可得
(2.25) $\begin{equation} W_{I}(t,\widehat{x},l) =E_{t,\widehat{x},l}[\widehat{X}^{u^{*}_{I},u_{R}}(T)]-\frac{\gamma_{1}}{2}Var_{t,\widehat{x},l}[\widehat{X}^{u^{*}_{I},u_{R}}(T)]=J_{I}^{u^{*}_{I},u_{R}}(t,\widehat{x},l)=V_{I}(t,\widehat{x},l). \end{equation}$
步骤二 我们证明 $u^{*}_{I}$ $J_{I}^{u^{\epsilon}_{I},u_{R}}(t,\widehat{x},l)=E_{t,\widehat{x},l}[\widehat{X}^{u^{\epsilon}_{I},u_{R}}(T)]-\frac{\gamma_{1}}{2}Var_{t,\widehat{x},l}[\widehat{X}^{u^{\epsilon}_{I},u_{R}}(T)]$ $u^{\epsilon}_{I}$
(2.26) $\begin{align*} J_{I}^{u^{\epsilon}_{I},u_{R}}(t, \widehat{x},l) &=E_{t, \widehat{x},l}\left[ \widehat{X}^{u^{\epsilon}_{I},u_{R}}(T)\right] - \frac{\gamma_{1}}{2}Var_{t,\widehat{x},l}\left[ \widehat{X}^{u_{I}^{\epsilon},u_{R}}(T)\right] \\ &=E_{t, \widehat{x},l}\left[ \widehat{X}^{u_{I}^{\epsilon},u_{R}}(T)- \frac{\gamma_{1}}{2}(X^{u^{\epsilon}_{I},u_{R}}(T))^{2}\right] + \frac{\gamma_{1}}{2}\left(E_{t,\widehat{x},l}\left[ \widehat{X}^{u^{\epsilon}_{I},u_{R}}_{I}(T)\right]\right)^{2} \\ &=E_{t,\widehat{x},l}\left[E_{t+\epsilon,\widehat{X}^{\widehat{u}_{I},u_{R}}(t+\epsilon),l(t+\epsilon)}\left[ \widehat{X}^{u_{I}^{*},u_{R}}(T)- \frac{\gamma_{1}}{2}\left(X^{u_{I}^{*},u_{R}}(T)\right)^{2}\right]\right] \\ &\,\,\,\,\,\,\,+\frac{\gamma_{1}}{2}\left(E_{t, \widehat{x},l} \left[E_{t+\epsilon,\widehat{X}^{\widehat{u}_{I},u_{R}}(t+\epsilon),l(t+\epsilon)}\left[\widehat{X}^{u^{*}_{I},u_{R}}(T)\right]\right]\right)^{2} \\ &=E_{t, \widehat{x},l}\left[J^{{u}^{*}_{I},u_{R}}_{I}\left( t+\epsilon,\widehat{X}^{\widehat{u}_{I},u_{R}}(t+\epsilon),l(t+\epsilon) \right)\right] \\ &\,\,\,\,\,\,\,-\frac{\gamma_{1}}{2}E_{t, \widehat{x},l}\left[ \left( E_{t+\epsilon,\widehat{X}^{\widehat{u}_{I},u_{R}}(t+\epsilon),l(t+\epsilon)}\left[\widehat{X}^{u^{*}_{I},u_{R}}(T) \right] \right)^{2}\right] \\ &\,\,\,\,\,\,\,+\frac{\gamma_{1}}{2}\left(E_{t, \widehat{x},l}\left[ E_{t+\epsilon,\widehat{X}^{\widehat{u}_{I},u_{R}}(t+\epsilon),l(t+\epsilon)}\left[\widehat{X}^{u^{*}_{I},u_{R}}(T) \right] \right]\right)^{2} \\ &=E_{t, \widehat{x},l}\left[ J_{I}^{u_{I}^{*},u_{R}}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right] \\ &\,\,\,\,\,\,\,- \frac{\gamma_{1}}{2}E_{t, \widehat{x},l}\left[ g_{I}^{2}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right] \\ &\,\,\,\,\,\,\,+\frac{\gamma_{1}}{2}\left(E_{t, \widehat{x},l}\left[ g_{I}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right]\right)^{2}. \end{align*}$
然后我们把 $g^{2}_{I}(t,\widehat{x},l)$ $W_{I}(t,\widehat{x},l)$
(2.27) $\begin{equation} \begin{aligned} J_{I}^{u_{I}^{\epsilon},u_{R}}(t, \widehat{x},l) &=E_{t, \widehat{x},l}\left[ W_{I}^{u_{I}^{*},u_{R}}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right]\\ &\,\,\,\,\,\,\,- \frac{\gamma_{1}}{2}\left\{ E_{t, \widehat{x},l }\left[ g_{I}^{2}(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon) )\right] -g^{2}_{I}(t, \widehat{x},l )\right\}\\ &\,\,\,\,\,\,\,+ \frac{\gamma_{1}}{2}\left\{\left(E_{t,\widehat{x},l}\left[ g_{I}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{1},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right]\right)^{2}-g^{2}_{I}(t, \widehat{x},l)\right\}. \end{aligned} \end{equation}$
对于任意的 $u_{I}\in U_{I}$ $\epsilon>0$ $W_{I}(t,\widehat{x},l)\in D_{p}^{1,2,2}([T]\times R \times R^{+})$
(2.28) $\begin{equation} \mathcal{L}_{1 \epsilon}^{u_{I},u_{R}}W_{I}(t, \widehat{x},l):=E_{t,\widehat{x},l}\left[ W_{I}\left(t+ \epsilon, \widehat{X}^{u_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right] -W_{I}(t, \widehat{x},l). \end{equation}$
(2.29) $\begin{equation} \mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}W_{I}(t, \widehat{x},l)= \lim _{\epsilon \downarrow 0}\frac{\mathcal{L} _{1\epsilon}^{\widehat{u}_{I},u_{R}}W_{I}(t, \widehat{x},l)}{\epsilon}. \end{equation}$
(2.30) $\begin{equation} \begin{aligned} J_{I}^{u_{I}^{\epsilon},u_{R}}(t, \widehat{x},l) &=W_{I}(t,\widehat{x},l)+\mathcal{L}^{\widehat{u}_{I},u_{R}}_{1\epsilon}W_{I}(t,\widehat{x},l)-\frac{\gamma_{1}}{2}\mathcal{L}^{\widehat{u}_{I},u_{R}}_{1\epsilon}g^{2}_{I}(t,\widehat{x},l)\\ &\,\,\,\,\,\,\,+ \frac{\gamma_{1}}{2}\left\{\left(E_{t,\widehat{x},l}\left[ g_{I}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{1},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right]\right)^{2}-g^{2}_{I}(t, \widehat{x},l)\right\}. \end{aligned} \end{equation}$
(2.31) $\begin{equation} \begin{aligned} & E_{t, \widehat{x},l}\left[ g_{I}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right]\\ &=g_{I}(t, \widehat{x},l)+E_{t,\widehat{x},l} \left[ \int _{t}^{t+ \epsilon}\mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}g_{I}\left(s, \widehat{X}^{\widehat{u}_{I},u_{R}}(s),l(t+\epsilon)\right){\rm d}s \right], \end{aligned} \end{equation}$
(2.32) $\begin{equation} \begin{aligned} & \left\{ E_{t, \widehat{x},l}\left[ g_{I}\left(t+ \epsilon, \widehat{X}^{\widehat{u}_{I},u_{R}}(t+ \epsilon),l(t+\epsilon)\right)\right] \right\} ^{2}-g^{2}(t, \widehat{x},l )\\ &=2g_{I}(t, \widehat{x},l)E_{t, \widehat{x},l}\left[ \int _{t}^{t+ \epsilon}\mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}g_{I}\left(s, \widehat{X}^{\widehat{u}_{I},u_{R}}(s),l(s)\right){\rm d}s\right]\\ &\,\,\,\,\,\,\,+ \left\{ E_{t, \widehat{x},l}\left[ \int _{t}^{t+ \epsilon}\mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}g_{I}\left(s, \widehat{X}^{\widehat{u}_{I},u_{R}}(s),l(s)\right){\rm d}s \right] \right\} ^{2}. \end{aligned} \end{equation}$
将 (2.32) 式代入到 (2.30) 式中, 可得
(2.33) $\begin{equation} \begin{aligned} J_{I}^{u_{I}^{\epsilon},u_{R}}(t, \widehat{x},l) &=W_{I}(t,\widehat{x},l)+\mathcal{L}^{\widehat{u}_{I},u_{R}}_{1\epsilon}W_{I}(t,\widehat{x},l)-\frac{\gamma_{1}}{2}\mathcal{L}^{\widehat{u}_{I},u_{R}}_{1\epsilon}g^{2}_{I}(t,\widehat{x},l)\\ &\,\,\,\,\,\,\,+\gamma_{1}g_{I}(t, \widehat{x})E_{t, \widehat{x}}\left[ \int _{t}^{t+ \epsilon}\mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}g_{I}\left(s, \widehat{X}^{\widehat{u}_{I},u_{R}}(s)\right){\rm d}s\right]\\ &\,\,\,\,\,\,\,+\frac{\gamma_{1}}{2}\left\{ E_{t, \widehat{x},l}\left[ \int _{t}^{t+ \epsilon}\mathcal{L}_{1}^{\widehat{u}_{I},u_{R}}g_{I}\left(s, \widehat{X}^{\widehat{u}_{I},u_{R}}(s),l(s)\right){\rm d}s \right] \right\} ^{2}. \end{aligned} \end{equation}$
由 (2.14) 式中的扩展 HJB 方程, 可得
因此, $u^{*}_{I}$
3 主要结果
我们依次求解问题的纳什均衡策略和相应的值函数, 为了简化计算和表达, 我们记
(3.1) $\begin{equation} \begin{aligned} &\Theta= \frac{\alpha ^{4}\sigma ^{2}(1- \rho ^{2})}{2\gamma_{1}(\beta + \alpha \rho \sigma)^{2}},\quad \Phi= \frac{\alpha ^{3}\rho \sigma}{\gamma_{1}(\beta + \alpha \rho \sigma)},\quad \Psi= \frac{\alpha ^{2}}{2\gamma_{1}}-(\Theta + \Phi),\\ &\xi= \frac{2 \Theta + \Phi}{\alpha \rho \sigma}- \frac{\Theta}{\beta +2 \alpha \rho \sigma}- \frac{\Psi}{\beta},\quad H=\frac{\gamma_{1}(1+k)+\gamma_{2}}{2\gamma_{1}(1+k)+\gamma_{2}},\\ &H^{\theta}=\frac{\theta \lambda_{0}\mu_{z}} {\gamma_{1}(b^{2}+\lambda_{0} \sigma^{2}_{z}) } {\rm e}^{r(t-T)},\quad H^{\bar{\theta}}=\frac{\bar{\theta}\lambda_{0}\mu_{z}}{\gamma_{1}(b^{2}+\lambda_{0}\sigma^{2}_{z})} {\rm e}^{r(t-T)}. \end{aligned} \end{equation}$
步骤一 在 Stackelberg 博弈中, 再保险公司 (即领导者) 首先宣布其任何可接受的策略 $(p(\cdot),\ \pi_{R}(\cdot)) \in U_{R};$
步骤二 在观测到再保险公司的策略后, 保险公司 (即追随者) 在均值方差准则下解决优化问题 (2.10). 首先利用变分算子 (2.12), 我们可以把等式 (2.14) 简化为
(3.2) $\begin{equation} \begin{aligned} &\underset{u_{I}\in U_{I}}{\rm{max}} \left \{\frac{\partial W_{I}}{\partial t}+\Big[r\widehat{x}+\alpha l (\pi_{I}(t)-k\pi_{R}(t))+\theta a -(1+k)(1-q(t))\right.\\ &\left.(p(t)-a)\Big]\frac{\partial W_{I}}{\partial \widehat{x}}+\frac{1}{2}\Big[(bq(t)-kb+kbq(t))^{2}+(\pi_{I}(t)-k\pi_{R}(t))^{2}l\Big]\frac{\partial ^{2} W_{I}} {\partial \widehat{x}^{2}}\right.\\ &\left.+\beta(\delta-l)\frac{\partial W_{I}}{\partial l}+\frac{1}{2}\sigma^{2}l\frac{\partial^{2} W_{I} }{\partial {l}^{2}}+(\pi_{I}(t)-k\pi_{R}(t))\sigma l \rho \frac{\partial^{2}W_{I}}{\partial \widehat{x} \partial l}\right.\\ &\left.+\lambda_{0}E\Big[ W_{I} (t,\widehat{x}-z(kq(t)+q(t)-k),l)-W_{I}(t,\widehat{x},l)\Big]\right.\\ &\left.-\frac{\gamma_{1}}{2}\Big[(bq(t)-kb+kbq(t))^{2}+(\pi_{I}(t)-k\pi_{R}(t))^{2}l\Big]\left(\frac{\partial g_{I}}{\partial \widehat{x}}\right)^{2}\right.\\ &\left.-\frac{\gamma_{1}}{2}\sigma^{2}l\left(\frac{\partial g_{I}}{\partial l}\right)^{2}-\gamma_{1} (\pi_{I}(t)-k\pi_{R}(t) )\sigma l \rho \left(\frac{\partial g_{I}}{\partial \widehat{x}}\right)\left(\frac{\partial g_{I}}{\partial l}\right)\right.\\ &\left.-\frac{\gamma_{1}}{2}\lambda_{0}E\Big[g_{I}(t,\widehat{x}-z(kq(t)+q(t)-k),l)-g_{I}(t,\widehat{x},l)\Big]^{2} \right\}=0.\\ \end{aligned} \end{equation}$
为了求解 (2.15) 和 (3.2) 式, 我们推测保险公司的解有如下形式
(3.3) $\begin{align*} &\underset{u_{I}\in U_{I}}{\rm{max}} \Big\{A^{\prime}_{1}(t)\widehat{x}+B^{\prime}_{1}(t)l+C^{\prime}_{1}(t)+[r\widehat{x}+\alpha l (\pi_{I}(t)-k\pi_{R}(t))+\theta a-(1+k)(1-q(t)) \\ &(p(t)-a)]A_{1}(t)+\beta(\delta-l)B_{1}(t)-\lambda_{0}(kq(t)+q(t)-k)\mu_{z}A_{1}(t) \\ &-\frac{\gamma_{1}}{2} [(bq(t)-kb+kbq(t))^{2}+(\pi_{I}(t)-k \pi_{R}(t))^{2}l ]A^{2}_{2}(t) \\ &-\frac{\gamma_{1}}{2}\sigma^{2}lB^{2}_{2}(t)-\gamma_{1}(\pi_{I}(t)-k\pi_{R}(t))\sigma l \rho A_{2}(t)B_{2}(t) \\ &-\frac{\gamma_{1}}{2}\lambda_{0}\sigma^{2}_{z}\Big(kq(t)+q(t)-k\Big)^{2}A^{2}_{2}(t) \Big\}=0. \end{align*}$
通过上面两个等式, 可知投资策略和再保险策略是独立的. 因此, $f^{*}(\cdot,\ p(\cdot), \ \pi _{R}(\cdot))$ $g^{*}(\cdot,\ p(\cdot),$ $ \pi _{R}(\cdot))$
可以分别写为 $f^{*}(\cdot,\ p(\cdot))$
和 $g^{*}(\cdot,\ \pi _{R}(\cdot)),$ $q(t)\in[0, 1]$
(3.4) $q^{*}(t,p(t))=f^{*}(t,p(t))= \left[ \frac{(p(t)- \lambda_{0} \mu_{z}-a)A_{1}(t)}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z}){A}^{2}_{2}(t)}+ \frac{k}{1+k}\right] \vee 0\wedge 1,$
(3.5) $\pi _{I}^{*}(t)=g^{*}(t, \pi _{R}(t))= \frac{\alpha A_{1}(t)-\gamma_{1}\sigma \rho A_{2}(t)B_{2}(t)}{\gamma_{1} A^{2}_{2}(t)}+k \pi _{R}(t).$
那么 $q^{*}(t,p(t))=1$ $q^{*}(t,p(t))=1$ $\pi^{*}_{I}(t)$
通过分离变量 $\widehat{x}$ $l$
结合边值条件 $A_{1}(T)=A_{2}(T)=1,\ B_{1}(T)=B_{2}(T)=0,\ C_{1}(T)=C_{2}(T)=0$
(3.6) $ A_{1}(t)={\rm e}^{r(T-t)},\quad A_{2}(t)={\rm e}^{r(T-t)},$
(3.7) $B_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta},$
(3.8) $B_{2}(t)=\frac{\alpha^{2}}{\gamma_{1}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right],$
(3.9) $\begin{align*}& C_{1}^{Ia}(t)=\delta \Psi(T-t)+\frac{\theta \lambda_{0}\mu_{z}}{r}[{\rm e}^{r(T-t)-1}]-\frac{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{4r}[{\rm e}^{2r(T-t)}-1] \\ &\qquad\qquad+\delta \xi[1-{\rm e}^{\beta(t-T)}]-\frac{\beta\delta(2\Theta+\Phi)}{\alpha\sigma\rho(\beta+\alpha\sigma\rho)}[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}] \\ &\qquad\qquad+\frac{\beta\delta\theta}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}], \end{align*}$
(3.10) $\begin{align*}& C_{2}^{Ia}(t)=\frac{\theta\lambda_{0}\mu_{z}}{r}[{\rm e}^{r(T-t)}-1]+\frac{\beta\delta\alpha^{2}}{\gamma_{1}(\beta+\alpha\sigma\rho)} +\frac{\beta\delta\alpha^{2}}{\gamma_{1}(\beta+\alpha\sigma\rho)}(T-t) \\[2mm] &\qquad\qquad-\frac{\beta\delta\alpha^{2}}{\gamma_{1}(\beta+\alpha\sigma\rho)^{2}}[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]. \end{align*}$
把等式 (3.6) 代入到 (3.5) 式, 我们可以得到保险公司的最优策略
(3.11) $\begin{equation} q^{*}(t,p(t))=1,\quad \pi^{*}_{I}(t)=\frac{\alpha-\gamma_{1}\sigma\rho B_{2}(t)}{\gamma_{1}{\rm e}^{r(T-t)}}+k\pi_{R}(t). \end{equation}$
我们把 $q^{*}(t,p(t))$ $\pi^{*}_{I}(t)$
通过分离变量 $\widehat{x}$ $l$
结合边值条件 $A_{1}(T)=A_{2}(T)=1,\ B_{1}(T)=B_{2}(T)=0,\ C_{1}(T)=C_{2}(T)=0$
(3.12) $A_{1}(t)={\rm e}^{r(T-t)},\quad A_{2}(t)={\rm e}^{r(T-t)},$
(3.13) $B_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta},$
(3.14) $B_{2}(t)=\frac{\alpha^{2}}{\gamma_{1}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right],$
(3.15) $\begin{align*} C_{1}^{Ib}(t)&=\int_{t}^{T}\frac{(p(t)-a-\lambda_{0}\mu_{z})^{2}}{2\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{\rm d}s-\int_{t}^{T}(p(t)-a)A_{1}(s){\rm d}s \\ & +\frac{\beta \delta\theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho (\beta+\alpha\sigma\rho)} \\ & +\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}]+\frac{\theta a }{r}[{\rm e}^{r(T-t)}-1],\end{align*}$
(3.16) $\begin{align*} C_{2}^{Ib}(t)&=\frac{\theta a }{r}[{\rm e}^{r(T-t)}-1]+\frac{\alpha^{2}\beta\delta(T-t)}{\gamma_{2}(\beta+\alpha\sigma\rho)}+\frac{\alpha^{2}\beta\delta}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}-1] \\ & -\int_{t}^{T}(p(s)-a)A_{2}(s){\rm d}s+\int_{t}^{T}\frac{(p(s)-a-\lambda_{0}\mu_{z})^{2}}{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{\rm d}s. \end{align*}$
(3.17) $\begin{align*} &q^{*}(t,p(t))=\frac{(p(t)- \lambda_{0} \mu_{z}-a)}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z})A_{2}(t)}+ \frac{k}{1+k}, \\ &\pi^{*}_{I}(t)=\frac{\alpha-\gamma_{1}\sigma\rho B_{2}(t)}{\gamma_{1}A_{2}(t)}+k\pi_{R}(t). \end{align*}$
步骤三 再保险公司现在知道保险公司将根据等式 (3.4) 和 (3.5) 采取策略, 再保险公司将决定最优策略 $(p^{*}(t),\ \pi^{*}_{R}(t))\in U_{R}$
(3.18) $\begin{aligned} &\underset{u_{R}\in U_{R}}{\rm{max}} \Big\{\frac{\partial W_{R}}{\partial t}+[ry+\alpha l\pi_{R}(t)+(1-q^{*}(t))(p(t)-a)]\frac{\partial W_{R}}{\partial y}+\frac{1}{2}[(1-q^{*}(t))^{2}b^{2}\\ &+\pi^{2}_{R}(t)l]\frac{\partial ^{2} W_{R}} {\partial y^{2}}+\beta(\delta-l)\frac{\partial W_{R}}{\partial l}+\frac{1}{2}\sigma^{2}l\frac{\partial^{2} W_{R}}{\partial {l}^{2}} +\sigma\rho l \pi_{R}(t)\frac{\partial^{2} W_{R}}{\partial y \partial l}\\ &+\lambda_{0}E\left[ W_{R} (t,y-z(1-q^{*}(t)),l)-W_{R}(t,y,l)\right]-\frac{\gamma_{2}}{2}[(1-q^{*}(t))^{2}b^{2}\\ &+\pi^{2}_{R}(t)l] \left(\frac{\partial g_{R}}{\partial y}\right)^{2}-\frac{\gamma_{2}}{2}\sigma^{2}l\left(\frac{\partial g_{R}}{\partial l} \right)^{2}-\gamma_{2}\sigma\rho l\pi_{R}(t)\frac{\partial g_{R}}{\partial y}\frac{\partial g_{R} }{\partial l}\\ &-\frac{\gamma_{2}}{2}\lambda_{0}E[g_{R}(t,y-z(1-q^{*}(t)),l)-g_{R}(t,y,l)]^{2} \Big\}=0. \end{aligned}$
(3.19) $\begin{aligned} &\underset{u_{R}\in U_{R}}{\rm{max}} \Big\{D^{\prime}_{1}(t)y+E_{1}^{\prime}(t)l+F_{1}^{\prime}(t)+[ry+\alpha l \pi_{R}(t)+(1-q^{*}(t))(p(t)-a)]D_{1}(t)\\ &+\beta(\delta-l)E_{1}(t)-\lambda_{0}\mu_{z}(1-q^{*}(t))D_{1}(t)-\frac{\gamma_{2}}{2}[(1-q^{*}(t))^{2}b^{2}+\pi_{R}^{2}(t)l]D_{2}^{2}(t)\\ &-\frac{\gamma_{2}}{2}\sigma^{2} l E_{2}^{2}(t)-\gamma_{2}\sigma l \rho \pi_{R}(t)D_{2}(t)E_{2}(t)-\frac{\gamma_{2}}{2}\lambda_{0}\sigma_{z}^{2}(1-q^{*}(t))^{2}D_{2}^{2}(t)\Big\}=0. \end{aligned}$
在情况 (Ia) 下, 我们把 $q^{*}(t,p(t))=1$
(3.20) $\begin{equation} \begin{aligned} &\underset{u_{R}\in U_{R}}{\rm{max}} \Big\{D^{\prime}_{1}(t)y+E_{1}^{\prime}(t)l+F_{1}^{\prime}(t)+[ry+\alpha l\pi_{R}(t)]D_{1}(t) +\beta(\delta-l)E_{1}(t)\\ &-\frac{\gamma_{2}}{2}\pi_{R}^{2}(t)lD_{2}^{2}(t)-\frac{\gamma_{2}}{2}\sigma^{2} l E_{2}^{2}(t)-\gamma_{2}\sigma l \rho \pi_{R}(t)D_{2}(t)E_{2}(t) \Big\}=0. \end{aligned} \end{equation}$
上式对 $\pi_{R}(t)$
(3.21) $\begin{equation} \pi^{*}_{R}(t)=\frac{\alpha D_{1}(t)-\gamma_{2}\sigma\rho D_{2}(t)E_{2}(t)}{\gamma_{2}D_{2}^{2}(t)},\quad p^{*}(t)=p, \end{equation}$
这里 $p$ $[c,\ \bar{c}]$
通过分离变量 $y$ $l$
结合边值条件 $D_{1}(T)=D_{2}(T)=1,\ E_{1}(T)=E_{2}(T)=0,\ F_{1}(T)=F_{2}(T)=0$
(3.22) $D_{1}(t)={\rm e}^{r(T-t)},\quad D_{2}(t)={\rm e}^{r(T-t)},$
(3.23) $E_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta},$
(3.24) $E_{2}(t)=\frac{\alpha^{2}}{\gamma_{2}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right],$
(3.25) $\begin{align*} &F_{1}^{Ia}(t)=\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+2\alpha\sigma\rho)(\beta+\alpha\sigma\rho)}- \frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha \sigma\rho)(t-T)}]}{\alpha\sigma\rho(\beta+\alpha\sigma\rho)} \\ &\qquad\qquad+\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}], \end{align*}$
(3.26) $F_{2}^{Ia}(t)=\frac{\alpha^{2}\beta\delta(T-t)}{\gamma_{2}(\beta+\alpha\sigma\rho)}+\frac{\alpha^{2}\beta\delta}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}-1].$
这里先验条件 $\frac{(p(t)- \lambda_{0} \mu_{z}-a)A_{1}(t)}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z}){A}^{2}_{2}(t)}+ \frac{k}{1+k}\geq1$ $H^{\theta} \geq 1$ . 把等式 (3.22) 代入到等式 (3.21) 并结合等式 (3.11), 可以得到最优策略
这里 $p$ $[c,\ \bar{c}]$
在情况 (Ib) 中, 我们把$ q^{*}(t,p(t))=\frac{p(t)-a-\lambda_{0}\mu_{z}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z})A_{2}(t)}+\frac{k}{1+k}$
(3.27) $\begin{equation} \begin{aligned} &\underset{u_{R}\in U_{R}}{\rm{max}}\bigg\{ D^{\prime}_{1}(t)y+E^{\prime}(t)l+F^{\prime}_{1}(t)+ryD_{1}(t)+\alpha l \pi_{R}(t)D_{1}(t)+\beta(\delta-l)E_{1}(t)\\[2mm] &-\frac{\gamma_{2}}{2}\sigma^{2}lE_{2}^{2}(t)-\frac{\gamma_{2}}{2}\pi_{R}^{2}(t)lD_{2}^{2}(t)-\gamma_{2}\pi_{R}(t)\sigma l \rho D_{2}(t)E_{2}(t)\\[2mm] &+(p(t)-a-\lambda_{0}\mu_{z})D_{1}(t)\left(\frac{1}{1+k}-\frac{p(t)-a-\lambda_{0}\mu_{z}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})A_{2}(t)}\right)\\[2mm] &-\frac{\gamma_{2}}{2}D_{2}^{2}(t)(b^{2}+\lambda_{0}\sigma_{z}^{2})\left(\frac{1}{1+k}-\frac{p(t)- a-\lambda_{0}\mu_{z}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})A_{2}(t)} \right)^{2} \bigg \}=0. \end{aligned} \end{equation}$
通过对 $p(t)$ $\pi_{R}(t)$
我们取 $p^{*}(t)=\bar{c}$ $ q^{*}(t)=\frac{\bar{\theta}\lambda_{0}\mu_{z}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z})A_{2}(t)}+\frac{k}{1+k}=\frac{H^{\bar{\theta}}+k}{1+k},$
通过分离变量 $y$ $l$
结合边值条件 $D_{1}(T)=D_{2}(T)=1,\ E_{1}(T)=E_{2}(T)=0,\ F_{1}(T)=F_{2}(T)=0$
(3.28) $\begin{align*} &D_{1}(t)={\rm e}^{r(T-t)},\quad D_{2}(t)={\rm e}^{r(T-t)}, \nonumber\\[1mm] &E_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta}, \nonumber\\[2mm] &E_{2}(t)=\frac{\alpha^{2}}{\gamma_{2}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right], \nonumber\\[2mm] &F_{1}^{Ib1}(t)=\frac{\bar{\theta}\lambda_{0}\mu_{z}}{r(1+k)}[{\rm e}^{r(T-t)}-1]-\frac{\bar{\theta}^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t)\nonumber\\[2mm] &\qquad\qquad-\frac{\gamma_{2}}{4r(1+k)^{2}}(b^{2}+\lambda_{0}\sigma_{z}^{2})[{\rm e}^{2r(T-t)}-1]+\frac{\gamma_{2}}{\gamma_{1}}\frac{\bar{\theta}\lambda_{0}\mu_{z}}{r(1+k)^{2}}[{\rm e}^{r(T-t)}-1]\nonumber\\[2mm] &\qquad\qquad-\frac{\gamma_{2}\bar{\theta}^{2}\lambda_{0}^{2}\mu_{z}^{2}}{2\gamma_{1}^{2}(1+k)^{2}(b^{2}+\lambda_{0}\sigma_{z}^{2})}[T-t] +\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}\nonumber\\[2mm] &\qquad\qquad-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho(\beta+\alpha\sigma\rho)} +\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}],\end{align*}$
(3.29) $\begin{align*} &F_{2}^{Ib1}(t)=\frac{\bar{\theta}\lambda_{0}\mu_{z}}{r(1+k)}[{\rm e}^{r(T-t)}-1]-\frac{\bar{\theta}^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t)\nonumber\\[2mm] &\qquad\qquad+\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)}(T-t)-\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}].\end{align*}$
变为 $H^{\bar{\theta}}\leq H$ $H^{\theta}<H^{\bar{\theta}}\leq H<1$
自然就是正确的.等式 (3.15) 和 (3.16) 变为
(3.30) $\begin{align*} C^{Ib1}_{1}(t)&=\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho(\beta+\alpha\sigma\rho)} \\ & +\frac{(\theta-\bar{\theta})a}{r}[{\rm e}^{r(T-t)}-1]+\frac{\bar{\theta}^{2}\lambda_{0}^{2}\mu_{z}^{2}}{2\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t)\\ & +\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}], \end{align*}$
(3.31) $\begin{equation} \begin{aligned} C^{Ib1}_{2}(t)&=\frac{(\theta-\bar{\theta})a}{r}[{\rm e}^{r(T-t)}-1]+\frac{\alpha^{2}\beta\delta(T-t)}{\gamma_{2}(\beta+\alpha\sigma\rho)}\\ & +\frac{\alpha^{2}\beta\delta}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}-1] +\frac{\bar{\theta}^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t). \end{aligned} \end{equation}$
我们取 $p^{*}(t)=c$ $ q^{*}(t)=\frac{\theta\lambda_{0}\mu_{z}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma^{2}_{z})A_{2}(t)}+\frac{k}{1+k}=\frac{H^{\theta}+k}{1+k},$
通过分离变量 $y$ $l$
结合边值条件 $D_{1}(T)=D_{2}(T)=1,\ E_{1}(T)=E_{2}(T)=0,\ F_{1}(T)=F_{2}(T)=0$
(3.32) $\begin{align*} &D_{1}(t)={\rm e}^{r(T-t)},\quad D_{2}(t)={\rm e}^{r(T-t)}, \nonumber\\ &E_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta}, \nonumber\\ &E_{2}(t)=\frac{\alpha^{2}}{\gamma_{2}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right], \nonumber\\ &F_{1}^{Ib2}(t)=\frac{\theta\lambda_{0}\mu_{z}}{r(1+k)}[{\rm e}^{r(T-t)}-1]-\frac{\theta^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t)\nonumber\\ &\qquad\qquad-\frac{\gamma_{2}}{4r(1+k)^{2}}(b^{2}+\lambda_{0}\sigma_{z}^{2})[{\rm e}^{2r(T-t)}-1]+\frac{\gamma_{2}}{\gamma_{1}}\frac{\theta\lambda_{0}\mu_{z}}{r(1+k)^{2}}[{\rm e}^{r(T-t)}-1]\nonumber\\ &\qquad\qquad-\frac{\gamma_{2}\theta^{2}\lambda_{0}^{2}\mu_{z}^{2}}{2\gamma_{1}^{2}(1+k)^{2}(b^{2}+\lambda_{0}\sigma_{z}^{2})}[T-t] +\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}\nonumber\\ &\qquad\qquad-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho(\beta+\alpha\sigma\rho)} +\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}],\end{align*}$
(3.33) $\begin{align*} &F_{2}^{Ib2}(t)=\frac{\theta\lambda_{0}\mu_{z}}{r(1+k)}[{\rm e}^{r(T-t)}-1]-\frac{\theta^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(1+k)(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t)\nonumber\\ &\qquad\qquad+\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)}(T-t)-\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]. \end{align*}$
意味着 $H\leq H^{\theta}$ $H^{\theta}<1$ $H\leq H^{\theta}<1$ . 因此等式 (3.15) 和 (3.16) 变为
(3.34) $\begin{align*} C^{Ib2}_{1}(t)&=\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho(\beta+\alpha\sigma\rho)} \\ & +\frac{\theta^{2}\lambda_{0}^{2}\mu_{z}^{2}}{2\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t) +\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}],\end{align*}$
(3.35) $\begin{align*} C^{Ib2}_{2}(t)&=\frac{\alpha^{2}\beta\delta(T-t)}{\gamma_{2}(\beta+\alpha\sigma\rho)} +\frac{\alpha^{2}\beta\delta}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}-1] \\ & +\frac{\theta^{2}\lambda_{0}^{2}\mu_{z}^{2}}{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}(T-t). \end{align*}$
把它们代入到等式 (2.17) 和 (3.27) 可得
通过分离变量 $y$ $l$
结合边值条件 $D_{1}(T)=D_{2}(T)=1,\ E_{1}(T)=E_{2}(T)=0\ F_{1}(T)=F_{2}(T)=0$
(3.36) $\begin{align*} &D_{1}(t)={\rm e}^{r(T-t)},\quad D_{2}(t)={\rm e}^{r(T-t)}, \\ &E_{1}(t)=\frac{\Theta {\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}}{\beta+2\alpha\sigma\rho}-\frac{(2\Theta+\Phi){\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}}{\alpha \sigma \rho}+\xi {\rm e}^{\beta(t-T)}+\frac{\Psi}{\beta}, \\ &E_{2}(t)=\frac{\alpha^{2}}{\gamma_{2}(\beta+\alpha \sigma \rho)}\left[1-{\rm e}^{(\beta+\alpha \sigma \rho)(t-T)}\right], \\ &F_{1}^{Ib3}(t)=\frac{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{2r(1+k)}(H-H^{2}){\rm e}^{2r(T-t)}-\frac{\gamma_{1}^{2}\gamma_{2}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{4r[2\gamma_{1}(1+k)+\gamma_{2}]^{2}} {\rm e}^{2r(T-t)} \\ &\qquad\qquad+\frac{\beta\delta\Theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)} -\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho(\beta+\alpha\sigma\rho)} \\ &\qquad\qquad+\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}],\end{align*}$
(3.37) $\begin{align*}&F_{2}^{Ib3}(t)=\frac{\gamma_{1}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{2r(1+k)}(H-H^{2}){\rm e}^{2r(T-t)}+\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)}(T-t) \\ &\qquad\qquad-\frac{\beta\delta\alpha^{2}}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]. \end{align*}$
变为 $H^{\theta}<H<H^{\bar{\theta}}$ $ p^{*}(t)=a+\lambda_{0}\mu_{z}+(b^{2}+\lambda_{0}\sigma^{2}_{z})\gamma_{1}A_{2}(t)H, $ $q^{*}(t)=\frac{(1+2k)\gamma_{1}+\gamma_{2}}{2(1+k)\gamma_{1}+\gamma_{2}}$
(3.38) $\begin{align*} C_{1}^{Ib3}(t)=\,&\frac{\gamma_{1}H^{2}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{4r}[{\rm e}^{2r(T-t)}-1]-\frac{\lambda_{0}\mu_{z}}{r}[{\rm e}^{r(T-t)}-1] -\frac{\gamma_{1}H(b^{2}+\lambda_{o}\sigma_{z}^{2})} {2r}[{\rm e}^{2r(T-t)}-1] \\ &+\frac{\beta \delta\theta[1-{\rm e}^{2(\beta+\alpha\sigma\rho)(t-T)}]}{2(\beta+\alpha\sigma\rho)(\beta+2\alpha\sigma\rho)}-\frac{\beta\delta(2\Theta+\Phi)[1-{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}]} {\alpha\sigma\rho (\beta+\alpha\sigma\rho)} \\ &+\delta\Psi(T-t)+\delta\xi[1-{\rm e}^{\beta(t-T)}]+\frac{\theta a }{r}[{\rm e}^{r(T-t)}-1],\end{align*}$
(3.39) $\begin{align*}C_{2}^{Ib3}(t)=\,&\frac{\theta a }{r}[{\rm e}^{r(T-t)}-1]+\frac{\alpha^{2}\beta\delta(T-t)}{\gamma_{2}(\beta+\alpha\sigma\rho)}+\frac{\alpha^{2}\beta\delta}{\gamma_{2}(\beta+\alpha\sigma\rho)^{2}}[{\rm e}^{(\beta+\alpha\sigma\rho)(t-T)}-1] \\ &+\frac{\gamma_{1}H^{2}(b^{2}+\lambda_{0}\sigma_{z}^{2})}{2r}[{\rm e}^{2r(T-t)}-1]-\frac{\lambda_{0}\mu_{z}}{r}[{\rm e}^{r(T-t)}-1] \\ &-\frac{\gamma_{1}H(b^{2}+\lambda_{o}\sigma_{z}^{2})} {2r}[{\rm e}^{2r(T-t)}-1]. \end{align*}$
定理3.1 对于问题 (2.10) 和 (2.11), 保险公司和再保险公司的 Stackelberg 微分博弈的纳什均衡策略由($q^{*}(t),\ \pi_{I}^{*}(t),\ p^{*}(t),\ \pi_{R}^{*}(t)$ ) 给出, 其中 $q^{*}(t)$ $p^{*}(t)$ 表格1 分情况给出, $\pi_{I}^{*}(t)$ $\pi_{R}^{*}(t)$
(3.40) $\pi_{I}^{*}(t)=\frac{\alpha-\gamma_{1}\sigma\rho B_{2}(t)}{\gamma_{1}{\rm e}^{r(T-t)}}+k\frac{\alpha-\gamma_{2}\sigma\rho E_{2}(t)}{\gamma_{2}{\rm e}^{r(T-t)}},$
(3.41) $\pi_{R}^{*}(t)=\frac{\alpha-\gamma_{2}\sigma\rho E_{2}(t)}{\gamma_{2}{\rm e}^{r(T-t)}},$
其中 $H$ $H^{\bar{\theta}}$ $H^{\theta}$ $B_{2}(t)$ $E_{2}(t)$
(3.42) $V_{I}(t,\widehat{x})=A_{1}(t)\widehat{x}+B_{1}(t)l+C_{1}(t),$
(3.43) $V_{R}(t,y)=D_{1}(t)y+E_{1}(t)l+F_{1}(t),$
$C_{1}^{Ia}(t),\ C_{1}^{Ib1}(t),\ C_{1}^{Ib2}(t),\ C_{1}^{Ib3}(t),\ F_{1}^{Ia}(t),\ F_{1}^{Ib1}(t),\ F_{1}^{Ib2}(t),\ F_{1}^{Ib3}(t)$
(3.34), (3.38), (3.25),(3.28),(3.32),(3.36)给出.
命题3.1 定理 3.1中的 $q^{*}(t)$ $k$
证 在 (2), (3), (4) 分别对 $k$
很容易看出 $q^{* \prime}(t)$ $q^{*}(t)$ $k$
注3.1 从命题 3.1 中我们可以看出均衡保留水平 $q^{*}(t)$ $q^{*}(t)=1$ $k$ $k$ $k$
注3.2 从定理 3.1, 我们可以得到以下两个结论: 均衡再保险-投资策略与当前财富无关; 保险公司的投资策略独立于再保险策略. 这与大多数文献的结论相一致,如文献[23 ,32 ,33 ].
注3.3 与文献[20 ]和[23 ]相似, 在定理3.1中的情况 (Ib3), 最优再保险保费遵循方差保费原则. 也就是说, 对于每一单位的风险, 与让出比例 $1-q^{*}(t)$
4 数值分析
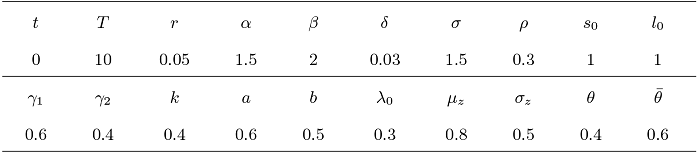
在本节中, 我们将给出一些数值例子, 对第 3 节推导的均衡再保险投资策略进行敏感性分析. 下面作为基准使用的基本模型参数如表2 所示, 除非另有说明, 否则这些参数不变.
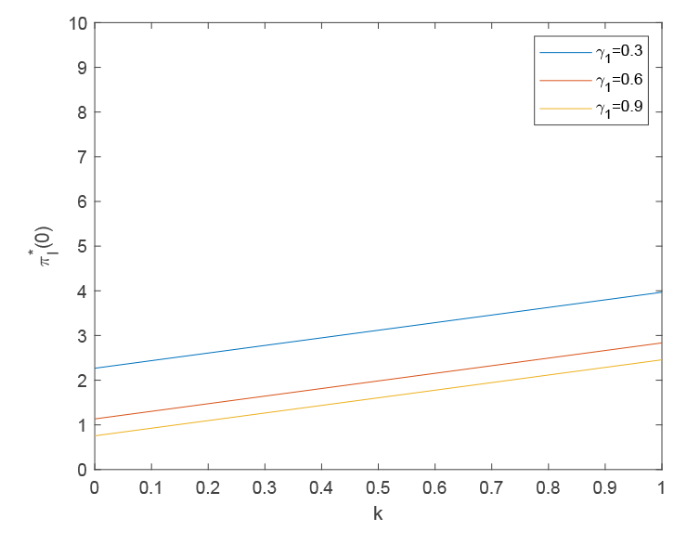
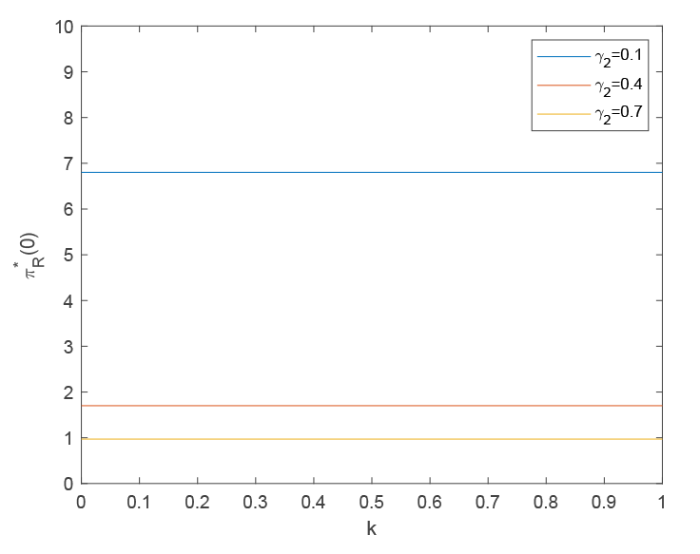
图1 显示了敏感性系数 $k$ $\gamma_{1}$ $\gamma_{1}$ $k$ $k$ $k = 0$ $\gamma_{2}$ 图2 描述了敏感性参数 $k$ $\gamma_{2}$ $\gamma_{2}$ $k$ $\gamma_{2}$
图1
图1
$k$ $\gamma_{1}$ $\pi_{I}^{*}(0)$
图2
图2
$k$ $\gamma_{2}$ $\pi_{R}^{*}(0)$
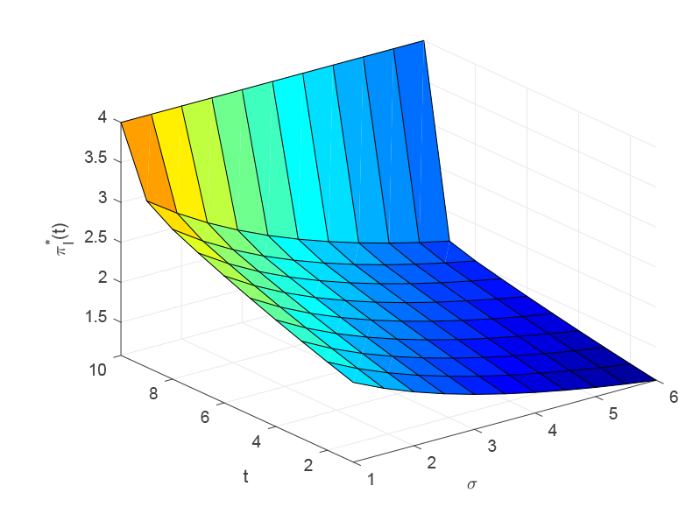
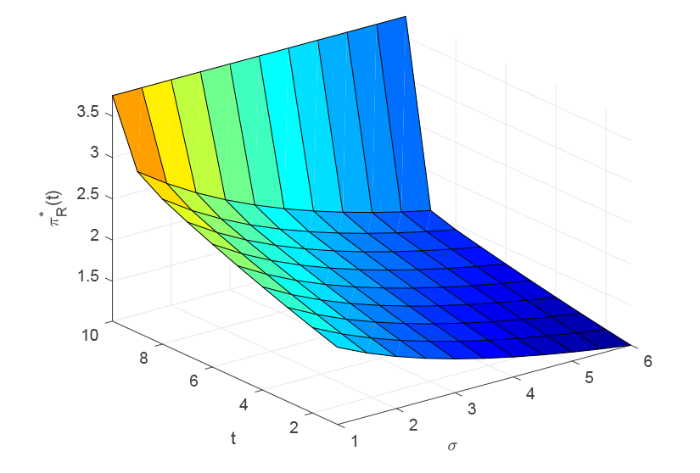
图3 和图4 描述了 $t$ $\sigma$ $\pi_{I}^{*}(t)$ $\pi_{R}^{*}(t)$ 图3 和图4 可以看出 $\pi_{I}^{*}(t)$ $\pi_{R}^{*}(t)$ $t$ $\pi_{I}^{*}(t)$ $\pi_{R}^{*}(t)$ $\sigma$
图3
图3
$t$ $\sigma$ $\pi_{I}^{*}(t)$
图4
图4
$t$ $\sigma$ $\pi_{R}^{*}(t)$
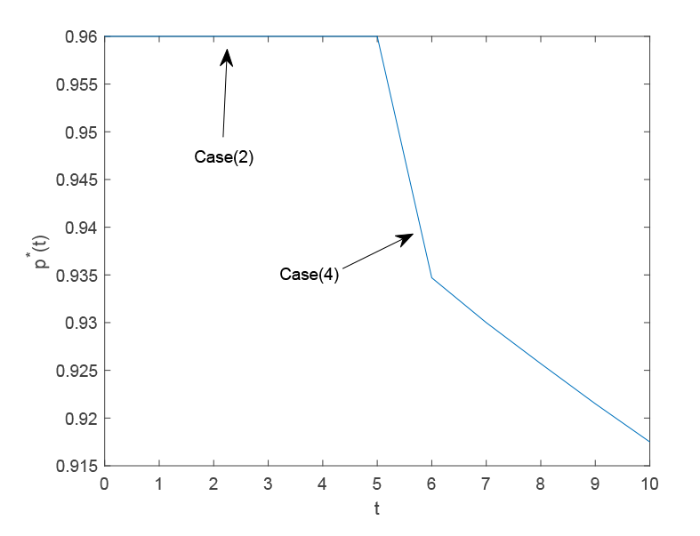
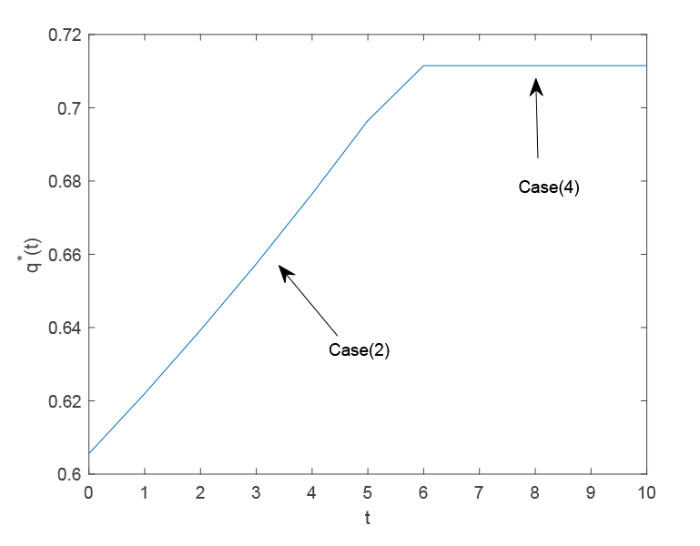
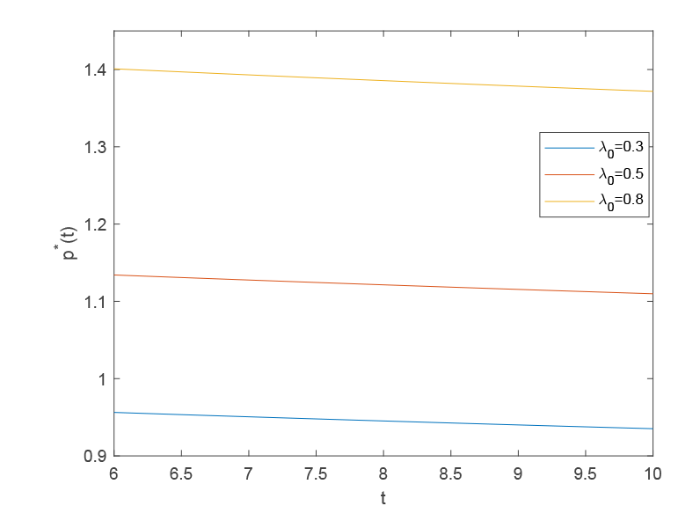
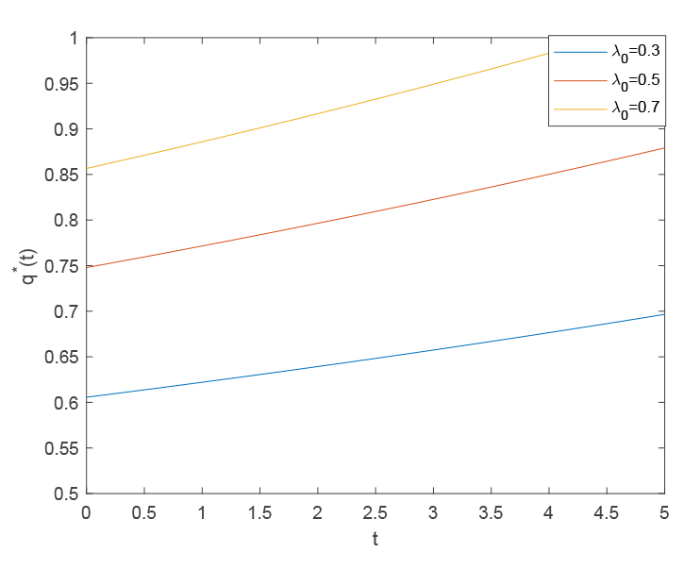
图5 和图6 描述了再保险公司的最优保费定价策略 $p^{*}(t)$ $q^{*}(t)$ 图5 和图6 对应的数值结果如表3 所示, 我们可以看出, 由于保险公司的财富水平不足以支持其早期的所有索赔, 因此保险公司有强烈的愿望与再保险公司签订再保险合同, 以降低其索赔风险. 因此, 由于再保险公司在供需关系中的优势地位, 再保险公司提供最昂贵的再保险保费价格作为其最优保费定价策略. 随着时间的推移, 保险公司也试图通过增加保留水平 $q^{*}(t)$ $q^{*}(t)$ $t$ $H^{\theta}<H<H^{\bar{\theta}}$ $\frac{(1+2k)\gamma_{1}+\gamma_{2}}{2(1+k)\gamma_{1}+\gamma_{2}}$ ) , 其再保险策略保持不变. 而再保险公司则降低其安全负荷, 以刺激保险公司增加再保险比例, 这是图5 中的 Case(4) 和表3 中 $t>5$
图5
图6
图7 描述了在 Case(4) 中 $\lambda_{0}$ $p^{*}(t)$ $\lambda_{0}$ $p^{*}(t)$ $t$ $t$ 图8 中我们可以看出, 在 Case(2) 中 $q^{*}(t)$ $t$ $t$ $q^{*}(t)$ $\lambda_{0}$
图7
图7
$\lambda_{0}$ $t$ $p^{*}(t)$
图8
图8
$\lambda_{0}$ $t$ $q^{*}(t)$
参考文献
View Option
[1]
Azcue P Muler N . Optimal investment strategy to minimize the ruin probability of an insurance company under borrowing constraints
Insurance: Mathematics and Economics , 2009 , 44 1 ): 26 -34
[本文引用: 1]
[2]
Han X Liang Z . Minimizing the probability of absolute ruin under the mean-variance premium principles
Optimal Control Applications and Methods , 2021 , 42 3 ): 786 -806
[3]
Ma J Bai L Liu J . Minimizing the probability of ruin under interest force
Applied Mathematical Sciences , 2008 , 17 2 ): 843 -851
[本文引用: 1]
[4]
Li D Rong X Zhao H . The optimal investment problem for an insurer and a reinsurer under the constant elasticity of variance model
IMA Journal of Management Mathematics , 2016 , 27 2 ): 255 -280
[本文引用: 1]
[5]
Wang Y Rong X Zhao H . Optimal investment strategies for an insurer and a reinsurer with a jump diffusion risk process under the CEV model
Journal of Computational and Applied Mathematics , 2018 , 3.8 414 -431
[6]
Zhou J Deng Y Huang Y Yang X . Optimal proportional reinsurance and investment for a constant elasticity of variance model under variance principle
Acta Math Sci , 2015 , 35B 2 ): 303 -312
[7]
王雨薇 , 荣喜民 , 赵慧 . 基于模型不确定性的保险人最优投资再保险问题研究
工程数学学报 , 2022 , 39 1 ): 1 -19
[本文引用: 1]
Wang Y W Rong X M Zhao H . Optimal reinsurance and investment strategies for insurers with ambiguity aversion: minimizing the probability of ruin
Chinese Journal of Engineering Mathematics , 2022 , 39 1 ): 1 -19
[本文引用: 1]
[8]
Bi J Meng Q Zhang Y . Dynamic mean-variance and optimal reinsurance problems under the no-bankruptcy constraint for an insurer
Annals of Operations Research , 2014 , 2.2 1 ): 43 -59
[本文引用: 1]
[9]
Liu J . Optimal investment for the insurer in the Levy market under the mean-variance criterion
Journal of Applied Mathematics and Informatics , 2010 , 28 863 -875
[10]
Zhou J Yang X Guo J . Portfolio selection and risk control for an insurer in the Lévy market under mean-variance criterion
Statistics and Probability Letters , 2017 , 1.6 : 139 -149
[本文引用: 1]
[11]
Borch K . The optimal reinsurance treaty
Astin Bulletin: The Journal of the International Actuarial Association , 1969 , 5 2 ): 293 -297
[本文引用: 1]
[12]
Zhang N Jin Z Qian L Wang R . Optimal quota-share reinsurance based on the mutual benefit of insurer and reinsurer
Journal of Computational and Applied Mathematics , 2018 , 3.2 337 -351
[本文引用: 1]
[13]
Yang P Chen Z . Optimal reinsurance pricing, risk sharing and investment strategies in a joint reinsurer-insurer framework
IMA Journal of Management Mathematics , 2023 , 34 4 ): 661 -694
[本文引用: 1]
[14]
杨鹏程 . 均值方差准则下保险集团的最优投资再保险问题研究 . 成都 : 西南财经大学 , 2022
[本文引用: 1]
Yang P C . Research on optimal investment reinsurance for insurance groups under mean-variance criterion . Chengdu : Southwest University of Finance and Economics , 2022
[本文引用: 1]
[15]
Cai J Fang Y Li Z Willmot G E . Optimal reciprocal reinsurance treaties under the joint survival probability and the joint profitable probability
Journal of Risk and Insurance , 2013 , 80 1 ): 145 -168
[本文引用: 1]
[16]
Zhao H Weng C Shen Y Zeng Y . Time-consistent investment-reinsurance strategies towards joint interests of the insurer and the reinsurer under CEV models
Science China Mathematics , 2017 , 60 2 ): 317 -344
[本文引用: 1]
[17]
Elliott R J Siu T K . A BSDE approach to a risk-based optimal investment of an insurer
Automatica , 2011 , 47 2 ): 253 -261
[本文引用: 1]
[18]
Wang N Zhang N Jin Z Qian L . Reinsurance-investment game between two mean-variance insurers under model uncertainty
Journal of Computational and Applied Mathematics , 2021 , 3.2 113095
[本文引用: 1]
[19]
Yan M Peng F Zhang S . A reinsurance and investment game between two insurance companies with the different opinions about some extra information
Insurance: Mathematics and Economics , 2017 , 75 58 -70
[本文引用: 1]
[20]
Chen L Shen Y . On a new paradigm of optimal reinsurance: A stochastic Stackelberg differential game between an insurer and a reinsurer
Astin Bulletin: The Journal of the International Actuarial Association , 2018 , 48 2 ): 905 -960
[本文引用: 3]
[21]
Chen L Shen Y . Stochastic Stackelberg differential reinsurance games under time-inconsistent mean-variance framework
Insurance: Mathematics and Economics , 2019 , 88 120 -137
DOI:10.1016/j.insmatheco.2019.06.006
[本文引用: 2]
We study optimal reinsurance in the framework of stochastic Stackelberg differential game, in which an insurer and a reinsurer are the two players, and more specifically are considered as the follower and the leader of the Stackelberg game, respectively. An optimal reinsurance policy is determined by the Stackelberg equilibrium of the game, consisting of an optimal reinsurance strategy chosen by the insurer and an optimal reinsurance premium strategy by the reinsurer. Both the insurer and the reinsurer aim to maximize their respective mean-variance cost functionals. To overcome the time-inconsistency issue in the game, we formulate the optimization problem of each player as an embedded game and solve it via a corresponding extended Hamilton-Jacobi-Bellman equation. It is found that the Stackelberg equilibrium can be achieved by the pair of a variance reinsurance premium principle and a proportional reinsurance treaty, or that of an expected value reinsurance premium principle and an excess-of-loss reinsurance treaty. Moreover, the former optimal reinsurance policy is determined by a unique, model-free Stackelberg equilibrium; the latter one, though exists, may be non-unique and model-dependent, and depend on the tail behavior of the claim-size distribution to be more specific. Our numerical analysis provides further support for necessity of integrating the insurer and the reinsurer into a unified framework. In this regard, the stochastic Stackelberg differential reinsurance game proposed in this paper is a good candidate to achieve this goal. (C) 2019 Elsevier B.V.
[22]
Li D Young V R . Stackelberg differential game for reinsurance: Mean-variance framework and random horizon
Insurance: Mathematics and Economics , 2022 , 1.2 42 -55
[本文引用: 1]
[23]
Bai Y Zhou Z Xiao H Gao R . A Stackelberg reinsurance-investment game with asymmetric information and delay
Optimization , 2021 , 70 10 ): 2131 -2168
[本文引用: 5]
[24]
French K R Schwert G W Stambaugh R F . Expected stock returns and volatility
Journal of Financial Economics , 1987 , 19 1 ): 3 -29
[本文引用: 1]
[25]
Pagan A R Schwert G W . Alternative models for conditional stock volatility
Journal of Econometrics , 1990 , 45 1/2 ): 267 -290
[本文引用: 1]
[26]
Heston S L . A closed-form solution for options with stochastic volatility with applications to bond and currency options
The Review of Financial Studies , 1993 , 6 2 ): 327 -343
[本文引用: 1]
[27]
Guan G Liang Z Song Y . A Stackelberg reinsurance-investment game under $\alpha$ - maxmin mean-variance criterion and stochastic volatility
Scandinavian Actuarial Journal , 2024 , 20.4 1 ): 28 -63
[本文引用: 1]
[28]
Zhou G Qiu Z Li S . A Stackelberg reinsurance-investment game under Heston's stochastic volatility model
Journal of Industrial and Management Optimization , 2023 , 19 6 ): 4350 -4380
[本文引用: 1]
[29]
Björk T Murgoci A . A general theory of markovian time inconsistent stochastic control problems
Ssrn Electronic Journal , 2010 , 18 3 ): 545 -592
[本文引用: 1]
[30]
Yang P Chen Z Xu Y . Time-consistent equilibrium reinsurance-investment strategy for $n$
Insurance: Mathematics and Economics , 2020 , 3.4 : 112769
[本文引用: 2]
[31]
Yang Y Wang G Yao J . Time-consistent reinsurance-investment games for multiple mean-variance insurers with mispricing and default risks
Insurance: Mathematics and Economics , 2024 , 1.4 79 -107
[本文引用: 3]
[32]
Bensoussan A Siu C C Yam S C P Yang H L . A class of non-zero-sum stochastic differential investment and reinsurance games
Automatica , 2014 , 50 8 ): 2025 -2037
[本文引用: 1]
[33]
Deng C Zeng X Zhu H . Non-zero-sum stochastic differential reinsurance and investment games with default risk
European Journal of Operational Research , 2018 , 2.4 3 ): 1144 -1158
[本文引用: 1]
Optimal investment strategy to minimize the ruin probability of an insurance company under borrowing constraints
1
2009
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
Minimizing the probability of absolute ruin under the mean-variance premium principles
2021
Minimizing the probability of ruin under interest force
1
2008
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
The optimal investment problem for an insurer and a reinsurer under the constant elasticity of variance model
1
2016
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
Optimal investment strategies for an insurer and a reinsurer with a jump diffusion risk process under the CEV model
2018
Optimal proportional reinsurance and investment for a constant elasticity of variance model under variance principle
2015
基于模型不确定性的保险人最优投资再保险问题研究
1
2022
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
基于模型不确定性的保险人最优投资再保险问题研究
1
2022
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
Dynamic mean-variance and optimal reinsurance problems under the no-bankruptcy constraint for an insurer
1
2014
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
Optimal investment for the insurer in the Levy market under the mean-variance criterion
2010
Portfolio selection and risk control for an insurer in the Lévy market under mean-variance criterion
1
2017
... 近年来, 投资和再保险是保险公司提高承保能力、控制风险、保证保险业务持续健康发展的重要业务活动. 因此, 有关保险公司最优投资和再保险问题在保险精算领域引起了广泛的关注, 对不同优化准则下的保险公司的最优再保险投资策略进行了大量的研究, 其中应用最广泛的准则包括最小化破产概率[1 3 ] 和最大化终端财富期望效用[4 7 ] 以及均值-方差准则[8 10 ] . ...
The optimal reinsurance treaty
1
1969
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
Optimal quota-share reinsurance based on the mutual benefit of insurer and reinsurer
1
2018
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
Optimal reinsurance pricing, risk sharing and investment strategies in a joint reinsurer-insurer framework
1
2023
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
1
2022
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
1
2022
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
Optimal reciprocal reinsurance treaties under the joint survival probability and the joint profitable probability
1
2013
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
Time-consistent investment-reinsurance strategies towards joint interests of the insurer and the reinsurer under CEV models
1
2017
... 在上述文章中, 大多数只从保险公司的角度考虑最优策略而忽略了再保险公司. 1969 年, Borch[11 ] 表明双方在再保险保费上存在利益冲突, 再保险保费应该是双方共同达成的协议, 只涉及一方利益的再保险策略可能不会被另一方所接受. 一般来说, 从保险公司和再保险公司的共同角度来研究再保险有两种方法: 一种方法是研究保险公司和再保险公司的加权目标,Zhang 等[12 ] 在五种不同的标准下, 研究了基于保险公司和再保险公司的共同利益的最优份额再保险问题.Yang 和 Chen[13 ] 考虑了保险公司和再保险公司之间的共同利益, 保险公司和再保险公司分别从各自角度出发, 在最大化终端时刻期望值同时减小其方差的目标下, 得到了最优再保险合同及投资策略. Yang[14 ] 在均值-方差准则下研究了保险集团的最优投资再保险策略, 通过对保险公司和再保险公司的财富赋予不同的权重, 研究了模型参数对最优策略的影响.Cai 等[15 ] 考虑了保险公司和再保险公司的利益, 研究了保险公司与再保险公司的共同生存和盈利概率, 在一般再保险保费原则下, 得到了在一类保险政策中存在最优再保险条约的充分条件.Zhao 等[16 ] 在 CEV 模型下研究了兼顾保险公司和再保险公司利益的最优投资再保险策略. ...
A BSDE approach to a risk-based optimal investment of an insurer
1
2011
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
Reinsurance-investment game between two mean-variance insurers under model uncertainty
1
2021
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
A reinsurance and investment game between two insurance companies with the different opinions about some extra information
1
2017
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
On a new paradigm of optimal reinsurance: A stochastic Stackelberg differential game between an insurer and a reinsurer
3
2018
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
... 目前, 保险公司和再保险公司在保险市场上的地位并不平等, 因为在保险市场上保险公司的数量很多, 保险公司之间竞争很激烈, 而再保险公司的数量却很少, 再保险业务被少量再保险公司所垄断. 因此, 在保险市场中有一个领导者. 在下面, 我们将再保险公司和保险公司分别作为博弈的领导者和追随者. 根据文献[20 ]和[23 ], 我们的目标是依次求解优化问题. 更具体地来说, 我们可以将求解 Stackelberg 随机微分优化问题分为以下三个步骤 ...
... 注3.3 与文献[20 ]和[23 ]相似, 在定理3.1中的情况 (Ib3), 最优再保险保费遵循方差保费原则. 也就是说, 对于每一单位的风险, 与让出比例 $1-q^{*}(t)$
Stochastic Stackelberg differential reinsurance games under time-inconsistent mean-variance framework
2
2019
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
... 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
Stackelberg differential game for reinsurance: Mean-variance framework and random horizon
1
2022
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
A Stackelberg reinsurance-investment game with asymmetric information and delay
5
2021
... 另一种方法是制定保险公司和再保险公司之间的 Stackelberg 博弈, 在博弈中再保险公司是领导者, 保险公司是追随者. 再保险公司首先给出任意的再保险保费策略, 保险公司根据再保险公司给定的保费策略得到最优的保险策略, 最后再保险公司根据保险公司的最优策略调整其再保险保费, 从而得到 Stackelberg 均衡策略.事实上, 保险业务中的随机微分博弈已经在几个竞争的保险公司或保险公司和市场之间进行了广泛的研究. 在保险公司与市场零和博弈的框架下,2011 年, Elliott 和 Siu[17 ] 通过求解倒向随机微分方程解决了最优投资问题,它给出了一种简单自然的方法, 在没有马尔可夫假设的情况下验证了最优投资策略的存在性和唯一性. 在均值-方差效用准则下,Wang 等[18 ] 研究了两家竞争保险公司的最优策略, 这两家保险公司的索赔过程由复合泊松风险模型和扩散近似模型描述, 两者的目标都是最大化相对于对手的预期终端盈余, 得到了均衡再保险投资策略和相应的值函数. Yan 等[19 ] 研究了两家保险公司之间的再保险和投资博弈, 两者对开始时获得的索赔信息采取不同态度, 以最大化终端时刻与竞争对手盈余差额为目标, 在指数效用下得到了均衡策略. 然而, 这些文章没有涉及到保险公司和再保险公司之间的博弈. Chen[20 ] 首先从保险公司和再保险公司相互影响的角度, 运用 Stackelberg 微分博弈分析了最优再保险问题, 在期望效用最大化准则下, 得到了最优保费定价策略和特殊情况下的最优再保险策略. Chen 与 Shen[21 ] 在均值-方差框架下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值保费准则和方差保费准则下分别得到了再保险策略和值函数. Li 与 Young[22 ] 进一步推广了文献[21 ], 在随机时刻下研究了保险公司和再保险公司之间的 Stackelberg 微分博弈, 在均值-方差保费准则下得到最优再保险策略为超额损失再保险策略. 同时, 还分析了不同风险分布对均衡再保险和保费策略的影响, 如果索赔分布是轻尾的, 那么均衡再保险就是纯粹的超额损失再保险,对损失的方差没有负荷; 如果索赔分布是重尾的, 那么均衡再保险就有一个非平凡共保, 对损失的方差有相应的正负荷. Bai[23 ] 考虑到保险公司和再保险公司在金融市场上信息不对称, 还考虑到当前财富受到过去业绩的影响, 在常数绝对风险厌恶效用函数下得到最优再保险和投资策略. ...
... 目前, 保险公司和再保险公司在保险市场上的地位并不平等, 因为在保险市场上保险公司的数量很多, 保险公司之间竞争很激烈, 而再保险公司的数量却很少, 再保险业务被少量再保险公司所垄断. 因此, 在保险市场中有一个领导者. 在下面, 我们将再保险公司和保险公司分别作为博弈的领导者和追随者. 根据文献[20 ]和[23 ], 我们的目标是依次求解优化问题. 更具体地来说, 我们可以将求解 Stackelberg 随机微分优化问题分为以下三个步骤 ...
... 类似文献[23 ], 作为 Stackelberg 博弈中的追随者, 保险公司的财富远低于再保险公司. 由于比较心理, 保险公司既关心自己的最终财富, 也关心自己与再保险公司之间的财富差距, 即保险人的目标是寻找一种再保险投资策略, 使下面定义的均值-方差成本函数在其相对绩效下最大化. 这里我们将保险公司的相对绩效定义为 $ \widehat{X}(t):=(1-k)X(t)+k(X(t)-Y(t))=X(t)-kY(t),$ $k\in[0, 1]$ $k$ $k=0$
... 注3.2 从定理 3.1, 我们可以得到以下两个结论: 均衡再保险-投资策略与当前财富无关; 保险公司的投资策略独立于再保险策略. 这与大多数文献的结论相一致,如文献[23 ,32 ,33 ]. ...
... 注3.3 与文献[20 ]和[23 ]相似, 在定理3.1中的情况 (Ib3), 最优再保险保费遵循方差保费原则. 也就是说, 对于每一单位的风险, 与让出比例 $1-q^{*}(t)$
Expected stock returns and volatility
1
1987
... 在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产. ...
Alternative models for conditional stock volatility
1
1990
... 在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产. ...
A closed-form solution for options with stochastic volatility with applications to bond and currency options
1
1993
... 在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产. ...
A Stackelberg reinsurance-investment game under $\alpha$ -maxmin mean-variance criterion and stochastic volatility
1
2024
... 在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产. ...
A Stackelberg reinsurance-investment game under Heston's stochastic volatility model
1
2023
... 在上述的大多数文献中, 大多数假设风险资产的价格过程遵循几何布朗运动, 这意味着风险资产的波动率是恒定的. 然而, 这与波动率为随机的实证研究结果相冲突, 比如文献[24 ]和[25 ]. 因此, 我们有必要考虑风险资产的波动率为随机的模型. Heston 随机波动率模型是最受欢迎的随机波动率模型之一, 它考虑了波动率的均值回归特性、长时期和短时期的波动率特性, 这使得模型在捕捉市场现实波动的特点时表现得更为合理. 同时, Heston 模型可以解释很多众所周知的发现, 比如波动率微笑, 波动率聚类, 收益分布的重尾性质等. Heston 模型还为欧式看涨和看跌期权提供了半解析闭式解,在某些情况下, Heston 模型可以在没有计算机模拟或复杂数值方法的情况下得到期权价格, 这对于市场参与者来说是一个很大的优点. 为了使模型更加贴近现实, Heston[26 ] 提出了风险资产的波动率是平方根扩散过程驱动的模型, 该模型具有一定的计算优势. 在保险公司和再保险公司对金融市场中的信息了解程度不同时, Guan 等[27 ] 在 Heston 随机波动率模型和 Alpha-maxmin 均值-方差准则下研究了保险公司和再保险公司的 $\alpha$ - Robust 策略.Zhou 等[28 ] 在 Heston 随机波动率模型下研究了保险公司和再保险公司的 Stackelberg 随机微分博弈, 在均值-方差效用准则下得到了保险公司和再保险公司的均衡策略和值函数. 后来许多学者将其引入到优化问题中, 用 Heston 随机波动率来描述风险资产. ...
A general theory of markovian time inconsistent stochastic control problems
1
2010
... 众所周知, 均值-方差准则下的再保险投资问题是时间不一致的. 按照文献[29 ]的方法, 我们寻求问题 (2.10) 和 (2.11) 的均衡策略和均衡值函数, 定义如下 ...
Time-consistent equilibrium reinsurance-investment strategy for $n$ competitive insurers under a new interaction mechanism and a general investment framework
2
2020
... 根据命题2.1, 我们将保险公司和再保险公司的值函数简化为 $V_{I}(t,\widehat{x},l)$ $V_{R}(x,y,l)$ . 令 $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $t$ $x$ $l$ $\psi(t,x,l)$ $\psi(t,x,l)$ $\psi_{t}(t,x,l),\psi_{x}(t,x,l),\ \psi_{xx}(t,x,l),\ \psi_{l}(t,x,l),\ \psi_{ll}(t,x,l),\ \psi_{xl}(t,x,l)$ $[T]\times R \times R^{+}$ $D_{p}^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $x$ $l$ $\psi(t,x,l)$ 30 ]和[31 ]). 对于任意的函数 $\psi(t,\widehat{x},l)\in C^{1,2,2}$ $\mathcal{L}^{u_{I},u_{R}}_{1}$
... 类似文献[30 ]和[31 ], 下面给出假设. ...
Time-consistent reinsurance-investment games for multiple mean-variance insurers with mispricing and default risks
3
2024
... 根据命题2.1, 我们将保险公司和再保险公司的值函数简化为 $V_{I}(t,\widehat{x},l)$ $V_{R}(x,y,l)$ . 令 $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $t$ $x$ $l$ $\psi(t,x,l)$ $\psi(t,x,l)$ $\psi_{t}(t,x,l),\psi_{x}(t,x,l),\ \psi_{xx}(t,x,l),\ \psi_{l}(t,x,l),\ \psi_{ll}(t,x,l),\ \psi_{xl}(t,x,l)$ $[T]\times R \times R^{+}$ $D_{p}^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $C^{1,2,2}(\left[ 0,T \right] \times R \times R^{+})$ $x$ $l$ $\psi(t,x,l)$ 30 ]和[31 ]). 对于任意的函数 $\psi(t,\widehat{x},l)\in C^{1,2,2}$ $\mathcal{L}^{u_{I},u_{R}}_{1}$
... 类似文献[30 ]和[31 ], 下面给出假设. ...
... 类似文献[31 ] 可得, 积分 ...
A class of non-zero-sum stochastic differential investment and reinsurance games
1
2014
... 注3.2 从定理 3.1, 我们可以得到以下两个结论: 均衡再保险-投资策略与当前财富无关; 保险公司的投资策略独立于再保险策略. 这与大多数文献的结论相一致,如文献[23 ,32 ,33 ]. ...
Non-zero-sum stochastic differential reinsurance and investment games with default risk
1
2018
... 注3.2 从定理 3.1, 我们可以得到以下两个结论: 均衡再保险-投资策略与当前财富无关; 保险公司的投资策略独立于再保险策略. 这与大多数文献的结论相一致,如文献[23 ,32 ,33 ]. ...