1 引言
随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究.
近期, 学者们加大了对违约债券的研究, 根据中国人民银行发布的《中国金融稳定报告 (2023)》 中数据显示1 (1数据来源: 《中国金融稳定报告 (2023)》. http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/5177895/index.html .), 截止 2022 年末, 我国债券型基金占比 28.73% 高于股票型基金占比的 9.53%, 因此考虑养老金基金在可违约债券上的投资也是很有必要的. 目前也有学者在混合养老金计划框架中引入了对违约风险的研究. 如 Wang等[18 ] 在目标收益型养老金计划的模型中考虑了违约风险并分别推导出了违约前和违约后的最优投资和收益支付策略.张欣茹等[27 ] 在考虑违约风险和工资是随机的情况下研究了目标收益型养老金计划的鲁棒最优投资和收益支付调整策略.
在以上的研究中考虑的是 Black-Scholes 模型和 Heston 随机波动率模型, 但 Black-Scholes 模型假设的不变波动率无法刻画期权市场中的波动聚集和波动率
"微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题.
本文在 Wang 等[19 ] 提出的具有代际风险分担的混合型养老金模型的基础上, 引入了价格服从 4/2 随机波动率模型的股票和违约债券来描述金融市场, 考虑了模型不确定性下的混合型养老金的最优投资和缴款--给付调整策略. 本文的目标是在 CARA 效用函数基础上最大化盈余和缴款--给付调整额的贴现值或当盈余和缴款--给付调整额为负时将其贴现值最小化. 接着通过求解扩展的 Hamilton-Jacobi-Bellman (HJB) 方程系统分别得到违约前和违约后情况下的混合型养老金的最优投资和缴款--给付调整策略的闭式表达式. 最后, 通过一些数值模拟分析了模型参数和金融市场参数对最优策略的影响.
本文的剩余部分结构如下: 第 2 节介绍了混合型养老金计划的模型和假设; 第 3 节给出鲁棒最优控制问题; 第 4 节是相关模型的求解; 第 5 节是数值分析; 第 6 节是结论与展望.
2 混合型养老金计划模型和假设
令 $(\Omega,\mathbb{F},P)$ $T$ $P$ $\mathbb{F}:=\left\{\mathcal{F}_{t}\right\}_{0\leq t\leq T}$ $\mathbb{Z}:=\left\{\mathcal{Z}_{t}\right\}_{0\leq t\leq T}$ $\{Z(t)\}$ $\mathbb{G}:=\left\{\mathcal{G}_{t}\right\}_{0\leq t\leq T}$ $\mathbb{F}$ $\mathbb{Z}$ $\mathcal{G}_{t}:=\mathcal{F}_{t}\bigvee\mathcal{Z}_{t}$ .
2.1 金融市场
假设金融市场由无风险资产, 价格服从 4/2 随机波动率模型的股票和违约债券三部分组成. 定义 $t$ $S_0(t)$
(2.1) $\begin{equation} {\rm d}S_0(t)=rS_0(t){\rm d}t, S_0(0)=s_0>0, \end{equation}$
定义 $t$ $S(t)$
(2.2) $\begin{equation} \begin{aligned} \left\{ \begin{array}{rcl} &&{\rm d}S(t)=(r+\lambda(c_1V(t)+c_2))S(t){\rm d}t+(c_1\sqrt{V(t)}+\frac{c_2}{\sqrt{V(t)}})S(t){\rm d}W_1(t),\\ &&{\rm d}V(t)=k(\theta_v-V(t)){\rm d}t+\sigma_v\sqrt{V(t)}(\rho {\rm d}W_1(t)+\sqrt{1-\rho^{2}}{\rm d}W_2(t)), \end{array} \right. \end{aligned} \end{equation}$
其中 $S(0)=s_1>0$ $V(0)=v_0>0$ . $W_1(t), W_2(t)$ $\lambda>0$ $k>0$ $\theta_v>0$ $\sigma_v>0$ $V(t)$ $2k\theta_v\geq\sigma_v^2$ $V(t)>0$ . 这里我们假设 $c_1, c_2$ $\rho\in[-1,1]$ .
注2.1 4/2 随机波动率模型结合了 Heston 模型和 3/2 模型.
当 $c_1=1, c_2=0$
当 $c_1=0, c_2=1$
令 $(\Omega, \mathbb{F}, P)$ $\tau$ $P$ $h^P>0$ $\tau$ $h^P$ $t\geq0$
其中 $\mathbb{I}$ $Z(t)=1$ $Z(t)=0$ $\mathbb{G}:=\left\{\mathcal{G}_{t}\right\}_{0\leq t\leq T}$ $\tau$
根据 Bielecki[1 ] , 得到 $P$ $P(t,T_1)$
(2.3) $\begin{equation} {\rm d}P(t,T_1)=P(t-,T_1)[r{\rm d}t+(1-Z(t))\delta(1-\Delta){\rm d}t-(1-Z(t-))\zeta {\rm d}M^P (t)], \end{equation}$
其中 $T_1$ $T<T_1$ . $\zeta\in[0, 1]$ $\delta=h^{P^*}\zeta$ $1/\Delta:=h^{P^*}/h^P$ $h^{P^*}$ $P^*$ $P^*$ $P$ $1/\Delta\geq1$ . 假设如果违约发生, 养老金计划投资者在违约前收回违约债券的部分市场价值, 另一方面, 违约发生后将不再投资该风险资产.
2.2 混合型养老金计划的基本假设与模型
此处考虑一定时期内非平稳的, 按照年龄结构划分的人口演化过程. 参考 Wang等[19 ] 进行以下几个假设
假设2.1 混合型养老金计划成员在年龄 $a$ $b$ $\omega$ . 年龄为 $x$ $s(x)$
假设2.2 $n(t)$ $t$ $t$ $x$ $n(t-(x-a))\bar s(x)$ . 值得注意的是, $t-(x-a)$ $t(\geq0)$ $x$ $x-a$
假设2.3 $w(x,t), a\leq x\leq b$ $t$ $x$
此处假设到达退休年龄 $b$ $\xi$ $t$ $\xi w(b,t)$ .
假设2.4 $h(x)$ $x-b$ $t$ $x$ $\xi w(b,t-x+b)h(x)$ .
假设2.5 假设 $\bar a_x^h$ $h(y)$
(2.4) $\begin{equation} \bar a_x^h=\int_{x}^{\omega}{\rm e}^{-\varepsilon(y-x)}h(y)\frac{\bar s(y)}{\bar s(x)}{\rm d}y, b\leq x\leq\omega. \end{equation}$
记 $^TP_t$ $t$ $b$ $^TP_t$
接下来, 根据 Wang 等[19 ] 定义应计函数 $M(x)$
(2.5) $\begin{equation} M(x)=\int_{a}^{x}m(y){\rm d}y, a\leq x\leq b, \end{equation}$
其中当 $x>b$ $m(x)=0$ . 且以该密度 $m(x)$ $a$ $b-a$ $M(b)=1$
根据应计负债函数, 用 $NC(t)$ $t$ $t$ $NC(t)$
(2.6) $\begin{equation}\begin{aligned} NC(t)&=\int_{a}^{b}{\rm e}^{-\varepsilon(b-x)}\cdot ^TP_{t+b-x}m(x){\rm d}x\\ &=\xi\cdot\bar s(b)\bar a_b^h\int_{a}^{b}{\rm e}^{-\varepsilon(b-x)}w(b,t+b-x)n(t-x+a)m(x){\rm d}x, 0\leq t\leq T. \end{aligned} \end{equation}$
定义 $t$ $PB(t)$ $PB(t)$
(2.7) $\begin{equation} PB(t)=\int_{b}^{\omega}{n(t-x+a)\bar s(x)\xi\cdot w(b,t-x+b)h(x){\rm d}x}, 0\leq t\leq T. \end{equation}$
受 Khorasanee[12 ] 和 Wang等[19 ] 改进的混合型养老金计划模型的启发, 定义两个控制变量 $\lambda_1(t)$ $\lambda_2(t)$
(2.8) $\begin{equation} \underline B(t)=PB(t)+\lambda_1(t); \end{equation}$
(2.9) $\begin{equation} \underline C(t)=NC(t)-\lambda_2(t), \end{equation}$
其中 $ \underline C(t)$ $ \underline B(t)$ $t$ $F(t)$ $L(t)$ $t$ $SP(t)=F(t)-L(t)$ $SP(t)>0$ $\lambda_1(t)$ $\lambda_2(t)$ $SP(t)<0$ $\lambda_1(t)$ $\lambda_2(t)$
根据 Bowers 等[2 ] 描述的终端融资方法, 集体混合型养老金计划的累计精算负债是所有计划参与者退休后应享给付总额的贴现, 即未来养老金应计给付总额的贴现值. 更确切地说, 这些负债包括在职成员的未来退休收益和承诺给当前退休人员的给付总额. 根据上面给出的符号, 可以将 $t$ $AL(t)$
(2.10) $\begin{equation} AL(t)=\int_{a}^{b}{\rm e}^{-\varepsilon(b-x)}\cdot^TP_{t+b-x}M(x){\rm d}x+\int_{b}^{\omega}\xi w(b,t-y+b)n(t-y+a)\bar s(y)\cdot\bar a_y^h{\rm d}y, \end{equation}$
(2.11) $\begin{equation} {\rm d}AL(t)=\varepsilon AL(t){\rm d}t+(NC(t)-PB(t)){\rm d}t, t\geq0, \end{equation}$
其中 (2.10) 式到 (2.11) 式的推导中用到了下面的式子
下面定义了混合型养老金计划的实际负债 $L(t)$
(2.12) $\begin{equation} {\rm d}L(t)=[\varepsilon L(t)+\kappa SP(t)]{\rm d}t+(NC(t)-PB(t)){\rm d}t, L(0)=l_0, \end{equation}$
(2.13) $\begin{equation} {\rm d}L(t)=L(t)[\varepsilon+\kappa(\frac{F(t)}{L(t)}-1)]{\rm d}t+(NC(t)-PB(t)){\rm d}t, L(0)=l_0, \end{equation}$
其中 $0<\kappa<1$ $\varepsilon>0$ . $\frac{F(t)}{L(t)}$ $L(t)$ $t$ $\kappa SP(t)$ . 从 (2.13) 式中可以看出, 当资金比率大于 1 时, 表明资产水平大于负债水平, 则有多余的收益, 此时负债增加一个额外的乘数率, 乘以资金比率与 1 之间的差额. 否则当资金比率小于 1 时, 表明资产水平小于负债水平, 没有多余的收益, 养老基金出现了赤字, 此时负债增加率以小于利息力 $\varepsilon$
假设 $t$ $\pi_1(t)$ $\pi_2(t)$ $F(t)-\pi_1(t)-\pi_2(t)$ . 混合型养老金计划的资产过程为
(2.14) $\begin{equation} {\rm d}F(t)=\pi_1(t)\frac{{\rm d}S(t)}{S(t)}+\pi_2(t)\frac{{\rm d}P(t,T_1)}{P(t-,T_1)}+(F(t)-\pi_1(t)-\pi_2(t))\frac{{\rm d}S_0(t)}{S_0(t)}+( \underline C(t)- \underline B(t)){\rm d}t. \end{equation}$
根据 (2.1)-(2.3) 式可以将方程 (2.14) 重写为
(2.15) $\begin{equation} \left\{ \begin{array}{rcl} &&{\rm d}F(t)=[F(t)r+\pi_1(t)\lambda(c_1V(t)+c_2)+\pi_2(t)(1-Z(t))\delta+ \underline C(t)- \underline B(t)]{\rm d}t\\ && +\pi_1(t)(c_1\sqrt{V(t)}+\frac{c_2}{\sqrt{V(t)}}){\rm d}W_1(t)-\pi_2(t)(1-Z(t-))\zeta {\rm d}Z(t),\\ &&{\rm d}V(t)=k(\theta_v-V(t)){\rm d}t+\sigma_v\sqrt{V(t)}(\rho {\rm d}W_1(t)+\sqrt{1-\rho^2}{\rm d}W_2(t)),\\ &&F(0)=f_0. \end{array} \right. \end{equation}$
在时间间隔 $[T]$ [18 ] 的启发, 使用 CARA 效用给出目标函数
(2.16) $\begin{equation} \begin{aligned} W(t,f,l,v,z)&=\sup\limits_{\pi\in\Pi}E^P\bigg[-\int_{0}^{T}(\frac{Q_1}{m}{\rm e}^{-m\lambda_1(s)}+\frac{Q_2}{m}{\rm e}^{-m\lambda_2(s)}){\rm e}^{-\beta s}{\rm d}s\\ & -\frac{Q_3}{m}{\rm e}^{-mSP(T)}{\rm e}^{-\beta T}|F(t)=f,L(t)=l,V(t)=v,Z(t)=z\bigg]. \end{aligned} \end{equation}$
其中 $Q_1, Q_2, Q_3$ $m$ $\beta$
注2.2 在此目标函数中, 使用指数效用函数来衡量终端资产与实际负债之间的差 (即 $SP(t)$ ) 和实际给付与目标给付之间的差 (即 $\lambda_1(t)$ ) 以及正常成本与实际缴款之间的差 (即 $\lambda_2(t)$ ). 当 $SP(t)$ $\lambda_1(t)$ $\lambda_2(t)$ $SP(t)$ $\lambda_1(t)$ $\lambda_2(t)$ . 然而当 $SP(t)$ $\lambda_1(t)$ $\lambda_2(t)$ $SP(t)$ $\lambda_1(t)$ $\lambda_2(t)$ . 这保持了养老金计划的稳定性和可持续性.
3 最优控制问题
一般地, 我们假设养老金计划管理者和参与者都是模糊中性的, 即他们认为参考测度就是真实的概率测度. 然而金融市场中存在很多超出养老金计划管理者认知范围的因素, 导致养老金计划管理者对参考模型和参考测度持怀疑态度, 故我们这里引入了模糊性, 下面定义一组与 $P$
在可替代测度 $Q^\phi$ $P$ $Q^\phi\in\mathcal{Q}$ $\{\phi(t):=(\phi_1(t), \phi_2(t), \phi_3(t))|t\in[T]\}$
(3.1) $\begin{equation} \frac{{\rm d}Q^\phi}{{\rm d}P}|_\mathcal{G}(t):=\Lambda^\phi(t), \end{equation}$
$\phi(t):=(\phi_1(t), \phi_2(t), \phi_3(t))$
(1) 对于 $\forall t\in[T]$ $\phi_1(t), \phi_2(t), \phi_3(t)$ $\mathcal{G}_t$
(2) $\int_{0}^{T}[(\phi_1(s))^2+(\phi_2(s))^2+(\phi_3(s))^2]{\rm d}s<\infty$
(3) 对于 $\forall (t,\omega)\in[T]\times\Omega$ $\phi_3(t)=\phi_3(t,\omega)>0$ .
$\phi(t):=(\phi_1(t), \phi_2(t), \phi_3(t))$ $\Lambda^\phi(t)$ $P$ - 鞅. 令 $\Theta$ $Q^\phi$ $W_1^\phi(t)$ $W_2^\phi(t)$
(3.2) $\begin{equation} {\rm d}W_1^\phi(t)={\rm d}W_1(t)+\phi_1(t){\rm d}t; \end{equation}$
(3.3) $\begin{equation} {\rm d}W_2^\phi(t)={\rm d}W_2(t)+\phi_2(t){\rm d}t. \end{equation}$
此外, 泊松过程 $Z(t)$ $Q^\phi$ $h^P\phi_3(t)$ $Z^\phi(t)$ . 综上所述, 我们得到了 $Q^\phi$
(3.4) $\begin{equation} \left\{ \begin{array}{rcl} {\rm d}F(t)&=&[F(t)r+\pi_1(t)\lambda(c_1V(t)+c_2)+\pi_2(t)(1-Z(t))\delta-\pi_1(t)(c_1\sqrt{V(t)}\\&&+\frac{c_2}{\sqrt{V(t)}})\phi_1(t) +NC(t)-\lambda_2(t)-PB(t)-\lambda_1(t)]{\rm d}t+\pi_1(t)(c_1\sqrt{V(t)}\\ &&+\frac{c_2}{\sqrt{V(t)}}){\rm d}W_1^\phi(t)-\pi_2(t)(1-Z(t-))\zeta {\rm d}Z^\phi(t),\\ {\rm d}V(t)&=&[k(\theta_v-V(t))-\sigma_v\sqrt{V(t)}\rho\phi_1(t)-\sqrt{1-\rho^2}\sigma_v\sqrt{V(t)}\phi_2(t)]{\rm d}t\\ &&+\sigma_v\sqrt{V(t)}\rho {\rm d}W_1^\phi(t)+\sigma_v\sqrt{V(t)}\sqrt{1-\rho^2}{\rm d}W_2^\phi(t). \end{array} \right. \end{equation}$
定义3.1 (容许策略) 如果策略 $\pi=\{(\pi_{1}(t),\pi_{2}(t)),\lambda_1(t), \lambda_2(t))\}_{t\in[T]}$ $\pi$
(1) $\pi$ $\mathcal{G}_t$
(2) 对 $\forall t\in[T]$ $\lambda_1(t)<\infty,\lambda_2(t)<\infty$
(3) $(F^\pi, \pi)$
养老金计划管理者尝试在最坏情况的模型中寻求最优策略, 受 Wang等[18 ] 的启发, 构建鲁棒最优控制问题如下
(3.5) $\begin{equation} \begin{aligned} &\sup\limits_{\pi\in\Pi}\inf\limits_{\phi\in\Theta}E^\phi\bigg[-\int_{0}^{T}(\frac{Q_1}{m}{\rm e}^{-m\lambda_1(s)}+\frac{Q_2}{m}{\rm e}^{-m\lambda_2(s)}){\rm e}^{-\beta s}{\rm d}s-\frac{Q_3}{m}{\rm e}^{-mSP(T)}{\rm e}^{-\beta T}\\ &+\int_{0}^{T}g_\beta(\phi(s)){\rm d}s|F(t)=f,L(t)=l,V(t)=v,Z(t)=z\bigg]. \end{aligned} \end{equation}$
在鲁棒控制中当可替代测度偏离参考测度时会受到惩罚, 参考Maenhout[13 ] , 这里惩罚函数 $g_\beta(\phi)$
(3.6) $\begin{equation}\begin{aligned} g_\beta(\phi)=\frac{\phi^2_1(s)}{2\beta_1}+\frac{\phi^2_2(s)}{2\beta_2}+\frac{h^P(\phi_3(s)\ln\phi_3(s)-\phi_3(s)+1)(1-z)}{\beta_3}, \end{aligned} \end{equation}$
其中 $\beta_1$ $\beta_2$ $\beta_3$ $\beta_1$ $\beta_2$ $\beta_3$ [13 ] , 对 $\beta_i$
其中 $\rho_1, \rho_2, \rho_3$ $W_1(t)$ $W_2(t)$ $Z(t)$
4 最优策略
假设4.1 假设容许策略集 $\Pi$ $\Theta$
在这一部分中, 我们推导了基于模型不确定性有违约风险的混合型养老金计划的最优投资策略和最优缴款-给付调整策略的闭式解以及相应的值函数.根据 Yong[23 ] , Fleming[7 ] 以及 Wang 等[18 ] , 最优值函数 $J(t,f,l,v,z)\in C^{1,2,2,2}([T]\times\mathcal{R}\times\mathcal{R}^{+}\times\mathcal{R}^{+}\times(0,1))$
(4.1) $\begin{equation}\begin{aligned} &\sup\limits_{\pi\in\Pi}\{J_t+J_f[fr+\pi_1(t)\lambda(c_1v+c_2)+\pi_2(t)(1-z)\delta+NC(t)-\lambda_2(t)-PB(t)\\&-\lambda_1(t)] +J_l[\varepsilon l+\kappa (f- l)+NC(t)-PB(t)]+J_v(k\theta_v-kv)+\frac{1}{2}J_{vv}\sigma_v^2v\\&+\frac{1}{2}J_{ff}\pi_1^2(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}})^2+J_{fv}\pi_1(t)(c_1v+c_2)\sigma_v\rho -\frac{Q_1}{m}{\rm e}^{-m\lambda_1(t)-\beta t}\\&-\frac{Q_2}{m}{\rm e}^{-m\lambda_2(t)-\beta t} +\inf\limits_{\phi\in\Theta}[-\pi_1(t)(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}})\phi_1(t)J_f-\sigma_v\sqrt{v}\rho\phi_1(t)J_v\\& -\sqrt{1-\rho^2}\sigma_v\sqrt{v}\phi_2(t)J_v +[J(t,f-\pi_2\zeta,l,v,1)-J(t,f,l,v,0)]\phi_3h^P(1-z)\\&+g_\beta(\phi)]\}=0, \end{aligned} \end{equation}$
边界条件: $J(T,f,l,v,z)=-\frac{Q_3}{m}{\rm e}^{-mSP(T)}\cdot {\rm e}^{-\beta T}$ . 这里 $J_t, J_f, J_l, J_v, J_{fv}, J_{ff}, J_{vv}$ $J(t,f,l,v,z)$ $t, f, l, v$ $(t,f,l,v,z)$ .
4.1 违约后情况
在本小节中, 将考虑违约债券违约后情况, 即 $z=1$
(4.2) $\begin{equation} \begin{aligned} &\sup\limits_{\pi\in\Pi}\bigg\{J_t+J_f[fr+\pi_1(t)\lambda(c_1v+c_2)+NC(t)-\lambda_2(t)-PB(t)-\lambda_1(t)]\\ &+J_l[\varepsilon l+\kappa (f-l)+NC(t)-PB(t)]+J_v(k\theta_v-kv)+J_{fv}\pi_1(t)(c_1v+c_2)\sigma_v\rho\\ &+\frac{1}{2}\pi_1^2(t)\Big(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}}\Big)^2J_{ff}+\frac{1}{2}J_{vv}\sigma^2_vv-\frac{Q_1}{m}{\rm e}^{-m\lambda_1(t)-\beta t}-\frac{Q_2}{m}{\rm e}^{-m\lambda_2(t)-\beta t}\\ &+\inf\limits_{\phi\in\Theta}\bigg(-\pi_1(t)(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}})\phi_1(t)J_f-\sigma_v\sqrt{v}\rho\phi_1(t)J_v-\sqrt{1-\rho^2}\sigma_v\sqrt{v}\phi_2(t)J_v\\&-\frac{\phi_1^2mJ}{2\rho_1}-\frac{\phi_2^2mJ}{2\rho_2}\bigg)\bigg\}=0, \end{aligned} \end{equation}$
根据边界条件: $J(T,f,l,v,1)=-\frac{Q_3}{m}{\rm e}^{-mSP(T)}\cdot {\rm e}^{-\beta T}$
(4.3) $\begin{equation}\begin{aligned} &J_t=[-A_{1t}B_1(t)l-A_1(t)B_{1t}l-fA_{1t}+C_{1t}v+D_{1t}-\beta]J,\\ &J_f=-A_1(t)J, J_l=-B_1(t)A_1(t)J, J_v=C_1(t)J,\\ &J_{ff}=A_1^2(t)J, J{vv}=C_1^2(t)J, J_{fv}=-A_1(t)C_1(t)J. \end{aligned} \end{equation}$
根据 $\phi_1$ $\phi_2$
(4.4) $\begin{equation}\begin{aligned} &\phi_1^*=-\frac{\pi_1(t)(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}})\rho_1 J_f+\sigma_v\sqrt{v}\rho\rho_1J_v}{mJ};\\ &\phi_2^*=-\frac{\sqrt{1-\rho^2}\sigma_v\sqrt{v}\rho_2J_v}{mJ}. \end{aligned} \end{equation}$
(4.5) $\begin{equation}\begin{aligned} &\sup\limits_{\pi\in\Pi}\bigg\{J_t+J_f[fr+\pi_1(t)\lambda(c_1v+c_2)+NC(t)-\lambda_2(t)-PB(t)-\lambda_1(t)] +J_l[\varepsilon l +\kappa (f-l)\\ &+NC(t)-PB(t)]+J_v(k\theta_v-kv)+J_{fv}\pi_1(t)(c_1v+c_2)\sigma_v\rho+\frac{1}{2}\pi_1^2(t)\Big(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}}\Big)^2J_{ff}\\& +\frac{1}{2}J_{vv}\sigma_v^2v-\frac{Q_1}{m}{\rm e}^{-m\lambda_1(t)-\beta t} -\frac{Q_2}{m}{\rm e}^{-m\lambda_2(t)-\beta t}+\frac{\pi_1(t)\sigma_v\rho\rho_1(c_1v+c_2)J_vJ_f}{mJ}\\&+\frac{\pi_1^2(t)(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}})^2\rho_1J_f^2+\sigma_v^2v\rho^2\rho_1J_v^2+(1-\rho^2)\sigma_v^2v\rho_2J_v^2)}{2mJ} \bigg\}=0. \end{aligned} \end{equation}$
对方程 (4.5) 关于 $\pi_1, \lambda_1, \lambda_2$
(4.6) $\begin{equation}\begin{aligned} &\pi_1^*(t)=-\frac{vm\lambda JJ_f+vm\sigma_v\rho JJ_{fv}+v\sigma_v\rho\rho_1J_fJ_v}{m(c_1v+c_2)JJ_{ff}+(c_1v+c_2)\rho_1J_f^2},\\ &\lambda_1^*(t)=-\frac{1}{m}\ln(\frac{J_f{\rm e}^{\beta t}}{Q_1}),\\ &\lambda_2^*(t)=-\frac{1}{m}\ln(\frac{J_f{\rm e}^{\beta t}}{Q_2}). \end{aligned} \end{equation}$
下面将 (4.3), (4.6) 式带回方程 (4.5) 后分离变量得到
(4.7) $\begin{equation}\begin{aligned} &f\bigg\{-A_{1t}-A_1(t)r+\frac{A_1^2(t)}{m}+\frac{A_1^2(t)}{m}-B_1(t)A_1(t)\kappa\bigg\}+l\{-A_{1t}B_1(t)-A_1(t)B_{1t}\\&+\frac{A_1^2(t)B_1(t)}{m}+\frac{A_1^2(t)B_1(t)}{m}+A_1(t)B_1(t)(\kappa-\varepsilon)\} +v\{C_{1t}+C_1(t)\varphi_1\\ &+C^2_1(t)\varphi_2+\varphi_3\}+1\cdot\bigg\{D_{1t}-(\frac{A_1(t)}{m}+\frac{A_1(t)}{m})D_1(t)+g_1(t)\bigg\}=0. \end{aligned} \end{equation}$
(4.8) $\varphi_1=-\lambda\sigma_v\rho-k-\frac{A_1(t)}{m}-\frac{A_1(t)}{m},$
(4.9) $\varphi_2=-\frac{1}{2}\sigma_v^2\rho^2+\frac{1}{2}\sigma_v^2+\frac{(1-\rho^2)\sigma_v^2\rho_2}{2m},$
(4.10) $\varphi_3=\frac{-m\lambda^2}{2(m+\rho_1)},$
(4.11) $\begin{equation}\begin{aligned} g_1(t)&=-\beta+C_1(t)k\theta_v-A_1(t)(1+B_1(t))(NC(t)-PB(t))\\ & -\frac{A_1(t)}{m}\bigg[\ln\bigg(\frac{A_1(t)Q_3}{Q_1m}\bigg)-1\bigg]-\frac{A_1(t)}{m}\bigg[\ln\bigg(\frac{A_1(t)Q_3}{Q_2m}\bigg)-1\bigg]. \end{aligned} \end{equation}$
根据分离变量结果, 令 $f, l, v, 1$
(4.12) $\begin{equation} \begin{aligned} &A_{1t}+A_1(t)r-\frac{A^2_1(t)}{m}-\frac{A^2_1(t)}{m}+B_1(t)A_1(t)\kappa=0,\\ &A_{1t}B_1(t)+A_1(t)B_{1t}-\frac{A^2_1(t)B_1(t)}{m}-\frac{A^2_1(t)B_1(t)}{m}+A_1(t)B_1(t)(\varepsilon-\kappa)=0,\\ &C_{1t}+C_1(t)\varphi_1+C^2_1(t)\varphi_2+\varphi_3=0,\\ &D_{1t}-\bigg(\frac{A_1(t)}{m}+\frac{A_1(t)}{m}\bigg)D_1(t)+g_1(t)=0,\\ \end{aligned} \end{equation}$
方程组 (4.12) 的求解见附录. 最后将解得的 $A_1(t)$ $B_1(t)$ $C_1(t)$ $D_1(t)$
4.2 违约前情况
在本小节中, 将考虑违约债券违约前情况, 即 $z=0$ . 本小节的解法参考了 Wang等[16 ] 和 Wang 等[18 ] 中违约前情况下的相关解法. 则 (4.1) 式的 HJB 方程可以整理为
(4.13) $\begin{equation}\begin{aligned} &\sup\limits_{\pi\in\Pi}\bigg\{J_t+J_f[fr+\pi_1(t)\lambda(c_1v+c_2)+\pi_2(t)\delta+NC(t)-\lambda_2(t)-PB(t)-\lambda_1(t)]\\ &+J_l[\varepsilon l+\kappa (f-l)+NC(t)-PB(t)]+J_v(k\theta_v-kv)+J_{fv}\pi_1(t)(c_1v+c_2)\sigma_v\rho\\ &+\frac{1}{2}J_{ff}\pi_1^2(t)\Big(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}}\Big)^2+\frac{1}{2}J_{vv}\sigma_v^2v-\frac{Q_1}{m}{\rm e}^{-m\lambda_1(t)-\beta t}-\frac{Q_2}{m}{\rm e}^{-m\lambda_2(t)-\beta t}\\ &+\inf\limits_{\phi\in\Theta}\bigg(-\pi_1(t)\Big(c_1\sqrt{v}+\frac{c_2}{\sqrt{v}}\Big)\phi_1(t)J_f -\sigma_v\sqrt{v}\rho\phi_1(t)J_v-\sqrt{1-\rho^2}\sigma_v\sqrt{v}\phi_2(t)J_v\\&-\frac{\phi_1^2mJ}{2\rho_1}-\frac{\phi_2^2mJ}{2\rho_2} -\frac{h^P(\phi_3\ln\phi_3-\phi_3+1)mJ}{\rho_3}+[J(t,f-\pi_2(t)\zeta,l,v,1)\\ &-J(t,f,l,v,0)]\phi_3h^P\bigg) \bigg\}=0. \end{aligned} \end{equation}$
根据边界条件: $J(T,f,l,v,0)=-\frac{Q_3}{m}{\rm e}^{-mSP(T)}\cdot {\rm e}^{-\beta T}$
(4.14) $\begin{equation}\begin{aligned} &J_t=[-A_{2t}B_2(t)l-A_2(t)B_{2t}l-fA_{2t}+C_{2t}v+D_{2t}-\beta]J,\\ &J_f=-A_2(t)J, J_l=-B_2(t)A_2(t)J, J_v=C_2(t)J, \\ &J_{ff}=A^2_2(t)J, J{vv}=C^2_2(t)J, J_{fv}=-A_2(t)C_2(t)J,\\ &J(t,f-\pi_2(t)\zeta,l,v,1)-J(t,f,l,v,0)=[\exp\{-f(A_1(t)-A_2(t))+\zeta\pi_2(t)A_1(t)\\&-B_1(t)lA_1(t) )+B_2(t)lA_2(t)+(C_1(t)-C_2(t))v+(D_1(t)-D_2(t))\}-1]J(t,f,l,v,0). \end{aligned} \end{equation}$
将 (4.14) 式带回方程 (4.13) 整理后, 根据 $\pi_1$ $\pi_2$ $\lambda_1$ $\lambda_2$
(4.15) $\begin{equation}\begin{aligned} \pi_1^*(t)=-\frac{\sqrt{v}{\phi}_1(t)-\lambda v-\sigma_v\rho vC_2(t)}{(c_1v+c_2)A_2(t)}, \end{aligned} \end{equation}$
(4.16) $\begin{equation}\begin{aligned} \pi_2^*(t)&=\frac{1}{\zeta A_1(t)}[\ln(\frac{\delta A_2(t)}{\zeta A_1(t) h^P{\phi}_3})+fA_1(t)-fA_2(t)+B_1(t)lA_1(t)\\ & -B_2(t)lA_2(t)-C_1(t)v+C_2(t)v-D_1(t)+D_2(t)], \end{aligned} \end{equation}$
(4.17) $\begin{equation}\begin{aligned} &\lambda_1^*(t)=-\frac{1}{m}\ln(\frac{A_2(t)Q_3}{Q_1m})-\frac{1}{m}[-(f+B_2(t)l)A_2(t)+C_2(t)v+D_2(t)], \end{aligned} \end{equation}$
(4.18) $\begin{equation}\begin{aligned} &\lambda_2^*(t)=-\frac{1}{m}\ln(\frac{A_2(t)Q_3}{Q_2m})-\frac{1}{m}[-(f+B_2(t)l)A_2(t)+C_2(t)v+D_2(t)]. \end{aligned} \end{equation}$
将 (4.15)-(4.18) 式带回方程 (4.13), 并关于 $\phi$
(4.19) $\begin{equation}\begin{aligned} {\phi}_1^*=\frac{\lambda\rho_1\sqrt{v}}{\rho_1+m}, \end{aligned} \end{equation}$
(4.20) $\begin{equation}\begin{aligned} {\phi}_2^*=-\frac{\sqrt{1-\rho^2}\sigma_v\rho_2\sqrt{v}C_2(t)}{m}, \end{aligned} \end{equation}$
(4.21) $\begin{equation} \begin{aligned} &{\phi}_3^*h^P+\frac{h^P{\phi}_3^*m}{\rho_3}\ln{\phi}_3^*-\frac{A_2(t)\delta}{\zeta A_1(t)}=0. \end{aligned} \end{equation}$
将 (4.19)-(4.21) 式带回方程 (4.13), 分离变量有
其中 $\varphi_1$ $\varphi_2$ $\varphi_3$
(4.23) $\begin{equation}\begin{aligned} g_2(t)&=-\beta+C_2(t)k\theta_v-A_2(t)(1+B_2(t))(NC(t)-PB(t))-\frac{A_2(t)}{m}\bigg[\ln\bigg(\frac{A_2(t)Q_3}{Q_1m}\bigg)-1\bigg]\\ & -\frac{A_2(t)}{m}\bigg[\ln\bigg(\frac{A_2(t)Q_3}{Q_2m}\bigg)-1\bigg]-\frac{\delta A_2(t)}{\zeta A_1(t)}\bigg[\ln\bigg(\frac{\delta A_2(t)}{\zeta A_1(t) h^P{\phi}_3^*}\bigg)-D_1(t)-1\bigg]\\ & -h^P{\phi}_3^* -\frac{mh^P}{\rho_2}({\phi}_3^*\ln{\phi}_3^*-{\phi}_3^*+1). \end{aligned} \end{equation}$
引理4.1 方程 ${\phi}_3^*h^P+\frac{h^P{\phi}_3^*m}{\rho_3}\ln{\phi}_3^*-\frac{\delta}{\zeta }=0$
证 此引理的证明类似于 Sun 等[14 ] , 这里不再赘述.
定理4.1 对于混合型养老金计划的鲁棒最优控制问题 (3.5), HJB 方程的最优解为
(4.24) $\begin{equation}\begin{aligned} V(t,f,l,v,z)=J(t,f,l,v,z)=(1-z)J(t,f,l,v,0)+zJ(t,f,l,v,1). \end{aligned} \end{equation}$
(4.25) $\begin{equation}\begin{aligned} \pi_1^*(t)=\frac{vm\lambda+vmC(t)\sigma_v\rho+C(t)v\sigma_v\rho\rho_1}{m(c_1v+c_2)A(t)+(c_1v+c_2)A(t)\rho_1}, \end{aligned} \end{equation}$
(4.26) $\begin{equation} \pi_2^{*}(t)= \begin{cases} \frac{1}{\zeta A(t)}[\ln(\frac{\delta}{\zeta h^P{\phi}_3^*})-D_1(t)+D_2(t)],&t\in[0,\tau\wedge T),\\ 0,&t\in[\tau\wedge T,T], \end{cases} \end{equation}$
(4.27) $\begin{equation} \lambda_1^{*}(t)= \begin{cases} -\frac{1}{m}\ln(\frac{A(t)Q_3}{Q_1m})-\frac{1}{m}[-(f+B(t)l)A(t)+C(t)v+D_2(t)],&t\in[\\ -\frac{1}{m}\ln(\frac{A(t)Q_3}{Q_1m})-\frac{1}{m}[-(f+B(t)l)A(t)+C(t)v+D_1(t)],&t\in[\tau\wedge T,T], \end{cases} \end{equation}$
(4.28) $\begin{equation} \lambda_2^{*}(t)= \begin{cases} -\frac{1}{m}\ln(\frac{A(t)Q_3}{Q_2m})-\frac{1}{m}[-(f+B(t)l)A(t)+C(t)v+D_2(t)],&t\in[\\ -\frac{1}{m}\ln(\frac{A(t)Q_3}{Q_2m})-\frac{1}{m}[-(f+B(t)l)A(t)+C(t)v+D_1(t)],&t\in[\tau\wedge T,T], \end{cases} \end{equation}$
$\varphi_1, \varphi_2, \varphi_3$
$g_2(t)$ ${\phi}_1^*$ ${\phi}_2^*$ ${\phi}_3^*$
推论4.1 若 $\rho_1=\rho_2=\rho_3=0$
5 数据分析
在本节中, 我们将分别研究不同模型参数和金融市场参数对最优策略的影响. 在进行数值分析前, 先做几点假设
假设5.1 死亡力遵循 Makeham 定律, 即年龄为 $x$
该式满足 $\bar s(a)=1$ . 接下来数值分析中, 参考 Dickson等[6 ] 设 $\mathcal{A}=2.2\times10^{-4}, \mathcal{B}=2.7\times10^{-6},$ $\theta=1.124$ .
假设5.2 根据 Bowers 等[2 ] 第二十章的进入年龄精算成本法以及 Wang 等[19 ] 假定养老金应计密度函数 $m(x)$
其中 $\alpha_1$ $\eta$ [19 ] 取 $\alpha_1=0.02, \eta=0.01$ .
假设5.4 随着经济的发展与社会的进步, 本文假设退休员工的生活成本不断进行调整
$\varsigma$ [19 ] 取 $\varsigma=0.03$ .
假设5.5 除非特别说明, 本文采用的其他相关数值可参考Zhang[24 ] , Wang 等[19 ] 和 Wang 等[18 ] :$T=15$ $a=30$ $b=65$ $\omega=100$ $n(t)=10$ $\varepsilon=0.015$ $r=0.05$ $\beta=0.01$ $\xi=0.5$ $w_0=1$ $l=6277$ $f=7000$ $\kappa=0.1$ $\delta=0.01$ $\zeta=0.4$ $h^{P^*}=0.025$ $h^P=0.00625$ $c_1=0.9051$ $c_2=0.0023$ $\sigma_v=0.6612$ $\lambda=2.9428$ $\theta_v=0.0328$ $\rho=-0.7689$ $k=7.3479$ $Q_1=6$ $Q_2=5$ $Q_3=1$ $\rho_1=1$ $\rho_2=1$ $\rho_3=2$ $m=1$ $v_0=0.02$ .
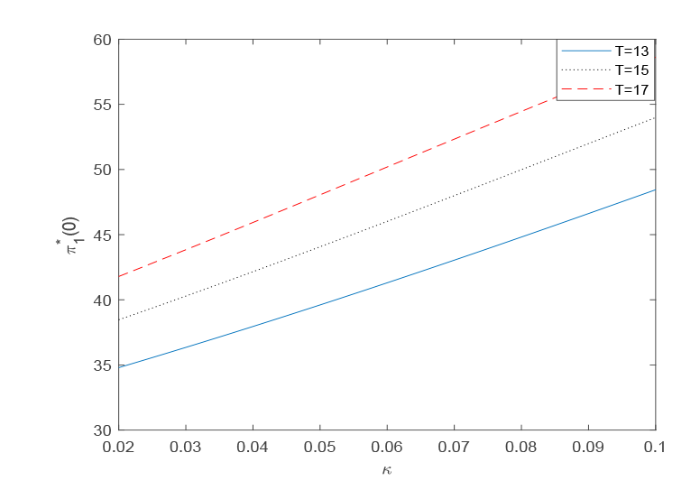
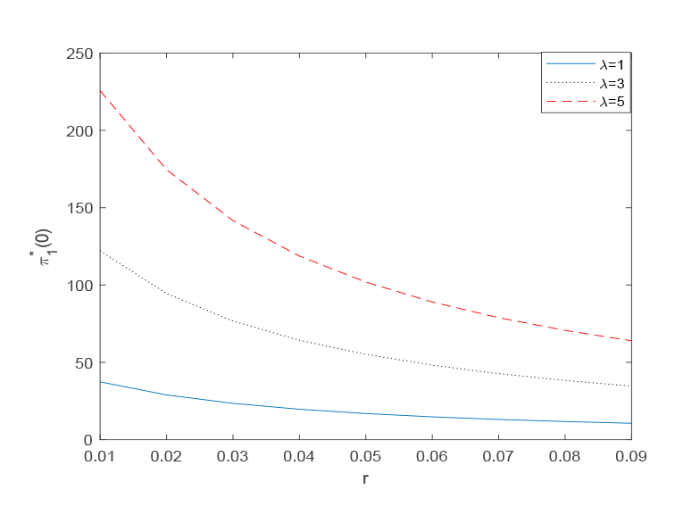
为作图方便, 不失一般性, 我们取 $t=0$ 图1 研究了 $\pi_1^*(0)$ $\kappa$ $T$ $\pi_1^*(0)$ $\kappa$ $T$ 图2 研究的是 $\pi_1^*(0)$ $r$ $\lambda$ $r$ $\pi_1^*(0)$ $\lambda$ $\pi_1^*(0)$ $\lambda$
图1
图1
$\pi_1^*(0)$ $\kappa,T$
图2
图2
$\pi_1^*(0)$ $r,\lambda$
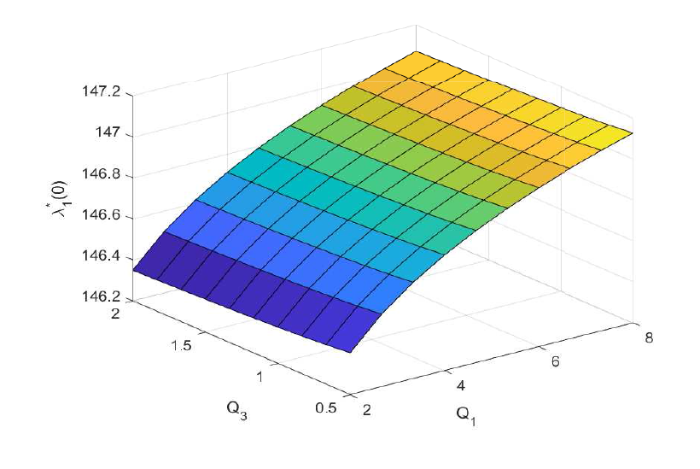
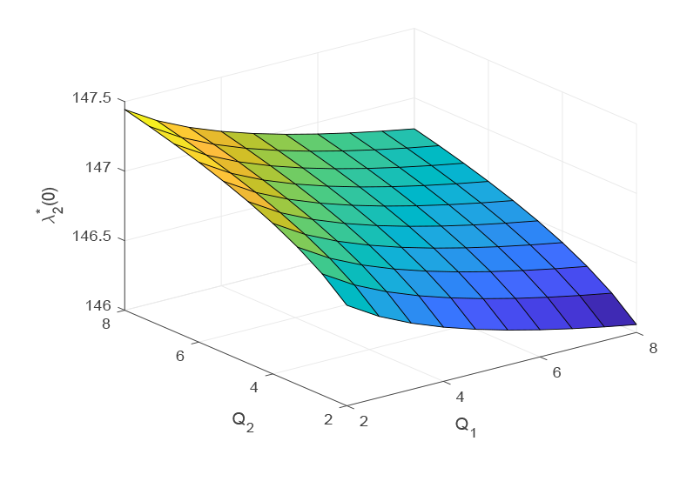
+图3 -图4 研究的是最优调整策略关于权重参数的敏感性. 从图3 可以看出 $\lambda_1^*(0)$ $Q_1$ $Q_3$ $Q_1$ $Q_3$ 图4 可以看出 $\lambda_2^*(0)$ $Q_1$ $Q_2$ $Q_1$ $Q_2$
图3
图3
$\lambda_1^*(0)$ $Q_1,Q_3$
图4
图4
$\lambda_2^*(0)$ $Q_1,Q_2$
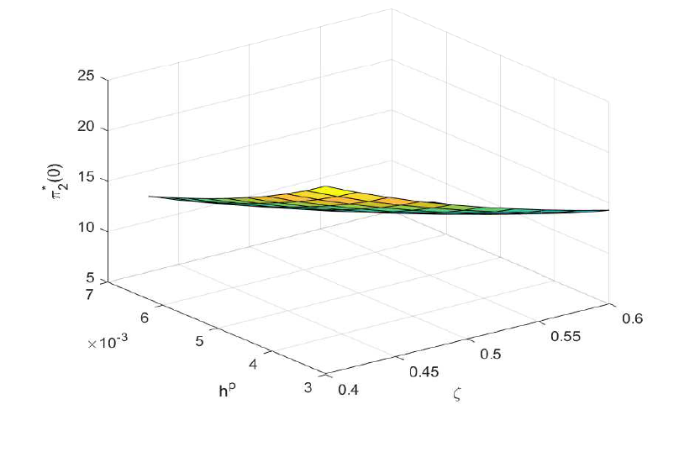
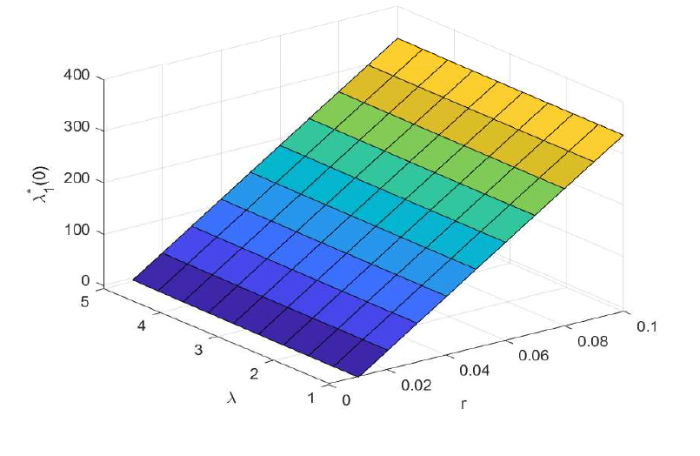
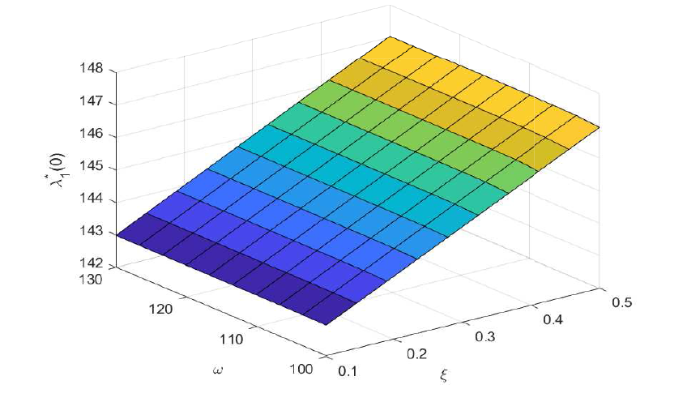
图5 反映 $\zeta$ $h^P$ $\pi_2^*(0)$ $\pi_2^*(0)$ $\zeta$ $h^P$ 图6 刻画了违约前情况下参数 $r$ $\lambda$ $r$ $\lambda$ 图7 研究的是违约前情况下最优给付调整策略 $\lambda_1^*(0)$ $\xi$ $\omega$ $\omega$ $\lambda_1^*(0)$ $\xi$ $\xi$ $\xi$ $\lambda_1^*(0)$ $\omega$ $\omega$
图5
图5
$\pi_2^*(0)$ $\zeta,h^P$
图6
图6
$\lambda_1^*(0)$ $r,\lambda$
图7
图7
$\lambda_1^*(0)$ $\xi,\omega$
6 结论与展望
本文的主要研究内容是基于模型不确定性有违约风险的混合型养老金计划的最优投资策略和最优缴款--给付调整策略. 本文的目标是从养老金计划管理者和参与者两个角度出发, 寻找最优策略. 其次可以发现基金盈余 (赤字) 可通过收益和缴款调整策略实现代际之间的利益共享 (缓冲金融市场萧条时期的经济下滑). 最后对其进行数值模拟, 得到结论: (1) 金融市场参数和模型参数对最优投资和最优缴款-给付调整策略有影响. (3) 根据图7 可得将长寿风险纳入混合型养老金计划模型中是有必要的, 这也是我们接下来工作的重心.
A 附录
(A.1) $\begin{equation}\begin{aligned} &A_{1t}+A_1(t)r-\frac{A^2_1(t)}{m}-\frac{A^2_1(t)}{m}+B_1(t)A_1(t)\kappa=0.\\ \end{aligned} \end{equation}$
(A.2) $\begin{equation} \begin{aligned} &A_{1t}B_1(t)+A_1(t)B_{1t}-\frac{A^2_1(t)B_1(t)}{m}-\frac{A^2_1(t)B_1(t)}{m}+A_1(t)B_1(t)(\varepsilon-\kappa)=0.\\ \end{aligned} \end{equation}$
根据边界条件可得到一个关于 $B_1(t)$
(A.3) $\begin{equation} A_1(t)=\frac{1}{(\frac{1}{m}+\int_{t}^{T}\frac{2}{m}{\rm e}^{\int_{u}^{T}(r+\kappa B_1(s)){\rm d}s}{\rm d}u)\cdot {\rm e}^{-\int_{t}^{T}(r+\kappa B_1(s)){\rm d}s}}. \end{equation}$
当 $\varepsilon\neq\kappa+r$ $B_1(t)$
(A.4) $\begin{align*} {\rm e}^{\int_{t}^{T}(r+\kappa B_1(s)){\rm d}s} &={\rm e}^{\int_{t}^{T}(r+\kappa \frac{r+\kappa-\varepsilon}{(\varepsilon-r){\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\kappa}){\rm d}s}\\ &={\rm e}^{r(T-t)}{\rm e}^{\int_{t}^{T}\frac{-\kappa}{(\varepsilon-r){\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\kappa}{\rm d}(r+\kappa-\varepsilon)(T-s)}\\ &={\rm e}^{r(T-t)}{\rm e}^{\int_{t}^{T}\frac{-\frac{\kappa}{\varepsilon-r}+{\rm e}^{(r+\kappa-\varepsilon)(T-s)}-{\rm e}^{(r+\kappa-\varepsilon)(T-s)}}{{\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\frac{\kappa}{\varepsilon-r}} {\rm d}(r+\kappa-\varepsilon)(T-s)}\\ &={\rm e}^{r(T-t)}{\rm e}^{\int_{t}^{T}(1-\frac{{\rm e}^{(r+\kappa-\varepsilon)(T-s)}}{{\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\frac{\kappa}{\varepsilon-r}}) {\rm d}(r+\kappa-\varepsilon)(T-s)}\\ &={\rm e}^{(\varepsilon-\kappa)(T-t)}\cdot {\rm e}^{-\int_{t}^{T} \frac{{\rm d e}^{(r+\kappa-\varepsilon)(T-s)}}{{\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\frac{\kappa}{\varepsilon-r}}}\\ &={\rm e}^{(\varepsilon-\kappa)(T-t)}\cdot {\rm e}^{-\int_{t}^{T} \frac{{\rm d}({\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\frac{\kappa}{\varepsilon-r})}{{\rm e}^{(r+\kappa-\varepsilon)(T-s)}-\frac{\kappa}{\varepsilon-r}}}\\ &={\rm e}^{(\varepsilon-\kappa)(T-t)}{\rm e}^{\ln{\frac{{\rm e}^{(r+\kappa-\varepsilon)(T-t)}-\frac{\kappa}{\varepsilon-r}}{1-\frac{\kappa}{\varepsilon-r}}}}\\ &={\rm e}^{(\varepsilon-\kappa)(T-t)}(\frac{{\rm e}^{(r-\varepsilon+\kappa)(T-t)}-\frac{\kappa}{\varepsilon-r}}{1-\frac{\kappa}{\varepsilon-r}})\\ &=\frac{(\varepsilon-r){\rm e}^{r(T-t)}-\kappa {\rm e}^{-(\kappa-\varepsilon)(T-t)}}{\varepsilon-r-\kappa}. \end{align*}$
(A.5) $\begin{equation} \begin{aligned} \int_{t}^{T}\frac{2}{m}&\frac{(\varepsilon-r){\rm e}^{r(T-u)}-\kappa {\rm e}^{-(\kappa-\varepsilon)(T-u)}}{\varepsilon-r-\kappa}{\rm d}u\\ &=-\frac{2}{m}\bigg(\int_{t}^{T}\frac{(\varepsilon-r){\rm e}^{r(T-u)}}{r(\varepsilon-r-\kappa)}{\rm d}[r(T-u)]\\ &+\int_{t}^{T}\frac{\kappa {\rm e}^{(\varepsilon-\kappa)(T-u)}}{(\varepsilon-r-\kappa)(\kappa-\varepsilon)}{\rm d}[-(\kappa-\varepsilon)(T-u)]\bigg)\\ &=-\frac{2}{m}\bigg(\frac{(\varepsilon-r)(1-{\rm e}^{r(T-t)}}{r(\varepsilon-r-\kappa)}+\frac{\kappa(1-{\rm e}^{-(\kappa-\varepsilon)(T-t)})}{(\varepsilon-r-\kappa)(\kappa-\varepsilon)}\bigg). \end{aligned} \end{equation}$
将 (A.4)-(A.5) 式带入 (A.3) 式, 经过简单化简即可得到
当 $\varepsilon=\kappa+r$
方程组 (4.12) 中第三个方程的求解参考了 Wang等[17 ] 中附录 $A$
参考文献
View Option
[1]
Bielecki T Jang I . Portfolio optimization with a defaultable security
Asia-Pacific Financial Markets , 2006 , 13 2 ): 113 -127
[本文引用: 1]
[2]
Bowers N L Gerber H U , et al . Actuarial Mathematics
Schaumburg Illinois: Society of Actuaries , 1997
[本文引用: 2]
[3]
Cheng Y Y Escobar-Anel M . Optimal investment strategy in the family of 4/2 stochastic volatility models
Quantitative Finance , 2021 , 21 10 ): 1723 -1751
[本文引用: 1]
[4]
Cui J Jong F D Ponds E . Intergenerational risk sharing within funded pension schemes
Journal of Pension Economics and Finance , 2011 , 10 1 ): 1 -29
[本文引用: 1]
[5]
Cui Z Y Kirkby J L Nguyen D . Equity-linked annuity pricing with cliquet-style guarantees in regime-switching and stochastic volatility models with jumps
Insurance Mathematics and Economics , 2017 , 74 46 -62
[本文引用: 1]
[6]
Dickson D C Hardy M R Waters H R . Actuarial Mathematics for Life Contingent Risks . London : Cambridge University Press , 2013
[本文引用: 1]
[7]
Fleming W H Soner H M . Controlled Markov Processes and Viscosity Solutions . Pittsburgh : Springer , 2006
[本文引用: 1]
[8]
Gollier C . Intergenerational risk-sharing and risk-sharing of a pension fund
Journal of Public Economics , 2008 , 92 5 ): 1463 -1485
[本文引用: 1]
[9]
Grasselli M . The 4/2 stochastic volatility model: A unified approach for the Heston and the 3/2 model
Mathematical Finance , 2017 , 27 4 ): 1013 -1034
[本文引用: 1]
[10]
He L Liang Z X Wang S . Dynamic optimal adjustment policies of hybrid pension plans
Insurance Mathematics and Economics , 2022 , 1.6 46 -68
[本文引用: 1]
[11]
Heston S L . A simple new formula for options with stochastic volatility
Social Science Electronic Publishing , 1997 , 15 4 ): 23 -44
[本文引用: 1]
[12]
Khorasanee Z M . Risk-sharing and benefit smoothing in a hybrid pension plan
North American Actuarial Journal , 2012 , 16 4 ): 449 -461
[本文引用: 2]
[13]
Maenhout P J . Robust portfolio rules and asset pricing
The Review of Financial Studies , 2004 , 17 4 ): 951 -983
[本文引用: 2]
[14]
Sun Z Y Zheng X X Zhang X . Robust optimal investment and reinsurance of an insurer under variance premium principle and default risk
Journal of Mathematical Analysis and Applications , 2017 , 4.6 1666 -1686
[本文引用: 1]
[15]
Turner J A Center P P . Hybrid Pensions: Risk Sharing Arrangements for Pension Plan Sponsors and Participants . Shawburger : Society of Actuaries , 2014
[本文引用: 1]
[16]
Wang N Zhang N Jin Z Qian L Y . Robust non-zero-sum investment and reinsurance game with default risk
Insurance: Mathematics and Economics , 2019 , 84 115 -132
DOI:10.1016/j.insmatheco.2018.09.009
[本文引用: 1]
This paper investigates a non-zero-sum stochastic differential game between two competitive CARA insurers, who are concerned about the potential model ambiguity and aim to seek the robust optimal reinsurance and investment strategies. The ambiguity-averse insurers are allowed to purchase reinsurance treaty to mitigate individual claim risks; and can invest in a financial market consisting of one risk-free asset, one risky asset and one defaultable corporate bond. The objective of each insurer is to maximize the expected exponential utility of his terminal surplus relative to that of his competitor under the worst-case scenario of the alternative measures. Applying the techniques of stochastic dynamic programming, we derive the robust Nash equilibrium reinsurance and investment policies explicitly and present the corresponding verification theorem. Finally, we perform some numerical examples to illustrate the influence of model parameters on the equilibrium reinsurance and investment strategies and draw some economic interpretations from these results. (C) 2018 Elsevier B.V.
[17]
Wang P Li Z F . Robust optimal investment strategy for an AAM of DC pension plans with stochastic interest rate and stochastic volatility
Insurance Mathematics and Economics , 2018 , 80 67 -83
[本文引用: 1]
[18]
Wang P Q Rong X M Zhao H Wang S X . Robust optimal investment and benefit payment adjustment strategy for target benefit pension plans under default risk
Journal of Computational and Applied Mathematics , 2021 , 3.1 : 113382
[本文引用: 6]
[19]
Wang S X Lu Y . Optimal investment strategies and risk-sharing arrangements for a hybrid pension plan
Insurance: Mathematics and Economics , 2019 , 89 46 -62
[本文引用: 9]
[20]
Wang S X Lu Y Sanders B . Optimal investment strategies and intergenerational risk sharing for target benefit pension plans
Insurance: Mathematics and Economics , 2018 , 80 1 -14
[本文引用: 1]
[21]
Wang S X Rong X Zhao H . Optimal investment and benefit payment strategy under loss aversion for target benefit pension plans
Applied Mathematics and Computation . 2019 , 3.6 205 -218
[本文引用: 1]
[22]
Wang W Y Muravey D Shen Y Zeng Y . Optimal investment and reinsurance strategies under 4/2 stochastic volatility model
Scandinavian Actuarial Journal , 2023 , 20.3 5 ): 413 -449
[本文引用: 1]
[23]
Yong J Zhou X . Stochastic Controls:Hamiltonian Systems and HJB Equations . New York : Springer , 1999
[本文引用: 1]
[24]
Zhang Y M . Dynamic optimal mean-variance investment with mispricing in the family of 4/2 stochastic volatility models
Mathematics , 2021 , 9 18 ): 2293
[本文引用: 2]
[25]
Zhu S Wang B . Unified approach for the affine and non-affine models: An empirical analysis on the S&P 500 volatility dynamics
Computational Economics , 2019 , 53 1421 -1442 .
[本文引用: 1]
[26]
王奕 , 王传玉 , 刘帅 . 违约风险下混合养老金的最优投资策略
安徽工程大学学报 , 2022 , 37 4 ): 84 -94
[本文引用: 1]
Wang Y Wang C Y Liu S . Optimal investment strategy under default risk for hybrid pension plans
Journal of Anhui Polytechnic , 2022 , 37 4 ): 84 -94
[本文引用: 1]
[27]
张欣茹 , 马世霞 , 张雨萌 , 慕蕊 . 带随机工资的目标收益养老金计划的鲁棒最优投资和收益支付调整策略
运筹学学报 , 2022 , 29 1 ): 127 -141
[本文引用: 1]
Zhang X R Ma S X Zhang Y M Mu R . Robust optimal investment and benefit payment adjustment strategy for target benefit pension plans with stochastic salary
Operations Research Transactions , 2022 , 29 1 ): 127 -141
[本文引用: 1]
Portfolio optimization with a defaultable security
1
2006
... 根据 Bielecki[1 ] , 得到 $P$ $P(t,T_1)$
Actuarial Mathematics
2
1997
... 根据 Bowers 等[2 ] 描述的终端融资方法, 集体混合型养老金计划的累计精算负债是所有计划参与者退休后应享给付总额的贴现, 即未来养老金应计给付总额的贴现值. 更确切地说, 这些负债包括在职成员的未来退休收益和承诺给当前退休人员的给付总额. 根据上面给出的符号, 可以将 $t$ $AL(t)$
... 假设5.2 根据 Bowers 等[2 ] 第二十章的进入年龄精算成本法以及 Wang 等[19 ] 假定养老金应计密度函数 $m(x)$
Optimal investment strategy in the family of 4/2 stochastic volatility models
1
2021
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
Intergenerational risk sharing within funded pension schemes
1
2011
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
Equity-linked annuity pricing with cliquet-style guarantees in regime-switching and stochastic volatility models with jumps
1
2017
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
1
2013
... 该式满足 $\bar s(a)=1$ . 接下来数值分析中, 参考 Dickson等[6 ] 设 $\mathcal{A}=2.2\times10^{-4}, \mathcal{B}=2.7\times10^{-6},$ $\theta=1.124$ . ...
1
2006
... 在这一部分中, 我们推导了基于模型不确定性有违约风险的混合型养老金计划的最优投资策略和最优缴款-给付调整策略的闭式解以及相应的值函数.根据 Yong[23 ] , Fleming[7 ] 以及 Wang 等[18 ] , 最优值函数 $J(t,f,l,v,z)\in C^{1,2,2,2}([T]\times\mathcal{R}\times\mathcal{R}^{+}\times\mathcal{R}^{+}\times(0,1))$
Intergenerational risk-sharing and risk-sharing of a pension fund
1
2008
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
The 4/2 stochastic volatility model: A unified approach for the Heston and the 3/2 model
1
2017
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
Dynamic optimal adjustment policies of hybrid pension plans
1
2022
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
A simple new formula for options with stochastic volatility
1
1997
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
Risk-sharing and benefit smoothing in a hybrid pension plan
2
2012
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
... 受 Khorasanee[12 ] 和 Wang等[19 ] 改进的混合型养老金计划模型的启发, 定义两个控制变量 $\lambda_1(t)$ $\lambda_2(t)$
Robust portfolio rules and asset pricing
2
2004
... 在鲁棒控制中当可替代测度偏离参考测度时会受到惩罚, 参考Maenhout[13 ] , 这里惩罚函数 $g_\beta(\phi)$
... 其中 $\beta_1$ $\beta_2$ $\beta_3$ $\beta_1$ $\beta_2$ $\beta_3$ [13 ] , 对 $\beta_i$
Robust optimal investment and reinsurance of an insurer under variance premium principle and default risk
1
2017
... 证 此引理的证明类似于 Sun 等[14 ] , 这里不再赘述. ...
1
2014
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
Robust non-zero-sum investment and reinsurance game with default risk
1
2019
... 在本小节中, 将考虑违约债券违约前情况, 即 $z=0$ . 本小节的解法参考了 Wang等[16 ] 和 Wang 等[18 ] 中违约前情况下的相关解法. 则 (4.1) 式的 HJB 方程可以整理为 ...
Robust optimal investment strategy for an AAM of DC pension plans with stochastic interest rate and stochastic volatility
1
2018
... 方程组 (4.12) 中第三个方程的求解参考了 Wang等[17 ] 中附录 $A$
Robust optimal investment and benefit payment adjustment strategy for target benefit pension plans under default risk
6
2021
... 近期, 学者们加大了对违约债券的研究, 根据中国人民银行发布的《中国金融稳定报告 (2023)》 中数据显示1 (1数据来源: 《中国金融稳定报告 (2023)》. http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/5177895/index.html .), 截止 2022 年末, 我国债券型基金占比 28.73% 高于股票型基金占比的 9.53%, 因此考虑养老金基金在可违约债券上的投资也是很有必要的. 目前也有学者在混合养老金计划框架中引入了对违约风险的研究. 如 Wang等[18 ] 在目标收益型养老金计划的模型中考虑了违约风险并分别推导出了违约前和违约后的最优投资和收益支付策略.张欣茹等[27 ] 在考虑违约风险和工资是随机的情况下研究了目标收益型养老金计划的鲁棒最优投资和收益支付调整策略. ...
... 在时间间隔 $[T]$ [18 ] 的启发, 使用 CARA 效用给出目标函数 ...
... 养老金计划管理者尝试在最坏情况的模型中寻求最优策略, 受 Wang等[18 ] 的启发, 构建鲁棒最优控制问题如下 ...
... 在这一部分中, 我们推导了基于模型不确定性有违约风险的混合型养老金计划的最优投资策略和最优缴款-给付调整策略的闭式解以及相应的值函数.根据 Yong[23 ] , Fleming[7 ] 以及 Wang 等[18 ] , 最优值函数 $J(t,f,l,v,z)\in C^{1,2,2,2}([T]\times\mathcal{R}\times\mathcal{R}^{+}\times\mathcal{R}^{+}\times(0,1))$
... 在本小节中, 将考虑违约债券违约前情况, 即 $z=0$ . 本小节的解法参考了 Wang等[16 ] 和 Wang 等[18 ] 中违约前情况下的相关解法. 则 (4.1) 式的 HJB 方程可以整理为 ...
... 假设5.5 除非特别说明, 本文采用的其他相关数值可参考Zhang[24 ] , Wang 等[19 ] 和 Wang 等[18 ] :$T=15$ $a=30$ $b=65$ $\omega=100$ $n(t)=10$ $\varepsilon=0.015$ $r=0.05$ $\beta=0.01$ $\xi=0.5$ $w_0=1$ $l=6277$ $f=7000$ $\kappa=0.1$ $\delta=0.01$ $\zeta=0.4$ $h^{P^*}=0.025$ $h^P=0.00625$ $c_1=0.9051$ $c_2=0.0023$ $\sigma_v=0.6612$ $\lambda=2.9428$ $\theta_v=0.0328$ $\rho=-0.7689$ $k=7.3479$ $Q_1=6$ $Q_2=5$ $Q_3=1$ $\rho_1=1$ $\rho_2=1$ $\rho_3=2$ $m=1$ $v_0=0.02$ . ...
Optimal investment strategies and risk-sharing arrangements for a hybrid pension plan
9
2019
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
... 本文在 Wang 等[19 ] 提出的具有代际风险分担的混合型养老金模型的基础上, 引入了价格服从 4/2 随机波动率模型的股票和违约债券来描述金融市场, 考虑了模型不确定性下的混合型养老金的最优投资和缴款--给付调整策略. 本文的目标是在 CARA 效用函数基础上最大化盈余和缴款--给付调整额的贴现值或当盈余和缴款--给付调整额为负时将其贴现值最小化. 接着通过求解扩展的 Hamilton-Jacobi-Bellman (HJB) 方程系统分别得到违约前和违约后情况下的混合型养老金的最优投资和缴款--给付调整策略的闭式表达式. 最后, 通过一些数值模拟分析了模型参数和金融市场参数对最优策略的影响. ...
... 此处考虑一定时期内非平稳的, 按照年龄结构划分的人口演化过程. 参考 Wang等[19 ] 进行以下几个假设 ...
... 接下来, 根据 Wang 等[19 ] 定义应计函数 $M(x)$
... 受 Khorasanee[12 ] 和 Wang等[19 ] 改进的混合型养老金计划模型的启发, 定义两个控制变量 $\lambda_1(t)$ $\lambda_2(t)$
... 假设5.2 根据 Bowers 等[2 ] 第二十章的进入年龄精算成本法以及 Wang 等[19 ] 假定养老金应计密度函数 $m(x)$
... 其中 $\alpha_1$ $\eta$ [19 ] 取 $\alpha_1=0.02, \eta=0.01$ . ...
... $\varsigma$ [19 ] 取 $\varsigma=0.03$ . ...
... 假设5.5 除非特别说明, 本文采用的其他相关数值可参考Zhang[24 ] , Wang 等[19 ] 和 Wang 等[18 ] :$T=15$ $a=30$ $b=65$ $\omega=100$ $n(t)=10$ $\varepsilon=0.015$ $r=0.05$ $\beta=0.01$ $\xi=0.5$ $w_0=1$ $l=6277$ $f=7000$ $\kappa=0.1$ $\delta=0.01$ $\zeta=0.4$ $h^{P^*}=0.025$ $h^P=0.00625$ $c_1=0.9051$ $c_2=0.0023$ $\sigma_v=0.6612$ $\lambda=2.9428$ $\theta_v=0.0328$ $\rho=-0.7689$ $k=7.3479$ $Q_1=6$ $Q_2=5$ $Q_3=1$ $\rho_1=1$ $\rho_2=1$ $\rho_3=2$ $m=1$ $v_0=0.02$ . ...
Optimal investment strategies and intergenerational risk sharing for target benefit pension plans
1
2018
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
Optimal investment and benefit payment strategy under loss aversion for target benefit pension plans
1
2019
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
Optimal investment and reinsurance strategies under 4/2 stochastic volatility model
1
2023
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
1
1999
... 在这一部分中, 我们推导了基于模型不确定性有违约风险的混合型养老金计划的最优投资策略和最优缴款-给付调整策略的闭式解以及相应的值函数.根据 Yong[23 ] , Fleming[7 ] 以及 Wang 等[18 ] , 最优值函数 $J(t,f,l,v,z)\in C^{1,2,2,2}([T]\times\mathcal{R}\times\mathcal{R}^{+}\times\mathcal{R}^{+}\times(0,1))$
Dynamic optimal mean-variance investment with mispricing in the family of 4/2 stochastic volatility models
2
2021
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
... 假设5.5 除非特别说明, 本文采用的其他相关数值可参考Zhang[24 ] , Wang 等[19 ] 和 Wang 等[18 ] :$T=15$ $a=30$ $b=65$ $\omega=100$ $n(t)=10$ $\varepsilon=0.015$ $r=0.05$ $\beta=0.01$ $\xi=0.5$ $w_0=1$ $l=6277$ $f=7000$ $\kappa=0.1$ $\delta=0.01$ $\zeta=0.4$ $h^{P^*}=0.025$ $h^P=0.00625$ $c_1=0.9051$ $c_2=0.0023$ $\sigma_v=0.6612$ $\lambda=2.9428$ $\theta_v=0.0328$ $\rho=-0.7689$ $k=7.3479$ $Q_1=6$ $Q_2=5$ $Q_3=1$ $\rho_1=1$ $\rho_2=1$ $\rho_3=2$ $m=1$ $v_0=0.02$ . ...
Unified approach for the affine and non-affine models: An empirical analysis on the S&P 500 volatility dynamics
1
2019
... "微笑" 两个典型特征, 而且 Heston 模型被校准到真实数据时, Feller 条件往往得不到满足. 因此 Heston[11 ] 提出了进一步克服 Heston 模型局限性的 3/2 随机波动率模型, 其中它的瞬时波动率由 Cox-Ingersoll-Ross (CIR) 过程的倒数刻画. 继而, 为了更好地模拟风险资产的价格变化,Grasselli[9 ] 引入了一种包含 Heston 模型和 3/2 模型的双因子 4/2 随机波动率模型. 该模型的两因子之间虽然密切相关, 但在解释隐含波动率方面展现出不同的性质, 因而可以更好地描绘金融市场的复杂多变. 由于 4/2 随机波动率模型能够更准确地刻画金融市场隐含波动率曲面的演变, 这个新模型已经被广泛应用于衍生品的定价和校准, 如 Cui 等[5 ] 和 Zhu 等[25 ] . 其次也有很多学者将其应用于保险的投资组合问题. Cheng 等[3 ] 一文推导出了 4/2 随机波动率模型下的最优投资策略并进行了全面的实证分析. Zhang[24 ] 研究了4/2 随机波动率模型下包含股票错误定价的均值-方差动态最优投资策略. Wang 等[22 ] 在 4/2 随机波动率模型下利用一类抛物偏微分方程研究了均值-方差再保险投资问题. ...
违约风险下混合养老金的最优投资策略
1
2022
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
违约风险下混合养老金的最优投资策略
1
2022
... 随着人口老龄化程度的加深, 养老金问题已成为社会热点. 目前各国根据缴费和给付方式的不同将养老金计划分为确定给付 (Defined Benefit, DB) 型和确定缴费 (Defined Contribution, DC) 型. DB 型养老金计划为员工提供稳定的退休收益, 但金融风险由养老金计划受托人承担. 而在 DC 型养老金计划框架中, 员工的缴款是预先确定的, 退休收益取决于养老基金的投资表现, 由此可见 DC 型养老金计划完全将财务风险外化, 并由计划参与者承担. 随着预期寿命的增加和人口结构的转变, 让养老金计划受托人或参与者一方独立承担所有风险的方案愈显不合理. 基于此背景下, 各国陆续开始研究与发展兼具 DB 型计划与 DC 型计划优点的混合型养老金计划. 这种混合型养老金计划旨在可持续、稳定和负担的起的基础上为计划参与者提供更好的退休保障, 并在所有的参与者和不同年龄群体之间分担风险. Turner等[15 ] 总结了混合型养老金计划的四种典型方案: 荷兰的混合型 DB 计划 (Hybrid DB Plans), 瑞典的非金融 DC 计划 (Nonfinancial DC Plan), 美国、加拿大和日本的现金余额计划 (Cash Balance Plans) 以及德国的李斯特计划 (Riester Plans). Gollier[8 ] 提出并证明了混合型养老金计划可以更好地实现代际风险分担, 这种风险分担方式除了提高时间分散化的主要收益外, 还允许养老基金更好地利用股权溢价带来的高额收益.Wang 等[19 ] 提出一种连续时间框架下的集体混合型养老金计划模型, 在这种混合型养老金计划模型中, 缴款和退休给付水平都根据计划的绩效进行调整, 并在所有的参与者和不同年龄群体间分担风险. Wang等[20 ] 和 Wang 等[21 ] 也在目标收益型养老金计划模型下分别考虑了连续时间的投资和代际风险分担模式以及损失厌恶条件下的最优投资和收益支付策略.此外, Cui 等[4 ] ,Khorasanee[12 ] , He 等[10 ] 和王奕等[26 ] 等文献中都有关于混合型养老金计划的研究. ...
带随机工资的目标收益养老金计划的鲁棒最优投资和收益支付调整策略
1
2022
... 近期, 学者们加大了对违约债券的研究, 根据中国人民银行发布的《中国金融稳定报告 (2023)》 中数据显示1 (1数据来源: 《中国金融稳定报告 (2023)》. http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/5177895/index.html .), 截止 2022 年末, 我国债券型基金占比 28.73% 高于股票型基金占比的 9.53%, 因此考虑养老金基金在可违约债券上的投资也是很有必要的. 目前也有学者在混合养老金计划框架中引入了对违约风险的研究. 如 Wang等[18 ] 在目标收益型养老金计划的模型中考虑了违约风险并分别推导出了违约前和违约后的最优投资和收益支付策略.张欣茹等[27 ] 在考虑违约风险和工资是随机的情况下研究了目标收益型养老金计划的鲁棒最优投资和收益支付调整策略. ...
带随机工资的目标收益养老金计划的鲁棒最优投资和收益支付调整策略
1
2022
... 近期, 学者们加大了对违约债券的研究, 根据中国人民银行发布的《中国金融稳定报告 (2023)》 中数据显示1 (1数据来源: 《中国金融稳定报告 (2023)》. http://www.pbc.gov.cn/goutongjiaoliu/113456/113469/5177895/index.html .), 截止 2022 年末, 我国债券型基金占比 28.73% 高于股票型基金占比的 9.53%, 因此考虑养老金基金在可违约债券上的投资也是很有必要的. 目前也有学者在混合养老金计划框架中引入了对违约风险的研究. 如 Wang等[18 ] 在目标收益型养老金计划的模型中考虑了违约风险并分别推导出了违约前和违约后的最优投资和收益支付策略.张欣茹等[27 ] 在考虑违约风险和工资是随机的情况下研究了目标收益型养老金计划的鲁棒最优投资和收益支付调整策略. ...