1 引言
体力作用下的一维等熵磁气动力学欧拉方程在欧拉坐标中可以写成
(1.1) $ \left\{\begin{array}{ll} \rho_{t}+(\rho u)_{x}=0,\\(\rho u)_{t}+(\rho u^{2} +p+\frac{B^{2}}{2\mu})_{x}=\beta\rho,\end{array}\right. $
其中 $\rho, u, p, \mu > 0 $ $B$
(1.2) $p=\varepsilon_{1}\ln\rho,\,\,\,\,\,B=\varepsilon_{2}\rho, $
其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
Shen[2 ] 考虑了具有库仑类摩擦项的无压欧拉系统, 并通过引入新的速度得到了非自相似黎曼解
(1.3) $v(t,x)=u(t,x)-\beta t,$
且 Faccanoni 和 Mangeney[9 ] 也引入了这个方法, 用于研究具有库仑类摩擦项的浅水方程的黎曼问题.
如果 $\beta=0$ $B=0$
(1.4) $ \left\{\begin{array}{ll} \rho_{t}+(\rho u)_{x}=0,\\(\rho u)_{t}+ (\rho u^{2}+p)_{x}=0.\end{array}\right. $
Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态.
在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26] 及其引用的参考文献.
如果压力 $p$ $B$ $\epsilon_{1},\epsilon_{2} \to 0,$
(1.5) $ \left\{\begin{array}{ll} \rho_{t}+(\rho u)_{x}=0,\\(\rho u)_{t}+(\rho u^{2} )_{x}=\beta\rho,\end{array}\right. $
它也可以通过恒定压力获得, 其中力被假定为重力, $\beta$ [27 ] . 该系统 (1.4) 可以描述自由粒子在低温下碰撞粘附的运动学过程, 以及有关宇宙大尺度结构的信息[28 ] . Shen[2 ] 考虑了系统 (1.4) 的黎曼问题.
受文献 [17 20] 的启发, 本文重点研究了体力作用下等熵磁气体动力学方程组 (1.1)-(1.2) 的黎曼解当消失压力和磁场时的极限. 与齐次情况不同, 黎曼解不再是自相似的. $\epsilon_{1},\epsilon_{2}. \rightarrow0$
本文的其余部分组织如下. 为了完整起见, 我们在第 2 节中简要回顾了(1.4) 的黎曼解. 在第 3 节中, 我们展示了 (1.1)-(1.2) 的黎曼解的一些结果. 最后, 在第 4 节中, 我们严格地展示了当压力和磁场消失时 (1.1)-(1.2) 的黎曼解中 $\delta$ - 激波和真空态的形成.
2 对零压零磁场欧拉方程黎曼解的回顾
为了完整起见, 在本节中, 我们简要回顾一下系统 (1.4) 的黎曼解. 更多细节可以在文献 [2 ,29 ] 中找到. 系统 (1.4) 可以通过更改变量 (1.3) 的形式重写
(2.1) $ \left\{\begin{array}{ll} \rho_{t}+(\rho (v+\beta t))_{x}=0,\\(\rho v)_{t}+(\rho v(v+\beta t))_{x}=0.\end{array}\right. $
在本节中, 我们对具有初始数据的 (2.1) 的黎曼问题感兴趣
(2.2) $ (\rho, v)(0, x) =\left\{\begin{array}{ll} (\rho_{-}, u_{-}),\,\,\,\,x< 0,\\(\rho_{+}, u_{+}),\,\,\,\,x> 0,\end{array} \right.$
其中 $\rho_{\pm}>0$ $u_{\pm}$ $(\rho, u)(t, x)=(\rho, v+ \beta t)(t, x),$
根据前人的研究[2 ,29 ] , 我们可以分别通过接触间断、真空状态和 $\delta$ - 激波连接两个常数状态 $(\rho_{\pm},u_{\pm})$
(1) 对于 $u_{-} >u_{+}$
(2.3) $(\rho, u)(t,x)=\left\{ \begin{array}{ll} (\rho_{-}, u_{-}+\beta t),& \hbox{$x<x(t)$,}\\(w(t)\delta(x-x(t)),u_{\delta} (t)), & \hbox{$x=x(t)$,}\\ (\rho_{+}, u_{+}+\beta t), & \hbox{$x>x(t)$,} \end{array} \right. $
(2.4) $ x(t)=\frac{\sqrt{\rho_{-}}u_{-}+\sqrt{\rho_{+}}u_{+}}{\sqrt{\rho_{-}}+\sqrt{\rho_{+}}}t+\frac{1}{2}\beta t^{2}, ~~ w(t)=\sqrt{\rho_{-}\rho_{+}}(u_{-}-u_{+})\,t, ~~u_{\delta}(t)=\frac{\sqrt{\rho_{-}}u_{-}+\sqrt{\rho_{+}}u_{+}}{\sqrt{\rho_{-}}+\sqrt{\rho_{+}}}+\beta t;$
(2) 对于 $u_{-}<u_{+}$
(2.5) $ (\rho,u)(t,x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-\infty<x<u_{-}t+\frac{1}{2}\beta t^{2}, \\(0,\frac{x+\frac{1}{2}\beta t}{t}),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,u_{-}t+\frac{1}{2}\beta t^{2} \leq x \leq u_{+}t+\frac{1}{2}\beta t^{2},\\(\rho_{+},u_{+}+\beta t), \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, u_{+}t+\frac{1}{2}\beta t^{2}<x<+\infty, \end{array}\right. $
其中两个接触不连续 $J_{1}$ $J_{2}$
(3)对于 $u_{-}=u_{+}$
(2.6) $ (\rho,u)(t,x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-\infty<x<u_{-}t+\frac{1}{2}\beta t^{2}, \\(\rho_{+},u_{+}+\beta t), \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, u_{-}t+\frac{1}{2}\beta t^{2}<x<+\infty, \end{array}\right. $
其中, 接触不连续 $J$
3 等熵磁气动力学欧拉方程的黎曼问题
在本节中, 我们构造了在体力作用下的带对数气体的等熵磁气动力学方程组黎曼解. 代入 (1.2)、(1.3) 式, 系统 (1.1) 可以重写为
(3.1) $ \left\{\begin{array}{ll} \rho_{t}+(\rho (v+\beta t))_{x}=0,\\(\rho v)_{t}+(\rho v (v+\beta t)+\epsilon_{1}\ln\rho+\frac{\epsilon_{2}^{2}\rho^{2}}{2\mu})_{x}=0.\end{array}\right. $
我们关注的是 (3.1) 式的黎曼问题, 初始数据为
(3.2) $ (\rho, v)(0, x) =\left\{\begin{array}{ll} (\rho_{-}, u_{-}),\,\,\,\,x< 0,\\(\rho_{+}, u_{+}),\,\,\,\,x> 0,\end{array} \right.$
其中 $\rho_{\pm}>0$ $u_{\pm}$
(3.3) $\left( \begin{array}{ccc}1& 0 \\v & \rho \end{array}\right)\left(\begin{array}{cc}\rho\\v \end{array}\right)_t+\left( \begin{array}{ccc}v+\beta t& \rho \\v(v+\beta t)+\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu} & \rho(2v+\beta t) \end{array}\right)\left(\begin{array}{cc}\rho\\v \end{array}\right)_x=\left(\begin{array}{cc}0\\0 \end{array}\right). $
通过 (3.3) 式, 很容易看出系统 (3.1) 有两个特征值
(3.4) $ \lambda_{1}=v+\beta t-\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}},\,\,\,\,\,\,\,\lambda_{2}=v+\beta t+\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}}, $
因此, 当 $\rho>0$
(3.5) $w^{1} =v+\int^{\rho}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau, \,\,\,\,w^{2} =v-\int^{\rho}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau,$
分别满足 $\bigtriangledown w^{i} \cdot \overrightarrow{r_i}=0$ ( $i$
在相平面上, 给定一个状态 $(\rho_{-}, u_{-})$
(3.6) $R_{1}(\rho_{-},u_{-}):\,\,\left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=\lambda_{1}=v+\beta t-\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}}, \\v+\int^{\rho}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau=u_{-}+\int^{\rho_{-}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau, \,\,\,\,\rho<\rho_{-}, v>u_{-},\\ \lambda_{1}(\rho_{-},u_{-})<\lambda_{1}(\rho,v)\end{array} \right.$
(3.7) 和$R_{2}(\rho_{-},u_{-}):\,\,\left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=\lambda_{2}=v+\beta t+\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}}, \\v-\int^{\rho}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau=u_{-}-\int^{\rho_{-}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau, \,\,\,\,\rho>\rho_{-}, v<u_{-},\\\lambda_{2}(\rho_{-},u_{-})<\lambda_{2}(\rho,v).\end{array} \right.$
对方程 (3.6) 的第二个方程 $v$ $\rho$
这意味着 1-稀疏波曲线 $R_{1}(\rho_{-},u_{-})$ $(\rho, v)$ $v$ $\rho$ $\frac{{\rm d}v}{{\rm d}\rho}>0$ $\frac{{\rm d}^{2} v}{{\rm d}\rho^{2}}<0$ $R_{2}(\rho_{-},u_{-})$ $(\rho, v)(\rho>0)$
取极限 $\rho \to 0^{+}$ $\textstyle \lim_{\rho \to 0^{+}} v=+\infty $ $R_{1}(\rho_{-},u_{-})$ $u$ $\textstyle \lim_{\rho \to +\infty} v=+\infty $
设 $\sigma(t)=\frac{{\rm d}x(t)}{{\rm d}t}$ $x=x(t)$
(3.8) $\left\{ \begin{array}{ll} -\sigma(t)[\rho]+[\rho (v+\beta t)]=0, \\ -\sigma(t)[\rho v]+[\rho v(v+\beta t)+\varepsilon_{1}\ln\rho+\frac{\varepsilon_{2}^{2}\rho^{2}}{2\mu}]=0, \end{array} \right. $
其中 $[\rho]=\rho-\rho_{-}$
(3.9) $v=v_{-}\pm\sqrt{\frac{(\rho-\rho_{-})(\epsilon_{1}(\ln\rho-\ln\rho_{-})+\frac{\epsilon_{2}^{2}}{2\mu}(\rho^{2}-\rho_{-}^{2}))}{\rho \rho_{-}}}, $
其中 $(\rho_{-},v_{-})$ $(\rho_{},v_{})$
Lax 熵条件说明 1-激波 $S_{1} $ $\sigma_{1} (t)$
(3.10) $\sigma_{1} (t)<\lambda_{1} (\rho_{-},v_{-}),\,\,\,\,\lambda_{1} (\rho,v)<\sigma_{1} (t)<\lambda_{2} (\rho,v).$
类似地, Lax 熵条件意味着 2-激波 $S_{2} $ $\sigma_{2} (t)$
(3.11) $\sigma_{1} (t)>\lambda_{1} (\rho,v),\,\,\,\,\lambda_{1} (\rho_{-},v_{-})<\sigma_{1} (t)<\lambda_{2} (\rho_{-},v_{-}).$
然后, 将 (3.8) 式代入 (3.10) 式的第一个不等式, 我们有
这表明 $v - v_{-}$ $\rho- \rho_{-}$
$v - v_{-}$ $\rho- \rho_{-}$
对于给定的左状态 $(\rho_{-},u_{-})$
(3.12) $S_{1} (\rho_{-},u_{-}):\left\{\begin{array}{ll} v=u_{-}-\sqrt{\frac{(\rho-\rho_{-})(\epsilon_{1}(\ln\rho-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho^2- \rho_{-}^2))}{\rho\rho_{-}}},~~~\\\rho>\rho_{-},v<u_{-}\end{array} \right.$
(3.13) 和$S_{2} (\rho_{-},u_{-}):\left\{\begin{array}{ll} v=u_{-}-\sqrt{\frac{(\rho-\rho_{-})(\epsilon_{1}(\ln\rho-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho^2- \rho_{-}^2))}{\rho\rho_{-}}},~~~\\\rho<\rho_{-},v<u_{-}.\end{array} \right.$
对 (3.12) 式的第二个方程 $v$ $\rho$ $\rho>\rho_{-}$
(3.14) $v_{\rho}=-\frac{1}{2\sqrt{\frac{(\rho-\rho_{-})(\epsilon_{1}(\ln\rho-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho^2- \rho_{-}^2))}{\rho\rho_{-}}}} \Big(\frac{(\epsilon_{1}(\ln\rho-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho^2- \rho_{-}^2))}{\rho^2}+\frac{\rho-\rho_{-}}{\rho\rho_{-}}(\frac{\epsilon_{1}}{\rho} +\frac{\epsilon_{2}^{2}\rho}{\mu})\Big),$
这意味着对于 1-激波曲线, $v_{\rho}<0$ $\rho>\rho_{-}$ $S_{1}(\rho_{-},u_{-})$ $(\rho, v) $ $v_{\rho}>0$ $\rho<\rho_{-}$ $S_{2}(\rho_{-},u_{-})$ $(\rho, v) $ $S_{1}(\rho_{-},u_{-})$ $\lim_{\rho \to +\infty}v=-\infty $ $S_{2}(\rho_{-},u_{-})$ $\lim_{\rho \to 0^{+}}v=-\infty $ .
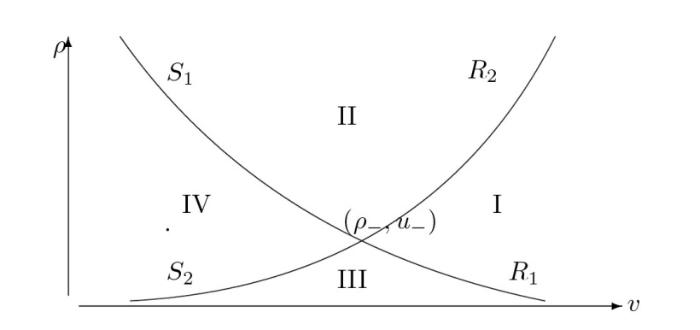
在相平面 $(\rho, v) $ $(\rho_{-}, u_{-})$ $R_{j} (\rho_{-}, u_{-})$ $S_{j} (\rho_{-}, u_{-})$ $j$ $(\rho, v)$ 图 1 ). 根据不同区域的右状态 $(\rho_{+},u_{+})$
(1) $(\rho_{+},u_{+})\in I (\rho_{-},u_{-}):$ $(\rho_{-},u_{-})+R_{1} +(\rho_{\ast},v_{\ast})+R_{2} +(\rho_{+},u_{+});$
(2) $(\rho_{+},u_{+})\in II(\rho_{-},u_{-}):$ $(\rho_{-},u_{-})+S_{1} +(\rho_{\ast},v_{\ast})+R_{2} +(\rho_{+},u_{+});$
(3) $(\rho_{+},u_{+})\in III(\rho_{-},u_{-}):$ $(\rho_{-},u_{-})+R_{1} +(\rho_{\ast},v_{\ast})+S_{2} +(\rho_{+},u_{+});$
(4) $(\rho_{+},u_{+})\in IV (\rho_{-},u_{-}):$ $(\rho_{-},u_{-})+S_{1} +(\rho_{\ast},v_{\ast})+S_{2} +(\rho_{+},u_{+}),$ $(\rho_{\ast},v_{\ast})$
图 1
使用 (1.3), 得到了 (1.1)-(1.2) 的黎曼解, 如下所示
(1) $(\rho_{+},u_{+})\in I(\rho_{-},u_{-}):$ $(\rho_{-},u_{-}+\beta t)+R_{1} +(\rho_{\ast},v_{\ast}+\beta t)+R_{2} +(\rho_{+},u_{+}+\beta t);$
(2) $(\rho_{+},u_{+})\in II(\rho_{-},u_{-}):$ $(\rho_{-},u_{-}+\beta t)+S_{1} +(\rho_{\ast},v_{\ast}+\beta t)+R_{2} +(\rho_{+},u_{+}+\beta t);$
(3) $(\rho_{+},u_{+})\in III (\rho_{-},u_{-}):$ $(\rho_{-},u_{-}+\beta t)+R_{1} +(\rho_{\ast},v_{\ast}+\beta t)+S_{2} +(\rho_{+},u_{+}+\beta t);$
(4) $(\rho_{+},u_{+})\in IV (\rho_{-},u_{-}):$ $(\rho_{-},u_{-}+\beta t)+S_{1} +(\rho_{\ast},v_{\ast}+\beta t)+S_{2} +(\rho_{+},u_{+}+\beta t).$
让我们回到黎曼问题 (1.1)-(1.2) 和 (3.2). 如果 $(\rho_{+},u_{+})\in I $ $R_{1}+R_{2}$
(3.15) $ (\rho,u)(t, x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x<x_{1}^{-}(t), \\R_{1},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{1}^{-}(t) < x <x_{1}^{+}(t),\\(\rho_{\ast},u_{\ast}+\beta t), \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{1}^{+}(t) < x <x_{2}^{-}(t),\\R_{2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{2}^{-}(t) < x <x_{2}^{+}(t),\\(\rho_{+},u_{+}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x >x_{2}^{+}(t) \end{array}\right. $
其中 $x_{1}^{\pm}(t)$ $x_{2}^{\pm}(t)$ $(\rho_{\ast},v_{\ast})$ 图 2 中的 (a) 来详细说明这种情况, 其中稀疏波扇 $R_{1}$ $R_{2}$
图 2
图 2
当 $\beta>0$
如果 $(\rho_{+},u_{+})\in II$ $S_{1}+R_{2}$
(3.16) $ (\rho,u)(t, x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x<x_{1}(t), \\(\rho_{\ast},u_{\ast}+\beta t), \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{1}(t) < x <x_{2}^{-}(t),\\ R_{2},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{2}^{-}(t) < x <x_{2}^{+}(t),\\(\rho_{+},u_{+}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x >x_{2}^{+}(t) \end{array}\right. $
其中 $x_{1}^{\pm}(t)$ $x_{2}^{\pm}(t)$ $(\rho_{\ast},v_{\ast})$ 图 2 中的 (b) 来详细说明这种情况, 其中激波曲线 $S_{1}$ $R_{2}$
如果 $(\rho_{+},u_{+})\in III$ $R_{1}+S_{2}$ $(\rho_{+},u_{+})\in II$ 图 2 中的 (c).
如果 $(\rho_{+},u_{+})\in IV$ $S_{1}+S_{2}$
(3.17) $ (\rho,u)(t, x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x<x_{1}(t), \\(\rho_{\ast},u_{\ast}+\beta t), \,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x_{1}(t) < x <x_{2}(t),\\(\rho_{+},u_{+}+\beta t),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x >x_{2}(t) \end{array}\right. $
其中 $x_{1}(t)$ $x_{2}^{\pm}(t)$ $(\rho_{\ast},v_{\ast})$ 图 2 中的 (d) 来详细说明这种情况, 其中激波曲线 $S_{1}$ $S_{2}$
4 极限 $\epsilon_{1},\epsilon_{2}\rightarrow 0$ $\delta$ - 激波和真空状态的形成
在本节中, 我们将研究压力场和磁场都消失的极限过程, 即 $\epsilon_{1},\epsilon_{2}\rightarrow 0$ . 由于当 $\epsilon_{1},\epsilon_{2}\rightarrow 0$ $(\rho,v)$ $II$ $III$ $(\rho_{+}, u_{+}) \in I$ $(\rho_{+}, u_{+}) \in IV$
4.1 $\delta$ - 激波
在本小节中, 我们将讨论当 $u_{-}>u_{+}$ $\epsilon_{1},\epsilon_{2}\rightarrow 0$ $\delta$ - 激波的形成. 如果 $(\rho_{+}, u_{+})\in IV(\rho_{-}, u_{-})$ $\epsilon_{1},\epsilon_{2}>0$ $S_1$ $S_2$ $(\rho_{\ast},u_{\ast})$ $(\rho_{\pm},u_{\pm})$
(4.1) $ S_{1}^{\epsilon_{1}\epsilon_{2}}: \left\{ \begin{array}{ll} \sigma_{1}^{\epsilon_{1}\epsilon_{2}}=\frac{\rho_{\ast} v_{\ast}-\rho_{-}u_{-} }{\rho_{\ast}-\rho_{-}}+\beta t, \\[3mm] v_{\ast} = u_{-}-\sqrt{\frac{(\rho_{\ast}-\rho_{-})(\epsilon_{1}(\ln\rho_{\ast}-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho_{\ast}^2- \rho_{-}^2))}{\rho_{\ast}\rho_{-}}},\\[3mm] \rho_{\ast}>\rho_{-},\,\,\,\,\,\,\,\,\, \end{array} \right. $
(4.2) $S_{2}^{\epsilon_{1}\epsilon_{2}}: \left\{ \begin{array}{ll} \sigma_{2}^{\epsilon_{1}\epsilon_{2}}=\frac{\rho_{+} v_{+}-\rho_{\ast}u_{\ast} }{\rho_{+}-\rho_{\ast}}+\beta t, \\[3mm] u_{+} = v_{\ast}-\sqrt{\frac{(\rho_{+}-\rho_{\ast})(\epsilon_{1}(\ln\rho_{+}-\ln\rho_{\ast})+\frac{\epsilon_{2}^2}{2\mu}(\rho_{+}^2- \rho_{\ast}^2))}{\rho_{+}\rho_{\ast}}},\\[3mm] \rho_{+}<\rho_{\ast}.\,\,\,\,\,\,\,\,\,\, \end{array} \right. $
通过 (4.1) 和 (4.2) 式的第二个方程, 我们有
(4.3) $ u_{-}-u_{+}=\sqrt{\frac{(\rho_{\ast}-\rho_{-})(\epsilon_{1}(\ln\rho_{\ast}-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho_{\ast}^2- \rho_{-}^2))}{\rho_{\ast}\rho_{-}}}$ $\qquad\qquad\qquad+\sqrt{\frac{(\rho_{+}-\rho_{\ast})(\epsilon_{1}(\ln\rho_{+}-\ln\rho_{\ast})+\frac{\epsilon_{2}^2}{2\mu}(\rho_{+}^2- \rho_{\ast}^2))}{\rho_{+}\rho_{\ast}}}. $
对于任何给定的 $\rho_{\pm}>0,$ $\epsilon_{1},\epsilon_{2}\to 0$
(4.4) $ u_{-}-u_{+}= \lim_{\epsilon_{1},\epsilon_{2} \to 0}\sqrt{\epsilon_{1}\ln\rho_{\ast}+\frac{(\epsilon_{2}\rho_{\ast})^2}{2\mu}} \cdot\Big(\sqrt{\frac {\rho_{\ast}-\rho_{-}}{\rho_{\ast}\rho_{-}}}+\sqrt{\frac{\rho_{\ast}-\rho_{+}}{\rho_{+}\rho_{\ast}}}\Big), $
这意味着 $\lim_{\epsilon_{1},\epsilon_{2}\to 0}\rho_{\ast}=+\infty,$
${\bf引理4.2}$ $\sigma=\frac{\sqrt{\rho_{-}}u_{-}+\sqrt{\rho_{+}}u_{+}}{\sqrt{\rho_{-}}+\sqrt{\rho_{+}} }$
(4.5) $ \lim_{\epsilon_{1},\epsilon_{2} \to 0} u_{\ast}=\lim_{\epsilon_{1},\epsilon_{2} \to 0}\sigma _{1}^{\epsilon_{1}\epsilon_{2}}=\lim_{\epsilon_{1},\epsilon_{2} \to 0}\sigma_{2}^{\epsilon_{1}\epsilon_{2}}=\sigma+\beta t. $
${\bf证}$ 使用 (4.1) 式和引理 4.1, 可以计算出
(4.6) $\begin{matrix} \lim_{\epsilon_{1},\epsilon_{2} \to 0} v_{\ast} &=u_{-}-\lim_{\epsilon_{1},\epsilon_{2} \to 0} \sqrt{\frac{(\rho_{\ast}-\rho_{-})(\epsilon_{1}(\ln\rho_{\ast}-\ln\rho_{-})+\frac{\epsilon_{2}^2}{2\mu}(\rho_{\ast}^2- \rho_{-}^2))}{\rho_{\ast} \rho_{-}}} \\ &=u_{-}-\frac{\sqrt{\rho_{+}}(u_{-}-u_{+})}{\sqrt{\rho_{-}}+\sqrt{\rho_{+}}}\\ & =\frac{\sqrt{\rho_{-}}u_{-}+\sqrt{\rho_{+}}u_{+}}{\sqrt{\rho_{-}}+\sqrt{\rho_{+}} }=\sigma, \end{matrix}$
从 (4.1) 和 (4.2) 式的第一个方程中, 我们有
可得 $\lim\limits_{\epsilon_{1},\epsilon_{2} \rightarrow 0} u_{\ast}=\lim\limits_{\epsilon_{1},\epsilon_{2} \rightarrow 0}\sigma _{1}^{\epsilon_{1}\epsilon_{2}}=\lim\limits_{\epsilon_{1},\epsilon_{2} \rightarrow 0}\sigma_{2}^{\epsilon_{1}\epsilon_{2}}=\sigma+\beta t.$
(4.7) $\begin{matrix} \lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}} t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}} t}\rho_{\ast} {\rm d}x=\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t, \end{matrix}$
(4.8) $\begin{matrix}\lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}} t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}} t}\rho_{\ast}u_{\ast}{\rm d}x=(\sigma+\beta t)\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t. \end{matrix}$
${\bf证}$ $S_{1}^{\epsilon_{1}\epsilon_{2}}$ $S_{2}^{\epsilon_{1}\epsilon_{2}}$
(4.9) $\lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}}t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}}t}\rho_{\ast} {\rm d}x =\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t. $
(4.10) $\begin{matrix} \lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}}t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}}t}\rho_{\ast}u_{\ast}{\rm d}x &=\lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}}t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}}t}\rho_{\ast}v_{\ast}{\rm d}x +\beta t\lim_{\epsilon_{1},\epsilon_{2} \to 0}\int_{\sigma_{1}^{\epsilon_{1}\epsilon_{2}}t}^{\sigma_{2}^{\epsilon_{1}\epsilon_{2}}t}\rho_{\ast}{\rm d}x \\ &=(\sigma+\beta t)\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t. \end{matrix}$
上述引理表明, 当 $ \epsilon_{1},\epsilon_{2}\rightarrow 0$ $S_{1}^{\epsilon_{1}\epsilon_{2}}$ $S_{2}^{\epsilon_{1}\epsilon_{2}}$ $\delta$ - 激波. 接下来, 我们将根据引理 4.3 给出 $\delta$ - 激波的确切位置、传播速度和强度. 从 (4.7) 和 (4.8) 式中
(4.11) $\omega(t)=\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t,$
(4.12) $\omega(t)u_{\delta}=(\sigma+\beta t)\sqrt{\rho_{+}\rho_{-}}(u_{-}-u_{+})t,$
(4.13) $u_{\delta}=\sigma+\beta t, $
这与 $\sigma(t)$ $\frac{{\rm d}x(t)}{{\rm d}t}=\sigma(t) $
(4.14) $ x(t)=\sigma t+\frac{1}{2}\beta t^2.$
从 (4.11)-(4.14) 式中, 我们可以看到上面定义的量与第 2 节给出的量完全一致. 因此, 它唯一地确定, 当 $ \epsilon_{1},\epsilon_{2} \rightarrow 0$ $(\rho_{+},u_{+}) \in IV$ $u_{-}>u_{+}$ $\delta$ - 激波解. 因此, 我们得到以下结果, 该结果表征了 $(\rho_{+},u_{+}) \in IV$ $u_{-}>u_{+}$
${\bf定理4.1}$ $u_{-}>u_{+}$ $\epsilon_{1},\epsilon_{2},(\rho_{+},u_{+}) \in IV$ $(\rho,u)$ $ \epsilon_{1},\epsilon_{2}\rightarrow 0,(\rho,u)$ $\delta$ - 激波解.
4.2 真空态
在本小节中, 我们展示在 $(\rho_{+},u_{+})\in I$ $u_{-}< u_{+}$ $ \rho_{\pm} > 0 $ $\epsilon_{1},\epsilon_{2}>0$ $(\rho_{\ast},u_{\ast})=$ $(\rho_{\ast},v_{\ast}+\beta t)$ $(\rho_{-},u_{-}+\beta t)$ $(\rho_{\ast},v_{\ast}+\beta t)$ $R_{1}^{\epsilon_{1}\epsilon_{2}}$ $\lambda_{1}^{\epsilon_{1}\epsilon_{2}}$ $(\rho_{\ast},u_{\ast}+\beta t)$ $(\rho_{+},v_{+}+\beta t)$ $R_{2}^{\epsilon_{1}\epsilon_{2}}$ $\lambda_{2}^{\epsilon_{1}\epsilon_{2}}$ . 有
(4.15) $R_{1}^{\epsilon_{1}\epsilon_{2}}:\,\,\left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=\lambda_{1}^{\epsilon_{1}\epsilon_{2}}=v+\beta t-\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}}, \\v_{\ast}=u_{-}-\int^{\rho_{\ast}}_{\rho_{-}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau, \,\,\,\,\rho_{\ast}\leq\rho\leq\rho_{-}\end{array} \right.$
(4.16) 和$R_{2}^{\epsilon_{1}\epsilon_{2}}:\,\,\left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=\lambda_{2}^{\epsilon_{1}\epsilon_{2}}=v+\beta t+\sqrt{\frac{\epsilon_{1}}{\rho}+\frac{\epsilon_{2}^{2}\rho}{\mu}}, \\v_{\ast}=u_{+}+\int^{\rho_{\ast}}_{\rho_{+}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau, \,\,\,\,\rho_{\ast}\leq\rho\leq\rho_{+}.\end{array} \right.$
${\bf定理4.2}$ $u_{-}<u_{+}$ $(\rho_{+},u_{+})\in I(\rho_{-},u_{-})$ $\epsilon_{1},\epsilon_{2} \to 0.$
${\bf证}$
(4.17) $\begin{matrix} u_{+}-u_{-}&=\int^{\rho_{+}}_{\rho_{\ast}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau +\int^{\rho_{-}}_{\rho_{\ast}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau \\ &\leq\frac{1}{\rho_{\ast}}\int^{\rho_{+}}_{\rho_{\ast}}\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{+}}{\mu}}{\rm d}\tau +\frac{1}{\rho_{\ast}}\int^{\rho_{-}}_{\rho_{\ast}}\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{-}}{\mu}}{\rm d}\tau \\ & \leq\frac{\rho_{+}}{\rho_{\ast}}\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{+}}{\mu}} +\frac{\rho_{-}}{\rho_{\ast}}\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{-}}{\mu}} \end{matrix}$
(4.18) $2v_{\ast}-u_{-}-u_{+}=\int_{\rho_{+}}^{\rho_{-}}\frac{\sqrt{\frac{\epsilon_{1}}{\tau}+\frac{\epsilon_{2}^{2}\tau}{\mu}}}{\tau}{\rm d}\tau. $
假设 $\lim_{\epsilon_{1}\epsilon_{2} \to 0} \rho_{\ast} = M \in (0,\min(\rho_{-},\rho_{+})],$ $u_{+}=u_{-}$ $u_{-}<u_{+}$ $\lim_{\epsilon_{1}\epsilon_{2} \to 0} \rho_{\ast}=0,$ $\epsilon_{1},\epsilon_{2}\to 0$ $\lim\limits_{\epsilon_{1},\epsilon_{2} \rightarrow 0} v_{\ast}=\frac{u_{-}+u_{+}}{2}.$ $ \lim\limits_{\epsilon_{1},\epsilon_{2} \rightarrow 0} u_{\ast}=\frac{u_{-}+u_{+}}{2}+\beta t.$
系统 (1.1) 和 (1.2) 的黎曼解可以明确表示为
(4.19) $(\rho_{},u_{})(t, x)=\left\{\begin{array}{ll} (\rho_{-}, u_{-}+\beta t),\,\,\,\,\,\,x< x_{1}^{\epsilon_{1}\epsilon_{2}}(t),\\ R_{1}^{\epsilon_{1}\epsilon_{2}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\qquad x_{1}^{\epsilon_{1}\epsilon_{2}}(t)\leq x\leq x_{2}^{\epsilon_{1}\epsilon_{2}}(t),\\(\rho_{\ast}^{}, v_{\ast}^{}+\beta t),\,\,\,\,\,\,\,\,x_{2}^{\epsilon_{1}\epsilon_{2}}(t)<x< x_{3}^{AB}(t),\\ R_{2}^{\epsilon_{1}\epsilon_{2}},\,\,\,\,\,\,\,\,\,\qquad\quad x_{3}^{\epsilon_{1}\epsilon_{2}}(t)\leq x\leq x_{4}^{\epsilon_{1}\epsilon_{2}}(t),\\(\rho_{+}, u_{+}+\beta t),\,\,\,\,\ x> x_{4}^{\epsilon_{1}\epsilon_{2}}(t),\end{array} \right.$
(4.20) $\left\{\begin{array}{ll} x_{1}^{\epsilon_{1}\epsilon_{2}}(t)=\int_{0}^{t}\lambda_{1}^{\epsilon_{1}\epsilon_{2}}(\rho_{-}, u_{-})(\tau) {\rm d}\tau=\bigg(u_{-}-\sqrt{\frac{\epsilon_{1}}{\rho_{-}}+\frac{\epsilon_{2}^{2}\rho_{-}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2}, \\x_{2}^{\epsilon_{1}\epsilon_{2}}(t)=\int_{0}^{t}\lambda_{1}^{\epsilon_{1}\epsilon_{2}}(\rho_{\ast}^{}, v_{\ast}^{})(\tau) {\rm d}\tau=\bigg(v_{\ast}^{}-\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{\ast}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2}, \\x_{3}^{\epsilon_{1}\epsilon_{2}}(t)=\int_{0}^{t}\lambda_{2}^{\epsilon_{1}\epsilon_{2}}(\rho_{\ast}^{}, v_{\ast}^{})(\tau) {\rm d}\tau=\bigg(v_{\ast}^{}+\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{\ast}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2},\\ x_{4}^{\epsilon_{1}\epsilon_{2}}(t)=\int_{0}^{t}\lambda_{2}^{\epsilon_{1}\epsilon_{2}}(\rho_{+}, u_{+})(\tau) {\rm d}\tau=\bigg(u_{+}+\sqrt{\frac{\epsilon_{1}}{\rho_{+}}+\frac{\epsilon_{2}^{2}\rho_{+}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2}. \end{array} \right.$
在 (4.17) 式的第一行中取极限 $\epsilon_{2}\to 0$
令 $\epsilon_{1}\to 0,$
(4.21) $ \lim_{\epsilon_{1}\to 0 }\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}(\epsilon_{1},0)}}=\frac{u_{+}-u_{-}}{4}. $
(4.22) $\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}x_{1}^{\epsilon_{1}\epsilon_{2}}(t)=\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}\bigg(u_{-}-\sqrt{\frac{\epsilon_{1}}{\rho_{-}}+\frac{\epsilon_{2}^{2}\rho_{-}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2}=u_{-}t+\frac{1}{2}\beta t^{2}, $
(4.23) $\begin{matrix} \lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}x_{2}^{\epsilon_{1}\epsilon_{2}}(t)&=\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}\bigg(v_{\ast}-\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{\ast}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2} \\ &=\bigg(\frac{u_{-}+u_{+}}{2}-\lim_{\epsilon_{1}\to 0 }\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}(\epsilon_{1},0)}}\bigg)t+\frac{1}{2}\beta t^{2}\\ &=\frac{3u_{-}+u_{+}}{4}t+\frac{1}{2}\beta t^{2}. \end{matrix}$
(4.24) $\begin{matrix} \lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}x_{3}^{\epsilon_{1}\epsilon_{2}}(t)& =\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}\bigg(v_{\ast}+\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}}+\frac{\epsilon_{2}^{2}\rho_{\ast}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2} \\ & =\bigg(\frac{u_{-}+u_{+}}{2}+\lim_{\epsilon_{1}\to 0 }\sqrt{\frac{\epsilon_{1}}{\rho_{\ast}(\epsilon_{1},0)}}\bigg)t+\frac{1}{2}\beta t^{2}\\ &=\frac{u_{-}+3u_{+}}{4}t+\frac{1}{2}\beta t^{2}, \end{matrix}$
(4.25) $\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}x_{4}^{\epsilon_{1}\epsilon_{2}}(t)=\lim\limits_{\epsilon_{1},\epsilon_{2}\rightarrow 0}\bigg(u_{+}-\sqrt{\frac{\epsilon_{1}}{\rho_{+}}+\frac{\epsilon_{2}^{2}\rho_{+}}{\mu}}\bigg)t+\frac{1}{2}\beta t^{2}=u_{+}t+\frac{1}{2}\beta t^{2}. $
另一方面, $R_{1}$ $\epsilon_{2}\to 0$
(4.26) $ \lim_{\epsilon_{2}\to 0}R_{1}: \left\{ \begin{array}{ll} \frac{{\rm d}x}{{\rm d}t}=\lambda_{1}=v+\beta t-\sqrt{\frac{\epsilon _{1}}{\rho}}, \\[3mm] v=u_{-}+2\sqrt{\frac{\epsilon_{1}}{\rho}}-2\sqrt{\frac{\epsilon_{1}}{\rho_{-}}}, \,\,\,\,\,\,\, \rho<\rho_{-}. \end{array} \right. $
(4.27) $ \rho_{1}(t,x)=\frac{\epsilon_{1}}{(\frac{x}{t}-u_{-}-\frac{1}{2}\beta t+2\sqrt{\frac{\epsilon_{1}}{\rho_{-}}})^2},\, \,\,v_{1}(t,x)=2\frac{x}{t}-u_{-}-\beta t+2\sqrt{\frac{\epsilon_{1}}{\rho_{-}}}, $
(4.28) $ \,u_{1}(t,x)=2\frac{x}{t}-u_{-}+2\sqrt{\frac{\epsilon_{1}}{\rho_{-}}}. $
因此, 在 (4.27) 和 (4.28) 式中令 $\epsilon_{1}\to 0$
同样, 在 $R_{2}$ $(\rho_{2}(t,x),u_{2}(t,x))$
(4.29) $\qquad\quad~~ \rho_{2}(t,x)=\frac{\epsilon_{1}}{(u_{+}+\frac{1}{2}\beta t-\frac{x}{t}+2\sqrt{\frac{\epsilon_{1}}{\rho_{+}}})^2},$
因此, 在 (4.29) 式中让 $\epsilon_{1}\to 0$
那么, 上面的讨论表明, 在 $(\rho_{+},u_{+})\in I(\rho_{-},u_{-})$ $u_{+}>u_{-}$ $\epsilon_{1},\epsilon_{2}\to 0$
(4.30) $ \lim_{\epsilon_{1},\epsilon_{2}\to 0}(\rho,u)(t, x) = \left\{ \begin{array}{ll} (\rho_{-},u_{-}+\beta t), \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-\infty<x<u_{-}t+\frac{1}{2}\beta t^{2},\\ (0,2\frac{x}{t}-u_{-}), \,\,\,\,\,\,\,\,\,\,\qquad u_{-}t+\frac{1}{2}\beta t^{2}< x<\frac{3u_{-}+u_{+}}{4}t+\frac{1}{2}\beta t^{2}, \\ (0,\frac{u_{-}+u_{+}}{2}+\beta t), \\\frac{3u_{-}+u_{+}}{4}t+\frac{1}{2}\beta t^{2}<x<\frac{u_{-}+3u_{+}}{4}t+\frac{1}{2}\beta t^{2},\\ (0,2\frac{x}{t}-u_{+}), \,\,\,\,\,\,\,\,\,\qquad \frac{u_{-}+3u_{+}}{4}t+\frac{1}{2}\beta t^{2}< x< u_{+}t+\frac{1}{2}\beta t^{2}, \\ (\rho_{+},u_{+}+\beta t), \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,u_{+}t+\frac{1}{2}\beta t^{2}<x< +\infty. \end{array} \right. $
这与输运方程的黎曼解不同. 因此, 从上面我们已证明了以下结果.
${\bf定理4.3}$ $u_{+}>u_{-}$ $(\rho_{+},u_{+})\in I (\rho_{-},u_{-})$ $\epsilon_{1},\epsilon_{2}>0$ $\epsilon_{1},\epsilon_{2} \to 0$
${\bf定理4.4}$ $(\rho_{+},u_{+})\in I (\rho_{-},u_{-})$ $u_{-}<u_{+}$ $\epsilon_{1},\epsilon_{2}\to 0$ $u_{+}>u_{-}$
参考文献
View Option
[1]
Sekhar T R Sharma V D Riemann problem and elementary wave interactions in isentropic magnetogasdynamics
Nonlinear Anal Real World Appl , 2010 , 11 619 -636
[本文引用: 1]
[2]
Shen C The limits of Riemann solutions to the isentropic magnetogasdynamics
Appl Math Lett , 2011 , 24 1124 -1129
[本文引用: 5]
[3]
Shao Z Delta shocks and vacuum states for the isentropic magnetogasdynamics equations for Chaplygin gas as pressure and magnetic field vanish
Anal Math Phys , 2022 , 12 85
[本文引用: 1]
[4]
Chen J Sheng W The Riemann problem and the limit solutions as magnetic field vanishes to magnetogasdynamics for generalized Chaplygin gas
Commun Pure Appl Anal , 2018 , 17 127 -142
[本文引用: 1]
[5]
Chavanis P H Sire C Logotropic distributions
Physica A: Stat Mech Appl , 2007 , 375 140 -158
[本文引用: 1]
[6]
Chavanis P H The logotropic dark fluid as a unification of dark matter and dark energy
Phys Lett B , 2016 , 758 59 -66
[7]
Ferreira V M C Avelino P P New limit on logotropic unified energy models
Phys Lett B , 2017 , 770 213 -216
[8]
Odintsov S D Oikonomou V K Timoshkin A V et al . Cosmological fluids with logarithmic equation of state
Ann Physics , 2018 , 398 238 -253
[本文引用: 1]
[9]
Faccanoni G Mangeney A Exact solution for granular flows
Internat J Numer Anal Meth Geomech , 2012 , 37 10 ): 1408 -1433
[本文引用: 1]
[10]
Sun M Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state
Nonlinear Anal Real World Appl , 2020 , 53 103068
[本文引用: 1]
[11]
Brenier Y Solutions with concentration to the Riemann problem for one-dimensional Chaplygin gas equations
J Math Fluid Mech , 2005 , 7 S326 -S331
[本文引用: 1]
[12]
Guo L Sheng W Zhang T The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system
Commun Pure Appl Anal , 2010 , 9 431 -458
[本文引用: 1]
[13]
Serre D Multidimensional shock interaction for a Chaplygin gas
Arch Ration Mech Anal , 2009 , 191 539 -577
[本文引用: 1]
[14]
Sheng W Wang G Yin G Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes
Nonlinear Anal Real World Appl , 2015 , 22 115 -128
[本文引用: 1]
[15]
Wang G The Riemann problem for one dimensional generalized Chaplygin gas dynamics
J Math Anal Appl , 2013 , 403 434 -450
[本文引用: 1]
[16]
Sheng W Zhang T The Riemann Problem for the Transportation Equations in Gas Dynamics
Providence, RI: Amer Math Soc , 1999
[本文引用: 1]
[17]
Chen G Q Liu H Formation of $\delta$ - shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids
SIAM J Math Anal , 2003 , 34 925 -938
[本文引用: 2]
[18]
Chen G Q Liu H Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids
Physica D , 2004 , 189 141 -165
[本文引用: 1]
[19]
Li J Note on the compressible Euler equations with zero temperature
Appl Math Lett , 2001 , 14 519 -523
[本文引用: 1]
[20]
Ibrahim M Liu F Liu S Concentration of mass in the pressureless limit of Euler equations for power law
Nonlinear Anal Real World Appl , 2019 , 47 224 -235
[本文引用: 2]
[21]
Shen C Sun M Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model
J Differential Equations , 2010 , 249 3024 -3051
[本文引用: 1]
[22]
Tong M Shen C Lin X The asymptotic limits of Riemann solutions for the isentropic extended Chaplygin gas dynamic system with the vanishing pressure
Boundary Value Problems , 2018 , 2018 144
[23]
Yang H Wang J Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas
J Math Anal Appl , 2014 , 413 800 -820
[24]
Yin G Sheng W Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases
J Math Anal Appl , 2009 , 355 594 -605
[25]
Yin G Song K Vanishing pressure limits of Riemann solutions to the isentropic relativistic Euler system for Chaplygin gas
J Math Anal App , 2014 , 411 506 -521
[26]
Li H Shao Z Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas
Commun Pure Appl Ana , 2016 , 15 2373 -2400
[本文引用: 1]
[27]
Daw D A E Nedeljkov M Shadow waves for pressureless gas balance laws
Appl Math Lett , 2016 , 57 54 -59
[本文引用: 1]
[28]
Weinan E Rykov Y G Sinai Y G Generalized variational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics
Comm Math Phys , 1996 , 177 349 -380
[本文引用: 1]
[29]
Sheng S Shao Z The vanishing adiabatic exponent limits of Riemann solutions to the isentropic Euler equations for power law with a Coulomb-like friction term
J Math Phys , 2019 , 60 101504
[本文引用: 2]
Riemann problem and elementary wave interactions in isentropic magnetogasdynamics
1
2010
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
The limits of Riemann solutions to the isentropic magnetogasdynamics
5
2011
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
... Shen[2 ] 考虑了具有库仑类摩擦项的无压欧拉系统, 并通过引入新的速度得到了非自相似黎曼解 ...
... 它也可以通过恒定压力获得, 其中力被假定为重力, $\beta$ [27 ] . 该系统 (1.4) 可以描述自由粒子在低温下碰撞粘附的运动学过程, 以及有关宇宙大尺度结构的信息[28 ] . Shen[2 ] 考虑了系统 (1.4) 的黎曼问题. ...
... 为了完整起见, 在本节中, 我们简要回顾一下系统 (1.4) 的黎曼解. 更多细节可以在文献 [2 ,29 ] 中找到. 系统 (1.4) 可以通过更改变量 (1.3) 的形式重写 ...
... 根据前人的研究[2 ,29 ] , 我们可以分别通过接触间断、真空状态和 $\delta$ - 激波连接两个常数状态 $(\rho_{\pm},u_{\pm})$
Delta shocks and vacuum states for the isentropic magnetogasdynamics equations for Chaplygin gas as pressure and magnetic field vanish
1
2022
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
The Riemann problem and the limit solutions as magnetic field vanishes to magnetogasdynamics for generalized Chaplygin gas
1
2018
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
Logotropic distributions
1
2007
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
The logotropic dark fluid as a unification of dark matter and dark energy
0
2016
New limit on logotropic unified energy models
0
2017
Cosmological fluids with logarithmic equation of state
1
2018
... 其中 $\varepsilon_{1}$ $\varepsilon_{2}$ [1 ] 研究了黎曼问题解的存在性和唯一性, 并讨论了等熵磁气体动力学中基本波的相互作用. 各种气体模型的系统 (1.1) 的极限解的研究一直备受关注. Shen[2 ] 、Shao[3 ] 、Chen 和 Sheng[4 ] 分别研究了多方气体等熵磁气体动力学的黎曼解、Chaplygin 气体的黎曼解和广义 Chaplygin 气体的黎曼解的极限行为. 在某些宇宙学理论中, 作为宇宙暗能量的可能模型, Chaplygin 气体可以描述当前宇宙的加速膨胀. 最新的工作[5 8 ] 引入了状态 $p=\epsilon_{1}\ln\rho$ $\rho>1$ $p=\epsilon_{1}\ln\rho$ $0<\rho<1$
Exact solution for granular flows
1
2012
... 且 Faccanoni 和 Mangeney[9 ] 也引入了这个方法, 用于研究具有库仑类摩擦项的浅水方程的黎曼问题. ...
Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state
1
2020
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
Solutions with concentration to the Riemann problem for one-dimensional Chaplygin gas equations
1
2005
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system
1
2010
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
Multidimensional shock interaction for a Chaplygin gas
1
2009
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes
1
2015
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
The Riemann problem for one dimensional generalized Chaplygin gas dynamics
1
2013
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
The Riemann Problem for the Transportation Equations in Gas Dynamics
1
1999
... Sun[10 ] 研究了带对数状态方程的等熵欧拉系黎曼解在压力消失过程中的浓度和空化现象. 对于等熵欧拉系统, Brenier[11 ] 首先研究了一维黎曼问题, 得到了当初始数据属于相平面中某个域时的集中解. 此外, Guo、Sheng 和 Zhang[12 ] 放弃了这种约束, 构造性地获得了一维黎曼问题的全局解, 其中发现了 $\delta$ - 激波. 此外, 他们还系统地研究了等熵 Chaplygin 气体方程的二维黎曼问题. 对于二维情况, 我们也可以参考文献 [13 ], 其中 Serre 研究了二维等熵不旋转 Chaplygin 气体的压力波相互作用, 并构造性地证明了二维黎曼问题的鞍形和涡旋两种情况的跨音速解的存在. 最近, Sheng, Wang, Yin[14 ] 和 Wang[15 ] 研究了广义 Chaplygin 气体的黎曼问题, 得到了黎曼问题的解和基本波的相互作用. Sheng 和 Zhang 在文献 [16 ] 中提出了气体动力学中零压流输运方程的黎曼解, 其中出现了 $\delta$ - 激波和真空态. ...
Formation of $\delta$ -shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids
2
2003
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
... 受文献 [17 20 ] 的启发, 本文重点研究了体力作用下等熵磁气体动力学方程组 (1.1)-(1.2) 的黎曼解当消失压力和磁场时的极限. 与齐次情况不同, 黎曼解不再是自相似的. $\epsilon_{1},\epsilon_{2}. \rightarrow0$
Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids
1
2004
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
Note on the compressible Euler equations with zero temperature
1
2001
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
Concentration of mass in the pressureless limit of Euler equations for power law
2
2019
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
... 受文献 [17 20 ] 的启发, 本文重点研究了体力作用下等熵磁气体动力学方程组 (1.1)-(1.2) 的黎曼解当消失压力和磁场时的极限. 与齐次情况不同, 黎曼解不再是自相似的. $\epsilon_{1},\epsilon_{2}. \rightarrow0$
Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model
1
2010
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
The asymptotic limits of Riemann solutions for the isentropic extended Chaplygin gas dynamic system with the vanishing pressure
0
2018
Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas
0
2014
Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases
0
2009
Vanishing pressure limits of Riemann solutions to the isentropic relativistic Euler system for Chaplygin gas
0
2014
Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas
1
2016
... 在 $\delta$ - 激波的相关研究中, 一个非常重要和有趣的话题是研究黎曼解中集中和空化现象以及 $\delta$ - 激波和真空态的形成. 在早期的开创性论文中, Chen 和 Liu[17 ] 首先通过在模型 $p(\rho)=\varepsilon\rho^{\gamma}/\gamma ( \gamma >1)$ $\varepsilon \rightarrow 0+$ $\delta$ - 激波和真空状态的形成, 它严格地描述了数学中的集中和空化现象. 此外, 他们还在文献 [18 ] 中获得了非等熵流体欧拉方程组的相同结果. Li[19 ] 研究了等温情况的等温欧拉方程的相同问题, 证明当温度降至零时, 包含两个激波的解收敛到输运方程的 $\delta$ - 激波解, 包含两个稀疏波的解收敛到涉及真空的输运方程的解. 最近, Ibrahim、Liu 和 Liu[20 ] 表明, 在 $p(\rho) =\rho^{\gamma}$ $(0 < \gamma < 1)$ 21 26 ] 及其引用的参考文献. ...
Shadow waves for pressureless gas balance laws
1
2016
... 它也可以通过恒定压力获得, 其中力被假定为重力, $\beta$ [27 ] . 该系统 (1.4) 可以描述自由粒子在低温下碰撞粘附的运动学过程, 以及有关宇宙大尺度结构的信息[28 ] . Shen[2 ] 考虑了系统 (1.4) 的黎曼问题. ...
Generalized variational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics
1
1996
... 它也可以通过恒定压力获得, 其中力被假定为重力, $\beta$ [27 ] . 该系统 (1.4) 可以描述自由粒子在低温下碰撞粘附的运动学过程, 以及有关宇宙大尺度结构的信息[28 ] . Shen[2 ] 考虑了系统 (1.4) 的黎曼问题. ...
The vanishing adiabatic exponent limits of Riemann solutions to the isentropic Euler equations for power law with a Coulomb-like friction term
2
2019
... 为了完整起见, 在本节中, 我们简要回顾一下系统 (1.4) 的黎曼解. 更多细节可以在文献 [2 ,29 ] 中找到. 系统 (1.4) 可以通过更改变量 (1.3) 的形式重写 ...
... 根据前人的研究[2 ,29 ] , 我们可以分别通过接触间断、真空状态和 $\delta$ - 激波连接两个常数状态 $(\rho_{\pm},u_{\pm})$