超可积系统作为可积系统的一类重要推广, 与量子场论和弦理论之间存在着紧密的联系, 在理论和数学物理中具有重要的应用 ^[1-3]. 经典可积系统经历了多种形式的超延拓 (也称费米扩张), 这一领域的研究历史悠久且成果丰硕, 见文献[4-7]. 追溯其起源, 早在 1985 年, Manin 和 Radul 运用超拟微分算子的语言首次刻画了超 KP 可积系统 ^[6]. 此后, 其他版本的超可积系统相继涌现^[4,5,7], 其中 Kac-van de Leur 版本 ^[7-9] 和 Jacobian 版本 ^[4,5] 引起了学者的较多关注. 前者侧重于利用无穷维李超代数和表示论的语言来刻画超可积系统, 而后者更多利用代数和几何的工具来描述超可积系统. 当前, 关于超可积系统的研究正广泛开展, 吸引了大量学者与科研人员的深入探索 ^[10-15]. 该文主要关注 Kac-van de Leur 版本下超 KP 可积系列的一类推广系统. 我们先回顾 Kac-van de Leur 版本下超 KP 可积系列的构造, 更多细节请参阅文献 [9,16].

克利福德超代数 $Cl=Cl_{\bar{0}}\oplus Cl_{\bar{1}}$ 的生成子 $\psi_i^+$ 与 $\psi_i^-~ (i\in \mathbb{Z}/2)$ (也称自由超费米子) 满足如下关系

其中 $\mathbb{Z}_2$-分次指: 当 $i\in\mathbb{Z}$ 时, $\psi_i^{\pm}\in Cl_{\bar{0}}$ (也称 $\psi_i^{\pm}$ 是偶的, 标记为 $p(\psi_i^{\pm})=0$), 当 $i\in\mathbb{Z}+1/2$ 时, $\psi_i^{\pm}\in Cl_{\bar{1}}$ (也称 $\psi_i^{\pm}$ 是奇的, 标记为 $p(\psi_i^{\pm})=1$).

不可约的 $Cl$-模 (也称超费米 Fock 空间)

这里 $j_n>\cdots >j_1>0\geq i_1\geq\cdots> i_m $ 且当 $ i_r~(\text{resp} ~j_r)\in\mathbb{Z}$ 时, $l_r=1~(\text{resp}~ k_r=1)$, 其中偶元素 $|0\rangle$ 称为真空向量且满足

对于 $n \in \mathbb{Z}$, 定义 $M$ 中的元素 $|n\rangle $ 为

定义电荷$(|0\rangle)=0$, 电荷$(\psi_i^+)=-$电荷$(\psi_i^-)=1$, 电荷的引入使得 $M$ 分解为不可约模的直和, 即 $M=\oplus_{n\in\mathbb{Z}}M_n,$ 其中 $M_n=\Big\{f\in M\Big|\text{电荷}(f)=n \Big\}$.

令 $\mathfrak{g}$ 是复数域 $\mathbb{C}$ 上的一固定超代数, $\bar{a}_{\infty|\infty}$ 是由以下 Chevalley 生成子所生成的复数域 $\mathbb{C}$ 上的李超代数

这里 $(E_{ij})_{kl}=\delta_{i,k}\delta_{j,l}$. $\bar{a}_{\infty|\infty}$ 的中心扩张所成的李超代数 ${a_{\infty|\infty}}= {\bar{a}_{\infty|\infty}}\oplus\mathbb{C}c $ 上的李超括号定义为 $[a+\lambda c,b+\mu c]=ab-(-1)^{p(a)p(b)}ba+C(a,b)c, $ 其中, $ \text{当} ~i\leq0<j~ \text{时},~C(E_{ij},E_{ji})=-(-1)^{2(i+j)}C(E_{ij},E_{ji})=(-1)^{2i},\nonumber $ 其余情况下, $C(E_{ij},E_{kl})=0.$

张量积 $a_{\infty|\infty}\otimes\mathfrak{g}$ 的偶部分是一个李代数, 记为 $a_{\infty|\infty}(\mathfrak{g})$ (更多细节请参阅文献 [16]).

定义 $a_{\infty|\infty}$ 在 $M$ 上的表示

注意 $a_{\infty|\infty}$ 在 $M$ 上的模结构将诱导出 $a_{\infty|\infty}(\mathfrak{g})$ 在 $M(\mathfrak{g})$ 上的模结构. 定义 $a_{\infty|\infty}(\mathfrak{g})$ 在 $M(\mathfrak{g})\otimes M(\mathfrak{g})$ 上的表示 $r\otimes r$

其中 $gl(V)$ 代表空间 $V$ 上的全体线性变换, 且 $g_{i,j}\in \mathfrak{g}$.

记 $A_{\infty|\infty}(\mathfrak{g})$ 是李代数 ${a}_{\infty|\infty}(\mathfrak{g})$ 所对应的群, $\overline{A_{\infty|\infty}(\mathfrak{g})}$ 是 $A_{\infty|\infty}(\mathfrak{g})$ 的极大子群^[17]. 指数映射诱导出群 $A_{\infty|\infty}(\mathfrak{g})$ 在 $M(\mathfrak{g})$ 上的表示 $ R$. 群 $\overline{A_{\infty|\infty}(\mathfrak{g})}$ 的轨道记为 $\textrm{O}_l=R(\overline{A_{\infty|\infty}(\mathfrak{g})})|l\rangle (l\in \mathbb{Z}).$

引入作用在 $M(\mathfrak{g})\otimes M(\mathfrak{g})$ 上的两个算子

文献 [16] 中已经证明算子 $S$ (resp $T$) 与群 $\overline{A_{\infty|\infty}(\mathfrak{g})}$ 在 $M(\mathfrak{g})\otimes M(\mathfrak{g})$ 上的作用可以相互交换.

对于任意元素 $g\in\overline{A_{\infty|\infty}(\mathfrak{g})}$, 恒等式 $ S(g|0\rangle\otimes g|0)=0 $ 与 $ S(g|0\rangle\otimes g|1\rangle)=|1\rangle\otimes |0\rangle $ 分别是 Kac-van de Leur 版本下的超 KP (SKP) 可积系列与超修正 KP (SmKP) 可积系列 ^[9,16]的定义. 该文将利用 Kac-van de Leur 方法构造一个包含 SKP 可积系列的系统, 该系统比 SKP 可积系列包含更多的偏微分方程, 称为 $s$-次推广超 KP 可积系列 (见命题 2.2).

该文的结构如下. 第 2 节介绍 $s$-次推广超 KP 可积系列的费米描述. 第 3 节给出了$s$-次推广超 KP 可积系列的玻色对应物. 第 4 节在超玻色 Fock 空间中研究了该系统的超双线性恒等式, 并得到了 KP 和超 KP 方程. 第 5 节将 2-4 节的内容推广到多分量情形.

利用等式 (1.2) 可证明下面的引理.

${\bf引理2.1}$ 对于 $n \in \mathbb{Z}$, $i\in \mathbb{Z}/2$, 以下结论成立

(i) $\psi_i^+|n\rangle=0$ 成立当且仅当两种情形: $n\geq0,~i\leq 0$ 或 $n<0,~i\leq -1$;

(ii) $\psi_i^-|n\rangle=0$ 成立当且仅当两种情形: $n>0,~i\geq 1$ 或 $n\leq0,~i> 0$.

关于算子 $S$ 和 $T$, 有如下引理.

${\bf引理2.2}$ 对于 $k,s\in\mathbb{Z}$, 以下结论成立

(i) $S(|k+s\rangle\otimes |k\rangle)=0$ 当且仅当 $-s\leq k\leq0$;

(ii) $T(|k\rangle\otimes |k+s\rangle)=0$ 当且仅当 $-s\leq k\leq0$.

${\bf证}$ (i) 直接计算可得

利用引理 2.1 可知 $i>0,~k\leq0$ 时有 $\psi^-_{i}|k\rangle=0$, 同时 $i\leq0,~ k+s\geq0$ 时有 $\psi^+_{i}|k+s\rangle=0$. 因此由条件 $-s\leq k\leq0$ 可得到 $S(|k+s\rangle\otimes |k\rangle)=0$. 反之亦成立. 用类似的方法可证明 (ii).

${\bf命题2.1}$ 对于 $s\in\mathbb{Z_+}$, 有以下结论

${\bf证}$ 当 $s\in\mathbb{Z_+}$ 时, 有 $|s\rangle= {\psi^+_{\frac{1}{2}}}^s|0\rangle.$ 利用克里福德超代数关系 (1.1) 与 (1.3) 式计算可得

进一步, 利用引理 2.1 与引理 2.2 计算可得

下面考虑 $s>1$ 的情形, 类似计算可得

$S$ 再次作用在 $S^2(|0\rangle\otimes|s\rangle)$ 上有

下面考虑 $s>3$ 的情形并执行类似的计算过程可得

将算子 $S$ 作用在 $|0\rangle\otimes |s\rangle$ 上 $s$ 次可得

进一步, 利用引理 2.2 (取 $k=0$) 计算可得 $S^{s+1}(|0\rangle\otimes |s\rangle)=0$. 类似的方法可以证明 (2.2) 式.

${\bf注 2.1}$ 对于 $s\in\mathbb{Z_+}$, $S^s(|k\rangle\otimes |k+s\rangle)=(-1)^{\frac{s(s-1)}{2}}s!|s\rangle\otimes |k\rangle$ 当且仅当 $k=0$ 时成立, 这一结论与非超情形 (见文献 [18])不同, 注意非超情形下拥有更强的结论.

现引入 $\tau$ 函数 $\tau_l \in \textrm{O}_l\subseteq M,~l\in \mathbb{Z}$. 利用引理 2.2, 可得到如下费米形式恒等式的命题.

${\bf命题2.2}$ 对于 $k,s\in\mathbb{Z}$, $-s\leq k\leq0$, 恒等式

成立.

恒等式 (2.3) 是 $s$-次超 KP 可积系列的费米表现形式. 显然, 在 (2.3) 式中 $s=0$ 时对应 SKP 可积系列 [7–9].

${\bf注 2.2}$ 对于 $-s\leq k\leq0$, 观察到 $p(|k+s\rangle)\equiv k+s,~p(|k\rangle)\equiv-k-1+\delta_{k,0}$, 且 $\forall~ g\in \overline{A_{\infty|\infty}(\mathfrak{g})}$ 均有 $p(g)=0$. 因此可得 $p(\tau_{k+s})\equiv k+s,~p(\tau_{k})\equiv-k-1+\delta_{k,0},$ 和 $\tau_{k+s}\in M_{k+s,\overline{k+s}},~\tau_{k}\in M_{k,\overline{\mathrm{-k+1+\delta_{k,0}}}}.$

${\bf注 2.3}$ 在等式 (2.1) 中取 $s=1$, 则得到超修正 KP 可积系列的费米形式 $S(\tau_{0}\otimes\tau_{1})=\tau_{1}\otimes\tau_{0}$, 关于超修正 KP 可积系列的更多内容可参阅文献 [16]. 事实上, 在非超情形中, 文献 [18] 指出修正 KP 可积系列具有两种定义方式, 即 $S(\tau_{0}\otimes\tau_{1})=\tau_{1}\otimes\tau_{0}$ 与 $S(\tau_{1}\otimes\tau_{0})=0$, 且两种定义是等价的. 然而, 在超的情形中这一结论并不成立.

引入费米场

$s$-次推广超 KP 可积系列 (2.3) 可用费米场表达为

其中 ${\rm Res}_{z} \sum_{i\in \mathbb{Z}}a_iz^i=a_{-1}.$

在本节中, $Cl$-模 $M$ 将由超玻色 Fock 空间表达.

$\mathbb{C}[t_i,\theta_j]$ 指由交换变量 $t_i,~i\in \mathbb{Z}-\{0\}$, 生成的多项式代数与由反交换变量 $\theta_j,~j\in \mathbb{Z}- \{0\}$, 生成的 Grassmann 代数的张量积. $q$ 是一个新的变量满足: $ qt_i\!=\!t_iq ~\text{与} ~q\theta_i\!=\!-\theta_iq, ~\text{其中}~i\in \mathbb{Z}-\{0\}$. 超的玻色 Fock 空间是一个含有超变量的多项式空间

为表达方便, 这里我们引入一些记号

${\bf命题3.1}$^[7] $ \textbf{A 型超玻色-费米对应关系 }$ 超玻色 Fock 空间 $M$ 与超费米 Fock 空间 $B$ 之间存在唯一的线性空间同构

使得超费米场的对应物为

将同构张量积 $\sigma\otimes\sigma'$ 作用在 (2.4) 式上可得

为了更方便地描述 $\tau$ 函数, 从这里开始, 我们将固定的超代数 $\mathfrak{g}$ 取为 $\mathfrak{g}=\mathbb{C}\oplus\mathbb{C}\eta$, 其中 $\eta$ 是奇元素. 观察到

为书写方便, 我们在 $\tau$ 函数表达式中省略奇元素 $\eta$, 但应时刻注意

$\tau_{k+s}(t',\theta)=\tau_{k+s}(t',\theta,\eta)=(\tau_{k+s}(t',\theta))_{{\overline{k+s}}}+ (\tau_{k+s}(t',\theta))_{{\overline{k+s+1}}}\eta,$

$\tau_k(t'',\varsigma)=\tau_k(t'',\varsigma,\eta)=(\tau_{k}(t'',\varsigma))_{\overline{-k+1+\delta_{k,0}}}+ (\tau_{k}(t'',\varsigma))_{\overline{-k+\delta_{k,0}}}\eta.$

更具体地, $\tau_{k+s}(t',\theta)$ 可以表达成 $\Lambda(\theta)$ 的特征向量之和

使得

且 $\tau_{{k+s},{n}}$ 具有如下形式: 对于 $j_{l},\iota_{m},j'_{l},\iota'_{m}>0$,

当 $n\equiv k+s+1 $ 时

当 $n\equiv k+s$ 时

类似地, $\tau_{k}(t'',\varsigma)$ 可以表达成 $\Lambda(\varsigma)$ 的特征向量之和

使得

且 $\tau_{{k},{n}}$ 具有如下形式

当 $n\equiv -k+\delta_{k,0} $ 时

当 $n\equiv -k+\delta_{k,0}+1$ 时

基于上述准备, 现给出 $s$-次推广超 KP 可积系列 (2.3) 的玻色描述.

${\bf命题3.2}$ 对于 $n,n',k,s\in\mathbb{Z}$, $-s\leq k\leq0$, $s$-次推广超 KP 可积系列在超玻色 Fock 空间中的形式是

其中 $l>0$,

${\bf证}$ 该命题的证明思路可参阅文献 [16].

${\bf注 3.1}$ 当 $s=0$ 时, 系统 (3.9) 是文献 [9] 中所构造的超 KP 可积系列.

在等式 (5.7) 中做变量替换

并对变量替换之后的结果利用基本的 Schur 多项式

这里 $p_n(t_{\pm})\in \mathbb{C}[t_{ \pm1},t_{\pm2},\cdots]$. 接着利用超 Hirota 双线性方程的定义

可以把 (3.9) 式表达成超 Hirota 双线性形式的生成级数.

${\bf命题4.1}$ 设 $n,n',k,s \in\mathbb{Z}$, $-s\leq k\leq0$, $s$-次推广超 KP 可积系列的超 Hirota 双线性形式是

这里

当 $l>0$,

当 $k, s, n,$ 和 $n'$ 被赋予不同的具体数值时, (4.1) 式对应着不同的含有超变量的非线性偏微分方程系统, 并从该系统中可以推导出具体的超 Hirota 双线性方程. 令 ${\rm deg}~ y_{\pm i}=2i, ~{\rm deg}~ \theta_{\pm i}={\rm deg}~ \varsigma_{\pm i}=2i\mp1,$ 通过在命题 4.1 中考虑 $y_i,~\theta_i, ~\varsigma_i$ 等单项式系数, 下面给出超 Hirota 双线性方程的一些具体例子.

${\bf情况 1}$$\textbf{取}$$s$=$k$=0.

若取 $n=n'$, 则由 $y_3$ 确定的 deg = 8 的方程是

令 $t_{-}=(t_{-1},t_{-2},t_{-3},\cdots)=\theta_{\pm}=(\theta_{\pm1},\theta_{\pm2},\theta_{\pm3},\cdots) =0,$ 当 $i>3$ 时令 $t_{+i}=0$, 则 $\tau_{0,n}$ 依赖于 3 个偶变量

此时, (4.2) 式是 KP 方程的 Hirota 双线性形式. 进一步, 令 $x=t_1,~y=t_2,~t=t_3,$ 且利用变换 $u(x,y,t)=2\frac{\partial^2}{\partial x^2}\log\tau_{0,n}(x,y,t)$, 方程 (4.2) 可化为

若取 $n=-1,~n'=1$, 则由 $\theta_3\varsigma_{-2}$ 确定的 ${\rm deg}=8$ 的方程是

令 $t_{+}=0$, 当 $i>3$ 时令 $t_{-i}=\theta_{\pm i}=0$, 则偶函数 $\tau_{0,0}$ 依赖于 3 个偶变量和 6 个奇变量

一般地, 若含有超变量的方程在去掉超的部分后可以退化为 KP 方程 (4.2), 我们将这样的方程视为超 KP 方程, 显然 (4.3) 式可看作是超 KP 方程, 但应注意 KP 方程的超延拓不是唯一的.

${\bf情况 2}$$\textbf{取}$$s$=1, $k$=0.

若令 $n=n'$, 则由 $y_1$ 所确定的 deg = 6 的方程是

则由 $y_2$ 所确定的 deg = 8 的方程是

在利用玻色-费米子的语言描述可积系统时, 系统的费米形式是唯一的. 然而, 不同方式的玻色化将产生不同的偏微分方程系统. 本节主要利用文献 [19] 中所构建的多分量 A 型超玻色-费米对应关系来考虑 $s$-次超 KP 可积系列的多分量情形.

当 $j \in \mathbb{Z}/2$, $a=1,2,\cdots,m$ 时, 按如下方式重排自由超费米子

可得到 $m$-分量的超费米子. 在此重排下, 克里福德超代数的代数运算变成

其中 $b=1,2,\cdots,m$. $4m$ 组超费米场的定义如下

现在超玻色 Fock 空间是一个由 $m$ 组奇变量与偶变量生成的超代数多项式, 记为

这里 $q_a$ 满足

类似于一分量的情形, 满足关系 (5.1) 生成的克里福德 $Cl$-模 $\hat{M}$ 可由含有 $m$ 组分量的超玻色 Fock 空间来 $\hat{B}$ 实现.

${\bf命题5.1}$^[19]$\textbf{多分量 A 型超玻色-费米对应关系}$

超费米 Fock 空间 $\hat{M}$ 与超玻色 Fock 空间 $\hat{B}$ 之间存在唯一的向量空间同构

使得

其中

类似于一分量情形 (见命题 3.2), 可利用命题 5.1 给出 $m$-分量 $s$-次推广超 KP 可积系列

的玻色形式, 如下命题所示.

${\bf命题5.2}$ 设 $\vec{n},\vec{n}',\vec{l},\vec{l'}\in \mathbb{Z}^m,~|\vec{l}|=k+s+1,~|\vec{l'}|=k-1,$$e_a$ 是第 $a$ 个向量为 1 其余向量为 0 的 $m$ 维行向量, 则有

${\bf证}$ 将同构映射 $\hat{\sigma}\otimes \hat{\sigma}'$ 作用在 (5.6) 式上可得

先考虑 $A_1$ 项. 把 (5.2) 式代入 $A_1$ 并注意

其中

且它们具有如下形式

这里当 $n_b\equiv k+s+1$ 时

当 $n_c\equiv k+s$ 时

利用公式

进一步计算可得

用类似的方法计算可得

在等式

的两边同时取 $q^{\vec{l}}q'^{\vec{l}'} (|\vec{l}|=k+s+1,~|\vec{l}'|=k-1)$ 的系数可得

经计算可知

其中

事实上, $\Omega^{(a)}_{\vec{n}\vec{n}'}$ 是属于算子 $\Lambda(\varsigma^{(a)})\Lambda(\theta^{(a)})$ 的特征值为 $n_an'_a$ 的特征向量. 由于属于不同特征值的特征向量线性无关, 因此可以在 (5.8) 式中消掉关于$\vec{n},\vec{n}' \in\mathbb{Z}^m$ 的求和来得到 (5.7) 式.

基于命题 5.2 给出多分量 $s$-次广义超 KP 可积系列的超 Hirota 双线性形式.

${\bf命题5.3}$ 设 $\vec{n},\vec{n}',\vec{l},\vec{l'}\in \mathbb{Z}^m,~|\vec{l}|=k+s+1,~|\vec{l'}|=k-1,$ 多分量 $s$-次推广超 KP 可积系列的 Hirota 双线性形式是

其中

${\bf注 5.1}$ 注意 (5.9) 式中当 $s=k=0$ 时该系统对应多分量超 KP 可积系列 [19], 当 $m=1$ 时该系统对应超 KP 可积系列.

定义 deg$~ y^{(a)}_{\pm i}=2i, ~{\rm deg}~ \theta^{(a)}_{\pm i}={\rm deg}~ \varsigma^{(a)}_{\pm i}=2i\mp1,$ 现从多分量超 Hirota 双线性生成级数系统 (5.9) 中剥离具体的超 Hirota 双线性方程.

${\bf情况 3}$$\textbf{ 取}$$s$=$k$=0, $m$=2.

若取 $\vec{l}=(0,1),~\vec{l}'=(0,-1),~\vec{n}=(1,0),~\vec{n}'=(1,2),$ 则由 $\theta_2^{(2)}\varsigma_{-3}^{(2)}$ 所决定的 deg = 8 的方程是

令 $t_+^{(a)}=\theta_+^{(a)}=0,$ 当 $i>3$ 时令 $~t^{(a)}_{-i}=\theta^{(a)}_{- i}=0$, 则偶的函数

等式 (5.10) 可以看成 2 分量的超 KP 方程.

${\bf情况 4}$$\textbf{取}$$s$=1, $k$=0, $m$=2.

若取 $\vec{l}=(1,1),~\vec{l}'=(0,-1),~\vec{n}=(1,0),~\vec{n}'=(1,0),$ 则由 $y_2^{(2)}$ 确定的 deg = 6 的方程是

由 $\theta_2^{(1)}\varsigma_1^{(1)}$ 确定的 deg = 6 的方程是

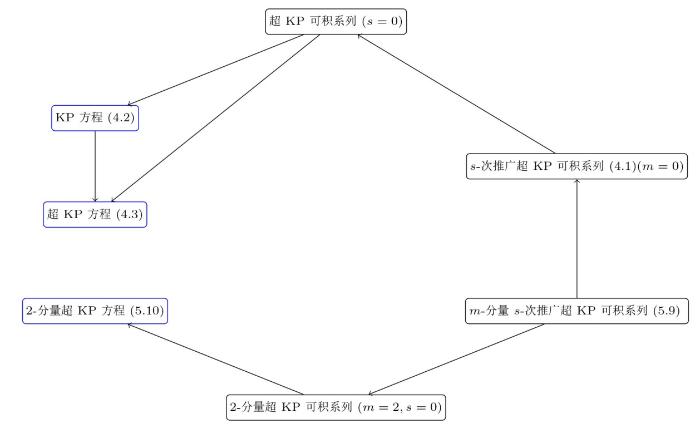
该文构造了 $s$-次推广超 KP 可积系列, 这是一个包括 Kac-van de Leur 版本下超 KP 可积系列 (即 $s=0$) 的更大的系统, 如命题 2.2 所示, 该系统比超 KP 可积系列拥有更多的方程. 命题 3.2 给出了 $s$-次推广超 KP 可积系列的玻色形式. 借助超 Hirota 双线性算子的定义, 命题 4.1 中给出该系统的超 Hirota 双线性形式. 在此基础上给出了超 Hirota 双线性方程的具体例子, 包括 KP 和超 KP 方程. 最后讨论了 $s$-次推广超 KP 可积系列的多分量情形, 并利用多分量 A 型超玻色-费米对应关系在命题 5.3 中给出 $m$-分量 $s$-次推广超 KP 可积系列的玻色对应物. 本文涉及的超可积系列和方程之间的关系如下图所示

迄今为止, 关于 Kac-van de Leur 版本的超可积系统的相关研究主要集中在 A 型无穷维李超代数 ^[9,16,19] 与 B 型无穷维李超代数 ^[8,20] 所对应的超可积系统上. 遗憾的是该版本下的超可积系统缺少相应的 Lax 对, 构造该版本下超可积系统的 Lax 对将是我们未来的研究课题之一. 此外, 在非超情况下，通过将有限维仿射李代数嵌入到无穷维李代数中, 可以构造约化情况下的可积系统 ^[21-23]. 然而, 这一思想尚未应用于超可积系统, 研究超可积系统的约化情形也是我们未来的研究课题之一. 文献 [24]研究了可积系列与其扭结不变量之间的联系,并启示我们进一步探索这一思想在超空间中的拓展. 具体而言，将研究范围延伸至超对称 KP 可积系列, 进而考察其推广形式-超对称 UC 可积系列, 以及与之相关的扭结不变量, 将构成一个富有意义的研究课题.