1 引言
分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3] . 其中, Filippov 系统[4 6] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9] .
近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] .
Faraday 圆盘发电机是一种基于 Faraday 电磁感应原理的装置, 通过旋转导体在磁场中切割磁力线, 将机械能高效转换为电能. 近年来, 由于其结构简单以及出色的能量转换效率, 这种发电机在可再生能源与小型发电系统中的应用引起了广泛关注. 目前, 大部分学者的研究主要集中于提升发电机的性能优化、电磁模拟以及新材料的应用等领域. Galvan 等人 [21 ] 对 Faraday 圆盘发电机的设计进行了全面优化, 其着重于材料改进和能量采集技术的提升, 以增强发电效率. Patrinos[22 ] 进一步探讨了由 Faraday 单极感应器引发的感应电动势现象, 并揭示了法拉第对磁场动态线的视角与相对论理论之间的差异. 该研究通过基于法拉第的实验设置进行了理论和实验的深入探索, 计算了感应电动势, 测量了磁场成分以验证结果, 为理解感应电动势的基本原理及其相关理论提供了重要的参考. Galvan 等人 [23 ] 在他们的研究中使用了在恒定磁场中以不同速度旋转的环形导电固体材料, 探讨了其相互作用所产生的电位差, 并进行测量, 同时强调了理解 Faraday 圆盘这一小型直流发电机中电磁感应现象的重要性. 经典的 Faraday 模型具有以下形式 [24 ]
(1.1) $\begin{equation} \begin{cases} \dfrac{{\rm d}x(t)}{{\rm d}t} = x(t) y(t) - x(t) - \beta z(t),\\[2mm] \dfrac{{\rm d}y(t)}{{\rm d}t} = \alpha(1 - x(t)^2) - k y(t), \\[2mm] \dfrac{{\rm d}z(t)}{{\rm d}t} = x(t) - \lambda z(t), \end{cases} \end{equation}$
其中 $ x(t) $ $ y(t) $ $ z(t) $ $ k $ $ \lambda $ $ \alpha $ $ \beta^{-1} $ $ y(t) $ $ Y_0 $ $ y(t) $ $ y(t) $ $ Y_0 $ $ y(t) $
本文将针对 Filippov 型 Faraday 系统的滑动区域进行深入研究, 重点讨论阈值控制策略对于该电路系统的分岔与混沌的影响, 以便于更好地提升发电设备的运行效率, 尽可能避免故障的发生. 该方法对各类发电设备和能源管理系统优化设计具有重要意义, 有利于推动能源管理系统的智能化发展, 从而实现更加可持续的能源利用.
2 模型构建与基本定义
2.1 模型构建
(2.1) $\begin{equation}\label{1} \dfrac{{\rm d}X(t)}{{\rm d}t} = \begin{cases} x(t) y(t) - x(t) - \beta z(t) + \epsilon f_1(x(t)), \\ \alpha(1 - x(t)^2) - k y(t) + \epsilon f_2(y(t)), \\ x(t) - \lambda z(t) + \epsilon f_3(z(t)), \end{cases} \end{equation}$
其中, $ X=(x,y,z)^{T} $ $ \epsilon=\begin{cases} 0, Q(X)<0,\\ 1, Q(X)>0, \end{cases} $ $ Q(X)=y-Y_0 $ $ Y_0 $ $ f_1(x)=0 $ $ f_2(y)=-m_1 y $ $ f_3(z)=0 $ . 系统 (2.1) 拥有两个子区域: $ S_1=\{X \in R^3|Q(X)<0\} $ $ S_2=\{X \in R^3|Q(X)>0\} $ . 当 $ \epsilon=0 $ $ F_{S_{1}} $ $ S_1 $ . 当 $ \epsilon=1 $ $ F_{S_{2}} $ $ S_2 $ . 定义切换边界为 $ \Sigma=\{X \in R^3|Q(X)=0\} $ $ S_1 $ $ S_2 $ $ R^3=S_1\cup \Sigma \cup S_2 $ .
2.2 基本定义
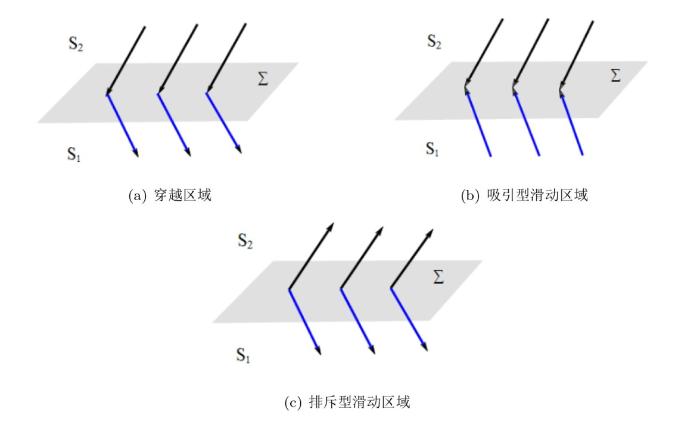
切换边界 $ \Sigma $ $ (\Sigma_C) $ $ \Sigma $ $ \Sigma $ 图 1(a) 所示; (ii) 吸引的滑动区域 $ (\Sigma_{as}) $ $ F_{S_1} $ $ F_{S_2} $ $ \Sigma $ 图 1(b) 所示; (iii) 排斥的滑动区域 $ (\Sigma_{rs}) $ $ F_{S_1} $ $ F_{S_2} $ $ \Sigma $ 图 1(c) 所示
图1
图1
不同切换边界类型图: (a) 穿越区域 $ \Sigma_C $ $ \Sigma_{as} $ $ \Sigma_{rs} $
为了研究系统 (2.1) 在切换边界 $ \Sigma $ $ F_{S_i} $ $ Q(X) $ [25 ] : $ L_{F_{S_i}}Q(X)=\left \langle \nabla Q(X), F_{S_i}(X)\right \rangle $ $ i=1,2 $ $ \nabla Q(X) $ $ Q(X) $ $ \langle \cdot,\cdot \rangle $ [26 ] : $ L^{n}_{F_{S_i}} Q(X) = \left\langle \nabla^{n-1}_{F_{S_i}} Q(X), F_{S_i}(X) \right\rangle, ~ n=2,3,\cdots $ . 因此, 可以明确地定义滑动区域 ( $ \Sigma_S $ ) 和穿越区域 ( $ \Sigma_C $ ) 如下所示
滑动集 $ \Sigma_{as} \bigcup \Sigma_{rs} $ $ F_{\Sigma_S} $ $ F_{S_1} $ $ F_{S_2} $ [4 ,26 ]
(2.2) $\begin{equation}\label{2} F_{\Sigma_S}(X) = \rho F_{S_1}(X) + (1 - \rho) F_{S_2}(X), \end{equation} $
并且对于每一个 $ X \in \Sigma_{as} \bigcup \Sigma_{rs} $ $ \rho $ $ L_{F_{S}} Q(X)=0 $
(2.3) $\begin{equation}\label{3} \rho = \rho(X) = \dfrac{L_{F_{S_2}} Q(X)}{L_{F_{S_2}} Q(X) - L_{F_{S_1}} Q(X)}, \end{equation}$
需要注意的是上式中的分母不为 0, 即 $ L_{F_{S_2}} Q(X)\ne L_{F_{S_1}} Q(X) $ . 因此, 对于所有的 $ X \in \Sigma_{as} \bigcup \Sigma_{rs} $ $ \rho \in (0,1) $ . 当 $ \rho=0 $ $ L_{F_{S_2}} Q(X)=0 $ $ X $ $ F_{S_2} $ $ \Sigma $ $ \rho=1 $ $ L_{F_{S_1}} Q(X)=0 $ $ X $ $ F_{S_1} $ $ \Sigma $
${\bf定义2.1}$ $ M(x,y,z) $ $ F_{S_i}(M)=0 $ $ i=1,2 $ $ M(x,y,z) $ $ M(x,y,z) $ $ F_{S_1}(M)=0 $ $ Q(M)<0 $ $ F_{S_2}(M)=0 $ $ Q(M)>0 $ $ M(x,y,z) $ $ M(x,y,z) $ $ F_{S_1}(M)=0 $ $ Q(M)>0 $ $ F_{S_2}(M)=0 $ $ Q(M)<0 $ $ M(x,y,z) $
${\bf定义2.2}$ $ M(x,y,z) $ $ F_{S_i}(M)=0 $ $ i=1,2 $ $ F_{S_1}(M)=0 $ $ Q(M)=0 $ $ F_{S_2}(M)=0 $ $ Q(M)=0 $ $ M(x,y,z) $
${\bf定义2.3}$ $ M(x,y,z) $ $ M(x,y,z) $ $ M(x,y,z) $ $ F_{\Sigma_S}(M)=0 $ $ Q(M)=0 $ $ M(x,y,z) $ $ M(x,y,z) $ $ F_{\Sigma_S}(M)=0 $ $ Q(M)\ne 0 $ $ M(x,y,z) $
${\bf定义2.4}$ $ M(x,y,z) $ $ Q(M)=0 $ $ L_{F_{S_1}}Q(M)=0 $ $ Q(M)=0 $ $ L_{F_{S_2}}Q(M)=0 $ $ M(x,y,z) $ $ T(x,y,z) $ .
${\bf定义2.5}$ $ T(x,y,z) $ $ L^2_{F_{S_i}}Q(T) \ne 0 $ $ T(x,y,z) $ $ T(x,y,z) $ $ L^2_{F_{S_1}}Q(T)<0 $ $ L^2_{F_{S_2}}Q(T)>0 $ $ T(x,y,z) $ $ T(x,y,z) $ $ L^2_{F_{S_1}}Q(T)>0 $ $ L^2_{F_{S_2}}Q(T)<0 $ $ T(x,y,z) $
${\bf定义2.6}$ $ T(x,y,z) $ $ L^2_{F_{S_i}}Q(T)=0 $ $ L^3_{F_{S_i}}Q(T) \ne 0 $ $ (\nabla Q(T),\nabla L_{F_{S_i}}Q(T),\nabla L^2_{F_{S_i}}Q(T)) $ $ T(x,y,z) $
${\bf定义2.7}$ $ S_1 $ $ S_2 $ ) 区域, 那么称这个周期解为 Filippov 系统 (2.1)的标准周期解; 同样的, 如果一个周期解完全位于滑动区域 $ \Sigma_S $ $ F_{S_1} $ $ F_{S_2} $ ) 的轨道段和 $ F_{\Sigma_S} $ $ \Sigma_C $ $ S_1 $ $ S_2 $
3 子系统动力学
根据 Filippov 系统 (2.1) 区分的子系统 $ S_1 $ $ S_2 $
(3.1) $\begin{equation}\label{4} \dfrac{{\rm d}X(t)}{{\rm d}t} = \begin{cases} F_{S_1}(X(t)) = \begin{pmatrix} x(t)y(t) - x(t) - \beta z(t) \\ \alpha(1 - x(t)^2) - ky(t) \\ x(t) - \lambda z(t) \end{pmatrix}, & X(t) \in S_1, \\ F_{S_2}(X(t)) = \begin{pmatrix} x(t)y(t) - x(t) - \beta z(t) \\ \alpha(1 - x(t)^2) - ky(t) - m_1y \\ x(t) - \lambda z(t) \end{pmatrix}, & X(t) \in S_2. \end{cases} \end{equation}$
对于系统 (3.1), 存在四种平衡点: 实平衡点, 虚拟平衡点, 边界平衡点和伪平衡点, 其中实平衡点和虚拟平衡点称为 Filippov 系统 (3.1) 的正则平衡点[27 ] . 首先对子系统 $ S_1 $ $ S_2 $ $ S_1 $
为了便于计算, 令 $ \overline{\alpha} = \dfrac{\alpha}{k} $ $ \overline{\beta} = \dfrac{\beta}{\lambda} $
${\bf引理3.1}$ $ S_1 $
(1) 平衡点 $ E_{S_1}^0 = (0, \overline{\alpha}, 0) $
(2) 当且仅当参数满足条件 $ 1-\dfrac{1}{\overline{\alpha}}(1+\overline{\beta})>0 $ $ \overline{\beta}<Y_{0} -1 $ $ E_{S_1}^1 = (x_1, y_1, z_1) $ $ E_{S_1}^2 = (x_2, y_2, z_2) $
(3) 当且仅当参数满足条件 $ 1-\dfrac{1}{\overline{\alpha}}(1+\overline{\beta})>0 $ $ \overline{\beta}>Y_{0} -1 $ $ E_{S_1}^1 = (x_1, y_1, z_1) $ $ E_{S_1}^2 = (x_2, y_2, z_2) $
(4) 当且仅当参数满足条件 $ 1-\dfrac{1}{\overline{\alpha}}(1+\overline{\beta})>0 $ $ \overline{\beta}=Y_{0} -1 $ $ E_{S_1}^1 = (x_1, y_1, z_1) $ $ E_{S_1}^2 = (x_2, y_2, z_2) $
${\bf证}$
${\bf定理3.1}$ $ S_1 $
(i) 当 $ 1-\overline{\alpha}+\lambda>0 $ $ 0<\lambda(1-\overline{\alpha})+\beta<\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ E_{S_1}^0 $
(ii) 当 $ 1-\overline{\alpha}+\lambda<0 $ $ \lambda(1-\overline{\alpha})+\beta<0 $ $ E_{S_1}^0 $
(iii) 当 $ 1-\overline{\alpha}+\lambda>0 $ $ \lambda(1-\overline{\alpha})+\beta>\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ E_{S_1}^0 $
(iv) 当 $ 1-\overline{\alpha}+\lambda<0 $ $ \lambda(1-\overline{\alpha})+\beta>\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ E_{S_1}^0 $
(v) 当 $ k + 1 - y + \lambda>0 $ $ (k + 1 - y + \lambda)(\beta + k - y k + 2 \alpha x^2 + \lambda k + \lambda - y \lambda)>\beta k + \lambda k - y \lambda k + 2 \alpha \lambda x^2 $ $ E_{S_1}^1 $ $ E_{S_1}^2 $
${\bf证}$ $ S_1 $
(1) 矩阵 $ J_{S_1} $ $ E_{S_1}^0 $
因此平衡点 $ E_{S_1}^0 $
当 $ 1-\overline{\alpha}+\lambda>0 $ $ 0<\lambda(1-\overline{\alpha})+\beta<\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ \xi_i<0 $ $ i=1,2,3 $ $ E_{S_1}^0 $ $ 1-\overline{\alpha}+\lambda<0 $ $ \lambda(1-\overline{\alpha})+\beta<0 $ $ \xi_1<0,\xi_2>0,\xi_3<0 $ $ E_{S_1}^0 $ $ 1-\overline{\alpha}+\lambda>0 $ $ \lambda(1-\overline{\alpha})+\beta>\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ E_{S_1}^0 $ $ 1-\overline{\alpha}+\lambda<0 $ $ \lambda(1-\overline{\alpha})+\beta>\dfrac{(1-\overline{\alpha}+ \lambda)^2}{4} $ $ E_{S_1}^0 $
(2) 矩阵 $ J_{S_1} $ $ E_{S_1}^1 $ $ E_{S_1}^2 $
根据 Routh-Hurwitz 准则 [28 ] , 当 $ \alpha^2_{S_1}>0 $ $ \alpha^2_{S_1}\alpha^1_{S_1}>\alpha^0_{S_1} $ $ E_{S_1}^1 $ $ E_{S_1}^2 $
${\bf引理3.2}$ $ S_2 $
(1) 平衡点 $ E_{S_2}^0 = (0, \dfrac{\alpha}{k + m_1}, 0) $
(2) 当且仅当参数满足条件 $ \dfrac{(k + m_1)(1 + \overline{\beta})}{\alpha}<1 $ $ \overline{\beta} > Y_0 - 1 $ $ E_{S_2}^1 = (x_1, y_1, z_1) $ $ E_{S_2}^2 = (x_2, y_2, z_2) $
(3) 当且仅当参数满足条件 $ \dfrac{(k + m_1)(1 + \overline{\beta})}{\alpha}<1 $ $ \overline{\beta}<Y_0 - 1 $ $ E_{S_2}^1 = (x_1, y_1, z_1) $ $ E_{S_2}^2 = (x_2, y_2, z_2) $
(4) 当且仅当参数满足条件 $ \dfrac{(k + m_1)(1 + \overline{\beta})}{\alpha}<1 $ $ \overline{\beta} =Y_0 - 1 $ $ E_{S_2}^1 = (x_1, y_1, z_1) $ $ E_{S_2}^2 = (x_2, y_2, z_2) $
${\bf证}$
${\bf定理3.2}$ $ S_2 $
(i) 当 $ 1-\frac{\alpha}{k + m_1} + \lambda > 0 $ $ 0 < \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta < \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ \xi_i<0 $ $ i=1,2,3 $ $ E_{S_2}^0 $
(ii) 当 $ 1-\frac{\alpha}{k + m_1} + \lambda <0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta<0 $ $ \xi_1<0,\xi_2>0,\xi_3<0 $ $ E_{S_2}^0 $
(iii) 当 $ 1-\frac{\alpha}{k + m_1} + \lambda > 0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta > \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ E_{S_2}^0 $
(iv) 当 $ 1-\frac{\alpha}{k + m_1} + \lambda <0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta > \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ E_{S_2}^0 $
(v) 当 $ k + m_1 + 1 - y + \lambda>0 $ $ (k + m_1 + 1 - y + \lambda)(\beta + k + m_1 - yk- y m_1 + 2 \alpha x^2 + \lambda k + \lambda m_1 + \lambda - \lambda y)>\beta k + \beta m_1 + \lambda k + \lambda m_1 - \lambda y k - y \lambda m_1 + 2 \alpha \lambda x^2 $ $ E_{S_2}^1 $ $ E_{S_2}^2 $
${\bf证}$ $ S_2 $
(1) 矩阵 $ J_{S_2} $ $ E_{S_2}^0 $
因此平衡点 $ E_{S_2}^0 $
当且仅当 $ 1-\frac{\alpha}{k + m_1} + \lambda > 0 $ $ 0 < \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta < \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ \xi_i<0 $ $ i=1,2,3 $ $ E_{S_2}^0 $ $ 1-\frac{\alpha}{k + m_1} + \lambda <0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta<0 $ $ \xi_1<0,\xi_2>0,\xi_3<0 $ $ E_{S_2}^0 $ $ 1-\frac{\alpha}{k + m_1} + \lambda > 0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta > \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ E_{S_2}^0 $ $ 1-\frac{\alpha}{k + m_1} + \lambda <0 $ $ \lambda \left( 1 - \frac{\alpha}{k + m_1} \right) + \beta > \frac{\left( 1 - \frac{\alpha}{k + m_1} + \lambda \right)^2}{4} $ $ E_{S_2}^0 $
(2) 矩阵 $ J_{S_2} $ $ E_{S_2}^1 $ $ E_{S_2}^2 $
根据 Routh-Hurwitz 准则[28 ] , 当 $ \alpha^2_{S_2}>0 $ $ \alpha^2_{S_2}\alpha^1_{S_2}>\alpha^0_{S_2} $ $ E_{S_2}^1 $ $ E_{S_2}^2 $
4 滑动向量场动力学
本节将对于滑动向量场进行分析. 首先根据 2.2 节中对于切换边界的定义, 将切换边界划分为不同区域. 令 $ \mu(M) $ $ Q(M) $ $ \Sigma $
(1)穿越区域: $ \Sigma_C = \{M(x,y,z) \,|\, M \in \Sigma, \, \mu(E) > 0\} $
(2)滑动区域: $ \Sigma_S = \{M(x,y,z) \,|\, M \in \Sigma, \, \mu(E) < 0\} $
(3)边界切线: $ T = \{M(x,y,z) \,|\, M \in \Sigma, \, \mu(E) = 0\} $ .
4.1 滑动区域的存在性
根据滑动区域 $ \Sigma_S $ $ \mu(E) < 0 $
(1) 当 $ m_1<0 $ $ \alpha(1 - x^2) - kY_0 <\alpha(1 - x^2) - kY_0 - m_1 Y_0 $ $ L_{F_{S_1}}<0 $ $ L_{F_{S_2}}>0 $
(2) 当 $ m_1>0 $ $ \alpha(1 - x^2) - kY_0 >\alpha(1 - x^2) - kY_0 - m_1 Y_0 $ $ L_{F_{S_1}}>0 $ $ L_{F_{S_2}}<0 $
(3) 根据定义 2.4 可以得出子系统 $ S_1 $ $ S_2 $
4.2 滑动向量场
Filippov 系统 (3.1) 可能会出现一个滑动向量场, 该向量场是否存在取决于切换面是否存在滑动区域. 滑动区域 $ \Sigma_S $ [4 ,26 ] 来表示
(4.1) $\begin{equation}\label{5} \begin{cases} \dfrac{{\rm d}x(t)}{{\rm d}t} = x(t) Y_0 - x(t) - \beta z(t), \\[2mm] \dfrac{{\rm d}y(t)}{{\rm d}t} = 0, \\[2mm] \dfrac{{\rm d}z(t)}{{\rm d}t} = x(t) - \lambda z(t), \end{cases} \end{equation}$
由定义 2.4 知, 若 $ F_{\Sigma_S}(M)=0 $ $ M(x,y,z) $ $ (0,Y_0,0)\in \Sigma_C $ $ (x,y,z) \to (-x,y,-z) $ $ E_P(x^P, Y_0, z^P) $
(4.2) $\begin{equation}\label{6} \begin{cases} \dfrac{{\rm d}x(t)}{{\rm d}t} = x(t) Y_0 - x(t) - \beta z(t) \doteq P(x, z), \\[2mm] \dfrac{{\rm d}z(t)}{{\rm d}t} = x(t) - \lambda z(t) \doteq Q(x, z), \end{cases} \end{equation}$
因此, 对于非平凡伪平衡点 $ E_P(x^P, Y_0, z^P) $
其特征方程为: $ \xi^2 - (Y_0 - 1 - \lambda) \xi + (1 - Y_0) \lambda + \beta = 0 $ . 则有定理如下
${\bf定理4.1}$
(1) 当 $ \Delta = (Y_0 - 1 - \lambda)^2-4[(1 - Y_0) \lambda + \beta]\geq 0 $ $ (1-Y_0) \lambda + \beta<0 $ $ E_P(x^P, Y_0, z^P) $
(2) 当 $ \Delta = (Y_0 - 1 - \lambda)^2-4[(1 - Y_0) \lambda + \beta]\geq 0 $ $ (1-Y_0) \lambda + \beta>0 $ $ Y_0-1- \lambda<0 $ $ E_P(x^P, Y_0, z^P) $ $ Y_0-1- \lambda>0 $ $ E_P(x^P, Y_0, z^P) $
(3) 当 $ \Delta = (Y_0 - 1 - \lambda)^2-4[(1 - Y_0) \lambda + \beta]<0 $ $ Y_0-1- \lambda<0 $ $ E_P(x^P, Y_0, z^P) $ $ Y_0-1- \lambda>0 $ $ E_P(x^P, Y_0, z^P) $
${\bf定理4.2}$ $ E_P(x^P, Y_0, z^P) $ $ x^P=T_{S_i},i=1,2 $ $ E_P(x^P, Y_0, z^P) $ $ S_1 $
5 分岔与混沌分析
本节基于前三节的结果进行数值模拟. 为了研究阈值控制对于 Filippov 型 Faraday 系统的影响, 设置分岔参数为 $ Y_0 $ $ Y_0 $ $ (0,15) $ . 其余参数固定如下
根据 Hide 等人在 1996 年的研究[17 ] , 该组参数适用于 Faraday 系统, 是系统能够表现出混沌行为的一组参数, 该参数已在类似研究中得到验证 [24 ,29 ] .
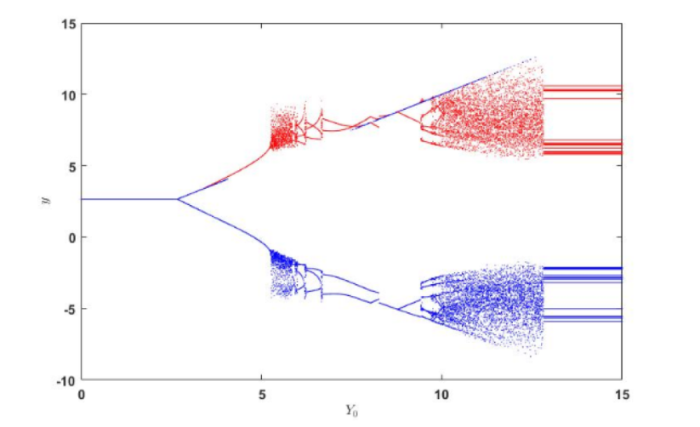
图 2 给出了初始值为 $ (x,y,z)=(0.9,2.6,0.7) $ 图 3 -12 显示了当阈值参数 $ Y_0 $ $ x-y $
图2
图2
Filippov 系统 (3.1) 关于参数 $ Y_0 $
图3
图3
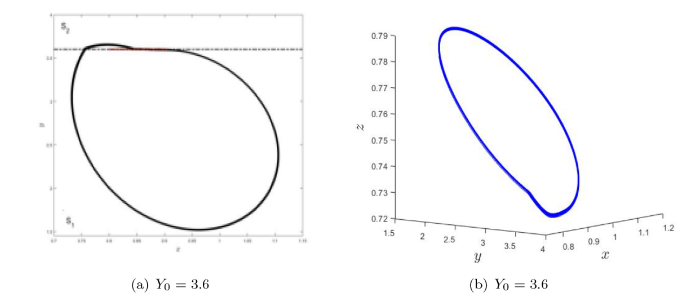
(a) Filippov 系统 (3.1) 当参数 $ Y_0=3.6 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=3.6 $
图4
图4
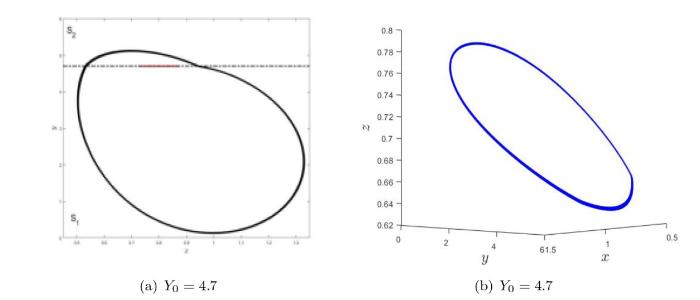
(a) Filippov 系统 (3.1) 当参数 $ Y_0=4.7 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=4.7 $
图5
图5
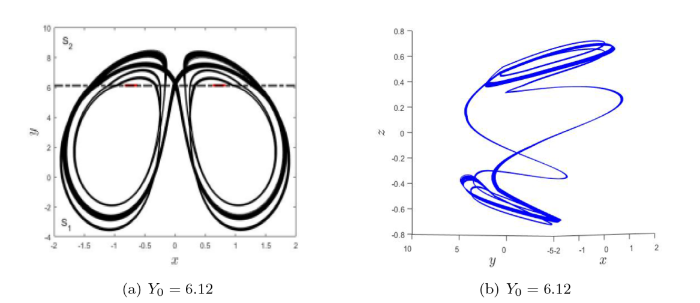
(a) Filippov 系统 (3.1) 当参数 $ Y_0=6.12 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=6.12 $
图6
图6
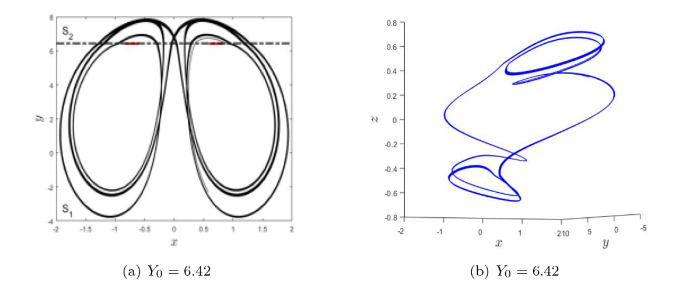
(a) Filippov 系统 (3.1) 当参数 $ Y_0=6.42 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=6.42 $
图7
图7
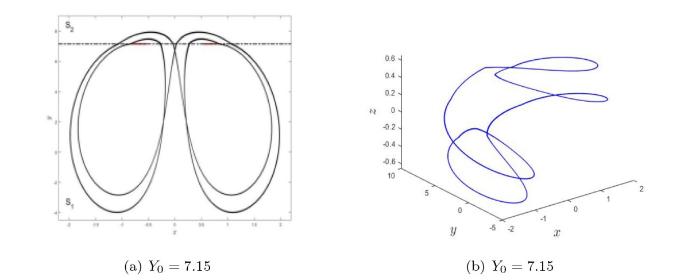
(a) Filippov 系统 (3.1) 当参数 $ Y_0=7.15 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=7.15 $
图8
图8
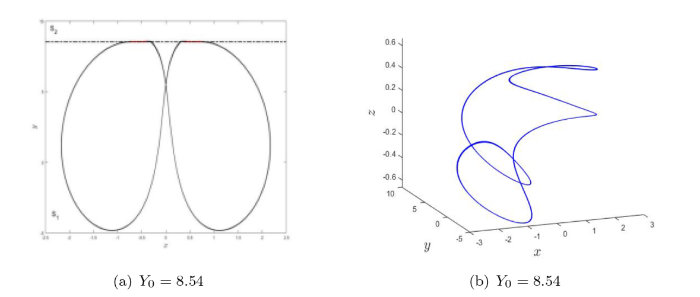
(a) Filippov 系统 (3.1) 当参数 $ Y_0=8.54 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=8.54 $
图9
图9
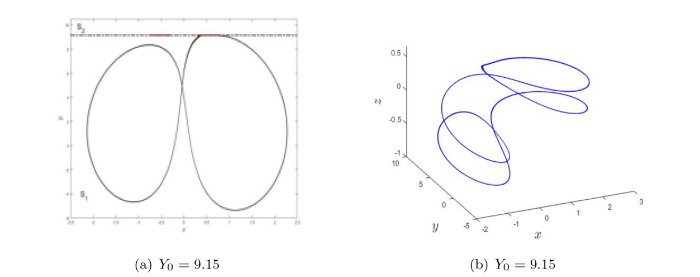
(a) Filippov 系统 (3.1) 当参数 $ Y_0=9.15 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=9.15 $
图10
图10
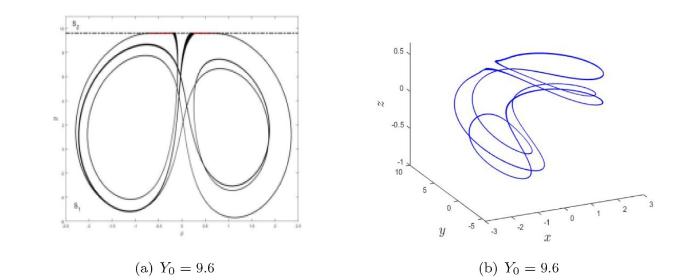
(a) Filippov 系统 (3.1) 当参数 $ Y_0=9.6 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=9.6 $
图11
图11
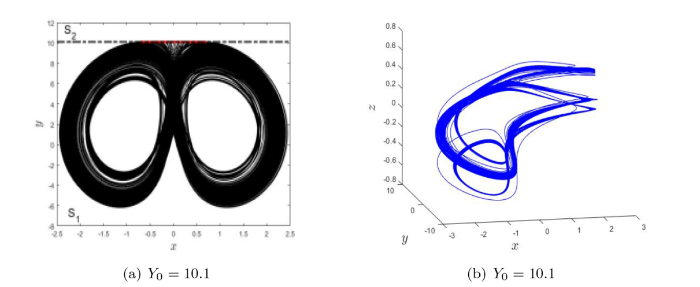
(a) Filippov 系统 (3.1) 当参数 $ Y_0=10.1 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=10.1 $
图12
图12
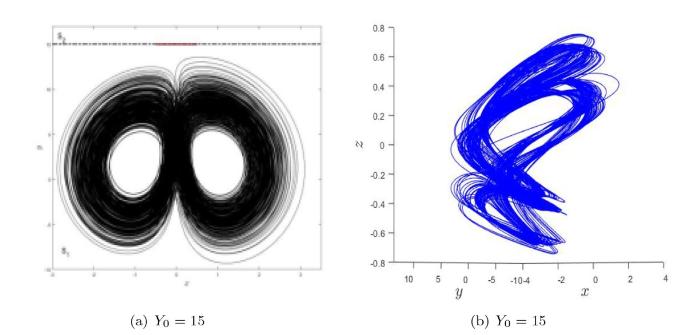
(a) Filippov 系统 (3.1) 当参数 $ Y_0=15 $ $ x-y $ $ \Sigma $ $ S_1 $ $ S_2 $ $ Y_0=15 $
(1) 当 $ Y_0=3.6 $ $ S_1 $ $ \Sigma $ $ S_2 $ 图 3(a) 所示;
(2) 当 $ Y_0=4.7 $ 图 3(b) 所示;
(3) 当 $ Y_0=6.12 $ 图 3(c) 所示;
(4) 当 $ Y_0=6.42 $ 图 3(d) 所示;
(5) 当 $ Y_0=7.15 $ 图 3(e) 所示;
(6) 当 $ Y_0=8.54 $ $ S_1 $ $ \Sigma $ $ S_1 $ 图 3(f) 所示;
(7) 当 $ Y_0=9.15 $ $ S_1 $ $ \Sigma $ $ S_1 $ 图 3(g) 所示;
(8) 当 $ Y_0=9.6 $ $ S_1 $ $ \Sigma $ $ S_1 $ 图 3(h) 所示;
(9) 当 $ Y_0=10.1 $ 图 3(i) 所示;
(10) 当 $ Y_0=15 $ $ S_1 $ 图 3(j) 所示.
6 结论
本文建立了一类三维 Filippov 型 Faraday 模型, 并分析了其在阈值控制策略下的稳定性和多种分岔行为. 首先, 计算了子系统的平衡点及其稳定性, 并探讨了滑动向量场的动力学及其分岔现象. 通过对切换面上的不同区域进行分类, 重点分析了不连续边界和滑动区域稳定性对系统动力学的影响. 研究发现, 相较于传统 Faraday 系统, 该非光滑系统中出现了混沌吸引子、穿越分岔等复杂动力学行为. 此外, 本文基于研究内容进行了数值模拟, 使用切换面阈值作为参数从而观察阈值控制对于 Filippov 型 Faraday 模型的影响, 同时验证了在特定条件下参数阈值的变化对倍周期分岔及混沌现象的影响, 这说明了设置合理的阈值控制有助于进一步优化 Filippov 型 Faraday 模型, 从而设计出更加稳定、运行效率更高且故障发生率更低的发电机.
基于 Filippov 型 Faraday 系统的研究在电路设计应用领域拓展具有一定实际意义. 这一研究的开展不仅有助于设置合理的阈值控制, 为优化电路提供更加可行的解决方案, 同时也将促进更多关于非光滑动力系统的深入研究, 从而推动智能电网及可再生能源应用的发展.
参考文献
View Option
[1]
Zheng Y Chen X Degenerate T-singularity bifurcation and crossing periodic orbits in a 3-dimensional piecewise smooth system
Journal of Differential Equations , 2023 , 354 296 -324
[本文引用: 1]
[2]
Wang F Wei Z Zhang W Sliding homoclinic orbits and chaotic dynamics in a class of 3D piecewise-linear Filippov systems
Nonlinear Dynamics , 2024 , 112 22 ): 20461 -20481
[3]
Huang L Wang J Global dynamics of piecewise smooth systems with switches depending on both discrete times and status
SIAM Journal on Applied Dynamical Systems , 2024 , 23 3 ): 2533 -2556
[本文引用: 1]
[4]
Filippov A F Differential equations with discontinuous right-hand side
Matematicheskii Sbornik , 1960 , 93 1 ): 99 -128
[本文引用: 3]
[5]
Bernardo M Budd C Champneys A R et al . Piecewise-Smooth Dynamical Systems:Theory and Apxinplications . Berlin : Springer Science , 2008
[6]
杨静 , 柯昌成 , 魏周超 . 一类连续和不连续分段线性系统的周期解研究
数学物理学报 , 2021 , 41A 4 ): 1053 -1065
[本文引用: 1]
Yang J Ke C C Wei Z C A study of periodic solutions for a class of continuous and discontinuous piecewise linear systems
Acta Math Sci , 2021 , 41A 4 ): 1053 -1065
[本文引用: 1]
[7]
Wei Z Li Y Moroz I et al . Melnikov-type method for a class of planar hybrid piecewise-smooth systems with impulsive effect and noise excitation: Heteroclinic orbits
Chaos: An Interdisciplinary Journal of Nonlinear Science , 2022 , 32 10 ): Art 103127
[本文引用: 1]
[8]
Wang F Wei Z Zhang W et al . Coexistence of three heteroclinic cycles and chaos analyses for a class of 3D piecewise affine systems
Chaos: An Interdisciplinary Journal of Nonlinear Science , 2023 , 33 2 ): Art 023108
[9]
Duan J Wei Z Li G et al . Strange nonchaotic attractors in a class of quasiperiodically forced piecewise smooth systems
Nonlinear Dynamics , 2024 , 112 14 ): 12565 -12577
[本文引用: 1]
[10]
Yang Q Huang Y Chaotic Dynamics arising from sliding heteroclinic cycles in 3D Filippov systems
International Journal of Bifurcation and Chaos , 2023 , 33 1 ): Art 2350009
[本文引用: 1]
[11]
Hamdallah S A A Arafa A A Tang S et al . Complex dynamics of a Filippov three-species food chain model
International Journal of Bifurcation and Chaos , 2021 , 31 5 ): Art 2150074
[本文引用: 1]
[12]
Zhou W Zhao T Wang A et al . Bifurcations and dynamics of a Filippov epidemic model with nonlinear threshold control policy and medical-resource constraints
Chaos Solitons & Fractals , 2024 , 184 114992
[本文引用: 1]
[13]
Zhou H Tang S Complex dynamics and sliding bifurcations of the Filippov Lorenz-Chen system
International Journal of Bifurcation and Chaos , 2022 , 32 12 ): Art 2250182
[本文引用: 1]
[14]
Deng Q Wang C Lin H Chaotic dynamical system of Hopfield neural network influenced by neuron activation threshold and its image encryption
Nonlinear Dynamics , 2024 , 112 8 ): 6629 -6646
[本文引用: 1]
[15]
Mohammadi H Challenor P Goodfellow M Emulating complex dynamical simulators with random Fourier features
SIAM/ASA Journal on Uncertainty Quantification , 2024 , 12 3 ): 788 -811
[16]
Wu F Xi F Zhu C On a class of McKean-Vlasov stochastic functional differential equations with applications
Journal of Differential Equations , 2023 , 371 31 -49
[本文引用: 1]
[17]
Hide R Skeldon A C Acheson D J A study of two novel self-exciting single-disk homopolar dynamos: theory
Proceedings of the Royal Society of London , 1996 , 452 1949 ): 1369 -1395
[本文引用: 2]
[18]
Brandenburg A Ntormousi E Galactic dynamos
Annual Review of Astronomy and Astrophysics , 2023 , 61 1 ): 561 -606
[本文引用: 1]
[19]
Foldes R Lévêque E Marino R et al . Efficient kinetic Lattice Boltzmann simulation of three-dimensional Hall-MHD turbulence
Journal of Plasma Physics , 2023 , 89 4 ): Art 905890413
[本文引用: 1]
[20]
方秀珍 , 彭爱武 , 刘保林 . 盘式磁流体发电机通道结构对等离子体稳定性的影响研究
电工电能新技术 , 2020 , 39 9 ): 13 -19
DOI:10.12067/ATEEE2003006
[本文引用: 1]
盘式磁流体发电机工质因其主要吸收切线方向法拉第电流产生的自激焦耳热而形成非平衡电离等离子体。当盘式通道型线一定时,等离子体松弛区域的变化将改变发电通道入口等离子体吸收自激焦耳热区域的大小,引起发电通道入口等离子体电离状态变化,导致等离子体非平衡电离不稳定,严重影响发电机输出性能。本文采用非平衡盘式磁流体发电机的非稳态准一维数学模型进行数值模拟,分析较高磁感应强度下盘式磁流体发电机等离子体松弛区域对等离子体稳定性和磁流体流动特性的影响。分析结果表明:当发电通道型线和气体滞止状态一定时,等离子体松弛区域的改变抑制发电通道中电子数密度的波动,维持等离子非平衡电离的稳定性,促进发电机性能的提高;磁感应强度越高,等离子体松弛区域越小,最优阳极位置越靠近圆盘中心,发电通道中等离子体越容易达到非平衡电离的稳定;等离子体松弛区域的改变抑制了发电通道中或发电通道前等离子体流动中激波的产生,维持了发电通道中等离子体适当的超音速流动,促进发电机性能的提高;磁感应强度越大,发电通道中激波的产生越受等离子体松弛区域的影响,发电机的性能极易恶化。
Fang X Z Peng A W Liu B L A study of the effect of disk magnetohydrodynamic generator channel structure on plasma stability
Advanced Technology of Electrical Engineering and Energy , 2020 , 39 9 ): 13 -19
DOI:10.12067/ATEEE2003006
[本文引用: 1]
盘式磁流体发电机工质因其主要吸收切线方向法拉第电流产生的自激焦耳热而形成非平衡电离等离子体。当盘式通道型线一定时,等离子体松弛区域的变化将改变发电通道入口等离子体吸收自激焦耳热区域的大小,引起发电通道入口等离子体电离状态变化,导致等离子体非平衡电离不稳定,严重影响发电机输出性能。本文采用非平衡盘式磁流体发电机的非稳态准一维数学模型进行数值模拟,分析较高磁感应强度下盘式磁流体发电机等离子体松弛区域对等离子体稳定性和磁流体流动特性的影响。分析结果表明:当发电通道型线和气体滞止状态一定时,等离子体松弛区域的改变抑制发电通道中电子数密度的波动,维持等离子非平衡电离的稳定性,促进发电机性能的提高;磁感应强度越高,等离子体松弛区域越小,最优阳极位置越靠近圆盘中心,发电通道中等离子体越容易达到非平衡电离的稳定;等离子体松弛区域的改变抑制了发电通道中或发电通道前等离子体流动中激波的产生,维持了发电通道中等离子体适当的超音速流动,促进发电机性能的提高;磁感应强度越大,发电通道中激波的产生越受等离子体松弛区域的影响,发电机的性能极易恶化。
[21]
Galvan-Ruiz J L Sellschopp-Sanchez F S Rivero M et al . Theoretical, numerical and experimental investigation of a Faraday disc generator for energy harvesting applications
IEEE Latin America Transactions , 2023 , 21 7 ): 849 -857
[本文引用: 1]
[22]
Patrinos K On the Unipolar generator: An experimental and theoretical study
Journal of Applied Mathematics and Physics , 2024 , 12 8 ): 2928 -2958
[本文引用: 1]
[23]
Galvan-Ruiz J L Sellschopp-Sanchez F S álvarez-Macías C et al . Theoretical and experimental investigation of a Faraday disc generator//2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC)
IEEE , 2022 , 6 1 -6
[本文引用: 1]
[24]
Moroz I M The Hide, Skeldon, Acheson dynamo revisited
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences , 2007 , 463 2077 ): 113 -130
[本文引用: 2]
[25]
Cristiano R Carvalho T Tonon D J et al . Hopf and homoclinic bifurcations on the sliding vector field of switching systems in R3
Nonlinear Phenomena , 2017 , 347 12 -20
[本文引用: 1]
[26]
Kuznetsov Y A Rinaldi S Gragnani A One-parameter bifurcations in planar Filippov systems
International Journal of Bifurcation and Chaos , 2003 , 13 8 ): 2157 -2188
[本文引用: 3]
[27]
Wang A Xiao Y Smith R Multiple equilibria in a nonsmooth epidemic model with medical resource constraints
Bulletin of Mathematical Biology , 2019 , 81 4 ): 963 -994
[本文引用: 1]
[28]
DeJesus E X Kaufman C Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations
Physical Review A , 1987 , 35 12 ): Art 5288
PMID:9898166
[本文引用: 2]
[29]
Moroz I M Template analysis of a Faraday disk dynamo
The European Physical Journal Special Topics , 2008 , 165 1 ): 211 -220
[本文引用: 1]
Degenerate T-singularity bifurcation and crossing periodic orbits in a 3-dimensional piecewise smooth system
1
2023
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
Sliding homoclinic orbits and chaotic dynamics in a class of 3D piecewise-linear Filippov systems
0
2024
Global dynamics of piecewise smooth systems with switches depending on both discrete times and status
1
2024
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
Differential equations with discontinuous right-hand side
3
1960
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
... 滑动集 $ \Sigma_{as} \bigcup \Sigma_{rs} $ $ F_{\Sigma_S} $ $ F_{S_1} $ $ F_{S_2} $ [4 ,26 ] ...
... Filippov 系统 (3.1) 可能会出现一个滑动向量场, 该向量场是否存在取决于切换面是否存在滑动区域. 滑动区域 $ \Sigma_S $ [4 ,26 ] 来表示 ...
一类连续和不连续分段线性系统的周期解研究
1
2021
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
一类连续和不连续分段线性系统的周期解研究
1
2021
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
Melnikov-type method for a class of planar hybrid piecewise-smooth systems with impulsive effect and noise excitation: Heteroclinic orbits
1
2022
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
Coexistence of three heteroclinic cycles and chaos analyses for a class of 3D piecewise affine systems
0
2023
Strange nonchaotic attractors in a class of quasiperiodically forced piecewise smooth systems
1
2024
... 分段光滑动力系统广泛应用于机械工程、航空航天、土木工程、交通与能源等领域, 是数学、力学与工程学的重要研究热点 [1 3 ] . 其中, Filippov 系统[4 6 ] 作为经典分段光滑自治系统, 具有典型的不连续特性. 研究 Filippov 系统的滑动模式与非光滑动力学, 有助于揭示传统线性与非线性理论难以解释的现象[7 9 ] . ...
Chaotic Dynamics arising from sliding heteroclinic cycles in 3D Filippov systems
1
2023
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Complex dynamics of a Filippov three-species food chain model
1
2021
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Bifurcations and dynamics of a Filippov epidemic model with nonlinear threshold control policy and medical-resource constraints
1
2024
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Complex dynamics and sliding bifurcations of the Filippov Lorenz-Chen system
1
2022
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Chaotic dynamical system of Hopfield neural network influenced by neuron activation threshold and its image encryption
1
2024
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Emulating complex dynamical simulators with random Fourier features
0
2024
On a class of McKean-Vlasov stochastic functional differential equations with applications
1
2023
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
A study of two novel self-exciting single-disk homopolar dynamos: theory
2
1996
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
... 根据 Hide 等人在 1996 年的研究[17 ] , 该组参数适用于 Faraday 系统, 是系统能够表现出混沌行为的一组参数, 该参数已在类似研究中得到验证 [24 ,29 ] . ...
Galactic dynamos
1
2023
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Efficient kinetic Lattice Boltzmann simulation of three-dimensional Hall-MHD turbulence
1
2023
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
盘式磁流体发电机通道结构对等离子体稳定性的影响研究
1
2020
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
盘式磁流体发电机通道结构对等离子体稳定性的影响研究
1
2020
... 近年来, 众多学者对 Filippov 系统的分岔和混沌问题进行了深入研究. Yang 等人[10 ] 建立了 Filippov 系统中三个 Shil'nikov 型异宿定理, 可以解析证明在某些假设条件下 Filippov 系统在奇异环附近具有混沌不变量集. Hamdallah 等人 [11 ] 利用阈值策略控制分析了 Filippov 食物链模型滑动和交叉段的区域以及伪平衡点的分岔集等. Zhou 等人[12 ] 提出了具有非线性阈值函数的 Filippov 模型, 并推导出了滑动段、滑动动力学和不同类型平衡点的存在条件, 揭示了不连续诱导的局部和全局分岔等. Tang 等人 [13 ] 研究了一类三维 Filippov 型 Lorenz-Chen 系统, 探讨了滑模分岔、滑动 Hopf 分岔与类 Hopf 边界平衡点分岔的现象. 在现代工程和科学研究中, 复杂动力系统因其展现出的丰富行为而受到广泛关注[14 16 ] . 作为一种典型的非线性动力学模型, Faraday 系统[17 ] 利用电磁感应原理, 广泛应用于各类发电设备和能源管理系统. 随着可再生能源的迅速发展, 对 Faraday 系统动力学特性的深入探讨变得愈发重要[18 ] . 具体而言, 研究 Faraday 系统在不同操作条件下的稳定性与分岔现象, 不仅有助于提高设备的整体性能, 还能为新型发电技术的开发提供重要的理论依据 [19 ,20 ] . ...
Theoretical, numerical and experimental investigation of a Faraday disc generator for energy harvesting applications
1
2023
... Faraday 圆盘发电机是一种基于 Faraday 电磁感应原理的装置, 通过旋转导体在磁场中切割磁力线, 将机械能高效转换为电能. 近年来, 由于其结构简单以及出色的能量转换效率, 这种发电机在可再生能源与小型发电系统中的应用引起了广泛关注. 目前, 大部分学者的研究主要集中于提升发电机的性能优化、电磁模拟以及新材料的应用等领域. Galvan 等人 [21 ] 对 Faraday 圆盘发电机的设计进行了全面优化, 其着重于材料改进和能量采集技术的提升, 以增强发电效率. Patrinos[22 ] 进一步探讨了由 Faraday 单极感应器引发的感应电动势现象, 并揭示了法拉第对磁场动态线的视角与相对论理论之间的差异. 该研究通过基于法拉第的实验设置进行了理论和实验的深入探索, 计算了感应电动势, 测量了磁场成分以验证结果, 为理解感应电动势的基本原理及其相关理论提供了重要的参考. Galvan 等人 [23 ] 在他们的研究中使用了在恒定磁场中以不同速度旋转的环形导电固体材料, 探讨了其相互作用所产生的电位差, 并进行测量, 同时强调了理解 Faraday 圆盘这一小型直流发电机中电磁感应现象的重要性. 经典的 Faraday 模型具有以下形式 [24 ] ...
On the Unipolar generator: An experimental and theoretical study
1
2024
... Faraday 圆盘发电机是一种基于 Faraday 电磁感应原理的装置, 通过旋转导体在磁场中切割磁力线, 将机械能高效转换为电能. 近年来, 由于其结构简单以及出色的能量转换效率, 这种发电机在可再生能源与小型发电系统中的应用引起了广泛关注. 目前, 大部分学者的研究主要集中于提升发电机的性能优化、电磁模拟以及新材料的应用等领域. Galvan 等人 [21 ] 对 Faraday 圆盘发电机的设计进行了全面优化, 其着重于材料改进和能量采集技术的提升, 以增强发电效率. Patrinos[22 ] 进一步探讨了由 Faraday 单极感应器引发的感应电动势现象, 并揭示了法拉第对磁场动态线的视角与相对论理论之间的差异. 该研究通过基于法拉第的实验设置进行了理论和实验的深入探索, 计算了感应电动势, 测量了磁场成分以验证结果, 为理解感应电动势的基本原理及其相关理论提供了重要的参考. Galvan 等人 [23 ] 在他们的研究中使用了在恒定磁场中以不同速度旋转的环形导电固体材料, 探讨了其相互作用所产生的电位差, 并进行测量, 同时强调了理解 Faraday 圆盘这一小型直流发电机中电磁感应现象的重要性. 经典的 Faraday 模型具有以下形式 [24 ] ...
Theoretical and experimental investigation of a Faraday disc generator//2022 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC)
1
2022
... Faraday 圆盘发电机是一种基于 Faraday 电磁感应原理的装置, 通过旋转导体在磁场中切割磁力线, 将机械能高效转换为电能. 近年来, 由于其结构简单以及出色的能量转换效率, 这种发电机在可再生能源与小型发电系统中的应用引起了广泛关注. 目前, 大部分学者的研究主要集中于提升发电机的性能优化、电磁模拟以及新材料的应用等领域. Galvan 等人 [21 ] 对 Faraday 圆盘发电机的设计进行了全面优化, 其着重于材料改进和能量采集技术的提升, 以增强发电效率. Patrinos[22 ] 进一步探讨了由 Faraday 单极感应器引发的感应电动势现象, 并揭示了法拉第对磁场动态线的视角与相对论理论之间的差异. 该研究通过基于法拉第的实验设置进行了理论和实验的深入探索, 计算了感应电动势, 测量了磁场成分以验证结果, 为理解感应电动势的基本原理及其相关理论提供了重要的参考. Galvan 等人 [23 ] 在他们的研究中使用了在恒定磁场中以不同速度旋转的环形导电固体材料, 探讨了其相互作用所产生的电位差, 并进行测量, 同时强调了理解 Faraday 圆盘这一小型直流发电机中电磁感应现象的重要性. 经典的 Faraday 模型具有以下形式 [24 ] ...
The Hide, Skeldon, Acheson dynamo revisited
2
2007
... Faraday 圆盘发电机是一种基于 Faraday 电磁感应原理的装置, 通过旋转导体在磁场中切割磁力线, 将机械能高效转换为电能. 近年来, 由于其结构简单以及出色的能量转换效率, 这种发电机在可再生能源与小型发电系统中的应用引起了广泛关注. 目前, 大部分学者的研究主要集中于提升发电机的性能优化、电磁模拟以及新材料的应用等领域. Galvan 等人 [21 ] 对 Faraday 圆盘发电机的设计进行了全面优化, 其着重于材料改进和能量采集技术的提升, 以增强发电效率. Patrinos[22 ] 进一步探讨了由 Faraday 单极感应器引发的感应电动势现象, 并揭示了法拉第对磁场动态线的视角与相对论理论之间的差异. 该研究通过基于法拉第的实验设置进行了理论和实验的深入探索, 计算了感应电动势, 测量了磁场成分以验证结果, 为理解感应电动势的基本原理及其相关理论提供了重要的参考. Galvan 等人 [23 ] 在他们的研究中使用了在恒定磁场中以不同速度旋转的环形导电固体材料, 探讨了其相互作用所产生的电位差, 并进行测量, 同时强调了理解 Faraday 圆盘这一小型直流发电机中电磁感应现象的重要性. 经典的 Faraday 模型具有以下形式 [24 ] ...
... 根据 Hide 等人在 1996 年的研究[17 ] , 该组参数适用于 Faraday 系统, 是系统能够表现出混沌行为的一组参数, 该参数已在类似研究中得到验证 [24 ,29 ] . ...
Hopf and homoclinic bifurcations on the sliding vector field of switching systems in R3
1
2017
... 为了研究系统 (2.1) 在切换边界 $ \Sigma $ $ F_{S_i} $ $ Q(X) $ [25 ] : $ L_{F_{S_i}}Q(X)=\left \langle \nabla Q(X), F_{S_i}(X)\right \rangle $ $ i=1,2 $ $ \nabla Q(X) $ $ Q(X) $ $ \langle \cdot,\cdot \rangle $ [26 ] : $ L^{n}_{F_{S_i}} Q(X) = \left\langle \nabla^{n-1}_{F_{S_i}} Q(X), F_{S_i}(X) \right\rangle, ~ n=2,3,\cdots $ . 因此, 可以明确地定义滑动区域 ( $ \Sigma_S $ ) 和穿越区域 ( $ \Sigma_C $ ) 如下所示 ...
One-parameter bifurcations in planar Filippov systems
3
2003
... 为了研究系统 (2.1) 在切换边界 $ \Sigma $ $ F_{S_i} $ $ Q(X) $ [25 ] : $ L_{F_{S_i}}Q(X)=\left \langle \nabla Q(X), F_{S_i}(X)\right \rangle $ $ i=1,2 $ $ \nabla Q(X) $ $ Q(X) $ $ \langle \cdot,\cdot \rangle $ [26 ] : $ L^{n}_{F_{S_i}} Q(X) = \left\langle \nabla^{n-1}_{F_{S_i}} Q(X), F_{S_i}(X) \right\rangle, ~ n=2,3,\cdots $ . 因此, 可以明确地定义滑动区域 ( $ \Sigma_S $ ) 和穿越区域 ( $ \Sigma_C $ ) 如下所示 ...
... 滑动集 $ \Sigma_{as} \bigcup \Sigma_{rs} $ $ F_{\Sigma_S} $ $ F_{S_1} $ $ F_{S_2} $ [4 ,26 ] ...
... Filippov 系统 (3.1) 可能会出现一个滑动向量场, 该向量场是否存在取决于切换面是否存在滑动区域. 滑动区域 $ \Sigma_S $ [4 ,26 ] 来表示 ...
Multiple equilibria in a nonsmooth epidemic model with medical resource constraints
1
2019
... 对于系统 (3.1), 存在四种平衡点: 实平衡点, 虚拟平衡点, 边界平衡点和伪平衡点, 其中实平衡点和虚拟平衡点称为 Filippov 系统 (3.1) 的正则平衡点[27 ] . 首先对子系统 $ S_1 $ $ S_2 $ $ S_1 $
Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations
2
1987
... 根据 Routh-Hurwitz 准则 [28 ] , 当 $ \alpha^2_{S_1}>0 $ $ \alpha^2_{S_1}\alpha^1_{S_1}>\alpha^0_{S_1} $ $ E_{S_1}^1 $ $ E_{S_1}^2 $
... 根据 Routh-Hurwitz 准则[28 ] , 当 $ \alpha^2_{S_2}>0 $ $ \alpha^2_{S_2}\alpha^1_{S_2}>\alpha^0_{S_2} $ $ E_{S_2}^1 $ $ E_{S_2}^2 $
Template analysis of a Faraday disk dynamo
1
2008
... 根据 Hide 等人在 1996 年的研究[17 ] , 该组参数适用于 Faraday 系统, 是系统能够表现出混沌行为的一组参数, 该参数已在类似研究中得到验证 [24 ,29 ] . ...