时间序列数据广泛存在于多个领域, 如金融股票、医疗健康、气象、机械故障诊断等 ^[1-3]. 时间序列数据的独特之处在于数据点按时间顺序排列, 这使得对它的分析方法与传统静态数据分析方法截然不同. 时间序列分类 (Time Series Classification, TSC)^[4] 作为时间序列分析的重要任务之一, 旨在通过对时间序列数据的特征提取和模式识别, 实现对不同类别的有效区分 ^[5].

近年来, 时间序列分类的研究受到广泛关注, 特别是在机器学习和深度学习技术的推动下^[6]. 这些技术不仅提高了分类的准确性, 还扩展了应用范围. 例如, 卷积神经网络 ^[7]和递归神经网络 ^[8]等深度学习模型已被成功应用于时间序列分类任务中, 展现出优异的性能. 此外, 传统的特征工程方法, 如动态时间规整 ^[9]和基于距离 ^[10] 的分类方法, 依然在许多实际应用中具有重要价值.

由于时间序列数据的动态性、复杂性和不确定性等多种因素影响分类性能, 分类方法仍有提升空间. 此外, 数据的多样性、噪声、缺失值以及类间和类内的变异性等问题^[11], 均可能导致分类准确度的下降. 数据量的爆发式增长和数据维度的提升, 导致传统分类方法难以满足实际需求. 因此, 如何有效提取和分析时间序列特征以实现准确分类, 开发更为稳健和高效的时间序列分类算法显得尤为重要.

本文首先对现有的一些分类指标 ^[12-14]在模拟的时间序列数据上进行了实验研究, 发现这些指标在处理复杂度较高的非线性时间序列时准确性不高, 这表明在面对数量众多且复杂度较高的非线性时间序列时, 这些方法仍具有局限性. 此外, 以往的分类方法研究通常未充分考虑噪声对结果的影响, 而噪声问题在实际数据中却是一个常见的挑战. 本文提出了 CID-CIDMDS 分类方法, 系统地探讨了噪声对分类方法的影响, 以期提高分类模型在实际应用中的稳健性. 通过对有噪声的模拟数据分类结果表明 CID-CIDMDS 方法具有较强的准确性和稳健性. 并且不受序列长度的影响,分类效果在不同序列长度下保持一致. 该方法采用网络形式展示序列分类结果, 具有直观性和多维数据展示的优势, 能够清晰展示时间序列之间的关系, 增强交互性和灵活性, 便于分类分析和异常点识别. 本文的结构安排如下: 第 2 节介绍复杂度不变距离、多维尺度方法、基于复杂度不变距离的多维尺度和 CID-CIDMDS 理论; 第 3 节介绍四个模型; 第 4 节分析并比较现有的一些分类指标与 CID-CIDMDS 方法的分类结果, 分析时间序列长度对本方法的影响,并探讨噪声干扰下的分类情况; 第 5 节在股票市场进行实证研究; 最后, 第 6 节给出结论.

在许多领域中, 不同类别的时间序列可能表现出不同的复杂性. 相较于复杂度较低的时间序列, 复杂度较高的时间序列通常会出现大量的 "尖峰'', 这些尖峰在数量、周期和变异性上各不相同. 即使在与同一类别的时间序列进行匹配时, 这些特征也难以达到高度一致, 因此许多微小的局部差异可能迅速聚合成一个较大的总欧几里得距离, 从而导致同一类别的对象被误判为不同类别.

为了解决复杂度较高的时间序列分类问题, Gustavo 等^[15] 提出了复杂度不变距离(Complexity-Invariant Distance, CID). 与传统的欧几里得距离相比, CID 引入复杂因子 (CF), 该因子在保持其复杂度的同时, 能够有效调整时间序列 $X$ 和 $Y$ 之间的距离.

该方法对复杂度相同的序列, 使用欧几里得距离, 而对于复杂度不同的序列, 则通过 CF 增加距离. 复杂度相似的序列之间的 CF 相对较小, 而复杂度不同的序列之间的 CF 则较大. 以此达到能够有效区分不同复杂度的时间序列的目的. 因此, CID 在进行距离度量时更具可比性和准确性.

复杂度不变距离的定义为

其中, $ED(X,Y)$是两个时间序列$X$、$Y$之间的欧式距离, $CF(X,Y)$ 是 CID 的复杂因子

CID 主要是通过复杂度不变量对时间序列进行分类, $CE$ 就是实现这个目标的核心内容. 时间序列 $Z$ 的复杂度估计 $CE(Z)$ 定义为

其中, $N$ 表示时间序列 $Z$ 的数据点.

多维尺度方法 (Multidimensional Scaling, MDS) 最早由心理学家 Shepard 于 1962 年提出 [16], 作为一种用于数据降维和可视化的统计方法. MDS 旨在帮助研究者更直观地理解数据, 通过将高维空间中的数据点映射到低维空间 (通常为二维或三维). 该方法能够揭示数据的相似性: 在低维空间中, 差异较小的数据点被映射得较近, 而差异较大的数据点则被映射得较远. 这一特性有助于识别数据的群集或分类. 与主成分分析不同, MDS 更侧重于原始空间的相似性或距离度量, 而非单纯的方差最大化. 此外, 通过一些扩展的 MDS 方法, 研究者可以分析距离矩阵的特征值, 这些特征值的大小反映出不同维度的重要性, 从而帮助选择与数据结构相关的特征. 因此, MDS 在降维过程中主要关注样本之间的距离与相似性关系, 以及数据的全局结构, 使其成为测量和可视化高维数据相似性的有效工具.

CIDMDS 的实现步骤

(1) 构建距离矩阵 $D$: 计算每对时间序列之间的欧式距离, 构建距离矩阵 $D$;

(2) 中心化距离矩阵 $H$: 对距离矩阵 $D$ 进行中心化处理. 中心化处理的主要目的是将数据的均值调整为零. 这一过程消除了数据中可能存在的整体偏移, 从而确保分析的焦点集中在数据的相对距离, 而不是绝对位置. 这有助于消除可能影响相似性或距离计算的干扰因素. 中心化矩阵 $H$ 的计算方法是

其中, $I$ 是单位矩阵, $n$ 是时间序列的数量, $i$ 是一个全 1 的 $n$ 维向量, $i^T$ 是该向量转置;

(3) 计算内积矩阵 $B$: 在原数据中, 内积提供了点之间的相似性度量, 内积的结果构造出一个距离矩阵. 通过这些距离, 后续的 MDS 分析可以基于相似性进行映射. 内积矩阵 $B$ 通过中心化矩阵 $H$ 和距离矩阵 $D$ 的平方形式计算得到

(4) 计算特征值和特征向量: 内积矩阵的特征值和特征向量反映了数据的主要变化方向. 通过对内积矩阵进行特征值分解, 提取出代表数据的主要成分, 从而在低维空间中重构样本之间的距离关系. 这些特征向量决定了降维后的空间坐标. 通过选取最大的 $k$ 个特征值及其对应的特征向量, 作为降维后的 $k$ 维空间的基;

(5) 计算降维后的坐标: 将原始时间序列投影到选定的 $k$ 维基上, 我们可以得到降维后的坐标, 降维后的坐标由特征向量矩阵乘以特征值矩阵的平方根得到.

在时间序列分析中, 复杂度是一个至关重要的因素. 然而, 传统的多维尺度方法主要基于欧氏距离, 虽然易于实现和理解, 却忽视了时间序列的复杂度. 因此, 引入复杂度不变距离可以显著改善分析效果. 针对这一问题, Shang 等 (2014) 提出了一种基于复杂度不变距离的多维尺度方法 (Complexity-Invariant Distance Multidimensional Scaling, CIDMDS)^[17]. 与经典的基于欧氏距离的多维尺度方法相比, CIDMDS 引入了复杂度不变距离, 使其在处理复杂度较高的时间序列数据时表现出明显的优势, 从而得到更为有效和合理的分析结果.

基于复杂度不变距离的多维尺度方法在计算步骤上与经典的多维尺度方法相似, 均包括构建距离矩阵、中心化距离矩阵、计算内积矩阵、计算特征值和特征向量, 以及计算降维后的坐标等步骤. 不同之处在于, 在构建距离矩阵时, CIDMDS 需计算时间序列间的复杂度不变距离.

CID 方法通过引入复杂因子, 考虑时间序列之间的复杂度差异, 提高了序列分类的准确性. 但 CID 方法对时间序列中的噪声较为敏感, 数据中的噪声或异常值可能会影响复杂度的计算. 此外, CID 方法在处理少量数据时表现良好, 但在数据量较大时, 分类结果可能会受到影响. CIDMDS 方法通过特征值的选择, 保留了数据中的关键信息, 减少了冗余信息, 从而增强了序列分类的有效性. 但在处理长度较长和带噪声的时间序列时, 多维尺度变换过程中可能出现维度问题, 导致在低维空间中难以准确表示其特征, 从而影响分类效果.

为了解决这些问题, 并考虑到序列数据的复杂度以及数量的急剧增加, 本文提出了一种新的分类方法: CID-CIDMDS. 该方法有效整合了距离方法和特征选取方法, 旨在提升分类准确性, 增强了模型在噪声影响下的稳健性与可解释性, 并且不受序列长度的限制. 在实际应用中, 特别是在医疗、金融等领域, CID-CIDMDS 展现出了潜力与价值.

CID-CIDMDS 方法是一种基于距离度量判断相似性并实现分类的技术. 其核心思想是通过计算对象在特征空间中的距离, 以评估其相似程度. 一般而言, 距离越小表示对象之间的相似性越高. 该方法通过设定阈值进行分类: 当两个序列的相似性大于给定阈值时, 便将其归类为同一类别; 而当相似性小于阈值时, 则将这两个序列划分为不同类别. CID-CIDMDS 方法的具体实现包括以下六个步骤

CID-CIDMDS 的实现步骤

$\textbf{步骤一 计算 CID 距离}$

在本步骤中, 首先计算 CID 来表示时间序列之间的相关性. 序列间的距离与其相似性呈负相关关系; 即序列间的距离越大, 其相似性越小.

设时间序列个数为 n, 序列数据集合在一个矩阵 $A$ 中, $A=[a_1,a_2,\cdots,a_n]^T$, 这里, $a_1,a_2,\cdots,a_n\in R^D$, $R^D$ 表示 $D$ 维向量空间.

复杂度不变距离的公式为

其中, $a_i$ 表示第 $i$ 个时间序列; $a_j$ 表示第 $j$ 个时间序列; $ED(a_i,a_j)$ 是第 $i$ 个时间序列和第 $j$ 个时间序列的欧式距离; $CF(a_i,a_j)$ 是第 $i$ 个时间序列和第 $j$ 个时间序列的复杂因子.

$\textbf{步骤二 计算 CIDMDS 距离}$

接下来, 通过计算 CIDMDS 距离, 以获取时间序列间的相关性. 与 CID 类似, CIDMDS 距离同样具有负相关的特性: 序列之间的距离越大, 其相似性越小. 设时间序列 $i$ 和时间序列 $j$ 的差异性由 $b_{ij}$ 给出

其中, $d_{ij}$ 是时间序列 $a_i$ 和时间序列 $a_j$ 的复杂度不变距离.

其中, $n$ 是时间序列的数量.

接下来, 计算矩阵 $b_{ij}$ 的特征值 $\lambda$ 和特征向量 $v$. 选取最大的两个特征值 $\lambda_{ij}$ 及其各自对应的特征向量 $v_{ij}$, 作为二维空间的基向量.

降维后的坐标 $X$ 通过以下公式计算

其中, $\Lambda=(\lambda_{ij})$ 是特征值矩阵, $V=(v_{ij})$ 是特征向量矩阵, $i=1$、$2$, $j$ 则代表第 $j$ 个时间序列.

最后计算 $X$ 中任意两列之间的欧式距离, 记为 $ED(X)$. 假设 $X$ 的第 $p$ 列向量为 $x_p$, 第 $q$ 列向量为 $x_q$, 则两列向量间的欧式距离计算公式为

$\textbf{步骤三 确定阈值}$

在获取 CID 和 CIDMDS 距离矩阵后, 第三步是利用这两种距离的分布特征来确定各自的阈值. 基于数据的分布特征灵活确定阈值是一种科学的分类判断方法, 可以使判定标准高度适配不同的数据特性. 对于波动较大的时间序列数据, 可以适当增大阈值, 以避免将离群值误分类; 而对于较为平稳的数据, 则可设定较小的阈值, 以精准地判断这些序列的相似性. 这种自适应的阈值设定策略在一定程度上显著提升了相似性判断的精准度.

$\textbf{步骤四 序列转换为网络节点}$

第四步将时间序列转换为网络中的节点, 以网络的形式展现分类结果. 在这个过程中, 每一个时间序列都被视为网络中的一个节点, 节点之间的连边情况由序列间的相似性决定. 这种网络结构能有效展示时间序列的关系, 有助于后续分类步骤的进行.

$\textbf{步骤五 基于 CID 距离判断连边}$

在构建了网络节点后, 下一步是利用前面确定的阈值对 CID 距离所代表的相关性判断节点的连边情况. 若两个节点的 CID 距离小于设定的阈值, 则将其归类为同一类别, 两节点的连边相连, 形成一个子网络; 而当 CID 距离大于阈值时, 则这两个节点之间的连边断开. 这一步的目的是明确时间序列之间的相关性, 以便后续的分类分析.

$\textbf{步骤六 基于 CIDMDS 距离判断连边}$

最后, 在第五步形成的网络基础上, 将利用前面确定的阈值对 CIDMDS 距离所代表的相关性进行进一步的判断节点连边情况. 若两个节点的 CIDMDS 距离小于相关阈值, 则将其归类为同一类别; 而当 CIDMDS 距离大于阈值时, 这两个节点之间的连边断开. 通过这两个步骤得到的最终网络结构, 达到了序列分类的目标.

通过以上六个步骤 CID-CIDMDS 方法有效地对非线性时间序列数据进行分类, 实现了理想的分类效果.

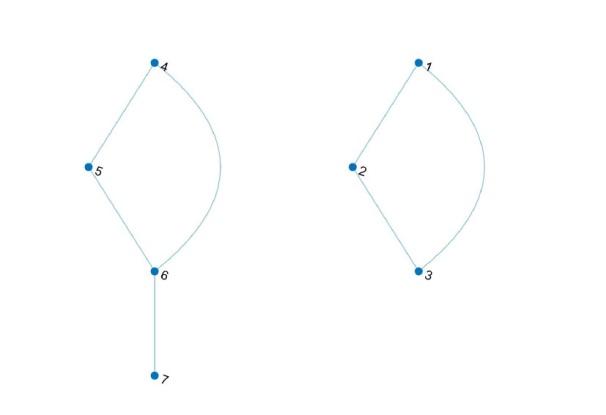
在本研究中, 采用网络的形式展示分类结果, 将时间序列集转化为节点. 对网络中的节点、边以及阈值的相关定义如下: 将每个时间序列视为网络中的一个节点, 节点之间的连边情况基于其相似性 (距离度量) 来确定. 设 $S_{ij}$ 表示第 $i$ 个节点和第 $j$ 个节点之间的距离, $S_{ij}$ 的值越小, 意味着第 $i$ 个节点和第 $j$ 个节点之间的相关性越高. 进一步地, 根据数据的分布特点, 给定一个阈值 $\omega$, 当且仅当 $S_{ij}>\omega$ 时, 节点 $i$ 和节点 $j$ 之间的连接将被断开. 如图 1 所示, 节点 1 与节点 2、节点 1 与节点 3、 节点 2 与节点 3 之间的距离均小于给定的阈值, 因此这三个节点被划分为同一类, 形成一个子网络; 同样, 节点 4 与节点 5、节点 4 与节点 6、 节点 5 与节点 6、 节点 6 与节点 7 之间的距离小于给定的阈值, 因此这四个节点也被归为同一类, 形成一个子网络. 通过这种方式, 可以根据时间序列之间的相似程度, 在网络结构中清晰地刻画节点间的关系.

若某分类方法效果理想, 通常至少存在一个阈值, 使得表征不同模型的时间序列节点间连边断开, 而表征同一模型的时间序列节点间形成连边. 反之, 若分类效果欠佳, 则可能出现表征不同模型的时间序列节点间形成连边、表征同一模型的时间序列节点间未形成连边的错误分类情况, 即不存在可使所有节点正确连边的阈值. 可取阈值范围越宽, 表明相应分类方法在处理多样化数据时, 具有更强的适应性与稳定性, 进而反映出该分类方法的稳健性更高.

本研究在分段线性 Lorenz 映射 ^[18]、Logistic 映射、帐篷映射和二次映射模型上展开时间序列的分类测试. 这四个模型在混沌动力学领域具有广泛研究和应用, 同时它们还代表了不同类型和级别的复杂系统, 有助于更深入地分析数据中存在的模式和规律. 这四个模型的定义如下

分段线性 Lorenz 映射模型定义为

其中, 选取参数 $a$、$b$、$c$ 的组合为 [1.8,1.2,0.5]、[1.8,1,0.4]、[1.5,1,0.4]、[1.5,1,0.5]、[1.8,1.2,0.3]、[1.8,1,0.5]、[1.8,1.2,0.4] [1.8,1,0.3]、[1.2,1,0.3]、[1.5,1,0.4], 即得到 10 个时间序列. 对于 $a$、$b$、$c$ 的每个值, 设 $x_1=0.4$.

Logistic 映射模型定义为

其中, 选取参数 $a$ 的取值范围为 $a\in[3.58,3.68]$, 步长为 0.01, 即得到 10 个时间序列. 对于 $a$ 的每个值, 设 $x_1=0.4$.

帐篷映射模型定义为

其中, 选取参数 $r$ 的取值范围为 $r\in[1.61,1.79]$, 步长为 0.02, 即得到 10 个时间序列. 对于 $r$ 的每个值, 设 $x_1=0.4$.

二次映射模型定义为

其中, 选取参数 $r$ 的取值范围为 $r\in[3.58,3.68]$, 步长为 0.01, 即得到 10 个时间序列. 对于 $r$ 的每个值, 设 $x_1=0.4$. 综上一共可以得到 40 个时间序列, 每个时间序列的长度为 100.

本研究基于以上四种动力模型生成 40 个时间序列, 每个模型生成 10 个长度为 100 的序列. 第 1 至第 10 个时间序列由分段线性 Lorenz 映射模型生成, 第 11 至第 20 个时间序列由 Logistic 映射模型生成, 第 21 至第 30 个时间序列由帐篷映射模型生成, 而第 31 至第 40 个时间序列则由二次映射模型生成.

依据 2.4 节所述的网络构建规则, 将每个时间序列转化为网络节点. 节点 1 至节点 10 分别代表分段线性 Lorenz 映射模型生成的 10 个时间序列; 节点 11 至节点 20 分别代表 Logistic 映射模型生成的 10 个序列; 节点 21 至节点 30 分别代表帐篷映射模型生成的 10 个序列; 节点 31 至节点 40 分别代表二次映射模型生成的 10 个序列.

由于同一模型生成的时间序列具备相似的特征空间分布, 研究将每个模型定义为一个独立类别. 通过分析计算每个时间序列的特征距离, 并设定阈值, 动态构建节点间的连接关系来进行分类. 理想分类状态下, 网络将形成四个独立的子网络: 子网络 A: 由节点 1 至节点 10 构成; 子网络 B: 由节点 11 至节点 20 构成; 子网络 C: 由节点 21 至节点 30 构成; 子网络 D: 由节点 31 至节点 40 构成, 分别对应四类动力学模型, 以此验证方法对不同类别序列的判别能力.

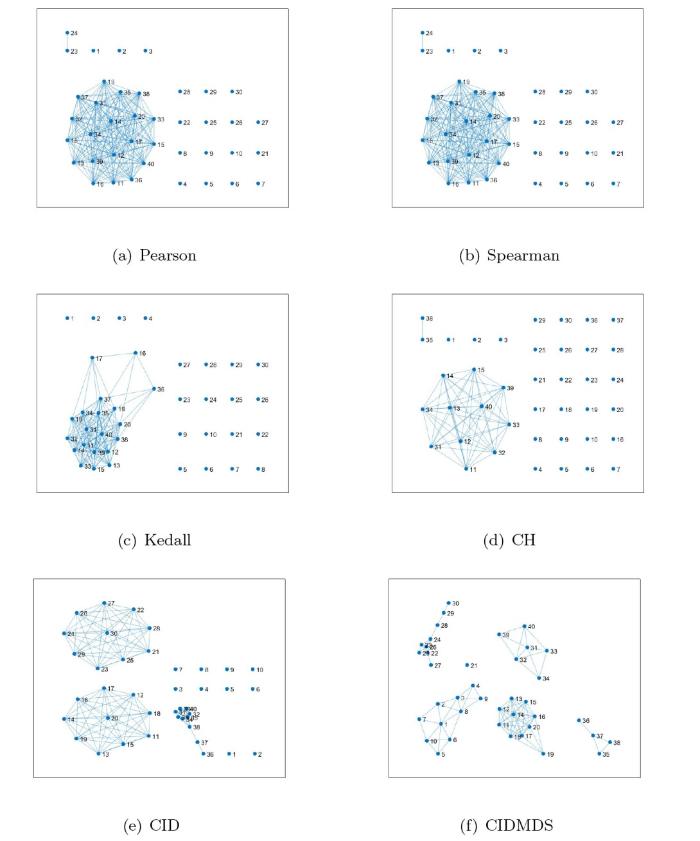
为了验证所提方法的有效性, 现对六种分类指标进行了比较, 包括 Pearson 相关系数、Spearman 秩相关系数、Kendall 相关系数、相干性 (CH)、CID 和 CIDMDS. 各方法的分类结果如图 2 所示.

根据图 1 中的 (a) 、 (b) 和 (c) 所示, Pearson 相关系数、Spearman 秩相关系数和 Kendall 相关系数在处理复杂系统模型生成的时间序列时, 分类效果均不理想. 图中结果表明, 这三种方法的分类结果相似, 其中节点 11 至节点 20 和节点 31 至节点 40 被连接在一起形成一个网络, 而节点 1 至节点 10 和节点 21 至节点 30 则被完全断开. 这一现象说明这三种方法无法有效区分帐篷映射模型和二次映射模型生成的序列, 导致它们的相关节点被错误地连接在一起. 同时, 它们也无法识别分段线性 Lorenz 映射模型和 Logistic 映射模型生成序列的相关性, 导致相关节点完全断开.

根据图 1 中的 (d) 所示, 相干性 (CH) 将节点 11 至节点 15、节点 31 至节点 34 以及节点 39 连接在一起, 形成了一个明显的网络结构, 整个网络共包括 11 个节点. 其余节点之间则完全断开, 没有任何连接. 这一现象表明, 基于相干性所呈现的分类效果相比于前面提到的 Pearson 相关系数、Spearman 秩相关系数和 Kendall 相关系数三种方法的分类效果更差.

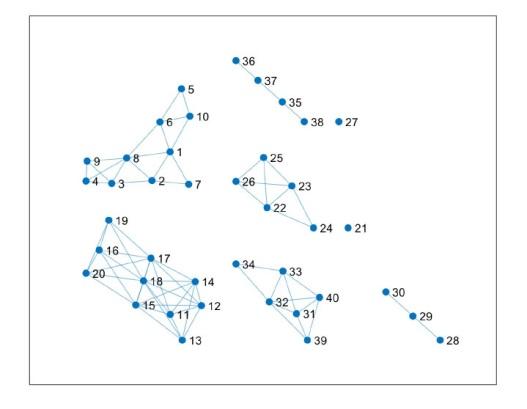
根据图 1 中的 (e) 所示, 通过 CID 方法形成的网络由三个子网络构成, 具体节点分布如下: 子网络 A: 由节点 11 至 节点 20 构成; 子网络 B: 由节点 21 至 节点 30 构成; 子网络 C: 由节点 31 至 节点 40 构成. 对该网络的分析表明, 节点 11 至节点 40 的分类结果较为理想, 形成了一个良好的网络结构. 其中, Logistic 映射模型、帐篷映射模型和二次映射模型生成的序列均得到了较为准确的分类. 然而, 节点 1 至节点 10 则形成了单节点网络, 表明分段线性 Lorenz 映射模型生成的序列未能有效归入同一类. 尽管该方法仍未能构建出理想的网络结构, 但相较于前面四种方法的分类效果展现出一定的优势.

根据图 1 中的 (f) 所示, CIDMDS 方法最终形成了五个子网络: 子网络 A: 由节点 1 至节点 10 构成; 子网络 B: 由节点 11 至节点 20 构成; 子网络 C: 由节点 21 至节点 30 构成; 子网络 D: 由节点 35 至节点 38 构成; 子网络E: 由节点 31 至节点 34 及节点 39 至节点 40 构成. 对该网络的分析表明, 节点 1 至 30 的分类结果较为理想, 形成了一个良好的网络结构. 其中, 分段线性 Lorenz 映射模型和 Logistic 映射模型生成的序列得到了正确分类, 而帐篷映射模型生成的序列则出现了断开的情况, 此外, 二次映射模型生成的序列被分为两类. 总体而言, CIDMDS 方法在对分段线性 Lorenz 映射模型、Logistic 映射模型和帐篷映射模型的分类效果上表现明显优越, 但对二次映射模型的分类效果则不理想.

目前所述的六种现有方法在对复杂系统模型产生的时间序列进行分类时均存在不同程度的问题. Pearson 相关系数、Spearman 秩相关系数、Kendall 相关系数及相干性方法在分类过程中未能有效区分任一种模型生成的序列. 相比之下, CID 方法在分类 Logistic 映射模型、帐篷映射模型和二次映射模型方面表现良好, 但在处理分段线性 Lorenz 映射模型时效果不佳. CIDMDS 方法在分段线性 Lorenz 映射模型和 Logistic 映射模型的分类上表现出色, 而在对二次映射模型的分类上则效果较差.

在本次实验中, 序列 1--10 由分段线性 Lorenz 映射模型生成, 序列 11--20 由 Logistic 映射模型生成, 序列 21--30 由帐篷映射模型生成, 序列 31--40 由二次映射模型生成. 计算得到了这 40 个时间序列间的 CID 和 CIDMDS 两种距离, 其距离矩阵分别显示在图 3 和图 6 中. 通过分析距离分布特征, 确定合理的阈值得到的两种分类结果如图 5 和图 7 所示.

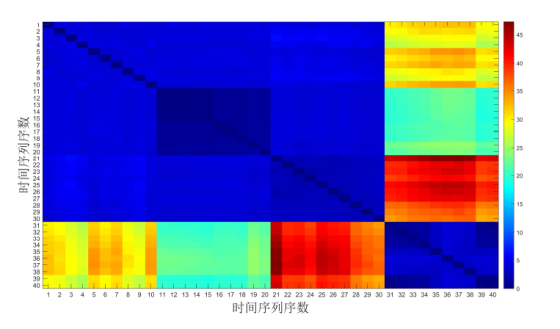
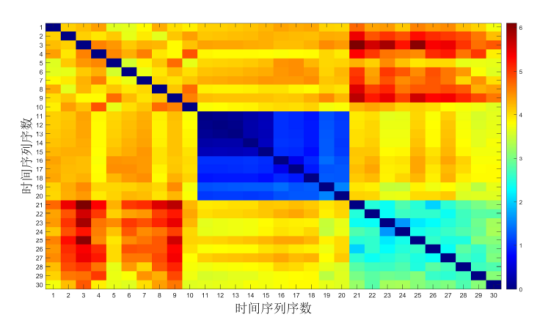
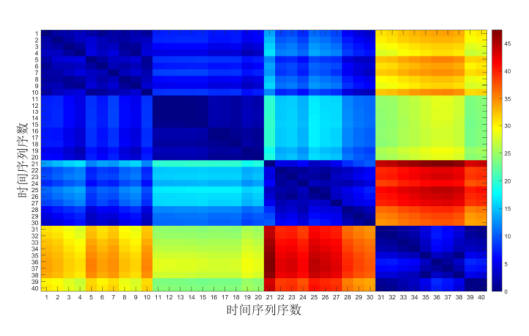
通过分析 CID 和 CIDMDS 距离的数据分布特征以确定合理阈值. 图 3 所示的 CID 距离矩阵显示, 序列 31-40 (二次映射模型) 的内部距离集中在 1-10 区间, 显著小于其与外部序列的距离 (17-45), 体现出该类数据的高内聚性. 进一步放大前 30 个序列的 CID 距离 (见图 4), 序列 11-20 (Logistic 映射) 和 21-30 (帐篷映射) 的内部距离分布于 0-3, 而类间距离为 3.5-6; 序列 1-10 (分段线性 Lorenz 映射) 的类内与类间距离区间重叠, 显示出较低的类别可分性. 基于上述特征, 将阈值优化区间设定为 2-3. 敏感性分析表明: 若阈值高于 3, 将导致不同模型序列因距离小于阈值被错误归为同一类 (如序列 4 与序列 11); 若阈值低于 2, 则会造成模型内序列因距离大于阈值无法正确连接 (如序列 8 与序列 10). 综合分析, 通过最大化类间分离度准则, 确定 CID 的最优阈值为 3.3.

将时间序列转换为网络节点后, 基于 CID 距离的分布特征分析确定阈值 3.3, 以此构建分类网络. 具体连接规则为: 当序列间距离大于阈值时, 节点间不形成连边; 当距离小于或等于阈值时, 节点间生成连边. 实验依据该规则获得如图 5 所示的分类结果. 图 5 显示, 在 CID 方法分类过程中, 序列 1-10 未能实现正确分类, 而序列 11-40 均被准确归类. 结合图 4 分析, 序列 1-10 未被正确分类在于其内部 CID 距离显著偏大, 超出阈值 3.3, 导致节点因距离过大无法形成有效类内连接. 该结果表明, 利用 CID 分类时, 分段线性 Lorenz 映射序列表现出较高的内部异质性.

图 6 展示了 CIDMDS 的距离矩阵, 结果表明不同模型内部的距离通常较小, 范围在 0-10 之间. 第一个模型和第二个模型的时间序列间的距离也相对较小. 因此, 为了达到更好的分类效果, 建议在距离范围 0-3 之间设定阈值. 因此, CIDMDS 的最佳阈值为 2.

通过将时间序列转化为网络中的节点, 采用 CIDMDS 的阈值 2 进行分类实验, 得到了如图 7 的分类结果. CIDMDS 方法在序列 1-20 的分类中达到了正确分类, 而序列 21-40 则未能获得正确分类. 由图 6 可知, 序列 21-40 的 CIDMDS 距离有连续的较大距离, 这造成了节点间的断连.

尽管 CID 和 CIDMDS 方法未能对所有模型实现准确分类, 但 CID 方法在某些模型的分类表现上展现出良好的有效性, CIDMDS 方法在其他一些模型的分类中同样显示出理想的分类效果. 因此, 为了提升分类的整体性能, 研究将这两种方法结合起来: 首先利用 CID 距离对序列进行初步分类, 然后在 CID 分类的基础上进一步进行 CIDMDS 分类. 最终的分类结果如图 8 所示.

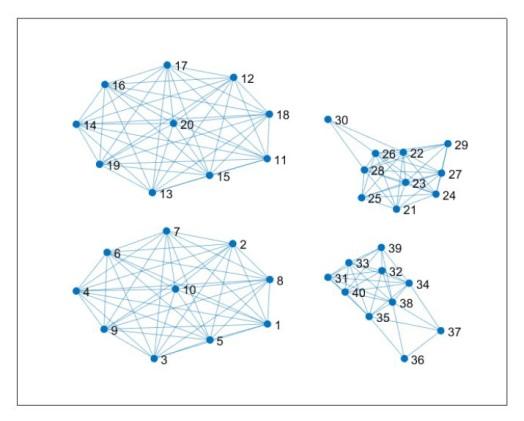
本次实验采用 CID-CIDMDS 方法对模拟时间序列进行分类. 根据距离的分布特征, CID 选取 3.3 作为阈值, CIDMDS 选取 2.3 作为阈值, 以此判定节点的连接情况. 最终实验结果呈现出四个显著的子网络. 其中, 子网络 A 由节点 1 至节点 10 构成, 代表分段线性 Lorenz 映射模型生成的 10 个序列; 子网络 B 则由节点 11 至节点 20 构成, 代表 Logistic 映射模型的 10 个序列; 子网络 C 包含节点 21 至节点 30, 代表帐篷映射模型的 10 个序列; 子网络 D 由节点 31 至节点 40 构成, 代表二次映射模型的 10 个序列.

实验结果表明, 当面对数量繁多且复杂度高的非线性时间序列时, CID-CIDMDS 方法展现出了卓越的准确性与有效性. 从网络结构特性来看, 各子网络彼此独立, 这一显著特征直观地反映出不同模型所生成的时间序列在特征维度上存在着明显的区分度. 而在各个子网络内部, 节点之间紧密相连, 这种紧密联系进一步有力地验证了 CID-CIDMDS 方法能够精准识别出同一模型生成的时间序列所共有的相似性特征. 这一系列研究成果充分凸显了 CID-CIDMDS 方法在处理复杂时间序列数据方面的独特优势.

在本章第二节所开展的实验中, 对 Pearson 相关系数、Spearman 秩相关系数、Kendall 相关系数、相干性、CID 以及 CIDMDS 这六种方法在模拟时间序列分类任务中的结果显示, 上述六种方法分类准确性较低. 鉴于此, 本文不再针对这几种方法开展序列长度影响的分析, 而是将研究重点放在 CID-CIDMDS 方法, 对其受序列长度的影响展开检验.

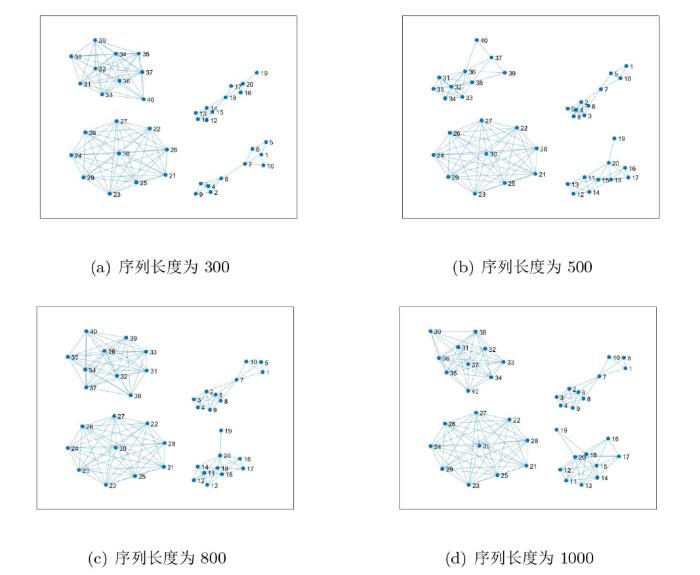
为实现本研究的目的, 依据相关模型随机生成了四组时间序列, 其长度分别设定为 300、500、800 和 1000. 实验选取合适的阈值后, 结果如图 9 所示. 在不同序列长度条件下, CID-CIDMDS 方法在模拟时间序列的分类任务中均展现出较高的准确性. 这一结果充分表明, 该方法对于序列长度的变化具备一定的稳健性, 同时具有良好的泛化能力.

进一步观察网络结构发现, 由节点 11 至节点 20 构成的子网络、由节点 21 至节点 30 构成的子网络以及由节点 31 至节点 40 构成的子网络, 其内部节点之间的连接相对紧密. 这一现象表明, Logistic 映射、帐篷映射和二次映射模型所生成的时间序列, 在不同序列长度下具有较强的抗干扰能力. 相较而言, 由节点 1 至节点 10 构成的子网络 (对应分段线性 Lorenz 映射模型生成的时间序列) 内节点连接相对较少, 这意味着分段线性 Lorenz 映射模型生成的时间序列在序列长度发生变化时, 更容易受到影响.

前面的实验中, 六种分类指标在时间序列分类中并未能准确分类所有时间序列. 这表明这些方法在处理非线性时间序列时的准确性不高. 因此不再对这些方法进行稳健性检验. 下面将对 CID-CIDMDS 进行稳健性检验, 也就是在噪声干扰下的分类效果.

在信号处理中, 通常采用相加或相乘的方式对信号添加噪声, 以检验实验方法的稳健性. 选择相加的方式能够灵活地模拟多种类型的噪声, 如白噪声和高斯噪声, 从而真实再现信号传输过程中的变化. 这种方法有助于研究人员更好地理解信号处理算法的性能. 此外, 该方法常用于评估和测试信号处理技术的有效性, 以系统地检测算法在不同噪声条件下的表现.

为避免实验结果的偶然性, 本次实验分别添加了白噪声、高斯噪声和脉冲噪声, 并对每种噪声进行了 8 次实验. 研究通过信噪比 (SNR) 来衡量噪声对信号的干扰程度,信噪比越低, 噪声所产生的干扰越严重. 当信噪比低于 20dB 时, 表明噪声对原信号产生了显著干扰; 而当信噪比低于 0dB 时, 原信号被噪声完全淹没, 无法进行有效实验. 为确保实验的有效性, 本次实验确保添加噪声的信号的信噪比均处于 10dB 到 20dB 之间.

通过实验选取阈值, 获得了图 10-12, 这三组图展示在不同信噪比区间下添加不同类型噪声后的时间序列分类效果. 图 3.10 展示添加白噪声后的序列分类效果, 图 11 展示添加高斯噪声后的序列分类效果, 图 12 展示添加脉冲噪声后的时间序列分类效果. 其中, 图 2 的子图在采用 CID-CIDMDS 方法时, CID 选取 3.3 作为阈值, CIDMDS 选取 5.5 作为阈值, 以此确定节点的连接情况. 当相关数值大于所设定阈值时, 节点间不形成连边; 若数值小于或等于阈值, 则节点间产生连边.

从图 10 可以看出, 在添加白噪声后, 序列在信噪比区间 13dB-14dB 和 12dB-13dB 分别出现一个节点断开的情况, 而在其他信噪比区间内则没有出现分类错位. 因此, 添加白噪声后的序列分类错分率为 $5\%$. 图 11 显示, 在添加高斯噪声后, 序列在信噪比区间 12dB-13dB 出现了一个节点断开的情况, 但在其他信噪比区间内无分类错位. 因此, 添加高斯噪声后的序列分类错分率为 $2.5\%$. 图 12 表明, 在添加脉冲噪声后, 序列在所有信噪比区间内均未出现分类错位现象. 因此, 添加脉冲噪声后的序列分类错分率为 0.

添加不同噪声后的时间序列的分类正确率一直保持在 $95\%$ 以上, 这充分证明了 CID-CIDMDS 方法的稳健性. 此外还观察到, 同一模型产生的序列所形成的节点之间存在断开现象, 但不同模型生成的序列节点并未出现相互连接的情况. 这一现象表明, 尽管在噪声的干扰下, CID-CIDMDS 方法可能导致分类不完全, 但并未出现分类错误的情况.

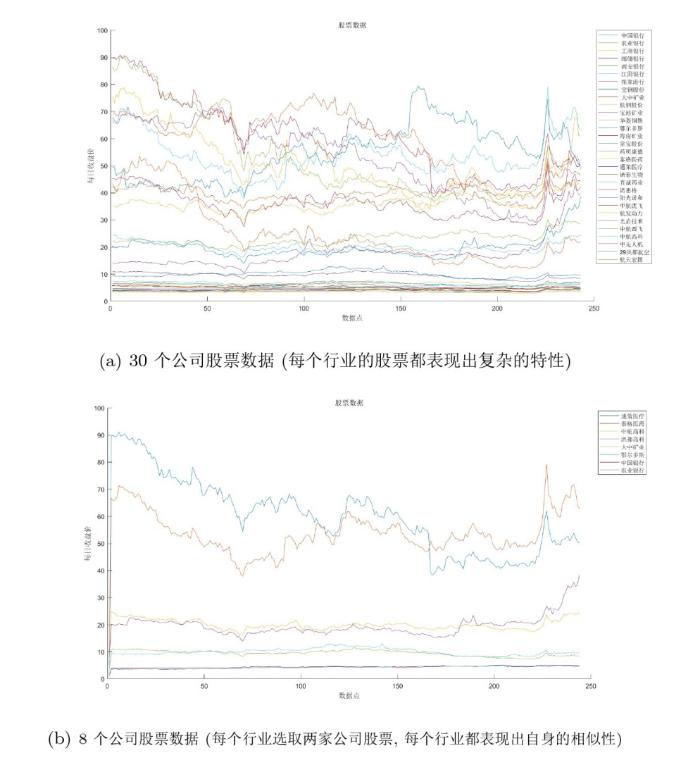
为了验证 CID-CIDMDS 方法在现实数据中的实用性, 本研究将该方法应用于股票的时间序列分析, 以对不同行业的股票进行分类. 选取了国内 30 个股票公司的日收盘数据, 具体包括 7 个银行行业股票、8 个钢铁行业股票、7 个医疗服务行业股票和 8 个航天航空行业股票. 表 1 列出了这 30 家公司, 图 6(a) 展示了这 30 家公司的股票数据, 而图 6(b) 则呈现了每个行业的两家公司的股票数据. 从图 6 中可以看出, 各行业的股票数据具有复杂的特性, 但每个行业内部也展现出自身的相似性. 原始股票数据来源于东方财富网站 [19], 数据的时间范围为 2023 年 10 月 31 日至 2024 年 10 月 31 日, 每个时间序列包含 243 个数据点.

根据图 13 的分析, 同一行业内不同公司的股票序列呈现出相似的内部特征. 因此, 本实验将每个行业定义为一个类. 通过计算 CID 和 CIDMDS 距离, 并分析这两种距离的分布特征, 我们能够确定一个合适的阈值, 以判断股票序列之间的相关性.

在实验过程中, 股票时间序列被转换为网络节点. 具体来说, 银行行业的七家公司股票序列被标记为节点 1 至节点 7; 钢铁行业的八家公司股票序列被标记为节点 8 至节点 15; 医疗服务行业的七家公司股票序列被标记为节点 16 至节点 22; 航天航空行业的八家公司股票序列被标记为节点 23 至节点 30. 在分类结果理想的情况下, 网络将呈现出四个不同的子网络, 每个子网络中的节点由同一行业的公司股票构成. 具体如下: 子网络 A: 由节点 1 至节点 7 构成; 子网络 B: 由节点 8 至节点 15 构成; 子网络 C: 由节点 16 至节点 22 构成; 子网络 D: 由节点 23 至节点 30 构成.

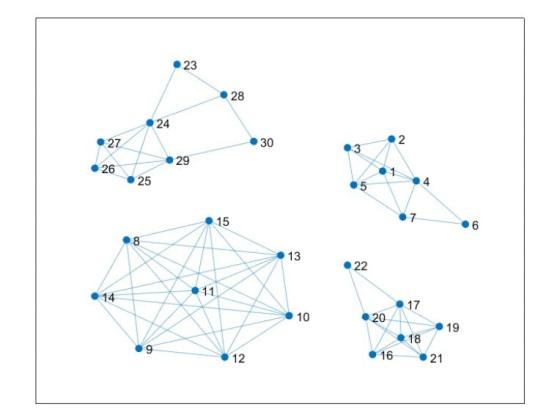
如图 14 所示, 本研究运用 CID-CIDMDS 方法对不同行业的股票序列开展分类研究. 其中, CID 选取 350 作为阈值, CIDMDS 选取 4400 作为阈值, 以此判定节点的连接情况. 实验结果呈现出四个特征显著且相互独立的子网络, 在每个子网络内部, 节点之间联系紧密.

左上方的子网络由节点 23 至节点 30 构成, 这些代表航天航空行业的各家公司; 右上方的子网络由节点 1 至节点 7 构成, 对应银行行业的各家公司; 左下方的子网络由节点 8 至节点 15 构成, 代表钢铁行业的各家公司; 右下方的子网络由节点 16 至节点 22 构成, 代表医疗服务行业的各家公司. 这种网络结构直观地反映出同一行业内时间序列在特征上具有高度相似性. 研究结果表明, CID-CIDMDS 方法在实际时间序列分类应用中, 能够有效地识别并分离具有不同特征的股票时间序列集合, 展现出良好的分类性能与应用潜力.

进一步分析显示, 钢铁行业构成的子网络呈现全连接特征, 表明这些公司之间存在较强的相互联系, 可能反映出它们在市场表现及行业特征上的高度相似性. 而在银行行业构成的子网络中, 节点 6 所代表的工商银行相较于其他银行表现出相对独立性, 或在市场波动中呈现较低的相似度特征.

通过对图中网络的分析, CID-CIDMDS 方法在股票市场分类方面表现出显著的效果. 该方法不仅准确反映了时间序列数据内在的相似性与差异性, 同时也为研究者提供了更高效的数据分析与处理能力. 这一结果的实现为股票市场的分类提供了技术支持.

在本研究中, 为探讨序列长度对 CID-CIDMDS 分类效果的影响, 本次实验选取了序列长度为 200、250、300 和 350 的股票序列进行分析.

通过选取合适的阈值, 获得了如图 15 所示的实验结果. 根据图 15 中的四张子图, 可以观察到, 在变更时间序列长度的情况下, CID-CIDMDS 对股票序列的分类准确性依然得以保持. 此外, 图中显示, 节点 1 至节点 7 所代表的银行行业以及节点 23 至节点 30 所代表的航天航空行业内各公司的相似性较容易受到时间序列长度的影响. 这可能与这两个行业的市场动态及外部环境因素的波动性较大有关. 因此, 在实际应用中, 研究这些行业时需特别关注时间序列长度的选择及其对结果的潜在影响.

节点 8 至节点 15 所代表的钢铁行业的公司之间始终表现出全连接网络的特征, 表明该行业内部的公司在业务及市场环境方面具有高度一致性, 因此其相似性不受不同时间序列长度的影响. 而在节点 16 至节点 22 所代表的医药服务行业中, 各公司的相似性受到时间序列长度的影响则相对较小. 这说明医药服务行业在面对时间序列数据时具备一定的适应性, 这可能源于其市场特征及竞争环境的相对稳定性.

为深入探究 CID-CIDMDS 分类方法的稳健性, 本研究在原始的股票时间序列上随机添加了白噪声, 以评估该方法在不确定性条件下的分类性能. 研究过程中, 所添加的白噪声使得股票序列的信噪比控制在 15dB 至 20dB 之间, 这一范围的选择, 旨在最大程度模拟实际市场中各类不确定因素引发的波动情况, 从而增强实验的真实性和有效性. 为避免实验结果受偶然因素干扰而产生偏差, 本研究严格遵循实验设计原则, 开展了六次独立重复实验, 每次实验均确保在完全相同的条件下进行.

通过选取合适的阈值, 获得了如图 16 所示的实验结果. 从图 16 呈现的六张子图中可以清晰观察到, 尽管股票序列中引入了噪声干扰, 但 CID-CIDMDS 分类方法依旧能够准确得出分类结果, 这一现象充分彰显了该方法具备较强的适应能力. 进一步深入分析实验所得的子网络结构发现, 节点之间存在紧密的连接关系. 这种紧密连接特性表明, 在面对不同程度的噪声干扰时, 各个节点仍能保持较为一致的分类表现, 有力地证实了 CID-CIDMDS 方法在复杂数据环境下的有效性与稳健性.

在本研究中, 首先分析了现有的一些时间序列分类方法, 包括 Pearson 相关系数、Spearman 秩相关系数、Kendall 相关系数、相干性、CID 和 CIDMDS. 研究表明, 这些方法在处理非线性时间序列分类问题时存在准确性不高等问题. 为了解决这些不足, 我们提出了一种新的分类方法—CID-CIDMDS, 该方法展现出较强的准确性和稳健性. 同时, 提出以网络形式表现分类效果, 以直观展示不同类别之间的关系和模式, 增强分类结果的解释性和可视化效果.

为了验证所提方法的有效性, 我们在分段线性 Lorenz 映射、Logistic 映射、帐篷映射和二次映射模型模拟的时间序列上进行了实验. 实验结果表明, CID-CIDMDS 方法在分类准确性上表现优异. 此外, 通过对不同序列长度的实验, 结果显示该方法的性能不受序列长度的影响. 我们还在序列上添加了不同的噪声, 以进一步系统验证该方法的稳健性. 最后, 通过对股票数据的应用实验, 我们进一步证明了 CID-CIDMDS 方法在实际数据中的有效性.

综上所述, 我们提出的 CID-CIDMDS 方法在时间序列分类中展现了良好的有效性和稳健性, 并且不受序列长度的影响, 为处理有噪声的非线性时间序列分类提供了新的解决方案.