1 引言
(1.1) $\begin{equation}\label{eq1} F(x)=0, \end{equation}$
其中底层映射 $F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$
(1.2) $\begin{matrix}\label{1.2} \left(F(x)-F(y)\right)^{\top}(x-y) \geq 0,~\forall~x,~y\in \mathbb{R}^{n}. \end{matrix}$
非线性方程组 (1.1) 在工程计算中具有广泛应用, 如压缩感知, 经济均衡系统, 化学平衡系统等. 由于其自身非线性特性, 获得解析解将具有一定挑战性. 求解 (1.1) 的数值方法主要有两类, 一是基于导数方法, 如牛顿法, 拟牛顿法及其改进版本等, 二是无导数方法, 如谱梯度投影法, 共轭梯度投影法等.
为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献.
惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等.
基于上述研究, 该文首先拓展 BFGS 搜索方向提出一个改进的三项搜索方向框架. 同时给出一种新的惯性步策略, 即使用三步迭代信息产生惯性迭代点, 这与现有多数求解非线性方程组惯性算法 (根据两步迭代信息) 不同. 进而结合投影技术, 提出一种有效的惯性三项共轭梯度投影法用于求解无约束非线性单调方程组 (1.1). 所提惯性算法具有如下理论特征: (i) 独立于任何线搜索, 其搜索方向具有充分下降性和信赖域性质; (ii) 无需 Lipschitz 连续性假设, 建立所提算法的全局收敛性.
该文余下结构安排为: 第二部分基于 BFGS 更新, 给出一类新的三项搜索方向, 进而结合惯性策略和超平面投影技术提出惯性三项共轭梯度投影法; 第三部分在较弱假设下, 论证所提算法的全局收敛性; 第四部分对新算法进行数值测试和报告, 并与其它同类方法进行比较.
2 惯性三项共轭梯度投影法
为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为
其中 $y_{k-1}=F_{k} - F_{k-1}$ $s_{k-1}=x_{k}-x_{k-1}$ . 为发展 BFGS 方法, Li[14 ] 基于 HS 方法, 提出如下近似 BFGS 拟牛顿方法的三项搜索方向
其中 $0\leq \chi_k \leq \bar{\chi} <1$
上式中 $1-\frac{y_{k-1}^{\top}s_{k-1}}{\|y_{k-1}\|^2}$ $\min\limits_{\chi \in \mathbb{R}} \|(y_{k-1}-s_{k-1})-\chi y_{k-1}\|^2$ [20 ] 给出三项搜索方向的一般定义, 即
其中 $p_{k} \in \mathbb{R}^{n} $ $\beta_k$ $p_k$ $d^{\rm N}_{k}$ $\beta_k$ $p_k$
借鉴文献 [14 ] 中 $d_{k}^{\rm THS}$ 20 ] 中 $d^{\rm N}_{k}$ $p_k$ $d_{k}^{\rm THS}$ $y_{k-1}$
其中 $0\leq \chi_k \leq \bar{\chi} <1$ . 搜索方向 $d_k^{\rm TCG}$ $p_{k}$ $p_{k}$ $y_{k-1}$ $d_k^{\rm TCG}$ $d_{k}^{\rm THS}$ $p_{k}$ $F_{k}$ $d_k^{\rm TCG}$ 6 ]的一种三项推广. 为使 $d_k^{\rm TCG}$ 14 ] 令
(2.1) $\begin{matrix}\label{A2.2} \chi_k = {\rm min} \left\{ \bar{\chi}, {\rm max}\left\{0, \ \frac{p_{k}^{\top}(y_{k-1}-s_{k-1})}{\|p_{k}\|^2}\right\} \right\}, \end{matrix}$
其中 $\frac{p_{k}^{\top}(y_{k-1}-s_{k-1})}{\|p_{k}\|^2}$ $\min\limits_{\chi \in \mathbb{R}} \|(y_{k-1}-s_{k-1})- \chi p_{k}\|^2$ $d_k^{\rm TCG}$
(2.2) $\begin{matrix}\label{AQ2.1} d_k = -F_{k}+{\beta^{\rm ITCG}_k}{d_{k - 1}}+\theta_{k}^{\rm ITCG} p_{k}, \ k\geq 1, \ d_0 = -F_0, \end{matrix}$
$\begin{matrix}\label{AQ2.2} \beta^{\rm ITCG}_k = \frac{F_{k}^{\top} p_{k}}{\varpi_{k}}-\frac{\|p_{k}\|^{2}F_{k}^{\top}d_{k-1}}{{\varpi_{k}}^{2}}, \ \ \theta_{k}^{\rm ITCG} = {\chi_{k}}\frac{{F^{\top}_{k}}d_{k-1}}{{\varpi_k}} \ (0 \leq \chi_{k} \leq \bar{\chi} < 1), \end{matrix} $ 2.3)
(2.4) $\begin{matrix}\label{AQ2.2b} \ {\varpi_{k}} = \max\{\tau({\|d_{k-1}\|}^{2}+\|p_{k}\|^{2}), \ {d^{\top}_{k-1}}{y_{k-1}}\} \ (\tau > 0). \end{matrix}$
数值试验中 $\chi_{k}$
基于搜索方向 (2.2)-(2.4) 式, 结合惯性策略和超平面投影技术, 给出惯性三项共轭梯度投影法 (算法 iITCGP) 求解问题 (1.1). 下面给出具体迭代步骤.
${\bf 步骤 0}$ $x_{-2}, \ x_{-1}, \ x_{0} \in \mathbb{R}^n$ . 参数 $\epsilon \geq 0,$ $\varepsilon>0$ $\phi \geq 0$ $\psi \geq 0$ $\tau > 0$ $0 \leq \chi_{k} \leq \bar{\chi} < 1$ $\varsigma > 0$ $\sigma > 0$ $\rho \in (0,1),$ $0<\mu_1 \leq \mu_2,$ $0 < \underline{\gamma} \leq \gamma_k \leq \bar{\gamma} < 2$ . 选取任意非零向量 $p_{k}$ . 惯性步控制序列 $\{\epsilon_k\}$ $\epsilon_k \in [0, \epsilon)$ ) 和 $\{\hat{\epsilon}_k\}$ $\hat{\epsilon}_k \in [0, \epsilon)$ ) 分别满足 $\sum\limits_{k=0}^{+\infty} \epsilon_k < +\infty$ $\sum\limits_{k=0}^{+\infty} \hat{\epsilon}_k < +\infty.$ $k:=0$ .
${\bf 步骤 1}$ $F(x_k)$ . 若 $\|F(x_k)\|\leq \varepsilon$
(2.5) $\begin{equation}\label{C1} \hspace{-.7cm}\phi_{k}=\begin{cases} \min\left\{\phi, \ \frac{\epsilon_k}{\|x_k-x_{k-1}\|}\right\},\:& \text{若} \ x_k\neq x_{k-1}, \\ \phi,\: & \text{否则}, \end{cases} \end{equation}$
(2.6) $\begin{equation}\label{C1a} \psi_{k}=\begin{cases} \min\left\{\psi, \ \frac{\hat{\epsilon}_k}{\|x_{k-1} -x_{k-2}\|}\right\},\:& \text{若} \ x_{k-1} \neq x_{k-2}, \\ \psi,\: & \text{否则}, \end{cases} \end{equation}$
产生惯性迭代点为 $v_k=x_k+\phi_k(x_k-x_{k-1}) + \psi_k(x_{k-1} -x_{k-2})$ $F(v_k)$ . 若 $\|F(v_k)\|\leq\varepsilon$
${\bf 步骤 3}$ $d_{k}$
(2.7) $d_{k}=\left\{\begin{array}{ll} -F\left(v_{k}\right), & \text { 若 } k=0, \\ -F\left(v_{k}\right)+\beta_{k}^{\mathrm{ITCG}} d_{k-1}+\theta_{k}^{\mathrm{ITCG}} p_{k}, & \text { 若 } k \geq 1, \end{array}\right.$
(2.8) $\begin{matrix}\label{d2} \beta^{\rm ITCG}_k = \frac{F(v_k)^{\top} p_{k}}{\varpi_{k}}-\frac{\|p_{k}\|^{2}F(v_k)^{\top}d_{k-1}}{{\varpi_{k}}^{2}}, \ \ \theta_{k}^{\rm ITCG} = {\chi_{k}}\frac{F(v_k)^{\top} d_{k-1}}{{\varpi_k}}, \end{matrix}$
(2.9) $\begin{matrix}\label{d2b} \ {\varpi_{k}} = \max\{\tau({\|d_{k-1}\|}^{2}+\|p_{k}\|^{2}), \ {d^{\top}_{k-1}}{\bar{y}_{k-1}}\}, \ \bar{y}_{k-1} = F(v_{k})-F(v_{k-1}). \end{matrix}$
${\bf 步骤 4}$ $z_k=v_k+t_k d_k$ $t_{k}= \varsigma {\rho}^{i_{k}}$ $i_{k}$ $i$
(2.10) $\begin{matrix}\label{eq10} -F(v_k+t_k d_k)^{\top}d_{k} \geq \sigma t_{k} \mathcal{P}_{[\mu_1,\mu_2]}[\|F(v_k+t_k d_k)\|] \|d_{k}\|^{2}. \end{matrix}$
若 $\|F(z_{k})\|\leq \varepsilon$
${\bf 步骤 5}$ $x_{k+1} = v_{k}- \gamma_k \xi_k F(z_k),$
${\bf注 2.1}$ $\mathcal{P}_{\mathcal{D}}[x]=\arg\min\{\|y-x\|~|~y\|F(z_{k})\|\in \mathcal{D}\}$ . 对于自适应线搜索 (2.10) 式 [30 ,31 ], 使用投影技术 $\mu_1 \leq \mathcal{P}_{[\mu_1,\mu_2]}[\cdot] \leq \mu_2$
${\bf注 2.2}$ $k$ $\phi_k \|x_{k}-x_{k-1}\| \leq \epsilon_k$ $\psi_k \|x_{k-1}-x_{k-2}\| \leq \hat{\epsilon}_k$
下面引理 2.1 表明独立于任意线搜索, 搜索方向 (2.7)-(2.9) 式具有充分下降性和信赖域性质.
${\bf引理2.1}$ $k \geq 0$
(2.11) $\begin{matrix}\label{3.2} \ F (v_{k})^{\top}d_{k} \leq -\left(1-\frac{(1+\bar{\chi})^{2}}{4}\right){\|F(v_{k})\|^{2}} \end{matrix}$
(2.12) $\left(1-\frac{(1+\bar{\chi})^{2}}{4}\right)\left\|F\left(v_{k}\right)\right\| \leq\left\|d_{k}\right\| \leq\left(1+\frac{1+\bar{\chi}}{2 \tau}+\frac{1}{4 \tau^{2}}\right)\left\|F\left(v_{k}\right)\right\|.$
${\bf证}$ $k=0$ $d_{0} = -F(v_{0})$ $F(v_{0})^{\top}d_{0} = -{\|F(v_{0})\|^{2}}$ $d_k$ $k \geq 1$
其中第一个不等式利用 $a^2 + b^2 \geq 2ab$
由 $d_{0} = -F(v_{0})$ $\|d_0\| = \|F(v_{0})\|$ $k = 0$ $k \geq 1$ $k$ $d_{k} \neq 0$ . 利用 (2.11) 式和柯西-施瓦茨不等式, 知 (2.12) 式的第一个不等式成立. 接下来, 根据 $\varpi_{k}$ $a^2 + b^2 \geq 2ab$
(2.13) $\begin{matrix}\label{0611A1} \ \varpi_{k} = \max\{\tau({\|d_{k-1}\|}^{2}+\|p_{k}\|^{2}), \ {d^{\top}_{k-1}}{y_{k-1}}\} \geq \tau({\|d_{k-1}\|}^{2}+\|p_{k}\|^{2}) \geq 2 \tau \|d_{k-1}\| \|p_{k}\|. \ \ \ \ \end{matrix}$
根据 $\beta^{\rm ITCG}_k$
其中第一个不等式使用柯西-施瓦茨不等式, 第二个不等式使用 (2.13) 式. 同理, 由 $\theta_{k}^{\rm ITCG}$
3 全局收敛性
该节分析算法 iITCGP 的全局收敛性. 首先给出如下假设.
${\bf 假设 1}$ $Sol_{F}$ $F$ $\mathbb{R}^{n}$ $F$
${\bf引理3.1}$ 23 ] 对于非负实序列 $\{p_{k}\}$ $\{q_{k}\}$ $p_{k+1}\leq p_k+ q_k$ . 若 $\sum\limits_{k=0}^{+\infty} q_k < +\infty$ $\{p_{k}\}$
${\bf引理3.2}$ $\{x_{k}\},\ \{v_{k}\}$ $\{z_{k}\}$ $x^{\ast}\in Sol_{F}$ . 若假设 1 成立, 则序列 $\{\|x_k-x^{\ast}\|\}$
${\bf证}$ $z_k=v_k+t_k d_k$
此结合假设 1 及 $x^{\ast}\in Sol_{F}$
(3.1) $\begin{matrix}\label{3.12} F(z_{k})^{\top}(v_{k}-x^{\ast}) &=& F(z_{k})^{\top}(v_{k}-z_{k})+F(z_{k})^{\top}(z_{k}-x^{\ast}) \nonumber \\ &=& F(z_{k})^{\top}(v_{k}-z_{k})+ [F(z_{k})- F(x^{\ast})]^{\top}(z_{k}-x^{\ast}) \nonumber \\ &\geq& F(z_{k})^{\top}(v_{k}-z_{k}) \nonumber \\ &\geq& \sigma \mu_1 \|v_{k}-z_{k}\|^{2}>0, \end{matrix}$
其中第一不等式由 $F$
(3.2) $\begin{matrix}\label{3.13} \nonumber \|x_{k+1}-x^{\ast}\|^{2}&=& \|v_{k}-\gamma_{k} \xi_{k}F(z_{k})- x^{\ast}\|^{2} \nonumber \\ &=& \|v_{k}-x^{\ast}\|^{2}-2\gamma_{k} \xi_{k}F(z_{k})^{\top}(v_{k}-x^{\ast})+\gamma_{k}^{2}\xi_{k}^{2}\|F(z_{k})\|^{2} \nonumber \\ &\leq& \|v_{k}-x^{\ast}\|^{2}-2\gamma_{k} \xi_{k}F(z_{k})^{\top }(v_{k}-z_{k})+\gamma_{k}^{2}\xi_{k}^{2}\|F(z_{k})\|^{2} \nonumber \\ &=& \|v_{k}-x^{\ast}\|^{2}-\gamma_{k}(2-\gamma_{k})\frac{[F(z_{k})^{\top}(v_{k}-z_{k})]^{2}}{\|F(z_{k})\|^{2}} \nonumber \\ &\leq& \|v_{k}-x^{\ast}\|^{2}-\gamma_{k}(2-\gamma_{k})\frac{{\sigma}^2 \mu^{2}_1\|v_{k}-z_{k}\|^{4}}{\|F(z_{k})\|^{2}} \nonumber \\ &\leq& \|v_{k}-x^{\ast}\|^{2}-\underline{\gamma} (2-\overline{\gamma} )\frac{{\sigma}^2 \mu^{2}_1\|v_{k}-z_{k}\|^{4}}{\|F(z_{k})\|^{2}}, \end{matrix}$
其中第一个不等式由 (3.1) 式放缩得到. 再根据 $0 < \underline{\gamma} \leq \overline{\gamma} <2$
结合 $\sum\limits_{k=0}^{+\infty} \epsilon_k < +\infty$ $\sum\limits_{k=0}^{+\infty} \hat{\epsilon}_k < +\infty$ $\{\|x_{k}-x^{\ast}\|\}$
${\bf引理3.3}$ $\{x_{k}\},\ \{v_{k}\}$ $\{z_{k}\}$
(i) 序列 $\{x_{k}\}$ $\{v_{k}\}$ $\{z_{k}\}$
(ii) $\lim\limits_{k\rightarrow +\infty}\|v_{k}-z_{k}\|= \lim\limits_{k\rightarrow +\infty}t_{k}\|d_{k}\|=0$
${\bf证}$ $\{\|x_{k}-x^{\ast}\|\}$ $\{\|x_{k}-x^{\ast}\|\}$ $x^{\ast}\in Sol_{F}$ $\{x_k\}$ $N_1$ $N_2$
此结合 $\phi_{k}$ $\psi_{k}$
即 $\{v_k\}$ $F$ $\{F(v_k)\}$ $\{d_k\}$ $z_k= v_k+t_k d_k$ $t_k\in (0, \varsigma]$ $\{z_k\}$
(ii) 考虑到 $x^{\ast}\in Sol_{F}$ $v_k$
(3.3) $\begin{matrix}\label{3.14} \nonumber \|v_k-x^*\|^2 &=& \|x_k+\phi_{k}(x_k-x_{k-1}) +\psi_{k}(x_{k-1}-x_{k-2}) -x^* \|^2 \nonumber \\ &=& \|x_k-x^*\|^2+2 (x_k-x^*)^{\top} [\phi_k (x_{k}-x_{k-1} )+\psi_k (x_{k-1}-x_{k-2} ) ] \nonumber \\ && + \|\phi_k (x_k-x_{k-1} )+\psi_k (x_{k}-x_{k-2} )\|^2 \nonumber \\ & \leq& \|x_k-x^*\|^2+2 \|x_k-x^*\| [ \phi_k \|x_{k-1}-x_{k-1}\| +\psi_k \|x_{k-1}-x_{k-2}\| ] \nonumber \\ && + 2(\phi_k \|x_k-x_{k-1}\|)^2 + 2 (\psi_k \|x_{k-1}-x_{k-2}\|)^2 \nonumber \\ & \leq& \|x_k-x^*\|^2+ 2 N_1 (\epsilon_k + \hat{\epsilon}_k) + 2 \epsilon_k^2 + 2 \hat{\epsilon}_k^2. \end{matrix}$
(3.4) $\begin{matrix}\label{3.15} \|x_{k+1}-x^{\ast}\|^{2} \leq \|x_{k}-x^{\ast}\|^{2}+ \left[2 N_1 (\epsilon_k + \hat{\epsilon}_k) + 2 \epsilon_k^2 + 2 \hat{\epsilon}_k^2\right] -\underline{\gamma} (2-\overline{\gamma} ) \frac{{\sigma}^2{\mu^{2}_1}\|v_{k}-z_{k}\|^{4}}{\|F(z_{k})\|^{2}}. \end{matrix}$
另一方面, 根据 $F$ $\{z_k\}$ $\{F(z_k)\}$ $k\geq 0$ $N_3$ $\|F(z_{k})\|\leq N_3$ .
再利用 $\sum\limits_{k=0}^{+\infty} \epsilon_k < +\infty$ $\sum\limits_{k=0}^{+\infty} \hat{\epsilon}_k < +\infty$
于是有 $\lim\limits_{k\rightarrow +\infty}\|v_{k}-z_{k}\| = \lim\limits_{k\rightarrow +\infty}t_k\|d_{k}\|=0$ .
${\bf定理3.1}$ $\{x_{k}\},\ \{v_{k}\}$ $\{z_{k}\}$
(i) $\liminf\limits_{k\rightarrow +\infty}\|F(v_{k})\|=0;$
(ii) $\{x_{k}\},\ \{v_{k}\}$ $\{z_{k}\}$
${\bf证}$ $\Lambda >0$
再利用 (2.12) 式知, 对任意 $k\geq 0$ $\|d_{k}\| \geq \left(1-\frac{(1+\bar{\chi})^{2}}{4}\right) \|F(v_{k})\| \geq \left(1-\frac{(1+\bar{\chi})^{2}}{4}\right) \Lambda > 0$ . 结合引理 3.3 (ii), 有 $\lim\limits_{k\rightarrow +\infty}t_k=0.$ $\{d_{k}\}$ $\{v_{k}\}$ $\{d_{k_{j}}\}$ $\{v_{k_{j}}\}$ $\lim\limits_{j\rightarrow +\infty,j\in \mathcal{K}}d_{k_{j}} = \tilde{d}, \ \lim\limits_{j\rightarrow +\infty,j\in \mathcal{K}}v_{k_{j}} = \tilde{v},$ $\mathcal{K}$
上式中令 $j \rightarrow + \infty$ $F$
(3.5) $\begin{matrix}\label{3.18} -{F(\tilde{v})}^{\top}\tilde{d} \geq \left(1-\frac{(1+\bar{\chi})^{2}}{4}\right) {\|F(\tilde{v})\|^{2}} \geq \left(1-\frac{(1+\bar{\chi})^{2}}{4}\right) \Lambda^{2} > 0. \end{matrix}$
类似的, 上式中令 $j \rightarrow + \infty$ $F$ $-{F(\tilde{v})}^{\top}\tilde{d} \leq 0$ . 此与不等式(3.5) 产生矛盾. 因此, $\liminf\limits_{k\rightarrow +\infty}\|F(v_{k})\|=0$
(ii) 考虑到 $\{v_k = x_k+\phi_k(x_k-x_{k-1}) + \psi_k(x_{k-1} -x_{k-2})\}$ $\phi_{k}$ $\psi_{k}$
上式两边同时取极限, 结合 $\lim\limits_{k\rightarrow +\infty} \epsilon_k =0$ $\lim\limits_{k\rightarrow +\infty} \hat{\epsilon}_k =0$ $\lim\limits_{k\rightarrow +\infty} \|x_{k}-v_{k}\|=0$ . 令
从而 $\lim\limits_{i\rightarrow +\infty}\|F(x_{k_i})\|=\|F(v^{*})\|=0$ . 令 $x^{*} := v^{*} \in Sol_{F}$ $\{\|x_k-x^{\ast}\|\}$
因此, $\{x_{k}\}$ $x^{*} \in Sol_{F}$ $\{v_{k}\}$ $x^{*}$ . 此结合引理 3.3 (ii) 知 $\lim\limits_{k\rightarrow + \infty} \|z_{k}- v_{k}\| = 0$ $\{z_{k}\}$ $x^{*}$ .
4 数值试验
为验证算法 iITCGP 的数值有效性, 该节将其应用于求解 10 个无约束非线性方程组问题. 数值试验分为两部分, 即试验 I 和试验 II, 所有程序均使用 Matlab R2022a 实现, 在 Lenovo 笔记本电脑上执行, 其配置为 Intel(R) Core(TM) i5-1135G7 CPU (2.40 GHz), 16 GB 内存.
$\textbf{试验 I}$ $p_k$ $\bar{y}_{k-1} = F(v_{k})-F(v_{k-1})$ $F(v_{k})$ $F(v_{k-1})$ $d_{k-1}$ $\sigma=0.001$ $\varsigma=0.45$ $\rho=0.43$ $\gamma_k \equiv 1.99$ $\phi=0.01$ $\psi=0.01$ $\mu_1=0.001$ $\mu_2=0.8$ $\tau=0.99$ $\bar{\chi}=0.5$ $\epsilon_k=\hat{\epsilon}_k=\frac{1}{k^2}$ $k=0$ $\epsilon_k=\hat{\epsilon}_k= 1$ ).
$\textbf{试验 II}$ [9 ] , MITTCGP [18 ] 和 ISTCP [10 ] , 其搜索方向和线搜索参数的取值均与原文献保持一致.
记 $F(x)=\left(f_{1}(x), f_{2}(x), \dots, f_{n}(x)\right)^{\top}$
$\textbf{问题 4}$
$\textbf{问题 8}$ $f_{i}(x)=({\rm e}^{x_i})^2+3\sin x_i\cos x_i-1,\ i=1,2,3,\dots,n.$
$\textbf{问题 9}$
$\textbf{问题 10}$ [问题 16] 令 $f_{i}(x)= \frac{i}{n}{\rm e}^{x_i}-1,\ i=1,2,3,\dots,n.$
对上述 10 个测试问题分别取 5 个不同维度 ($n=1000, \ 5000, \ 10000, \ 50000$ $100000$ ) 进行求解, 表 1 列出算法所需不同初始点的选取情况. 所有算法满足如下一种终止准则时, 迭代停止. (i) $\|d_k\| \leq 10^{-7}$ $\|F_k\| \leq 10^{-6}$ $F_k$ $F(x_k)$ $F(v_k)$ $F(z_k)$ .
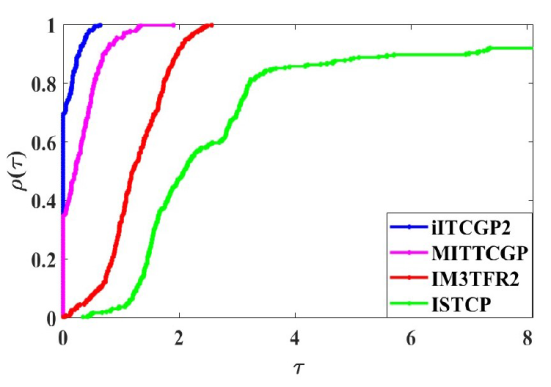
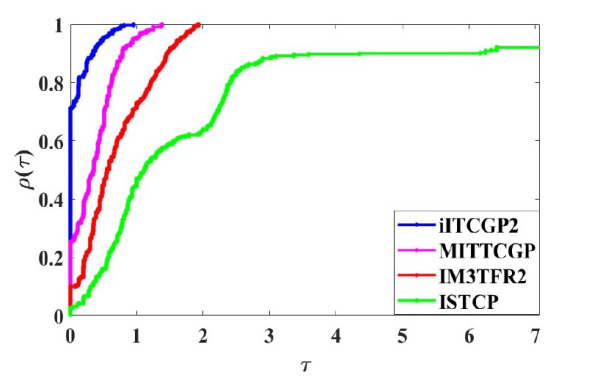
试验 I 和试验 II 的具体测试结果见 https://www.cnblogs.com/kekoukelele/p/18470451 . 其中, "Case" 表示 7 种不同初始点选择情形, "n" 表示测试问题维度除以 $10^3$ $F$ $\|F^{*}\|$ $\|F_k\|$ $\|F^{*}\|$ 5 ] 提出的性能曲线图以展示每种算法关于三个指标的计算结果 (即计算时间, 函数 $F$
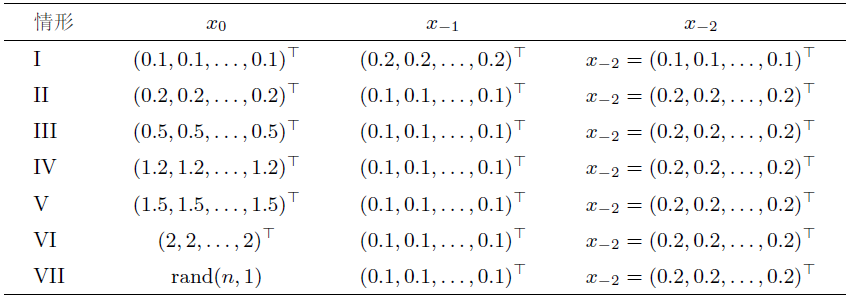
(i) 对于试验 I, 从图 1 -3 中可观察到, $p_{k}$ $F(v_{k})$ $p_{k}$ $\bar{y}_{k-1}$
图1
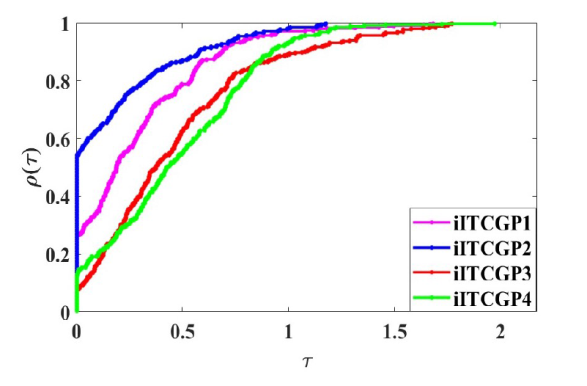
图2
图3
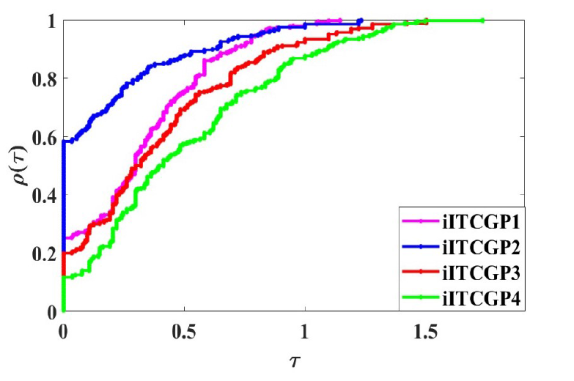
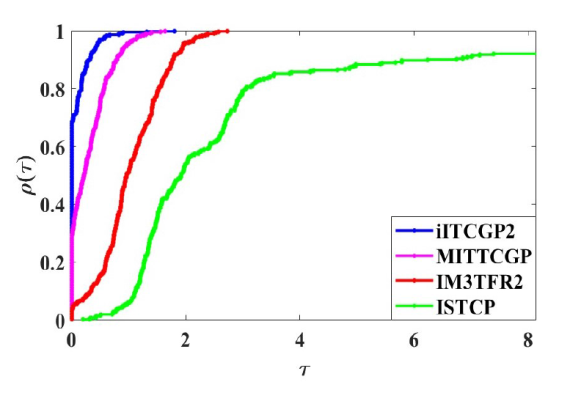
(ii) 对于测试 II, 结果见图 4 -6 . 多数情况下, 算法 iITCGP2 在迭代次数, 函数 $F$
图4
图5
图5
试验 II 中函数 $F$
图6
参考文献
View Option
[1]
Awwal A M Kumam P Sitthithakerngkiet K et al . Derivative-free method based on DFP updating formula for solving convex constrained nonlinear monotone equations and application
AIMS Math , 2021 , 6 8 ): 8792 -8814
[2]
Bing Y Lin G An efficient implementation of Merrill's method for sparse or partially separable systems of nonlinear equations
SIAM J Optimiz , 1991 , 1 2 ): 206 -221
[3]
Cheng W Y A PRP type method for systems of monotone equations
Math Comput Modell , 2009 , 50 15 -20
[本文引用: 1]
[4]
Cruz W L A spectral algorithm for large-scale systems of nonlinear monotone equations
Numer Algorithms , 2017 , 76 1109 -1130
[5]
Dolan E D Moré J J Benchmarking optimization software with performance profiles
Math Program , 2002 , 91 2 ): 201 -213
[本文引用: 1]
[6]
Dai Y H Yuan Y X A nonlinear conjugate gradient method with a strong global convergence property
SIAM J Optim , 1999 , 10 1 ): 177 -182
[本文引用: 1]
[7]
Gao P T He C J An efficient three-term conjugate gradient method for nonlinear monotone equations with convex constraints
Calcolo , 2018 , 55 4 ): Article 53
[8]
Hu Y P Wei Z X A modified Liu-Storey conjugate gradient projection algorithm for nonlinear monotone equations
Int J Math , 2014 , 9 1767 -1777
[9]
Ibrahim A H Kumama P Rapajić S et al . Approximation methods with inertial term for large-scale nonlinear monotone equations
Appl Numer Math , 2022 , 181 417 -435
[本文引用: 2]
[10]
Ibrahim A H Kumam P Sun M et al . Projection method with inertial step for nonlinear equations: Application to signal recovery
J Ind Manag Optim , 2023 , 19 1 ): 30 -55
[本文引用: 2]
[11]
Jian J B Yin J H Tang C M et al . A family of inertial derivative-free projection methods for constrained nonlinear pseudo-monotone equations with applications
Comput Appl Math , 2022 , 41 7 ): Article 309
[本文引用: 1]
[12]
Kou C X Dai Y H A modified self-scaling memoryless Broyden-Fletcher-Goldfarb-Shanno method for unconstrained optimization
J Optim Theory Appl , 2015 , 165 209 -224
[本文引用: 1]
[13]
La Cruz W Martínez J M Raydan M Spectral residual method without gradient information for solving large-scale nonlinear systems of equations
Math Comput , 2006 , 75 255 ): 1429 -1448
[14]
Li M A modified Hestense-Stiefel conjugate gradient method close to the memoryless BFGS quasi-Newton method
Optim Methods Softw , 2018 , 33 2 ): 336 -353
[本文引用: 4]
[15]
刘金魁 , 孙悦 , 赵永祥 . 凸约束伪单调方程组的无导数投影算法
计算数学 , 2021 , 43 3 ): 388 -400
DOI:10.12286/jssx.j2020-0659
[本文引用: 1]
Based on the structure of the HS conjugate gradient method, we propose an iterative projection algorithm for solving nonlinear pseudo-monotone equations with convex constraints under one weak assumption. Since the proposed method does not need any gradient or Jacobian matrix information of equations, it is suitable to solve large-scale problems. The proposed algorithm generates a sufficient descent direction in per-iteration, which is independent of any line search. Moreover, the global convergence and R-linear convergence rate of the proposed method are proved without the assumption that nonlinear equations satisfies Lipschitz condition.The numerical results show that the proposed method is stable and effective for the given large-scale nonlinear equations with convex constraints.
Liu J K Sun Y Zhao Y X A derivative-free projection algorithm for solving pseudo-monotone equations with convex constraints
Math Numer Sin , 2021 , 43 3 ): 388 -400
DOI:10.12286/jssx.j2020-0659
[本文引用: 1]
Based on the structure of the HS conjugate gradient method, we propose an iterative projection algorithm for solving nonlinear pseudo-monotone equations with convex constraints under one weak assumption. Since the proposed method does not need any gradient or Jacobian matrix information of equations, it is suitable to solve large-scale problems. The proposed algorithm generates a sufficient descent direction in per-iteration, which is independent of any line search. Moreover, the global convergence and R-linear convergence rate of the proposed method are proved without the assumption that nonlinear equations satisfies Lipschitz condition.The numerical results show that the proposed method is stable and effective for the given large-scale nonlinear equations with convex constraints.
[16]
Liu P J Shao H Yuan Z H et al . A family of three-term conjugate gradient projection methods with a restart procedure and their relaxed-inertial extensions for the constrained nonlinear pseudo-monotone equations with applications
Numer Algorithms , 2023 , 94 1055 -1083
[本文引用: 1]
[17]
Liu P J Wu X Y Shao H et al . Three adaptive hybrid derivative-free projection methods for constrained monotone nonlinear equations and their applications
Numer Linear Algebra Appl , 2023 , 30 2 ): e2471
[本文引用: 1]
[18]
Ma G D Jin J C Jian J B et al . A modified inertial three-term conjugate gradient projection method for constrained nonlinear equations with applications in compressed sensing
Numer Algorithms , 2023 , 92 3 ): 1621 -1653
[本文引用: 2]
[19]
Moré J J Garbow B S Hillstrom K E Testing unconstrained optimization software
ACM Trans Math Softw , 1981 , 7 1 ): 17 -41
[20]
Narushima Y Yabe H Ford J A A three-term conjugate gradient method with sufficient descent property for unconstrained optimization
SIAM J Optim , 2011 , 21 1 ): 212 -230
[本文引用: 2]
[21]
Nocedal J Updating quasi-Newton matrices with limited storage
Math Comput , 1980 , 35 151 ): 773 -782
[本文引用: 1]
[22]
Polyak B T Some methods of speeding up the convergence of iteration methods
USSR Comput Math Math Phys , 1964 , 4 5 ): 1 -17
[本文引用: 1]
[23]
Polyak B T Introduction to Optimization . New York : Inc Publications Division , 1987
[本文引用: 1]
[24]
Rao J Y Huang N A derivative-free scaling memoryless DFP method for solving large scale nonlinear monotone equations
J Glob Optim , 2023 , 87 2 ): 641 -677
[25]
Shanno D F Conjugate gradient methods with inexact searches, Math Oper Res , 1978 , 3 3 ): 244 -256
[本文引用: 1]
[26]
Solodov M V Svaiter B F A globally convergent inexact Newton method for systems of monotone equations//Fukushima M, Qi L. Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods
Dordrecht: Kluwer , 1998 . 355 -369
[本文引用: 1]
[27]
Song T Y Liu Z X An efficient inertial subspace minimization CG algorithm with convergence rate analysis for constrained nonlinear monotone equations
J Comput Appl Math , 2024 , 446 115873
[本文引用: 1]
[28]
Stanimirović P S Ivanov B Djordjević S et al . New hybrid conjugate gradient and Broyden-Fletcher-Goldfarb-Shanno conjugate gradient methods
J Optim Theory Appl , 2018 , 178 860 -884
[本文引用: 1]
[29]
Wu X Y Shao H Liu P J et al . An inertial spectral CG projection method based on the memoryless BFGS update
J Optim Theory Appl , 2023 , 198 1130 -1155
[本文引用: 1]
[30]
尹江华 , 简金宝 , 江羡珍 . 凸约束非光滑方程组基于自适应线搜索的谱梯度投影算法
计算数学 , 2020 , 42 4 ): 457 -471
DOI:10.12286/jssx.2020.4.457
[本文引用: 1]
Based on three classic line search techniques for finding separating hyperplane, this paper proposes an adaptive line search method. Combining this with the spectral gradient projection method, a spectral gradient projection algorithm for nonsmooth monotone equations with convex constraints is proposed. The proposed method does not calculate and store any matrix, so it is suitable for solving large-scale nonsmooth monotone nonlinear equations. Under mild conditions, the global convergence of the proposed method is proved, and its rate of convergence is analyzed. Numerical experiments show that the proposed algorithm is efficient and robust.
Yin J H Jian J B Jiang X J A spectral gradient projection algorithm for convex constrained nonsmooth equations based on an adaptive line search
Math Numer Sin , 2020 , 42 4 ): 457 -471
DOI:10.12286/jssx.2020.4.457
[本文引用: 1]
Based on three classic line search techniques for finding separating hyperplane, this paper proposes an adaptive line search method. Combining this with the spectral gradient projection method, a spectral gradient projection algorithm for nonsmooth monotone equations with convex constraints is proposed. The proposed method does not calculate and store any matrix, so it is suitable for solving large-scale nonsmooth monotone nonlinear equations. Under mild conditions, the global convergence of the proposed method is proved, and its rate of convergence is analyzed. Numerical experiments show that the proposed algorithm is efficient and robust.
[31]
Yin J H Jian J B Jiang X Z et al . A hybrid three-term conjugate gradient projection method for constrained nonlinear monotone equations with applications
Numer Algorithms , 2021 , 88 389 -418
[本文引用: 2]
[32]
Yin J H Jian J B Jiang X Z et al . A family of inertial-relaxed DFPM-based algorithms for solving large-scale monotone nonlinear equations with application to sparse signal restoration
J Comput Appl Math , 2023 , 419 114674
[本文引用: 1]
[33]
Yu G H Niu S Z Ma J H et al . An adaptive prediction-correction method for solving large-scale nonlinear systems of monotone equations with applications
Abstr Appl Anal , 2013 , 2013 1 -13
[34]
Zhang L Zhou W J Spectral gradient projection method for solving nonlinear monotone equations
J Comput Appl Math , 2006 , 196 478 -484
[本文引用: 1]
[35]
张宁 , 刘金魁 . 非线性伪单调方程组的谱 LS 型投影算法
数学物理学报 , 2022 , 42A 6 ): 1886 -1897
[本文引用: 1]
Zhang N Liu J K Spectral LS-type projection algorithm for solving nonlinear pseudo-monotone equations
Acta Math Sci , 2022 , 42A 6 ): 1886 -1897
[本文引用: 1]
[36]
Zhang N Liu J K Zhang L Q et al . A fast inertial self-adaptive projection based algorithm for solving large-scale nonlinear monotone equations
J Comput Appl Math , 2023 , 426 115087
[本文引用: 1]
[37]
Zhou W J Shen D M Convergence properties of an iterative method for solving symmetric non-linear equations
J Optim Theory Appl , 2015 , 164 277 -289
Derivative-free method based on DFP updating formula for solving convex constrained nonlinear monotone equations and application
0
2021
An efficient implementation of Merrill's method for sparse or partially separable systems of nonlinear equations
0
1991
A PRP type method for systems of monotone equations
1
2009
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
A spectral algorithm for large-scale systems of nonlinear monotone equations
0
2017
Benchmarking optimization software with performance profiles
1
2002
... 试验 I 和试验 II 的具体测试结果见 https://www.cnblogs.com/kekoukelele/p/18470451 . 其中, "Case" 表示 7 种不同初始点选择情形, "n" 表示测试问题维度除以 $10^3$ $F$ $\|F^{*}\|$ $\|F_k\|$ $\|F^{*}\|$ 5 ] 提出的性能曲线图以展示每种算法关于三个指标的计算结果 (即计算时间, 函数 $F$
A nonlinear conjugate gradient method with a strong global convergence property
1
1999
... 其中 $0\leq \chi_k \leq \bar{\chi} <1$ . 搜索方向 $d_k^{\rm TCG}$ $p_{k}$ $p_{k}$ $y_{k-1}$ $d_k^{\rm TCG}$ $d_{k}^{\rm THS}$ $p_{k}$ $F_{k}$ $d_k^{\rm TCG}$ 6 ]的一种三项推广. 为使 $d_k^{\rm TCG}$ 14 ] 令 ...
An efficient three-term conjugate gradient method for nonlinear monotone equations with convex constraints
0
2018
A modified Liu-Storey conjugate gradient projection algorithm for nonlinear monotone equations
0
2014
Approximation methods with inertial term for large-scale nonlinear monotone equations
2
2022
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
... $\textbf{试验 II}$ [9 ] , MITTCGP [18 ] 和 ISTCP [10 ] , 其搜索方向和线搜索参数的取值均与原文献保持一致. ...
Projection method with inertial step for nonlinear equations: Application to signal recovery
2
2023
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
... $\textbf{试验 II}$ [9 ] , MITTCGP [18 ] 和 ISTCP [10 ] , 其搜索方向和线搜索参数的取值均与原文献保持一致. ...
A family of inertial derivative-free projection methods for constrained nonlinear pseudo-monotone equations with applications
1
2022
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
A modified self-scaling memoryless Broyden-Fletcher-Goldfarb-Shanno method for unconstrained optimization
1
2015
... 为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为 ...
Spectral residual method without gradient information for solving large-scale nonlinear systems of equations
0
2006
A modified Hestense-Stiefel conjugate gradient method close to the memoryless BFGS quasi-Newton method
4
2018
... 为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为 ...
... 其中 $y_{k-1}=F_{k} - F_{k-1}$ $s_{k-1}=x_{k}-x_{k-1}$ . 为发展 BFGS 方法, Li[14 ] 基于 HS 方法, 提出如下近似 BFGS 拟牛顿方法的三项搜索方向 ...
... 借鉴文献 [14 ] 中 $d_{k}^{\rm THS}$ 20 ] 中 $d^{\rm N}_{k}$ $p_k$ $d_{k}^{\rm THS}$ $y_{k-1}$
... 其中 $0\leq \chi_k \leq \bar{\chi} <1$ . 搜索方向 $d_k^{\rm TCG}$ $p_{k}$ $p_{k}$ $y_{k-1}$ $d_k^{\rm TCG}$ $d_{k}^{\rm THS}$ $p_{k}$ $F_{k}$ $d_k^{\rm TCG}$ 6 ]的一种三项推广. 为使 $d_k^{\rm TCG}$ 14 ] 令 ...
凸约束伪单调方程组的无导数投影算法
1
2021
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
凸约束伪单调方程组的无导数投影算法
1
2021
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
A family of three-term conjugate gradient projection methods with a restart procedure and their relaxed-inertial extensions for the constrained nonlinear pseudo-monotone equations with applications
1
2023
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
Three adaptive hybrid derivative-free projection methods for constrained monotone nonlinear equations and their applications
1
2023
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
A modified inertial three-term conjugate gradient projection method for constrained nonlinear equations with applications in compressed sensing
2
2023
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
... $\textbf{试验 II}$ [9 ] , MITTCGP [18 ] 和 ISTCP [10 ] , 其搜索方向和线搜索参数的取值均与原文献保持一致. ...
Testing unconstrained optimization software
0
1981
A three-term conjugate gradient method with sufficient descent property for unconstrained optimization
2
2011
... 上式中 $1-\frac{y_{k-1}^{\top}s_{k-1}}{\|y_{k-1}\|^2}$ $\min\limits_{\chi \in \mathbb{R}} \|(y_{k-1}-s_{k-1})-\chi y_{k-1}\|^2$ [20 ] 给出三项搜索方向的一般定义, 即 ...
... 借鉴文献 [14 ] 中 $d_{k}^{\rm THS}$ 20 ] 中 $d^{\rm N}_{k}$ $p_k$ $d_{k}^{\rm THS}$ $y_{k-1}$
Updating quasi-Newton matrices with limited storage
1
1980
... 为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为 ...
Some methods of speeding up the convergence of iteration methods
1
1964
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
1
1987
... ${\bf引理3.1}$ 23 ] 对于非负实序列 $\{p_{k}\}$ $\{q_{k}\}$ $p_{k+1}\leq p_k+ q_k$ . 若 $\sum\limits_{k=0}^{+\infty} q_k < +\infty$ $\{p_{k}\}$
A derivative-free scaling memoryless DFP method for solving large scale nonlinear monotone equations
0
2023
1
1978
... 为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为 ...
A globally convergent inexact Newton method for systems of monotone equations//Fukushima M, Qi L. Reformulation: Nonsmooth, Piecewise Smooth, Semismooth and Smoothing Methods
1
1998
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
An efficient inertial subspace minimization CG algorithm with convergence rate analysis for constrained nonlinear monotone equations
1
2024
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
New hybrid conjugate gradient and Broyden-Fletcher-Goldfarb-Shanno conjugate gradient methods
1
2018
... 为发挥拟牛顿法的性能优势, 研究人员利用其潜在理论特点构造近似于拟牛顿方向的算法求解无约束优化问题 $\min\limits_{x\in \mathbb{R}^n} f(x)$ 12 ,14 ,28 ]. 记 $F_k := F(x_k)= \nabla f(x_k)$ . 对于 Nocedal 和 Shanno 给出的无记忆 BFGS 方法 [21 ,25 ] , 其搜索方向为 ...
An inertial spectral CG projection method based on the memoryless BFGS update
1
2023
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
凸约束非光滑方程组基于自适应线搜索的谱梯度投影算法
1
2020
... ${\bf注 2.1}$ $\mathcal{P}_{\mathcal{D}}[x]=\arg\min\{\|y-x\|~|~y\|F(z_{k})\|\in \mathcal{D}\}$ . 对于自适应线搜索 (2.10) 式 [30 ,31 ], 使用投影技术 $\mu_1 \leq \mathcal{P}_{[\mu_1,\mu_2]}[\cdot] \leq \mu_2$
凸约束非光滑方程组基于自适应线搜索的谱梯度投影算法
1
2020
... ${\bf注 2.1}$ $\mathcal{P}_{\mathcal{D}}[x]=\arg\min\{\|y-x\|~|~y\|F(z_{k})\|\in \mathcal{D}\}$ . 对于自适应线搜索 (2.10) 式 [30 ,31 ], 使用投影技术 $\mu_1 \leq \mathcal{P}_{[\mu_1,\mu_2]}[\cdot] \leq \mu_2$
A hybrid three-term conjugate gradient projection method for constrained nonlinear monotone equations with applications
2
2021
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
... ${\bf注 2.1}$ $\mathcal{P}_{\mathcal{D}}[x]=\arg\min\{\|y-x\|~|~y\|F(z_{k})\|\in \mathcal{D}\}$ . 对于自适应线搜索 (2.10) 式 [30 ,31 ], 使用投影技术 $\mu_1 \leq \mathcal{P}_{[\mu_1,\mu_2]}[\cdot] \leq \mu_2$
A family of inertial-relaxed DFPM-based algorithms for solving large-scale monotone nonlinear equations with application to sparse signal restoration
1
2023
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
An adaptive prediction-correction method for solving large-scale nonlinear systems of monotone equations with applications
0
2013
Spectral gradient projection method for solving nonlinear monotone equations
1
2006
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
非线性伪单调方程组的谱 LS 型投影算法
1
2022
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
非线性伪单调方程组的谱 LS 型投影算法
1
2022
... 为使算法求解结构简单和内存需求低, Solodov 和 Svaiter[26 ] 提出仅使用函数值信息的无导数投影法, 每次迭代无需存储矩阵. 在此基础上, Zhang 和 Zhou[34 ] 结合谱梯度法建立求解无约束非线性单调方程组的谱梯度型投影法. Cheng[3 ] 将经典 Polak-Ribi\`{e}re-Polyak 共轭梯度法拓展至求解无约束非线性单调方程组, 在底层映射满足单调性和 Lipschitz 连续性时, 证明其全局收敛性. 刘金魁等 [15 ] 基于 Hestenes-Stiefel (HS) 共轭参数结构, 提出一种无导数投影法用于求解大规模凸约束伪单调方程组. 无需 Lipschitz 连续性, 得到算法的全局收敛性和 R-线性收敛率. 张宁和刘金魁 [35 ] 使用 Liu-Storey (LS) 共轭参数, 借助充分下降条件获得谱参数, 进而得到一种谱 LS 型无导数投影法. 在 Lipschitz 连续假设下, 建立算法的全局收敛性. Yin 等 [31 ] 提出一个混合三项共轭梯度投影法, 其搜索方向类似无记忆 Broyden-Fletcher-Goldfarb-Shanno (BFGS) 结构, 无需任何线搜索具有充分下降性和信赖域性质. 基于 BFGS 结构的更多无导数投影法见文献 [17 ,18 ,29 ] 及其参考文献. ...
A fast inertial self-adaptive projection based algorithm for solving large-scale nonlinear monotone equations
1
2023
... 惯性作为一种有效加速策略, 其源于 Polyak[22 ] 提出的重球法. 传统迭代算法中, 每一步仅考虑当前迭代点信息产生新的迭代点, 而惯性加速策略则使用至少两步迭代点信息. 最近一些学者将惯性策略应用于无导数投影法以解决非线性方程组问题. Ibrahim 等[9 ] 将惯性外推法扩展到 Fletcher-Reeves 型无导数投影法中, 用于求解单调且 Lipschitz 连续的非线性方程组. Jian 等[11 ] 基于惯性加速技术提出一类惯性无导数投影法以求解凸约束非线性伪单调方程组, 无需 Lipschitz 连续性, 建立算法的全局收敛性. Zhang 等 [36 ] 通过将惯性外推步嵌入到搜索方向中, 提出一种改进的混合谱共轭梯度投影法, 其独立于任何线搜索, 即可获得搜索方向的充分下降性. 有关解决非线性方程组的更多惯性方法, 见文献 [10 ,16 ,27 ,32 ] 等. ...
Convergence properties of an iterative method for solving symmetric non-linear equations
0
2015