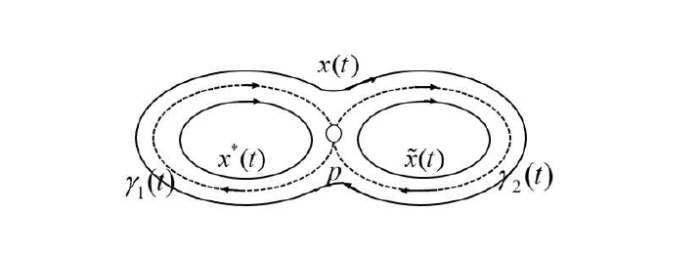
在非线性动力系统理论中, 双同宿环是一类很特殊的不变集, 其附近蕴含了丰富的动力学行为^[1]. 以经典的 Duffing 方程 $ x^{''}=x-2x^{3} $ 为例, 该系统在原点处存在由两条对称的同宿轨 $ \gamma_{1}={\rm sech}(t),\gamma_{2}=-{\rm sech}(t) $ 构成的双同宿环结构. 2001 年, Kapper 和 Zou 等在文献 [2] 中对广义 Liénard 系统进行了数值模拟, 发现当参数 $ k=1.10957905740 $, $ \eta=-0.5547906048 $ 时, 系统会出现双同宿环且构成 8 字型, 见图 1. 在双同宿环附近, 系统的动力学行为复杂多样, 这使得研究其分支行为已成为非线性动力系统理论中的重要问题,相关研究成果可参考文献 [3-5].

Cheng 和 Huang 在研究双同宿环的分支问题时, 给出了一个具有双同宿环的二维系统的例子, 其构成双同宿环的同宿轨道是非退化的, 在自治扰动下可分支出一个稳定的周期解 ^[6]. 2016 年, Xiong 在文献 [7] 中考虑了一类分段近 Hamiltonian 系统, 假设未扰动系统具有双同宿环, 当参数取值不同时, 系统会从双同宿环附近分支出周期解 $ x(t),\tilde{x}(t) $ 与 $ x^{*}(t) $, 分支现象见图 2. 在图 2 中, 把位于同宿轨 $ \gamma_{1} $ 和 $ \gamma_{2} $ 附近的周期解 $ x(t) $ 称为双同宿环附近的大周期解, 把 $ \gamma_{1} $ 附近的周期解 $ x^{*}(t) $ 与 $ \gamma_{2} $ 附近的周期解 $ \tilde{x}(t) $ 称为双同宿环附近的小周期解. Zhang 和 Zhu 在文献 [8] 中应用指数二分性、推广的 Floquet 理论和 Poincaré 映射研究了四维系统中具有轨道翻转的双同宿环分支, 证明了双同宿环附近同宿轨和周期轨的存在性. 随后, 张伟鹏在文献 [9,10] 中应用 Poincaré 映射, 分别考虑了非共振与共振条件下扰动系统在原双同宿环附近分支出大 1-周期轨和大 1-同宿轨的问题. 吴家伟在文献 [11] 中, 利用活动坐标架, 研究了三维系统中具有轨道翻转 $ R $ 对称双同宿环的分支, 得到了 $ R $ 对称双同宿环与 $ R $ 对称周期轨的共存性条件. 张利群在文献 [12] 中, 使用局部坐标系研究了高维系统中退化双同宿环在非扭曲和扭曲情况下经扰动分支出双同宿环, 同宿轨以及周期轨的唯一性 Lu 在文献 [13] 中, 利用 Poincaré 映射考虑了高维系统中余维 2 的扭曲双同宿环附近同宿轨与周期轨的存在性与唯一性. Jin 在文献 [14] 中, 通过局部坐标系来构建 Poincaré 映射, 考虑了具有共振条件的双扭同宿环的分支出大周期轨和大同宿环的问题并给出了相应的分支图. 目前, 仍有许多学者在研究双同宿环附近的动力学行为, 见文献 [15-18].

基于以上背景, 本文将应用 Lin 方法 ^[19]来研究高维系统中具有高余维的双同宿环附近分支出大周期解的问题.

考虑一个自治微分方程

其中 $ x \in\mathbb{R} ^{n} $. 对于方程 (1.1), 假设其满足以下条件

$({\bf H1})$$ f \in \mathbb{C} ^{3} $;

$({\bf H2})$ 方程 (1.1) 有一个鞍点 p, 即 $ f(p)=0 $ 且矩阵 $ Df(p) $ 的特征值只有正实部和负实部;

$({\bf H3}) $ 方程 (1.1) 有两个同宿于平衡点 $ p $ 的同宿解 $ \gamma_1(t) $ 和 $ \gamma_2(t) $. 即 $ \gamma'_i(t)=f(\gamma_i(t)) $, 且

其中 $ i=1,2 $;

$({\bf H4})$$ \dim(W^{s}(p))=w $, $ W^{s}(p) $ 是鞍点 p 的稳定流形.

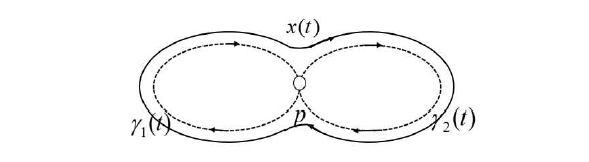
由 (H3) 可知, 方程 (1.1) 具有同宿于鞍点 $ p $ 的双同宿环 $ \Gamma $, 其中, $ \Gamma=\{\gamma_{1}(t),t\in \mathbb{R}\}\cup\{p\}\cup\{\gamma_{2}(t),t\in \mathbb{R}\} $, 假设其构成 8-型, 见图 3.

方程 (1.1) 沿着轨道 $ \gamma_i $ 的变分方程为

因此, $ \gamma'_i(t) $ 是方程 (1.2) 的一个有界解. 假设方程 (1.2) 有 $ d_i $ 个线性无关的有界解, 由 $ \gamma^{''}_i(t)=Df(\gamma_i(t))\gamma'_i(t) $ 可知, $ d_i\geqslant1 $, $ i=1,2 $.

${\bf定义1.1}$^[20] 若方程 (1.2) 只有一个线性无关的有界解, 即 $ d_i=1 $, 则称轨道 $ \gamma_{i}(t) $ 是非退化的; 若该方程存在两个以上的线性无关的有界解, 即 $ d_i>1 $, 则称轨道 $ \gamma_{i}(t) $ 是退化的.

$({\bf H5})$

其中, $ T_{\gamma_i(0)}W^{s/u}(p) $ 表示相应不变流形在 $ \gamma_i(0) $ 处的切空间, 且 $ d_{i}>1,i=1,2 $.

由于同宿轨 $ \gamma_1 $ 和 $ \gamma_2 $ 位于平衡点 $ p $ 的稳定流形和不稳定流形的交, 而变分方程有界解的个数等于相应稳定流形与不稳定流形的切空间相交子空间的维数. 因此, 同宿轨 $ \gamma_{1} $ 和 $ \gamma_{2} $ 是退化的.

同宿与异宿轨道分支问题之所以重要, 究其原因是由于其附近的混沌行为. 而混沌现象的产生通常与横截同宿或异宿点的出现密切相关, 自治系统是不会出现横截同宿或异宿点的, 因此需要通过增加扰动项来促使系统的稳定流形和不稳定流形发生横截相交, 从而为分支现象的产生创造条件. 在未受扰动的情况下, 双同宿环通常不会自发产生分支现象, 但通过引入适当的扰动, 可以研究双同宿环附近的复杂动力学行为, 尤其是混沌现象的产生机制. 因此, 我们通常会在未扰动系统的方程中加入周期性的扰动项, 以便更好地探索双同宿环附近的动力学行为.

因此, 我们考虑在方程 (1.1) 中加入周期扰动项, 建立如下的扰动方程

其中 $ x\in\mathbb{R}^{n} $, $ \mu:=(\mu_1,\mu_2)\in\mathbb{R}^{2} $.

对于方程 (1.3), 假设其满足以下条件

$({\bf H6})$$ g_{j} \in\mathbb{C} ^{3} $, $ g_j $ ( $ x $,0, $ t $ ) $ =0 $, $ g_j(x,\mu,t+2)=g_j(x,\mu,t) $.

由于轨道 $ \gamma_i(t) $ 位于 $ W^{s}(p)\cap W^{u}(p) $ 上, 若 $ \gamma_i(t) $ 在平衡点 $ p $ 处的稳定流形与不稳定流形是非横截相交的, 那么未扰动的双同宿环在周期扰动下将会发生分岔现象. 通过计算, 可得 $ \gamma_i(t) $ 的余维数为

由于 $ d_i $ 是变分方程 (1.2) 的线性无关的有界解的个数, 由 (H5) 可知, codim$(\gamma_i(t))>1 $. 所以, 未扰动的双同宿环是结构不稳定的, 从而在周期扰动下会发生分支现象. 因此, 本文将应用 Lin 方法来研究扰动方程 (1.3) 从未扰动方程 (1.1) 的双同宿环附近分支出大周期解的问题.

本节, 我们首先给出了变分方程 (1.2) 的双边指数二分性; 其次, 为了叙述结论, 简要介绍了一些记号; 最后, 给出了本文的主要结论.

由点 $ p $ 是方程 (1.1) 的双曲平衡点以及 (H3) 可知, 对于 $ i=1,2 $, 有

由指数二分性的粗糙性定理[21], 可知变分方程 (1.2) 在 $ \mathbb{R^{+}} $ 和 $ \mathbb{R^{-}} $ 上具有指数二分性. 假设 $ U_i $ 是变分方程 (1.2) 的一个标准基解矩阵, 关于变分方程 (1.2) 有如下结论.

${\bf引理2.1}$^[22] 若 (H4) 和 (H5) 成立, 那么对于方程 (1.2), 存在常数 $ K>0,N>0 $, 可逆矩阵 $ A $ 以及投影 $ P_{ss}^{i},P_{us}^{i},P_{su}^{i}, P_{uu}^{i} $, 使得以下结论成立

其中投影 $ P_{ss}^{i},P_{us}^{i},P_{su}^{i}, P_{uu}^{i} $ 满足 $ P_{ss}^{i}+P_{us}^{i}+P_{su}^{i}+P_{uu}^{i}=I $, $ I $ 是一个 $ n\times n $ 的单位矩阵, $ I_{s} $ 和 $ I_{u} $ 分别是 $ w\times w $, $ (n-w)\times (n-w) $ 的单位矩阵, 且 Rank$(P_{ss}^{i})= {\rm Rank}(P_{uu}^{i})=d_{i} $, $ i=1,2 $.

设 $ u_{k}^{i} $ 表示 $ U_i $ 的第 $ k $ 列, 对于投影 $ P_{uu}^{i} $ 和 $ P_{ss}^{i} $, 有

其中 $ I_{d_i} $ 和 $ 0_{d_i} $ 分别为 $ d_i\times d_i $ 的单位矩阵和零矩阵, 且 $ i= 1,2 $.

因此, 对于 $ i=1,2 $, 有

令 $ U_{i}^{-1} $ 是 $ U_i $ 的逆矩阵, 则

对 (2.2) 式两边同时关于 t 求导, 可得

从而

因此, 方程 (1.2) 的对偶方程的标准基解矩阵是 $ (U_{i}^{-1})^{T} $. 对方程 (1.2) 的两边同时进行共轭转置, 可知方程 (1.2) 的对偶方程在 $ \mathbb{R}^{+} $ 和 $ \mathbb{R}^{-} $ 上也具有指数二分性.

令 $ (u_{l}^{i})^{\bot} $ 表示 $ U_i^{-1} $ 的第 $ l $ 行, 对于 $ i=1,2 $, 有

对于 $ i,j=1,2 $, $ l=1,2,\cdots,d_{i} $, $ m,n=1,2,\cdots,d_{i}-1 $, 我们定义 Melnikov 积分为

定义函数 $ \tilde{M}_{i}(\beta,\mu,\alpha_i):\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}\rightarrow\mathbb{R}^{d_i} $:

其中

定义函数 $ M(\beta,\mu,\alpha):\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2}\rightarrow\mathbb{R}^{d_1+d_2} $:

其中 $ \alpha=(\alpha_{1},\alpha_{2}). $

最后, 我们给出本文的主要结论.

${\bf定理2.1}$ 假设 (H1)-(H6) 成立, 若存在 $ (\beta_0,\mu_0,\alpha_0)\in\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2} $ 使得

且 $ D_{(\beta,\mu)}M(\beta_0,\mu_0,\alpha_0) $ 是一个 $ (d_1+d_2)\times (d_1+d_2) $ 的可逆矩阵, 则存在常数 $ T_0>0 $, $ r_1>0 $, $ \mathbb{R}^{2} $ 中以 $ \alpha_{0} $ 为圆心, $ r_{1} $ 为半径的开球 $ B_2(\alpha_0,r_1) $, $ \mathbb{R}^{d_1+d_2} $ 中以 $ 0 $ 为圆心, $ r_{1} $ 为半径的闭球 $ \overline{B_1(r_1)} $, 以及可微函数 $ \phi=(\tilde{\phi}_{11},\tilde{\phi}_{12}):B_2(\alpha_0,r_1)\times(T_0,+\infty)\to \overline{B_1(r_1)} $, 使得扰动方程 (1.3) 在未扰动的双同宿环附近存在一个大周期解.

本节, 是关于定理 2.1 的详细证明. 我们应用 Lin 方法在原双同宿环附近建立分段连续解, 构造相应的边界条件使分段连续解可以连接起来形成周期解, 并由此推导出分支函数. 在一定条件下, 证明该分支函数存在零点, 从而可以证明扰动方程 (1.3) 在未扰动的双同宿环 $ \Gamma $ 附近存在大周期解.

构造辅助函数 $ v_{i}:\mathbb{R}^{d_{1}+d_{2}-2}\times (0,+\infty)\rightarrow\mathbb{R}^{n}: $

其中 $ \beta=(\beta_{1}^{1},\beta_{2}^{1},\cdots,\beta_{d_1-1}^{1},\beta_{1}^{2},\cdots,\beta_{d_2-1}^{2}) $, $ i=1,2 $, 且当 $ \beta $ 有界时, $ v_i(\beta,t) $ 以指数形式双边趋于 $ 0 $, 即

任取 $ T\in\mathbb{R} $, $ \alpha_i\in\mathbb{R} $, $ i=1,2 $, 设 $ x_i(t) $ 是扰动方程 (1.3) 的一个解, 作以下变换

从而, $ z_i(t) $ 满足方程

其中

假设 $ z_{i}(t),i=1,2 $ 是方程 (3.3) 在 $ t\in[-T,T] $ 上的两个解, 若 $ z_{1}(T)=z_{2}(-T),z_{1}(-T)=z_{2}(T) $, 由 $ v_{i}(\beta,t) $ 的定义以及变换 (3.1) 式和 (3.2) 式可知, $ x_{1}(T+\alpha_{1})=x_{2}(-T+\alpha_{2}),x_{1}(-T+\alpha_{1})=x_{2}(T+\alpha_{2}) $. 因此, 寻找方程 (1.3) 的周期解 $ x(t) $ 等价于寻找方程 (3.3) 满足 $ z_{1}(T)=z_{2}(-T),z_{1}(-T)=z_{2}(T) $ 的解 $ z(t) $.

设 $ D_{i} $ 表示一个多元函数关于第 $ i $ 个变量的一阶导, $ D_{ij} $ 表示关于第 $ i $ 个和第 $ j $ 个变量的二阶导.通过计算, 可知函数 $ h_i(z_i,\beta,\mu,\alpha_i,T) $ 满足如下性质.

${\bf引理3.1}$ 函数 $ h_i(z_i,\beta,\mu,\alpha_i,T) $ 满足以下性质

(1)$\displaystyle\lim_{T\to+\infty}h_i(0,0,0,\alpha_i,T)=0, $$\displaystyle\lim_{T\to+\infty}D_1h_i(0,0,0,\alpha_i,T)=0; $

(2)$\displaystyle\lim_{T\to+\infty}D_{11}h_i(0,0,0,\alpha_i,T)=D_{11}f(\gamma_i); $

(3)$\displaystyle\lim_{T\to+\infty}\cfrac{\partial h_i}{\partial\mu_j}(0,0,0,\alpha_i,T)=g_j(\gamma_i,0,t+\alpha_i); $

(4)$\displaystyle\lim_{T\to+\infty}\cfrac{\partial h_i}{\partial\beta_m^{i}}(0,0,0,\alpha_i,T)=0, $$\displaystyle\lim_{T\to+\infty}\cfrac{\partial^{2} h_i}{\partial\beta_m^{i}\beta_n^{i}}(0,0,0,\alpha_i,T)=D_{11}f(\gamma_i)u_{d_{i}+m}^{i}u_{d_{i}+n}^{i}. $

记 $ C^{1}([c,d],\mathbb{R}^{n}) $ 是由从 $ [c,d] $ 到 $ \mathbb{R}^{n} $ 的所有具有一阶连续偏导数的函数全体构成. 取范数 $ \|y\|=\max_{t\in[c,d]}|y(t)| $, 则 $ C^{1}([c,d],\mathbb{R}^{n}) $ 是一个 Banach 空间.

对任意的 $ \varphi_j,\omega_j\in\mathbb{R}^{n},j=1,2,3,4 $, 应用常数变易公式和不变流形理论构造如下函数: $ y_{1},y_{3}\in C^{1}([-T,0],\mathbb{R}^{n}) $, $ y_{2},y_{4}\in C^{1}([T],\mathbb{R}^{n}) $, 其具体表达式如下

${\bf引理3.2}$ 对于 $ j=1,2,3,4 $, 给定 $ \varphi_{j},\omega_{j} $, 则 $ y_{1},y_{3} $ 是方程 (3.3) 在 $ t\in[-T,0] $ 上的解, $ y_{2},y_{4} $ 是方程 (3.3) 在 $ t\in[T] $ 上的解.

${\bf证}$ 对于给定的 $ \varphi_{j},\omega_{j} $, 由 $ y_{i}(t) $ 的定义可知, 若 $ y_{i}(t) $ 是积分方程 (3.6) 的连续解, 对 $ y_{i}(t) $ 表达式两边同时关于时间 $ t $ 求导, 可知 $ y_{i}(t) $ 也是微分方程 (3.3) 的解. 因此, 只需证明 (3.6) 式中相应积分方程具有连续解. 以 $ y_{1}(t) $ 的证明为例, $ y_{2}(t) $, $ y_{3}(t) $, $ y_{4}(t) $ 的证明与其类似.

由 (3.6) 式中 $ y_{1}(t) $ 的表达式, 定义算子 $ L_{1} $, $ L_{1} $ 作用于 $ y_{1}(t) $ 就等于 $ y_{1}(t) $ 表达式的右边. 即对于任意的 $ y_{1}(t)\in C^{1}([-T,0],\mathbb{R}^{n}) $, 有

接下来, 我们将应用压缩映像原理来证明算子 $ L_{1} $ 在 $ C^1{([-T,0],\mathbb{R}^n)} $ 上存在不动点.

在 $ C^1{([-T,0],\mathbb{R}^n)} $ 中取一个以原点为圆心, 半径为 $ \delta(\delta>0) $ 的闭球, 记为 $ \overline{B(0,\delta)}=\{y_1 \in C^1{([-T,0],\mathbb{R}^n)}:\|y_1\| \leq \delta \} $, 定义如下的 Banach 空间

取常数 $ K $, $ N $ 与引理 2.1 中一致, 取常数 $ \delta_{1}>0,\delta_{2}>0 $, 令$ \overline{B_{1}(0,\delta_{1})}=\{\beta\in\mathbb{R}^{d_{1}+d_{2}-2}:\|\beta\|\leq\delta_{1}\}\subseteq\mathbb{R}^{d_{1}+d_{2}-2} $, $ \overline{B_{2}(0,\delta_{2})}=\{\mu\in\mathbb{R}^{2}:\|\mu\|\leq\delta_{2}\}\subseteq\mathbb{R}^{2} $. 由引理 3.1 以及函数 $ f $ 和 $ g $ 的光滑性可知, 当 $ \delta_{1},\delta_{2} $ 充分小, $ T_{0} $ 充分大时, 对于任意的 $ (\beta,\mu,\alpha_{1},T)\in\overline{B_{1}(0,\delta_{1})}\times\overline{B_{2}(0,\delta_{2})}\times R\times[T_{0},+\infty) $, $ (y_1,\tilde{y}_1)\in\overline{B(0,\delta)} $, $ t\in[-T,0] $, 有

特别地, 取 $ \varphi_1,\omega_1 $ 满足 $ \|\varphi_1\|\leq\cfrac{\delta}{4K},\|\omega_1\|\leq\cfrac{\delta}{4K} $, 则对于任意的 $ t\in[-T,0],y_{1}\in\overline{B(0,\delta)} $, 有

且

因此, $ L_1:\mathbb{Y}^{2}\rightarrow\mathbb{Y}^{2} $.

对于任意的 $ (y_1,\tilde{y}_1)\in\overline{B(0,\delta)},t\in[-T,0] $, 有

因此, $ L_{1} $ 是 Banach 空间 $ \mathbb{Y}^{2} $ 上的一个压缩映射. 故 $ L_{1} $ 在 $ \mathbb{Y}^{2} $ 上存在一个不动点, 记为 $ y_{1}(\beta,\mu,\alpha_{1},T) $. 从而, $ y_{1}(\beta,\mu,\alpha_{1},T) $ 是方程 (3.3) 在 $ [-T,0] $ 上的一个解. 同理 $ y_{2}(\beta,\mu,\alpha_{1},T) $, $ y_{3}(\beta,\mu,\alpha_{2},T) $, $ y_{4}(\beta,\mu,\alpha_{2},T) $ 也是方程 (3.3) 的解. 因此, 方程 (3.3) 在 $ [-T,T] $ 上有四个分段连续的解, 其中 $ y_{1}(\beta,\mu,\alpha_{1},T),y_{3}(\beta,\mu,\alpha_{2},T)\in[-T,0] $, $ y_{2}(\beta,\mu,\alpha_{1},T),y_{4}(\beta,\mu,\alpha_{2},T)\in[T] $. 综上, 说明了 $ y_{1},y_{2} $, $ y_{3},y_{4} $ 是方程 (3.3) 在未扰动双同宿环附近的四个分段连续解.

如果我们可以找到 $ \varphi_{j},\omega_{j},j=1,2,3,4 $, 使得 $ y_{1}(0)=y_{2}(0),y_{3}(0)=y_{4}(0),y_{1}(-T)=y_{4}(T),y_{2}(T)=y_{3}(-T) $, 则方程 (3.3) 存在一个由 $ z_{1}(t) $ 与 $ z_{2}(t) $ 构成的周期解 $ z(t) $, 即

从而, 扰动方程 (1.3) 在未扰动的双同宿环附近存在一个由 $ x_{1}(t) $ 与 $ x_{2}(t) $ 构成的大周期解 $ x(t) $, 见图 4.

${\bf引理3.3}$ 当 $ (\beta,\mu)=(0,0) $ 时, 函数 $ z_{i} $ 满足以下性质

(1)$\displaystyle\lim_{T\to+\infty}z_i(0,0,\alpha_i,T)=0; $

(2)$\displaystyle\lim_{T\to+\infty}\cfrac{\partial z_i}{\partial\mu_j}(0,0,0,\alpha_i,T)=0, $$\displaystyle\lim_{T\to+\infty}\cfrac{\partial z^{2}_i}{\partial\mu_l \partial\mu_j}(0,0,0,\alpha_i,T)=0; $

(3)$\displaystyle\lim_{T\to+\infty}\cfrac{\partial z_i}{\partial\beta_m^{i}}(0,0,0,\alpha_i,T)=0, $$\displaystyle\lim_{T\to+\infty}\cfrac{\partial z^{2}_i}{\partial\beta_m^{i}\partial\mu_j}(0,0,0,\alpha_i,T)=0 $,

因此, 为了构造出周期扰动下未扰动双同宿环附近的周期解, 我们需要寻找使 $ y_1(0)=y_2(0),$$y_3(0)=y_4(0) $, $ y_1(-T)=y_4(T) $ 以及 $ y_2(T)=y_3(-T) $ 这四个等式成立的条件.

由 $ y_1(0)=y_2(0) $ 可得

由 $ P_{ss}^{1}+P_{su}^{1}+P_{us}^{1}+P_{uu}^{1}=I $ 可知, 上述表达式等价于

同理, 由 $ y_3(0)=y_4(0) $ 可得

则上述表达式等价于

由 $ y_1(-T)=y_4(T) $ 可得

同理, 由 $ y_2(T)=y_3(-T) $ 可得

在 (3.13) 式中, 当 $ T $ 充分大时, 有

令 $ A^{-1}\omega_1= \begin{pmatrix} \eta_1\\ 0 \end{pmatrix}, A^{-1}\omega_4= \begin{pmatrix} 0\\ -\eta_2 \end{pmatrix}, \eta= \begin{pmatrix} \eta_1\\ \eta_2 \end{pmatrix}. $

因此, 由 (3.15) 式, 可得

从而在 (3.13) 式中, 存在 $ T_0>0 $, 当 $ T>T_0 $ 时, 可解出 $ \omega_1,\omega_4 $, 将其记为 $ \omega_1^{*}=\omega_1^{*}(\beta,\mu,\alpha_1,T) $, $ \omega_4^{*}=\omega_4^{*}(\beta,\mu,\alpha_2,T) $. 同理, 在 (3.14) 式中可解出 $ \omega_2,\omega_3 $, 将其记为 $ \omega_2^{*}=\omega_2^{*}(\beta,\mu,\alpha_1,T),\omega_3^{*}=\omega_3^{*}(\beta,\mu,\alpha_2,T) $. 对于 $ j=1,2,3,4 $, $ \omega_j^{*} $ 满足 $ \displaystyle\lim_{T\rightarrow+\infty}\omega_j^{*}(0,0,\alpha_i,T)=0 $. 将 $ \omega_1^{*} $ 代入 (3.8) 式可解出 $ \varphi_2 $. 同理, 将 $ \omega_2^{*},\omega_3^{*},\varphi_4 $ 分别代入 (3.7) 式, (3.11) 式以及 (3.10) 式可解出 $ \varphi_1,\varphi_4,\varphi_3 $.

因此, 由以上分析可知, 若 $ \omega_j^{*} $ 也满足 (3.9) 式与 (3.12) 式, 则扰动方程 (1.3) 在未扰动的双同宿环附近存在一个大周期解 $ x(t) $. 从而, 对于方程 (1.3), 有以下结论成立.

${\bf引理3.4}$ 设 $ U_{1},U_{2},P_{uu}^{1},P_{uu}^{2} $ 与引理 2.1 中一致, 存在 $ T_{0}>0 $, 当 $ T>T_{0} $ 时, 若

则扰动方程 (1.3) 在未扰动的双同宿环附近存在一个大周期解.

定义 $ G^{*}_{i}(\beta,\mu,\alpha_i,T):\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}\times [T_0,+\infty)\rightarrow\mathbb{R}^{n} $:

由于 $ \displaystyle\lim_{T\rightarrow+\infty}\omega_j^{*}(0,0,\alpha_i,T)=0 $, $ \displaystyle\lim_{T\rightarrow+\infty}h_i(0,0,0,\alpha_i,T)=0 $. 通过计算, 可得

当 $ T $ 充分大时, 设

由于

对于 $ l=1,2,\cdots,d_i $, $ i=1,2 $, 记

故

由引理 3.1 和 3.3 可知, 当 $ (\beta,\mu)=(0,0) $ 时, 对函数 $ h_i $ 进行泰勒展开, 展开式的低阶项如下

当 $ i,j=1,2 $, $ l=1,2,\cdots,d_{i} $, $ m,n=1,2,\cdots,d_{i}-1 $ 时, 令

从而

因此, 对于 $ i=1,2 $, 有

定义 $ \tilde{M}_{i}(\beta,\mu,\alpha_i):\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}\rightarrow\mathbb{R}^{d_i} $, 则

因此

令 $ \tilde{G}_i(\beta,\mu,\alpha_i,T)=\tilde{M}_i(\beta,\mu,\alpha_i)+H.O.T, $

故 $ {G}^{*}_{i}(\beta,\mu,\alpha_i,T)=(\tilde{G}_{i}(\beta,\mu,\alpha_i,T),0,\cdots,0). $

因此, $ G^{*}_{i}(\beta,\mu,\alpha_i,T)=0 $ 等价于 $ \tilde{G}_{i}(\beta,\mu,\alpha_i,T)=0 $. 定义函数 $ G(\beta,\mu,\alpha,T): \mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2}\times\mathbb{R}\rightarrow\mathbb{R}^{d_1+d_2} $, 则

其中 $ \alpha=(\alpha_{1},\alpha_{2}). $

若存在 $ (\beta,\mu,\alpha,T)\in\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2}\times[T_0,+\infty)\rightarrow\mathbb{R}^{d_1+d_2} $, 使得 $ G(\beta,\mu,\alpha,T)=0 $, 则方程 (3.16) 和方程 (3.17) 成立. 进而方程 (1.3) 在未扰动的双同宿环附近存在一个周期解.

定义函数 $ M(\beta,\mu,\alpha):\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2}\rightarrow\mathbb{R}^{d_1+d_2} $, 则

其中 $ \alpha=(\alpha_{1},\alpha_{2}). $

因此

${\bf引理3.5}$ 若存在 $ (\beta_0,\mu_0,\alpha_0)\in\mathbb{R}^{d_1+d_2-2}\times\mathbb{R}^{2}\times\mathbb{R}^{2} $, 使得

且 $ D_{(\beta,\mu)}M(\beta_0,\mu_0,\alpha_0) $ 是一个 $ (d_1+d_2)\times (d_1+d_2) $ 的可逆矩阵, 则存在常数 $ T_0>0 $, $ r_1>0 $ 以及可微函数 $ \phi=(\tilde{\phi}_{11},\tilde{\phi}_{12}) :B_2(\alpha_0,r_1)\times(T_0,+\infty)\to \overline{B_1(r_1)} $, 使得对于任意的 $ (\alpha,T)\in B_2(\alpha_0,r_1)\times(T_0,+\infty) $ 时, 有 $ G(\beta_0+\tilde{\phi}_{11}(\alpha,T),\mu_0+\tilde{\phi}_{12}(\alpha,T),\alpha,T)=0 $. 其中 $ B_2(\alpha_0,r_1)\subset\mathbb{R}^{2},\overline{B_1(r_1)}\subset\mathbb{R}^{d_1+d_2} $, 且 $ \displaystyle\lim_{T\to +\infty}\phi(\alpha_0,T)=\displaystyle\lim_{T\to +\infty}(\tilde{\phi}_{11}(\alpha_0,T),\tilde{\phi}_{12}(\alpha_0,T))=0 $.

${\bf证}$ 设 $ \zeta_0=(\beta_0,\mu_0) $, $ \zeta=(\beta,\mu)-\zeta_0 $ 以及 $ {\cal F}= D_{(\beta,\mu)}M(\beta_0,\mu_0,\alpha_0)^{-1} $.

定义

由 $ {\cal G} $ 的定义可知, $ {\cal G}(\cdot,\alpha_0,T) $ 的不动点 $ \phi $ 等价于 $ G(\zeta_0+\phi,\alpha,T)=0 $. 经过计算, 可得

由 (3.21) 式和 (3.22) 式, 可得

设 $ B_1(r) $ 是 $ \mathbb{R}^{d_1+d_2} $ 中以原点为圆心, 半径 $ r>0 $ 的开球; $ B_2(\alpha_0,r) $ 是 $ \mathbb{R}^2 $ 中以 $ \alpha_0 $ 为圆心, 半径 $ r>0 $ 的开球. 由 $ (3.23) $ 式可知, 存在 $ r_1>0 $, 使得对于任意的$ (\zeta,\alpha)\in B_1(r_1)\times B_2(\alpha_0,r_1) $, 有

特别地, $ {\cal M}(0,\alpha_0)=0 $. 由 (3.24) 式可知, 存在一个常数 $ T_0>0 $, 使得对于任意的 $ (\zeta,\alpha,T)\in$$ B_1(r_1)\times B_2(\alpha_0,r_1)\times (T_{0},+\infty) $, 有

因此, 由 (3.25) 式和 (3.26) 式可得, 对于任意的 $ (\zeta,\alpha,T)\in B_1(r_1)\times B_2(\alpha_0,r_1)\times (T_{0},+\infty) $, 有

对于任意的 $ (\zeta,\alpha,T)\in B_1(r_1)\times B_2(\alpha_0,r_1)\times(T_0,+\infty) $, 定义映射 $ \phi_1:[0,1]\rightarrow \mathbb{R}^{d_1+d_2} $, 则 $ \phi_1(s)={\cal G}(s\zeta,\alpha,T) $, 有

因此, $ {\cal G}(\cdot,\alpha,T):\overline{B_1(r_1)}\rightarrow\overline{B_1(r_1)} $.

对于任意的 $ {\zeta_{1}},{\zeta_{2}}\in \overline{B_1(r_1)} $, $ (\alpha,T)\in B_2(\alpha_0,r_1)\times(T_0,+\infty) $, 定义映射 $ \phi_2:[0,1]\rightarrow\mathbb{R}^{d_1+d_2} $, 则 $ \phi_2(s)={\cal G}(s{\zeta_{1}}+(1-s){\zeta_{2}},\alpha,T) $. 显然, $ \phi_2 $ 是 $ C^2 $ 函数, 从而存在 $ s_0\in(0,1) $, 使得

因此, 对于任意的 $ (\alpha,T)\in B_2(\alpha_0,r_1)\times(T_0,+\infty) $, $ {\cal G}(\cdot,\alpha,T) $ 是 $ \overline{B_1(r_1)} $ 上的一个压缩映射.

由压缩映像原理可知, 存在一个 $ C^2 $ 函数 $ \phi(\alpha,T):B_2(\alpha_0,r_1)\times(T_0,+\infty)\to \overline{B_1(r_1)} $, 使得

且

通过 $ {\cal G} $ 的定义可知, 上述表达式等价于

其中, $ \phi=(\tilde{\phi}_{11},\tilde{\phi}_{12})\in \mathbb{R}^{d_1+d_2-1}\times\mathbb{R}^{2}. $

因此, 对于任意的 $ (\alpha,T)\in B_2(\alpha_0,r_1)\times(T_0,+\infty) $, 函数 $ G $ 的零点为 $ (\beta_0+\tilde{\phi}_{11}(\alpha,T),\mu_0+\tilde{\phi}_{12},\alpha_0,T) $.

由以上分析可知, 扰动方程 (1.3) 在未扰动的双同宿环附近存在一个大周期解 $x(t)$, 即

其中, $\tilde{\phi}_{11}=(\tilde{\phi}_{11}^1,\tilde{\phi}_{11}^2)\in \mathbb{R}^{d_1-1}\times\mathbb{R}^{d_2-1},\alpha_{0}=(\alpha_{01},\alpha_{02}).$