奇异摄动 Volterra 积分微分方程参数一致的数值方法

奇异摄动 Volterra 积分微分方程参数一致的数值方法

刘利斌^,^*, 廖仪戈^,, 隆广庆^,

南宁师范大学应用数学中心南宁 530100

A Parameter-Uniform Numerical Method for a Singularly Perturbed Volterra Integro-Differential Equation

Liu Libin^,^*, Liao Yige^,, Long Guangqing^,

Center for Applied Mathematics of Guangxi, Nanning Normal University, Nanning 530100

通讯作者: * 刘利斌，E-mail:liulibin969@163.com

收稿日期: 2022-10-10 修回日期: 2024-10-6

基金资助:

国家自然科学基金(12361087)
国家自然科学基金(12261062)

Received: 2022-10-10 Revised: 2024-10-6

Fund supported:

NSFC(12361087)
NSFC(12261062)

作者简介 About authors

廖仪戈，E-mail:lyg199600@163.com;

隆广庆，E-mail:longgq@amss.ac.cn

摘要

针对一类奇异摄动 Volterra 积分微分方程, 在 Vulanović-Bakhvalov 网格上构造了一个一阶参数一致收敛的有限差分格式. 进一步, 基于 Richardson 外推技术, 将数值格式的收敛阶从 $O(N^{-1})$ 提高到 $O(N^{-2})$, 其中 $N$ 是网格剖分数. 最后, 数值实验证明了数值方法的有效性.

关键词： 奇异摄动; Volterra 积分微分方程; Richardson 外推; Vulanović-Bakhvalov 网格

Abstract

A singularly perturbed Volterra integro-differential equation is considered. The problem is discretized by using a simple first-order finite difference scheme on a Vulanović-Bakhvalov mesh, the accuracy of which is first-order uniformly convergent with respect to the perturbation parameter $\varepsilon$. Furthermore, based on the Richardson extrapolation technique, the $\varepsilon$-uniform accuracy of the presented approximation scheme can be improved from $O(N^{-1})$ to $O(N^{-2})$, where $N$ is the number of mesh intervals. Finally, the theoretical finds are illustrated by two numerical experiments.

Keywords： singularly perturbed; Volterra integro-differential equation; Richardson extrapolation; Vulanović-Bakhvalov mesh

PDF (618KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘利斌, 廖仪戈, 隆广庆. 奇异摄动 Volterra 积分微分方程参数一致的数值方法[J]. 数学物理学报, 2025, 45(2): 576-583

Liu Libin, Liao Yige, Long Guangqing. A Parameter-Uniform Numerical Method for a Singularly Perturbed Volterra Integro-Differential Equation[J]. Acta Mathematica Scientia, 2025, 45(2): 576-583

1 引言

考虑如下奇异摄动 Volterra 积分微分方程

(1.1)$\mathcal{L} u:=\varepsilon u'(x)+b(x)u(x)+\int_{0}^{x} K(x,t)u(t){\rm d}t=f(x),\ x\in \Omega:=(0,1],$

(1.2)$u(0)=\eta,$

其中 $b(x)\geq\beta>0$, $0<\varepsilon\ll 1$. $b(x)$, $f(x)$ 和 $K(x,t)$ 为足够光滑的函数. $\eta$ 为给定常数. 当 $\varepsilon$ 趋于 $0$ 时, 该问题的解 $u(x)$ 在 $x = 0$ 处具有指数边界层, 即, 精确解及其导数满足如下估计^[1]

(1.3)$\begin{matrix} &&|u^{(k)}(x)|\leq C\left(1+\varepsilon^{-k}{\rm e}^{-\beta x/\varepsilon}\right), x\in \Omega, k=0,1,2,3.\label{1.3} \end{matrix}$

众所周知, 这类问题广泛存在于物理和生物系统中, 如流行病动力学、扩散耗散过程、同步控制等领域 (见文献 [2],[3],[4]). 因此, 研究奇异摄动 Volterra 积分微分方程的数值方法是计算数学领域的热点问题. 在现有的方法中, 层适应网格方法^[1],[5],[6]和基于网格均匀分布原理的自适应网格方法^{[7], Sumit}是两类非常重要的方法。更具体地说, 文献 [5] 的作者在分段均匀 Shishkin 网格上提出了一种拟合算子差分方法, 并证明了该离散化方案在离散最大范数上几乎是二阶参数一致收敛的. Şevgin^[6] 在 Bakhvalov 型网格上构造了参数一致一阶收敛有限差分格式来求解非线性奇摄动 Volterra 积分微分方程. Iragi 和 Munyakazi^[1] 在 Bakhvalov 型网格上设计了一种新的有限差分方法, 该方法将微分部分的向后欧拉格式与积分部分的复合求积规则相结合, 作者证明了该方法在最大范数上是一阶一致收敛的. 最近, Huang 等^[7]研究了一类弱奇异核奇异摄动 Volterra 积分-微分方程的后验误差估计, 并设计了自适应网格生成算法. 作者在文献 [8] 中考虑了非线性奇摄动 Volterra 积分微分方程, 并推导了一种基于后验误差界的自适应网格算法.

最近 Nhan 和 Vulanović 在文献 [9] 中, 研究了在 Vulanović-Bakhvalov 型网格 (VB 网格) 上的一种参数一致的数值方法, 用于求解离散于的奇摄动对流扩散方程. 这里, 我们考虑上述奇异摄动 Volterra 积分微分方程 (1.1)-(1.2), 并在 VB 网格上构造有限差分格式. 基于截断误差估计, 证明了该方法具有一阶 $\varepsilon$ 一致收敛性. 此外, 与文献 [10],[11] 中给出的分析方法类似, 另一个主要目标是提出一种简单 Richardson 外推技术的收敛分析, 该技术将数值方法的精度从一阶提高到二阶.

本文大纲如下: 第 2 节介绍了 VB 网格的生成方式及其相应的性质. 第 3 节给出了截断误差估计和 $\varepsilon$ 一致收敛性分析. 在第 4 节中, 结合 Richardson 外推方法, 提高了数值方法的收敛阶, 并在第 5 节中通过一些数值实验验证理论结果. 最后, 在第 6 节中进行了一些结论性的讨论.

2 Vulanović-Bakhvalov 网格

设 $\bar{\Omega}^{N}:=\{0=x_0<x_1<\cdots<x_N=1\}$ 为任意非均匀网格, 其网格步长为 $h_i=x_i-x_{i-1}$, $i=1,2,\cdots,N$. 记 $\bar{\Omega}^N$ 网格上的网格函数表示为 $w^N=(w_0^N,w_1^N,\cdots,w_N^N)^T$. 对于在 $\Omega$ 上定义的连续函数 $g(x)$, 记 $g_i=g(x_i)$ 及 $\|g\|=\max\limits_{x\in \Omega}|g(x)|$. 用 $C$ 表示和网格参数 $N$ 与 $\varepsilon$ 无关的正常数, 在不同的地方取值可能不同.

Bakhvalov 网格 (B 网格)^[12]是奇异摄动问题数值方法的第一个离散网格, B 网格的主要思想是构造以下网格生成函数

(2.1)$\lambda(t)=\begin{cases}\psi(t), &t\in[\alpha],\\\psi(\alpha)+\psi'(\alpha)(t-\alpha), &t\in[\alpha,1],\end{cases}$

其中 $\psi(t)$ 是一个正函数, $\alpha$ 是网格过渡点, 满足

(2.2)$\begin{matrix} \psi(\alpha)+\psi'(\alpha)(1-\alpha)=1. \end{matrix}$

那么, 由 $x_i=\lambda(t_i)$ 可生成 B 网格的网格点 $x_i$, 其中 $t_i=i/N$, $i=0,1,\cdots,N$. 显然, 从 (2.1) 可以看出, 任何 B 网格的关键问题是如何选择函数 $\psi(t)$, 为此, 许多学者通过构造不同的函数 $\psi(t)$ 生成不同的 B 网格 (例如, 文献 [13],[14], Kopteva,[16]). Vulanović^[17] 通过选择提出了另一种改进 B 网格, 称为 Vulanović-Bakhvalov (VB mesh), 其网格生成函数如下

(2.3)$\begin{matrix} \psi(t)=a\varepsilon\phi(t)=\frac{a\varepsilon t}{q-t}.\label{2.3} \end{matrix}$

其中, $a$ 和 $q$ 为正的网格参数, 通过 $\phi$ 的选择, 参数 $a$ 和 $q$ 有如下关系

$\begin{eqnarray*} \alpha=\frac{q-\sqrt{a\varepsilon q(1-q+a\varepsilon)}}{1+a\varepsilon}. \end{eqnarray*}$

引理2.1 设 $\left\{x_i\right\}_{i=0}^N$ 为 (2.1) 和 (2.3) 式生成的 VB 网格, 那么

$\begin{eqnarray*} &&\int_{x_{i-1}}^{x_{i}}1+\varepsilon^{-1}{\rm e}^{-\frac{\beta t}{2\varepsilon}}{\rm d}t\leq CN^{-1}, i=1,\cdots,N. \end{eqnarray*}$

证详见文献 [18],[19].

3 离散格式与误差分析

在上述 VB 网格上, 构造如下有限差分格式离散方程 (1.1)-(1.2)

(3.1)$\mathcal{L}^{N} u_{i}^{N}:=\varepsilon\frac{u_{i}^{N}-u_{i-1}^{N}}{h_{i}}+b_{i}u_{i}^{N}+\sum_{j=1}^{i}h_{j}K_{i,j-1}u_{j-1}^{N}=f_{i},$

(3.2)$u_{0}^{N}=\eta,$

其中 $u_{i}^{N}$ 是 $u(x)$ 在 $x=x_{i}$ 处的近似解, $K_{i,j}=K(x_i,x_j)$. 接下来, 为了导出 (3.1)-(3.2) 格式解的收敛性结果, 首先给出如下稳定性结果

引理3.1 文献 [20,定理 4.2] 离散格式 (3.1)-(3.2) 的解满足如下估计

(3.3)$\begin{matrix} &&\max\limits_{0\leq i\leq N}|u_{i}^{N}|\leq {\rm e}^{\frac{\|K\|}{\beta}} \left(|\eta|+\frac{1}{\beta}\max\limits_{0\leq i\leq N}|f_i|\right), \end{matrix}$

其中 $\|K\|:=\max\limits_{(x,t)\in \Omega\times\Omega}\left|K(x,t)\right|$.

引理3.2 文献 [21,定理 2.1] 问题 (1.1)-(1.2) 的解满足如下估计

(3.4)$\begin{matrix} &&\|u\|\leq {\rm e}^{\frac{\|K\|}{\beta}} \left(|\eta|+\frac{1}{\beta}\|f\|\right). \end{matrix}$

记 $e_{i}^{N} := u_{i}-u_{i}^{N}$, $i=1,2,3,\cdots,N$, 为点 $x=x_i$ 处的误差, 可得

(3.5)$\begin{matrix}\label{3.5xx} &&\mathcal{L}^{N} {\rm e}^{N}_{i}=R_i, \end{matrix}$

其中 $R_i=R_{1,i}+R_{2,i}$ 是 $x=x_i$ 处的局部截断误差

(3.6)$R_{1,i}=\varepsilon h_{i}^{-1}\int_{x_{i-1}}^{x_{i}}u"(t)(t-x_{i-1}){\rm d}t,$

(3.7)$R_{2,i}=-\sum_{j=1}^{i}\int_{x_{j-1}}^{x_{j}}(s-x_{j-1})\frac{\rm d}{{\rm d}s}\left[K(x_{i},s)u(s)\right]{\rm d}s.$

引理3.3 在上述 VB 网格 $\left\{x_i\right\}_{i=0}^N$ 下, 有 $ |R_i|\leq CN^{-1}, i=1,2,\cdots,N. $

证对于 (3.6) 式, 由 (1.3) 式和定理 2.1 可知

$\begin{align*} |R_{1,i}|&\leq\varepsilon h_{i}^{-1}\int_{x_{i-1}}^{x_{i}}\left|u"(t)\left(t-x_{i-1}\right)\right|{\rm d}t\leq \varepsilon\int_{x_{i-1}}^{x_{i}}\left|u"(t)\right|{\rm d}t\leq C\int_{x_{i-1}}^{x_{i}}1+\varepsilon^{-1}{\rm e}^{\frac{-\beta t}{\varepsilon}}{\rm d}t\leq CN^{-1}. \end{align*}$

同样, 对于 (3.7) 式, 有

$\begin{align*} |R_{2,i}|&\leq C\sum_{j=1}^{i}\left[\int_{x_{j-1}}^{x_{j}}\left(t-x_{j-1}\right)\left(\left|u(t)\right|+\left|u'(t)\right|\right){\rm d}t\right]\\ &\leq C\sum_{j=1}^{i}h_j\left(\int_{x_{j-1}}^{x_{j}}1+\varepsilon^{-1}{\rm e}^{\frac{-\beta t}{\varepsilon}}{\rm d}t\right)\\ &\leq CN^{-1} \sum_{j=1}^{i}h_j\leq CN^{-1}, \end{align*}$

引理得证.

根据引理 3.1 和 3.3, 可得本文第一个主要收敛性结果.

定理3.1 设 $u(x)$ 为上述 VB 网格 $\left\{x_i\right\}_{i=0}^N$ 上 (1.1)-(1.2) 式的精确解, $u_i^N$ 为 (3.1)-(3.2) 式的解, 可得

$\begin{matrix} &&\max\limits_{0\leq i\leq N}|u(x_i)-u_{i}^{N}|\leq CN^{-1}. \end{matrix}$

4 Richardson 外推

本节将利用 Richardson 外推技术提高离散格式 (3.1)-(3.2) 的精度, 为此, 首先给出如下引理

引理4.1 对于任意在 $[a,b]$ 上的正单调递减函数 $\phi$, 有

$\begin{eqnarray*} \int_a^b \phi(s)(s-a){\rm d}s\leq \frac{1}{2}\left[\int_a^b \sqrt{\phi(s)}{\rm d}s\right]^2.\label{4.10a} \end{eqnarray*}$

设 $\bar{\Omega}^{2N}=\bar{\Omega}^{N}\cup \left\{x_{i-1/2}=\frac{x_i+x_{i-1}}{2}\right\}_{i=1}^{N}$ 是通过等分 $\bar{\Omega}^{N}$ 得到的加密网格, 在此网格 $\bar{\Omega}^{2N}$ 上, 式 (1.1) 的离散方案如下

(4.1)$\mathcal{L}^{2N} u_{i}^{2N}:=\varepsilon\frac{u_{i}^{2N}-u_{i-1/2}^{2N}}{h_{i}/2}+b_{i}u_{i}^{2N}+\sum_{j=1}^{i}\frac{h_j}{2}\left(K_{i,j-1}u^{2N}_{j-1}+K_{i,j-1/2}u^{2N}_{j-1/2}\right)=f_{i}$

(4.2)$u_{0}^{2N}=\eta.\label{doub2}$

由定理 3.1, 当 $i=1,\cdots,N$ 时,

(4.3)$\left(u_i-u_i^N\right)=CN^{-1}+\mathcal{R}_i^N,$

(4.4)$\left(u_i-u_i^{2N}\right)=C(2N)^{-1}+\mathcal{R}_i^{2N},$

其中 $\mathcal{R}_i^N$ 和 $\mathcal{R}_i^{2N}$ 为 $o(N^{-1})$. 利用如下公式消去 $O(N^{-1})$,

(4.5)$\begin{matrix}\label{4.5axxx} &&\left(u_i-(2u_i^{2N}-u_i^N)\right)=2\mathcal{R}_i^{2N}-\mathcal{R}_i^N=o(N^{-1}). \end{matrix}$

因此, 基于上述离散化方案 (3.1)-(3.2) 和 (4.1)-(4.2), 定义 Richardson 外推解如下

(4.6)$\begin{matrix}\label{4.1xxx} &&u_{i,extp}^{N}:=2u^{2N}_{i}-u^{N}_{i}. \end{matrix}$

显然, 通过使用 (3.5) 式, 引理 4.1 和泰勒展开公式, 有

(4.7)$\begin{matrix} \begin{split}\label{4.4xxx} \left|R_{1,i}\right|&\leq CN^{-1}+\frac{\varepsilon}{h_i}\int_{x_{i-1}}^{x_i}(t-x_{i-1})^2 \left|u"'(t)\right|{\rm d}t\\ &\leq CN^{-1}+C\int_{x_{i-1}}^{x_{i}}(1+\varepsilon^{-2}{\rm e}^{\frac{-\beta t}{\varepsilon}})(t-x_{i-1}){\rm d}t\\ &\leq CN^{-1}+C\left[\int_{x_{i-1}}^{x_{i}}1+\varepsilon^{-1}{\rm e}^{\frac{-\beta t}{2\varepsilon}}{\rm d}t\right]^2\leq CN^{-1}+CN^{-2}, \end{split} \end{matrix}$

与

(4.8)$\begin{matrix} \begin{split}\label{4.4xxxx} \left|R_{2,i}\right|&\leq CN^{-1}+ \sum_{j=1}^{i}\int_{x_{j-1}}^{x_{j}}\int_{x_{j-1}}^{x}(t-x_{j-1})[K(x_i,t)u(t)]"{\rm d}t{\rm d}x\\ &\leq CN^{-1}+C\sum_{j=1}^{i}\int_{x_{j-1}}^{x_{j}}\int_{x_{j-1}}^{x_{j}}\left(1+\varepsilon^{-2}{\rm e}^{\frac{-\beta t}{\varepsilon}}\right)(t-x_{j-1}){\rm d}t{\rm d}x\\ &\leq CN^{-1}+C\max\limits_{1\leq j\leq i}\left[\int_{x_{j-1}}^{x_j} 1+\varepsilon^{-1}{\rm e}^{\frac{-\beta t}{2\varepsilon}}{\rm d}t\right]^2\sum_{j=1}^{i}\int_{x_{j-1}}^{x_{j}}{\rm d}x\\ &\leq CN^{-1}+CN^{-2}. \end{split} \end{matrix}$

那么, 从 (4.7)-(4.8) 式, 有

(4.9)$\begin{matrix}\label{4.7xxx} \max\limits_{i=1\cdots,N}\left|u_{i}-u^{N}_{i}\right|\leq CN^{-1}+CN^{-2}. \end{matrix}$

定理4.1 设 $u(x)$ 和 $u_{i,extp}^N$ 分别为 (1.1) 和 (4.6) 式的解, 那么 $ \max\limits_{0\leq i\leq N}|u_i-u_{i,extp}^{N}|\leq CN^{-2}. $

证显然, 由于(4.7)-(4.8) 式可知, $\mathcal{R}_i^N$ 和 $\mathcal{R}_i^{2N}$ 等于 $O(N^{-2})$. 由给出的外推式 (4.5) 可得

(4.10)$\begin{aligned} u_i-u_{i,extp}^{N} =2\left(u_i-u_i^{2N}\right)-\left(u_i-u_i^{N}\right) =2\mathcal{R}_i^{2N}-\mathcal{R}_i^N=O(N^{-2}). \end{aligned}$

5 数值实验

在本节中, 利用两个数值算例验证前文理论结果的有效性, 采用如下公式来计算数值解的绝对误差

$\begin{eqnarray*} E^N:=\max\limits_{0\leq i\leq N}\left|u(x_i)-u_i^N\right|, \end{eqnarray*}$

其中 $u(x_i)$ 为连续问题 (1.1)-(1.2) 的精确解, $u_i^N$ 为离散格式 (3.1)-(3.2) 的解, $x_i$ 为第 2 节定义的 VB 网格点. 于是, 相应的收敛速率可定义为

$\begin{eqnarray*} r^N=\log_2\left(\frac{E^N}{E^{2N}}\right). \end{eqnarray*}$

在所有的数值算例中, 取 $a=2.5, q=1/2$.

5.1 例 1: 线性算例

考虑如下奇摄动 Volterra 积分微分方程

$\begin{eqnarray*} \varepsilon u'(x)+(x+1)u(x)+\int_0^x \sin(x+t)u(t){\rm d}t=1,\;\;\;0<x<1,\;\;\; u(0)=0. \end{eqnarray*}$

由于该问题的精确解没有给出, 采用如下公式来计算数值解的绝对误差

$\begin{eqnarray*} &&E^N:=\max_{0\leq i\leq N}\left|u^{N}_i-u^{2N}_{i}\right|, \end{eqnarray*}$

其中 $u^{2N}_i$ 为离散格式 (3.1) 在 $\bar{\Omega}^{2N}$ 上的解. 外推后, 最大逐点误差如下

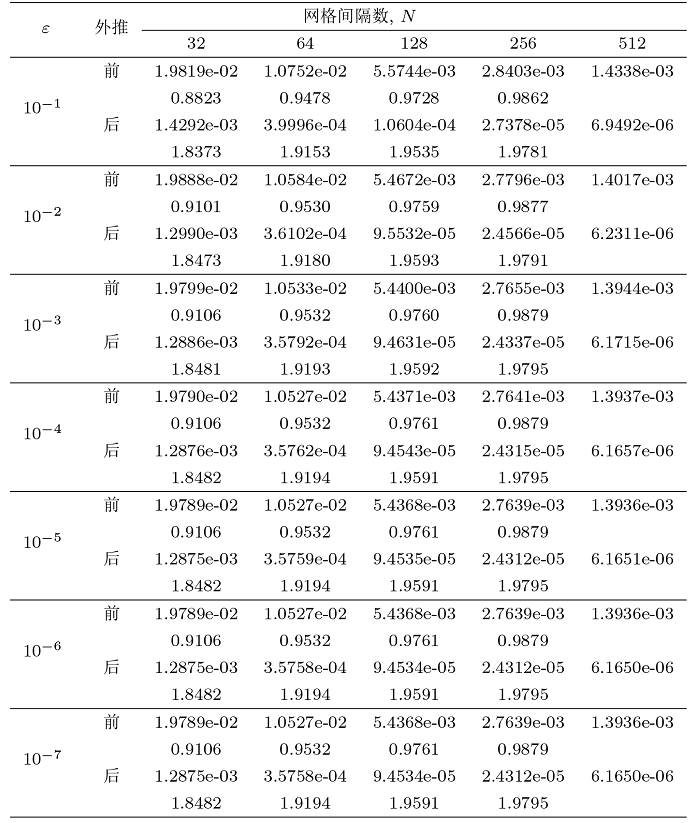
$\begin{eqnarray*} &&E_{extp}^N:=\max_{0\leq i\leq N}\left|u_{i,extp}^{N}-u_{i,extp}^{2N}\right|. \end{eqnarray*}$

对 $\varepsilon=10^{-k}(k=1,\cdots,7)$ 和 $N=32,64,128,256,512$, 表 1 中列出了例 1 在外推前后的最大误差和相应的收敛阶. 由表 1 可以看出, 所提数值方法在 $\varepsilon$ 上一致收敛, 经过 Richardson 外推, 数值解的收敛阶由一阶提高到二阶, 这验证了本文的理论结果. 事实上, VB 网格属于 B 型网格, 不像分段均匀的 Shishkin 网格那样受到 $\ln N$ 因子的影响. 因此, 这种 $\varepsilon$ 均匀收敛的阶数是最优的.

表1 例 1: 外推前后数值结果表

新窗口打开| 下载CSV

5.2 例 2: 非线性式例

为了说明本文结果可以推广到非线性奇异摄动 Volterra 积分微分方程, 考虑如下测试算例^[10]

(5.1)$\varepsilon u'(x)+u(x)+(1+\varepsilon)\int_0^x u^2(s){\rm d}s=f(x,\varepsilon), \;0<x\leq 1$

(5.2)$u(0)=1+\exp(-1),$

选择适当的 $f$, 使得方程的精确解为 $u(x)=\exp(x-1)+\exp\left[-\frac{x}{\varepsilon}(1+\varepsilon)\right]$.

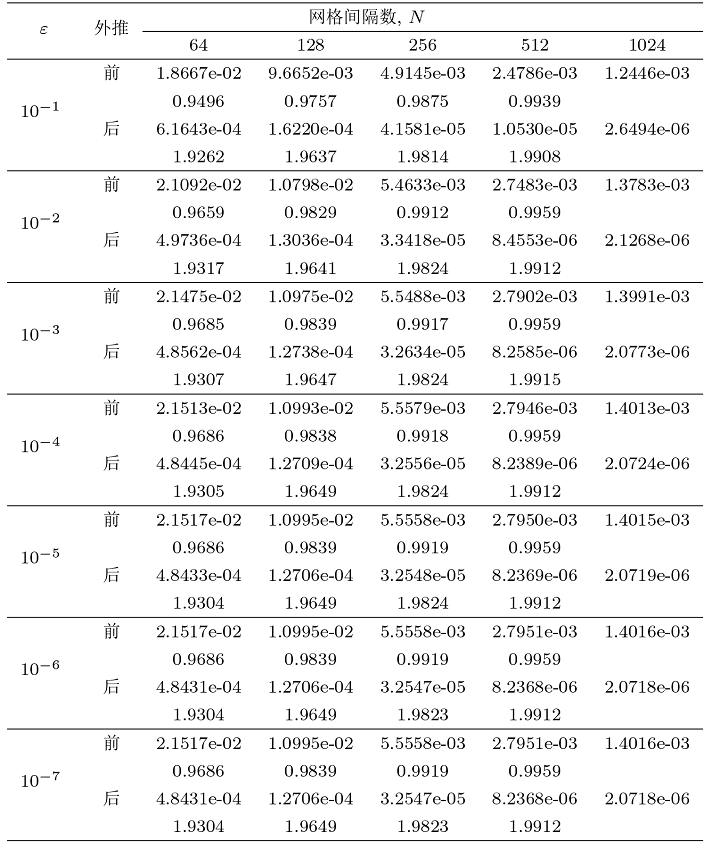
对于不同的 $\varepsilon$ 和 $N$, 利用所提出的数值方法来解决问题 (5.1)-(5.1). 表 2 给出了外推前后的数值结果, 在 VB 网格上的离散格式 (3.1)-(3.2) 是有效的, 对于较大的 $N$ 值, 误差相对于 $\varepsilon$ 具有鲁棒性, 经过外推后, 数值解的收敛速度从一阶提高到二阶.

表2 例 2: 外推前后数值结果表

新窗口打开| 下载CSV

6 总结

首先, 在 VB 网格上分析了奇异摄动 Volterra 积分微分方程离散格式 (3.1)-(3.2) 的 $\varepsilon$ 一致收敛性. 另外, 还通过 Richardson 外推在 VB 网格上给出了离散格式 (3.1)-(3.2) 的严格收敛证明. 需要指出的是, 本文给出的分析方法可以推广到其他奇异摄动问题外推方法的收敛性分析.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Iragi

B C

, Munyakazi

J B

A uniformly convergent numerical method for a singularly perturbed Volterra integro-differential equation

Int J Comput Math, 2020, 97(4): 759-771

[本文引用: 3]

[2]

Hoppensteadt

F C

An algorithm for approximate solutions to weakly filtered synchronous control systems and nonlinear renewal processes

SIAM J Appl Math, 1983, 43(4): 834-843