1 引言
肺结核 (Tuberculosis, TB) 是由结核分枝杆菌引起的一种传染病, 据世界卫生组织 (World Health Organization, WHO) 报告, 每年有 1000 万人感染肺结核. 尽管结核病是一种可预防和可治愈的疾病, 但每年仍有 150 万人死于结核病, 使其成为世界上最大的传染病杀手.据估计, 全球约有四分之一的人口感染了结核病细菌, 但大多数人不会继续发展为结核病, 有些人会清除感染.感染结核病细菌的人一生中患结核病的风险为 $5\%-10\%$ . 那些免疫系统受损的人, 如艾滋病毒感染者、营养不良者、糖尿病患者或吸烟者患病的风险更高[1 ] .
结核病的常见症状包括: 长期咳嗽、胸痛、虚弱或疲劳、体重减轻、发烧、盗汗. 通常, 这些症状在数月内都很轻微, 从而导致寻求治疗的延迟, 并增加了将感染传播给他人的风险. 结核病是可以治愈的, 但需要 3-6 个月的治疗期, 在某些情况下, 结核杆菌对标准药物没有反应, 在这种情况下, 患者患有耐药结核病, 治疗时间更长、更复杂. 如果没有坚持治疗或治疗没有正确完成, 这种疾病可能会产生耐药性并传播. 那些已感染但尚未患病的人可以进行结核病预防性治疗以阻止疾病的发作, 治疗时间可缩短至仅 1 或 3 个月, 此阶段无传染性[1 ] . 结核病同样是可预防的, 卡介苗 (BCG Vaccine) 在很大程度上对儿童的某些类型的结核病有效, 然而, BCG 在成年人中的作用差异很大, 并且疫苗有效性在接种疫苗 10-15 年后降低, 接种者仍然具有未来感染结核病的可能性[2 ,3 ] .
数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的.
特别地, 反应扩散模型在流行病学中被用于描述疾病如何在空间上扩散和在局部环境中的动态变化,对于肺结核这样的传染病, 该模型能够帮助理解肺结核在不同地理区域内的扩散模式以及疾病的局部传播动态.为此, Bhih 和 Laaroussi 等人[13 ] 建立了 SEIR-TB 的时空模型, 该模型通过考虑空间异质性来表征结核病的动态.Wang 和 Xu[14 ] 将空间效应引入到具有复发延迟的 SIR 模型中, 研究了稳态的稳定性和行波解的存在性.Zhang 和 Liu 等[15 ] 应用次超解方法、Schauder 不动点定理和李雅普诺夫泛函, 建立了一类具有快慢级数的扩散 TB 模型行波解的存在性.本文继续此方面的研究, 将空间因素引入模型, 探讨在多种控制措施下, 如何达到肺结核传播的最佳控制效果.
2 模型建立
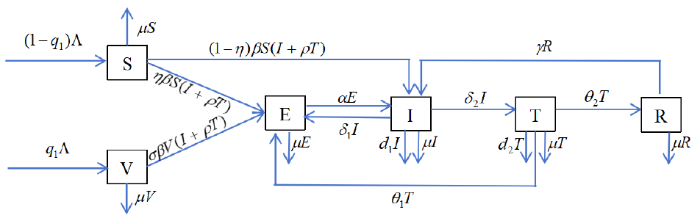
在 2022 年, Li 和 Liu 等人[7 ] 建立了一个 SVEITR 模型描述肺结核的传播, 将整个人群 $N$ $S(t)$ $V(t)$ $E(t)$ $I(t)$ $T(t)$ $R(t)$ [2 ,3 ] , 因此本文不考虑成人接种疫苗,各仓室传播过程见图 1.
图1
又因为人口运动和空间分布的交互作用在结核病传播中发挥着重要作用, 因此每个仓室加入扩散项.而在实际中, 为了达到更好的防控效果, 相关部门付出了很大努力, 例如: 开展肺结核预防和控制的宣传教育以提高个人防护意识 ($u_{1}$ ) ,及时的检测和治疗 ($u_{2}$ ) , 提高治疗水平 ($u_{3}$ ) , 以及降低复发率 ($u_{4}$ ) 等.将扩散和控制措施引入图 1 , 可以得到下面模型
(2.1) $\begin{equation} \left\{\begin{array}{l} \left.\begin{array}{l} \frac{\partial S}{\partial t}-D_{1}\Delta S=(1-q_{1})\Lambda-\beta(1-u_{1}) S(I+\rho T)-\mu S,\\ \frac{\partial V}{\partial t}-D_{2}\Delta V=q_{1}\Lambda-\sigma\beta(1-u_{1}) V(I+\rho T)-\mu V,\\ \frac{\partial E}{\partial t}-D_{3}\Delta E=\eta\beta(1-u_{1}) S(I+\rho T)+\sigma\beta(1-u_{1}) V(I+\rho T)\\ \quad\quad\quad\quad\quad\quad\quad+\delta_{1}I+\theta_{1}T-(\alpha+\mu)E,\\ \frac{\partial I}{\partial t}-D_{4}\Delta I=(1-\eta)\beta(1-u_{1}) S(I+\rho T)+\alpha E+\gamma(1-u_{4}) R\\ \quad\quad\quad\quad\quad\quad\quad-(\delta_{1}+\delta_{2}(1+u_{2})+\mu+d_{1})I,\\ \frac{\partial T}{\partial t}-D_{5}\Delta T=\delta_{2}(1+u_{2}) I-(\theta_{1}+\theta_{2}(1+u_{3})+\mu+d_{2})T,\\ \frac{\partial R}{\partial t}-D_{6}\Delta R=\theta_{2}(1+u_{3}) T-(\gamma(1-u_{4})+\mu)R,\\ \end{array}\right\}(x,t)\in Q=\Omega\times(0,T),\\ \left.\begin{array}{l} S(x,0)=S_{0}(x)\geq0, V(x,0)=V_{0}(x)\geq0, E(x,0)=E_{0}(x)\geq0, \\ I(x,0)=I_{0}(x)\geq0, T(x,0)=T_{0}(x)\geq0, R(x,0)=R_{0}(x)\geq0,\\ \end{array}\right\} x\in\Omega,\\ \frac{\partial S}{\partial \textbf{n}}=0, \frac{\partial V}{\partial \textbf{n}}=0, \frac{\partial E}{\partial \textbf{n}}=0, \frac{\partial I}{\partial \textbf{n}}=0, \frac{\partial T}{\partial \textbf{n}}=0, \frac{\partial R}{\partial \textbf{n}}=0, (x,t)\in\partial\Omega\times(0,T), \end{array}\right. \end{equation}$
其中$\Omega$ $\mathbb{R}^{n}$ $\partial\Omega.$ $\Delta$ $\textbf{n}$ $\partial\Omega$ 表 1.
对于最优控制问题, 我们希望以最少的花费实现最少的感染人数, 因此建立如下目标泛函
(2.2) $\begin{equation} \begin{array}{l} J(u_{1},u_{2},u_{3},u_{4})=\int_{0}^{T}\int_{\Omega}\big[A_{1}E+A_{2}I+\sum\limits_{i=1}^{4}\frac{1}{2}B_{i}u_{i}^{2}\big]\text{d}x\text{d}t\\ \quad\quad\quad\quad\quad\quad\quad =\int_{Q}\big[A_{1}E+A_{2}I+\sum\limits_{i=1}^{4}\frac{1}{2}B_{i}u_{i}^{2}\big]\text{d}x\text{d}t, \end{array} \end{equation}$
其中$T$ $A_{i}(i=1,2)$ $E$ $I$ $B_{i}(i=1,2,3,4)$
其中$M_{i}$ $i$ $u_{i}$
我们需要寻找最优控制$(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*})\in U,$
(2.3) $J(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*})=\inf\limits_{U} J(u_{1},u_{2},u_{3},u_{4}).$
由文献 [16 ] 第 25 章 25.1 部分的内容可知: 模型 (2.1) 中的任意状态解在$\Omega\times(0,T)$ $L^{2}((0,T);H^{1}(\Omega))$ ( 状态函数所属空间) 和 $L^{2}((0,T);H^{1}(\Omega)^{*})$ ( 偏导函数所属空间) 内,系统 (2.1) 的弱解是存在唯一的; 并且最优控制问题 (2.1), (2.2), (2.3) 存在唯一的最优控制.
3 问题求解
下面求解最优控制问题 (2.1), (2.2), (2.3).由文献 [16 ] 知道可以使用一组伴随偏微分方程来求解最优控制和相应的状态系统: 伴随函数类似于连接状态系统和成本目标泛函的 Lagrange 乘子. 通过求解由状态偏微分方程、伴随偏微分方程和最优控制特征组成的最优性系统, 就可以获得最优控制问题的解.
3.1 灵敏度系统
构造 “控制-状态” 映射$(u_{1},u_{2},u_{3},u_{4})\rightarrow \textbf{X}(u_{1},u_{2},u_{3},u_{4}),$ $\textbf{X}=(S,V,E,I,T,R).$ $u_{i}(i=1,2,3,4),$ $u_{i}^{\epsilon}=u_{i}+\epsilon l_{i},$ $l_{i}$ $\epsilon>0.$ $X_{j}=X_{j}(u_{1},u_{2},u_{3},u_{4}),$ $X_{j}^{\epsilon}=X_{j}(u_{1}^{\epsilon},u_{2}^{\epsilon},u_{3}^{\epsilon},u_{4}^{\epsilon}),$ $X_{j}$ $\textbf{X}$ $j(j=1,2,\cdots,6)$
下面定义灵敏度函数{$\psi_{i}~(i=1,2,\cdots,6)$
(3.1) $\frac{X_{j}^{\epsilon}-X_{j}}{\epsilon},$
满足$\epsilon\rightarrow0$ $X_{j}^{\epsilon}\rightarrow X_{j}$ $\frac{X_{j}^{\epsilon}-X_{j}}{\epsilon}\rightarrow \psi_{j} (j=1,2,\cdots,6).$
差商(3.1)的收敛性以及灵敏度函数及其对应偏微分方程的存在性可参考文献 [16 ]. 灵敏度函数满足与状态方程的线性化形式相对应的系统, 下面计算$\psi_{1}$ $\frac{S^{\epsilon}-S}{\epsilon},$
(3.2) $\begin{aligned} &~~~~\frac{\frac{\partial S^{\epsilon}}{\partial t}-\frac{\partial S}{\partial t}}{\epsilon}-D_{1}\frac{\Delta S^{\epsilon}-\Delta S}{\epsilon}\\ &=\frac{\partial \left(\frac{S^{\epsilon}-S}{\epsilon}\right)}{\partial t}-D_{1}\Delta\left(\frac{S^{\epsilon}-S}{\epsilon}\right)\\ &=-\beta(1-u_{1})\left[\frac{(S^{\epsilon}-S)I^{\epsilon}}{\epsilon}+\frac{S(I^{\epsilon}-I)}{\epsilon} +\rho\frac{(S^{\epsilon}-S)T^{\epsilon}}{\epsilon}+\rho\frac{S(T^{\epsilon}-T)}{\epsilon}\right]\\ & \quad +\beta l_{1}S^{\epsilon}(I^{\epsilon}+\rho T^{\epsilon})-\mu\frac{S^{\epsilon}-S}{\epsilon}. \end{aligned}$
令$\epsilon\rightarrow0,$
对于$\psi_{k} (k=2,3,4,5,6)$ ${\psi}=(\psi_{1},\psi_{2},\psi_{3},\psi_{4},$ $\psi_{5},\psi_{6})$
(3.3) $\begin{equation} \mathcal{L}\left( \begin{array}{c} \psi_{1} \\ \psi_{2} \\ \psi_{3} \\ \psi_{4} \\ \psi_{5} \\ \psi_{6} \\ \end{array} \right)=\left( \begin{array}{c} l_{1}\beta S(I+\rho T) \\ l_{1}\sigma\beta V(I+\rho T) \\ -l_{1}\eta\beta S(I+\rho T)-l_{1}\sigma\beta V(I+\rho T) \\ -l_{1}(1-\eta)\beta S(I+\rho T)-l_{2}\delta_{2}I-l_{4}\gamma R \\ l_{2}\delta_{2}I-l_{3}\theta_{2}T \\ l_{3}\theta_{2}T+l_{4}\gamma R \\ \end{array} \right),(x,t)\in Q=\Omega\times(0,T), \end{equation}$
可以发现灵敏度函数满足状态方程(2.1)的线性化形式相对应的系统.
(3.4) $\psi_{1}(x,0)=\psi_{2}(x,0)=\psi_{3}(x,0)=\psi_{4}(x,0)=\psi_{5}(x,0)=\psi_{6}(x,0)=0, x\in\Omega.$
(3.5) $\frac{\partial \psi_{1}}{\partial \textbf{n}}=\frac{\partial \psi_{2}}{\partial \textbf{n}}= \frac{\partial \psi_{3}}{\partial \textbf{n}}=\frac{\partial \psi_{4}}{\partial \textbf{n}}= \frac{\partial \psi_{5}}{\partial \textbf{n}}=\frac{\partial \psi_{6}}{\partial \textbf{n}}=0, (x,t)\in\partial\Omega\times(0,T).$
3.2 伴随系统
对于伴随变量${\lambda}=(\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6}),$ $L^{2}(Q)$
(3.6) $\langle{\lambda},\mathcal{L}{\psi}\rangle=\langle\mathcal{L}^{*}{\lambda},{\psi}\rangle.$
伴随系统中各方程等号的右端表达式由目标泛函 (2.2) 中的被积函数分别关于状态变量求偏导得到.下面使用表达式 (3.6) 来导出伴随系统中的算子, 通过在$\langle{\lambda},\mathcal{L}{\psi}\rangle$
(3.7) $\begin{equation} \mathcal{L}^{*}\left( \begin{array}{c} \lambda_{1} \\ \lambda_{2} \\ \lambda_{3} \\ \lambda_{4} \\ \lambda_{5} \\ \lambda_{6} \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ A_{1} \\ A_{2} \\ 0 \\ 0 \\ \end{array} \right),(x,t)\in Q=\Omega\times(0,T), \end{equation}$
(3.8) $\lambda_{1}(x,T)=\lambda_{2}(x,T)=\lambda_{3}(x,T)=\lambda_{4}(x,T)=\lambda_{5}(x,T)=\lambda_{6}(x,T)=0, x\in\Omega.$
(3.9) $\begin{equation} \frac{\partial \lambda_{1}}{\partial \textbf{n}}=\frac{\partial \lambda_{2}}{\partial \textbf{n}}= \frac{\partial \lambda_{3}}{\partial \textbf{n}}=\frac{\partial \lambda_{4}}{\partial \textbf{n}}= \frac{\partial \lambda_{5}}{\partial \textbf{n}}=\frac{\partial \lambda_{6}}{\partial \textbf{n}}=0, (x,t)\in\partial\Omega\times(0,T). \end{equation}$
3.3 最优控制的特征
记$\textbf{u}=(u_{1},u_{2},u_{3},u_{4}),$ $\textbf{l}=(l_{1},l_{2},l_{3},l_{4}).$ $\textbf{u}\rightarrow J(\textbf{u})$ $\textbf{l}$ $\textbf{u}^{*}$
因为$J(u^{*})$ $J(u)$ ${u}^{*}$
记 $W=B_{1}l_{1}u_{1}^{*}+B_{2}l_{2}u_{2}^{*}+B_{3}l_{3}u_{3}^{*}+B_{4}l_{4}u_{4}^{*},$
(3.10) $\begin{array}{l} \quad \lim\limits_{\epsilon\rightarrow0^{+}}\frac{J(\textbf{u}^{*}+\epsilon \textbf{l})-J(\textbf{u}^{*})}{\epsilon}\\ =\lim\limits_{\epsilon\rightarrow0^{+}}\int_{Q}\big[A_{1}(\frac{E^{\epsilon}-E}{\epsilon})+A_{2}(\frac{I^{\epsilon}-I}{\epsilon}) +\sum\limits_{i=1}^{4}\frac{1}{2}B_{i}[\frac{(u_{i}^{*}+\epsilon l_{i})^{2}-(u_{i}^{*})^{2}}{\epsilon}]\big]\text{d}x\text{d}t\\ =\int_{Q}\big[A_{1}\psi_{3}+A_{2}\psi_{4}+W\big]\text{d}x\text{d}t\\ =\int_{Q}\big[(\psi_{1},\psi_{2},\psi_{3},\psi_{4},\psi_{5},\psi_{6})(0,0,A_{1},A_{2},0,0)^{T}+W\big]\text{d}x\text{d}t\\ =\int_{Q}\big[(\psi_{1},\psi_{2},\psi_{3},\psi_{4},\psi_{5},\psi_{6})\mathcal{L}^{*}(\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6})^{T}+W\big]\text{d}x\text{d}t\\ =\int_{Q}\big[(\lambda_{1},\lambda_{2},\lambda_{3},\lambda_{4},\lambda_{5},\lambda_{6})\mathcal{L}(\psi_{1},\psi_{2},\psi_{3},\psi_{4},\psi_{5},\psi_{6})^{T}+W\big]\text{d}x\text{d}t\\ =\int_{Q}\big\{l_{1}\big[\beta[{\lambda_{1}S+\lambda_{2}\sigma V-\lambda_{3}\eta S-\lambda_{3}\sigma V-\lambda_{4}(1-\eta) S ](I+\rho T)}+B_{1}u_{1}^{*}\big]\big. \\ \quad +l_{2}[{(\lambda_{5}-\lambda_{4})\delta_{2}I+B_{2}u_{2}^{*}]+l_{3}[(\lambda_{6}-\lambda_{5})\theta_{2}T+B_{3}u_{3}^{*}] +l_{4}[(\lambda_{6}-\lambda_{4})\gamma R}+B_{4}u_{4}^{*}]\big\}\text{d}x\text{d}t.\\ \end{array}$
定理 3.1 在控制容许集 $U$ $J(u_{1},u_{2},u_{3},u_{4})$ $(u_{1}^{*},u_{2}^{*},u_{3}^{*},u_{4}^{*})$
其中 $(S^*,V^*,E^*,I^*,T^*,R^*)$ $(\lambda_1^*,\lambda_2^*,\lambda_3^*,\lambda_4^*,\lambda_5^*,\lambda_6^*)$
证 由文献 [16 ] 可知, 因为在控制容许集$U$ $\textbf{l}$ $U$
所以当$B_{i}\neq0$ $u_{i}^{*}~(i=1,2,3,4)$
4 数值模拟
本部分对理论结果进行可视化展示, 以下所有图中同一仓室在空间上不同位置处初值一样,分别取为:$S(:,1)=501000,V(:,1)=79300,E(:,1)=126000,I(:,1)=36,T(:,1)=10,R(:,1)=5,$ $\mu=1/77.11,~\Lambda=1,q_{1}=0.9,~\beta=9.0000e-06,~\sigma=0.0011,~\rho=0.0102, \eta=0.9380,~\delta_{1}=0.7,~\delta_{2}=0.3,~\theta_{1}=0.5,~\theta_{2}=0.5, \alpha=0.5002;~\gamma=0.0100,d_{1}=7.0600e-04, d_{2}=7.8300e-04, D_{1}=0.3,D_{2}=0.3,D_{3}=0.3,D_{4}=0.1,D_{5}=0.2,D_{6}=0.3.$ $A_1=0.2,A_2=0.2,B_1=1,B_2=1,B_3=1,B_4=1.$ $M_{i}=0.8~(i=1,2,3,4).$ $x=10$ $0.2.$ $t=30$ $0.5.$
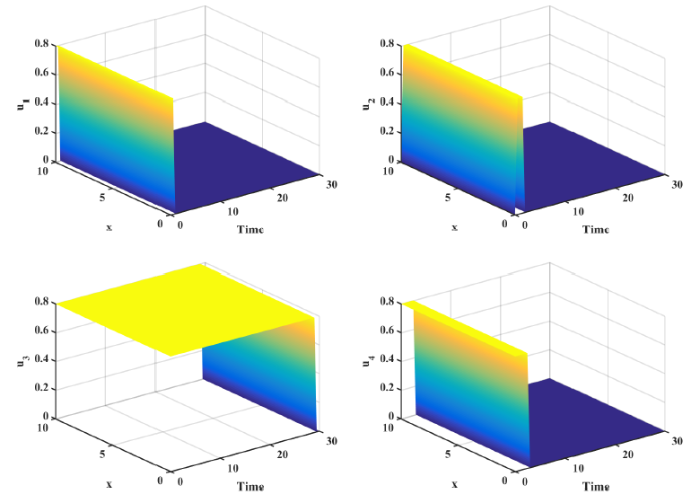
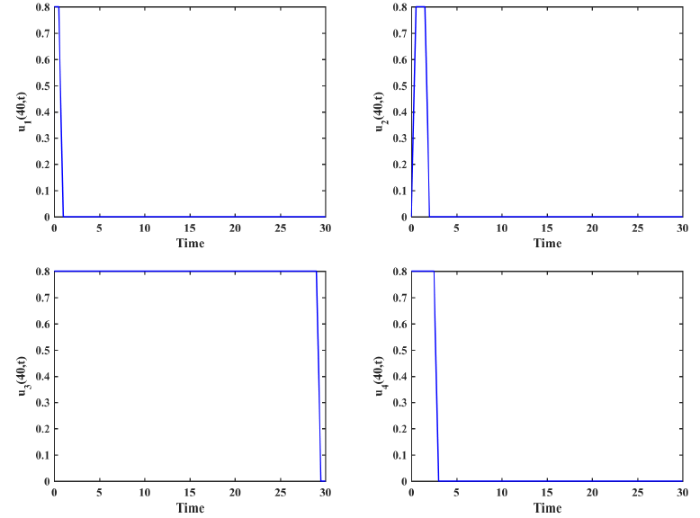
在最优控制下, 四个控制变量$u_{i}~(i=1,2,3,4)$ 图 2. 为了更直观地看出最优控制变量的变化情况, 可在图 2 中截取$x=8$ 图 3. 从图 3 可以看出, 对于控制变量$u_{1}$ $u_{2}$ $u_{3}$ $u_{4}$
图2
图2
最优控制变量的时间序列图.Time (单位: 天), $x$
图3
图3
最优控制变量在 $x=8$
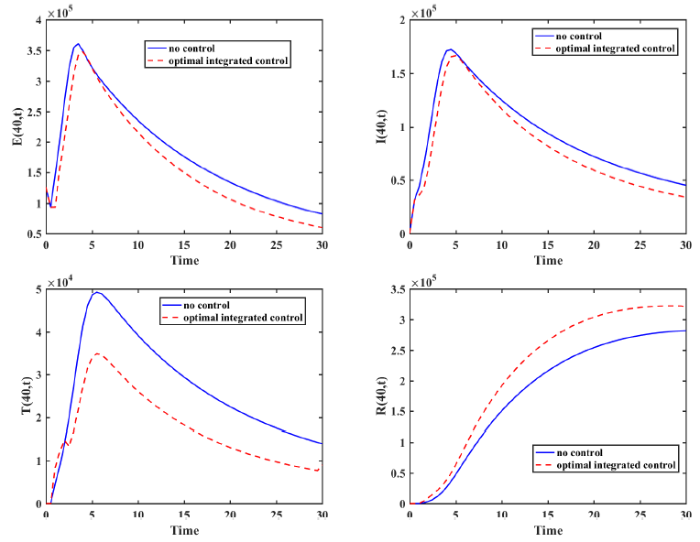
在上述最优控制水平下, 对于各状态变量的控制效果见图 4. 可以看出: 在最优控制下, 潜伏者、TB 活跃者和接受治疗者的数量均少于无控制的情形,而恢复者的数量却多于无控制的情形, 这说明最优综合控制策略对于肺结核的传播起到了较好的控制效果.
图4
图4
在 $x=8$
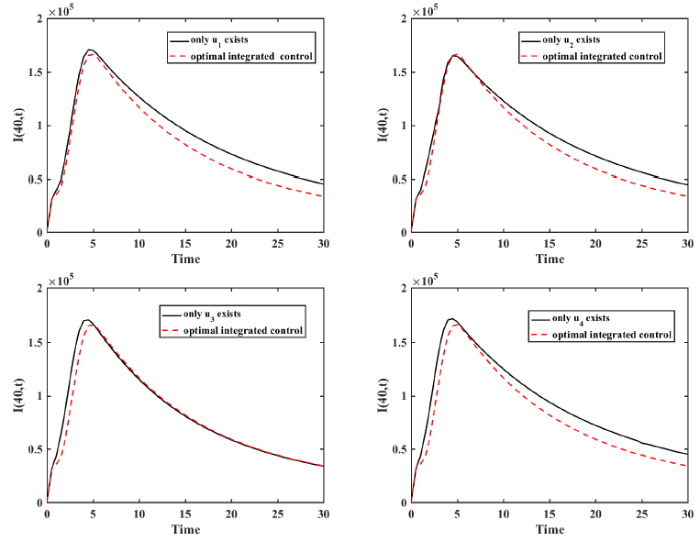
对于单一控制和综合控制, 其控制效果见图 5. 该图显示了两种控制策略下染病者数量在一个月内的变化情况, 可以看出:相比只有 $u_{1}$ $u_{2}$ $u_{2}$ $u_{3} $ $u_{3}$ $u_{4}$
图5
图5
在 $x=8$
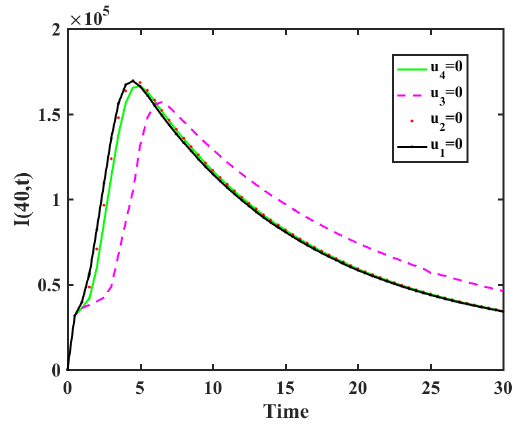
不同控制组合下的控制效果对比见图 6. 该图中给出了三种控制措施同时存在的情况下染病者的数量.共有四组不同的控制组合, 分别为: 组合 1: $u_{1},u_{2},u_{3}\neq0, u_{4}=0;$ $u_{1},u_{2},u_{4}\neq0, u_{3}=0;$ $u_{1},u_{3},u_{4}\neq0, u_{2}=0;$ $u_{2},u_{3},u_{4}\neq0, u_{1}=0.$
图6
图6
在 $x=8$
根据上述结果分析, 我们可以提出以下实际操作建议, 以优化肺结核的防控措施: (1) 个人防护意识提升方面: 在疫情初期, 迅速加强公众的防护意识教育, 通过宣传和教育活动使个人防护措施 (如佩戴口罩、保持社交距离等) 得到广泛普及. 建议在疾病暴发初期投入最大宣传力度, 然后根据防控效果逐渐减弱宣传强度. (2) 检测和治疗能力的提升方面: 在疫情初期, 快速提高检测和治疗的能力, 确保更多潜在病例能被及时发现并进行治疗. 此措施在初期保持高强度, 然后根据疫情的发展逐步减少检测频率, 但仍需保持一定的检测能力以防止疫情反弹. (3) 治疗水平的持续改进方面: 在整个疫情控制阶段, 保持高水平的治疗质量和能力, 这意味着需要足够的医疗资源和人员培训, 以确保患者能够得到及时有效的治疗. (4) 降低复发率的措施方面: 在疾病暴发初期, 集中采取措施降低复发率, 这可能包括针对康复者的后续监控和必要的医学干预, 以降低复发可能性. 总之, 应结合各方面的措施以达到更好的综合防控效果, 综合策略应根据疫情变化进行灵活调整, 确保各个环节的协调和优化. 另外, 还应建立持续的监测机制, 对防控措施的效果进行评估和反馈, 及时调整策略以适应新的挑战.
5 结束语
数学建模在肺结核研究中的应用是多方面的, 包括评估疫情发展、制定和评价干预策略、优化资源配置等. 通过对模型的不断完善和数据的更新, 数学建模将继续在控制肺结核传播和防治策略的制定中发挥关键作用. 本文对一个 SVEITR 模型加入了扩散和 4 个控制变量, 研究扩散存在下的最优控制策略. 理论分析得到了最优控制的特征, 并数值展示了最优控制变量的变化情况以及控制效果. 所得结果可为肺结核防控提供理论建议. 然而, 对于肺结核的研究仍有许多需要解决的问题, 例如, 在突发呼吸道传染病的各类非药物干预策略下, 我国肺结核在预防、传播、治疗和控制等各阶段将受到怎样的影响, 其发病率和死亡率如何变化, 如何建立动力学模型, 并定性研究其内在传播机制等均有待进一步研究.
参考文献
View Option
[1]
Global Tuberculosis report 2023 . Geneva : World Health Organization ; 2023 . Licence:CC BY-NC-SA 3.O IGO
[本文引用: 2]
[2]
Mao K X Zhen C X Hong Yan L U et al. Protective eff ect of vaccination of Bacille Calmette-Gnerin on children
Chin J Contemp Pediatr , 2003 , 5 4 ): 325 -327
[本文引用: 2]
[3]
Abubakar I Pimpin L et al. Systematic review and meta-analysis of the current evidence on the duration of protection by bacillus Calmette-Guerin vaccination against tuberculosis
Health Technol Assess , 2013 , 17 37 ): 1 -372
DOI:10.3310/hta17370
PMID:24021245
[本文引用: 2]
Recent evidence suggests that the duration of protection by bacillus Calmette-Guérin (BCG) may exceed previous estimates with potential implications for estimating clinical and cost-efficacy.To estimate the protection and duration of protection provided by BCG vaccination against tuberculosis, explore how this protection changes with time since vaccination, and examine the reasons behind the variation in protection and the rate of waning of protection.Electronic databases including MEDLINE, Excerpta Medica Database (EMBASE), Cochrane Databases, NHS Economic Evaluation Database (NHS EED), Database of Abstracts of Reviews of Effects (DARE), Web of Knowledge, Biosciences Information Service (BIOSIS), Latin American and Caribbean Health Sciences Literature (LILACs), MEDCARIB Database, Cumulative Index to Nursing and Allied Health Literature (CINAHL) were searched from inception to May 2009. Index to Theses, System for Information on Grey Literature in Europe (SIGLE), Centre for Agricultural Bioscience International (CABI) Abstracts, Scopus, Article First, Academic Complete, Africa-Wide Information, Google Scholar, Global Health, British National Bibliography for Report Literature, and clinical trial registration websites were searched from inception to October 2009.Electronic databases searches, screening of identified studies, data extraction and analysis were undertaken. Meta-analysis was used to present numerical and graphical summaries of clinical efficacy and efficacy by time since vaccination. Evidence of heterogeneity was assessed using the tau-squared statistic. Meta-regression allowed the investigation of observed heterogeneity. Factors investigated included BCG strain, latitude, stringency of pre-BCG vaccination tuberculin testing, age at vaccination, site of disease, study design and vulnerability to biases. Rate of waning of protection was estimated using the ratio of the measure of efficacy after 10 years compared with the efficacy in the first 10 years of a study.Study selection. A total of 21,030 references were identified, providing data on 132 studies after abstract and full-text review. Efficacy. Protection against pulmonary tuberculosis in adults is variable, ranging from substantial protection in the UK MRC trial {rate ratio 0.22 [95% confidence interval (CI) 0.16 to 0.31]}, to absence of clinically important benefit, as in the large Chingleput trial [rate ratio 1.05 (95% CI 0.88 to 1.25)] and greater in latitudes further away from the equator. BCG vaccination efficacy was usually high, and varied little by form of disease (with higher protection against meningeal and miliary tuberculosis) or study design when BCG vaccination was given only to infants or to children after strict screening for tuberculin sensitivity. High levels of protection against death were observed from both trials and observational studies. The observed protective effect of BCG vaccination did not differ by the strain of BCG vaccine used in trials.Reviewed studies showed that BCG vaccination protects against pulmonary and extrapulmonary tuberculosis for up to 10 years. Most studies either did not follow up participants for long enough or had very few cases after 15 years. This should not be taken to indicate an absence of effect: five studies (one trial and four observational studies) provided evidence of measurable protection at least 15 years after vaccination. Efficacy declined with time. The rate of decline was variable, with faster decline in latitudes further from the equator and in situations where BCG vaccination was given to tuberculin-sensitive participants after stringent tuberculin testing.The main limitation of this review relates to quality of included trials, most of which were conducted before current standards for reporting were formulated. In addition, data were lacking in some areas and the review had to rely on evidence from observational studies.BCG vaccination protection against tuberculosis varies between populations, to an extent that cannot be attributed to chance alone. Failure to exclude those already sensitised to mycobacteria and study latitude closer to the equator were associated with lower efficacy. These factors explained most of the observed variation. There is good evidence that BCG vaccination protection declines with time and that protection can last for up to 10 years. Data on protection beyond 15 years are limited; however, a small number of trials and observational studies suggest that BCG vaccination may protect for longer. Further studies are required to investigate the duration of protection by BCG vaccination.The National Institute for Health Research Health Technology Assessment programme.
[4]
徐瑞 , 周凯娟 , 白宁 . 一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型
数学物理学报 , 2024 , 44A 3 ): 771 -782
[本文引用: 1]
Xu R Zhou K J Bai N A with-in host HIV-1 infection dynamics model based on virus-to-cell infection and cell-to-cell transmission
Acta Math Sci , 2024 , 44A 3 ): 771 -782
[本文引用: 1]
[5]
杨俊元 , 张晨琳 , 杨丽 . 年龄结构流感模型综合控制策略研究
数学物理学报 , 2024 , 44A 3 ): 804 -814
Yang J Y Zhang C L Yang L Study on comprehensive control strategies of an age structured influenza model
Acta Math Sci , 44A 3 ): 804 -814
[6]
Liu J L Zhang T L Global stability for a tuberculosis model
Math Comput Model , 2011 , 54 836 -845
[本文引用: 2]
[7]
Li Y Liu X N Yuan Y Y et al. Global analysis of tuberculosis dynamical model and optimal control strategies based on case data in the United States
Appl Math Comput , 2022 , 422 126983
[本文引用: 4]
[8]
Yang Y L Tang S Y Ren X H et al. Global stability and optimal control for a tuberculosis model with vaccination and treatment
Discrete Contin Dyn Syst Ser B , 2017 , 21 3 ): 1009 -1022
[本文引用: 2]
[9]
Gao D P Huang N J A note on global stability for a tuberculosis model
Appl Math Lett , 2017 , 73 163 -168
[10]
Liu S Y Bi Y J Liu Y W Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control
Theor Biol Med Model , 2020 , 17 6 ): 1 -10
[11]
Gao D P Huang N J Optimal control analysis of a tuberculosis model
Appl Math Model , 2018 , 58 47 -64
[本文引用: 1]
[12]
Egonmwan A O Okuonghae D Mathematical analysis of a tuberculosis model with imperfect vaccine
Int J Biomath , 2019 , 12 7 ): 1950073
[本文引用: 1]
[13]
Bhih A E Laaroussi A E A Ghazzali R et al. An optimal chemoprophylaxis and treatment control for a spatiotemporal tuberculosis model
Commun Math Biol Neurosci , 2021 , 2021
[本文引用: 2]
[14]
Wang Z P Xu R Stability and traveling waves of an epidemic model with relapse and spatial diffusion
J Appl Anal Comput , 2014 , 4 3 ): 307 -322
[本文引用: 1]
[15]
Zhang R Liu L L Feng X M et al. Existence of traveling wave solutions for a diffusive tuberculosis model with fast and slow progression
Appl Math Lett , 2021 , 112 106848
[本文引用: 1]
[16]
Lenhart S Workman J T Optimal Control Applied to Biological Models . New York : Chapman & Hall/CRC , 2007
[本文引用: 4]
2
2023
... 肺结核 (Tuberculosis, TB) 是由结核分枝杆菌引起的一种传染病, 据世界卫生组织 (World Health Organization, WHO) 报告, 每年有 1000 万人感染肺结核. 尽管结核病是一种可预防和可治愈的疾病, 但每年仍有 150 万人死于结核病, 使其成为世界上最大的传染病杀手.据估计, 全球约有四分之一的人口感染了结核病细菌, 但大多数人不会继续发展为结核病, 有些人会清除感染.感染结核病细菌的人一生中患结核病的风险为 $5\%-10\%$ . 那些免疫系统受损的人, 如艾滋病毒感染者、营养不良者、糖尿病患者或吸烟者患病的风险更高[1 ] . ...
... 结核病的常见症状包括: 长期咳嗽、胸痛、虚弱或疲劳、体重减轻、发烧、盗汗. 通常, 这些症状在数月内都很轻微, 从而导致寻求治疗的延迟, 并增加了将感染传播给他人的风险. 结核病是可以治愈的, 但需要 3-6 个月的治疗期, 在某些情况下, 结核杆菌对标准药物没有反应, 在这种情况下, 患者患有耐药结核病, 治疗时间更长、更复杂. 如果没有坚持治疗或治疗没有正确完成, 这种疾病可能会产生耐药性并传播. 那些已感染但尚未患病的人可以进行结核病预防性治疗以阻止疾病的发作, 治疗时间可缩短至仅 1 或 3 个月, 此阶段无传染性[1 ] . 结核病同样是可预防的, 卡介苗 (BCG Vaccine) 在很大程度上对儿童的某些类型的结核病有效, 然而, BCG 在成年人中的作用差异很大, 并且疫苗有效性在接种疫苗 10-15 年后降低, 接种者仍然具有未来感染结核病的可能性[2 ,3 ] . ...
Protective eff ect of vaccination of Bacille Calmette-Gnerin on children
2
2003
... 结核病的常见症状包括: 长期咳嗽、胸痛、虚弱或疲劳、体重减轻、发烧、盗汗. 通常, 这些症状在数月内都很轻微, 从而导致寻求治疗的延迟, 并增加了将感染传播给他人的风险. 结核病是可以治愈的, 但需要 3-6 个月的治疗期, 在某些情况下, 结核杆菌对标准药物没有反应, 在这种情况下, 患者患有耐药结核病, 治疗时间更长、更复杂. 如果没有坚持治疗或治疗没有正确完成, 这种疾病可能会产生耐药性并传播. 那些已感染但尚未患病的人可以进行结核病预防性治疗以阻止疾病的发作, 治疗时间可缩短至仅 1 或 3 个月, 此阶段无传染性[1 ] . 结核病同样是可预防的, 卡介苗 (BCG Vaccine) 在很大程度上对儿童的某些类型的结核病有效, 然而, BCG 在成年人中的作用差异很大, 并且疫苗有效性在接种疫苗 10-15 年后降低, 接种者仍然具有未来感染结核病的可能性[2 ,3 ] . ...
... 在 2022 年, Li 和 Liu 等人[7 ] 建立了一个 SVEITR 模型描述肺结核的传播, 将整个人群 $N$ $S(t)$ $V(t)$ $E(t)$ $I(t)$ $T(t)$ $R(t)$ [2 ,3 ] , 因此本文不考虑成人接种疫苗,各仓室传播过程见图 1. ...
Systematic review and meta-analysis of the current evidence on the duration of protection by bacillus Calmette-Guerin vaccination against tuberculosis
2
2013
... 结核病的常见症状包括: 长期咳嗽、胸痛、虚弱或疲劳、体重减轻、发烧、盗汗. 通常, 这些症状在数月内都很轻微, 从而导致寻求治疗的延迟, 并增加了将感染传播给他人的风险. 结核病是可以治愈的, 但需要 3-6 个月的治疗期, 在某些情况下, 结核杆菌对标准药物没有反应, 在这种情况下, 患者患有耐药结核病, 治疗时间更长、更复杂. 如果没有坚持治疗或治疗没有正确完成, 这种疾病可能会产生耐药性并传播. 那些已感染但尚未患病的人可以进行结核病预防性治疗以阻止疾病的发作, 治疗时间可缩短至仅 1 或 3 个月, 此阶段无传染性[1 ] . 结核病同样是可预防的, 卡介苗 (BCG Vaccine) 在很大程度上对儿童的某些类型的结核病有效, 然而, BCG 在成年人中的作用差异很大, 并且疫苗有效性在接种疫苗 10-15 年后降低, 接种者仍然具有未来感染结核病的可能性[2 ,3 ] . ...
... 在 2022 年, Li 和 Liu 等人[7 ] 建立了一个 SVEITR 模型描述肺结核的传播, 将整个人群 $N$ $S(t)$ $V(t)$ $E(t)$ $I(t)$ $T(t)$ $R(t)$ [2 ,3 ] , 因此本文不考虑成人接种疫苗,各仓室传播过程见图 1. ...
一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型
1
2024
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
一类基于游离病毒感染和细胞-细胞传播的宿主体内 HIV-1 感染动力学模型
1
2024
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
Global stability for a tuberculosis model
2
2011
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
... 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
Global analysis of tuberculosis dynamical model and optimal control strategies based on case data in the United States
4
2022
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
... [7 ]在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
... 在 2022 年, Li 和 Liu 等人[7 ] 建立了一个 SVEITR 模型描述肺结核的传播, 将整个人群 $N$ $S(t)$ $V(t)$ $E(t)$ $I(t)$ $T(t)$ $R(t)$ [2 ,3 ] , 因此本文不考虑成人接种疫苗,各仓室传播过程见图 1. ...
... 注: 表 1 中各参数取值范围和来源主要参考文献 [7 ]. ...
Global stability and optimal control for a tuberculosis model with vaccination and treatment
2
2017
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
... [8 ]在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
A note on global stability for a tuberculosis model
2017
Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control
2020
Optimal control analysis of a tuberculosis model
1
2018
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
Mathematical analysis of a tuberculosis model with imperfect vaccine
1
2019
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
An optimal chemoprophylaxis and treatment control for a spatiotemporal tuberculosis model
2
2021
... 数学建模在理解传染病的流行趋势、传播机制、控制策略评估以及疫苗开发等方面发挥着重要作用[4 12 ] .SEIR (Susceptible-Exposed-Infectious-Recovered) 模型是研究传染病传播的基础模型, 可以用来模拟疾病的传播过程和流行趋势.在实际建模时, 只需根据所考虑因素的侧重点相应地扩充或修改SEIR模型. 例如: Liu 和 Zhang[6 ] 建立了一个 SVLIT (susceptible-vaccinated-latent-infective-treated) 模型, 分析了无病平衡点的全局稳定性和地方病平衡点的局部稳定性. Li 和 Liu等人[7 ] 考虑了疫苗接种和不完全的治疗, 将文献 [6 ] 的 SVLIT 模型推广为 SVEITR (susceptible-vaccinated-exposed-infective-treated-recovered) 模型, 讨论了美国结核病的流行率, 并研究了地方病平衡态的全局吸引性. Yang 和 Tang 等人[8 ] 考虑到了不完全疫苗接种和不完全治疗, 建立了一个 SVLIT 模型, 发现疫苗和治疗策略对减少肺结核是有效的. 在实际开展传染病的控制时, 总是希望在最少的成本下能实现最优的控制效果, 因此, 通过建立最优目标泛函, 结合最优控制理论寻找最优解也是学者感兴趣的领域. 例如, Li 和 Liu 等人[7 ] 在其所建模型中引入了三个控制变量讨论了最优控制策略, 得到了最优控制指标并开展了数值模拟实现最优控制的可视化. Yang 和 Tang 等人[8 ] 在其所建模型中引入了一个控制变量, 并评估了控制策略的成本, 然后根据庞特里亚金最大值原理进行了最优控制分析, 发现无论其疗效如何都应该实施最大疫苗接种策略. Gao 和 Huang[11 ] 在其模型中引入了三个控制变量, 以最小化疾病负担和干预成本为目标, 提出了最优控制策略. Bhih 和 Laaroussi 等人[13 ] 在其所建模型中引入化学预防和治疗控制讨论最优控制问题, 以减少潜在感染和主动感染的个体, 发现如果同时采用这两种控制策略, 干预措施是有效的. ...
... 特别地, 反应扩散模型在流行病学中被用于描述疾病如何在空间上扩散和在局部环境中的动态变化,对于肺结核这样的传染病, 该模型能够帮助理解肺结核在不同地理区域内的扩散模式以及疾病的局部传播动态.为此, Bhih 和 Laaroussi 等人[13 ] 建立了 SEIR-TB 的时空模型, 该模型通过考虑空间异质性来表征结核病的动态.Wang 和 Xu[14 ] 将空间效应引入到具有复发延迟的 SIR 模型中, 研究了稳态的稳定性和行波解的存在性.Zhang 和 Liu 等[15 ] 应用次超解方法、Schauder 不动点定理和李雅普诺夫泛函, 建立了一类具有快慢级数的扩散 TB 模型行波解的存在性.本文继续此方面的研究, 将空间因素引入模型, 探讨在多种控制措施下, 如何达到肺结核传播的最佳控制效果. ...
Stability and traveling waves of an epidemic model with relapse and spatial diffusion
1
2014
... 特别地, 反应扩散模型在流行病学中被用于描述疾病如何在空间上扩散和在局部环境中的动态变化,对于肺结核这样的传染病, 该模型能够帮助理解肺结核在不同地理区域内的扩散模式以及疾病的局部传播动态.为此, Bhih 和 Laaroussi 等人[13 ] 建立了 SEIR-TB 的时空模型, 该模型通过考虑空间异质性来表征结核病的动态.Wang 和 Xu[14 ] 将空间效应引入到具有复发延迟的 SIR 模型中, 研究了稳态的稳定性和行波解的存在性.Zhang 和 Liu 等[15 ] 应用次超解方法、Schauder 不动点定理和李雅普诺夫泛函, 建立了一类具有快慢级数的扩散 TB 模型行波解的存在性.本文继续此方面的研究, 将空间因素引入模型, 探讨在多种控制措施下, 如何达到肺结核传播的最佳控制效果. ...
Existence of traveling wave solutions for a diffusive tuberculosis model with fast and slow progression
1
2021
... 特别地, 反应扩散模型在流行病学中被用于描述疾病如何在空间上扩散和在局部环境中的动态变化,对于肺结核这样的传染病, 该模型能够帮助理解肺结核在不同地理区域内的扩散模式以及疾病的局部传播动态.为此, Bhih 和 Laaroussi 等人[13 ] 建立了 SEIR-TB 的时空模型, 该模型通过考虑空间异质性来表征结核病的动态.Wang 和 Xu[14 ] 将空间效应引入到具有复发延迟的 SIR 模型中, 研究了稳态的稳定性和行波解的存在性.Zhang 和 Liu 等[15 ] 应用次超解方法、Schauder 不动点定理和李雅普诺夫泛函, 建立了一类具有快慢级数的扩散 TB 模型行波解的存在性.本文继续此方面的研究, 将空间因素引入模型, 探讨在多种控制措施下, 如何达到肺结核传播的最佳控制效果. ...
4
2007
... 由文献 [16 ] 第 25 章 25.1 部分的内容可知: 模型 (2.1) 中的任意状态解在$\Omega\times(0,T)$ $L^{2}((0,T);H^{1}(\Omega))$ ( 状态函数所属空间) 和 $L^{2}((0,T);H^{1}(\Omega)^{*})$ ( 偏导函数所属空间) 内,系统 (2.1) 的弱解是存在唯一的; 并且最优控制问题 (2.1), (2.2), (2.3) 存在唯一的最优控制. ...
... 下面求解最优控制问题 (2.1), (2.2), (2.3).由文献 [16 ] 知道可以使用一组伴随偏微分方程来求解最优控制和相应的状态系统: 伴随函数类似于连接状态系统和成本目标泛函的 Lagrange 乘子. 通过求解由状态偏微分方程、伴随偏微分方程和最优控制特征组成的最优性系统, 就可以获得最优控制问题的解. ...
... 差商(3.1)的收敛性以及灵敏度函数及其对应偏微分方程的存在性可参考文献 [16 ]. 灵敏度函数满足与状态方程的线性化形式相对应的系统, 下面计算$\psi_{1}$ $\frac{S^{\epsilon}-S}{\epsilon},$
... 证 由文献 [16 ] 可知, 因为在控制容许集$U$ $\textbf{l}$ $U$