1 引言
为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的.
受到上面研究的启发, 本文提出一个新的排队模型, 在文献 [12 ] 的基础上加入服务员的耐烦行为, 即在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 该模型推广了文献 [12 ] 研究的情形, 使得系统模型的应用更加灵活, 也符合客观实际需求. 例如在一个加工订单所需产品的生产制造厂中, 由于启动生产的成本较高, 因此生产管理者为了减少频繁启动系统的费用, 只有当订单积累到一定数量 (例如 $N$ 个) 时才启动设备生产产品. 但是, 在碰到订单时间要求较紧急且积累的订单数又没有达到这个数量时, 管理者则以某个概率 $p\left( {0\leq p\leq1} \right)$ 来解决这种情形, 于是提出启动生产的 $(p,N)$-策略. 当系统完成所有订单需要的产品时, 系统就会从事一项辅助性工作来增加收入. 当这项辅助性工作结束后且系统中没有新的订单时, 管理者考虑到后面订单到来的可能性较大, 往往不会立即安排系统继续从事另一项辅助性工作, 而是让系统等待一段时间 (耐烦期), 以便能及时处理即将到达的订单. 若在这一段时间内还没有订单到达, 则系统又会去从事另一项辅助性工作. 我们使用直观的概率分解分析方法, 即应用全概率分解分析技术和更新过程理论分析了系统从任意初始状态出发的瞬态队长分布, 并且通过拉普拉斯变换工具得到队长的瞬态分布关于时间 $t$ 的拉普拉斯变换表达式, 再通过洛必达法则求得队长稳态分布的递推表达式, 同时获得了稳态队长分布的概率母函数和平均队长的表达式. 最后, 通过数值计算实例讨论了系统的容量优化设计问题, 以及系统的空闲率与附加平均队长对系统参数的敏感性.
2 模型的建立与描述
1) 系统中有一个服务员 (服务台) 提供服务, 并为顾客提供无限的等待空间. 顾客到达是速率为 $\lambda(\lambda>0)$ 的泊松过程, 即顾客相继到达独立, 且到达的时间间隔 $\tau $ 有分布函数 $F(t)=1-{{\rm e}^{-\lambda t}}, t \ge 0 $, 而且顾客之间的服务是独立的, 服务的规则是先到先服务, 每个顾客的服务时间 $\chi$ 有分布函数 $G(t)$, 其平均服务时间记为 ${1}/{\mu }\;(0<\mu <\infty )$.
2) 耐烦服务员的不中断多重休假机制与服务的 $(p,N)$-策略: 每当系统变空时, 服务员就去进行一次不中断的完整休假, 休假时间长度 $V$ 服从一般分布 $V(t)$. 当服务员休假回来时, 如果系统中等待服务的顾客数大于等于事先设置的阈值 $N(N\geq1)$ 时, 则服务员立即开始服务直到系统再次空竭, 若系统中有顾客但顾客数少于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务继续休假直到系统中的顾客数累积到 $N$ 个时才服务. 若服务员休假回来时系统中没有顾客, 则服务员呆在系统中经历一段随机长度 $U$ 的时间 (这段时间就称为服务员的耐烦期), 其分布为一般分布 $U(t)$. 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在耐烦期结束时仍无顾客到达, 则服务员就开启新一轮休假. 依次循环下去.
3) 顾客的到达间隔时间 $\tau $、顾客的服务时间 $\chi $、服务员的休假时间 $V$、 服务员的耐烦期 $U$ 是彼此独立的.
4) 为研究系统的瞬态特性, 假设在 $t=0$ 时刻, 如果系统中有顾客则立即开始服务, 如果系统是空的, 则服务员留在系统中等待顾客的到达并立即服务 (这样的假设更符合实际情况, 但稳态结果与初始状态假设无关).
3 系统队长的瞬态概率分布
为了方便后续问题讨论, 本文先给出一些定义、引理以及主要的符号说明.
定义 3.1 [4 ] “系统闲期” 是指从系统变空的时刻起, 直到其后的第一个顾客到达系统为止的这段时间. 令 ${\hat \tau _j}$ 表示第 $j$ 个系统闲期的长度, 因为顾客的到达是参数 $\lambda(\lambda>0)$ 的 Poisson 流, 于是 ${\hat \tau _j}$ 的分布为 $F(t) = P\{ {\hat \tau _j} \le t\} = 1 - {{\rm e}^{ - \lambda t}},t \ge 0,j = 1,2 \cdots.$
定义 3.2 “服务员非忙期” 是指从系统刚变空的时刻起, 直到其后服务员开始为顾客提供服务为止的这一段时间, 其中包含服务员的休假时间和耐烦时间.
定义 3.3 [4 ] “服务员忙期” 是指从服务员开始为顾客服务的时刻开始, 直到系统再次变空为止的这一段时间.由于服务员忙期开始时系统中可能有多个顾客, 因此若令 $b$ 表示从一个顾客开始的 “服务员忙期” 长度, 其分布记为 $B(t)=P\left\{ b\le t \right\}$, $b(s)$ 为其拉普拉斯--司梯阶 $(LS)$ 变换.
引理3.1 [4 ] 对 $\Re (s)>0, b(s)$ 是方程 $z=g(s+\lambda -\lambda z)$ 在 $\left| z \right|<1$ 内的唯一解, 且 $B(t)$ 表示为
其中, $\Re (s)$ 表示复变量 $s$ 的实部, $\rho =\frac{\lambda }{\mu }$ 表示系统的交通强度, $\omega (0<\omega <1)$ 是方程 $z=g(\lambda -\lambda z)$ 在$(0,1)$ 内的根. ${{G}^{(k)}}(t)$ 表示 $G(t)$ 的 $k$ 重卷积, $k=1,2\cdots$, 且 ${{G}^{(0)}}(t)=1,t\geq0$, $g(s)=\int_{0}^{\infty }{{{\rm e}^{-st}}{\rm d}G(t)}$ 为相应 $G(t)$ 的 $LS$ 变换. 以下出现具有相同的含义.
又令 ${b^{(i)}}$ 为从 $i$ 个顾客开始的服务员忙期长度, 由于顾客到达过程为 Poisson 过程, 则其分布为 $P\left\{ {b^{(i)}}\le \right.$$\left. t \right\}={{B}^{(i)}}(t)$, $t\ge 0$, $i\ge 1$.
若令 $N(t)$ 为系统在 $t$ 时刻的队长, ${{Q}_{j}}(t)=P\left\{ b>t\ge 0;N(t)=j \right\}$ 表示服务员忙期 $b$ 开始后时间长为 $t$ 的时刻 $t$ 处队长为 $j$ 的联合概率, 且 $t=0$ 时刻时只有一个顾客, 服务员忙期 $b$ 刚开始, 即 ${{Q}_{1}}(0)=1$, ${{Q}_{j}}(0)=0$, $j>1$.
引理 3.2 [4 ] 令 $q_{j}^{*}(s)=\int_{0}^{\infty }{{{\rm e}^{-st}}{{Q}_{j}}(t){\rm d}t}$ 为 ${{Q}_{j}}(t)$ 的拉普拉斯 $(L)$ 变换, 对 $\Re (s)>0$ 有
其中当 $j<0$ 时, 有 $q_{j}^{*}(s)=0,$ 且求和 $\sum\limits_{k=0}^{j}{(\cdot)_{k}=0}$.
下面讨论系统在任意时刻队长的瞬态概率分布. 令 $N(t)$ 为系统在任意 $t$ 时刻的队长, 且
表示系统在初始时刻有 $i$ 个顾客的条件下, 时刻 $t$ 队长为 $j$ 的瞬态概率, 其 $L$ 变换为$p_{ij}^{*}(s)=\int_{0}^{\infty}{\rm e}^{-st}{{p}_{ij}}(t){\rm d}t$, ${i,j = 0,1, \cdots }$.
定理 3.1 对 $\Re (s)>0$ 和 $i\ge 1$, 有
(3.1) $p_{00}^{*}(s) = \frac{{1 - f(s)}}{s}\left\{ {1 + \frac{{f\left( s \right)b\left( s \right)\left[ {1 - v\left( {s + \lambda } \right)u\left( {s + \lambda } \right)} \right]}}{{{\Delta _N}\left( s \right)}}} \right\},$
(3.2) $p_{i0}^{*}(s)= \frac{{1 - f\left( s \right)}}{s}\left\{ {\frac{{{b^i}\left( s \right)\left[ {1 - v\left( {s + \lambda } \right)u\left( {s + \lambda } \right)} \right]}}{{{\Delta _N}\left( s \right)}}} \right\}, i\geq1,$
证 令 $\{ {\tau _i},i \ge 1\}$ 表示顾客的到达间隔时间序列, ${s_k} = \sum\limits_{i = 1}^k {\left( {{V_i} + {U_i}} \right)}$, ${l_k} = \sum\limits_{i = 1}^k {{\tau _i}}, k \ge 1,$ 且 ${s_0} = {l_0} = 0,\bar F(t) = 1 - F(t)$. 因为在时刻 $t$ 系统的队长为 0 的充要条件是时刻 $t$ 处于系统没有顾客的时期 (系统的闲期) 内, 所以运用全概率分解技术和更新过程理论有
(3.3) $\begin{matrix} {{p}_{00}}(t)&=P\left\{ 0\le t<{{{\hat{\tau }}}_{1}} \right\}+P\left\{ {{{\hat{\tau }}}_{1}}+{{b}_{1}}\le t<{{{\hat{\tau }}}_{1}}+{{b}_{1}}+{{{\hat{\tau }}}_{2}} \right\}+P\left\{ {{{\hat{\tau }}}_{1}}+{{b}_{1}}+{{{\hat{\tau }}}_{2}}\le t,N(t)=0 \right\}\nonumber\\ &=\overline{F}(t)+\int_{0}^{t}{\bar{F}(t-x){\rm d}[F(x)*B(x)]}\nonumber\\ &~~~+\sum\limits_{k=1}^{\infty}P\left\{ {{{\hat \tau }_1} + {b_1} + {{\hat \tau }_2} \le t,{s_{k - 1}} + {V_k} \le {{\hat \tau }_2} < {s_k},N(t) = 0} \right\}\nonumber\\ &~~~+\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.\nonumber\\ &~~~\left. {{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t) = 0} \right\}\nonumber\\ &~~~+p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.\nonumber\\ &~~~\left. {{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t) = 0} \right\}\nonumber\\ &~~~+(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} + {l_{N - m}} \le t,} \right.{s_{k - 1}} \le {\hat \tau _2} < {s_{k - 1}} + {V_k}, \nonumber\\ &~~~\left. {{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},N(t) = 0} \right\}, \end{matrix}$
(3.4) $\begin{matrix} &\sum\limits_{k=1}^{\infty}\int_{0}^{t}{P\left\{ {{{\hat \tau }_2} \le t - x,{s_{k - 1}} + {V_k} \le {{\hat \tau }_2} < {s_k},N(t - x) = 0} \right\}}{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&\sum\limits_{k=1}^{\infty}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{10}}\left( {t - x - y - w} \right)\bar U\left( w \right)}{{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right)\nonumber\\ & \times{\rm d}\left[ {{V^{(k)}}(y) * {U^{(k - 1)}}(y)} \right] {{\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
(3.5) $\begin{matrix} &\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = 0\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{m0}}(t - x - y - w)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}{\rm d}V(w)\nonumber\\ &{\times {\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
(3.6) $\begin{matrix} &p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = 0\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{m0}}(t - x - y - w)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}{\rm d}V(w)\nonumber\\ &{\times {\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
(3.7) $\begin{matrix} &(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} + {l_{N - m}} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat{\tau} }_2} + {l_m}, } \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = 0\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}\int_{0}^{t-x-y-w}{{p_{N0}}(t - x - y - w - z)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}\nonumber\\ &{\times {{\rm d}{F^{(N - m)}}(z)}{\rm d}V(w){\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
将 (3.4)-(3.7) 式代入 (3.3) 式得
(3.8) $\begin{matrix} {p_{00}}\left(t\right)=&\bar F(t)+\int_0^t{\bar F(t-x){\rm d}\left[{F(x)*B(x)}\right]}\nonumber\\ &+ \sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{10}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}\nonumber\\ & {\times {\rm d}F\left( w \right)d\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F\left( x \right) * B\left( x \right)} \right]}\nonumber\\ &+ \sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{m0}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} } \nonumber\\ & {\times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F\left( x \right) * B\left( x \right)} \right]}\nonumber\\ &+ p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N-1 } {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{m0}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} } \nonumber\\ & {\times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F\left( x \right) * B\left( x \right)} \right]}\nonumber\\ &+ (1 - p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{N0}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } } \nonumber\\ & {\times {{{\rm e}^{ - \lambda \left( {w + y} \right)}}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w){\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
(3.9) $\begin{matrix} {p_{i0}}\left(t\right)=&\int_0^t {\bar F(t - x){\rm d}{B^{(i)}}(x)}\nonumber\\ &+ \sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{10}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}\nonumber\\ & {\times {\rm d}F\left( w \right){\rm d}\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]}{\rm d}{B^{(i)}}(x)\nonumber\\ &+ \sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{m0}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} } \nonumber\\ & {\times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]}{\rm d}{B^{(i)}}(x)\nonumber\\ &+ p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N-1 } {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{m0}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} } \nonumber\\ & {\times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]}{\rm d}{B^{(i)}}(x)\nonumber\\ &+ (1 - p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{N0}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } }\nonumber\\ & {\times {{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w){\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{\rm d}{B^{(i)}}(x), \end{matrix}$
对 (3.8) 与 (3.9) 式分别做 $L$ 变换, 得
(3.10) $\begin{matrix} p_{00}^{*}(s)=& \frac{{\left[ {1 - f(s)} \right]\left[ {1 + f(s)b(s)} \right]}}{s}\nonumber\\ & + \frac{{{{\left[ {f(s)} \right]}^2}b(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]p_{10}^{*}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\nonumber\\ &+\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{m0}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{m0}^{*}(s){v_m}(s + \lambda )} \nonumber\\ &+(1-p)p_{N0}^{*}(s)\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}, \end{matrix}$
(3.11) $\begin{matrix} p_{i0}^{*}(s) = &\frac{{\left[ {1 - f(s)} \right]{b^i}(s)}}{s}\nonumber\\ & + \frac{{f(s){b^i}(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]p_{10}^{*}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\nonumber\\ &+\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{m0}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{m0}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+(1-p)p_{N0}^{*}(s)\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}, \end{matrix}$
(3.12) $\begin{matrix} p_{i0}^{*}(s)=\frac{{{b^{i - 1}}(s)}}{{f(s)}}\left\{ { p_{00}^{*}(s)- \frac{{1 - f(s)}}{s}} \right\}, i\ge 1, \end{matrix}$
将 (3.12) 式代入 (3.10) 式可得到 (3.1) 式, 再把 (3.1) 式代入 (3.12) 式可得到 (3.2) 式.
定理 3.2 对 $\Re (s)>0$ 和 $i\geq1$ 有
1) 当 $j=1,2\cdots N-1$ 时,
(3.13) $\begin{matrix} p_{0j}^{*}(s)=f(s)\frac{{{\sigma _j}(s)}}{{{\Delta _N}(s)}} + f(s)q_{j}^{*}(s)\left\{ {1 + \frac{{f(s)b(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]}}{{{\Delta _N}(s)}}} \right\}, \end{matrix}$
(3.14) $\begin{matrix} p_{ij}^{*}(s)=\sum\limits_{k = 1}^i {q_{j-i+k}^{*}(s){b^{k - 1}}(s)} + \frac{{{b^{i - 1}}(s)\left\{ {{\sigma _j}(s) + f(s)q_{j}^{*}(s)b(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]} \right\}}}{{{\Delta _N}(s)}}, \end{matrix}$
(3.15) $\begin{matrix} p_{0j}^{*}(s)=f(s)\frac{{{\theta _j}(s)}}{{{\Delta _N}(s)}} + f(s)q_{j}^{*}(s)\left\{ {1 + \frac{{f(s)b(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]}}{{{\Delta _N}(s)}}} \right\}, \end{matrix}$
(3.16) $\begin{matrix} p_{ij}^{*}(s)=\sum\limits_{k = 1}^i {q_{j-i+k}^{*}(s) {b^{k - 1}}(s)} + \frac{{{b^{i - 1}}(s)\left\{ {{\theta _j}(s) + f(s)q_{j}^{*}(s)b(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]} \right\}}}{{{\Delta _N}(s)}}, \end{matrix}$
其中 ${\Delta _N}(s)$ 见定理 $3.1$, $q_{j}^{*}(s)$ 由引理 $3.2$ 给出.
证 当 $j=1,2,\cdots N-1$ 时, 时刻 $t$ 队长为 $j$ 可分为三种情况: 1) 时刻 $t$ 落在服务员忙期中且系统中的队长为 $j$; 2) 时刻 $t$ 落在服务员假期中且系统中的队长为 $j$; 3) 时刻 $t$ 落在假期结束后的服务员非忙期中且系统中的队长为 $j$. 运用全概率分解技术有
(3.17) $\begin{matrix} {p_{0j}}\left(t\right)=&P\left\{ {{{\hat \tau }_1} \le t < {{\hat \tau }_1} + {b_1},N(t) = j} \right\} + P{\rm{\{ }}{\hat \tau _1} + {b_1} + {\hat \tau _2} \le t,N(t) = j\}\nonumber\\ =&\int_{0}^{t}{Q_j}(t - x){\rm d}F(x)+\sum\limits_{k = 1}^\infty P\left\{ {{{\hat \tau }_1} + {b_1} + {{\hat \tau }_2} \le t,{s_{k - 1}} + {V_k} \le {{\hat \tau }_2} < {s_k},N(t) = j} \right\}\nonumber\\ &+ \sum\limits_{k = 1}^\infty {P\left\{ {{{\hat \tau }_1} + {b_1} + {{\hat \tau }_2} \le t < {{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k},{l_{j - 1}} \le t - ({{\hat \tau }_1} + {b_1} + {{\hat \tau }_2}) < {l_j},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k}\}\nonumber\\ &+\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\left. {N(t) = j} \right\}\nonumber\\ &+p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\left. {N(t) = j} \right\}\nonumber\\ &+ (1-p)\sum\limits_{k = 1}^{\infty}\sum\limits_{m = 1}^{N - 1}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} + {l_{N - m}} \le t,} \right.}{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},N(t) = j} \}\nonumber\\ &+(1\!-\! p)\sum\limits_{k = 1}^{\infty}\sum\limits_{m = 1}^j{P\left\{ {{{\hat \tau }_1} \!+\! {b_1} \!+\! {s_{k - 1}} \!+\! {V_k} \le t,{s_{k - 1}} \!\le\! {{\hat \tau }_2} \!+\! {l_{m - 1}} \!\le\! {s_{k - 1}}\! +\! {V_k} \!<\! {{\hat \tau }_2} \!+\! {l_m},} \right.}\nonumber\\ & {s_{k - 1}} \le {\hat \tau _2} < {s_{k - 1}} + {V_k},\left. {{l_{j - m}} \le t - ({{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k}) < {l_{j - m + 1}}} \right\}, \end{matrix}$
(3.18) $\begin{matrix} &\sum\limits_{k=1}^{\infty}\int_{0}^{t}{P\left\{ {{{\hat \tau }_2} \le t - x,{s_{k - 1}} + {V_k} \le {{\hat \tau }_2} < {s_k},N(t - x) = j} \right\}}{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&\sum\limits_{k=1}^{\infty}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{1j}}\left( {t - x - y - w} \right)\bar U\left( w \right)}{{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right){\rm d}\left[ {{V^{(k)}}(y) * {U^{(k - 1)}}(y)} \right]\nonumber\\ &{\times{{\rm d}\left[ {F(x) * B(x)} \right]}}, \end{matrix}$
(3.19) $\begin{matrix} &\sum\limits_{k = 1}^\infty {\int_0^t {P\left\{ {{{\hat \tau }_2} \le t - x < {s_{k - 1}} + {V_k},{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},{l_{j - 1}} \le t - x - {{\hat \tau }_2} < {l_j}} \right\}} } \nonumber\\ &{\times {\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ =&\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\bar V\left( {t - x - y} \right)\frac{{{{\left[ {\lambda \left( {t - x - y} \right)} \right]}^j}}}{{j!}}{{\rm e}^{ - \lambda (t - x)}}{\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]} } }\nonumber\\ &{\times {\rm d}\left[ {F(x) * B(x)} \right]}, \end{matrix}$
(3.20) $\begin{matrix} &\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = j\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{mj}}(t - x - y - w)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}{\rm d}V(w)\nonumber\\ &{\times {\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
(3.21) $\begin{matrix} &p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = j\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{{p_{mj}}(t - x - y - w)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}{\rm d}V(w)\nonumber\\ &{\times {\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
(3.22) $\begin{matrix} &(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}{P\left\{ {{s_{k - 1}} + {V_k} + {l_{N - m}} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} <{{\hat{\tau} }_2} + {l_m}, } \right.}\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},N(t - x) = j\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}\int_{0}^{t-x-y-w}{{p_{Nj}}(t - x - y - w - z)\frac{{{{(\lambda w)}^m}}}{{m!}}{{\rm e}^{ - \lambda (w + y)}}}\nonumber\\ &{\times {{\rm d}{F^{(N - m)}}(z)}{\rm d}V(w){\rm d}\left[ {{V^{(k - 1)}}(y) * {U^{(k - 1)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
(3.23) $\begin{matrix} &(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{j}\int_0^t {P\left\{ {{s_{k - 1}} + {V_k} \le t - x,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < } \right.} {{\hat \tau }_2} + {l_m},\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},{{l_{j - m}} \le t - x - {s_{k - 1}} - {V_k} < {l_{j - m + 1}}}\} }{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ =&(1-p)\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{j}\int_{0}^{t}\int_{0}^{t-x}\int_{0}^{t-x-y}{\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}\frac{{{{\left[ {\lambda (t - x - y - w)} \right]}^{j - m}}}}{{(j - m)!}}{{\rm e}^{ - (t - x)}}{\rm d}V(w)}\nonumber\\ &{\times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
将 (3.18)-(3.23) 式代入 (3.17) 式得
(3.24) $\begin{matrix} {p_{0j}}\left(t\right)=&\int_0^t {{Q_j}(t - x){\rm d}F(x)}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {{{\rm e}^{ - (t - x)}}\bar V(t - x - y)\frac{{{{\left[ {\lambda (t - x - y)} \right]}^j}}}{{j!}}} } } \nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{1j}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right)\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F\left( x \right) * B\left( x \right)} \right]}\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{Nj}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } } \nonumber\\ & { \times {{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w)d\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right]\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^j {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}\frac{{{{\left[ {\lambda (t - x - y - w)} \right]}^{j - m}}}}{{(j - m)!}}{{\rm e}^{ - (t - x)}}{\rm d}V(w)} } } } }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
(3.25) $\begin{matrix} {p_{ij}}\left(t\right)=&\sum\limits_{k = 1}^i {{Q_{j - i + k}}(t) * {B^{(k - 1)}}(t)}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {{{\rm e}^{ - (t - x)}}\bar V(t - x - y)\frac{{{{\left[ {\lambda (t - x - y)} \right]}^j}}}{{j!}}} } } \nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{1j}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right)\nonumber\\ & { \times{\rm d}\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{Nj}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } } \nonumber\\ & { \times {{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w){\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{{\rm d}{B^{(i)}}(x)}\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^j {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}\frac{{{{\left[ {\lambda (t - x - y - w)} \right]}^{j - m}}}}{{(j - m)!}}{{\rm e}^{ - (t - x)}}{\rm d}V(w)} } } } }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{{\rm d}{B^{(i)}}(x)}, \end{matrix}$
对 (3.24) 与 (3.25) 式分别做 $L$ 变换, 得
(3.26) $\begin{matrix} p_{0j}^{*}(s)=&f(s)q_{j}^{*}(s) + \frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\int_0^\infty {{{\rm e}^{ - (s + \lambda )t}}\frac{{{{\left( {\lambda t} \right)}^j}}}{{j!}}\bar V(t)}{\rm d}t\nonumber\\ &+\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}p_{1j}^{*}(s)f(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]\nonumber\\ &+\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{mj}^{*}(s){v_m}(s + \lambda )} \nonumber\\ &+(1-p)p_{Nj}^{*}(s)\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}\nonumber\\ &+(1-p)\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^j {{v_m}(s + \lambda )} \int_0^\infty {{{\rm e}^{ - \left( {s + \lambda } \right)t}}\frac{{{{\left( {\lambda t} \right)}^{j - m}}}}{{\left( {j - m} \right)!}}}{\rm d}t, \end{matrix}$
(3.27) $\begin{matrix} p_{ij}^{*}(s)=&\sum\limits_{k = 1}^i {q_{j-i+k}^{*}(s){b^{k - 1}}(s)}\nonumber\\ & + \frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\int_0^\infty {{{\rm e}^{ - (s + \lambda )t}}\frac{{{{\left( {\lambda t} \right)}^j}}}{{j!}}\bar V(t)}{\rm d}t\nonumber\\ &+\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}p_{1j}^{*}(s)f(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]\nonumber\\ &+\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+(1-p)p_{Nj}^{*}(s)\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}\nonumber\\ &+(1 - p)\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^j {{v_m}(s + \lambda )} \int_0^\infty {{{\rm e}^{(s + \lambda )t}}\frac{{{{(\lambda t)}^{j - m}}}}{{(j - m)!}}{\rm d}t}, \end{matrix}$
(3.28) $\begin{matrix} p_{ij}^{*}(s)=\sum\limits_{k=1}^{i}{q_{j-i+k}^{*}(s){{b}^{k-1}}(s)+\frac{{{b}^{i-1}}(s)}{f(s)}}\{p_{0j}^{*}(s)-f(s)q_{j}^{*}(s)\}, i\ge 1, \end{matrix}$
将 (3.28) 式代入 (3.26) 式可得到 (3.13) 式, 再把 (3.13) 式代入 (3.28) 式可得到 (3.14) 式.
当 $j\geq N$ 时, 时刻 $t$ 队长为 $j$ 的情况分为:1) 时刻 $t$ 落在服务员忙期中且系统中的队长为 $j$; 2) 时刻 $t$ 落在服务员假期中且系统中的队长为 $j$. 由全概率分解技术, 得
(3.29) $\begin{matrix} {p_{0j}}\left(t\right)=&P\left\{ {{{\hat \tau }_1} \le t < {{\hat \tau }_1} + {b_1},N(t) = j} \right\}\nonumber\\ &+\sum\limits_{k = 1}^\infty P\left\{ {{{\hat \tau }_1} + {b_1} + {{\hat \tau }_2} \le t,{s_{k - 1}} + {V_k} \le {{\hat \tau }_2} < {s_k},N(t) = j} \right\}\nonumber\\ &+ \sum\limits_{k = 1}^\infty {P\left\{ {{{\hat \tau }_1} + {b_1} + {{\hat \tau }_2} \le t < {{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k},{l_{j - 1}} \le t - ({{\hat \tau }_1} + {b_1} + {{\hat \tau }_2}) < {l_j},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k}\}\nonumber\\ &+\sum\limits_{k=1}^{\infty}\sum\limits_{m=N}^{\infty}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\left. {N(t) = j} \right\}\nonumber\\ &+p\sum\limits_{k=1}^{\infty}\sum\limits_{m=1}^{N-1}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} \le t,{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},} \right.}\nonumber\\ & {s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\left. {N(t) = j} \right\}\nonumber\\ &+ (1-p)\sum\limits_{k = 1}^{\infty}\sum\limits_{m = 1}^{N - 1}{P\left\{ {{{\hat \tau }_1} + {b_1} + {s_{k - 1}} + {V_k} + {l_{N - m}} \le t,} \right.}{s_{k - 1}} \le {{\hat \tau }_2} < {s_{k - 1}} + {V_k},\nonumber\\ &{{s_{k - 1}} \le {{\hat \tau }_2} + {l_{m - 1}} \le {s_{k - 1}} + {V_k} < {{\hat \tau }_2} + {l_m},N(t) = j} \}\nonumber\\ =&\int_0^t {{Q_j}(t - x)dF(x)}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {{{\rm e}^{ - (t - x)}}\bar V(t - x - y)\frac{{{{\left[ {\lambda (t - x - y)} \right]}^j}}}{{j!}}} } } \nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{1j}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right)\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F(x) * B(x)} \right]}\nonumber\\ &+p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{\rm d}\left[ {F\left( x \right) * B\left( x \right)} \right]}\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{Nj}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } } \nonumber\\ & { \times {{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w){\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{\rm d}\left[ {F(x) * B(x)} \right], \end{matrix}$
(3.30) $\begin{matrix} {p_{ij}}\left(t\right)=&\sum\limits_{k = 1}^i {{Q_{j - i + k}}(t) * {B^{(k - 1)}}(t)} +\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {{{\rm e}^{ - (t - x)}}\bar V(t - x - y)\frac{{{{\left[ {\lambda (t - x - y)} \right]}^j}}}{{j!}}} } } \nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{1j}}} \left( {t - x - y - w} \right)} } } \bar U\left( w \right){{\rm e}^{ - \lambda y}}{\rm d}F\left( w \right)\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( k \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+\sum\limits_{k = 1}^\infty {\sum\limits_{m = N}^\infty {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+p\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {{p_{mj}}} \left( {t - x - y - w} \right)} } \frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}{{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}V\left( w \right)} }\nonumber\\ & { \times {\rm d}\left[ {{V^{\left( {k - 1} \right)}}\left( y \right) * {U^{\left( {k - 1} \right)}}\left( y \right)} \right]{{\rm d}{B^{(i)}}(x)}}\nonumber\\ &+(1-p)\sum\limits_{k = 1}^\infty {\sum\limits_{m = 1}^{N - 1} {\int_0^t {\int_0^{t - x} {\int_0^{t - x - y} {\int_0^{t - x - y - w} {{p_{Nj}}\left( {t - x - y - w - z} \right)\frac{{{{\left( {\lambda w} \right)}^m}}}{{m!}}} } } } } } \nonumber\\ & { \times {{\rm e}^{ - \lambda \left( {w + y} \right)}}{\rm d}{F^{(N - m)}}(z){\rm d}V(w){\rm d}\left[ {{V^{\left( {k - 1} \right)}}(y) * {U^{\left( {k - 1} \right)}}(y)} \right]}{{\rm d}{B^{(i)}}(x)}, \end{matrix}$
对(3.29)与(3.30)式分别做 $L$ 变换
(3.31) $\begin{matrix} p_{0j}^{*}(s)=&f(s)q_{j}^{*}(s) + \frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\int_0^\infty {{{\rm e}^{ - (s + \lambda )t}}\frac{{{{\left( {\lambda t} \right)}^j}}}{{j!}}\bar V(t)}{\rm d}t \nonumber\\ &+\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}p_{1j}^{*}(s)f(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]\nonumber\\ &+\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{mj}^{*}(s){v_m}(s + \lambda )} \nonumber\\ &+(1-p)p_{Nj}^{*}(s)\frac{{f(s)b(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}, \end{matrix}$
(3.32) $\begin{matrix} p_{ij}^{*}(s)=&\sum\limits_{k = 1}^i {q_{j-i+k}^{*}(s){b^{k - 1}}(s)} + \frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\int_0^\infty {{{\rm e}^{ - (s + \lambda )t}}\frac{{{{\left( {\lambda t} \right)}^j}}}{{j!}}\bar V(t)}{\rm d}t\nonumber\\ &+\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}p_{1j}^{*}(s)f(s)v(s + \lambda )\left[ {1 - u(s + \lambda )} \right]\nonumber\\ &+\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = N}^\infty {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+p\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {p_{mj}^{*}(s){v_m}(s + \lambda )}\nonumber\\ &+(1-p)p_{Nj}^{*}(s)\frac{{{b^i}(s)}}{{1 - v(s + \lambda )u(s + \lambda )}}\sum\limits_{m = 1}^{N - 1} {{f^{N - m}}(s){v_m}(s + \lambda )}, \end{matrix}$
(3.33) $\begin{matrix} p_{ij}^{*}(s)=\sum\limits_{k=1}^{i}{q_{j-i+k}^{*}(s){{b}^{k-1}}(s)+\frac{{{b}^{i-1}}(s)}{f(s)}}\{p_{0j}^{*}(s)-f(s)q_{j}^{*}(s)\}, i\ge 1, \end{matrix}$
将 (3.33) 式代入 (3.31) 式可得到 (3.15) 式, 再把 (3.15) 式代入 (3.33) 式可得到 (3.16) 式.
定理 3.3 令 ${{p}_{j}}=\underset{t\to \infty }{\mathop{\lim }}\,P\left\{ N(t)=j \right\}$, $j=0,1,2,\cdots $, 则有
1) 当 $\rho= {\textstyle{\lambda \over \mu }}\ge 1$ 时, ${{p}_{j}}=0$, $j=0,1,2,\cdots $, 所以不构成概率分布;
2) 当 $\rho = {\textstyle{\lambda \over \mu }}<1$ 时, $p_{j}$ 有如下递推表达式
(3.34) ${{p}_{0}}=\left( {1 - \rho } \right)\frac{{1 - {v_0}u(\lambda )}}{{{\Delta _N}}}, $
(3.35) ${{p}_{j}}=\frac{{\lambda (1 - \rho )\left\{ {{\sigma _j} + {q_j}{v_0}\left[ {1 - u(\lambda )} \right]} \right\}}}{{{\Delta _N}}},j = 1,2, \cdots N - 1,$
(3.36) ${{p}_{j}}=\frac{{\lambda (1 - \rho )\left\{ {{\theta _j} + {q_j}{v_0}\left[ {1 - u(\lambda )} \right]} \right\}}}{{{\Delta _N}}},j = N,N + 1, \cdots,$
且此时 $\left\{ {{p_{j,}}j = 0,1,2 \cdots } \right\}$ 构成概率分布, 其中
证 由全概率公式和控制收敛定理得 ${{p}_{j}}=\sum\limits_{i=0}^{\infty }{P\left\{ N(0)=i \right\}\cdot \underset{t\to \infty }{\mathop{\lim }}\,{{p}_{ij}}(t)},\,j\geq0$, 且 $\underset{t\to \infty }{\mathop{\lim }}\,{{p}_{ij}}(t)=\underset{s\to {{0}^{+}}}{\mathop{\lim }}\,sp_{ij}^{*}(s)$.
当 $\rho > 1$ 时, 由引理 3.1 有 $\mathop {\lim }\limits_{s \to {0^ + }} b(s) = \omega \left( {0 < \omega < 1} \right)$, 且 $\mathop {\lim }\limits_{s \to {0^ + }} {\Delta _N}(s) \ne 0$, 此时直接计算可得 $\mathop {\lim }\limits_{s \to {0^ + }} s{p_{ij}}^*(s) = 0,i,j \ge 0$. 当 $\rho = 1$ 时, 由引理 3.1 有 $\mathop {\lim }\limits_{s \to {0^ + }} b(s) = 1$ 且 $E(b) = \infty$, 但 $\mathop {\lim }\limits_{s \to {0^ + }} {\Delta _N}(s)=0$, $\frac{\rm{d}}{{{\rm{d}}s}}[{\Delta _N}(s)]\left| {_{s = 0}} \right. = \infty $, 此时使用洛必达法则可得 $\mathop {\lim }\limits_{s \to {0^ + }} s{p_{ij}}^{*}(s) = 0$, $i,j \ge 0$, 从而当 $\rho \ge 1$ 时, ${p_j} = 0,j = 0,1,2 \cdots $.
当 $\rho < 1$ 时, 由引理 3.1 有 $\mathop {\lim }\limits_{s \to {0^ + }} b(s) = 1$, $E(b) =\frac{1}{{\mu - \lambda }}$, 而且
又使用洛必达法则, 经计算可得到 ${p_j}(j = 0,1,2 \cdots )$ 的递推表达式.
下面证明当 $\rho < 1$ 时 ${\rm{\{ }}{p_j},j = 0,1,2 \cdots {\rm{\} }}$ 构成概率分布. 由
(3.37) $\begin{matrix} \sum\limits_{j = 0}^\infty {p_j}=&{\frac{{\left( {1 - \rho } \right)\left[ {1 - {v_0}u(\lambda )} \right]}}{{{\Delta _N}}}}+\frac{{\lambda \left( {1 - \rho } \right)}}{{{\Delta _N}}}{v_0}\left[ {1 - u(\lambda )} \right]\sum\limits_{j = 1}^\infty {{q_j} + } \frac{{\lambda \left( {1 - \rho } \right)}}{{{\Delta _N}}}\sum\limits_{j = 1}^\infty {{\theta _j}}\nonumber\\ & + \frac{{(1 - p)(1 - \rho )}}{{{\Delta _N}}}\sum\limits_{j = 1}^{N - 1} {\sum\limits_{m = 1}^j {{v_m}} }, \end{matrix}$
(3.38) $\begin{matrix} \sum\limits_{j = 1}^\infty {{\theta _j}} = E(b)\left\{ {\lambda E(V) + (1 - p)\sum\limits_{m = 1}^{N - 1} {(N - m){v_m}} } \right\} + E(V) - \frac{{1 - {v_0}}}{\lambda }, \end{matrix}$
(3.39) $\begin{matrix} \sum\limits_{j = 1}^{N - 1} {\sum\limits_{m = 1}^j {{v_m}} = \sum\limits_{m = 1}^{N - 1} {\sum\limits_{j = m}^{N - 1} {{v_m}} = \sum\limits_{m = 1}^{N - 1} {\left( {N - m} \right){v_m}} } }, \end{matrix}$
(3.40) $\begin{matrix} \sum\limits_{j = 1}^\infty {{q_j} = \frac{1}{{\mu - \lambda }}}, \end{matrix}$
就可完成证明, 即 $\sum\limits_{j = 0}^\infty {{p_j} = } 1$.
定理 3.4 令 ${P}(z)$ 表示该系统稳态队长分布的概率母函数, 则当 $\rho <1$ 时, 有
(3.41) $\begin{matrix} P(z) = &\frac{{(1 - \rho )(1 - z)g(\lambda (1 - z))}}{{g(\lambda (1 - z)) - z}}\nonumber\\ &\times{\frac{{{v_0}\left[ {1 - u(\lambda )} \right](1 - z) + 1 - v(\lambda (1 - z)) + (1 - p)\sum\limits_{m = 1}^{N - 1} {({z^m} - {z^N}){v_m}} }}{{(1 - z){\Delta _N}}}},\ \left| z \right| < 1, \end{matrix}$
(3.42) $\begin{matrix} \bar L = \rho + \frac{{{\lambda ^2}E({\chi ^2})}}{{2(1 - \rho )}} + \frac{{{\lambda ^2}E({V^2}) + (1 - p)\sum\limits_{m = 1}^{N - 1} {\left[ {N(N - 1) - m(m - 1)} \right]{v_m}} }}{{2{\Delta _N}}}. \end{matrix}$
证 由 ${P}(z)=\sum\limits_{j=0}^{\infty }{{{z}^{j}}{{p}_{j}}}$ 可得
(3.43) $\begin{matrix} P(z) = &\frac{{\left( {1 - \rho } \right)\left[ {1 - {v_0}u(\lambda )} \right]}}{{{\Delta _N}}} + \frac{{\lambda \left( {1 - \rho } \right)}}{{{\Delta _N}}}{v_0}\left[ {1 - u(\lambda )} \right]\sum\limits_{j = 1}^\infty {{z^j}{q_j} + } \frac{{\lambda \left( {1 - \rho } \right)}}{{{\Delta _N}}}\sum\limits_{j = 1}^\infty {{\theta _j}} {z^j}\nonumber\\ &+\frac{{(1 - p)(1 - \rho )}}{{{\Delta _N}}}\sum\limits_{j = 1}^{N - 1} {{z^j}\sum\limits_{m = 1}^j {{v_m}} }, \end{matrix}$
(3.44) $\begin{matrix} \sum\limits_{j = 1}^\infty {{\theta _j}{z^j}} =&{\sum\limits_{m = N}^\infty {{v_m}\sum\limits_{k = 1}^m {\sum\limits_{j = 1}^\infty {{q_{j - m + k}}{z^j}} } } }+\left( {1 - p} \right)\sum\limits_{m = 1}^{N - 1} {{v_m}\sum\limits_{k = 1}^N {\sum\limits_{j = 1}^\infty {{q_{j - N + k}}{z^j}} } } \nonumber\\ &+{p\sum\limits_{m = 1}^{N - 1} {{v_m}\sum\limits_{k = 1}^m {\sum\limits_{j = 1}^\infty {{q_{j - m + k}}{z^j}} } } + \sum\limits_{j = 1}^\infty {{z^j}\int_0^\infty {{{\rm e}^{ - \lambda t}}\frac{{{{\left( {\lambda t} \right)}^j}}}{{j!}}\bar V(t){\rm d}t} } }\nonumber\\ =&\sum\limits_{m = N}^\infty {{v_m}\sum\limits_{k = 1}^m {{z^{m - k}}\sum\limits_{j = 1}^\infty {{q_j}{z^j} + } } } \left( {1 - p} \right)\sum\limits_{m = 1}^{N - 1} {{v_m}\sum\limits_{k = 1}^N {{z^{N - k}}\sum\limits_{j = 1}^\infty {{q_j}{z^j}} } } \nonumber\\ &+{p\sum\limits_{m = 1}^{N - 1} {{v_m}\sum\limits_{k = 1}^m {{z^{m - k}}\sum\limits_{j = 1}^\infty {{q_j}{z^j}} } } + \int_0^\infty {{{\rm e}^{ - \lambda t}}\sum\limits_{j = 1}^\infty {\frac{{{{\left( {\lambda tz} \right)}^j}}}{{j!}}\bar V(t)}{\rm d}t} }\nonumber\\ =&\sum\limits_{j = 1}^\infty {{q_j}{z^j}\left[ {\frac{{1 - v\left( {\lambda \left( {1 - z} \right)} \right)}}{{1 - z}} + (1 - p)\sum\limits_{m = 1}^{N - 1} {(\frac{{1 - {z^N}}}{{1 - z}} - \frac{{1 - {z^m}}}{{1 - z}}){v_m}} } \right]} \nonumber\\ &+\frac{{1 - v(\lambda (1 - z))}}{{\lambda (1 - z)}} - \frac{{1 - {v_0}}}{\lambda }, \end{matrix}$
(3.45) $\begin{matrix} \sum\limits_{j = 1}^{N - 1} {{z^j}} \sum\limits_{m = 1}^j {{v_m} = } \sum\limits_{m = 1}^{N - 1} {{v_m}} \sum\limits_{j = m}^{N - 1} {{z^j} = } \sum\limits_{m = 1}^{N - 1} {\frac{{{z^m} - {z^N}}}{{1 - z}}{v_m}}, \end{matrix}$
(3.46) $\begin{matrix} \sum\limits_{j = 1}^\infty {{q_j}} {z^j} = \frac{{z\left[ {1 - g(\lambda (1 - z))} \right]}}{{\lambda \left[ {g(\lambda (1 - z)) - z} \right]}}, \end{matrix}$
即可得到 (3.41) 式, 再由 $\bar L = {\textstyle{{\rm d} \over {{\rm d}z}}}{\left. {\left[ {P\left( z \right)} \right]} \right|_{z = 1}}$ 得到 (3.42) 式.
推论 3.1 $P\{ U = 0\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 即可得到与文献 [12 ] 完全一致的结果.
推论 3.2 当 $P\left\{ {U = \infty } \right\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断单重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = \infty } \right\} = 1$ 即可得到与文献 [11 ] 完全一致的结果.
推论 3.3 当 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$, 本文研究的系统等价于多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$ 即可得到与文献 [4 ] 完全一致的结果.
推论 3.4 当 $P\left\{ {U = 0} \right\} = 1,p = 0,P\left\{ {V = 0} \right\} = 1$ 时, 本文研究的系统等价于 $N$ 策略 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1,p = 0,P\left\{ {V = 0} \right\} = 1$ 即可得到与文献 [1 ] 完全一致的结果.
4 稳态队长分布的数值计算与系统容量的优化设计
为了体现稳态队长分布在应用方面的重要意义, 本文通过对稳态队长分布进行数值计算来讨论系统容量的优化设计问题.
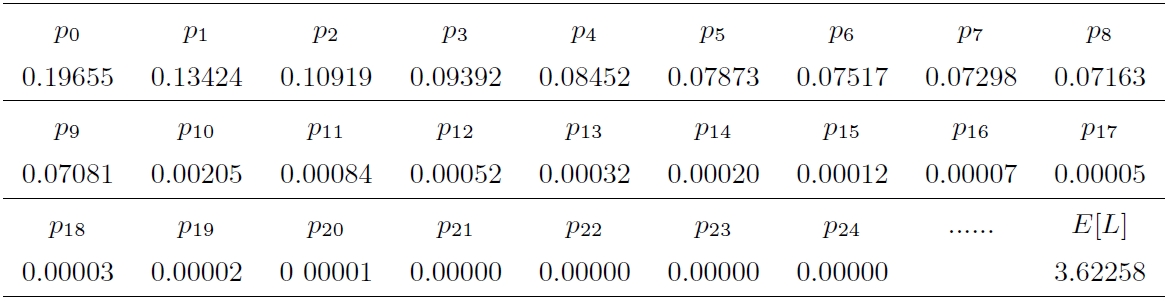
假设服务时间分布为 $G(t) = 1 - {{\rm e}^{ - \mu t}}$, 休假时间分布为 $V\left( t \right) = 1 - {{\rm e}^{ - \theta t}}$, 服务员耐烦时间分布为 $U\left( t \right) = 1 - {{\rm e}^{ - \alpha t}}$, 然后取参数值 $\lambda = 0.08,\mu = 8,\theta = 0.05,\alpha = 0.3,N = 10,p = 0.6$, 由定理 3.3, 再运用 Matlab 软件计算出稳态队长分布的数值结果如下 (见表 1 , 保留 5 位小数).
由表 1 可知, 在系统达到平稳状态时, 队长越来越大的概率逐渐变小, 而且当 $j$ 大于 21 时, 稳态队长分布 ${{p}_{j}}$ 的值接近于 0, 这是因为系统要达到平稳状态的特性决定的, 否则系统达不到平稳状态.所以在这样的参数取值下系统的容量不用设置为无穷大. 通过计算有
也就是说, 若按照平均队长为标准设计系统的容量, 则因容量不足而损失顾客的概率为 $46.61\%$, 即使比平均队长大一个单位作为标准设计系统的容量, 那么到达的顾客因为容量不足而损失的概率也达到 $38.158\%$, 流失的概率是相当大的. 所以若仅将平均队长作为容量设计的标准, 则会在实际应用中出现巨大的偏差.
为了降低顾客损失率, 我们就要将顾客的损失概率进行控制. 令 $M$ 表示系统容量, 如果要求顾客的损失概率不超过百分之 1, 即 $P\left\{ {L > M} \right\} \le 0.01$. 通过表 1 的数据可计算得到, $M \ge 11$, 即容量可设计为 11 个单位就可以达到要求. 因此得到便于做数值计算的稳态队长分布表达式 (定理 3.3) 不仅有重要的理论意义, 也有实际应用价值.
5 系统的空闲率和附加平均队长对系统参数的敏感性分析
本文涉及到的 “附加平均队长” 是指, 相对于标准的 $M/G/1$ 排队系统, 由于服务员的休假机制和系统采取的控制策略带来的平均队长的增加部分. 因此, 从上面 (3.42) 式可知本文所研究系统的附加平均队长是平均队长表达式中的第三项. 下面通过数值计算实例来讨论系统的空闲率 ${p_0}$ 与附加平均队长 ${\bar{L}_d}$ 随着参数 $p$ 与 $N$ 的变化情况.
则在 $\rho < 1$ 的情况下, 由定理 3.3 和定理 3.4 可进一步得到系统的空闲率 ${p_0}$ 与附加平均队长 ${\bar{L}_d}$ 的表达式为
(5.1) $ {p_0} = \frac{{\left( {1 - \rho } \right)\left\{ {1 - \frac{{\theta \cdot \alpha }}{{\left( {\lambda + \theta } \right)\left( {\lambda + \alpha } \right)}}} \right\}}}{{{\Delta _N}}}, $
(5.2) ${\bar L_d} = \frac{{2{{\left( {\frac{\lambda }{\theta }} \right)}^2} + (1 - p)\left( {1 - \frac{\lambda }{{\lambda + \theta }}} \right)\sum\limits_{m = 1}^{N - 1} {\left[ {N(N - 1) - m(m - 1)} \right]{{\left( {\frac{\lambda }{{\lambda + \theta }}} \right)}^m}} }}{{2\left\{ {\frac{{\theta \cdot \lambda }}{{\left( {\lambda + \theta } \right)\left( {\lambda + \alpha } \right)}} + \frac{\lambda }{\theta } + (1 - p)\left( {1 - \frac{\lambda }{{\lambda + \theta }}} \right)\sum\limits_{m = 1}^{N - 1} {\left( {N - m} \right){{\left( {\frac{\lambda }{{\lambda + \theta }}} \right)}^m}} } \right\}}},$
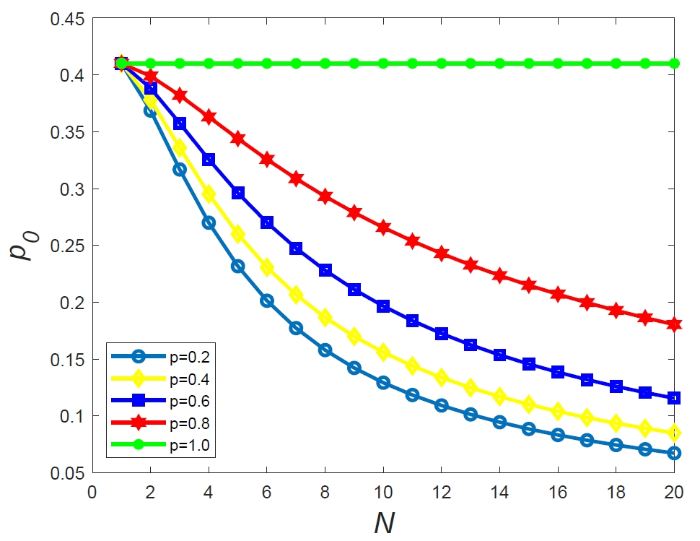
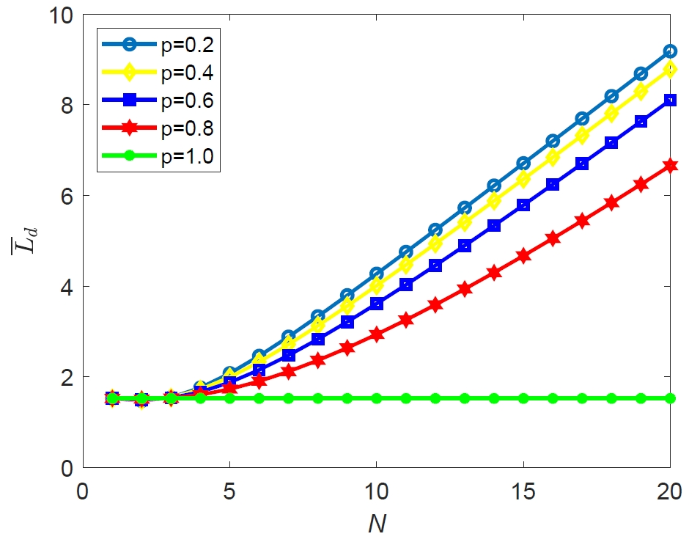
取 $\lambda = 0.08,\mu = 8,\theta = 0.05,\alpha = 0.3$, 然后运用 Matlab 软件进行数值计算, 见图 1 与图 2 . 图 1 反映了系统空闲率 ${p_0}$ 随着概率 $p$ 和控制值 $N$ 的变化情况, 图 2 反映了附加队长 ${\bar{L}_d}$ 随着概率 $p$ 和控制值 $N$ 的变化情况.
图1
图1
$p$ 取不同值时, ${p_0}$ 随着 $N$ 变化情况
图2
图2
$p$ 取不同值时, ${\bar {L}_d}$ 随着 $N$ 变化情况
由图 1 可得到, 当固定参数 $p$ 时, 系统空闲率 ${p_0}$ 随着 $N$ 的增大而减小, 控制值 $N$ 越大, 将使系统中等待服务的顾客数增多, 从而使系统空闲率 ${p_0}$ 减小. 当 $N$ 值不变, 参数 $p$ 不断增加时, 系统的空闲率 ${p_0}$ 增大, $p$ 值增加意味着顾客及时被服务的概率增加, 系统中等待的服务的顾客数减少, 从而使得系统的空闲率增加, 特别当 $p$ 值为 1 时, ${p_0}$ 将不会随着 $N$ 的增加而增加.
由图 2 可得到, 当固定参数 $p$ 时, 附加平均队长 ${\bar{L}_d}$ 随着 $N$ 的增大而增加, 说明当 $N$ 的值设定越大时, 将使系统中等待的顾客数增加, 从而使得附加平均队长增加. 当 $N$ 值不变, 参数 $p$ 不断增加时, 附加平均队长减少, 这是因为 $p$ 值增加使顾客及时被服务的概率增加, 从而使得附加队长降低, 且当 $p$ 值为 1 时, ${\bar{L}_d}$ 将不会随着 $N$ 的增加而变化.
6 结束语
本文依据实际背景建立了一个在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 然后使用直观的概率分解分析技术, 结合更新过程理论讨论了系统的排队性能指标, 求得了便于做数值计算的队长稳态分布的递推表达式. 一些特殊情况表明本文的研究推广了已有的文献研究. 最后, 通过数值计算实例分析了系统容量的优化设计, 以及系统的空闲率和附加平均队长对系统参数的敏感性, 使得本文的理论结果有更好的应用前景. 下一步我们将构建费用结构模型, 建立系统的费用函数来研究系统的最优控制策略问题.
参考文献
View Option
[1]
Levy Y Yechiali U Utilization of idle time in an M/G/1 queueing system
Management Science , 1975 , 22 2 ): 202 -211
[本文引用: 2]
[2]
田乃硕 . 休假随机服务系统 . 北京 : 北京大学出版 , 2001
[本文引用: 1]
Tian N S Stochastic Service System with Vacations . Beijing : Peking University Press , 2001
[本文引用: 1]
[3]
田乃硕 . 多级适应性休假的 M/G/1排队
应用数学 , 1992 , 5 4 ): 12 -18
[本文引用: 1]
Tian N S Queue M/G/1 with adaptive multistage vacation
Mathematica Applicata , 1992 , 5 4 ): 12 -18
[本文引用: 1]
[4]
唐应辉 , 唐小我 . 排队论-基础与分析技术 . 北京 : 科学出版社 , 2006
[本文引用: 6]
Tang Y H Tang X W Queueing Theory-Foundations and Analysis Techniques . Beijing : Science Press , 2006
[本文引用: 6]
[5]
唐应辉 , 吴文青 , 刘云颇 . 基于单重休假的 Min$(N,V)$-策略 M/G/1排队系统分析
应用数学学报 , 2014 , 37 6 ): 976 -996
[本文引用: 1]
Tang Y H Wu W Q Liu Y P Analysis of M/G/1 queueing system with Min$(N,V)$-policy based on single server vacation
Acta Mathematicae Applicatae Sinica , 2014 , 37 6 ): 976 -996
[本文引用: 1]
[6]
唐应辉 , 吴文青 , 刘云颇 , 等 . 基于多重休假的 Min$(N,V)$-策略排队系统的队长分布
系统工程理论与实践 , 2014 , 34 6 ): 1533 -1546
DOI:10.12011/1000-6788(2014)6-1533
[本文引用: 1]
运用全概率分解技术和拉普拉斯变换工具,研究了基于服务员多重休假的min(N,V)-策略M/G/1排队系统,其中N是预设的休假终止的门限值.讨论了从任意初始状态出发队长的瞬态分布,获得了队长瞬态分布的拉普拉斯变换的递推表达式和稳态队长分布的递推表达式,同时求出了附加队长分布的显示表达式.进一步讨论了当休假时间V分别服从负指数分布和定长分布P{V=T}=1,以及当N=1,N→∞,P{V=0}=1与P{V=∞}=1时的特殊情形.最后,通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
Tang Y H Wu W Q Liu Y P et al. The queue length distribution of M/G/ 1 queueing system with Min$(N,V)$-policy based on multiple server vacations
Systems Engineering-Theory & Practice , 2014 , 34 6 ): 1533 -1546
DOI:10.12011/1000-6788(2014)6-1533
[本文引用: 1]
运用全概率分解技术和拉普拉斯变换工具,研究了基于服务员多重休假的min(N,V)-策略M/G/1排队系统,其中N是预设的休假终止的门限值.讨论了从任意初始状态出发队长的瞬态分布,获得了队长瞬态分布的拉普拉斯变换的递推表达式和稳态队长分布的递推表达式,同时求出了附加队长分布的显示表达式.进一步讨论了当休假时间V分别服从负指数分布和定长分布P{V=T}=1,以及当N=1,N→∞,P{V=0}=1与P{V=∞}=1时的特殊情形.最后,通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
[7]
兰绍军 , 唐应辉 . 具有单重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队的离去过程分析
数学物理学报 , 2016 , 36A 2 ): 380 -392
[本文引用: 1]
Lan S J Tang Y H Analysis of the departure process for Geo/G/1 discrete-time queue with single server vacation and Min$(N,V)$-policy
Acta Mathematica Scientia , 2016 , 36A 2 ): 380 -392
[本文引用: 1]
[8]
兰绍军 , 唐应辉 . 具有多重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队
系统工程理论与实践 , 2015 , 35 3 ): 799 -810
DOI:10.12011/1000-6788(2015)3-799
[本文引用: 1]
考虑服务员具有多重休假和系统采用min(N,V)- 策略控制的离散时间Geo/G/1 排队系统, 使用全概率分解技术和更新过程理论, 研究了系统在任意时刻n<sup>+</sup> 的瞬态队长分布和稳态队长分布, 得到了瞬态队长分布的z- 变换表达式和稳态队长分布的递推表达式. 进一步, 得到了系统在时刻点n, n<sup>-</sup> 和外部观察时刻点的稳态队长分布. 特别地, 本文直接获得了一些特殊离散时间排队系统相应的结果. 最后, 通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
Lan S J Tang Y H Geo/G/1 discrete-time queue with multiple server vacations and Min$(N,V)$-policy
Systems Engineering-Theory & Practice , 2015 , 35 3 ): 799 -810
DOI:10.12011/1000-6788(2015)3-799
[本文引用: 1]
考虑服务员具有多重休假和系统采用min(N,V)- 策略控制的离散时间Geo/G/1 排队系统, 使用全概率分解技术和更新过程理论, 研究了系统在任意时刻n<sup>+</sup> 的瞬态队长分布和稳态队长分布, 得到了瞬态队长分布的z- 变换表达式和稳态队长分布的递推表达式. 进一步, 得到了系统在时刻点n, n<sup>-</sup> 和外部观察时刻点的稳态队长分布. 特别地, 本文直接获得了一些特殊离散时间排队系统相应的结果. 最后, 通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
[9]
高文萍 , 唐应辉 . 双阈值 $(m,N)$-策略不中断单重休假 M/G/1排队分析
数学学报 (中文版) , 2023 , 66 2 ): 363 -388
[本文引用: 1]
Gao W P Tang Y H Analysis of M/G/1 queue system with bi-level threshold $(m,N)$-policy and uninterrupted single vacation
Acta Mathematica Sinica , 2023 , 66 2 ): 363 -388
[本文引用: 1]
[10]
Feinberg E A Kim D J Bi-criterion optimization of an M/G/1 queue with a removable server
Probability in the Engineering and Informational Sciences , 1996 , 10 5 ): 57 -73
[本文引用: 1]
[11]
罗彦君 , 唐应辉 . 具有修正 $(p,N)$-策略与单重休假的 M/G/1排队分析
运筹学学报 , 2023 , 1 -17
[本文引用: 2]
Luo Y J Tang Y H Analysis of M/G/1 queue with single vacation and modified $(p,N)$-policy
Operations Research Transactions , 2023 , 1 -17
[本文引用: 2]
[12]
袁雨梅 , 唐应辉 , 刘雨欣 , 等 . 在随机启动 $(p,N)$-策略控制下不中断多重休假排队系统的性能分析
应用数学 , 2023 , 36 4 ): 1069 -1085
[本文引用: 4]
Yuan Y M Tang Y H Liu Y X et al. Performance analysis for a queueing system with uninterrupted multiple vacations under the control of randomized setup $(p,N)$-policy
Mathematica Applicata , 2023 , 36 4 ): 1069 -1085
[本文引用: 4]
[13]
Kuang X Y Tang Y H Yu M M et al. Performance analysis of an M/G/1 queue with bi-level randomized $(p,N_1,N_2)$-policy
RAIRO Operation Research 2022 , 56 1 ): 395 -414
[本文引用: 1]
[14]
Boxma O J Schlegel S Yechiali U A note on an M/G/1 queue with a waiting server, timer and vacations
American Mathematical Society Translations , 2002 , 207 25 -35
[本文引用: 2]
[15]
万思燕 , 兰绍军 , 唐应辉 . 具有耐烦服务员的 M/G/1休假排队系统性能分析与容量优化设计
系统科学与数学 , 2023 , 43 9 ): 2292 -2309
DOI:10.12341/jssms22707
[本文引用: 2]
考虑服务员具有耐烦行为的$M/G/1$休假排队系统.运用全概率分解技术和拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布,获得了瞬态队长分布的拉普拉斯变换表达式,并在此基础上导出了稳态队长分布的递推表达式.进一步给出了稳态队长的随机分解结构和一些重要的稳态性能指标.同时得到了一些特殊排队系统相应的结果.最后,通过数值实例讨论了系统的容量优化设计问题.
Wan S Y Lan S J Tang Y H Performance analysis and capacity optimization design of an M/G/1 queueing system with vacations and patient server
Journal of Systems Science and Mathematical Sciences , 2023 , 43 9 ): 2292 -2309
DOI:10.12341/jssms22707
[本文引用: 2]
考虑服务员具有耐烦行为的$M/G/1$休假排队系统.运用全概率分解技术和拉普拉斯变换工具,研究了系统从任意初始状态出发的瞬态队长分布,获得了瞬态队长分布的拉普拉斯变换表达式,并在此基础上导出了稳态队长分布的递推表达式.进一步给出了稳态队长的随机分解结构和一些重要的稳态性能指标.同时得到了一些特殊排队系统相应的结果.最后,通过数值实例讨论了系统的容量优化设计问题.
[16]
高文萍 , 唐应辉 , 唐蓓蕾 . 双水平控制策略和延迟不中断单重休假的 M/G/1排队系统分析
应用数学 , 2021 , 34 4 ): 829 -846
[本文引用: 1]
Gao W P Tang Y H Tang B L Analysis of M/G/1 queueing system with bi-level control policy and delayed uninterrupted single vacation
Mathematica Applicata , 2021 , 34 4 ): 829 -846
[本文引用: 1]
[17]
何亚兴 , 唐应辉 . 具有 $N$-策略和延迟单重休假且休假不中断的 M/G/1排队系统
应用数学 , 2021 , 34 1 ): 130 -145
[本文引用: 1]
He Y X Tang Y H M/G/1 Queueing system with $N$-policy and delayed single vacation without interruption
Mathematica Applicata , 2021 , 34 1 ): 130 -145
[本文引用: 1]
Utilization of idle time in an M/G/1 queueing system
2
1975
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 推论 3.4 当 $P\left\{ {U = 0} \right\} = 1,p = 0,P\left\{ {V = 0} \right\} = 1$ 时, 本文研究的系统等价于 $N$ 策略 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1,p = 0,P\left\{ {V = 0} \right\} = 1$ 即可得到与文献 [1 ] 完全一致的结果. ...
1
2001
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
1
2001
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
多级适应性休假的 M/G/1排队
1
1992
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
多级适应性休假的 M/G/1排队
1
1992
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
6
2006
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 定义 3.1 [4 ] “系统闲期” 是指从系统变空的时刻起, 直到其后的第一个顾客到达系统为止的这段时间. 令 ${\hat \tau _j}$ 表示第 $j$ 个系统闲期的长度, 因为顾客的到达是参数 $\lambda(\lambda>0)$ 的 Poisson 流, 于是 ${\hat \tau _j}$ 的分布为 $F(t) = P\{ {\hat \tau _j} \le t\} = 1 - {{\rm e}^{ - \lambda t}},t \ge 0,j = 1,2 \cdots.$ ...
... 定义 3.3 [4 ] “服务员忙期” 是指从服务员开始为顾客服务的时刻开始, 直到系统再次变空为止的这一段时间.由于服务员忙期开始时系统中可能有多个顾客, 因此若令 $b$ 表示从一个顾客开始的 “服务员忙期” 长度, 其分布记为 $B(t)=P\left\{ b\le t \right\}$, $b(s)$ 为其拉普拉斯--司梯阶 $(LS)$ 变换. ...
... 引理3.1 [4 ] 对 $\Re (s)>0, b(s)$ 是方程 $z=g(s+\lambda -\lambda z)$ 在 $\left| z \right|<1$ 内的唯一解, 且 $B(t)$ 表示为 ...
... 引理 3.2 [4 ] 令 $q_{j}^{*}(s)=\int_{0}^{\infty }{{{\rm e}^{-st}}{{Q}_{j}}(t){\rm d}t}$ 为 ${{Q}_{j}}(t)$ 的拉普拉斯 $(L)$ 变换, 对 $\Re (s)>0$ 有 ...
... 推论 3.3 当 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$, 本文研究的系统等价于多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$ 即可得到与文献 [4 ] 完全一致的结果. ...
6
2006
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 定义 3.1 [4 ] “系统闲期” 是指从系统变空的时刻起, 直到其后的第一个顾客到达系统为止的这段时间. 令 ${\hat \tau _j}$ 表示第 $j$ 个系统闲期的长度, 因为顾客的到达是参数 $\lambda(\lambda>0)$ 的 Poisson 流, 于是 ${\hat \tau _j}$ 的分布为 $F(t) = P\{ {\hat \tau _j} \le t\} = 1 - {{\rm e}^{ - \lambda t}},t \ge 0,j = 1,2 \cdots.$ ...
... 定义 3.3 [4 ] “服务员忙期” 是指从服务员开始为顾客服务的时刻开始, 直到系统再次变空为止的这一段时间.由于服务员忙期开始时系统中可能有多个顾客, 因此若令 $b$ 表示从一个顾客开始的 “服务员忙期” 长度, 其分布记为 $B(t)=P\left\{ b\le t \right\}$, $b(s)$ 为其拉普拉斯--司梯阶 $(LS)$ 变换. ...
... 引理3.1 [4 ] 对 $\Re (s)>0, b(s)$ 是方程 $z=g(s+\lambda -\lambda z)$ 在 $\left| z \right|<1$ 内的唯一解, 且 $B(t)$ 表示为 ...
... 引理 3.2 [4 ] 令 $q_{j}^{*}(s)=\int_{0}^{\infty }{{{\rm e}^{-st}}{{Q}_{j}}(t){\rm d}t}$ 为 ${{Q}_{j}}(t)$ 的拉普拉斯 $(L)$ 变换, 对 $\Re (s)>0$ 有 ...
... 推论 3.3 当 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$, 本文研究的系统等价于多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 且 $p = 1$ 或 $P\left\{ {U = 0} \right\} = 1$ 且 $N = 1$ 即可得到与文献 [4 ] 完全一致的结果. ...
基于单重休假的 Min$(N,V)$-策略 M/G/1排队系统分析
1
2014
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
基于单重休假的 Min$(N,V)$-策略 M/G/1排队系统分析
1
2014
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
基于多重休假的 Min$(N,V)$-策略排队系统的队长分布
1
2014
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
基于多重休假的 Min$(N,V)$-策略排队系统的队长分布
1
2014
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有单重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队的离去过程分析
1
2016
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有单重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队的离去过程分析
1
2016
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有多重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队
1
2015
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有多重休假和 Min$(N,V)$-策略控制的 Geo/G/1离散时间排队
1
2015
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
双阈值 $(m,N)$-策略不中断单重休假 M/G/1排队分析
1
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
双阈值 $(m,N)$-策略不中断单重休假 M/G/1排队分析
1
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
Bi-criterion optimization of an M/G/1 queue with a removable server
1
1996
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有修正 $(p,N)$-策略与单重休假的 M/G/1排队分析
2
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 推论 3.2 当 $P\left\{ {U = \infty } \right\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断单重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = \infty } \right\} = 1$ 即可得到与文献 [11 ] 完全一致的结果. ...
具有修正 $(p,N)$-策略与单重休假的 M/G/1排队分析
2
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 推论 3.2 当 $P\left\{ {U = \infty } \right\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断单重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = \infty } \right\} = 1$ 即可得到与文献 [11 ] 完全一致的结果. ...
在随机启动 $(p,N)$-策略控制下不中断多重休假排队系统的性能分析
4
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 受到上面研究的启发, 本文提出一个新的排队模型, 在文献 [12 ] 的基础上加入服务员的耐烦行为, 即在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 该模型推广了文献 [12 ] 研究的情形, 使得系统模型的应用更加灵活, 也符合客观实际需求. 例如在一个加工订单所需产品的生产制造厂中, 由于启动生产的成本较高, 因此生产管理者为了减少频繁启动系统的费用, 只有当订单积累到一定数量 (例如 $N$ 个) 时才启动设备生产产品. 但是, 在碰到订单时间要求较紧急且积累的订单数又没有达到这个数量时, 管理者则以某个概率 $p\left( {0\leq p\leq1} \right)$ 来解决这种情形, 于是提出启动生产的 $(p,N)$-策略. 当系统完成所有订单需要的产品时, 系统就会从事一项辅助性工作来增加收入. 当这项辅助性工作结束后且系统中没有新的订单时, 管理者考虑到后面订单到来的可能性较大, 往往不会立即安排系统继续从事另一项辅助性工作, 而是让系统等待一段时间 (耐烦期), 以便能及时处理即将到达的订单. 若在这一段时间内还没有订单到达, 则系统又会去从事另一项辅助性工作. 我们使用直观的概率分解分析方法, 即应用全概率分解分析技术和更新过程理论分析了系统从任意初始状态出发的瞬态队长分布, 并且通过拉普拉斯变换工具得到队长的瞬态分布关于时间 $t$ 的拉普拉斯变换表达式, 再通过洛必达法则求得队长稳态分布的递推表达式, 同时获得了稳态队长分布的概率母函数和平均队长的表达式. 最后, 通过数值计算实例讨论了系统的容量优化设计问题, 以及系统的空闲率与附加平均队长对系统参数的敏感性. ...
... ] 的基础上加入服务员的耐烦行为, 即在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 该模型推广了文献 [12 ] 研究的情形, 使得系统模型的应用更加灵活, 也符合客观实际需求. 例如在一个加工订单所需产品的生产制造厂中, 由于启动生产的成本较高, 因此生产管理者为了减少频繁启动系统的费用, 只有当订单积累到一定数量 (例如 $N$ 个) 时才启动设备生产产品. 但是, 在碰到订单时间要求较紧急且积累的订单数又没有达到这个数量时, 管理者则以某个概率 $p\left( {0\leq p\leq1} \right)$ 来解决这种情形, 于是提出启动生产的 $(p,N)$-策略. 当系统完成所有订单需要的产品时, 系统就会从事一项辅助性工作来增加收入. 当这项辅助性工作结束后且系统中没有新的订单时, 管理者考虑到后面订单到来的可能性较大, 往往不会立即安排系统继续从事另一项辅助性工作, 而是让系统等待一段时间 (耐烦期), 以便能及时处理即将到达的订单. 若在这一段时间内还没有订单到达, 则系统又会去从事另一项辅助性工作. 我们使用直观的概率分解分析方法, 即应用全概率分解分析技术和更新过程理论分析了系统从任意初始状态出发的瞬态队长分布, 并且通过拉普拉斯变换工具得到队长的瞬态分布关于时间 $t$ 的拉普拉斯变换表达式, 再通过洛必达法则求得队长稳态分布的递推表达式, 同时获得了稳态队长分布的概率母函数和平均队长的表达式. 最后, 通过数值计算实例讨论了系统的容量优化设计问题, 以及系统的空闲率与附加平均队长对系统参数的敏感性. ...
... 推论 3.1 $P\{ U = 0\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 即可得到与文献 [12 ] 完全一致的结果. ...
在随机启动 $(p,N)$-策略控制下不中断多重休假排队系统的性能分析
4
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... 受到上面研究的启发, 本文提出一个新的排队模型, 在文献 [12 ] 的基础上加入服务员的耐烦行为, 即在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 该模型推广了文献 [12 ] 研究的情形, 使得系统模型的应用更加灵活, 也符合客观实际需求. 例如在一个加工订单所需产品的生产制造厂中, 由于启动生产的成本较高, 因此生产管理者为了减少频繁启动系统的费用, 只有当订单积累到一定数量 (例如 $N$ 个) 时才启动设备生产产品. 但是, 在碰到订单时间要求较紧急且积累的订单数又没有达到这个数量时, 管理者则以某个概率 $p\left( {0\leq p\leq1} \right)$ 来解决这种情形, 于是提出启动生产的 $(p,N)$-策略. 当系统完成所有订单需要的产品时, 系统就会从事一项辅助性工作来增加收入. 当这项辅助性工作结束后且系统中没有新的订单时, 管理者考虑到后面订单到来的可能性较大, 往往不会立即安排系统继续从事另一项辅助性工作, 而是让系统等待一段时间 (耐烦期), 以便能及时处理即将到达的订单. 若在这一段时间内还没有订单到达, 则系统又会去从事另一项辅助性工作. 我们使用直观的概率分解分析方法, 即应用全概率分解分析技术和更新过程理论分析了系统从任意初始状态出发的瞬态队长分布, 并且通过拉普拉斯变换工具得到队长的瞬态分布关于时间 $t$ 的拉普拉斯变换表达式, 再通过洛必达法则求得队长稳态分布的递推表达式, 同时获得了稳态队长分布的概率母函数和平均队长的表达式. 最后, 通过数值计算实例讨论了系统的容量优化设计问题, 以及系统的空闲率与附加平均队长对系统参数的敏感性. ...
... ] 的基础上加入服务员的耐烦行为, 即在 $(p,N)$-策略控制下具有耐烦服务员和不中断多重休假的 $M/G/1$ 排队模型, 该模型推广了文献 [12 ] 研究的情形, 使得系统模型的应用更加灵活, 也符合客观实际需求. 例如在一个加工订单所需产品的生产制造厂中, 由于启动生产的成本较高, 因此生产管理者为了减少频繁启动系统的费用, 只有当订单积累到一定数量 (例如 $N$ 个) 时才启动设备生产产品. 但是, 在碰到订单时间要求较紧急且积累的订单数又没有达到这个数量时, 管理者则以某个概率 $p\left( {0\leq p\leq1} \right)$ 来解决这种情形, 于是提出启动生产的 $(p,N)$-策略. 当系统完成所有订单需要的产品时, 系统就会从事一项辅助性工作来增加收入. 当这项辅助性工作结束后且系统中没有新的订单时, 管理者考虑到后面订单到来的可能性较大, 往往不会立即安排系统继续从事另一项辅助性工作, 而是让系统等待一段时间 (耐烦期), 以便能及时处理即将到达的订单. 若在这一段时间内还没有订单到达, 则系统又会去从事另一项辅助性工作. 我们使用直观的概率分解分析方法, 即应用全概率分解分析技术和更新过程理论分析了系统从任意初始状态出发的瞬态队长分布, 并且通过拉普拉斯变换工具得到队长的瞬态分布关于时间 $t$ 的拉普拉斯变换表达式, 再通过洛必达法则求得队长稳态分布的递推表达式, 同时获得了稳态队长分布的概率母函数和平均队长的表达式. 最后, 通过数值计算实例讨论了系统的容量优化设计问题, 以及系统的空闲率与附加平均队长对系统参数的敏感性. ...
... 推论 3.1 $P\{ U = 0\} = 1$ 时, 本文研究的系统等价于在 $(p,N)$-策略控制下不中断多重休假的 $M/G/1$ 排队模型. 在上面所得结果中令 $P\left\{ {U = 0} \right\} = 1$ 即可得到与文献 [12 ] 完全一致的结果. ...
Performance analysis of an M/G/1 queue with bi-level randomized $(p,N_1,N_2)$-policy
1
2022
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
A note on an M/G/1 queue with a waiting server, timer and vacations
2
2002
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有耐烦服务员的 M/G/1休假排队系统性能分析与容量优化设计
2
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有耐烦服务员的 M/G/1休假排队系统性能分析与容量优化设计
2
2023
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
... ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
双水平控制策略和延迟不中断单重休假的 M/G/1排队系统分析
1
2021
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
双水平控制策略和延迟不中断单重休假的 M/G/1排队系统分析
1
2021
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有 $N$-策略和延迟单重休假且休假不中断的 M/G/1排队系统
1
2021
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...
具有 $N$-策略和延迟单重休假且休假不中断的 M/G/1排队系统
1
2021
... 为了有效利用系统的闲期, Levy 和 Yechiali[1 ] 于 1975 年将 “休假” 这一术语引入到排队论中. 目前有大量的文献对休假排队系统进行了研究, 而且经典的服务员休假机制有单重休假、多重休假、多级适应性休假等[2 ,3 ,4 ] . 在现实情况中, 系统若频繁从空闲状态转换到忙期状态会产生较大费用, 因此为了减少频繁启动系统的费用, 具有 $N$-策略与 $D$-策略等控制系统频繁启动的控制策略就提出来了. 文献 [5 ,6 ] 将 $N$-策略与单重休假和多重休假相结合, 分别研究了基于单重休假与多重休假的 Min$(N,V)$-策略 $M/G/1$ 排队系统, 文献 [7 ,8 ] 将 Min$(N,V)$-策略进一步应用到了离散时间排队系统中, 文献 [9 ] 结合实际情况提出了双阈值 $(m,N)$-策略, 其中$m$~为系统的启动阈值, $N$ 为服务员开始为顾客服务的阈值. 在文献 [10 ] 中, 作者首次提出了随机 $(p,N)$- 策略, 即当服务员休假回来时, 如果系统中等待的顾客数大于等于设定的阈值 $N(N\geq1)$, 则立即开始服务, 若系统中有顾客且小于 $N$ 个, 则服务员以概率 $p\left( {0 \le p \le 1} \right)$ 开始服务, 以概率 $\left( {1 - p} \right)$ 不服务直到系统中的顾客数积累到 $N$ 个才开始服务. 以上文献所涉及的服务员休假是可以根据控制策略中断休假的, 但实际情况并不完全是这样的, 例如当某医生在帮助抢救急重症病人时, 即使在该医生的就诊处的病人积累到了 $N$ 个, 该医生也不能立即中断当前帮助抢救急重症病人. 于是文献 [11 ] 提出了一个将不中断单重休假与 $(p,N)$-策略相结合的排队模型, 文献 [12 ] 则是将不中断多重休假与 $(p,N)$-策略相结合. 文献 [13 ] 将 $\left( {p,N} \right)$-策略推广, 提出了双水平随机 $(p,N_{1},N_{2})$-策略的 $M/G/1$ 排队系统. 文献 [14 ,15 ] 研究了具有耐烦服务员的 $M/G/1$ 排队休假系统, 在该系统中, 当服务员休假回来发现系统没有顾客时, 服务员则呆在系统经历一段随机长度时间的等待期, 这一段时间就称为服务员的耐烦期, 在耐烦期内若有顾客到达, 则服务员立即为顾客服务, 若在此期间没有顾客到达, 则开启新一轮休假. 但是文献 [16 ,17 ] 的服务员延迟休假行为不同于文献 [14 ,15 ] 服务员的耐烦行为, 服务员延迟休假行为不是在休假结束后而是在休假前发生的. ...