数学物理学报, 2025, 45(4): 1206-1216

具有季节性切换反应及脉冲扰动的鱼类单种群动力学模型

曾夏萍,, 卢文雯, 庞国萍, 梁志清,*

广西应用数学中心 (玉林师范学院), 广西高校复杂系统优化与大数据处理重点实验室 广西玉林 537000

Single Population Dynamics Model of Fish with Seasonal Switching and Impulsive Perturbations

Zeng Xiaping,, Lu Wenwen, Pang Guoping, Liang Zhiqing,*

Center for Applied Mathematics of Guangxi, Yulin Normal University, Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing, Yulin Normal University, Guangxi Yulin 537000

通讯作者: *E-mail: lzqysl@sohu.com

收稿日期: 2024-08-12   修回日期: 2025-04-14  

基金资助: 国家自然科学基金(12261096)
广西自然科学基金(2024GXNSFBA010395)
广西高校中青年教师科研基础能力提升项目(2021KY0592)
广西高校中青年教师科研基础能力提升项目(2022KY0582)
广西高校中青年教师科研基础能力提升项目(2025KY0675)
广西应用数学中心 (玉林师范学院) 开放课题(2023CAM005)

Received: 2024-08-12   Revised: 2025-04-14  

Fund supported: NSFC(12261096)
Natural Science Foundation of Guangxi Grants(2024GXNSFBA010395)
Project for enhancing Young and Middle-aged teacher's research basic ability in colleges of Guangxi(2021KY0592)
Project for enhancing Young and Middle-aged teacher's research basic ability in colleges of Guangxi(2022KY0582)
Project for enhancing Young and Middle-aged teacher's research basic ability in colleges of Guangxi(2025KY0675)
Systematic Project of Center for Applied Mathematics of Guangxi(2023CAM005)

作者简介 About authors

E-mail:xiaping062@163.com

摘要

该文考虑了一类具有季节性切换和脉冲扰动的鱼类单种群模型, 研究季节切换和脉冲扰动对鱼类种群动力学行为的影响. 利用离散动力系统频闪映射理论得到了鱼类单种群系统持久生存和灭绝的充分条件, 结合有理差分方程和不动点理论证明了该系统存在唯一全局吸引的正周期解. 最后, 通过数值模拟来验证结论.

关键词： 脉冲扰动; 持久生存; 季节切换; 周期解

Abstract

This paper considers a class of single population dynamics models for fish that incorporates seasonal switching and impulsive perturbations. It investigates the effects of these factors on fish population dynamics. By employing the discrete dynamical system theory and stroboscopic mapping, we derive the sufficient conditions for the permanence and extinction of the fish population system. Using rational difference equations and fixed point theory, we demonstrate the existence of a unique globally attractive positive periodic solution. Finally, numerical simulations are provided to validate the theoretical results.

Keywords： impulsive disturbance; permanence; seasonal switching; periodic solution

PDF (765KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

曾夏萍, 卢文雯, 庞国萍, 梁志清. 具有季节性切换反应及脉冲扰动的鱼类单种群动力学模型[J]. 数学物理学报, 2025, 45(4): 1206-1216

Zeng Xiaping, Lu Wenwen, Pang Guoping, Liang Zhiqing. Single Population Dynamics Model of Fish with Seasonal Switching and Impulsive Perturbations[J]. Acta Mathematica Scientia, 2025, 45(4): 1206-1216

1 引言

随着全球人口的增长和对海洋资源需求的加剧, 渔业可持续性成为国际社会关注的焦点. 渔业资源研究的背景之一就是对渔业资源的持续利用和管理. 研究人员通过对捕捞量、种类、渔业生产力等数据的收集和分析, 希望为渔业资源的可持续开发和管理提供科学依据, 以避免过度捕捞而造成生态系统崩溃[1-3].

由于南流江畔养猪场密布, 养猪产生的粪便、居民的生活污水直排江中, 导致南流江变成了 "黑水河", 以及南流江沙河段非法电鱼行为猖獗, 使得南流江中的鱼类成活率不高, 从而影响了渔业资源增殖的效益. 为了保持南流江鱼类种群持久生存, 从而获得最大的产量或最佳经济收益, 本文用数学模型来研究南流江鱼类资源的保护策略.

而季节切换对自然界和人类社会都有广泛的影响. 它会影响植物和动物的行为和生理过程, 还在物种传播、可再生资源、公共卫生等领域中扮演着重要角色. 比如, 种群传播速度受季节好坏的影响, 人们季节性接种疫苗也需要考虑传染病季节性传播的因素, 许多物种因季节变换而进行休眠. 如青蛙水下休眠以避寒, 亚洲黑熊进入巢穴休眠, 乌龟选择隐蔽处静卧休眠等. 害虫也会因为季节变换而进入休眠状态, 而鱼类的增长繁殖也会受季节变换的影响[4-7].

鱼类由于受自身或外部环境等因素的影响, 种群的数量会有所波动, 季节切换是造成这种波动的一个非常重要的因素, 在一定程度上不仅会影响种群增长速度, 而且还会影响内部. 季节性变化对动力系统造成的影响受到了很多研究人员的关注[8-15]. 文献[16]建立了如下模型

$\begin{equation} \left\{ \begin{array}{l} \begin{array}{*{20}c} {\frac{{{\rm d}x}}{{{\rm d}t}} = - \lambda _1 x,} & {n\tau < t \le n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {\frac{{{\rm d}x}}{{{\rm d}t}} = rx(1 - \frac{x}{K}),} & {n\tau + (1 - \phi )\tau < t \le (n + 1)\tau }, \\ \end{array} \\ x(0) = x_0 \in \mathbb{R}^ +. \\ \end{array} \right. \end{equation}$

其中, $x(t)$ 表示种群密度, $n \in N,\phi \in (0,1]$, $\lambda > 0$ 是鱼类种群的死亡率, $r$ 和 $K$ 分别是鱼类的内禀增长率和环境容纳量. 上述系统 (1.1) 由两个连续周期变化的季节组成 (季节 1 和季节 2), 即种群在时间区间 $[n\tau,n\tau + (1 - \phi )\tau ]$ 时生活在季节 1 中, 此时它的增长规律满足系统 (1.1) 的第一个方程; 在 $n\tau + (1 - \phi )\tau $时, 种群经历一次脉冲投放后开始在季节 2 生长, 此时, 鱼类种群的增长规律满足系统 (1.1) 的第二个方程. 在下一个脉冲时刻 $(n + 1)\tau $ 时种群数量经过脉冲变化后进入到下一个循环, 种群的增长规律也由此发生了变化, 并依次进行循环.

以上模型种群在经历环境变化时数量并没有增加或减少. 然而, 在现实生活中, 种群数量往往会受到很多外界因素的干扰, 并且这种扰动往往是瞬间完成的. 随着脉冲微分方程理论发展日益成熟, 许多学者已将该理论运用到种群动力学及其应用科学领域[17-23]. 脉冲捕捞模型是鱼类脉冲控制研究的核心. 经典的脉冲捕捞模型基于 Logistic 增长模型[24,25], 通过引入定期脉冲捕捞项, 描述捕捞对鱼类种群的影响. 许多学者对模型参数(如捕捞频率、捕捞强度) 进行了深入分析, 探讨了不同捕捞策略对种群稳定性和恢复能力的影响[26,27]. 但很少有学者考虑利用具有季节切换的脉冲微分方程的方法研究渔业资源管理.

为了能够充分考虑到瞬间变化对种群状态的影响, 本文通过脉冲来刻画这种扰动, 由此建立下列具有季节切换反应及脉冲扰动的南流江鱼类单种群系统

$\begin{equation} \left\{ \begin{array}{l} \begin{array}{*{20}c} {\frac{{{\rm d}x}}{{{\rm d}t}} = - \lambda _1 x - \lambda _2 x^2,} & {n\tau < t \le n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x^ + = a_1 x,} & {t = n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {\frac{{{\rm d}x}}{{{\rm d}t}} = rx(1 - \frac{x}{K}),} & {n\tau + (1 - \phi )\tau < t \le (n + 1)\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x^ + = a_2 x,} & {t = (n + 1)\tau }, \\ \end{array} \\ x(0) = x_0 \in \mathbb{R}^+. \\ \end{array} \right. \end{equation}$

其中, $x(t)$ 表示鱼类种群密度, $\lambda _1 > 0$ 是鱼类种群的死亡率, $\lambda _2 > 0$ 是鱼类种群种内竞争系数, $r$ 和 $K$ 分别是鱼类的内禀增长率和环境容纳量, $a_i > 0$$(i = 1,2)$ 表示脉冲投放系数, $\tau $ 为鱼类种群脉冲投放周期.

2 预备知识

首先给出下列的有理递归序列

$\begin{equation} x_{n + 1} = \frac{{a + bx_n }}{{1 + \sum\limits_{i = 0}^k {b_i x_{n - i} } }},\quad {\rm{ }}n \in N, \end{equation}$

其中

$\begin{equation} a,b_0, \cdots b_{i - 1} \in [0, + \infty ),{\rm{ }}b,b_k \in (0, + \infty ),k \in N. \end{equation}$

引理2.1[28] 若

$\begin{aligned} &a>0 \text {, 或者 }\\ &a=0, \quad b>1, \end{aligned}$

则方程 (2.1) 有唯一的正平衡点 $\overline x $. 即

$\overline x = \frac{{b - 1 + \sqrt {(b - 1)^2 + 4aB} }}{{2B}},$

其中

$B = \sum\limits_{i = 0}^k {b_i } > 0.$

引理2.2[28] 假设 (2.2) 式成立, 则下列结论成立

(a) 若 $a = 0$ 且 $0 \le b \le 1$, 则 (2.1) 式的每个解都趋向于 0;

(b) 若 (2.3) 式成立, 则 (2.1) 式持久;

(c) 若 (2.3) 式成立且下面条件之一满足

(1) $B\overline x k \le 1$ ;

(2) $(B - b_0 )\overline x k \le 1 + b_0 \overline x $ 且 $b - ab_0 \ge 0$ ;

(3) $B\overline x (k - 1) \le 1$ 且 $b[1 + \overline x (B - b_k ) - b_k a] \ge 0$;

则 $\overline x $ 全局吸引.

定义2.2[29] 若存在两个正常数 $m$ 和 $M$ 使得系统的任意解满足

$m \le \mathop {\lim \inf x(t) \le }\limits_{t \to \infty } \mathop {\lim \sup x(t) \le }\limits_{t \to \infty } M.$

则系统是持久的.

3 模型分析

令 $x_1 (t,x_{10} )$ 是方程 $\frac{{{\rm d}x}}{{{\rm d}t}} = - \lambda _1 x - \lambda _2 x^2 $满足初值 $x_{10} \in \mathbb{R}^+$ 的解, $x_2 (t,x_{20} )$ 是方程 $\frac{{{\rm d}x}}{{{\rm d}t}} = rx(1 - \frac{x}{K})$ 满足初值 $x_{20} $ 的解, 其中 $x_{20} = x_1 ((n\tau + (1 - \phi )\tau )^ +,x_{10} ) \in \mathbb{R}^+ $, 则 (1.2) 可以唯一的表示成如下的辅助系统

$x(t,x_0 ) = \left\{ \begin{array}{l} \begin{array}{*{20}c} {x_1 (t,x_{10} ) = - \frac{{\lambda _1 x(nt^ + ){\rm e}^{ - \lambda _1 (t - nt)} }}{{\lambda _1 + \lambda _2 x(n\tau,x_0 ) - \lambda _2 x(n\tau,x_0 ){\rm e}^{ - \lambda _1 (t - nt)} }}}, & {n\tau < t \le n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x_1 (t^ + ) = a_1 x_1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} & {} & {} \\ \end{array}} & {} & {} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array}} & {} & {} \\ \end{array}} & {} \\ \end{array}} \\ \end{array}} & {t = n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x_2 (t,x_{20} ) = x_2 (t - n\tau + (1 - \phi )\tau,x_{20} ),} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array}} & {} \\ \end{array}} & {} & {} \\ \end{array}n\tau + (1 - \phi )\tau < t \le (n + 1)\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x_2 (t^ + ) = a_2 x_2,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} & {} \\ \end{array}} & {} \\ \end{array}} & {} & {} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array}} & {} & {} & {} \\ \end{array}} \\ \end{array}} & {t = (n + 1)\tau }. \\ \end{array} \\ \end{array} \right.$

同理,对任意 $y_0 \in R^ + $, 令 $y(t,y_0 )$ 是 Logistics 方程的唯一解

$\frac{{{\rm d}y}}{{{\rm d}t}} = r_2 y\bigg(1 - \frac{y}{{K_2 }}\bigg), y(0,y_0 ) = y_0 \in \mathbb{R}^+.$

则该模型 (1.2) 的解可表示成如下形式

$\left\{ \begin{array}{l} \begin{array}{*{20}c} {x(t,x_0 ) = x(t - n\tau,x_0 ),} & {n\tau < t \le n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x(t^ + ) = a_1 x,} & {t = n\tau + (1 - \phi )\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {x(t,x_0 ) = y(t - (n\tau + (1 - \phi )\tau ), x(n\tau + (1 - \phi )\tau),x_0 ),} & {n\tau + (1 - \phi )\tau < t \le (n + 1)\tau }, \\ \end{array} \\ \begin{array}{*{20}c} {y(t^ + ) = a_2 x,} & {t = (n + 1)\tau }, \\ \end{array} \\ x(0) = x_0 \in \mathbb{R}^+, \\ \end{array} \right.$

对于模型 (1.2), 通过在脉冲点积分可得下列频闪映射

$\begin{equation} x_{1(n + 1)} = \frac{{a_1 \lambda _1 x_{2n} }}{{(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} }}, \\ x_{2(n + 1)} = \frac{{a_2 Kx_{1(n + 1)} }}{{(K - x_{1(n + 1)} )\frac{1}{{p_2 }} + x_{1(n + 1)} }}.\\ \end{equation}$

其中 $0 < p_1 = {\rm e}^{ - \lambda _1 (1 - \phi )\tau } < 1, p_2 = {\rm e}^{r\phi \tau } > 1$.

定理3.1 若条件 $\begin{array}{*{20}c} {a_1 a_2 p_1 p_2 > 1} & {( \le 1)} \\ \end{array}$ 成立, 则数学模型 (1.2) 持久 (灭绝).

证 首先, 证明 $a_1 a_2 p_1 p_2 > 1$ 成立, 数学模型 (1.2) 持久.

利用 (3.1) 式可得

$x_{2(n + 1)} = \frac{{a_2 Kx_{1(n + 1)} }}{{(K - x_{1(n + 1)} )\frac{1}{{p_2 }} + x_{1(n + 1)} }} < \frac{{a_2 K}}{{1 - \frac{1}{{p_2 }}}} = \frac{{a_2 K.p_2}}{{p_2 - 1}} = M_1,$
$x_{1(n + 1)} = \frac{{a_1 \lambda _1 x_{2n} }}{{(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} }} = \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \frac{{\lambda _1 }}{{x_{2n} }}}} < \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \frac{{\lambda _1 }}{{M_1 }}}} = M_2.$

另一方面, 利用 (3.1) 式, 可得

$\begin{equation} x_{1(n + 1)} = \frac{{a_1 \lambda _1 x_{2n} }}{{(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} }} = \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}}}, \end{equation}$

令

$\begin{equation} F_1 (x_{1n} ) = \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}}}, \end{equation}$

则

$\begin{align*} F'_1 (x_{1n} ) &= \frac{{ - a_1 \lambda _1 p_1 \bigg[\frac{{\lambda _1 [a_2 Kx_{1n} - a_2 Kx_{1n} \frac{1}{{p_2 }} - a_2 K^2 \frac{1}{{p_2 }} + a_2 Kx_{1n} \frac{1}{{p_2 }} - a_2 Kx_{1n} ]}}{{(a_2 Kx_{1n} )^2 }}\bigg]}}{{\bigg\{ (1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}\bigg\} ^2 }}\\[2mm] &= \frac{{a_1 a_2 \lambda _1^2 K^2 p_1 \frac{1}{{p_2 }}}}{{\bigg\{ (1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}\bigg\} ^2 }(a_2 Kx_{1n} )^2 } > 0. \end{align*}$

若存在 $N$, 使得 $x_{1(N + 1)} \le x_{1N},n \ge N$, 因为 $F_1 $ 是单调增函数, 有 $x_{1(n + 1)} \le x_{1n} $, 即

$x_{1(n + 1)} = \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}}} < x_{1n}.$

又因为 $a_1 a_2 p_1 p_2 > 1$, 故

$\begin{equation} x_{1n} > \frac{{\lambda _1 K(a_1 a_2 p_1 p_2 - 1)}}{{(1 - p_1 )p_2 a_2 \lambda _2 K + \lambda _1 (p_2 - 1)}} > 0. \end{equation}$

对上式两边同时取极限得

$\mathop {\lim }\limits_{} \mathop {\inf }\limits_{t \to + \infty } x_{1n} > \frac{{\lambda _1 K(a_1 a_2 p_1 p_2 - 1)}}{{(1 - p_1 )p_2 a_2 \lambda _2 K + \lambda _1 (p_2 - 1)}}.$

类似地, 对于

$\begin{equation} x_{2(n + 1)} = \frac{{a_2 K}}{{(1 - \frac{1}{{p_2 }}) + \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} ]}}{{a_1 \lambda _1 x_{2n} }}}}. \end{equation}$

记

$\begin{equation} F_2 (x_{2n} ) = \frac{{a_2 K}}{{(1 - \frac{1}{{p_2 }}) + \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} ]}}{{a_1 \lambda _1 x_{2n} }}}}. \end{equation}$

则

$\begin{align*} F'_2 (x_{2n} ) &= \frac{{ - a_2 K\bigg\{ \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _2 \frac{1}{{p_1 }} - \lambda _2 )a_2 \lambda _1 x_{2n} - a_2 \lambda _1 [(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} ]]}}{{(a_2 \lambda _1 x_{2n} )^2 }}\bigg\} }}{{\bigg\{ (1 - \frac{1}{{p_2 }}) + \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} ]}}{{a_1 \lambda _1 x_{2n} }}\bigg\} ^2 }}\\[2mm] &= \frac{{p_1 p_2 K^2 a_1^2 \lambda _1^2 }}{{\left\{ {p_1 (p_2 - 1)a_1 \lambda _1 x_{2n} + K[(\lambda _1 + \lambda _2 x_{2n} ) - p_1 \lambda _2 x_{2n} ]} \right\}^2 }} > 0. \end{align*}$

若存在 $N_1 $, 使得 $x_{1(N_1 + 1)} \le x_{1N_1 }, n \ge N_1 $, 因为 $F_2 $ 单调增加, 根据上述同样的方法, 可得

$x_{2(n + 1)} = \frac{{a_2 K}}{{(1 - \frac{1}{{p_2 }}) + \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_2 }} - \lambda _2 x_{2n} ]}}{{a_1 \lambda _1 x_{2n} }}}} < x_{2n}.$

而 $a_1 a_2 p_1 p_2 > 1$, 因此

$x_{2n} > \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{[a_1 \lambda _1 p_1 (p_2 - 1) + K\lambda _2 (1 - p_1 )]}} > 0.$

对上式两边同时取极限有

$\mathop {\lim \inf }\limits_{t \to \infty } x_{2n} > \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{[a_1 \lambda _1 p_1 (p_2 - 1) + K\lambda _2 (1 - p_1 )]}}.$

综上所述, 取

$m_1 = \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{Kp_2 a_2 \lambda _2 (1 - p_1 ) + \lambda _1 (p_2 - 1)}},\begin{array}{*{20}c} {} & {m_2 = \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{[a_1 \lambda _1 p_1 (p_2 - 1) + K\lambda _2 (1 - p_1 )]}}}. \end{array}$

令 $m = \min \{ m_1,m_2 \}, M = \max \{ M_1,M_2 \} $. 故

$m \le \mathop {\lim \inf }\limits_{t \to \infty } x(t) \le \mathop {\lim \sup }\limits_{t \to \infty } x(t) \le M.$

由持久性定义可知, 系统 (1.2) 持久.

其次, 证明 当 $a_1 a_2 p_1 p_2 \le 1$ 时, 系统 (1.2) 灭绝. 结合

$\begin{align*} & x_{1(n + 1)} = \frac{{a_1 \lambda _1 p_1 }}{{(1 - p_1 )\lambda _2 + \lambda _1 \frac{{[(K - x_{1n} )\frac{1}{{p_2 }} + x_{1n} ]}}{{a_2 Kx_{1n} }}}},\\ & x_{2(n + 1)} = \frac{{a_2 K}}{{(1 - \frac{1}{{p_2 }}) + \frac{K}{{p_2 }} \cdot \frac{{[(\lambda _1 + \lambda _2 x_{2n} )\frac{1}{{p_1 }} - \lambda _2 x_{2n} ]}}{{a_1 \lambda _1 x_{2n} }}}}, \end{align*}$

以及 $1 - \frac{1}{{p_2 }} > 0$, 有

$\begin{equation} x_{1(n + 1)} \le a_1 a_2 p_1 p_2 x_{1n} \le x_{1n}, x_{2(n + 1)} \le a_1 a_2 p_1 p_2 x_{2n} \le x_{2n}. \end{equation}$

故序列 $\{ x_{1n} \} $ 和 $\{ x_{2n} \} $ 非增. 设 $\xi _1,\xi _2 $ 分别为 $\{ x_{1n} \} $ 和 $\{ x_{2n} \} $ 的极限, 由数列极限的保号性知 $\xi _i \ge 0(i = 1,2)$. 另一方面, 对 (3.4) 和 (3.7) 等式两边同时取极限, 得

$\xi _1 = \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{Kp_1 a_2 \lambda _2 (1 - p_1 ) + \lambda _1 (p_2 - 1)}} \le 0,\begin{array}{*{20}c} {} & {\xi _2 = \frac{{K\lambda _1 (a_1 a_2 p_1 p_2 - 1)}}{{[a_1 \lambda _1 p_1 (p_2 - 1) + K\lambda _2 (1 - p_1 )]}}} \end{array} \le 0.$

因此

$\xi _i = 0, i = 1,2.$

这就表明系统 (1.2) 灭绝. 定理 3.1 得证.

定理3.2 若

$\begin{equation} a_1 a_2 > 1,{\rm{ }}r\phi - \lambda _1 (1 - \phi ) > 0. \end{equation}$

则系统 (1.2) 有唯一正 $\tau $-周期解 $x^* (t)$.

证 显然, $x(t,x_0 )$ 是 $\tau $-周期解当且仅当 $x(\tau ^ +,x_0 ) = x_0 $. 定义周期映射 $S:\mathbb{R}^+ \to \mathbb{R}^+ $

$\begin{equation} S(x_0 ) = x(\tau ^ +,x_0 ). \end{equation}$

则系统 (1.2) 有非平凡 $\tau $-周期解当且仅当 $S$ 在 $\mathbb{R}^+ $ 上有不动点. 由 (3.11) 式可知

$\begin{align*} & {S(x_0 )} = {x(\tau ^ +,x_0 ) = a_2 x_2 (\tau,x_0 )} = a_2 x_2 \Big(\phi \tau,\frac{{a_1 \lambda _1 x_0 }}{{(\lambda _1 + \lambda _2 x_0 )\frac{1}{{p_1 }} - \lambda _2 x_0 }}\Big), \\[1mm] & {S^2 (x_0 )} = a_2 x_2 (2\tau ^ +,x_0 ) = a_2 x_2 (\tau,S(x_0 )) = a_2 x_2 \Big(\phi \tau,\frac{{a_1 \lambda _1 S(x_0 )}}{{(\lambda _1 + \lambda _2 S(x_0 ))\frac{1}{{p_1 }} - \lambda _2 S(x_0 )}}\Big), \\[1mm] & {S^3 (x_0 )} = a_2 x_2 (3\tau ^ +,x_0 ) = a_2 x_2 (\tau,S^2 (x_0 )) = a_2 x_2 \Big(\phi \tau,\frac{{a_1 \lambda _1 S^2 (x_0 )}}{{(\lambda _1 + \lambda _2 S^2 (x_0 ))\frac{1}{{p_1 }} - \lambda _2 S^2 (x_0 )}}\Big), \\ & \qquad\quad \,{\rm{ }} \vdots \\ &{S^{n + 1} (x_0 )} = a_2 x_2 ((n + 1)\tau ^ +,x_0 ) = a_2 x_2 (\tau,S^n (x_0 )) \\ &\qquad\qquad = a_2 x_2 \Big(\phi \tau,\frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 ))\frac{1}{{p_1 }} - \lambda _2 S^n (x_0 )}}\Big). \end{align*}$

注意到 Logistic 方程的解 $x_2 (t,x_2 (0))$ 可以表示成

$\begin{equation} x_2 (t,x_2 (0)) = \frac{{Ka_2 x_2 (0)}}{{(K - x_2 (0)){\rm e}^{ - rt} + x_2 (0)}},\begin{array}{*{20}c} {} & {t \ge 0,x_2 (0) \in \mathbb{R}^+ }. \\ \end{array} \end{equation}$

因此, 周期映射 $S^{n + 1} (x_0 )$可表示为

$\begin{align*} S^{n + 1} (x_0 ) &= \frac{{Ka_2 \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}}}{{\Big[K - \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}\Big]{\rm e}^{ - rt} + \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}}} \\[2mm] & = \frac{{a_1 a_2 {\rm e}^{[r\phi - \lambda (1 - \phi )]\tau } }}{{1 + [\frac{{a_1 }}{K}{\rm e}^{[r\phi - \lambda _1 (1 - \phi )]\tau } (1 - {\rm e}^{ - r\phi \tau } ) + \frac{{\lambda _2 }}{{\lambda _1 }}(1 - {\rm e}^{ - \lambda _1 (1 - \phi )\tau } )]S^n (x_0 )}}. \end{align*}$

记

$\begin{array}{l} b = a_1 a_2 {\rm e}^{[r\phi - \lambda _1 (1 - \phi )]\tau }, \\ b_0 = \frac{{a_1 }}{K}{\rm e}^{[r\phi - \lambda _1 (1 - \phi )]\tau } (1 - {\rm e}^{ - r\phi \tau } ) + \frac{{\lambda _2 }}{{\lambda _1 }}(1 - {\rm e}^{ - \lambda _1 (1 - \phi )\tau } ). \\ \end{array}$

结合 (3.10) 和 (3.14) 式, 可知 $b > 1$. 再运用引理 2.1 得到 $S$ 有唯一不动点且 $\overline x = \frac{{b - 1}}{{b_0 }}$, 可得到系统 (1.2) 有唯一的正 $\tau $- 周期解 $x^* (t, \overline x )$.

定理3.3 若 $a_1 a_2 > 1$ 且 $r\phi - \lambda _1 (1 - \phi ) > 0$ 成立, 则系统满足任意初值 $x_0 > 0$ 的正解 $x(t,x_0 )$ 有

$\mathop {\lim }\limits_{t \to \infty } (x(t) - x^* (t)) = 0.$

证 因为

$\begin{align*} S^{n + 1} (x_0 ) &= \frac{{Ka_2 \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}}}{{[K - \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}]{\rm e}^{ - rt} + \frac{{a_1 \lambda _1 S^n (x_0 )}}{{(\lambda _1 + \lambda _2 S^n (x_0 )){\rm e}^{ - \lambda _1 (1 - \phi )} - \lambda _2 S^n (x_0 )}}}} \\ & = \frac{b}{{1 + b_0 S^n (x_0 )}}. \end{align*}$

这里 $b,b_0 $ 定义在 (3.14) 式中.

容易得到 $k = 0$, 所以有 $b_0 \overline x k = 0 \le 1$, 运用引理 2.2(c(1)), 知 $x^* (t, \overline x )$ 全局吸引.

定理3.4 若$a_1 a_2 > 1$ 且 $r\phi - \lambda _1 (1 - \phi ) \le 0,$则系统 (1.2) 的解 $x(t)$ 满足 $\mathop {\lim }\limits_{t \to \infty } x(t) = 0.$

证 由 $b = a_1 a_2 {\rm e}^{[r\phi - \lambda _1 (1 - \phi )]\tau }$可知

$0 < b \le 1.$

运用引理 2.2(a), 可以知道 $x = 0$ 全局吸引, 即种群最终灭绝.

4 数值模拟及生物意义

本文主要考虑一类具有季节性切换及脉冲扰动的鱼类单种群模型. 为了验证结果的准确性, 现对系统 (1.2) 进行数值模拟. 假设选取参数 $K = 4, {\rm{ }}\tau = 10, {\rm{ }}\phi {\rm{ = 0}}{\rm{.2, }}\lambda _1 = 0.3, {\rm{ }}\lambda _2 = 0.1, {\rm{ }}r = 1.8$. 令这些参数不变, 仅改变脉冲值 $a_1,{\rm{ }}a_2 $ 的大小. 根据上述的参数取值, 不难看出

$\begin{array}{*{20}c} {1.8 \times 0.2 > 0.3 \times 0.8} & {(r\phi > \lambda _1 (1 - \phi ))}. \end{array}$

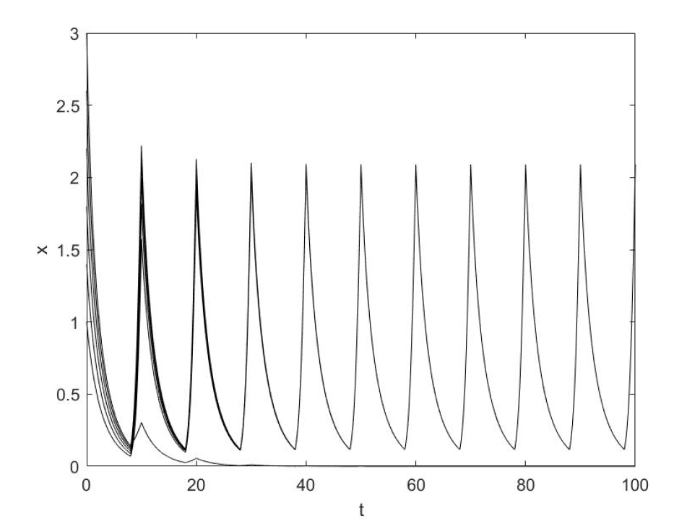
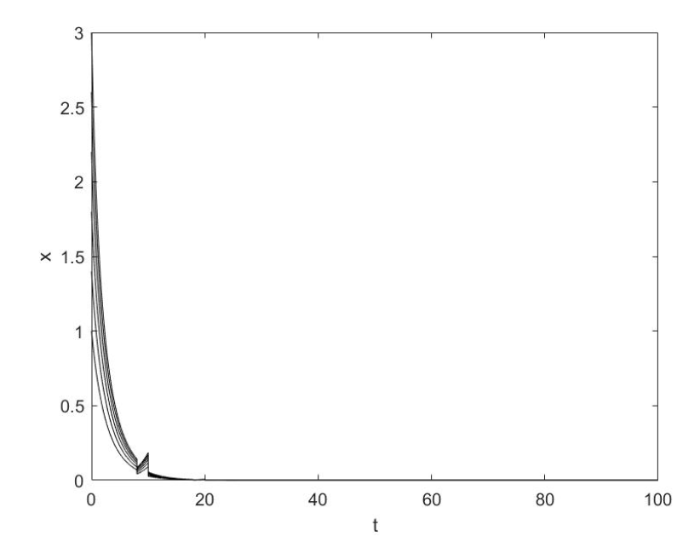
首先令 $a_1 = a_2 = 1$, 此时系统 (1.2) 变成连续系统 (在文献[16]中已研究) 且参数满足文献[16,引理 2.1] 的条件, 从数值模拟中可以看出系统有唯一全局渐近稳定的正周期解, 如图1 所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   当 $r\phi > \lambda _1 (1 - \phi )$ 时系统 (1.2) 具有稳定的正周期解


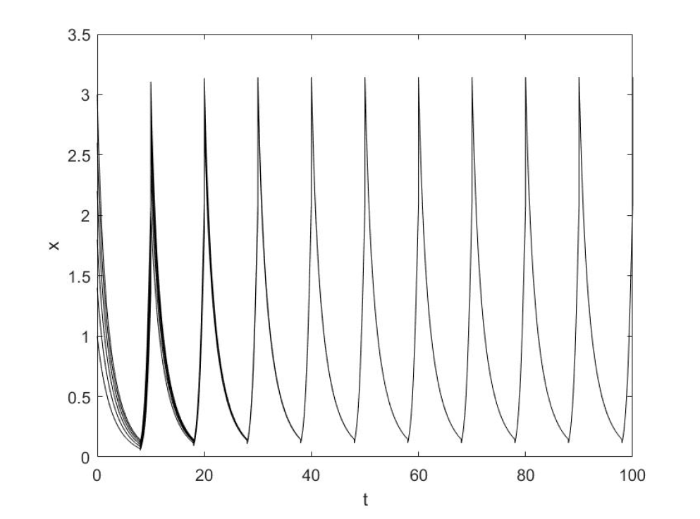
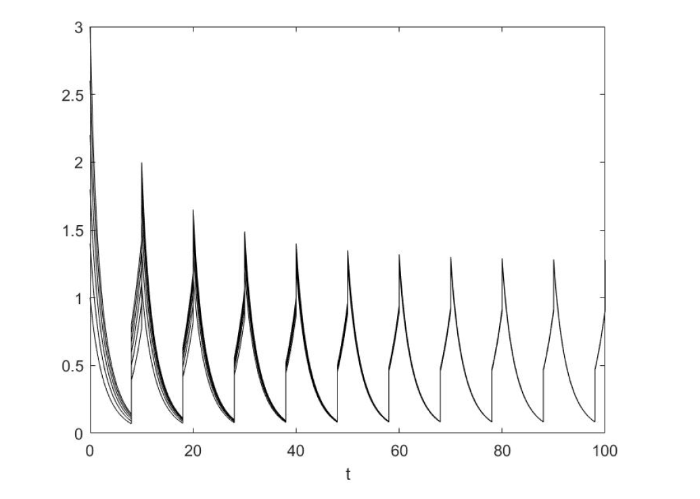
其次, 令 $a_1 = 0.8,{\rm{ }}a_2 = 1.5$, 并由此可得

$a_1 a_2 > 1$.

条件满足定理 3.2. 从模拟中我们可以看出系统 (1.2) 持久且有唯一全局吸引的正$\tau $-周期解, 这与我们的结论相符. 如图2 所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   当$a_1 a_2 > 1$时系统 (1.2) 持久且具有全局吸引的正周期解


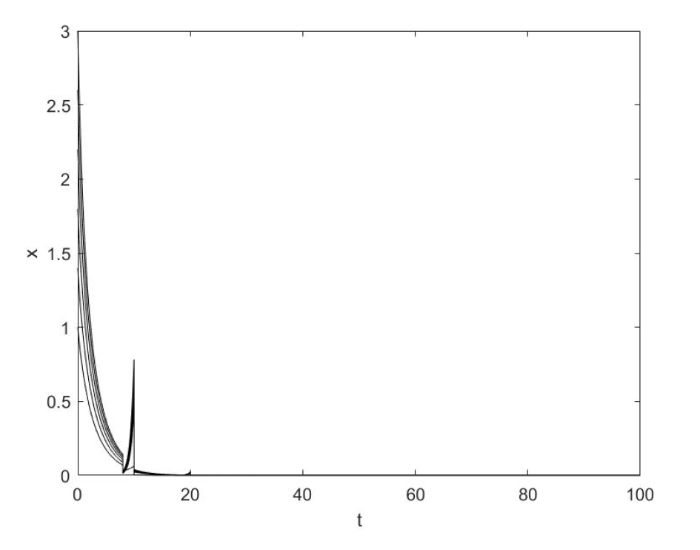
然而, 如果 $a_1 = 0.2,a_2 = 0.05$, 符合 $a_1 a_2 < 1$ (即种群在季节切换时由于认为投放或其他因素数量急剧减少), 系统 (1.2) 中的鱼类的数量最终趋于 0, 也就是说, 虽然 $r\phi > \lambda _1 (1 - \phi )$ 成立, 但是鱼类在季节切换时数量大幅度减少且减少的程度远远超过自身的回复调节能力, 鱼类仍会灭绝, 如图3 所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   当$a_1 a_2 < 1$时系统 (1.2) 灭绝


再设参数 $K = 4,{\rm{ }}\tau = 10,{\rm{ }}\phi = 0.2,{\rm{ }}\lambda _1 = 0.3,{\rm{ }}\lambda _2 = 0.1,{\rm{ }}r = 0.4$ 保持不变, $a_1,a_2 $ 是变量, 由上述参数可得

$0.4 \times 0.2 < 0.3 \times 0.8\begin{array}{*{20}c} {} & {(r\phi < \lambda _1 (1 - \phi ))}. \end{array}$

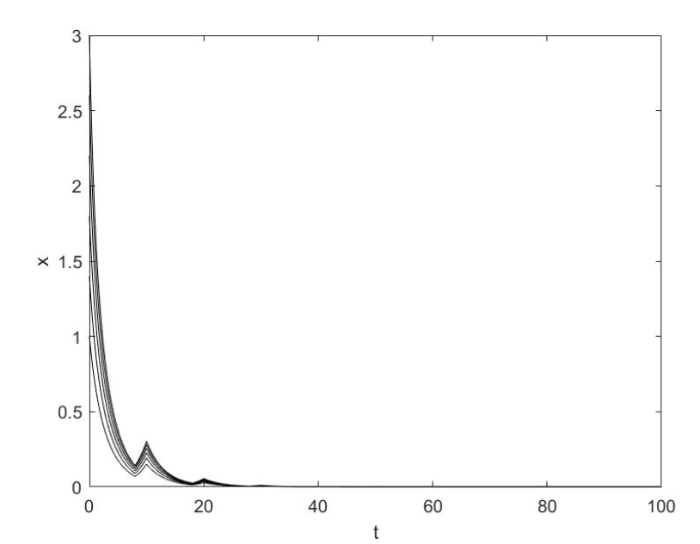
首先令 $a_1 = 1,a_2 = 1$, 系统 (1.2) 满足关于灭绝的条件, 如定理结果可得, 当 $t \to + \infty $ 时, 种群灭绝, 如图4 所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   当$r\phi < \lambda _1 (1 - \phi )$时系统 (1.2) 灭绝


其次, 令 $a_1 = 0.6,a_2 = 0.3$, 可得$a_1 a_2 < 1$.

由图可知定理 3.3 的结果得到验证, 如图5 所示.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   当$a_1 a_2 < 1$时系统 (1.2) 灭绝


然而, 当 $a_1 = 5.6,a_2 = 1.4$ (由于认为投放或其他因素, 种群在季节性过渡期间大幅度增加), 从数值模拟中可以看出, 种群不会像想象中那样无限增长, 而是会持久稳定, 这显然是符合自然生物系统的平衡性理论. 如图6 所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   当$a_1 = 5.6,a_2 = 1.4$时系统 (1.2) 持久稳定


5 结论

本文研究了一类具有季节性切换及脉冲投放的鱼类单种群动力学模型, 通过分析, 我们给出了正周期解的持久性、存在性、唯一性和全局稳定性的充分条件. 通过数值模拟结果可知, 如果系数 $\lambda _1,\lambda _2,a_1,a_2 $ 确定, 由从定理 3.1 到定理 3.4 的分析可知: 当 $a_1 a_2 p_1 p_2 > 1$ 时, 系统保持持久生存状态; 当 $a_1 a_2 p_1 p_2 \le 1$ 时, 系统就会灭绝; 当 $a_1 a_2 > 1$ 且 $r\phi > \lambda _1 (1 - \phi )$ 时, 系统持久生存且具有稳定的周期解; 当 $a_1 a_2 \le 1$ 且 $r\phi \le \lambda _1 (1 - \phi )$ 时, 系统就会灭绝. 数值模拟 (图1-6) 表明了脉冲扰动对鱼类种群持久生存与灭绝具有重要的影响, 对合理利用脉冲控制鱼类种群的发展趋势具有重要的意义, 我们的研究结论为渔业可再生资源的研究策略提供重要的数学理论依据. 综上可知，具有季节切换和脉冲扰动的种群模型的动力学行为更丰富，更加符合生物系统中种群发展的自然规律.

参考文献

马亚宸, 徐宾铎, 王晶, 等.

渔业信息船数对海洋捕捞产量估计的影响

中国海洋大学学报 (自然科学版), 2020, 50(S01): 71-77

[本文引用: 1]

Ma Y C, Xu B Y, Wang J, et al.

Effect of number of study fleets on the marine fisheries catch estimate in a fishery-dependent survey

Periodical of Oceanuniversity of China (Natural Science Edition), 2020, 50(S01): 71-77

[本文引用: 1]

黄振东.

海洋渔业对海洋生态系统的影响及其管理初探

中国农业信息, 2017, 29(10): 51-52

Huang Z D.

Preliminary study on the impact and management of marine fisheries on marine ecosystems

China Agricultural Information, 2017, 29(10): 51-52

茅克勤, 王鹏, 岳羲和, 等.

海洋渔业综合净效益评估研究

海洋环境科学, 2023, 42(5): 729-737

[本文引用: 1]

Mao K Q, Wang P, Yue X H, et al.

Study on the evaluation of comprehensive net performance of marine fishery

Marine Environmental Science, 2023, 42(5): 729-737

[本文引用: 1]

Peng R, Zhao X Q.

The diffusive logistic model with a free boundary and seasonal succession

Discrete and Continuous Dynamical Systems, 2012, 33(5): 2007-2031

[本文引用: 1]

Xing L, Chen Y, Zhang C L, et al.

Evaluating impacts of pulse fishing on the effectiveness of seasonal closure

Acta Oceanologica Sinica, 2020, 39: 89-99

Buonomo B, Chitnis N, d'Onofrio A.

Seasonality in epidemic models: a literature review

Ricerche di Matematica, 2018, 67: 7-25

Duarte J, Januario C, Martins N, et al.

Controlling infectious diseases: the decisive phase effect on a seasonal vaccination strategy

International Journal of Bifurcation and Chaos, 2021, 31(1): 134

[本文引用: 1]

李艳青. 具有季节演替及马尔科夫转换的种群模型研究. 乌鲁木齐: 新疆大学, 2017

[本文引用: 1]

Li Y Q. The Study of Population Models with Seasonal Succession and Markovian Switching. Urumqi: Xinjiang University, 2017

[本文引用: 1]

Wang M X, Zhang Q Y, Zhao X Q.

Traveling waves and spreading properties for a reaction-diffusion competition model with seasonal succession

Nonlinearity, 2022, 35(134): 135-169

Yan R, Sun Q W.

Uniqueness and stability of periodic solutions for an interactive wild and Wolbachia-infected male mosquito model

Journal of Biological Dynamics, 2022, 16(1): 254-276

Meng W, Yue Y, Ma M.

The minimal wave speed of the Lotka-Volterra competition model with seasonal succession

Discrete and Continuous Dynamical Systems-Series B, 2022, 27(9): 5085-5100

孙佳杰. 季节变换下害虫综合治理切换模型的数学模拟研究. 大连: 辽宁师范大学, 2023

Sun J J. Mathematical Simulation Study of Switching Models with Integrated Pest Management Under Seasonal Change. Dalian: Liaoning Normal University, 2023

Zhang Z W, Chang L J, Huang Q M, et al.

A mosquito population suppression modelwitha saturated Wolbachia release strategy in seasonal succession

Journal of Mathematical Biology, 2023, 86(51): 1-31

Feng X M, Liu Y F, Ruan S G, Yu J S.

Periodic dynamics of a single species model with seasonal Michaelis-Menten type harvesting

Journal of Differential Equations, 2023, 3.4: 237-263

Chen Y W, Li W X, Zhang Q M, et al.

The bistable wave speed in a reaction-diffusion system with seasonal succession

Journal of Mathematical Analysis and Applications, 2023, 5.8( 2): 126704

[本文引用: 1]

Hsu S B, Zhao X Q.

A Lotka-Volterra competition model with seasonal succession

J Math Biol, 2012, 64(1): 109-130

[本文引用: 3]

Tian Y, Tang S Y.

Dynamics of a density-dependent predator-prey biological system with nonlinearimpulsive control

Mathematical Biosciences and Engineering, 2021, 18(6): 7318-7343

[本文引用: 1]

Tang S Y, Tian Y, Cheke R A.

Dynamic complexity of a predator-prey model for IPM with nonlinear impulsive control incorporating a regulatory factor for predator releases

Mathematical Modelling and Analysis, 2019, 24(1): 134-154

Yan X X, Zhao Z, Hui Y X, Yang J G.

Dynamic analysis of a bacterial resistance model with impulsive state feedback control

Mathematical biosciences and engineering, 2023, 20(12): 20422-20436

DOI:10.3934/mbe.2023903      PMID:38124559     

Bacterial resistance caused by prolonged administration of the same antibiotics exacerbates the threat of bacterial infection to human health. It is essential to optimize antibiotic treatment measures. In this paper, we formulate a simplified model of conversion between sensitive and resistant bacteria. Subsequently, impulsive state feedback control is introduced to reduce bacterial resistance to a low level. The global asymptotic stability of the positive equilibrium and the orbital stability of the order-1 periodic solution are proved by the Poincaré-Bendixson Theorem and the theory of the semi-continuous dynamical system, respectively. Finally, numerical simulations are performed to validate the accuracy of the theoretical findings.

梁毅东. 脉冲微分方程在害虫治理模型中的应用. 长春: 长春工业大学, 2024

Liang Y D. Application of Impulse Differential Equation in Pest Management Model. Changchun: Changchun University of Technology, 2024

Fu J B, Chen L S.

Modelling and qualitative analysis of water hyacinth ecological system with two state-dependent impulse controls

Complexity, 2018, 20.8: Article 4543976

Huang Y, Shi W, Wei C, et al.

A stochastic predator-prey model with Holling II increasingfunction in the predator

Journal of Biological Dynamics, 2021, 15(1): 1-18

Shi Z Z, Cheng H D, Liu Y, et al.

Optimization of an integrated feedback control for a pest management predator-prey model

Mathematical Biosciences and Engineering, 2019, 16( 6): 7963-7981

DOI:10.3934/mbe.2019401      PMID:31698650      [本文引用: 1]

In this paper, a Leslie-Gower predator-prey model with ratio-dependence and state pulse feedback control is established to investigate the effect of spraying chemical pesticides and supplement amount of beneficial insects at the same time. Firstly, the existence, uniqueness and asymptotic stability of the periodic solution are proved by using successor function method and the analogue of the Poincaré criterion when the equilibria E and E are stable, and the existence of limit cycles without impulse system is verified when the equilibrium E is unstable. Furthermore, to obtain the minimum cost per period of controlling pests, we propose the optimization problem and calculate the optimal threshold. Finally, the feasibility of our model is proved by numerical simulation of a concrete example.

聂星屹, 焦建军.

具脉冲出生与脉冲收获切换的阶段结构单种群动力学模型

生物数学学报, 2020, 35(1): 155-159

[本文引用: 1]

Nei X Y, Jiao J J.

A Single population dynamics model with stage structure switching between pulse birth and pulse harvest

Journal of Biomathematics, 2020, 35(1): 155-159

[本文引用: 1]

王明靖.

具脉冲效应的渔业资源管理动力学模型

广东蚕业, 2023, 57(10): 35-38

[本文引用: 1]

Wang M J.

Dynamic model of fishery resource management with pulse effect

Guangdong Sericulture, 2023, 57(10): 35-38

[本文引用: 1]

吕宁.

双脉冲阶段结构的种群系统动力学特性

山东大学学报(理学版), 2021, 56(12): 100-110

[本文引用: 1]

Lv Ning.

Dynamics of the stage-structured population system with two kinds of pulses

Journal of Shandong University (Natural Science), 2021, 56(12): 100-110

[本文引用: 1]

刘兰兰. 具两系统切换脉冲效应的生物动力学模型. 贵阳: 贵州财经大学, 2019

[本文引用: 1]

Liu L L. Biodynamic Model with Two System Switching Pulse Effect. Guiyang: Guizhou University of Finance and Economics, 2019

[本文引用: 1]

Kocic V L, Ladas G. Global Behavior of Nonlinear Difference Equations of Higher Order with Application. London: Spinger-Verlag, 1993

[本文引用: 2]

Zhang L, Teng Z D, Donald L, Ruan S G.

Single species models with logistic growth and dissymmetric impulse dispersal

Math Biosci, 2013, 2.1(2): 188-197

DOI:10.1016/j.mbs.2012.11.005      PMID:23220292      [本文引用: 1]

In this paper, two classes of single-species models with logistic growth and impulse dispersal (or migration) are studied: one model class describes dissymmetric impulsive bi-directional dispersal between two heterogeneous patches; and the other presents a new way of characterizing the aggregate migration of a natural population between two heterogeneous habitat patches, which alternates in direction periodically. In this theoretical study, some very general, weak conditions for the permanence, extinction of these systems, existence, uniqueness and global stability of positive periodic solutions are established by using analysis based on the theory of discrete dynamical systems. From this study, we observe that the dynamical behavior of populations with impulsive dispersal differs greatly from the behavior of models with continuous dispersal. Unlike models where the dispersal is continuous in time, in which the travel losses associated with dispersal make it difficult for such dispersal to evolve e.g., [25,26,28], in the present study it was relatively easy for impulsive dispersal to positively affect populations when realistic parameter values were used, and a rich variety of behaviors were possible. From our results, we found impulsive dispersal seems to more nicely model natural dispersal behavior of populations and may be more relevant to the investigation of such behavior in real ecological systems.Copyright © 2012 Elsevier Inc. All rights reserved.

/

〈 〉

版权所有 © 《数学物理学报》杂志社
地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版)
E-mail: actams@apm.ac.cn
本系统由北京玛格泰克科技发展有限公司设计开发