1 引言
复杂信号处理于通信、雷达、环境监测等领域至关重要, 准确接收信号对提升系统性能与决策效率意义重大[1 ] . 但受测量仪器精度与环境干扰影响, 实测信号常因干扰和噪声畸变, 影响后续分析与应用[2 ] . 为了准确提取信号中的有用信息, 要在复杂环境中采用必要的降噪方法.
近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性.
我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪.
非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果.
本文提出了基于 CEEMDAN、小波阈值、Savitzky-Golay (SG) 滤波器和非平稳性度量相结合的降噪方法. 首先对复杂信号进行 CEEMDAN 分解, 得到各模态分量 IMF. 然后使用 NS 准则来区分高频噪声和非高频噪声模态分量, 对非高频噪声模态分量做 Savitzky-Golay 平滑处理, 对高频噪声模态分量采用改进的小波阈值去噪. 最后把处理后的高频噪声和非高频模态分量逆变换重构, 得到去噪后的复杂信号.
本文降噪方法采用 CEEMDAN 算法分解信号, 收敛性能好且能减少重构误差, 适用于非平稳性信号的分析. NS 指标过滤噪声时不受能量的影响, 能稳定地区分高低频模态分量. 改进对数阈值函数对高频分量做降噪处理, 进一步解决了恒定偏差问题; SG 滤波对低频分量进行平滑处理, 能有效去除噪声且保持信号的形状和趋势, 减少高频噪声的影响.
本文的余下结构为: 第 2 节介绍 CEEMDAN、NS准则、小波阈值和 SG 滤波器的基本理论; 第 3 节给出所提出方法的基本步骤; 第 4 节将该方法应用于模拟复杂信号和实测复杂信号中来验证本文方法去噪的有效性; 第 5 节给出结论.
2 理论介绍
2.1 CEEMDAN分解
EMD 算法分解过程中因异常事件干扰导致极值点分布不均匀产生了模式混叠现象, 为此集成经验模态分解 (ensemble empirical mode decomposition, EEMD) 将具有频率均匀分布特性的高斯白噪声加入信号, 使信号在不同尺度上连续, 从而克服信号间歇问题, 避免了模态混叠. 但在 EEMD 分解过程中, 添加到原始信号中的噪声无法消除, 这可能会导致重建误差[20 ] . Colominas 等[21 ] 提出了 CEEMDAN, 自适应白噪声被引入到每个残差分量, 以进一步消除模式混合现象. 由于迭代次数少、收敛性能好, 该算法适用于非平稳信号. 算法步骤如下
(1) 将噪声 ${\omega }^{i}(n)$ $x(n)$
(2.1) $\begin{equation} {X}^{i}(n)={x}({n})+{{\omega }}^{{i}}({n}), \end{equation}$
其中, ${\omega }^{i}\left ( n\right )\left ( i=1,2,\cdots,N\right )$
(2) 用 EMD 将信号 ${X}^{i}(n)$ ${{F}}_{{1}}^{{i}}$ ${{F}}_{{1}}^{{i}}$
(2.2) $\begin{equation} {\tilde{F}}_{1}\left ( n\right )=\frac{1}{N}\displaystyle\sum_{i=1}^{N}{F}_{1}^{i}; \end{equation}$
(2.3) $\begin{equation} {r}_{1}\left ( n\right )= x\left ( n\right )-{\tilde{F}}_{1}\left ( n\right ); \end{equation}$
(2.4) $\begin{equation} {\widetilde{F}}_{2}\left ( n\right )=\frac{1}{N}\displaystyle\sum_{i=1}^{N}{E}_{1}\left ( {r}_{1}\left ( n\right )+{\varepsilon }_{1}{E}_{1}\left [ {\omega }^{i}\left ( n\right )\right ]\right ), \end{equation}$
其中, ${E}_{j}\left ( \cdot \right )$ ${\varepsilon }_{j}$
(2.5) $\begin{equation} {r}_{k}\left ( n\right )={r}_{k-1}\left ( n\right )-{\widetilde{F}}_{k}\left ( n\right ), \end{equation}$
其中, $k=2,3,\cdots,K$ $K$
(2.6) $\begin{equation} {\widetilde{F}}_{k+1}\left ( n\right )=\frac{1}{N}\displaystyle\sum_{i=1}^{N}{E}_{1}\left ( {r}_{k}\left ( n\right )+{\varepsilon }_{k}{E}_{k}\left [ {\omega }^{i}\left ( n\right )\right ]\right ); \end{equation}$
(7) 重复步骤 (5) 和 (6), 直到剩余成分无法细分. 最终残留成分表示为
(2.7) $\begin{equation} R\left ( n\right )=x\left ( n\right )-\displaystyle\sum_{k=1}^{K}{\tilde{F}}_{k}\left ( n\right ); \end{equation}$
(2.8) $\begin{equation} x\left ( n\right )=\displaystyle\sum_{k=1}^{K}{\tilde{F}}_{k}\left ( n\right )+R\left ( n\right ). \end{equation}$
2.2 NS 准则
非平稳性度量 NS[17 ] 是一种专为分析和量化非平稳时间序列而设计的指标, 不同于常用的相关系数、样本熵、模糊熵、排列熵等, 该指标融合了概率论、统计学、遍历论和信息论的知识, 并定义了稳定集合与稳定信息结构的概念, 为非平稳性度量提供了新的视角和方法. NS指标的特点在于其能够适应不同的数据生成过程, 并通过四种算法进行计算, 这些算法考虑了有限样本的情况, 提高了度量的准确性和实用性. 并在模型选择、股票市场数据分析和彩票市场数据分析等实际应用[17 ] 中验证了该指标的有效性. 例如, 在模型选择中, NS可以作为新的准则, 通过保证拟合优度的情况下最小化模型残差序列的非平稳性度量值来选择最佳模型. 此外, NS 还能有效区分趋势平稳与差分平稳, 以及独立同分布、白噪声与鞅差等不同类型的序列.
谭秋衡等[19 ] 的参考文献, 验证了 NS 指标区分模态分量的有效性. 即 NS 准则能有效的将 EMD 分解后的 IMF 分量区分成信号和噪声. 同时, 本文提出方法本质是去除噪声, 而噪声具有高频且平稳的特点, 因此可用 NS 来过滤噪声, 进而用来区别分解信号的高低频状态.
在此基础上, 本文针对含噪信号使用 CEEMDAN 进行信号分解, 再用 NS 准则将其分成信号和噪声, 然后对区分后的模态分量进行去噪, 针对低频分量做平滑滤波, 针对高频分量做小波阈值去噪, 具体步骤如下
(1) 将含噪复杂信号经 CEEMDAN 分解后产生的 IMF 分量, 按照次序依次将 IMF 组合.
(2) 假设检验给定显著性水平为 0.05, 参数 ${\lambda}$ ${P}_{0}$
(2.9) $\begin{equation} M=\left \lfloor 1.87{\left ( N-1\right )}^{0.4}\right \rfloor. \end{equation}$
(3) 计算组合 IMF 信号的非平稳性. 在没有信号引入时噪声是平稳的, 一旦加入某个 IMF 使得噪声组合变得不平稳, 则认为加入的这个 IMF 是信号, 并在此处断开, 之前的 IMF 为噪声, 之后的 IMF 为信号. 同时为了弥补分界点靠前或者靠后用以下的方法寻找 IMF 的分界点 ${j}_{s}$
(2.10) $\begin{equation} {j}_{s}={j}_{0}-s, \end{equation}$
(2.11) $\begin{equation} s\ldotp t\ldotp {j}_{0}=\min_{k\geqslant 1}{\left \{ k-1:NS\left ( \displaystyle\sum_{i=1}^{k}{IMF}_{i}\right )> 0.1\right \}}, \end{equation}$
(2.12) $\begin{equation} s=\min_{k\geqslant 0}{\left \{ k:NS\left ({IMF}_{{j}_{0}-k} \right )\le 0.1\right \}}. \end{equation}$
2.3 SG 滤波器
SG 滤波器在数据上滑动一个窗口, 并在每个位置上对窗口内的数据进行多项式拟合来估计窗口中心的值. 对于原始复杂信号 $x\left [ n\right ]$ $n=0$ [22 ]
(2.13) $\begin{equation} f\left ( n\right )=\displaystyle\sum_{j=0}^{n}{n}^{j}{a}_{j}, \end{equation}$
(2.14) $\begin{equation} e=\displaystyle\sum_{n=-M}^{M}{\left ( f\left ( n\right )-x\left [ n\right ]\right )}^{2}=\displaystyle\sum_{n=-M}^{M}{\left ( \displaystyle\sum_{j=0}^{n}{n}^{j}{a}_{j}-x\left [ n\right ]\right )}^{2}. \end{equation}$
在近似区间内的 2M + 1 个输入样本可以通过一组固定的权重系数有效组合, 这些系数可以根据给定的多项式阶数N和长度为 2M + 1 的近似区间计算得出[23 ] . 最终, 输出样本可以通过以下形式的离散卷积来计算
(2.15) $\begin{equation} y\left [ n\right ]=\displaystyle\sum_{m=-M}^{M}h\left [ m\right ]x\left [ n-m\right ]=\displaystyle\sum_{m=n-M}^{n+M}h\left [ n-m\right ]x\left [ m\right ], \end{equation}$
其中, $h\left [ m\right ]$ 22 ,23 ]. 本文采用的窗口大小 21, 阶数为 3.
2.4 小波阈值
小波阈值去噪计算量较小, 具有实现简单和降噪效果相对较好等优点. 去噪效果与阈值估计和阈值函数的选取有关[24 ] , 如果阈值选择得太大, 则会导致部分有用信号被错误地滤除为噪声. 反之, 则会有噪声残留, 由于去噪不彻底, 导致信号失真. Donoho[25 ] 等人提出阈值估计为
(2.16) $\begin{equation} \lambda =\sigma \sqrt{2\log_{e}{N}}, \end{equation}$
(2.17) $\begin{equation} \sigma =median\left \{ \left | {W}_{s}\left ( {a}_{1:{n}_{v},b}\right )-median\left [ {W}_{s}\left ( {a}_{1:{n}_{v},b}\right )\right ]\right |\right \}/ 0.6745, \end{equation}$
式中, ${\lambda}$ ${\sigma }^{2}$
常用的阈值函数有硬阈值和软阈值如 (2.18) 和 (2.19) 式所示, 硬阈值函数能够保留更多的真实信号峰值特征, 但连续性较差, 在重构过程中会出现振荡. 软阈值函数具有更强的连续性, 重建的信号更平滑, 但也会导致重构信号出现一些误差.
(2.18) $\begin{equation} {\widehat{\omega }}_{j,k}=\begin{cases} {\omega }_{j,k},& \left |{\omega }_{j,k}\right |> \lambda, \\ 0,&\left |{\omega }_{j,k}\right |\leqslant \lambda, \end{cases} \end{equation}$
(2.19) $\begin{equation} {\widehat{\omega }}_{j,k}=\begin{cases} {\rm sgn}\left ( {\omega }_{j,k}\right )\left ( \left | {\omega }_{j,k}\right |-\lambda\right ),& \left |{\omega }_{j,k}\right |> \lambda, \\ 0,&\left |{\omega }_{j,k}\right |\leqslant \lambda, \end{cases} \end{equation}$
其中 ${\omega }_{j,k}$ ${\widehat{\omega }}_{j,k}$ ${\lambda}$
为了解决硬阈值和软阈值函数的缺点, 提高降噪的效果, 本文采用了逼近对数型阈值函数, 函数表达式如下
(2.20) $\begin{equation} {\widehat{\omega }}_{j,k}=\begin{cases} sgn\left ( {\omega }_{j,k}\right )\left ( \left | {\omega }_{j,k}\right |-\lambda\right / \log_{10}{\left (\left | {\omega }_{j,k}\right | -\lambda +10\right )}),& \left |{\omega }_{j,k}\right |> \lambda, \\ 0,&\left |{\omega }_{j,k}\right |\leqslant \lambda. \end{cases} \end{equation}$
3 组合的方法
CEEMDAN 是一种改进的信号分解算法, 在每次分解时添加白噪声的 IMF 分量, 添加噪声逐级减少, 固有模态分量中残留噪声更少, 有效减小了重构误差, 且在分解的每个阶段都有一个全局停止标准, 分解效率最高. 在使用 CEEMDAN 算法分解含噪声信号时, 如果直接舍弃含噪声较多的高频IMF分量, 可能会导致有效信息的缺失. 尽管 CEEMDAN 算法通过加入辅助噪声的 IMF 分量来减轻模态混叠问题, 但这种方法可能会在本征模态分量中残留一定的白噪声, 影响后续信号的分析和处理.
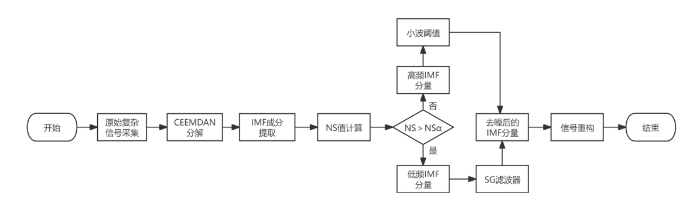
为克服这些缺点, 本文提出基于 CEEMDAN、小波阈值去噪、SG 滤波器和 NS 指标相结合的复杂信号去噪方法. 首先, 对含噪复杂信号做 CEEMDAN 分解, 得到各模态分量 IMF. 再用 NS 指标区分高频噪声和低频噪声模态分量, 对低频噪声模态分量做 S-G 平滑处理, 对高频噪声模态分量采用小波阈值去噪. 最后把处理后的高低频噪声模态分量逆变换重构, 得到去噪后的复杂信号. 本文流程图如图1 所示, 以下是去噪方法实现的步骤:
图1
(1) 对原始信号 $x\left ( n\right )$ $s\left ( n\right )$ . 对 $s\left ( n\right )$ ${F}_{i}\left ( n\right ),i=1,2,\cdots,K$ .
(2) 对分解得到的 IMF 分量 ${F}_{i}\left ( n\right )$ ${\lambda}$ ${P}_{0}$ ${\alpha}$ ${NS}_{\alpha}$ . 当小于值 ${NS}_{\alpha}$ ${F}_{h}\left ( n\right ),h=1,2,\cdots,{K}_{h}$ ${NS}_{\alpha}$ ${F}_{l}\left ( n\right ),l=1,2,\cdots,{K}_{l}$ .
(3) 低频 IMF 分量通过 SG 滤波器执行平滑和滤波过程, 利用 SG 的不同阶数和帧大小的系数, 对信号 ${F}_{l}\left ( n\right )$ ${F}_{h}\left ( n\right )$
(4) 将小波阈值去噪后的高频 IMF 分量 ${F}_{h}^{'}\left ( n\right )$ ${F}_{l}^{'}\left ( n\right )$ $f\left (x\right )$ .
4 实验验证
4.1 模拟仿真信号实验
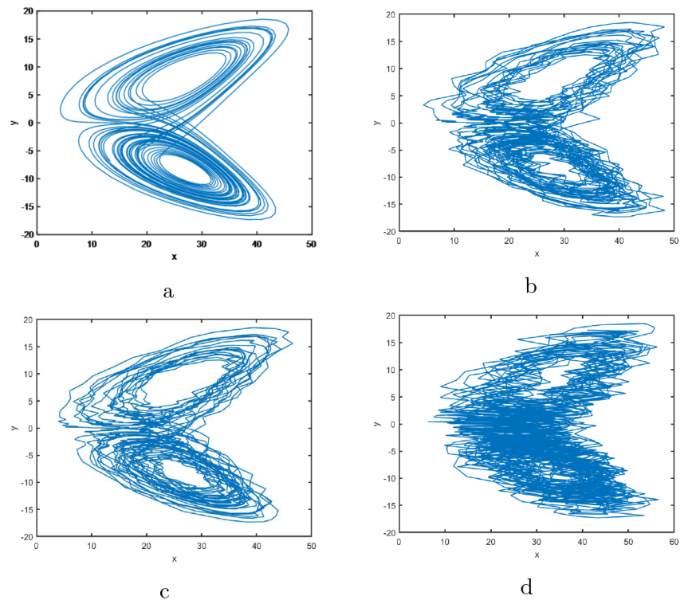
为验证本文提出的去噪算法对复杂信号去噪的可行性, 以 Lorenz 系统产生的复杂信号为研究对象. Lorenz 系统的动力学方程为
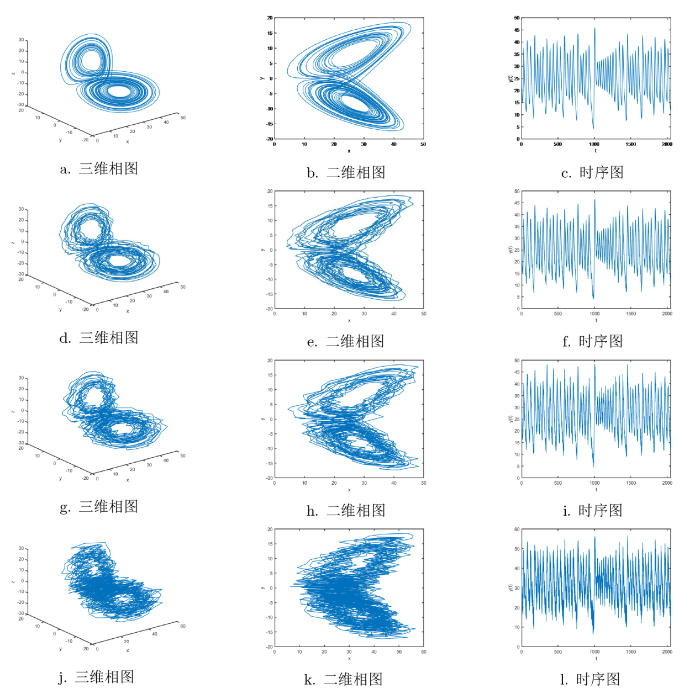
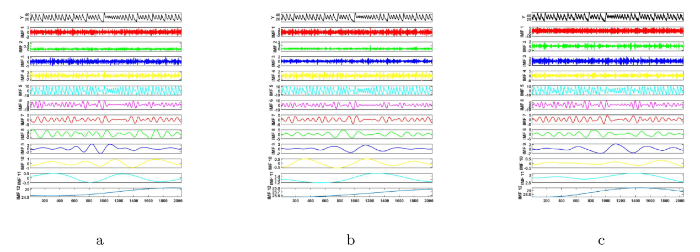
取参数 $\sigma$ $\gamma$ $x=5, y=0, z=10,$ $2.0001\times {10}^{4}$ 图2 中 a-c 为原始信号、d-f 为含高斯白噪声信号、g-i 为泊松噪声信号、j-l 为均匀噪声信号的三维相图, 二维相图和时序图对比图. 从图中发现, 因高斯白噪声、泊松噪声和均匀噪声的干扰, 对复杂信号的三维相图、二维相图和时序图产生显著影响, 图2 中 d、g、j 与 e、h、k 表现为轨迹或形状的扭曲、模糊不清及信号波形的失真. 将含高斯白噪声、均匀噪声和泊松噪声 Lorenz 信号用 CEEMDAN 分解分别得到 11 个 IMF 分量和 1 个残差项, 如图3 中 a-c 所示. 每次分解时分别添加白噪声、泊松噪声和均匀噪声的 IMF 分量, 添加的噪声逐级减少, 固有模态分量中残留噪声更少, 有效减少重构误差, 且在分解的每个阶段都有一个全局停止标准, 分解效率较高.
图2
图2
a-c 为原始信号、d-f 为含高斯白噪声信号、g-i 为含泊松噪声信号、j-l 为含均匀噪声信号
图3
图3
含高斯白噪声信号、泊松噪声信号和均匀噪声信号分解后模态分量图(三类含噪 Lorenz 信号用 CEEMDAN 分解得到各自的模态分量, 分解效率高)
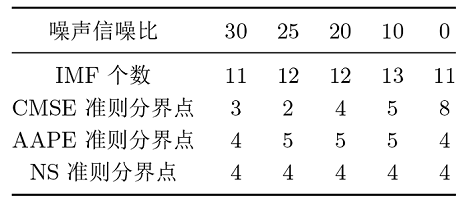
为验证 NS 指标的准确性, 在不同噪声信噪比下和常用的 AAPE 指标、CMSE 指标判别信号 IMF 的结果做比较. AAPE 值小于阈值时, 将模态分量划分为信号, 反之为噪声. 使 CMSE 值最小的那个 IMF 分量作为分界点, 在此模态分量之后的 IMF 分量为信号, 反之为噪声. NS 的值大于阈值时, 将模态分量划分为信号, 即 NS 值越接近 1 越好, 反之为噪声. 在不同噪声信噪比下把复杂信号用 CEEMDAN 分解后得出的模态分量, 计算不同的指标数据, 如表1 所示, 从而找到信号和噪声的分界点. 从表1 可以看出来, 在不同信噪比下用 NS 准则去寻找信号和噪声的分界点更加稳定, 故本文采用的是NS准则来划分高频模态分量和低频模态分量.
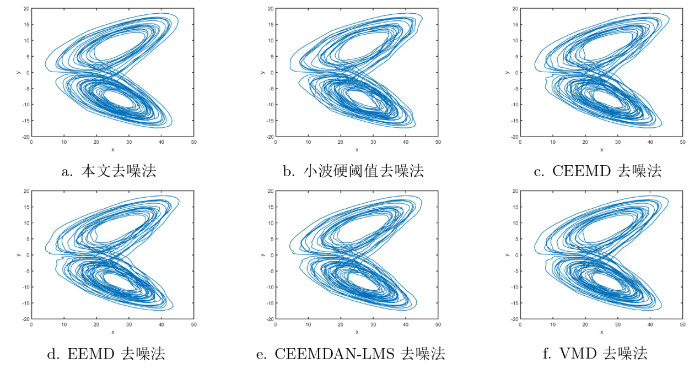
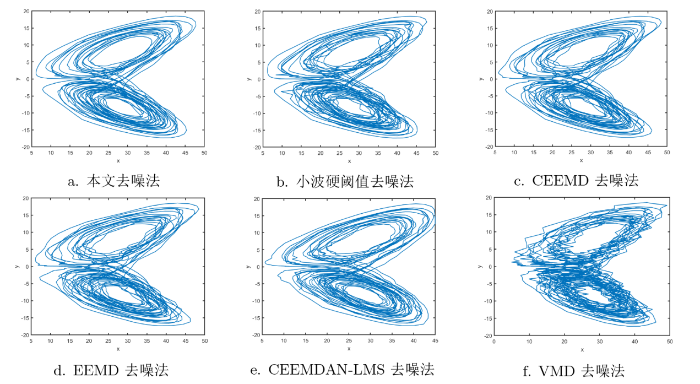
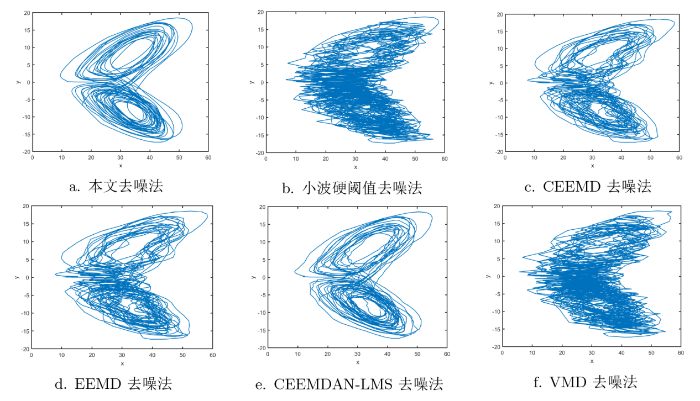
从复杂信号的特性观察不同算法的去噪效果, 原始信号、含高斯白噪声信号、泊松噪声信号、均匀噪声信号以及信噪比为 30dB 时 6 种不同的方法去噪后的二维相图如图4 中的 a-d 和图5 -7 中的 a-f 所示, 其中图5 -7 中的 a-f 分别是本文方法、小波硬阈值去噪法、CEEMD 去噪法、EEMD 去噪法、CEEMDAN-LMS 去噪法、VMD 去噪法去噪后的二维相图. 由图5 -7 中的 b-f 可以看出其他方法去噪后二维相图的轨迹仍有噪声存在的现象, 且不规则不光滑, 与图4 中的 a 原始信号图相似度比较低; 图5 -7 中的 a 本文方法去噪后相图轨迹清晰, 规则且光滑, 去噪效果更好, 与图4 中的 a 原始信号图相似度更高, 故本文提出的 CEEMDAN-NS-SG-WT 方法去噪效果更好.
图4
图4
原始信号、含高斯白噪声信号、含泊松噪声信号、含均匀噪声信号的二维相图
图5
图5
不同方法降噪后的信号对比图(高斯白噪声)(对比发现本文方法去噪后相图轨迹清晰, 规则且光滑, 去噪效果最好)
图6
图6
不同方法降噪后的信号对比图(泊松噪声) (对比发现本文方法去噪后相图轨迹清晰, 规则且光滑, 去噪效果最好)
图7
图7
不同方法降噪后的信号对比图(均匀噪声) (对比发现本文方法去噪后相图轨迹清晰, 规则且光滑, 去噪效果最好)
为了更好地比较本文方法和其他方法对复杂信号去噪效果的差别, 将信噪比 (signal noise ratio, SNR) 和均方根误差 (root mean square error, RMSE) 两个参数作为降噪效果的评价指标. 公式 (4.1) 和 (4.2) 中 $x\left ( n\right )$ $f\left ( n\right )$
(4.1) $\begin{equation} SNR=10\log_{10}{\frac{\displaystyle\sum_{i=1}^{N}{f\left ( n\right )}^{2}}{\displaystyle\sum_{i=1}^{N}{\left [ x\left ( n\right )-f\left ( n\right )\right ]}^{2}}}, \end{equation}$
(4.2) $\begin{equation} RMSE=\sqrt{\frac{\displaystyle\sum_{i=1}^{N}{\left [ x\left ( n\right )-f\left ( n\right )\right ]}^{2}}{N}}. \end{equation}$
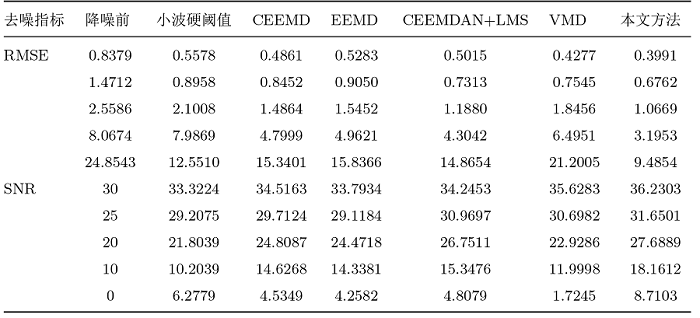
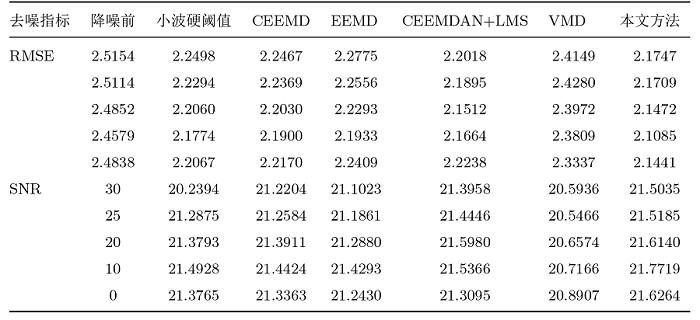
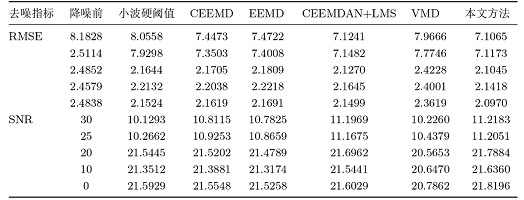
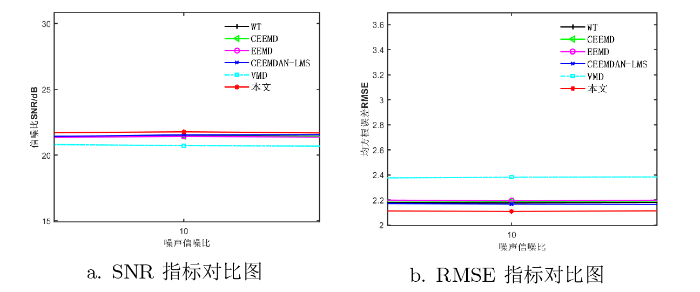
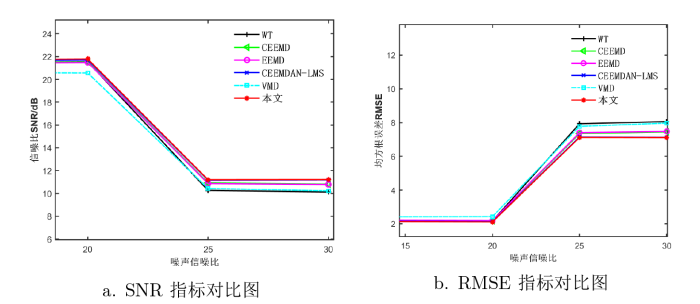
对实验数据分别加入信噪比为 30dB、25dB、20dB、10dB、0dB 的高斯白噪声、泊松噪声和均匀噪声. 采用本文方法、小波硬阈值去噪法、CEEEMD 去噪法、EEMD 去噪法、CEEMDAN+LMS 去噪法、VMD 去噪方法依次对复杂信号进行去噪, 取 5 次去噪结果的均值作为最终实验结果. 六种方法去噪后的 SNR 和 RMSE 如表2 -4 所示, 由表2 -4 可知: 本文方法去高斯白噪声、泊松噪声和均匀噪声后的 SNR 和 RMSE 得到了比较好的改善.
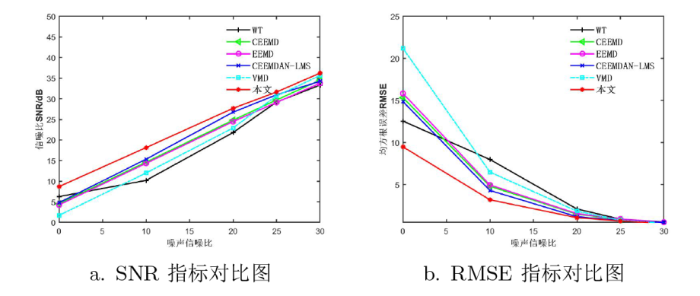
本文方法和其他五种去噪法降噪后SNR和RMSE指标对比图如图8 -10 所示, 从图8 -10 的 a 可以看出, 在不同的输入噪声信噪比下, 本文采用的降噪方法要比其他五种去噪方法的 SNR 更大, 则混在信号中的噪声最少. 从图8 -10 的 b 可以看出, 在不同的输入噪声信噪比下, 本文采用的降噪方法要比其他五种去噪方法的 RMSE 更小, 去噪后信号和原始信号相似度更高. 从图8 -10 可以更直观地比较出, 本文的降噪方法优于其他五种方法, 具有一定的抗噪性.
图8
图8
含高斯白噪声降噪后指标对比图 (对比可知本文去噪法的SNR最大, 则混在信号中的噪声最少; RMSE 最小, 与原始信号相似度最高)
图9
图9
含泊松噪声降噪后指标对比图 (对比可知本文去噪法的 SNR 最大, 效果最好, 信号更稳定; RMSE 最小, 与原始信号相似度最高)
图10
图10
含均匀噪声降噪后指标对比图 (对比可知本文去噪法的SNR最大, 效果最好, 信号更稳定; RMSE 最小, 与原始信号相似度最高)
因此, 本文对复杂信号加入高斯白噪声、泊松噪声和均匀噪声后, 通过六种降噪方法做对比实验, 可以看出本文采用的 CEEMDAN-NS-SG-WT 降噪方法的二维相图轨迹清晰, 规则且光滑, 降噪效果更好.
4.2 实测太阳黑子信号
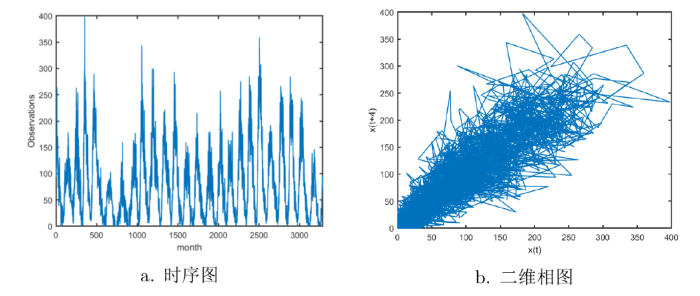
为验证 CEEMDAN-NS-SG-WT 去噪方法在实际应用中的可行性, 选取比利时皇家天文台布鲁塞尔世界数据中心 SILSO 的实测太阳黑子数据进行降噪处理. 该数据符合复杂信号部分特点, 具体采用 2023 年观测到的 3286 个太阳黑子数作为实测数据. 图11 中 a 和 b 分别是月太阳黑子信号的时序图与二维相图, 从图11 中 b 可以看出来, 受噪声的影响, 二维相图的轨迹杂乱, 不光滑且没有规则, 对后续的数据分析有影响.
图11
图11
实测月太阳黑子信号 (由 b 图看出, 受噪声的影响, 二维相图的轨迹杂乱, 不光滑且没有规则)
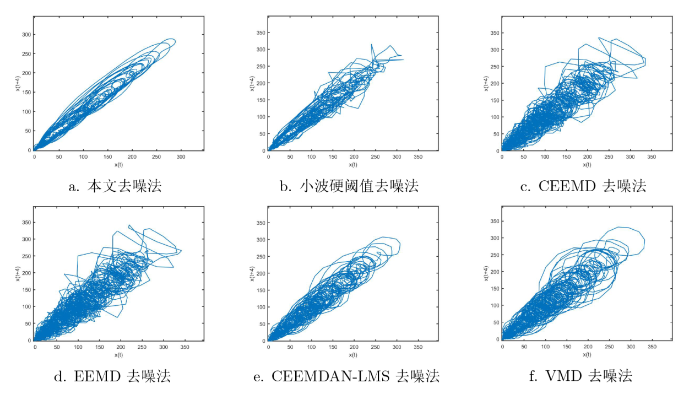
采用 6 种降噪方法对实测数据进行降噪处理, 图12 中 a-f 分别是本文去噪法、小波硬阈值去噪法、CEEMD 去噪法、EEMD 去噪法、CEEMDAN-LMS 去噪法、VMD 去噪法对信号降噪处理后的对比图. 由图12 中 a-f 和图11 中 b 的比较, 小波硬阈值、CEEMD 和 EEMD 法去噪后的相空间图轨迹杂乱, 降噪效果不好; CEEMDAN-LMS 和 VMD 方法去噪效果较好, 轨迹较光滑, 但 CEEMDAN-NS-SG-WT 去噪方法效果最好, 轨迹更光滑规则.
图12
图12
降噪后的太阳黑子信号对比图 (对比发现本文方法去噪效果最好, 轨迹更光滑规则)
将实测信号用六种降噪方法进行处理后, 对降噪后的信号分别计算它们的排列熵 PE, 振幅感知排列熵 AAPE, 如表5 所示. 时间序列复杂度越低对应的排列熵值越小, 从表5 的对比结果可知六个方法计算出的 PE 和 AAPE 值都小, 但本文方法降噪后的信号计算出的 PE 和 AAPE 值分别为 0.34 和 0.38, 是最小的, 表明经本文方法降噪后的信号更加规则, 降噪效果更好. 且本文方法降噪后信号的 CMSE 和 NS 值分别为 1.08 和 1, 说明降噪后的信号, 能量密度大且是平稳的, 具有明显的降噪效果.
4.3 实测滚动轴承的振动加速度信号
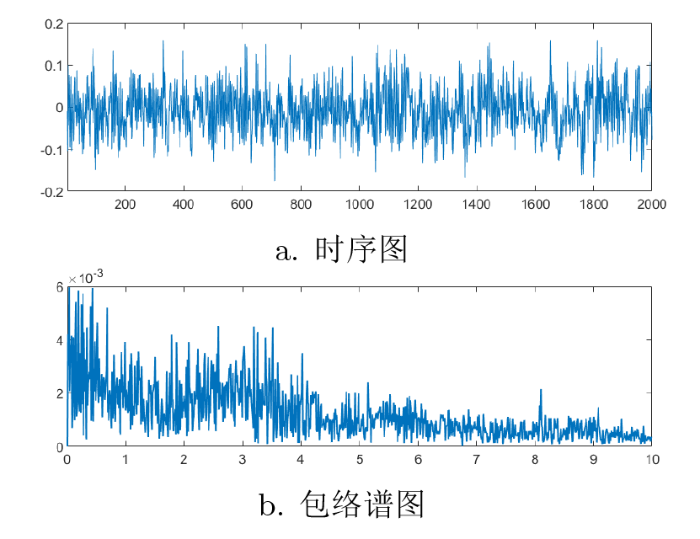
为再次验证本文 CEEMDAN-NS-SG-WT 去噪方法对实测数据的降噪效果, 对由美国辛辛那提大学、美国智能维护中心 (IMS) 提供的滚动轴承的振动加速度信号进行了降噪处理, 采样频率为 20Hz, 采样点数为 1.2$\times$ 105 , 取前 2000 个采样点作为实测轴承振动加速度数据. 图13 中 a 和 b 分别是原始滚动轴承的的振动加速度信号的时序图和包络谱图, 从图13 中 b 可以看出来, 信号中包含了多种频率成分, 且噪声水平较高. 由于噪声的存在, 原始信号的包络谱可能无法清晰地显示出轴承的频率特征.
图13
图13
实测滚动轴承的振动加速度信号(由 b 图看出, 信号中存在的噪声可能导致原始信号的包络谱无法清晰地显示出轴承的频率特征)
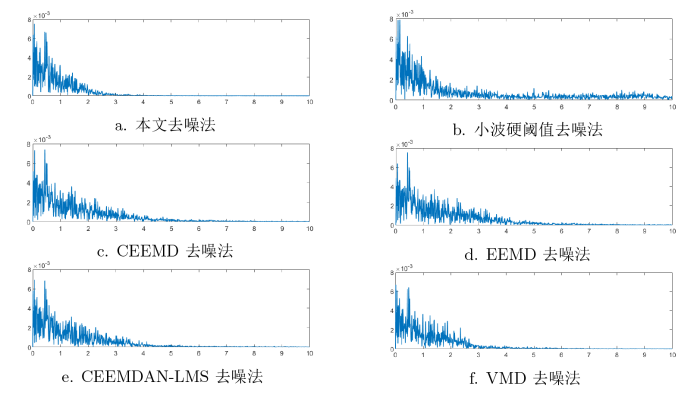
采用本文方法、小波硬阈值去噪法、CEEEMD 去噪法、EEMD 去噪法、CEEMDAN+LMS 去噪法、VMD 去噪方法对实测滚动轴承的振动加速度信号进行降噪处理, 图14 中 a-f 分别是降噪处理后信号的对比图. 比较图14 中 a-f 和图13 中 b, 小波硬阈值去噪法、CEEEMD 去噪法、EEMD 去噪法、CEEMDAN+LMS 去噪法、VMD 去噪法对信号处理后的效果明显, 但 CEEMDAN-NS-SG-WT 去噪法的降噪效果更好, 包络谱图中的信号变得更加清晰, 噪声水平显著降低, 包络谱图能更好表示轴承的频率特征.
图14
图14
降噪后的滚动轴承的振动加速度信号对比图(对比发现本文方法去噪效果最好, 包络谱图能更好表示轴承的频率特征)
5 结论
本文在单一去噪算法的基础上进行了改进, 提出了一种基于 CEEMDAN-NS-SG-WT 的复杂信号联合降噪方法.
(1) 将 CEEMDAN 分解后的模态分量使用 NS 指标划分为高频和低频模态分量, 对于高斯白噪声, 均匀噪声和泊松噪声都是有效的.
(2) 对高频模态分量做小波阈值降噪, 对低频模态分量做 SG 滤波降噪, 再对降噪后的高低频模态分量进行重构. 能够有效去除噪声, 保留信号, 并使得信号更加平滑.
通过模拟仿真复杂信号和实测复杂信号实验表明: 本文用 NS 指标划分高低频分量的效果更稳定; 本文降噪方法有效提升了信噪比 (SNR), 降低了均方根误差 (RMSE), 且使用改进的小波阈值函数, 降噪效果较硬、软阈值更好; CEEMDAN-NS-SG-WT 去噪法与小波硬阈值去噪法、CEEEMD 去噪法、EEMD 去噪法、CEEMDAN-LMS 去噪法、VMD 去噪法相比较, 本文方法去噪效果更好, 并且能较清晰地恢复出复杂信号吸引子内在的拓扑结构.
参考文献
View Option
[1]
柯水霞 . 信号降噪与解调技术研究 . 南昌 : 南昌大学 , 2016
[本文引用: 1]
Ke S X . Signal Denoising and Demodulation Techniques Research . Nanchang : Nanchang University , 2016
[本文引用: 1]
[2]
黄显高 , 徐健学 , 何岱海 , 等 . 利用小波多尺度分解算法实现混沌系统的噪声减缩
物理学报 , 1999 (10 ): 1810 -1817
[本文引用: 1]
Huang X G Xu J X He D H , et al . Noise reduction in chaotic systems via wavelet multiscale decomposition algorithm
Acta Physica Sinica , 1999 (10 ): 1810 -1817
[本文引用: 1]
[3]
雷达 , 钟诗胜 . 基于奇异值分解和经验模态分解的航空发动机健康信号降噪
吉林大学学报 (工学版) , 2013 , 43 3 ): 764 -770
[本文引用: 1]
Lei D Zhong S S . Aircraft engine health signal denoising based on singular value decomposition and empirical mode decomposition
Journal of Jilin University (Engineering Edition) , 2013 , 43 3 ): 764 -770
[本文引用: 1]
[4]
Lee D Shin S R Chung W , et al . Denoising sparker seismic data with Deep BiLSTM in fractional Fourier transform
Computers & Geosciences , 2024 , 1.4 : 105519
[本文引用: 1]
[5]
贾瑞生 , 赵同彬 , 孙红梅 , 等 . 基于经验模态分解及独立成分分析的微震信号降噪方法
地球物理学报 , 2015 , 58 3 ): 1013 -1023
DOI:10.6038/cjg20150326
[本文引用: 1]
针对微震信号具有高噪声、突变快、随机性强等特点,基于经验模态分解(EMD)及独立成分分析(ICA)提出一种微震信号降噪方法.首先,对含噪信号进行EMD分解,获得一系列按频率从高到低的内蕴模态函数(IMF),利用原信号与各IMF之间的互相关系数辨识出噪声与信号的分界,将分界之上的高频噪声滤除;其次,为有效去除分界IMF中的模态混叠噪声,基于ICA算法对分界IMF进行盲源分离,提取其中的微震有效信号,并将其与剩余的IMF累加重构,从而得到降噪后的微震信号;最后,利用快速傅里叶变换(FFT)时频谱对比分析降噪前后的信号特征,定性说明本文方法的有效性;引入信噪比和降噪后信号占原信号的能量百分比两个参数,定量说明本文方法能充分保留微震信号的瞬态非平稳特征,降噪效果明显.
Jia R S Zhao T L Sun H M , et al . Microseismic signal denoising method based on empirical mode decomposition and independent component analysis
Journal of Geophysics , 2015 , 58 3 ): 1013 -1023
DOI:10.6038/cjg20150326
[本文引用: 1]
针对微震信号具有高噪声、突变快、随机性强等特点,基于经验模态分解(EMD)及独立成分分析(ICA)提出一种微震信号降噪方法.首先,对含噪信号进行EMD分解,获得一系列按频率从高到低的内蕴模态函数(IMF),利用原信号与各IMF之间的互相关系数辨识出噪声与信号的分界,将分界之上的高频噪声滤除;其次,为有效去除分界IMF中的模态混叠噪声,基于ICA算法对分界IMF进行盲源分离,提取其中的微震有效信号,并将其与剩余的IMF累加重构,从而得到降噪后的微震信号;最后,利用快速傅里叶变换(FFT)时频谱对比分析降噪前后的信号特征,定性说明本文方法的有效性;引入信噪比和降噪后信号占原信号的能量百分比两个参数,定量说明本文方法能充分保留微震信号的瞬态非平稳特征,降噪效果明显.
[6]
Ma Y Cheng J Wang P , et al . A novel Lanczos quaternion singular spectrum analysis method and its application to bevel gear fault diagnosis with multi-channel signals
Mechanical Systems and Signal Processing , 2021 , 1.8 108679
[本文引用: 1]
[7]
Ma Y Cheng J Hu N , et al . Symplectic quaternion singular mode decomposition with application in gear fault diagnosis
Mechanical Systems and Signal Processing , 2021 , 1.0 104266
[本文引用: 1]
[8]
Zhou J Cheng J Wu X , et al . Adaptive quaternion multivariate local characteristic-scale decomposition and its application to gear fault diagnosis
Digital Signal Processing , 2022 , 1.9 103655
[本文引用: 1]
[9]
Zhong J Bi X Shu Q , et al . Partial discharge signal denoising based on singular value decomposition and empirical wavelet transform
IEEE Trans Instrum Meas , 2020 , 69 11 ): 8866 -8873
[本文引用: 1]
[10]
Bandt C Pompe B . Permutation entropy: A natural complexity measure for time series
Physical Review Letters , 2002 , 88 (17 ): 174102
[本文引用: 1]
[11]
Azami H Escudero J . Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation
Comput Methods Programs Biomed , 2016 , 1.8 40 -51
[本文引用: 1]
[12]
Huang J D Ling L Xiao Q X . Research on weak signal detection method for power system fault based on improved wavelet threshold
Energy Reports , 2022 , 8 12 ): 290 -296
[本文引用: 1]
[13]
陈克 , 张晓冬 , 李宁 . 基于 CEEMD 与自适小波阈值组合降噪在 OPAX 方法的应用
振动与冲击 , 2021 , 40 16 ): 192 -198
[本文引用: 1]
Chen K Zhang X D Li N . Application of CEEMD and adaptive wavelet thresholding combination denoising in the OPAX method
Vibration and Impact , 2021 , 40 16 ): 192 -198
[本文引用: 1]
[14]
Yang Y Li S S Li C , et al . Research on ultrasonic signal processing algorithm based on CEEMDAN joint wavelet packet thresholding
Measurement , 2022 , 2.1 : 111751
[本文引用: 1]
[15]
马星河 , 孔卫东 , 李自强 , 等 . 一种基于 S_VMD 与 Sdr_SampEn 的局部放电信号去噪方法
电力系统保护与控制 , 2022 , 50 18 ): 29 -38
[本文引用: 1]
Ma X H Kong W D Li Z Q , et al . A denoising method for partial discharge signals based on S_VMD and Sdr_SampEn
Power System Protection and Control , 2022 , 50 18 ): 29 -38
[本文引用: 1]
[16]
周怡娜 , 路敬祎 , 张勇 , 等 . VMD-SG-WT 去噪法及其在混沌去噪中的应用
东北石油大学学报 , 2020 , 44 4 ): 113 -120 ; 132; IX
[本文引用: 1]
Zhou Y N Lu J Y Zhang Y , et al . Denoising method based on VMD-SG-WT and its application in chaotic denoising
Journal of Northeast Petroleum University , 2020 , 44 4 ): 113 -120 ; 132; IX
[本文引用: 1]
[17]
谭秋衡 . 时间序列的非平稳性度量及其应用 . 武汉 : 中国科学院研究生院(武汉物理与数学研究所) , 2013
[本文引用: 3]
Tan Q H . Measurement of Nonstationarity in Time Series and Its Applications . Wuhan : Graduate School of the Chinese Academy of Sciences (Wuhan Institute of Physics and Mathematics) , 2013
[本文引用: 3]
[18]
张聪 , 丁义明 . 基于重对数律的非平稳性度量
数学物理学报 , 2023 , 43A 6 ): 1855 -1868
[本文引用: 1]
Zhang C Ding Y M . Non-stationarity measure based on logarithmic law.
Acta Math Sci , 2023 , 43A 6 ): 1855 -1868
[本文引用: 1]
[19]
谭秋衡 , 吴量 , 李波 . 基于 EMD 及非平稳性度量的趋势噪声分解方法
数学物理学报 , 2016 , 36A 4 ): 783 -794
[本文引用: 2]
Tan Q H Wu L Li B . Trend noise decomposition method based on EMD and non-stationarity measurement
Acta Math Sci , 2016 , 36A 4 ): 783 -794
[本文引用: 2]
[20]
Li S Qin N Huang D , et al . Damage localization of Stacker's track based on EEMD-EMD and DBSCAN cluster algorithms
IEEE Trans Instrum Meas , 2020 , 69 1981 -1992
[本文引用: 1]
[21]
Torres M Colominas M A Schlotthauer G , et al . A complete ensemble empirical mode decomposition with adaptive noise//Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)
Prague, Czech Republic: IEEE , 2011 : 4144 -4147
[本文引用: 1]
[22]
Savitzky A Golay M J E . Soothing and differentiation of data by simplifying least squares procedures
Anal Chem , 1964 , 36 1627 -39
[本文引用: 2]
[23]
Schafer R W . What is a Savitzky-Golay filter?
IEEE Signal Process Mag , 2011 , 28 4 ): 111 -117
[本文引用: 2]
[24]
Li H Li S S Sun J , et al . Ultrasound signal processing based on joint GWO-VMD wavelet threshold functions
Measurement , 2024 , 2.6 : 114143
[本文引用: 1]
[25]
Donoho D L Johnstone I M . Adapting to unknown smoothness via wavelet shrinkage
J Am Stat Assoc , 1995 , 90 1200 -1224
[本文引用: 1]
1
2016
... 复杂信号处理于通信、雷达、环境监测等领域至关重要, 准确接收信号对提升系统性能与决策效率意义重大[1 ] . 但受测量仪器精度与环境干扰影响, 实测信号常因干扰和噪声畸变, 影响后续分析与应用[2 ] . 为了准确提取信号中的有用信息, 要在复杂环境中采用必要的降噪方法. ...
1
2016
... 复杂信号处理于通信、雷达、环境监测等领域至关重要, 准确接收信号对提升系统性能与决策效率意义重大[1 ] . 但受测量仪器精度与环境干扰影响, 实测信号常因干扰和噪声畸变, 影响后续分析与应用[2 ] . 为了准确提取信号中的有用信息, 要在复杂环境中采用必要的降噪方法. ...
利用小波多尺度分解算法实现混沌系统的噪声减缩
1
1999
... 复杂信号处理于通信、雷达、环境监测等领域至关重要, 准确接收信号对提升系统性能与决策效率意义重大[1 ] . 但受测量仪器精度与环境干扰影响, 实测信号常因干扰和噪声畸变, 影响后续分析与应用[2 ] . 为了准确提取信号中的有用信息, 要在复杂环境中采用必要的降噪方法. ...
利用小波多尺度分解算法实现混沌系统的噪声减缩
1
1999
... 复杂信号处理于通信、雷达、环境监测等领域至关重要, 准确接收信号对提升系统性能与决策效率意义重大[1 ] . 但受测量仪器精度与环境干扰影响, 实测信号常因干扰和噪声畸变, 影响后续分析与应用[2 ] . 为了准确提取信号中的有用信息, 要在复杂环境中采用必要的降噪方法. ...
基于奇异值分解和经验模态分解的航空发动机健康信号降噪
1
2013
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
基于奇异值分解和经验模态分解的航空发动机健康信号降噪
1
2013
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Denoising sparker seismic data with Deep BiLSTM in fractional Fourier transform
1
2024
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
基于经验模态分解及独立成分分析的微震信号降噪方法
1
2015
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
基于经验模态分解及独立成分分析的微震信号降噪方法
1
2015
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
A novel Lanczos quaternion singular spectrum analysis method and its application to bevel gear fault diagnosis with multi-channel signals
1
2021
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Symplectic quaternion singular mode decomposition with application in gear fault diagnosis
1
2021
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Adaptive quaternion multivariate local characteristic-scale decomposition and its application to gear fault diagnosis
1
2022
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Partial discharge signal denoising based on singular value decomposition and empirical wavelet transform
1
2020
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Permutation entropy: A natural complexity measure for time series
1
2002
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation
1
2016
... 近年来, 各种去噪方法被应用到复杂信号的降噪中. 噪声分量变化快, 无规律, 在高频分量中占比较多; 信号分量变化缓慢, 波形平滑, 在低频分量中占比较多. 为有效去除噪声, 研究人员提出了傅里叶变换[3 ] , 奇异值分解[4 ] , 小波变换[5 ] 等降噪方法. Lee 等[6 ] 提出分数阶傅里叶变换与神经网络结合的去噪法, 用时频分布训练网络分离有用信号与噪声. 傅里叶变换对非平稳信号降噪效果有限, 且神经网络计算复杂、效率低. Ma 等[7 ] 和 Zhou 等[8 ] 采用四元数奇异值分解 (Quaternion Singular Value Decompositions, QSVD) 对齿轮故障信号去噪, 效果良好, 但受嵌入维数和分量阶数影响, 不适用于强噪声场景. Zhong 等[9 ] 结合 SVD 和经验小波变换对噪声信号进行降噪, 小波变换效果依赖于小波基和阈值选择, 对非线性和非静态数据降噪效果不佳. 在实际情况下, 信号分解通常分为高频和低频模态, 单一的降噪方法可能会忽略部分有效信息. 目前, 用于区分高频和低频的指标包括排列熵(Permutation Entropy, PE)[10 ] 和幅值感知排列熵 (Amplitude Perception Permutation Entropy, AAPE)[11 ] 等, 这些方法在稳定性上有其局限性. ...
Research on weak signal detection method for power system fault based on improved wavelet threshold
1
2022
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
基于 CEEMD 与自适小波阈值组合降噪在 OPAX 方法的应用
1
2021
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
基于 CEEMD 与自适小波阈值组合降噪在 OPAX 方法的应用
1
2021
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
Research on ultrasonic signal processing algorithm based on CEEMDAN joint wavelet packet thresholding
1
2022
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
一种基于 S_VMD 与 Sdr_SampEn 的局部放电信号去噪方法
1
2022
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
一种基于 S_VMD 与 Sdr_SampEn 的局部放电信号去噪方法
1
2022
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
VMD-SG-WT 去噪法及其在混沌去噪中的应用
1
2020
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
VMD-SG-WT 去噪法及其在混沌去噪中的应用
1
2020
... 我们提出了一种新的更稳定的高低频区分方法. 首先对信号进行分解, 经验模态分解(Empirical Mode Decomposition, EMD) 是数据驱动的非线性非平稳信号处理法, 依据信号局部特征时间尺度, 无需先验知识, 自适应将复杂信号分解为若干本征模态函数 (Intrinsic Mode Function, IMF) 之和, 广泛用于复杂信号分解. Huang等[12 ] 对 EMD 分解后的各模态分量直接采用小波软阈值算法滤波, 因会保留部分幅值较大的噪声系数, 影响降噪效果, 故需先划分模态分量再处理. Chen 等[13 ] 将互补集合经验模态分解 (Complementary Ensemble Empirical Mode Decomposition, CEEMD) 和自适小波阈值降噪相结合进行降噪, 采用样本熵划分模态分量. Yang 等[14 ] 将自适应噪声完全集合经验模态分解 (Complete Ensemble Empirical Mode Decomposition with Adaptive Noise Analysis, CEEMDAN) 与小波包阈值 (Wavelet Thresholding, WT) 相结合, 用相关系数划分模态分量, 改进单一EMD降噪方法可能丢失有用成分的缺点. 而低频分量中的少量噪声仍会影响复杂信号去噪效果, 因此需对其进一步处理. Ma 等[15 ] 和 Zhou等[16 ] 采用改进样本熵划分模态分量, 经 Savitzky-Golay (SG) 平滑滤波去噪, 取得较好降噪效果. 但仅以相关系数、样本熵等常用熵值作高低频分量划分指标, 易致误判, 影响去噪. ...
3
2013
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
... 非平稳性度量 NS[17 ] 是一种专为分析和量化非平稳时间序列而设计的指标, 不同于常用的相关系数、样本熵、模糊熵、排列熵等, 该指标融合了概率论、统计学、遍历论和信息论的知识, 并定义了稳定集合与稳定信息结构的概念, 为非平稳性度量提供了新的视角和方法. NS指标的特点在于其能够适应不同的数据生成过程, 并通过四种算法进行计算, 这些算法考虑了有限样本的情况, 提高了度量的准确性和实用性. 并在模型选择、股票市场数据分析和彩票市场数据分析等实际应用[17 ] 中验证了该指标的有效性. 例如, 在模型选择中, NS可以作为新的准则, 通过保证拟合优度的情况下最小化模型残差序列的非平稳性度量值来选择最佳模型. 此外, NS 还能有效区分趋势平稳与差分平稳, 以及独立同分布、白噪声与鞅差等不同类型的序列. ...
... [17 ]中验证了该指标的有效性. 例如, 在模型选择中, NS可以作为新的准则, 通过保证拟合优度的情况下最小化模型残差序列的非平稳性度量值来选择最佳模型. 此外, NS 还能有效区分趋势平稳与差分平稳, 以及独立同分布、白噪声与鞅差等不同类型的序列. ...
3
2013
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
... 非平稳性度量 NS[17 ] 是一种专为分析和量化非平稳时间序列而设计的指标, 不同于常用的相关系数、样本熵、模糊熵、排列熵等, 该指标融合了概率论、统计学、遍历论和信息论的知识, 并定义了稳定集合与稳定信息结构的概念, 为非平稳性度量提供了新的视角和方法. NS指标的特点在于其能够适应不同的数据生成过程, 并通过四种算法进行计算, 这些算法考虑了有限样本的情况, 提高了度量的准确性和实用性. 并在模型选择、股票市场数据分析和彩票市场数据分析等实际应用[17 ] 中验证了该指标的有效性. 例如, 在模型选择中, NS可以作为新的准则, 通过保证拟合优度的情况下最小化模型残差序列的非平稳性度量值来选择最佳模型. 此外, NS 还能有效区分趋势平稳与差分平稳, 以及独立同分布、白噪声与鞅差等不同类型的序列. ...
... [17 ]中验证了该指标的有效性. 例如, 在模型选择中, NS可以作为新的准则, 通过保证拟合优度的情况下最小化模型残差序列的非平稳性度量值来选择最佳模型. 此外, NS 还能有效区分趋势平稳与差分平稳, 以及独立同分布、白噪声与鞅差等不同类型的序列. ...
基于重对数律的非平稳性度量
1
2023
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
基于重对数律的非平稳性度量
1
2023
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
基于 EMD 及非平稳性度量的趋势噪声分解方法
2
2016
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
... 谭秋衡等[19 ] 的参考文献, 验证了 NS 指标区分模态分量的有效性. 即 NS 准则能有效的将 EMD 分解后的 IMF 分量区分成信号和噪声. 同时, 本文提出方法本质是去除噪声, 而噪声具有高频且平稳的特点, 因此可用 NS 来过滤噪声, 进而用来区别分解信号的高低频状态. ...
基于 EMD 及非平稳性度量的趋势噪声分解方法
2
2016
... 非平稳性度量 (Non-stationary measure, NS) 用于衡量时间序列或信号的非平稳性的指标. 最早由谭秋衡等[17 ] 提出, 基于 Shannon 熵的指标, 其值介于 0 到 1 之间, 越小表示时间序列越稳定. NS 指标通过计算非平稳熵与平稳熵的比值来衡量信号的非平稳程度, 这表明其能够反映信号的统计特性变化. 张聪等[18 ] 发现重对数律对自变量和的估计更加精确, 基于重对数律的非平稳性度量表示出更强的收敛性. 对噪声较强的模型, 能达到较低的相对误差, 提高模型选择精度, 有助于筛选模型.谭秋衡等[19 ] 结合非平稳性度量的准则来判定 EMD 分解后舍弃的本性模态函数的数目, 得到了比较准确的划分结果. ...
... 谭秋衡等[19 ] 的参考文献, 验证了 NS 指标区分模态分量的有效性. 即 NS 准则能有效的将 EMD 分解后的 IMF 分量区分成信号和噪声. 同时, 本文提出方法本质是去除噪声, 而噪声具有高频且平稳的特点, 因此可用 NS 来过滤噪声, 进而用来区别分解信号的高低频状态. ...
Damage localization of Stacker's track based on EEMD-EMD and DBSCAN cluster algorithms
1
2020
... EMD 算法分解过程中因异常事件干扰导致极值点分布不均匀产生了模式混叠现象, 为此集成经验模态分解 (ensemble empirical mode decomposition, EEMD) 将具有频率均匀分布特性的高斯白噪声加入信号, 使信号在不同尺度上连续, 从而克服信号间歇问题, 避免了模态混叠. 但在 EEMD 分解过程中, 添加到原始信号中的噪声无法消除, 这可能会导致重建误差[20 ] . Colominas 等[21 ] 提出了 CEEMDAN, 自适应白噪声被引入到每个残差分量, 以进一步消除模式混合现象. 由于迭代次数少、收敛性能好, 该算法适用于非平稳信号. 算法步骤如下 ...
A complete ensemble empirical mode decomposition with adaptive noise//Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)
1
2011
... EMD 算法分解过程中因异常事件干扰导致极值点分布不均匀产生了模式混叠现象, 为此集成经验模态分解 (ensemble empirical mode decomposition, EEMD) 将具有频率均匀分布特性的高斯白噪声加入信号, 使信号在不同尺度上连续, 从而克服信号间歇问题, 避免了模态混叠. 但在 EEMD 分解过程中, 添加到原始信号中的噪声无法消除, 这可能会导致重建误差[20 ] . Colominas 等[21 ] 提出了 CEEMDAN, 自适应白噪声被引入到每个残差分量, 以进一步消除模式混合现象. 由于迭代次数少、收敛性能好, 该算法适用于非平稳信号. 算法步骤如下 ...
Soothing and differentiation of data by simplifying least squares procedures
2
1964
... SG 滤波器在数据上滑动一个窗口, 并在每个位置上对窗口内的数据进行多项式拟合来估计窗口中心的值. 对于原始复杂信号 $x\left [ n\right ]$ $n=0$ [22 ] ...
... 其中, $h\left [ m\right ]$ 22 ,23 ]. 本文采用的窗口大小 21, 阶数为 3. ...
What is a Savitzky-Golay filter?
2
2011
... 在近似区间内的 2M + 1 个输入样本可以通过一组固定的权重系数有效组合, 这些系数可以根据给定的多项式阶数N和长度为 2M + 1 的近似区间计算得出[23 ] . 最终, 输出样本可以通过以下形式的离散卷积来计算 ...
... 其中, $h\left [ m\right ]$ 22 ,23 ]. 本文采用的窗口大小 21, 阶数为 3. ...
Ultrasound signal processing based on joint GWO-VMD wavelet threshold functions
1
2024
... 小波阈值去噪计算量较小, 具有实现简单和降噪效果相对较好等优点. 去噪效果与阈值估计和阈值函数的选取有关[24 ] , 如果阈值选择得太大, 则会导致部分有用信号被错误地滤除为噪声. 反之, 则会有噪声残留, 由于去噪不彻底, 导致信号失真. Donoho[25 ] 等人提出阈值估计为 ...
Adapting to unknown smoothness via wavelet shrinkage
1
1995
... 小波阈值去噪计算量较小, 具有实现简单和降噪效果相对较好等优点. 去噪效果与阈值估计和阈值函数的选取有关[24 ] , 如果阈值选择得太大, 则会导致部分有用信号被错误地滤除为噪声. 反之, 则会有噪声残留, 由于去噪不彻底, 导致信号失真. Donoho[25 ] 等人提出阈值估计为 ...