非均匀网格上时间分数阶扩散—波动方程的 BDF2 型有限元方法

非均匀网格上时间分数阶扩散—波动方程的 BDF2 型有限元方法

祝鹏^,¹, 陈艳萍^,²^,^*, 徐先宇^,³

¹嘉兴大学数据科学学院浙江嘉兴 314001

²南京邮电大学理学院南京 210023

³湘潭大学数学与计算科学学院湖南湘潭 411100

BDF2-Type Finite Element Method for Time-Fractional Diffusion-Wave Equations on Nonuniform Grids

Zhu Peng^,¹, Chen Yanping^,²^,^*, Xu Xianyu^,³

¹School of Data Science, Jiaxing University, Zhejiang Jiaxing 314001

²School of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023

³School of Mathematics and Computational Science, Xiangtan University, Hunan Xiangtan 411100

通讯作者: *E-mail: ypchen@njupt.edu.cn

收稿日期: 2024-09-19 修回日期: 2025-01-30

基金资助:

国家自然科学基金天元数学访问学者项目(12426616)
浙江省自然科学基金(LY23A010005)
南京邮电大学引进人才科研启动基金(NY223127)

Received: 2024-09-19 Revised: 2025-01-30

Fund supported:

Visiting scholar program of National Natural Science Foundation of China(12426616)
Zhejiang Provincial Natural Science Foundation of China(LY23A010005)
Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications(NY223127)

作者简介 About authors

E-mail:pzh@zjxu.edu.cn;

xuxianyuqdu@163.com

摘要

众所周知, 非均匀网格的研究可以有效地解决分数阶 Caputo 型导数的初值奇异现象. 在非均匀网格的理论分析中, 经常采用分数阶离散 Grönwall 不等式进行误差分析, 缺乏对误差结构的具体研究. 设计了一种非均匀网格上的误差卷积结构, 用于分析时间分数阶扩散-波动方程. 将二次插值近似应用于 Caputo 型导数, 通过使用降阶法和离散互补卷积核对 Caputo 型导数进行离散, 得到了非均匀网格上的 BDF2 型有限元方法. 离散互补卷积核在算法的收敛性分析中至关重要, 因为它简化有限元理论分析的过程, 并基于卷积核和插值估计的性质构建了全局一致性误差估计. 详细估计了非均匀网格上 BDF2 有限元格式的 $L^2$-范数误差和 $H^1$-范数误差, 并通过实验验证了所提出的有限元格式与理论收敛阶之间的一致性.

关键词： 时间分数阶扩散-波动方程; 离散卷积核; BDF2 型有限元格式; 误差卷积结构; 非均匀网格

Abstract

As is well known, the study of nonuniform grids can effectively solve the initial value singularity phenomenon of fractional Caputo -type derivatives. In the theoretical analysis of nonuniform grids, fractional discrete Grönwall inequality is often used for error analysis, but there is a lack of specific research on error structures. An error convolution structure (ECS) was designed on nonuniform grids for analyzing the time fractional diffusion wave equation. A quadratic interpolation approximation was applied Caputo -type derivatives, and the BDF2 -type finite element method on nonuniform grids was obtained by discretizing it using a reduction method and a discrete complementary convolution kernel. The discrete complementary convolution kernel is crucial in the convergence analysis of algorithms, as it simplify the process of finite element theory analysis and construct global consistency errors based on the properties of convolution kernels and interpolation estimates. The $L^2$-norm error and $H^1$-norm error of the BDF2 finite element scheme on nonuniform grids were estimated in detail, and verifies the consistency between the proposed finite element scheme and the theoretical convergence order through experiments.

Keywords： time fractional diffusion-wave equation; discrete complementary convolution kernels; BDF2 finite element format; error convolutional structure; nonuniform grids

PDF (672KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

祝鹏, 陈艳萍, 徐先宇. 非均匀网格上时间分数阶扩散—波动方程的 BDF2 型有限元方法[J]. 数学物理学报, 2025, 45(4): 1268-1290

Zhu Peng, Chen Yanping, Xu Xianyu. BDF2-Type Finite Element Method for Time-Fractional Diffusion-Wave Equations on Nonuniform Grids[J]. Acta Mathematica Scientia, 2025, 45(4): 1268-1290

1 引言

整数阶方程的局部性行为^[1,2]造成了在理论分析和数值模拟上的巨大困难, 因此对分数阶偏微分方程进行研究有着重要意义. 分数阶偏微分方程在经济、材料和生物学等各个领域有着广泛应用. 具体应用于分数阶布朗运动下的动力学模型^[3]、多孔介质中的扩散现象 (如亚扩散和超扩散)^[4]以及污染物浓度模型^[5]等. 在求解分数阶偏微分方程时, 主要的挑战在于离散具有非局部效应的分数阶导数, 本文提出了一个框架来设计快速稳定的算法解决此类问题.

Caputo 型导数作为常见的分数阶算子, 常常被用于时间分数阶方程的数值离散过程中. 近年来, 许多学者^[6,7]针对均匀网格和等级网格的 Caputo 型导数进行研究, 主要是针对 $t = 0$ 附近的弱奇异性进行分析. Jannelli^[8] 针对拟均匀网格下非线性两点分数阶边值问题进行误差分析, 通过数值实验展示了其一致性、稳定性和收敛性. Li 和 Sun 等^[9]在均匀网格和等级网格上采用 $s = {t^\beta }$ 进行变量替换, 处理 $t = 0$ 附近解的弱奇异性, 数值结果表明收敛阶为 $2-\alpha$ 阶.

具有 Caputo 型导数的扩散-波动方程是一种经典的时间分数阶偏微分方程. 对于此类方程的研究方法和数值格式很多, 常在时间上采用 L1 格式、L2-${1_\sigma}$ 格式、L2格式等, 在空间上采用有限差分方法和有限元方法进行求解. 如 Yu 和 Sun 等^[10]采用快速算法和 L1 格式来求解等级网格上的时间分数阶扩散方程, 数值结果表明收敛阶为 $2-\alpha$ 阶. Feng 和 Liu^[11] 采用 L1 型有限元方法求解多项时间分数阶扩散-波动方程, 给出了数值格式的稳定性和收敛性分析. Hu 和 Alikhanov 等^[12]采用 L2 型有限元格式来求解等级网格上的时间分数阶扩散方程, 给出了数值格式的稳定性分析. 由于 BDF2 格式是通过二次函数进行插值, 收敛阶数为 $3-\alpha$ 阶并可推广至 2 阶, 具有较高的精度, 本文重点研究 BDF2 格式求解时间分数阶扩散-波动方程.

Qiao 和 Guo 等^[13]在等级网格上采用 BDF2 格式求解二维时间分数阶积分-微分方程, 空间采用 ADI 算法, 得到了该方程的全离散隐式格式, 证明了 $L^2$-范数下的稳定性和收敛性. Yin 和 Liu 等^[14]在均匀网格上采用 BDF2 格式求解多项时间分数阶扩散-波动方程, 空间上采用有限元方法, 结合移位卷积求积方法, 证明了$L^2$-范数下的无条件稳定性. 在构造 BDF2 等高阶数值格式时, 往往通过指数和近似来进行理论分析. Liao等^[15]在非均匀网格上采用 L2-${1_\sigma}$ 格式求解时间分数阶次扩散方程, 通过指数和近似进行误差卷积结构 (ECS) 分析, 空间上采用有限差分法, 证明了 $L^2$-范数下的收敛性, 收敛阶数为 2 阶.

截止到目前, 尚未有在非均匀网格上采用 BDF2 有限元方法求解时间分数阶扩散-波动方程的论文, 这也是本文研究的主要目的. 由于有限元方法的理论分析较为完善, 因此选择该方法求解带有初值奇异性的 Caputo 型导数是合适的. 在现有求解分数阶扩散-波动方程的理论分析中, 往往需要离散分数阶 Gr$\rm\ddot o$nwall 不等式证明算法的稳定性与收敛性. 在本文中, 提出了一种不同于传统文献[16 -18]的数值方法, 将 BDF2 公式与互补卷积 (DCC) 核^[19]相结合, 以证明有限元格式的稳定性和收敛性. 本文利用时间的非均匀 BDF2 公式和空间的有限元方法来实现离散化的数值格式. 分析了离散化有限元公式在 $L^2$- 范数和 $H^1$-范数下的稳定性和误差, 通过数值算例验证了其在时间和空间上的收敛阶. 数值结果表明, 该有限元方法在时间和空间上都达到了最优收敛阶, 具有较高的精度和计算效率.

本文中的模型是一个时间分数阶超扩散波动方程^[20,21], 方程的具体形式如下

(1.1)$_0^CD_t^\beta v\left( {x,t} \right) = \Delta v\left( {x,t} \right) + f\left( {x,t} \right),\quad x \in \Omega,\quad t \in \left( {0,T} \right],$

(1.2)$v\left( {x,0} \right) = {g_1}\left( x \right),\quad {v_t}\left( {x,0} \right) = {g_2}\left( x \right),\quad x \in \overline \Omega.$

其中 $\Omega = {\left( {0,L} \right)^2} \subset {R^2}$ 是方程 (1.1) 中的区域, $\overline \Omega$ 是方程 (1.2) 的边界条件. $_0^CD_t^\beta v\left( t \right)$ 表示 $\beta,$$ \left( {1 < \beta < 2} \right)$阶 Caputo 分数阶导数, 具体形式如下

$_0^CD_t^\beta v\left( t \right) = \int _0^t {{\omega _{2 - \beta }}\left( {t - s} \right)\ddot v\left( s \right){\rm d}s},\quad {\omega _\gamma }\left( t \right) = \frac{{{t^{\gamma - 1}}}}{{\Gamma \left( \gamma \right)}}.\ $

本文的其余部分组织如下. 在第二节中, 首先对 Caputo 阶导数进行离散化, 并构造了非均匀网格上的 BDF2 型公式. 利用离散互补卷积核的相关性质和引理进行误差分析. 第 3 节构建了一个时间非均匀有限元公式, 并对时间收敛阶进行了理论分析. 第 4 节分析了 $L^2$-范数和 $H^1$-范数下有限元格式的稳定性和收敛性. 在第 5 节中, 通过数值实验验证理论分析结果. 本文在第 6 节中提供了总结和展望.

2 Caputo 导数的离散形式

在本节中, 我们的主要思想是使用二次插值函数构造非均匀半网格上离散 Caputo 导数的 BDF2 型公式. 首先, 我们采用了一些与离散系数核和离散卷积核相关的引理. 然后, 我们根据离散卷积核的性质分析了非均匀网格上的截断误差.

2.1 非均匀网格上的 BDF2 型公式

对于非均匀时间层 $0 = {t_0} < {t_1} < {t_2} < \cdots < {t_N} = T,$ 设 $N$ 为正整数, 设 $ {\tau _n} = {t_n} - {t_{n - 1}}$ 为第 $n$ 个步长并且${\tau _{n - \frac{1}{2}}} = \frac{{{\tau _n} + {\tau _{n - 1}}}}{2},{\tau _{\frac{1}{2}}} = \frac{{{\tau _1}}}{2},$ 设 ${t_{n - \frac{1}{2}}} = {t_{n - 1}} + \frac{{{\tau _n}}}{2},{t_{ - \frac{1}{2}}} = {t_0}.$ 设 ${\rho _n} = {\tau} _{n} / {\tau}_{n+1} $ 为步长比. 接下来, 令 ${\Pi _{1,n}}u$ 和 ${\Pi _{2,n}}u$ 分别为节点的线性插值和二次插值函数, 如参考文献[22]所定义,

(2.1)$\begin{align*} {\left( {{\Pi _{1,n}}u} \right)^\prime }\left( {{t_n}} \right) = \frac{{{\nabla _\tau }{u^n}}}{{{\tau _n}}},{\left( {{\Pi _{2,n}}u} \right)^\prime }\left( {{t_n}} \right) = \frac{{{\nabla _\tau }{u^n}}}{{{\tau _n}}} + \frac{{2\left( {t - {t_{n - \frac{1}{2}}}} \right)}}{{{\tau _n}\left( {{\tau _n} + {\tau _{n + 1}}} \right)}}\left( {\rho {}_n{\nabla _\tau }{u^{n + 1}} - {\nabla _\tau }{u^n}} \right).\ \end{align*}$

因此, 非均匀半网格上的插值函数公式可以如下获得

(2.2)$\begin{align*} {\left( {{\Pi _{1,n}}{u^{n - \frac{1}{2}}}} \right)^\prime }\ &=\frac{{{\nabla _\tau }{u^{n - \frac{1}{2}}}}}{{{\tau _{n - \frac{1}{2}}}}} = \frac{{{u^{n - \frac{1}{2}}} - {u^{n - \frac{3}{2}}}}}{{{\tau _{n - \frac{1}{2}}}}}, \\ {\left( {{\Pi _{2,n}}{u^{n - \frac{1}{2}}}} \right)^\prime }\ &=\frac{{{\nabla _\tau }{u^{n - \frac{1}{2}}}}}{{{\tau _{n - \frac{1}{2}}}}} + \frac{{2\left( {t - {t_{n - 1}}} \right)}}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}\left( {{\rho _{n - \frac{1}{2}}}{\nabla _\tau }{u^{n + \frac{1}{2}}} - {\nabla _\tau }{u^{n - \frac{1}{2}}}} \right) \\ &=\frac{{{u^{n - \frac{1}{2}}} - {u^{n - \frac{3}{2}}}}}{{{\tau _{n - \frac{1}{2}}}}} + \frac{{2\left( {t - {t_{n - 1}}} \right)}}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}\left( {{\rho _{n - \frac{1}{2}}}\left( {{u^{n + \frac{1}{2}}} - {u^{n - \frac{1}{2}}}} \right)} \right. \\ & -\left. {\left( {{u^{n - \frac{1}{2}}} - {u^{n - \frac{3}{2}}}} \right)} \right).\ \end{align*}$

设 ${u^n} \approx u\left( {{t_n}} \right)$ 为点 ${t_n}$ 处方程的数值近似. 其中, 相关算子如下

$ {u^{n - \frac{1}{2}}} = \frac{1}{2}\left( {{u^n} + {u^{n - 1}}} \right),\quad {\nabla _\tau }{u^{n - \frac{1}{2}}} = {u^{n - \frac{1}{2}}} - {u^{n - \frac{3}{2}}}.\ $

本文对非均匀时间网格的假设如下

(2.3)$\begin{align*} {\tau _{n{\rm{ - }}1}} \le {\tau _n},\quad 2 \le n \le N.\ \end{align*}$

我们在闭区间$\left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right]$ 上构造 BDF2 公式, 以近似 Caputo 型导数 $D_t^\alpha u\left( {x,{t_n}} \right),\left( {0 < \alpha \le 1} \right).$ 从方程 (2.2) 可以得到以下方程.

(2.4)$\begin{align*} {}_0^CD_t^\alpha u\left( {{t_{n - \frac{1}{2}}}} \right)\ &=\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right){{\left( {{\Pi _{1,n}}u} \right)}^\prime }\left( s \right){\rm d}s} \\ & + \sum _{k = 1}^{n - 1} {\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right){{\left( {{\Pi _{2,k}}u} \right)}^\prime }\left( s \right){\rm d}s} } \\ &= a_0^{\left( n \right)}{\nabla _\tau }{u^{n - \frac{1}{2}}} + \sum _{k = 1}^{n - 1} {\left( {a_{n - k}^{\left( n \right)}{\nabla _\tau }{u^{k - \frac{1}{2}}} + {\rho _{k - \frac{1}{2}}}b_{n - k}^{\left( n \right)}{\nabla _\tau }{u^{k + \frac{1}{2}}}} \right.} - \left. {b_{n - k}^{\left( n \right)}{\nabla _\tau }{u^{k - \frac{1}{2}}}} \right) \\ &= \sum _{k = 1}^n {d_{n - k}^{\left( n \right)}} {\nabla _\tau }{u^{k - \frac{1}{2}}} = D_\tau ^\alpha {u^{n - \frac{1}{2}}},\quad n \ge 1.\ \end{align*}$

其中 ${ \nabla _\tau }{u^{\frac{1}{2}}} = \frac{1}{2}\left( {{u^1} - {u^0}} \right),$ 并且离散系数核 $a_{n - k}^{\left( n \right)},b_{n - k}^{\left( n \right)}$ 的具体形式如下

(2.5)$\begin{align*} a_0^{\left( n \right)}\ &=\frac{1}{{{\tau _{n - \frac{1}{2}}}}}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right){\rm d}s},\\ a_{n - k}^{\left( n \right)}\ &=\frac{1}{{{\tau _{k - \frac{1}{2}}}}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right){\rm d}s},1 \le k \le n - 1, \\ b_{n - k}^{\left( n \right)}\ &=\frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {s - {t_{k - 1}}} \right){\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right){\rm d}s}.\ \end{align*}$

具有紧致形式的离散系数核 $ d_{n - k}^{\left( n \right)}$ 的定义如下

$d_0^{\left( 1 \right)} = a_0^{\left( 1 \right)},\quad n = 1,\ $

并且当 $n \ge 2,$

(2.6)$\begin{align*} d_{n - k}^{\left( n \right)} = \left\{ \begin{array}{l} a_0^{\left( n \right)} + {\rho _{n - \frac{3}{2}}}b_1^{\left( n \right)},\quad k = n,\\ a_{n - k}^{\left( n \right)} + {\rho _{k - \frac{3}{2}}}b_{n - k + 1}^{\left( n \right)} - b_{n - k}^{\left( n \right)},\quad 2 \le k \le n - 1,\\ a_{n - 1}^{\left( n \right)} - b_{n - 1}^{\left( n \right)},\quad k = 1. \end{array} \right.\ \end{align*}$

以下引理描述了离散系数核 $d_{n - k}^{\left( n \right)}$ 的性质, 给出了正定性和边界估计.

引理2.1 对于任意在 (2.6) 式定义的 $d_{n - k}^{\left( n \right)}$, 成立下式

(1)$d_k^{\left( n \right)} > 0,0 \le k \le n - 1$;

(2)$\frac{{d_0^{\left( k \right)}}}{{d_{k - 2}^{\left( k \right)}}} < \frac{{{{\left( {{t_{k - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)}^\alpha }}}{{\left( {1 - \alpha } \right){{\left( {{\tau _{k - \frac{1}{2}}}} \right)}^\alpha }}},2 \le k \le n$;

(3)$0 < {\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{1}{2}}}} \right) - {\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{3}{2}}}} \right) \le d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)},2 \le k \le n - 1$.

证这一结果的证明来自参考文献[23,引理 3.1].

2.2 DCC核的性质

离散卷积核在误差卷积结构 (ECS) 的理论分析中尤为重要. 在本节中, 我们将介绍离散卷积核 $D_{n - k}^{\left( n \right)}$ 的重要性质和引理, 以获得非均匀半网格下的全局一致性误差. 以下方程提供了离散卷积核的一般表达式,

(2.7)$\begin{align*} D_0^{\left( n \right)} = \frac{1}{{d_0^{\left( n \right)}}},D_{n - k}^{\left( n \right)} = \frac{1}{{d_0^{\left( k \right)}}}\sum\limits_{j = k + 1}^n {\left( {d_{j - k - 1}^{\left( j \right)} - d_{j - k}^{\left( j \right)}} \right)D_{n - j}^{\left( n \right)}},1 \le k \le n - 1.\ \end{align*}$

引理 2.2 给出了离散系数核 $D_{n - k}^{\left( n \right)}$ 的下界及其对步长 ${\rho _k}$ 的限制.

引理2.2 假设离散系数核 $D_{n - k}^{\left( n \right)}$ 有以下性质:

(A1) 当 $1 \le k \le N,$ 存在一个正常数 ${c_1} > 0,$ 满足,

$\begin{align*} d_{n - k}^{\left( n \right)} \ge \frac{1}{{{c_1}}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\frac{{{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}}{{{\tau _{k - \frac{1}{2}}}}}{\rm d}s.} \ \end{align*}$

(A2) 当 $1 \le k \le N - 1,$ 存在一个正数 $\rho$ 满足步长比 ${\rho _{k - \frac{1}{2}}} \le \rho.$

证首先我们对(A1)假设条件加以证明. 当 $k = 1$ 时, 由 (2.6) 式和中值定理得到,

(2.9)$\begin{align*} d_{n - 1}^{\left( n \right)}\ &= a_{n - 1}^{\left( n \right)} - b_{n - 1}^{\left( n \right)}\nonumber \\ &= \frac{1}{{{\tau _{\frac{1}{2}}}}}\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s - \frac{2}{{{\tau _{\frac{1}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {s{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{1}{{{\tau _{\frac{1}{2}}}}} - \frac{2}{{{\tau _{\frac{1}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}{t_{\frac{1}{2}}}} \right)\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{1}{{{\tau _{\frac{1}{2}}}}} - \frac{2}{{{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}}}} \right)\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{{{\tau _{\frac{3}{2}}} - {\tau _{\frac{1}{2}}}}}{{{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}}}} \right)\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s,\ \end{align*}$

由 (2.3) 式, 此时取 ${c_1} = \frac{{{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}}}{{{\tau _{\frac{1}{2}}}\left( {{\tau _{\frac{3}{2}}} - {\tau _{\frac{1}{2}}}} \right)}} > 0,$ (2.8) 式即可得证. 当 $k = n$ 时, 由 (2.6) 式和 ${t_{n - \frac{5}{2}}} = {t_{n - 2}} - \frac{{{\tau _{n - \frac{3}{2}}}}}{2},$ 得到下式

(2.10)$\begin{align*} d_0^{\left( n \right)}\ &= a_0^{\left( n \right)} + {\rho _{n - \frac{3}{2}}}b_1^{\left( n \right)}\nonumber \\ &= \frac{1}{{{\tau _{n - \frac{1}{2}}}}}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ & + \frac{{2{\rho _{n - \frac{3}{2}}}}}{{{\tau _{n - \frac{3}{2}}}\left( {{\tau _{n - \frac{3}{2}}} + {\tau _{n - \frac{1}{2}}}} \right)}}\int _{{t_{n - \frac{5}{2}}}}^{{t_{n - \frac{3}{2}}}} {\left( {s - {t_{n - 2}}} \right){\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \frac{1}{{{\tau _{n - \frac{1}{2}}}}}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ & + \frac{{2\left( {{t_{n - \frac{5}{2}}} - {t_{n - 2}}} \right)}}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{3}{2}}} + {\tau _{n - \frac{1}{2}}}} \right)}}\int _{{t_{n - \frac{5}{2}}}}^{{t_{n - \frac{3}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \frac{1}{{{\tau _{n - \frac{1}{2}}}}}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s - \frac{{{\tau _{n - \frac{3}{2}}}}}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{3}{2}}} + {\tau _{n - \frac{1}{2}}}} \right)}}\int _{{t_{n - \frac{5}{2}}}}^{{t_{n - \frac{3}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{1}{{{\tau _{n - \frac{3}{2}}} + {\tau _{n - \frac{1}{2}}}}}} \right)\int _{{t_{ - \frac{1}{2}}}}^{{t_{\frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s,\ \end{align*}$

由 (2.3) 式, 此时取 ${c_1} = \frac{1}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{3}{2}}} + {\tau _{n - \frac{1}{2}}}} \right)}} > 0,$ (2.8) 式即可得证. 当 $2 \le k \le n - 2$ 时, 由 (2.6) 式得到下式

(2.11)$\begin{align*} d_{n - k}^{\left( n \right)}\ &= a_{n - k}^{\left( n \right)} + {\rho _{k - \frac{3}{2}}}b_{n - k + 1}^{\left( n \right)} - b_{n - k}^{\left( n \right)} \nonumber \\ &= \frac{1}{{{\tau _{k - \frac{1}{2}}}}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ & + \frac{{2{\rho _{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {s - {t_{k - 1}}} \right){\omega _{1 - \alpha }}\left( {{t_{n + \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ & - \frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {s - {t_{k - 1}}} \right){\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \frac{1}{{{\tau _{k - \frac{1}{2}}}}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s - \frac{{{\tau _{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n + \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ & - \frac{{{\tau _k}}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{1}{{{\tau _{k - \frac{1}{2}}}}} - \frac{{{\tau _{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}} - \frac{{{\tau _k}}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s \nonumber \\ &\ge \left( {\frac{{{\tau _{k + 1}} - {\tau _{k - 2}}}}{{2{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - s} \right)}{\rm d}s. \end{align*}$

由 (2.3) 式, 此时取 ${c_1} = \frac{{{\tau _{k + 1}} - {\tau _{k - 2}}}}{{2\tau _{k - \frac{1}{2}}^2\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}} > 0,$ 综上 (2.8) 式即可得证. (A2)假设是对步长比的限制, 由参考文献[22, 引理 $2.1$]可证, 以下引理证明了离散卷积核在非均匀网格上具有正定性.

引理2.3 当 $1 \le k \le n,$ 在 $(2.7)$ 式中定义的离散卷积核 $D_{n - k}^{\left( n \right)}$ 是正定的, 并且满足以下方程,

(2.12)$\begin{align*} \sum _{j = k}^n {D_{n - j}^{\left( n \right)}d_{j - k}^{\left( j \right)}} = 1.\ \end{align*}$

如果非均匀网格满足 (2.3) 式,

(2.13)$\begin{align*} \sum _{j = 1}^{n - 1} {D_{n - j}^{\left( n \right)}{\omega _{1 + m\alpha - \alpha }}\left( {{t_j}} \right)} \le {\omega _{1 + m\alpha }}\left( {{t_{n - \frac{1}{2}}}} \right),n \ge 1,m \ge 1.\ \end{align*}$

证方程式 $(2.12)$-$(2.13)$ 的证明可以在参考文献[23,引理 2.1]中找到.

为了进行有限元的理论分析, 给出了以下假设,

(B1) 假设 A2 中的最大时间步长为 $\rho = 7/4$, BDF2 格式中的时间步长为 $\sigma = 1 - {\alpha / 2}.$

(B2) 存在一个正常数 ${C_\gamma }$ 满足, $\tau_k \leq C_\gamma \tau \min \left\{1, t_k^{1-1 / \gamma}\right\}$, $1 \le k \le N,{t_k} \le {C_\gamma }{t_{k - 1}},$ 并且 $\tau_k / t_k \leq C_\gamma \tau_{k-1} / t_{k-1}, 2 \leq k \leq N.$

为了分析截断误差, 以下引理给出了一个具有积分型余项的插值误差估计.

引理2.4 假设 $p \in {C^2}\left( {\left( {0,T} \right]} \right),1 \le k \le n,$ 并且令 ${\Pi _{1,k}}p\left( t \right)$ 和 ${\Pi _{2,k}}p\left( t \right) $ 是在区间 $\left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right]$ 上关于 $p\left( t \right)$ 的线性插值和二次插值. 线性插值误差表达式如下,

(2.14)$\begin{align*} p\left( t \right) - {\Pi _{1,k}}p\left( t \right) = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\chi _{1k}}\left( {t,\lambda } \right)\ddot p\left( \lambda \right)}{\rm d}\lambda,t \in \left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right].\ \end{align*}$

给出二次插值误差如下,

(2.15)$\begin{align*} p\left( t \right) - {\Pi _{2,k}}p\left( t \right) = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\chi _{2k}}\left( {t,\lambda } \right)\ddot p\left( \lambda \right)}{\rm d}\lambda,t \in \left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right].\ \end{align*}$

其中 ${\chi _{1k}} = \max \left\{ {t - \lambda,0} \right\} - \frac{{t - {t_{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}}}\left( {{t_{k - \frac{1}{2}}} - \lambda } \right)$是 Peano 核, 满足,

$- \frac{{{t_{k - \frac{1}{2}}} - \lambda }}{{{\tau _{k - \frac{1}{2}}}}}\left( {t - {t_{k - \frac{3}{2}}}} \right) \le {\chi _{1k}} \le 0,t,\lambda \in \left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right].\ $

${\chi _{2k}}$的具体表达式如下

$\begin{align*} {\chi _{2k}}\ &=\max \left\{ {t - \lambda,0} \right\} - \frac{{t - {t_{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}}}\left( {{t_{k - \frac{1}{2}}} - \lambda } \right) - \frac{{2\left( {t - {t_{k - 1}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\ \\ & \left( {{\rho _{k - \frac{1}{2}}}\frac{{\left( {t - {t_{k - \frac{1}{2}}}} \right)}}{{{\tau _{k + \frac{1}{2}}}}}\left( {{t_{k + \frac{1}{2}}} - \lambda } \right) - \frac{{t - {t_{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}}}\left( {{t_{k - \frac{1}{2}}} - \lambda } \right)} \right),\ \end{align*}$

下式成立

$\begin{align*} & - \frac{{t - {t_{k - \frac{3}{2}}}}}{{{\tau _{k - \frac{1}{2}}}}}\left( {{t_{k - \frac{1}{2}}} - \lambda } \right) - \frac{{2{\rho _{k - \frac{1}{2}}}\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{1}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\left( {{t_{k + \frac{1}{2}}} - \lambda } \right)\ \\ & + \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{\tau _{k - \frac{1}{2}}^2\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}\left( {{t_{k - \frac{1}{2}}} - \lambda } \right) \le {\chi _{2k}} \le 0,t,\lambda \in \left[ {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right].\ \end{align*}$

证引理 2.4 的证明过程可以从参考文献[23,引理 3.1]中获得.

我们将 $n \ge 1$ 时方程 (2.4) 的局部截断误差定义如下

${\xi ^n} = {}_0^CD_t^\alpha u\left( {{t_{n - \frac{1}{2}}}} \right) - D_\tau ^\alpha {u^{n - \frac{1}{2}}} = \sum\limits_{k = 1}^n {\xi _k^n}.\ $

下面我们提供了在非均匀半网格上估计全局近似误差 $\sum\limits_{j = 1}^n {D_{n - j}^{\left( n \right)}} \left| {{\xi ^j}} \right|$ 的相关引理.

引理2.5 假设 $u \in {C^2}\left( {\left( {0,T} \right]} \right),$ 其中 $ \int _0^T {t\left| {\ddot u\left( t \right)} \right|}{\rm d}t < \infty,\int _0^T {{t^2}\left| {\ddot u\left( t \right)} \right|}{\rm d}t < \infty.$ 如果非均匀网格满足 (2.3) 式, 我们有

$\begin{aligned} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \ & \le 2\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)}\int _{{t_{j - \frac{3}{2}}}}^{{t_{j - \frac{1}{2}}}} {\left( {2\left( {t - {t_{j - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{j - 1}}} \right)\left( {{t_{j - \frac{1}{2}}} - t} \right)}}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right.} \ \\ & + \left. {\frac{{2\left( {t - {t_{j - 1}}} \right)\left( {t - {t_{j - \frac{3}{2}}}} \right)}}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t.\ \end{aligned}$

证对于 $1 \le k \le n - 1, $ 通过使用引理 2.1 和引理 2.4, 我们得到

(2.16)$\begin{align*} & {{\tilde \Pi }_{1,k}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\\ & = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\chi _{1k}}\left( {t,\lambda } \right){{\ddot \omega }_{2 - \alpha }}} \left( {{t_{n - \frac{1}{2}}} - \lambda } \right){\rm d}\lambda \\ & \le \left( {{t_{k - \frac{3}{2}}} - t} \right)\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{{\ddot \omega }_{2 - \alpha }}} \left( {{t_{n - \frac{1}{2}}} - \lambda } \right){\rm d}\lambda \\ & = \left( {t - {t_{k - \frac{3}{2}}}} \right)\left[ {{\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{1}{2}}}} \right) - {\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{3}{2}}}} \right)} \right]\\ &\le \left( {t - {t_{k - \frac{3}{2}}}} \right)\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right),\forall t \in \left( {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right). \end{align*}$

对于 $\forall t \in \left( {{t_{k - \frac{3}{2}}},{t_{k - \frac{1}{2}}}} \right),$ 下式成立

(2.17)$\begin{align*} & {{\tilde \Pi }_{2,k}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\\ & =\! \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{\chi _{2k}}\left( {t,\lambda } \right){{\ddot \omega }_{2 - \alpha }}} \left( {{t_{n - \frac{1}{2}}} - \lambda } \right){\rm d}\lambda \\ & \le\!\! \left(\!\! {\left( {{t_{k - \frac{3}{2}}} \!-\! t} \right) \!-\! \frac{{2\left( {{t_{k - 1}} - t} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)}}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right.\left. { - \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{{\ddot \omega }_{2 - \alpha }}} \left( {{t_{n - \frac{1}{2}}} \!-\! \lambda } \right){\rm d}\lambda \\ & =\!\! \left(\!\! {\left( {t \!-\! {t_{k - \frac{3}{2}}}} \right) \!-\! \frac{{2\left( {t \!-\! {t_{k \!-\! 1}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)}}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right. \!+\! \left. {\frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\left[ \begin{array}{l} {\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{1}{2}}}} \right) - \\ {\omega _{1 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{k - \frac{3}{2}}}} \right) \end{array} \right]\\ & \le\!\! \left(\!\! {\left( {t - {t_{k - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)}}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right.\left. { + \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right). \end{align*}$

当 $k = n, $ 由于 ${\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right) $ 相对于 $t$ 单调递减, 以下方程成立

(2.18)$\begin{align*} 0\ & \le {{\tilde \Pi }_{1,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right) \\ & \le {\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{n - \frac{3}{2}}}} \right) - {\Pi _{1,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right) \\ &= \left( {t - {t_{n - \frac{3}{2}}}} \right)d_0^{\left( n \right)}.\ \end{align*}$

并且成立

(2.19)$\begin{align*} 0\ & \le {{\tilde \Pi }_{2,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right) \\ & \le {\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - {t_{n - \frac{3}{2}}}} \right) - {\Pi _{2,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right) \\ &\le \left( {\left( {t - {t_{k - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)}}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}} + \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)d_0^{\left( n \right)}.\ \end{align*}$

现在, 当 $1 \le k \le n - 1,$ 我们估计截断误差 $\xi _n^n,\xi _k^n,$ 并定义积分表达式如下

$\begin{align*} & G_1^k = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - \frac{3}{2}}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t,} \\ & G_2^k = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - 1}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t},\\ & G_3^k = \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t}. \end{align*}$

由 (2.18) 式

(2.20)$\begin{align*} \left| {\xi _n^n} \right|\ & \le \int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{{\tilde \Pi }_{1,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\left| {\ddot u\left( t \right)} \right|}{\rm d}t \\ & \le d_0^{\left( n \right)}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {\left( {t - {t_{n - \frac{3}{2}}}} \right)\left| {\ddot u\left( t \right)} \right|}{\rm d}t = d_0^{\left( n \right)}G_1^n.\ \end{align*}$

对于 $n \ge 1,$ 由 (2.19) 式

(2.21)$\begin{align*} \left| {Q_n^n} \right|\ & \le \int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {{{\tilde \Pi }_{2,n}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t} \\ & \le d_0^{\left( n \right)}\int _{{t_{n - \frac{3}{2}}}}^{{t_{n - \frac{1}{2}}}} {\left( {\left( {t - {t_{n - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{n - 1}}} \right)\left( {{t_{n - \frac{1}{2}}} - t} \right)}}{{{\tau _{n + \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}} \right.} \\ & + \left. {\frac{{2\left( {t - {t_{n - 1}}} \right)\left( {t - {t_{n - \frac{3}{2}}}} \right)}}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t \\ &= d_0^{\left( n \right)}\left( {G_1^n - \frac{2}{{{\tau _{n + \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}G_2^n} \right. \\ & + \left. {\frac{2}{{{\tau _{n - \frac{1}{2}}}\left( {{\tau _{n - \frac{1}{2}}} + {\tau _{n + \frac{1}{2}}}} \right)}}G_3^n} \right)\ \end{align*}$

当 $1 \le k \le n - 1,$ 通过 (2.16) 式

(2.22)$\begin{align*} \sum\limits_{k = 1}^{n - 1} {\left| {q_k^n} \right|} \ & \le \sum _{k = 1}^{n - 1} {\int\limits_{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{{\tilde \Pi }_{1,k}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\left| {\ddot u\left( t \right)} \right|} {\rm d}} t \\ & \le \sum _{k = 1}^{n - 1} {\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right)\int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - \frac{3}{2}}}} \right)\left| {\ddot u\left( t \right)} \right|} {\rm d}} t \\ & = \sum _{k = 1}^{n - 1} {\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right)} G_1^k.\ \end{align*}$

通过 (2.17) 式

(2.23)$\begin{align*} \sum _{k = 1}^{n - 1} {\left| {Q_k^n} \right|} \ & \le \sum _{k = 1}^{n - 1} {\int\limits_{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{{\tilde \Pi }_{2,k}}{\omega _{2 - \alpha }}\left( {{t_{n - \frac{1}{2}}} - t} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t} } \\ & \le \sum _{k = 1}^{n - 1} {\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right)} \int\limits_{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {\left( {t - {t_{k - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{k - 1}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)}}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right.} \\ & + \left. {\frac{{2\left( {t - {t_{k - 1}}} \right)\left( {t - {t_{k - \frac{3}{2}}}} \right)}}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t,\ \end{align*}$

对 (2.23) 式进行化简得到

(2.24)$\begin{align*} \sum _{k = 1}^{n - 1} {\left| {Q_k^n} \right|} \ &\le \sum _{k = 1}^{n - 1} {\left( {d_{n - k - 1}^{\left( n \right)} - d_{n - k}^{\left( n \right)}} \right)} \left( {G_1^k - \frac{2}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_2^k} \right. \\ & + \left. {\frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_3^k} \right).\ \end{align*}$

由 (2.20)-(2.24) 得到的误差估计表达式如下

(2.25)$\begin{align*} \left| {\xi {}^j} \right|\ &= \sum _{k = 1}^j {\left| {\xi _k^n} \right|} = \xi _n^n + Q_n^n + \sum _{k = 1}^{j - 1} {\left| {q_k^n} \right|} + \sum _{k = 1}^{j - 1} {\left| {Q_k^n} \right|} \\ & \le \sum _{k = 1}^{j - 1} {\left( {d_{j - k - 1}^{\left( j \right)} - d_{j - k}^{\left( j \right)}} \right)} \left( {2G_1^k - \frac{2}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_2^k} \right. \\ & + \left. {\frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_3^k} \right) + d_0^{\left( j \right)}\left( {2G_1^j} \right. \\ & - \left. {\frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j + \frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right).\ \end{align*}$

其中, $1 \le j \le n.$ 将方程 (2.25) 两端同乘 $D_{n - j}^{\left( n \right)}$ 将 $j$ 从 1 求和到 $n$, 然后交换求和顺序获得,

(2.26)$\begin{align*} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \ &\le \sum _{j = 2}^n {D_{n - j}^{\left( n \right)}} \sum _{k = 1}^{j - 1} {\left( {d_{j - k - 1}^{\left( j \right)} - d_{j - k}^{\left( j \right)}} \right)} \left( {2G_1^k - \frac{2}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_2^k} \right. \\ & + \left. {\frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_3^k} \right) + \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)}\left( {2G_1^j} \right. \\ & - \left. {\frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j + \frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right) \\ &= \sum _{k = 1}^{n - 1} {\left( {2G_1^k - \frac{2}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_2^k + \frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_3^k} \right)} \\ & \times\sum _{j = k + 1}^n {D_{n - j}^{\left( n \right)}\left( {d_{j - k - 1}^{\left( j \right)} - d_{j - k}^{\left( j \right)}} \right)} + \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)}\left( {2G_1^j} \right. \\ & - \left. {\frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j + \frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right),\ \end{align*}$

因此, 我们有

(2.27)$\begin{align*} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \ &\le \sum _{k = 1}^{n - 1} {\left( {2G_1^k - \frac{2}{{{\tau _{k + \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_2^k + \frac{2}{{{\tau _{k - \frac{1}{2}}}\left( {{\tau _{k - \frac{1}{2}}} + {\tau _{k + \frac{1}{2}}}} \right)}}G_3^k} \right)} D_{n - k}^{\left( n \right)}d_0^{\left( k \right)} \\ & + \sum _{j = 1}^n {\left( {2G_1^j - \frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j + \frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right)D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)} \\ & \le 2\sum _{j = 1}^n {\left( {2G_1^j - \frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j + \frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right)D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)} \\ &= 2\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}} d_0^{\left( j \right)}\int _{{t_{j - \frac{3}{2}}}}^{{t_{j - \frac{1}{2}}}} {\left( {2\left( {t - {t_{j - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{j - 1}}} \right)\left( {{t_{j - \frac{1}{2}}} - t} \right)}}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right.} \\ & + \left. {\frac{{2\left( {t - {t_{j - 1}}} \right)\left( {t - {t_{j - \frac{3}{2}}}} \right)}}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t.\ \end{align*}$

推论2.1 假设 $u \in {C^2}\left( {\left( {0,T} \right]} \right),$ 并且存在一个常数 ${c_u} > 0$, 满足

(2.28)$\begin{align*} \left| {\ddot u\left( t \right)} \right| \le {c_u}\left( {1 + {t^{\mu - 3}}} \right).\ \end{align*}$

其中 $\mu \in \left( {0,1} \right) \cup \left( {1,2} \right) \cup \left( {2,3} \right) $ 是一个正则化参数. 当 $n \ge 1,$ 如果方程 (2.3) 成立, 则全局误差估计的表达式如下

(2.29)$\begin{align*}\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \le {c_u}\left( {\tau _1^\mu + \frac{1}{{1 - \alpha }}\mathop {\max }\limits_{2 \le j \le n} {{\left( {{t_{j - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)}^\alpha }t_{_{j - \frac{3}{2}}}^{\mu - 3}\tau _{_{j - \frac{1}{2}}}^{3 - \alpha }} \right).\ \end{align*}$

证通过方程 (2.28),

(2.30)$\begin{align*} \begin{array}{l} G_1^1 \le c{c_u}\tau _1^\mu,G_1^k \le \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - \frac{3}{2}}}} \right)} {c_u}{t^{\mu - 3}}{\rm d}t \le c{c_u}{\left( {{\tau _{k - \frac{1}{2}}}} \right)^3}t_{k - \frac{3}{2}}^{\mu - 3},\\[3mm] G_2^1 \le {c_u}\tau _1^\mu,G_2^k \le \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {\left( {t - {t_{k - \frac{3}{2}}}} \right)\left( {{t_{k - \frac{1}{2}}} - t} \right)} {c_u}{t^{\mu - 3}}{\rm d}t \le {c_u}{\left( {{\tau _{k - \frac{1}{2}}}} \right)^3}t_{k - \frac{3}{2}}^{\mu - 3},\\[3mm] G_3^1 \le {c_u}\tau _1^\mu,G_3^k \le \int _{{t_{k - \frac{3}{2}}}}^{{t_{k - \frac{1}{2}}}} {{{\left( {t - {t_{k - \frac{3}{2}}}} \right)}^2}} {c_u}{t^{\mu - 3}}{\rm d}t \le {c_u}{\left( {{\tau _{k - \frac{1}{2}}}} \right)^3}t_{k - \frac{3}{2}}^{\mu - 3},2 \le k \le n. \end{array}\ \end{align*}$

其中, 常数 $c$ 能被 $c{\tau _1} \ge 1,c{\tau _{k - \frac{1}{2}}} \ge 1,2 \le k \le n$ 控制. 由于 $D_{n - k}^{\left( n \right)} > 0,d_{n - k}^{\left( n \right)} > 0$. 并且方程 (2.12) 满足 $\sum _{j = 2}^n {D_{n - j}^{\left( n \right)}d_{j - 2}^{\left( j \right)}} = 1.$ 通过引理 2.1 和引理 2.5, 我们得到

(2.31)$\begin{align*} & \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \\ &\le 2D_{n - 1}^{\left( n \right)}d_0^{\left( 1 \right)}\left( {2G_1^1 - \frac{2}{{{\tau _{\frac{3}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}G_2^1} \right. + \left. {\frac{{2G_3^1}}{{{\tau _{\frac{1}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}} \right) \\ & + 2\sum _{j = 2}^n {\left( {2G_1^j - \frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j} \right.} + \left. {\frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right)D_{n - j}^{\left( n \right)}d_0^{\left( j \right)},\ \end{align*}$

通过方程 (2.31), 我们有

(2.32)$\begin{align*} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \ & \le 2\left( {2G_1^1 - \frac{2}{{{\tau _{\frac{3}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}G_2^1 + \frac{2}{{{\tau _{\frac{1}{2}}}\left( {{\tau _{\frac{1}{2}}} + {\tau _{\frac{3}{2}}}} \right)}}G_3^1} \right) \\ & + \frac{2}{{1 - \alpha }}\sum _{j = 2}^n {\left( {2G_1^j - \frac{2}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_2^j} \right.} \\ & + \left. {\frac{2}{{{\tau _{j - \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}G_3^j} \right)D_{n - j}^{\left( n \right)}d_{j - 2}^{\left( j \right)}{\left( {{t_{j - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)^\alpha }{\left( {{\tau _{j - \frac{1}{2}}}} \right)^{ - \alpha }} \\ &\le {c_u}\tau _1^\mu + \frac{{{c_u}}}{{1 - \alpha }}\sum _{j = 2}^n {D_{n - j}^{\left( n \right)}d_{j - 2}^{\left( j \right)}} {\left( {{t_{j - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)^\alpha }t_{j - \frac{3}{2}}^{\mu - 3}{\left( {{\tau _{j - \frac{1}{2}}}} \right)^{3 - \alpha }} \\ &\le {c_u}\left( {\tau _1^\mu + \frac{1}{{1 - \alpha }}\mathop {\max } _{2 \le j \le n} {{\left( {{t_{j - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)}^\alpha }t_{j - \frac{3}{2}}^{\mu - 3}{{\left( {{\tau _{j - \frac{1}{2}}}} \right)}^{3 - \alpha }}} \right).\ \end{align*}$

3 非均匀 BDF2 型有限元格式

本节的主要工作是为时间分数阶扩散-波动方程开发一个非均匀 BDF2 型有限元格式. 首先, 使用降阶方法将原始问题 (1.1)-(1.2) 改写为等效方程组. 给出

(3.31)$\begin{align*} \alpha = \beta - 1,u\left( {x,t} \right) = \frac{{\partial v}}{{\partial t}}\left( {x,t} \right),\ \end{align*}$

将 (3.1) 式代入 (2.4) 式, 得到以下方程

(3.2)$\begin{align*} _0^CD_t^\beta v\left( {x,t} \right)\ & = \frac{1}{{\Gamma \left( {2 - \beta } \right)}}\int _0^t {\frac{{{\partial ^2}v}}{{\partial {s^2}}}\left( {x,s} \right)} \frac{1}{{{{\left( {t - s} \right)}^{\beta - 1}}}}{\rm d}s \\ & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\int _0^t {\frac{{{\partial ^2}v}}{{\partial {s^2}}}\left( {x,s} \right)} \frac{1}{{{{\left( {t - s} \right)}^\alpha }}}{\rm d}s \\ &= _0^CD_t^\alpha u\left( {x,t} \right).\ \end{align*}$

3.1 双线性有限元方法

定义 ${J_{h1}}$ 为 $\Omega {\rm{ = }}{\left( {0,L} \right)^2}$ 的矩形网格族, 其中对于任意 $K \in {J_{h1}},$ 定义 ${O_K} = \left( {{x_K},{y_K}} \right)$ 是 $K$ 的中心, $h_x^K$ 和 $h_y^K$ 分别是中心 ${O_K}$ 和平行于两个坐标平面的 $K$ 的两侧之间的垂直距离.

$A_1^K = \left( {{x_K} - h_x^K,{y_K} - h_y^K} \right),A_2^K = \left( {{x_K} + h_x^K,{y_K} - h_y^K} \right),A_3^K = \left( {{x_K} - h_x^K,{y_K} + h_y^K} \right),$

$A_4^K = \left( {{x_K} + h_x^K,{y_K} + h_y^K} \right)$ 表示 $K$ 的四个顶点. 定义 ${x_i} = ih,{y_j} = jh,{h_K} = \max \left\{ {h_x^K,h_y^K} \right\},$$h = \mathop {\max }\limits_{K \in {J_{h1}}} {h_K}.$ 然后, 设 $M$ 为正整数, 我们将离散空间网格定义为

${\Omega _h} = \left\{ {\left. {\left. {{x_h} = \left( {{x_i},{y_j}} \right)} \right|1 \le i,j \le M - 1} \right\}} \right.,{\overline \Omega _h} = \left\{ {\left. {\left. {{x_h}} \right|0 \le i,j \le M} \right\}} \right..\ $

有限元空间如下

(3.3)$\begin{align*} {V_h}\ & = \left\{ {\left. {{{\left. {v;v} \right|}_K} \in {Q_{11}}\left( K \right),{v_h}\left( {{x_h},0} \right) = {\varphi _1}\left( {{x_h}} \right)} \right\}} \right., \\ {U_h}\ & = \left\{ {\left. {{{\left. {v;v} \right|}_K} \in {Q_{11}}\left( K \right),{u_h}\left( {{x_h},0} \right) = {\varphi _2}\left( {{x_h}} \right)} \right\}} \right..\ \end{align*}$

其中 ${Q_{ij}} = {\rm span}\left\{ {{x^r}{y^s};\left( {x,y} \right) \in K,0 \le r \le i,0 \le s \le j} \right\}.$因此对于 ${u_h} \in {U_h},$ 我们在点 $\big( {x_h},$${t_{n - \frac{1}{2}}} \big)$ 处得到以下算子的离散形式. 其中,${\delta _x}{u_{i + \frac{1}{2},j}} = \frac{{\left( {{u_{i + 1,j}} - {u_{i,j}}} \right)}}{h},\ $${\delta _y}{u_{i,j + \frac{1}{2}}} = \frac{{\left( {{u_{i,j + 1}} - {u_{i,j}}} \right)}}{h}.$离散拉普拉斯算子和离散梯度向量定义如下

${\Delta _h}{u_{i,j}} = \delta _x^2{u_{i,j}} + \delta _y^2{u_{i,j}},{\nabla _h}{u_{i,j}} = {\left( {{\delta _x}{u_{i - \frac{1}{2},j}},{\delta _y}{u_{i,j - \frac{1}{2}}}} \right)^T}.\ $

3.2 BDF2 型有限元格式

首先我们构造方程 (1.1)-(1.2) 的弱形式如下: 找到 $ v,u \in H_0^1\left( \Omega \right),\ $ 对于任意 $ t \in \left( {0,T} \right],\ $ 满足

(3.4)$\begin{align*} \left\{ \begin{array}{rl} \left( {_0^CD_t^\alpha u,w} \right) + \left( {\nabla v,\nabla w} \right)& = \left( {f,w} \right),\ \\ \left( {u,w} \right) & = \left( {{v_t},w} \right),x \in \Omega,\forall w \in H_0^1\left( \Omega \right),\ \\ v\left( {x,0} \right) & = {g_1}\left( x \right),u\left( {x,0} \right) = {g_2}\left( x \right),x \in \overline \Omega.\ \end{array} \right. \end{align*}$

在 $ \left( {{x_h},{t_{n - \frac{1}{2}}}} \right) $ 点处 BDF2 有限元全离散格式由方程 (3.4) 定义如下: 找到 ${v_h} \in {V_h},{u_h} \in {U_h},$ 对于任意 $ t \in \left( {0,T} \right],\ $ 满足

(3.5)$\begin{align*} \left\{ \begin{array}{rl} \left( {D_\gamma ^\alpha u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)& = \left( {{\Delta _h}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {f_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {R_h^n,w_h^{n - \frac{1}{2}}} \right),\ \\ \left( {u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) & = \left( {{\delta _t}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {r_h^n,w_h^{n - \frac{1}{2}}} \right),{x_h} \in {\Omega _h},\forall {w_h} \in {U_h},\ \\ v_h^0 & = {g_1}\left( {{x_h}} \right),u_h^0 = {g_2}\left( {{x_h}} \right),{x_h} \in {\overline \Omega _h}.\ \end{array} \right. \end{align*}$

其中 $ 1 \le n \le N $, $R_h^n = \xi _h^n + \eta _h^n $, $\xi _h^n$ 表示时间方向上的截断误差, $\eta _h^n$ 表示空间方向上的截断误差. 具体估计式如下

(3.6)$\begin{align*} \left| {r_h^n} \right| \le {c_0}\tau _n^2,\left| {\eta _h^n} \right| \le {c_0}{h^2},{x_h} \in {\Omega _h}.\ \end{align*}$

其中 ${c_0}$ 是一个常数. 忽略截断误差, 我们构造 BDF2 有限元格式如下

(3.7)$\begin{align*} \left\{ \begin{array}{rl} \left( {D_\gamma ^\alpha u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) & = \left( {{\Delta _h}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {f_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right),\ \\ \left( {u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) & = \left( {{\delta _t}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right),{x_h} \in {\Omega _h},\forall {w_h} \in {U_h},\ \\ v_h^0 & = {g_1}\left( {{x_h}} \right),u_h^0 = {g_2}\left( {{x_h}} \right),{x_h} \in {\overline \Omega _h}.\ \end{array} \right. \end{align*}$

其中 $ 1 \le n \le N,$ 以下是关于非均匀网格上所提出的 BDF2 有限元格式的时间收敛阶定理.

定理3.1 BDF2 有限元格式 (3.7) 在非均匀网格上的时间收敛阶为 $O\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}} \right),$ 误差范数表达式如下

$\left\| {\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} } \right\| \le {c_u}{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}. $

特别是如果B2成立, 我们可以得到

$\left\| {\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} } \right\| \le {C_\Lambda }{N^{ - \min \left\{ {\gamma \mu,2} \right\}}}.\ $

其中 $ {c_u}$ 和 ${C_\Lambda }$ 是正常数, ${\xi ^j} = \sum _{j = 1}^n {{}_0^CD_t^\alpha v\left( {{t_{j - \frac{1}{2}}}} \right) - \sum _{j = 1}^n {D_\tau ^\alpha {v^{j - \frac{1}{2}}}} }$ 表示时间误差余项.

证我们考虑基于推论 2.1 的均匀网格 $\tau = \frac{T}{N}$ 可以得出

$\begin{aligned} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} \ & \le {c_u}\left( {{\tau ^\mu } + \frac{1}{{1 - \alpha }}{\tau ^{\min \left\{ {\mu,3 - \alpha } \right\}}}\mathop {\max } _{2 \le k \le n} t_{_{k - \frac{3}{2}}}^{\alpha + \mu - 3}{\tau ^{3 - \alpha - \min \left\{ {\mu,3 - \alpha } \right\}}}} \right)\ \\ & = {c_u}\left( {{\tau ^\mu } + \frac{1}{{1 - \alpha }}{\tau ^{\min \left\{ {\mu,3 - \alpha } \right\}}}\mathop {\max } _{2 \le k \le n} {{\left( {k - \frac{3}{2}} \right)}^{\alpha + \mu - 3}}{\tau ^{\mu - \min \left\{ {\mu,3 - \alpha } \right\}}}} \right)\ \\ & \le {c_u}\left( {{\tau ^\mu } + \frac{1}{{1 - \alpha }}\mathop {\max } _{2 \le k \le n} t_{_{k - \frac{3}{2}}}^{\mu - \min \left\{ {\mu,3 - \alpha } \right\}}{\tau ^{\min \left\{ {\mu,3 - \alpha } \right\}}}} \right).\ \end{aligned}$

从上述方程中得出, 在 $\mu \le 3 - \alpha$ 时有限元法 (3.7) 的时间收敛阶随着正则化参数 $\mu$ 的增加而增加. 当 $\mu \in \left[ {3 - \alpha,3} \right),$ 时间收敛阶是 $O\left( {{\tau ^{3 - \alpha }}} \right).$

我们现在将考虑等级网格 ${t_k} = T{\left( {\frac{k}{N}} \right)^\gamma },\gamma > 1$ 的情况

${\left( {{t_{\frac{3}{2}}} - {t_{\frac{1}{2}}}} \right)^\alpha }t_{\frac{1}{2}}^{\mu - 3}\tau _{\frac{3}{2}}^{3 - \alpha } \le {\left( {T{{\left( {\frac{2}{N}} \right)}^\gamma }} \right)^3}{\left( {T{{\left( {\frac{1}{{2N}}} \right)}^\gamma }} \right)^{\left( {\mu - 3} \right)}} = {2^{6\gamma - \mu \gamma }}{T^\mu }{N^{ - \mu \gamma }}. $

不难由 ${\tau _k} \le T{N^{ - \gamma }}\gamma {k^{\gamma - 1}}$ 得出并且当 $ k \le 3\left( {k - 2} \right),$ 可以获得以下方程

$\begin{aligned} \begin{array}{l} { \left( {{t_{k - \frac{1}{2}}} - {t_{\frac{1}{2}}}} \right)^\alpha }t_{k - \frac{3}{2}}^{\mu - 3}\tau _{k - \frac{1}{2}}^{3 - \alpha }\\ \le {T^\alpha }{\left( {\frac{k}{N}} \right)^{\alpha \gamma }}{T^{\left( {\mu - 3} \right)}}{\left( {\frac{{k - 2}}{N}} \right)^{\gamma \left( {\mu - 3} \right)}}{\left( {\gamma {k^{\gamma - 1}}T{N^{ - \gamma }}} \right)^{3 - \alpha }}\\ \le {T^\mu }{k^{\alpha + 3\left( {\gamma - 1} \right)}}{\left( {k - 2} \right)^{\gamma \left( {\mu - 3} \right)}}{\gamma ^{3 - \alpha }}{N^{ - \gamma \mu }} \le {T^\mu }{3^{\alpha + 3\left( {\gamma - 1} \right)}}{\left( {k - 2} \right)^{\gamma \mu + \alpha - 3}}{\gamma ^{3 - \alpha }}{N^{ - \gamma \mu }}\\ \le {T^\mu }{3^{\alpha + 3\left( {\gamma - 1} \right)}}{\left( {k - 2} \right)^{\min \left\{ {\gamma \mu,3 - \alpha } \right\} - \left( {3 - \alpha } \right)}}{\left( {\frac{{k - 2}}{N}} \right)^{\gamma \mu - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}{\gamma ^{3 - \alpha }}{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}\\ \le {T^{\min \left\{ {\mu,\frac{{3 - \alpha }}{\gamma }} \right\}}}{3^{\alpha + 3\left( {\gamma - 1} \right)}}t_{k - 2}^{\mu - \min \left\{ {\mu,\frac{{3 - \alpha }}{\gamma }} \right\}}{\gamma ^{3 - \alpha }}{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}\\ \le {T^\mu }{3^{\alpha + 3\left( {\gamma - 1} \right)}}{\gamma ^{3 - \alpha }}{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}},k \ge 3. \end{array}\ \end{aligned}$

基于上述不等式可以得出结论

(3.8)$\begin{align*} \sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right| \le {c_u}} {N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}}.\ \end{align*}$

网格假设条件 B2 意味着 ${\tau _1} \le {C_\gamma }{\tau ^\gamma },$ 并且获得以下方程

(3.9)$\begin{aligned}\left(t_{j-\frac{1}{2}}-t_{\frac{1}{2}}\right)^\alpha t_{j-\frac{3}{2}}^{\mu-3} \tau_{j-\frac{1}{2}}^{3-\alpha} & \leq t_{j-\frac{1}{2}}^{\alpha+\mu-3} \tau_{j-\frac{1}{2}}^{3-\alpha-\min \{\gamma \mu, 2\}}\left(C_\gamma \tau \min \left\{1, t_{j-\frac{1}{2}}^{1-1 / \gamma}\right\}\right)^{\min \{\gamma \mu, 2\}} \\& \leq\left(C_\gamma\right)^{\min \{\gamma \mu, 2\}} t_{j-\frac{1}{2}}^{\mu-\min \{\gamma \mu, 2\} / \gamma} \tau^{\min \{\gamma \mu, 2\}}.\end{aligned}$

根据 (3.9) 式和推论 2.1, 如果我们 ${t_n} \le T,$ 得到

(3.10)$\begin{align*} \left\| {\sum _{j = 1}^n {D_{n - j}^{\left( n \right)}\left| {{\xi ^j}} \right|} } \right\| \le {C_\Lambda }{N^{ - \min \left\{ {\gamma \mu,2} \right\}}}.\ \end{align*}$

4 BDF2 型有限元格式的稳定性和收敛性分析

本节利用离散卷积核 $D_{n - k}^{\left( n \right)}$ 的相关性质证明了非均匀有限元 BDF2 格式在 ${L^2}$-范数和 ${H^1}$-范数下的收敛性和稳定性, 并为稳定性分析和误差分析提供了定理. 首先, 我们证明了所提出的有限元格式 (3.7) 的稳定性.

4.1 有限元格式在 ${L}^2$-范数下的稳定性

下面，我们证明了所提出的有限元公式 (3.7) 在 ${L^2}$-范数下的稳定性定理.

定理4.1 所提出的 BDF2 型有限元公式 (3.7)依赖于初始值和右端项的无条件稳定性. 我们可以得到 $L^2$-范数下的稳定性估计

(4.1)$\begin{align*} \left\| {{v^n}} \right\| \le \sqrt {{{\left\| {{g_1}} \right\|}^2} + {{\left( {\sum _{k = 1}^n {{\tau _k}\left\| {\sum\limits_{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|} } \right)}^2}} + \sum _{k = 1}^n {{\tau _k}\left\| {\sum\limits_{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|}.\ \end{align*}$

证相应的非齐次有限元方程 (3.7)的解如下

(4.2)$\begin{align*} \left\{ \begin{array}{rlr} \left( {\sum _{k = 1}^n {d_{n - k}^{\left( n \right)}{\nabla _\tau }u_h^{k - \frac{1}{2}}},w_h^{n - \frac{1}{2}}} \right) & = \left( {{\Delta _h}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {f_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right), \\ \left( {u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)& = \left( {{\delta _t}v_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right),{x_h} \in {\Omega _h},\forall {w_h} \in {U_h}, \\ v_h^0 & = {g_1},u_h^0 = {g_2},{x_h} \in {\overline \Omega _h}.\ \end{array} \right. \end{align*}$

其中 $ 1 \le n \le N,\ $ 将 (4.2) 式中的第一个方程的两端同乘以 $D_{n - k}^{\left( n \right)},$ 并从 1 到 $n$ 求和

(4.3)$\begin{align*} & \,\left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}\sum _{j = 1}^n {d_{k - j}^{\left( k \right)}{\nabla _\tau }} } u_h^{j - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\\ &= \left( {\sum\limits_{k = 1}^n {D_{n - k}^{\left( n \right)}} {\Delta _h}v_h^{k - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} f_h^{k - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right).\ \end{align*}$

交换方程 (4.3) 的积分顺序并代入 (2.9) 式得到

(4.4)$\begin{align*} \begin{array}{l} \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}\sum\limits_{j = 1}^n {d_{k - j}^{\left( k \right)}{\nabla _\tau }} } u_h^{j - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\sum _{j = 1}^n {{\nabla _\tau }} u_h^{j - \frac{1}{2}}\sum _{k = j}^n {D_{n - k}^{\left( n \right)}d_{k - j}^{\left( k \right)}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {{\nabla _\tau }u_h^{\frac{1}{2}}{\rm{ + }}{\nabla _\tau }u_h^{\frac{3}{2}}{\rm{ + }} \cdots {\rm{ + }}{\nabla _\tau }u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\frac{1}{2}\left( {u_h^1 - u_h^0} \right){\rm{ + }}\left( {u_h^{\frac{3}{2}} - u_h^{\frac{1}{2}}} \right){\rm{ + }}\left( {u_h^{\frac{5}{2}} - u_h^{\frac{3}{2}}} \right){\rm{ + }} \cdots {\rm{ + }}\left( {u_h^{n - \frac{1}{2}} - u_h^{n - \frac{3}{2}}} \right),w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\frac{1}{2}\left( {u_h^1 - u_h^0} \right){\rm{ + }}\left( {u_h^{n - \frac{1}{2}} - \frac{1}{2}\left( {u_h^1 + u_h^0} \right)} \right),w_h^{n - \frac{1}{2}}} \right)\\ = \left( {u_h^{n - \frac{1}{2}} - u_h^0,w_h^{n - \frac{1}{2}}} \right) = \left( {u_h^{n - \frac{1}{2}} - {g_2},w_h^{n - \frac{1}{2}}} \right). \end{array}\ \end{align*}$

简化上述方程式得

(4.5)$\begin{align*} \left( {u_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) = \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}{\Delta _h}v_h^{k - \frac{1}{2}},w_h^{n - \frac{1}{2}}} } \right) + \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}f_h^{k - \frac{1}{2}} + {g_2},w_h^{n - \frac{1}{2}}} } \right). \end{align*}$

在 (4.5) 和 (4.2) 式中的第二个方程中取 ${w^{n - \frac{1}{2}}} = {v^{n - \frac{1}{2}}}$ 我们有

(4.6)$\begin{align*} \left\{ \begin{array}{rl} \left( {{u^{n - \frac{1}{2}}},{v^{n - \frac{1}{2}}}} \right)& = \sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} \left( {{\Delta _h}{v^{k - \frac{1}{2}}},{v^{n - \frac{1}{2}}}} \right) + \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} {f^{k - \frac{1}{2}}} + {g_2},{v^{n - \frac{1}{2}}}} \right),\ \\ \left( {{\delta _t}{v^{n - \frac{1}{2}}},{v^{n - \frac{1}{2}}}} \right) & = \left( {{u^{n - \frac{1}{2}}},{v^{n - \frac{1}{2}}}} \right).\ \end{array} \right. \end{align*}$

根据 ${\delta _t}$ 的定义和方程 $(4.6)$ 两端 $k$ 从 1 到 $n$ 的求和, 我们能得到

(4.7)$\begin{align*} & \sum _{k = 1}^n {\left( {{\nabla _\tau }{v^k},{v^{k - \frac{1}{2}}}} \right)}\\ & = \sum _{k = 1}^n {{\tau _k}\sum\limits_{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\Delta _h}{v^{l - \frac{1}{2}}},{v^{k - \frac{1}{2}}}} \right) + } \sum\limits_{k = 1}^n {{\tau _k}\left( {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2},{v^{k - \frac{1}{2}}}} \right)}. \end{align*}$

根据算子的定义, 我们能得到

(4.8)$\begin{align*} \sum _{k = 1}^n {\left( {{\nabla _\tau }{v^k},{v^{k - \frac{1}{2}}}} \right)} \ &= \sum _{k = 1}^n {\left( {{v^k} - {v^{k - 1}},\frac{1}{2}\left( {{v^k} + {v^{k - 1}}} \right)} \right)} \\ &= \frac{1}{2}\sum _{k = 1}^n {\left( {{{\left\| {{v^k}} \right\|}^2} - {{\left\| {{v^{k - 1}}} \right\|}^2}} \right)} \\ &= \frac{1}{2}\left( {{{\left\| {{v^n}} \right\|}^2} - {{\left\| {{v^0}} \right\|}^2}} \right) = \frac{1}{2}\left( {{{\left\| {{v^n}} \right\|}^2} - {{\left\| {{g_1}} \right\|}^2}} \right).\ \end{align*}$

从引理 2.3 可以得出离散卷积核 $D_{k - l}^{\left( k \right)}$ 具有正定性的结论, 我们得到

(4.9)$\begin{align*} \sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\Delta _h}{v^{l - \frac{1}{2}}},{v^{k - \frac{1}{2}}}} \right)} = - \sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\nabla _h}{v^{l - \frac{1}{2}}},{\nabla _h}{v^{k - \frac{1}{2}}}} \right)} \le 0. \end{align*}$

将 (4.8) 和 (4.9) 式代入方程式 (4.7) 得到

(4.10)$\begin{align*} {\left\| {{v^n}} \right\|^2} \le {\left\| {{g_1}} \right\|^2} + 2\sum _{k = 1}^n {{\tau _k}\left\| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|.\left\| {{v^{k - \frac{1}{2}}}} \right\|}. \end{align*}$

选择一些整数 ${n_0}\left( {0 \le {n_0} \le n} \right)$ 满足 $\left\| {{v^{{n_0}}}} \right\| = \mathop {\max }\limits_{0 \le k \le n} \left\| {{v^k}} \right\|,$ 在 (4.10) 式中取 $n = {n_0}$, 我们有

(4.11)$\begin{align*} {\left\| {{v^{{n_0}}}} \right\|^2} \le {\left\| {{g_1}} \right\|^2} + 2\sum _{k = 1}^n {{\tau _k}\left\| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|.\left\| {{v^{{n_0}}}} \right\|}. \end{align*}$

因此

(4.12)$\begin{align*} \left\| {{v^n}} \right\| \le \left\| {{v^{{n_0}}}} \right\| \le \sqrt {{{\left\| {{g_1}} \right\|}^2} + {{\left( {\sum _{k = 1}^n {{\tau _k}\left\| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|} } \right)}^2}} + \sum _{k = 1}^n {{\tau _k}\left\| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right\|}. \end{align*}$

4.2 有限元格式在${H^1}$-范数下的稳定性

下面，我们证明了所提出的有限元公式 (3.7) 在 ${H^1}$-范数下的稳定性定理.

定理4.2 所提出的 BDF2 型有限元公式 (3.7) 依赖于初始值和右端项的无条件稳定性. 我们可以得到 ${H^1}$-范数下的稳定性估计

(4.13)$\begin{align*} {\left| {{v^n}} \right|_1} \le \sqrt {\left| {{g_1}} \right|_1^2 + {{\left( {\sum _{k = 1}^n {{\tau _k}{{\left| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right|}_1}} } \right)}^2}} + \sum _{k = 1}^n {{\tau _k}{{\left| {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} {f^{l - \frac{1}{2}}} + {g_2}} \right|}_1}}.\ \end{align*}$

证证明过程类似于定理 4.1, 在 (4.5) 式中取 ${w^{n - \frac{1}{2}}} = - {\Delta _h}{v^{n - \frac{1}{2}}},$ 可得到定理 4.2 的结果.

4.3 有限元格式在 ${L^2}$-范数下的收敛性

下面, 我们证明了所提出的有限元公式 (3.7) 在 ${L^2}$-范数下的收敛性. 定义

$ e_h^n = V_h^n - v_h^n,\rho _h^n = U_h^n - u_h^n,{x_h} \in {\Omega _h},1 \le n \le N,\ $

考虑方程 (3.7) 中的误差项, 误差方程如下

(4.14)$\begin{align*} \left\{ \begin{array}{rl} \left( {D_\gamma ^\alpha \rho _h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)& = \left( {{\Delta _h}e_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {R_h^n,w_h^{n - \frac{1}{2}}} \right),\ \\ \left( {\rho _h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)& = \left( {{\delta _t}e_h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) + \left( {r_h^n,w_h^{n - \frac{1}{2}}} \right),{x_h} \in {\Omega _h},\forall {w_h} \in H_0^1\left( \Omega \right),\ \\ e_h^0& = 0,\rho _h^0 = 0,{x_h} \in {\overline \Omega _h}.\ \end{array} \right. \end{align*}$

定理4.3 所提出的 BDF2 型有限元公式 (3.7) 在 $L^2$-范数下是收敛的. 误差估计如下

$\left\| {{{\rm e}^n}} \right\| \le {c_v}\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}{h^2} + {t_n}\tau _n^2} \right).\ $

特别是如果 B2 成立, 我们得到

$\left\| {{{\rm e}^n}} \right\| \le {c_v}\left( {{N^{ - \min \left\{ {\gamma \mu,2} \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}{h^2} + {t_n}\tau _n^2} \right).\ $

证其中 $ 1 \le n \le N.$ 将 (4.14) 式中的第一个方程的两端同乘以 $D_{n - k}^{\left( n \right)},$ 并从 1 到 $n$ 求和

(4.15)$\begin{align*} \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}\sum _{j = 1}^n {d_{k - j}^{\left( k \right)}{\nabla _\tau }} } \rho _h^{j - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\! =\! \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} {\Delta _h}e_h^{k - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) \!+\! \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} R_h^k,w_h^{n - \frac{1}{2}}} \right).\ \end{align*}$

交换方程 (4.15) 的积分顺序并代入 (2.9) 式得到

(4.16)$\begin{align*} \begin{array}{l} \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}\sum _{j = 1}^n {d_{k - j}^{\left( k \right)}{\nabla _\tau }} } \rho _h^{j - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\sum _{j = 1}^n {{\nabla _\tau }} \rho _h^{j - \frac{1}{2}}\sum\limits_{k = j}^n {D_{n - k}^{\left( n \right)}d_{k - j}^{\left( k \right)}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {{\nabla _\tau }\rho _h^{\frac{1}{2}}{\rm{ + }}{\nabla _\tau }\rho _h^{\frac{3}{2}}{\rm{ + }} \cdots {\rm{ + }}{\nabla _\tau }\rho _h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\frac{1}{2}\left( {\rho _h^1 - \rho _h^0} \right){\rm{ + }}\left( {\rho _h^{\frac{3}{2}} - \rho _h^{\frac{1}{2}}} \right){\rm{ + }}\left( {\rho _h^{\frac{5}{2}} - \rho _h^{\frac{3}{2}}} \right){\rm{ + }} \cdots {\rm{ + }}\left( {\rho _h^{n - \frac{1}{2}} - \rho _h^{n - \frac{3}{2}}} \right),w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\frac{1}{2}\left( {\rho _h^1 - \rho _h^0} \right){\rm{ + }}\left( {\rho _h^{n - \frac{1}{2}} - \frac{1}{2}\left( {\rho _h^1 + \rho _h^0} \right)} \right),w_h^{n - \frac{1}{2}}} \right)\\ = \left( {\rho _h^{n - \frac{1}{2}} - \rho _h^0,w_h^{n - \frac{1}{2}}} \right) = \left( {\rho _h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right). \end{array}\ \end{align*}$

简化上述方程式得

(4.17)$\begin{align*} \left( {\rho _h^{n - \frac{1}{2}},w_h^{n - \frac{1}{2}}} \right) = \left( {\sum _{k = 1}^n {D_{n - k}^{\left( n \right)}{\Delta _h}e_h^{k - \frac{1}{2}} + \sum _{k = 1}^n {D_{n - k}^{\left( n \right)}R_h^k},w_h^{n - \frac{1}{2}}} } \right).\ \end{align*}$

在 $(4.14)$ 和 $(4.17)$ 式中的第二个方程中取 ${w^{n - \frac{1}{2}}} = {{\rm e}^{n - \frac{1}{2}}}$, 我们有

(4.18)$\begin{align*} \left\{ \begin{array}{rl} \left( {{\rho ^{n - \frac{1}{2}}},{{\rm e}^{n - \frac{1}{2}}}} \right) & = \sum _{k = 1}^n {D_{n - k}^{\left( n \right)}} \left( {{\Delta _h}{{\rm e}^{k - \frac{1}{2}}},{{\rm e}^{n - \frac{1}{2}}}} \right) + \sum _{k = 1}^n {D_{n - k}^{\left( n \right)}\left( {{R^k},{{\rm e}^{n - \frac{1}{2}}}} \right)},\ \\ \left( {{\rho ^{n - \frac{1}{2}}},{{\rm e}^{n - \frac{1}{2}}}} \right)& = \left( {{\delta _t}{{\rm e}^{n - \frac{1}{2}}},{{\rm e}^{n - \frac{1}{2}}}} \right) + \left( {{r^n},{{\rm e}^{n - \frac{1}{2}}}} \right).\ \end{array} \right. \end{align*}$

根据 ${\delta _t}$ 的定义和对方程 (4.18) 两端 $k$ 从 1 到 $n$ 的求和, 我们能得到

(4.19)$\begin{align*} \sum _{k = 1}^n {\left( {{\nabla _\tau }{{\rm e}^k},{{\rm e}^{k - \frac{1}{2}}}} \right)} \ &= \sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\Delta _h}{{\rm e}^{l - \frac{1}{2}}},{{\rm e}^{k - \frac{1}{2}}}} \right)} + \sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{R^l},{{\rm e}^{k - \frac{1}{2}}}} \right)} \\ & - \sum _{k = 1}^n {{\tau _k}\left( {{r^k},{{\rm e}^{k - \frac{1}{2}}}} \right)}.\ \end{align*}$

根据算子的定义, 我们能得到

(4.20)$\begin{aligned} \sum _{k = 1}^n {\left( {{\nabla _\tau }{{\rm e}^k},{{\rm e}^{k - \frac{1}{2}}}} \right)} \ & =\sum _{k = 1}^n {\left( {{{\rm e}^k} - {{\rm e}^{k - 1}},\frac{1}{2}\left( {{{\rm e}^k} + {{\rm e}^{k - 1}}} \right)} \right)} \ \\ & =\frac{1}{2}\sum _{k = 1}^n {\left( {{{\left\| {{{\rm e}^k}} \right\|}^2} - {{\left\| {{{\rm e}^{k - 1}}} \right\|}^2}} \right)} \ \\ & = \frac{1}{2}\left( {{{\left\| {{{\rm e}^n}} \right\|}^2} - {{\left\| {{e^0}} \right\|}^2}} \right) = \frac{1}{2}{\left\| {{{\rm e}^n}} \right\|^2}.\ \end{aligned}$

从引理 2.3 可以得出离散卷积核 $D_{n - k}^{\left( n \right)}$ 具有正定性的结论, 我们得到

(4.21)$\sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\Delta _h}{{\rm e}^{l - \frac{1}{2}}},{{\rm e}^{k - \frac{1}{2}}}} \right)} = - \sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {{\nabla _h}{{\rm e}^{l - \frac{1}{2}}},{\nabla _h}{{\rm e}^{k - \frac{1}{2}}}} \right)} \le 0. $

将 (4.20) 和 (4.21) 式代入方程式 (4.19) 得到

(4.22)$\left\|\mathrm{e}^n\right\|^2 \leq 2 \sum_{k=1}^n \tau_k \sum_{l=1}^k D_{k-l}^{(k)}\left\|R^l\right\| \cdot\left\|\mathrm{e}^{k-\frac{1}{2}}\right\|+2 \sum_{k=1}^n \tau_k\left\|r^k\right\| \cdot\left\|\mathrm{e}^{k-\frac{1}{2}}\right\|.$

选择一些整数 ${n_0}\left( {0 \le {n_0} \le n} \right)$ 满足 $ \left\| {{{\rm e}^{{n_0}}}} \right\| = \mathop {\max } _{0 \le k \le n} \left\| {{{\rm e}^k}} \right\|\ $, 在 (4.22) 式中取 $n = {n_0},$ 我们有

(4.23)${\left\| {{{\rm e}^{{n_0}}}} \right\|^2} \le 2\sum _{k = 1}^n {{\tau _k}\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left\| {{R^l}} \right\|.\left\| {{{\rm e}^{{n_0}}}} \right\|} + 2\sum _{k = 1}^n {{\tau _k}\left\| {{r^k}} \right\|.\left\| {{{\rm e}^{{n_0}}}} \right\|}.$

基于引理 2.3 和引理 2.5, 综合方程 (3.6) 和 (3.1) 可得

(4.24)$\begin{aligned} \left\| {{{\rm e}^n}} \right\|\ & \le \left\| {{{\rm e}^{{n_0}}}} \right\| \le 2\sum _{k = 1}^n {{\tau _k}\left( {\sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left\| {{R^l}} \right\|} \right)} + 2\sum _{k = 1}^n {{\tau _k}\left\| {{r^k}} \right\|} \ \\ & \le 2{c_0}{t_n}\tau _n^2 + 2{t_n}\mathop {\max } _{1 \le k \le n} \sum _{l = 1}^k {D_{k - l}^{\left( k \right)}} \left( {\left\| {{\xi ^l}} \right\| + \left\| {{\eta ^l}} \right\|} \right)\ \\ & \le {c_u}\left( {\mathop {\max } _{1 \le k \le n} \sum _{j = 1}^k {D_{k - j}^{\left( k \right)}} d_0^{\left( j \right)}\int _{{t_{j - \frac{3}{2}}}}^{{t_{j - \frac{1}{2}}}} {\left( {2\left( {t - {t_{j - \frac{3}{2}}}} \right) - \frac{{2\left( {t - {t_{j - 1}}} \right)\left( {{t_{j - \frac{1}{2}}} - t} \right)}}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right.} } \right.\ \\ & + \left. {\left. {\frac{{2\left( {t - {t_{j - 1}}} \right)\left( {t - {t_{j - \frac{3}{2}}}} \right)}}{{{\tau _{j + \frac{1}{2}}}\left( {{\tau _{j - \frac{1}{2}}} + {\tau _{j + \frac{1}{2}}}} \right)}}} \right)\left| {\ddot u\left( t \right)} \right|{\rm d}t + t_{n - \frac{1}{2}}^{\beta - 1}{h^2} + {t_n}\tau _n^2} \right)\ \\ & \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}{h^2} + {t_n}\tau _n^2} \right).\ \end{aligned}$

其中, ${c_u}$ 是一个独立常数. 如果 B2 成立, 我们将得到,

$\left\| {{{\rm e}^n}} \right\| \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,2} \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}{h^2} + {t_n}\tau _n^2} \right).\ $

4.4 有限元格式在 ${H^1}$-范数下的收敛性

最后, 我们证明了所提出的有限元公式 (3.7) 在 ${H^1}$-范数下的收敛性.

定理4.4 所提出的 BDF2 型有限元公式 (3.7) 在 $H^1$-范数下是收敛的. 误差估计如下

${\left\| {{{\rm e}^n}} \right\|_1} \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}h + {t_n}\tau _n^2} \right).\ $

特别是如果 B2 成立, 我们得到,

${\left\| {{{\rm e}^n}} \right\|_1} \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,2} \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}h + {t_n}\tau _n^2} \right).\ $

证时间误差由定理 4.3 得到, 空间误差由逆不等式得到,

(4.31)${\left| {{{\rm e}^n}} \right|_1} \le C{h^{ - 1}}\left\| {{{\rm e}^n}} \right\| \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}h + {t_n}\tau _n^2} \right). $

由 Poincare' 不等式,

${\left\| {{{\rm e}^n}} \right\|_1} \le C{\left| {{{\rm e}^n}} \right|_1} \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,3 - \alpha } \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}h + {t_n}\tau _n^2} \right).\ $

如果 (B2)成立, 我们将得到,

${\left\| {{{\rm e}^n}} \right\|_1} \le {\left| {{{\rm e}^n}} \right|_1} \le C{h^{ - 1}}\left\| {{{\rm e}^n}} \right\| \le {c_u}\left( {{N^{ - \min \left\{ {\gamma \mu,2} \right\}}} + t_{n - \frac{1}{2}}^{\beta - 1}h + {t_n}\tau _n^2} \right).\ $

5 数值实验

在本节中, 我们使用分数阶扩散—波动方程的数值算例来验证所提出的 BDF2 型有限元格式在非均匀网格上的收敛性. 分别在 $L^2$-范数和 $H^1$-半范数下计算了该方法的收敛阶和误差.

例 5.1 考虑以下的分数阶方程

$_0^CD_t^\beta v - \Delta v = f,{x_h} \in {\left( {0,1} \right)^2},t \in \left[ {0,1} \right],\ $

方程的源项为

$f\left( {x,t} \right) = (\frac{{\Gamma \left( 3 \right)}}{{\Gamma \left( {4 - \beta } \right)}}{t^{3 - \beta }} + 2{\pi ^2}{t^2})\sin \pi x\sin \pi y,\ $

方程的解析解为

$v\left( {x,t} \right) = {t^2}\sin \pi x\sin \pi y.\ $

定义

${e_1}\left( N \right) = \left\| {{V^N} - {v^N}} \right\|,{e_2}\left( N \right) = {\left| {{V^N} - {v^N}} \right|_1},\ $

作为 $L^2$-范数和 $H^1$-半范数.

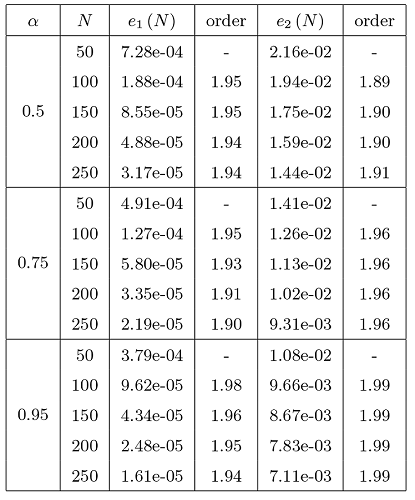
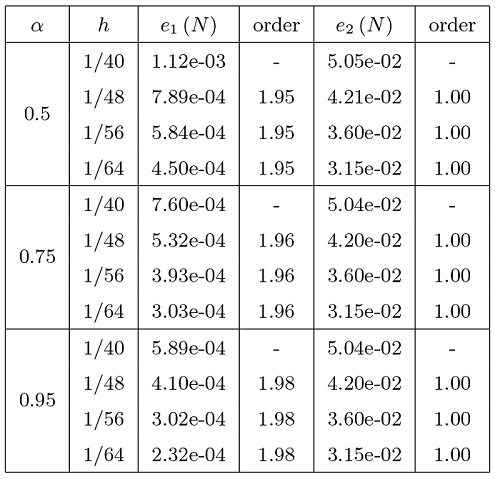
例 5.1 是线性时间分数阶扩散—波动方程的时间收敛阶和空间收敛阶的结果. 我们取等级网格${t_n} = T(n /N)^{2 / \mu }$. 在时间方向上选择 $50,100,150,200,250$ 个节点, 空间方向上选择 $40,48,56,64$ 个节点. 其中, $\mu = \beta-1,$表1 和表2 分别展示了有限元格式 (3.7) 在时间方向和空间方向上的 $L^2$-范数和 $H^1$-半范数误差和收敛阶数. 我们注意到表1 在不同参数$\gamma$下, 时间分数阶的 $L^2$-范数和 $H^1$-半范数收敛结果均为 2 阶. 表2 中有限元格式 (3.7) 在空间上分别为 2 阶和 1 阶收敛, 这与我们的理论结果相一致.

表1 有限元格式的 $L^2$-范数和 $H^1$-半范数在时间方向上误差.

新窗口打开| 下载CSV

表2 有限元格式的 $L^2$-范数和 $H^1$-半范数在空间方向上误差.

新窗口打开| 下载CSV

例 5.2 考虑以下的分数阶方程

$_0^CD_t^\beta v - \Delta v = f,{x_h} \in {\left( {0,1} \right)^2},t \in \left[ {0,1} \right],\ $

方程的源项为

$f\left( {x,t} \right) = (\Gamma \left( \beta \right) + 2{\pi ^2}{t^{\beta - 1}})\sin \pi x\sin \pi y,\ $

方程的解析解为

$v\left( {x,t} \right) = {t^{\beta - 1}}\sin \pi x\sin \pi y.\ $

定义

${e_1}\left( N \right) = \left\| {{V^N} - {v^N}} \right\|,{e_2}\left( N \right) = {\left| {{V^N} - {v^N}} \right|_1},\ $

作为 $L^2$-范数和 $H^1$-半范数.

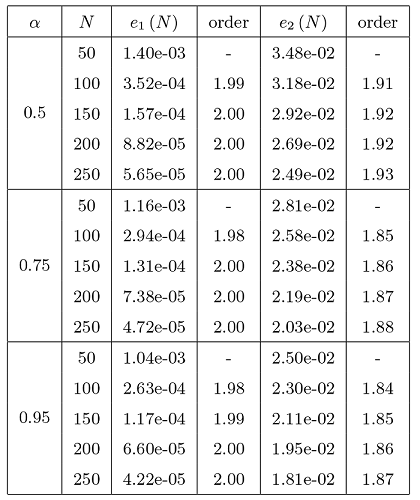
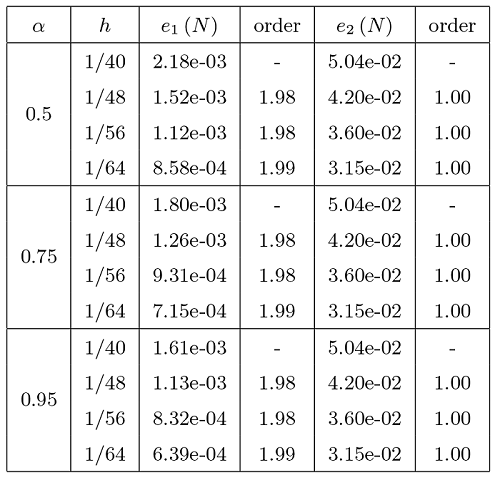
例 5.2 是线性时间分数阶扩散—波动方程的时间收敛阶和空间收敛阶的结果. 与例 5.1 相比, 该分数阶方程具有更强的初值奇异性. 我们取等级网格${t_n} = T(n /N)^{2 / \mu }$. 在时间方向上选择 $50,100,150,200,250$ 个节点, 空间方向上选择 $40,48,56,64$ 个节点. 其中, $ \mu = \beta-1,$表3 和表4 分别展示了有限元格式 (3.7) 在时间方向和空间方向上的$L^2$-范数和 $H^1$-半范数误差和收敛阶数. 我们注意到表3 在不同参数 $\gamma$ 下, 时间分数阶的 $L^2$-范数和 $H^1$-半范数收敛结果均为 2 阶. 表4 中有限元格式 (3.7) 在空间上分别为 2 阶和 1 阶收敛, 这与我们的理论结果相一致.

表3 有限元格式的 $L^2$-范数和 $H^1$-半范数在时间方向上误差.

新窗口打开| 下载CSV

表4 有限元格式的 $L^2$-范数和 $H^1$-半范数在空间方向上误差.

新窗口打开| 下载CSV

6 结论

基于 Caputo 导数初值 $t = 0$ 附近的弱奇异性问题, 本文研究了具有 $\beta,\left( {1 < \beta < 2} \right)$ 阶 Caputo 分数阶导数的分数阶扩散-波动方程. 首先, 在非均匀时间半网格上建立了具有离散系数核的 BDF2 公式, 并引入了离散系数核和离散卷积核的相关引理. 该工具简化了算法的理论分析过程, 具有高效性和创新性. 通过使用具有积分型余项的插值误差, 分析了误差卷积结构, 并构建了具有离散卷积核的时间全局误差.

由于有限元方法是一种构建空间网格的有效数值方法, 具有丰富的理论分析结果, 因此使用此方法进行空间离散化是适当的. 我们将降阶方法与具有离散系数核的 BDF2 公式相结合, 构建了一个全离散的 BDF2 型有限元格式, 并使用离散卷积核分析了该格式在 $L^2$-范数和 $H^1$-范数下的稳定性和收敛性.

在数值例子中, 我们使用等级网格进行验证, 并使用具有各种分级参数 $\gamma$ 的扩散-波动方程进行实验. 实验结果表明, 在 $L^2$-范数和 $H^1$-范数下, 所提出的有限元格式的时间收敛阶为 $\min \left\{ {\gamma \mu,2} \right\}$ 阶, 空间收敛阶为 2 阶和 1 阶. 一方面, 这与理论分析结果一致. 另一方面, 获得的时间收敛阶数不取决于正则化参数 $\mu$ 的选择. 在未来的研究中, 我们将探索求解非均匀网格上分布阶分数阶方程的高阶数值方法. 这将包括二阶 BDF2 格式和 L2-${1_\sigma}$ 格式, 以进一步研究稳定性结果.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zheng

, Wang

Variable-order space-fractional diffusion equations and a variable-order modification of constant-order fractional problems

Applicable Analysis, 2022, 1.1(6): 1848-1870