1 引言
Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生.
本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础.
我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
(1.1) $\begin{equation}\label{eqn-13} \begin{cases}\frac{\partial u}{\partial t}=-a \frac{\partial^4u}{\partial x^4}+\frac{\partial^2u}{\partial x^2}+\lambda u+bu^2-du^3,&(x,t)\in(0,L)\times(0,\infty),\\[2ex]u(x,0)=\varphi(x),&x\in(0,L),\end{cases} \end{equation}$
其中: $a> 0$ $b$ $d> 0$ $\lambda>0$
(1.2) $ -a \frac{\partial^4u}{\partial x^4}+\frac{\partial^2u}{\partial x^2}+\lambda u+bu^2-du^3=0,\qquad x\in(0,L), $
对于 Direchlet 边界条件, 取空间 $H_\mathrm{l}$
对于 Neumann 边界条件, 取空间 $H_\mathrm{1}$
然后定义算子 $L_\lambda=-A+B_\lambda:H_1\to H$
这样, 问题 (1.2) 在条件 (i) 或 (ii) 下均可化为抽象形式
(1.3) $L_{\lambda}u+G(u)=0. $
2 预备知识
令 $X,X_1,Y$ $X_1 \subset X$
(2.1) $L_{\lambda}u + G\left(u,\lambda\right) = 0, $
显然 (u, $\lambda$ ) =(0, $\lambda$ ) 是方程 (2.1) 的一个平凡解, 分歧问题就是寻求一个从某点 (0, $\lambda_0$ ) 产生出的一个非平凡解 ($u_\lambda$ $\lambda$ ) $\neq $ (0 , $\lambda$ ) 使得
${\bf定义2.1}$ [27 ] (分歧定义) 假设 $(2.1)$ $\lambda$ ) =(0, $\lambda_0$ ) 处分歧出一个解 ($u_\lambda,\lambda$ ) $\in X\times\mathbb{R}^1$ $(u_n,\lambda_n)$ $u_n \neq$ 0 , 使得
此时, $(0,\lambda_0)$
${\bf定义2.2}$ [19 ] (正则性定义) 令 $u_\lambda\in X_1$ $\lambda=\lambda_0$ $L_\lambda+G(.,\lambda)$ $u_\lambda$
对所有 $0<\mid\lambda-\lambda_0\mid<\varepsilon$
${\bf引理2.1}$ [27 ] (隐函数定理) 令 $U\subset X\times Y$ $(x_0,y_0)\in U$ $F\in C^{k}(U,Z)$ $k$ $(k\mathbf{\geqslant}1)$ $F(x_0,y_0)=0$ . 假设 $F$ $(x_0,y_0)$ $x$ $D_xF(x_0,y_0):X$ $\to\mathbb{Z}$
(1) 存在 $x_0$ $y_0$ $V\subset X$ $W\subset Y$ $\forall y \in W$ $F(x,y)=0$
(2) 映射 $\Phi{:}W{\to}V$ $k$ $F$ $\Phi$
(3) 如果 $F$ $y$ $m$ $x_0,y_0)$
${\bf引理2.2}$ [19 ] (一般线性全连续场谱理论) 令 $L:H_1\to H$
(1) 如果 $\{\lambda_k|k\geqslant1\}\subset C$ $L$ $L$ $\{\varphi_k\}\subset H_1$ $L^{*}$ $\{\varphi_k^*\}\subset H_1^*$
(2.2) $ \langle \varphi _{i}, \varphi _{j}^{* }\rangle _{H}\left \{ \begin{array} { l l } {= }0, & {\text{当 }i\neq j\text{ 时}, }\\ {\neq 0, }& {\text{当 }i= j\text{ 时}; }\end{array} \right. $
(2) 如果 $\rho=\lambda_k=\cdots=\lambda_{n+k}(n\geqslant1)$ $m=n+1$ $r=1$ $\sigma\neq0$ $L$ $\{\varphi_k,\cdots\,\varphi_{k+n}\}$ $L^*$ $\{\varphi_k^*,\cdots,\varphi_{k+n}^*\}$
(2.3) $\begin{cases}L\varphi_k = \rho\varphi_k,\\L\varphi_{k+1} = \rho\varphi_{k+1} + \sigma\varphi_k,\\...\\L\varphi_{k+n} = \rho\varphi_{k+n} + \sigma\varphi_{k+n-1},\end{cases} $
(2.4) $\begin{equation} \begin{cases}L^* \varphi_{k+n}^* = \rho\varphi_{k+n}^*,\\L^* \varphi_{k+n-1}^* = \rho\varphi_{k+n-1}^* + \sigma\varphi_{k+n}^*,\\...\\L^* \varphi_k^* = \rho\varphi_k^* + \sigma\varphi_{k+1}^* ;\end{cases} \end{equation}$
(4) $E_1$ $E_2$
并且 $\mathcal{L}=L|_{E_2}$ $ \mathcal{L}^{-1}:\overline{E}_2\to E_2\subset\overline{E}_2$
(5) 对任何 $u\in H$
3 主要结果及证明
对于 Dirichlet 边界条件, 问题 (1.2) 有如下结论
${\bf定理3.1}$ $u,\lambda)=\Big(0,\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}\Big)$
${\bf 第一步}$ $L_\lambda=-A+B_\lambda$ $\rho_k$ $e_k(k=1,2,\cdots)$ $k$
(3.1) $\begin{equation}\label{eq:a1} \begin{cases}-\frac{{\rm d}^2e_k}{{\rm d}x^2}=\rho_ke_k,\\e_k(0)=e_k(L)=0,\\[2ex]\int_0^Le_k^2 \mathrm{d}x=1, \end{cases} \end{equation}$
可得出方程 (3.1) 的特征值 $\left\{\rho_k\mid k=1,2,\cdots\right\}$
可得到算子 $L_\mathrm{\lambda}$ $\beta_{k}(\lambda)$
由文献 [19 ] 知, 算子 $L_\mathrm{\lambda}$ $\left\{e_k\mid k=1, 2\cdots\right\}$ $H_\mathrm{l}$ $L_\mathrm{\lambda}$
${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$
在 $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $H$
令 $u\in H_1$ $u=u_1+u_2$ $u_1\in E_1,u_2\in E_2$ . 不妨设
${\bf 第三步}$ [19 ] 求出问题 (1.2) 的分歧解, 将 $u_1,u_2$
(3.2) $\begin{equation}\label{eq:a2} \beta_{1}(\lambda)x_{1}+b<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{2},e_{1}>-\\d<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{3},e_{1}>=0, \end{equation}$
(3.3) $\beta_{j}(\lambda)y_{j}+b<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{2},e_{j}>-\\d<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{3},e_{j}>=0, $
又因为 $e_{1},e_{k}(k\geq1)$
(3.4) $\beta_1(\lambda)x_1+\frac{8b\sqrt{2}}{3\pi\sqrt{L}}x_1^2+o(x_1^2)=0, $
(3.5) $\beta_{1}\left(\lambda\right)x_{1}+\frac{8b\sqrt{2}}{3\pi\sqrt{L}}x_{1}^{2}=0, $
进而能得到所述的问题 (1.2) 的分歧解的表达式
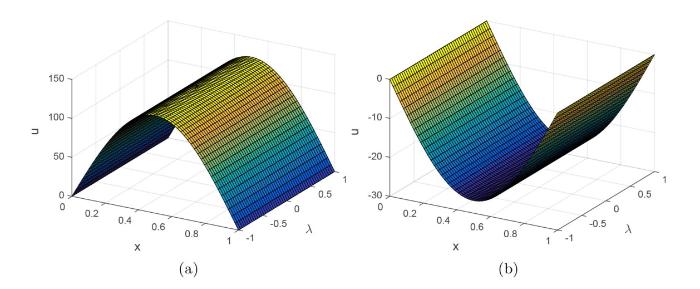
可见问题 (1.2) 在 $(u,\lambda)=(0,\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4})$ 图 1 所示.
图1
图1
当 $a=1,b=1,d=1,L=1$ $\lambda<\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $\lambda>\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$
${\bf 第四步}$ $\overline{u}$
(3.6) $\beta_1\left(\lambda\right)+\frac{16b\sqrt{2}}{3\pi\sqrt{L}}x_1$
代入 $x_1=-\frac{3\beta_1\pi\sqrt{L}}{8b\sqrt{2}}$ $-\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 式的分歧解 $\overline{u}$
对于 Neumann 边界条件, (1.2) 式有如下结论
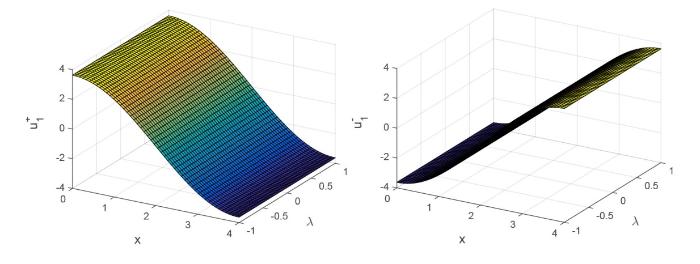
${\bf定理3.2}$ $2b^2L^4>9d\pi^2L^2+45ad\pi^4 $ $\lambda<\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $( u, \lambda ) = ( 0, \frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ ) 处产生次临界分歧, 共分歧出两个分歧解分支且每个分歧解都是正则的. 进一步, 分歧解表达为
(3.7) $\begin{aligned} \overline{u}_{1}^+&=\sqrt{\frac{4(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^8-9d\pi^2L^6-45ad\pi^4 L^4}}\cos\frac{\pi x}{L}\\[2mm] &~~~+o\Bigg(\sqrt{\frac{2(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^7-9d\pi^2L^5-45ad\pi^4 L^3}}\Bigg),\\[2mm] \overline{u}_{1}^-&=-\sqrt{\frac{4(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^8-9d\pi^2L^6-45ad\pi^4 L^4}}\cos\frac{\pi x}{L}\\[2mm] &~~~+o\Bigg(\sqrt{\frac{2(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^7-9d\pi^2L^5-45ad\pi^4 L^3}}\Bigg).\\ \end{aligned} $
(b) 若 $2b^2L^4<9d\pi^2L^2+45ad\pi^4 $ $\lambda>\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $(u,\lambda)=(0,\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4})$
${\bf证}$ ${\bf 第一步}$ $L_\lambda=-A+B_\lambda$ $L_\mathrm{\lambda}$
由文献 [19 ] 知, 算子 $L_\lambda$ $\{e_k,k=1$ $2,\ldots\}$ $H_{1}$
${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $H$
令 $u\in H_1$ $u=u_1+u_2$ $u_1\in E_1,u_2\in E_2$ . 不妨设
${\bf 第三步}$ [27 ] 求出问题 (1.2) 的分歧解, 将 $u_1,u_2$
(3.8) $\beta_{1}(\lambda)x_{1}+b<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{2},e_{1}>-\\d<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{3},e_{1}>=0, $
(3.9) $\beta_{j}(\lambda)y_{j}+b<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{2},e_{j}>-\\d<(x_{1}e_{1}+\sum_{j=2}^{\infty}y_{j}e_{j})^{3},e_{j}>=0, $
又因为 $e_{1},e_{k}(k\geq1)$
(3.10) $ \beta_1(\lambda)x_1-\Bigg(\frac{b^2}{L\beta_2}+\frac{3d}{2L}\Bigg)x_1^3+o(x_1^3)=0, $
(3.11) $ \beta_1(\lambda)x_1-\Bigg(\frac{2b^2+3d\beta_2 }{2L\beta_2}\Bigg)x_1^3=0. $
若 $2b^2L^4>9d\pi^2L^2+45ad\pi^4 $ $\lambda<\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $( x_1, \lambda ) = ( 0, \frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ ) 的领域内存在两个非平凡解, (3.11) 式此处产生次临界分歧, 两个分歧解分支为
(3.12) $\begin{aligned} &x_1^+=\sqrt{\frac{2(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^7-9d\pi^2L^5-45ad\pi^4 L^3}},\\[2mm] &x_1^-=-\sqrt{\frac{2(\pi^2 L^2+a\pi^{4}-\lambda L^{4})(3\pi^2 L^2+15a\pi^{4})}{2b^2L^7-9d\pi^2L^5-45ad\pi^4 L^3}}, \end{aligned} $
从而可得到问题 (1.2) 的分歧解表达式, 分歧解图如图 2 所示
图2
图2
当 $a=1,b=1,d=1,L=4,\lambda>\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$
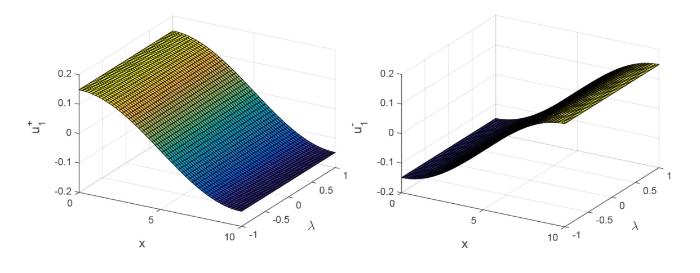
若 $2b^2L^4 <9d\pi^2L^2+45ad\pi^4 $ $\lambda>\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $( x_1, \lambda ) = \Big( 0, \frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}\Big)$ 图 3 所示.
图3
图3
当 $a=1,b=1,d=1,L=10,\lambda<\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$
${\bf 第四步}$ $\overline{u}$
(3.13) $ \beta_1(\lambda)-3\Bigg(\frac{2b^2+3d\beta_2 }{2L\beta_2}\Bigg)x_1^2, $
可得到 $-2\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 的分歧解 $\overline{u}$
4 总结
在本文中, 我们研究了 Extended Fisher-Kolmogorov (EFK) 系统的定态分歧解, 运用拓展的 Lyapunov-Schmidt 约化方法并结合线性全连续场谱分解定理给出了分歧解具体表达式, 并得到了该系统产生超临界分歧与次临界分歧的完整判据. 定理 3.1 讨论了系统在 Dirichlet 边界条件下的分歧解, 得到了当 $\lambda$ $\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$
定理 3.2 讨论了系统在 Neumann 边界条件下的分歧解, 当 $\lambda>\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $\lambda<\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$
参考文献
View Option
[1]
Fisher R A The wave of advance of advantageous genes
Annals of eugenics , 1937 , 7 4 ): 355 -369
[本文引用: 1]
[2]
Kolmogorov A N Petrovsky I G Piskunov N S Étude de l'équation de la diffusion avec croissance de la quantité de matière et son application à un problème biologigue
Moscow Univ Bull Math , 1937 , 1 1 -26
[本文引用: 1]
[3]
王玉兰 . 趋化-流体耦合模型研究进展
西华大学学报 (自然科学版) , 2016 , 35 4 ): 30 -34
[本文引用: 1]
Wang Y L Recent advances in chemotaxis-fluid coupled model research
Journal of Xihua University (Natur Sci Edi) , 2016 , 35 4 ): 30 -34
[本文引用: 1]
[4]
Pan Z G Jia L Mao Y Q Wang Q Transitions and bifurcations in couple stress fluid saturated porous media using a thermal non-equilibrium model
Appl Math Comput , 2022 , 415 126727
[本文引用: 1]
[5]
Fan Y L Li L Pan Z G On dynamics of double-diffusive magneto-convection in a non-Newtonian fluid layer
Math Method Appl Sci , 2023 , 46 13 ): 14596 -14621
[本文引用: 1]
[6]
Coullet P Elphick C Repaux D The nature of spatial chaos
Phys Rev Lett , 1987 , 58 5 ): 431 -434
PMID:10034937
[本文引用: 1]
[7]
Saarloose W Bistable systems with propagating fronts leading to pattern formation
Phys Rev Lett , 1988 , 60 25 ): 2641 -2644
PMID:10038411
[本文引用: 1]
[8]
Kopell N Howard LN Plane wave solutions to reaction-diffusion equations
Stud Appl Math , 1973 , 52 4 ): 291 -328
[本文引用: 1]
[9]
Bartuccelli M V On the asymptotic positivity of solutions for the extended Fisher-Kolmogorov equation with nonlinear diffusion
Math Method Appl Sci , 2002 , 25 701 -708
[本文引用: 1]
[10]
Peletier L Troy W Spatial patterns described by the extended Fisher-Kolmogorov equation: Periodic solutions
SIAM J Math Anal , 1997 , 28 6 ): 1317 -1353
[本文引用: 1]
[11]
Kwapisz J Uniqueness of the stationary wave for the extended Fisher-Kolmogorov equation
J Differ Equations , 2000 , 165 235 -253
[本文引用: 1]
[12]
Ma R Y Wei L Chen Z Evolution of bifurcation curves for one-dimensional Minkowski-curvature problem
Appl Math Lett , 2020 , 103 106176
[本文引用: 2]
[13]
罗宏 , 蒲志林 . Extended Fisher-Kolmogorov 系统的整体吸引子及其分形维数估计
四川师范大学学报 (自然科学版) , 2004 , 27 2 ): 135 -138
[本文引用: 1]
Luo H Pu Z L Global attractor and its fractal dimension estimate for the Extended Fisher-Kolmogorov system
Journal of Sichuan Normal University (Natur Sci Edi) , 2004 , 27 2 ): 135 -138
[本文引用: 1]
[14]
Ma R Y Xu L Existence of positive solutions of a nonlinear fourth-order boundary value problem
Appl Math Lett , 2010 , 23 5 ): 537 -543
[本文引用: 1]
[15]
钟吉玉 . 关于 Kuramoto-Sivashinsky 方程平衡解的分岔问题
四川大学学报 (自然科学版) , 2006 , 43 2 ): 277 -280
[本文引用: 1]
Zhong J Y Bifurcation problems of equilibrium solutions for the Kuramoto-Sivashinsky equation
Journal of Sichuan University (Natur Sci Edi) , 2006 , 43 2 ): 277 -280
[本文引用: 1]
[16]
张强 , 曾艳 , 李桂花 . 带 Neumann 边界条件的 Extended Fisher-Kolmogorov 系统的定态分歧
四川师范大学学报 (自然科学版) , 2014 , 37 2 ): 188 -191
[本文引用: 2]
Zhang Q Zeng Y Li G H Steady-state bifurcation of the Extended Fisher-Kolmogorov system with Neumann boundary conditions
Journal of Sichuan Normal University (Natur Sci Edi) , 2014 , 37 2 ): 188 -191
[本文引用: 2]
[17]
Sengul T Tiryakioglu B Dynamic transitions and bifurcations of 1D reaction-diffusion equations: the non-self-adjoint case
J Math Anal Appl , 2023 , 523 1 ): Art 127114
[本文引用: 1]
[18]
Drame A K Costa D G On positive solutions of one-dimensional semipositone equations with nonlinear boundary conditions
Appl Math Lett , 2012 , 25 12 ): 2411 -2416
[本文引用: 1]
[19]
马天 , 汪守宏 . 非线性演化方程的稳定性与分歧 . 北京 : 科学出版社 , 2007
[本文引用: 10]
Ma T Wang S H Stability and Bifurcation of Nonlinear Evolutionary Equations . Beijing : Science Press , 2007
[本文引用: 10]
[20]
张强 , 雷开洪 , 向丽 . Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
四川大学学报 (自然科学版) , 2013 , 50 1 ): 6 -10
[本文引用: 1]
Zhang Q Lei K H Xiang L Steady-state bifurcation of the Fisher-Kolmogorov-Petrovskii-Piskunov equation
Journal of Sichuan University (Natur Sci Edi) , 2013 , 50 1 ): 6 -10
[本文引用: 1]
[21]
郝清明 , 潘志刚 , 朱超 . 带 Robin 边界条件 Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
西华大学学报 (自然科学版) , 2025 , 44 3 ): 102 -106
[本文引用: 1]
Hao Q M Pan Z G Zhu C Steady-state bifurcation of the Fisher-Kolmogorov-Petrovskii-Piskunov equation with Robin boundary conditions
Journal of Xihua University (Natur Sci Edi) , 2025 , 44 3 ): 102 -106
[本文引用: 1]
[22]
曹倩 , 李艳玲 , 单炜华 . 含有猎物避难所和恐惧效应的反应扩散捕食者-食饵模型的动力学
山东大学学报 (理学版) , 2023 , 58 10 ): 43 -53
[本文引用: 1]
Cao Q Li Y L Shan W H Dynamics of a Reaction-Diffusion Predator-Prey model with prey eefuge and fear effect
Journal of Shandong University (Natur Sci Edi) , 2023 , 58 10 ): 43 -53
[本文引用: 1]
[23]
袁海龙 , 王玉萍 , 李艳玲 . 一类带有交叉扩散的捕食-食饵模型的正解
数学物理学报 , 2019 , 39A 3 ): 545 -559
[本文引用: 1]
Yuan H L Wang Y P Li Y L Positive solutions of a predator-prey model with cross-diffusion
Acta Math Sci , 2019 , 39A 3 ): 545 -559
[本文引用: 1]
[24]
张强 , 张正丽 . 一类反应扩散方程的定态分歧
四川大学学报 (自然科学版) , 2010 , 47 3 ): 461 -463
[本文引用: 1]
Zhang Q Zhang Z L Steady-state bifurcation of a class of reaction-diffusion equations
Journal of Sichuan University (Natur Sci Edi) , 2010 , 47 3 ): 461 -463
[本文引用: 1]
[25]
张正丽 , 张强 . 一类 Cahn-Hilliard 方程的定态分歧
四川大学学报(自然科学版) , 2011 , 48 4 ): 729 -732
Zhang Z L Zhang Q Steady-state bifurcation of a class of Cahn-Hilliard equations
Journal of Sichuan University (Natur Sci Edi) , 2011 , 48 4 ): 729 -732
[26]
帅鲲 , 蒲志林 , 潘志刚 . 一类带平均值约束的二元方程组的定态分歧
四川师范大学学报 (自然科学版) , 2013 , 36 6 ): 820 -823
[本文引用: 1]
Shuai K Pu Z L Pan Z G Steady-state bifurcation of a class of binary equation systems with mean value constraints
Journal of Sichuan Normal University (Natur Sci Edi) , 2013 , 36 6 ): 820 -823
[本文引用: 1]
[27]
Ma T Bifurcation Theory and Applications . Singapore: World Scientific , 2005
[本文引用: 3]
The wave of advance of advantageous genes
1
1937
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
étude de l'équation de la diffusion avec croissance de la quantité de matière et son application à un problème biologigue
1
1937
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
趋化-流体耦合模型研究进展
1
2016
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
趋化-流体耦合模型研究进展
1
2016
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
Transitions and bifurcations in couple stress fluid saturated porous media using a thermal non-equilibrium model
1
2022
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
On dynamics of double-diffusive magneto-convection in a non-Newtonian fluid layer
1
2023
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
The nature of spatial chaos
1
1987
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
Bistable systems with propagating fronts leading to pattern formation
1
1988
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
Plane wave solutions to reaction-diffusion equations
1
1973
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
On the asymptotic positivity of solutions for the extended Fisher-Kolmogorov equation with nonlinear diffusion
1
2002
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
Spatial patterns described by the extended Fisher-Kolmogorov equation: Periodic solutions
1
1997
... Fisher-Kolmogorov(FK)方程由 Fisher[1 ] 和 Kolmogorov[2 ] 在 1937 年提出, 其在生物学和物理学领域占据着重要的位置, 尤其是在描述生物种群的扩散及其适应性相互作用方面. 在此前趋化-流体耦合模型常被用于理解和预测生物群体在复杂环境中的行为, 其是一种用于描述生物群体在化学信号引导下运动, 并与周围流体相互作用的数学模型. 王[3 ] 对趋化-流体耦合模型的起源、研究进展、研究困难进行详细的分析, 并指出此类方程组研究中一些尚待解决的问题, 潘[4 ] 则采用热非平衡模型研究了耦合应力流体饱和多孔介质的稳定性和转变, 文献 [5 ]讨论了在垂直磁场作用下, 非牛顿流体水平层在热扩散和溶质扩散共同影响下的动力学转变. 而如今为了更准确地捕捉系统内复杂的动态行为, Coullet[6 ] 和 Saarloos[7 ] 对 FK[8 ] 方程进行了改进, 基于考虑长距离相互作用或非线性效应的情况下, 引入了一个稳定的四阶导数项, 这一改进使得方程能更真实地反映生态系统中种群的复杂动态, 由此 Extended Fisher-Kolmogorov (EFK) 系统[9 ,10 ] 应运而生. ...
Uniqueness of the stationary wave for the extended Fisher-Kolmogorov equation
1
2000
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
Evolution of bifurcation curves for one-dimensional Minkowski-curvature problem
2
2020
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
... 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
Extended Fisher-Kolmogorov 系统的整体吸引子及其分形维数估计
1
2004
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
Extended Fisher-Kolmogorov 系统的整体吸引子及其分形维数估计
1
2004
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
Existence of positive solutions of a nonlinear fourth-order boundary value problem
1
2010
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
关于 Kuramoto-Sivashinsky 方程平衡解的分岔问题
1
2006
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
关于 Kuramoto-Sivashinsky 方程平衡解的分岔问题
1
2006
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
带 Neumann 边界条件的 Extended Fisher-Kolmogorov 系统的定态分歧
2
2014
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
带 Neumann 边界条件的 Extended Fisher-Kolmogorov 系统的定态分歧
2
2014
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
Dynamic transitions and bifurcations of 1D reaction-diffusion equations: the non-self-adjoint case
1
2023
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
On positive solutions of one-dimensional semipositone equations with nonlinear boundary conditions
1
2012
... 本文我们将用 EFK 系统研究生物种群的复杂动态, 尽管 EFK 系统在解的渐近性质和结构问题[11 ] 上已有大量研究, 但在分歧现象方面的探索仍相对不足. 分歧现象对于理解生态系统的稳定性至关重要, 当生态系统内部环境或资源发生改变时, 生态系统可能会从一种稳定状态转变到另一种截然不同的稳定状态; 在数学上, 这指的是当系统参数发生变化时, 解集的结构会发生显著的变化. 这一现象在非线性偏微分方程的研究中尤为重要, 因为它有助于揭示系统的稳定性和行为转变. 在研究分歧现象时, Krein-Rutman 定理[12 ] 保证了最大特征值及其对应特征向量的存在, 这对于系统稳定性分析是非常关键的, 全局分歧技术被用于研究非线性动力系统在其参数跨越某个临界值时发生根本性变化的长期行为, 它不局限在某个时间段上, 而是研究整个时间区域, 这对于我们理解复杂系统的动态特性很有帮助, 文献 [12 ] 中基于 Krein-Rutman 定理和全局分歧技术研究了四阶边值问题正解的存在性, 罗[13 ]讨论了 EFK 系统的整体吸引子及其分形维数估计. 我们理解非线性动力系统的基本原理一般从一维系统的分歧问题入手, 在文献 [14 ] 中讨论了一维闵可夫斯基-曲率问题的分歧曲线的演化, 文献 [15 ] 运用了 Lyapunov-Schmidt 约化方法讨论了一维空间中的 Kuramoto-Sivashinsky 方程, 张[16 ] 讨论了 EFK 系统在 Neumann 边界下的定态分歧的工作, 且此类一维系统的分歧问题在齐次边界[17 ] 与非齐次边界[18 ] 上均有具体的讨论, 这些文献的研究为本文讨论 EFK 系统的分歧现象提供了理论基础. ...
10
2007
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
... ${\bf定义2.2}$ [19 ] (正则性定义) 令 $u_\lambda\in X_1$ $\lambda=\lambda_0$ $L_\lambda+G(.,\lambda)$ $u_\lambda$
... ${\bf引理2.2}$ [19 ] (一般线性全连续场谱理论) 令 $L:H_1\to H$
... 由文献 [19 ] 知, 算子 $L_\mathrm{\lambda}$ $\left\{e_k\mid k=1, 2\cdots\right\}$ $H_\mathrm{l}$ $L_\mathrm{\lambda}$
... ${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$
... ${\bf 第三步}$ [19 ] 求出问题 (1.2) 的分歧解, 将 $u_1,u_2$
... 代入 $x_1=-\frac{3\beta_1\pi\sqrt{L}}{8b\sqrt{2}}$ $-\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 式的分歧解 $\overline{u}$
... 由文献 [19 ] 知, 算子 $L_\lambda$ $\{e_k,k=1$ $2,\ldots\}$ $H_{1}$
... ${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $H$
... 可得到 $-2\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 的分歧解 $\overline{u}$
10
2007
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
... ${\bf定义2.2}$ [19 ] (正则性定义) 令 $u_\lambda\in X_1$ $\lambda=\lambda_0$ $L_\lambda+G(.,\lambda)$ $u_\lambda$
... ${\bf引理2.2}$ [19 ] (一般线性全连续场谱理论) 令 $L:H_1\to H$
... 由文献 [19 ] 知, 算子 $L_\mathrm{\lambda}$ $\left\{e_k\mid k=1, 2\cdots\right\}$ $H_\mathrm{l}$ $L_\mathrm{\lambda}$
... ${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$
... ${\bf 第三步}$ [19 ] 求出问题 (1.2) 的分歧解, 将 $u_1,u_2$
... 代入 $x_1=-\frac{3\beta_1\pi\sqrt{L}}{8b\sqrt{2}}$ $-\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 式的分歧解 $\overline{u}$
... 由文献 [19 ] 知, 算子 $L_\lambda$ $\{e_k,k=1$ $2,\ldots\}$ $H_{1}$
... ${\bf 第二步}$ [19 ] , 将空间 $H$ $L_\mathrm{\lambda}$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ $H$
... 可得到 $-2\beta_1\left(\lambda\right)$ $\lambda=\frac{\pi^2}{L^2}+a\frac{\pi^4}{L^4}$ 19 ] 可知, (1.2) 的分歧解 $\overline{u}$
Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
1
2013
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
1
2013
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
带 Robin 边界条件 Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
1
2025
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
带 Robin 边界条件 Fisher-Kolmogorov-Petrovskii-Piskunov 方程的定态分歧
1
2025
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
含有猎物避难所和恐惧效应的反应扩散捕食者-食饵模型的动力学
1
2023
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
含有猎物避难所和恐惧效应的反应扩散捕食者-食饵模型的动力学
1
2023
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类带有交叉扩散的捕食-食饵模型的正解
1
2019
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类带有交叉扩散的捕食-食饵模型的正解
1
2019
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类反应扩散方程的定态分歧
1
2010
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类反应扩散方程的定态分歧
1
2010
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类 Cahn-Hilliard 方程的定态分歧
0
2011
一类 Cahn-Hilliard 方程的定态分歧
0
2011
一类带平均值约束的二元方程组的定态分歧
1
2013
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
一类带平均值约束的二元方程组的定态分歧
1
2013
... 我们注意到对于系统在参数变化时可能出现的超临界和次临界分歧, 目前还缺乏系统性的研究. 本文旨在深入探讨 EFK 方程在 Dirichlet 边界和 Neumann 边界条件下的分歧问题, 利用拓展的 Lyapunov-Schmidt 约化方法[19 ] 来研究 EFK 系统的定态分歧, 并试图得到系统发生超临界和次临界分歧的具体判据及分歧解的具体表达式, 最后从相图分析其在无穷维空间中的超临界与次临界分歧. 张[20 ] 和郝[21 ] 研究了 FKPP 方程在 Dirichlet 边界、Neumann 边界和 Robin 边界条件下的定态分歧, 曹[22 ] 和袁[23 ] 讨论了捕食-食饵模型的稳定性和在 Dirichlet 边界条件下的分歧问题, 文献 [24 26 ] 则是讨论了 Cahn-Hilliard 方程在 Neumann 边界下的定态分歧以及产生超临界分歧与次临界分歧的完整判据. 基于文献 [16 ] 考虑了种群在某一生态环境固定区域无迁徙的情况, 我们在此基础上更进一步考虑了种群在该生态环境中边界无分布的情况, 且, 在实际生态系统中, 考虑到种群动态往往受到多种非线性效应的共同影响, 为了能更精准的反映生物种群密度作用机制, 我们考虑了具有合作与自限效应的情形并引入了 $bu^2$ $du^3$
3
2005
... ${\bf定义2.1}$ [27 ] (分歧定义) 假设 $(2.1)$ $\lambda$ ) =(0, $\lambda_0$ ) 处分歧出一个解 ($u_\lambda,\lambda$ ) $\in X\times\mathbb{R}^1$ $(u_n,\lambda_n)$ $u_n \neq$ 0 , 使得 ...
... ${\bf引理2.1}$ [27 ] (隐函数定理) 令 $U\subset X\times Y$ $(x_0,y_0)\in U$ $F\in C^{k}(U,Z)$ $k$ $(k\mathbf{\geqslant}1)$ $F(x_0,y_0)=0$ . 假设 $F$ $(x_0,y_0)$ $x$ $D_xF(x_0,y_0):X$ $\to\mathbb{Z}$
... ${\bf 第三步}$ [27 ] 求出问题 (1.2) 的分歧解, 将 $u_1,u_2$