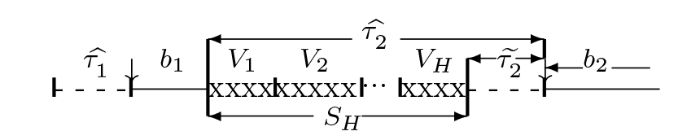1 引言
离散时间排队系统是顺应数字化技术发展趋势而建立起来的一套数学分析模型, 离散时间排队系统理论的不断发展, 不仅丰富和拓展了连续时间排队系统理论, 而且为计算机系统和通信网络的设计优化与性能分析提供了十分有效的数学方法和研究手段, 其精确性和适用性得到了广泛验证. 现有研究成果表明, 离散时间排队系统及其延伸的深入研究, 需要较多的数学工具, 其讨论过程比较复杂和繁琐, 其结果也很冗长和复杂, 更具难度和挑战. 近年来离散时间排队的分析取得了惊人的进展[1 7] , 为我们提供了有关离散时间排队的深入研究和广泛应用.
生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队.
在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限.
休假排队模型是在处理大量复杂系统的设计和控制问题的实际应用背景中产生的, 随着休假排队理论研究的进展, 所得结果迅速在众多领域取得了卓有成效的应用. 例如, 最优保养策略的拟定和实施、生产过程的经济效益分析、物流与仓储管理、通信网络与数据传输、柔性制造系统的生产调度、异步转换模式中的拥塞问题分析等等. 作为多重休假与单重休假的推广, 多级适应性休假[2 ] 仍以空竭服务规则作为控制休假开始的机制, 而何时终止休假既取决于服务员当前所要从事的辅助工作量的多少, 又适当的受到顾客到达过程的制约, 因此服务员的连续休假次数是不确定的. 多级适应性休假策略体现了在为主队列顾客服务和从事辅助工作之间权衡得失决定整个休假期长度的思想, 为系统的优化设计和运行控制提供了极大的灵活性.
在本文中, 我们所关注的问题与中转仓库的调度策略有关. 物流行业中, 包装好的货物暂时存放在中转站仓库中, 管理者需要安排货运车将货物运往相应的目的地. 由于货物到达的随机性, 一个自然方法是将货物装载过程建模为排队模型. 为了减少运输次数, 降低运输成本, 从中转站出发的一辆货运车装载不止一件货物包裹应该是合情合理的, 同时当仓库中货物的总重量远低于货运车的载重能力时, 将货物装载并运往目的地也是极不合理的. 因此, 如果需要运送的货物包裹不足 $N$ $N$ $N$ - 策略). 然而, 仓库中等待装载的货物也会导致库存成本, 货运车不能为了凑齐 $N$ $N$ $D$ $D$ - 策略). 另外, 每当中转站没有货物时, 装卸工人或处于休息或去做其他辅助工作 (对应服务员休假机制).
目前, 对联合策略控制的排队系统开展的研究工作主要集中在连续时间情形. 基于离散时间排队系统更适合于计算机通信网络的建模和性能分析的应用背景, 本文研究服务员具有多级适应性休假和系统采取修正的 Min$(N,D)$ - 控制策略的 Geo/G/1 离散时间排队系统, 通过瞬态分析和稳态分析, 获得队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并借助具体数值实例, 探讨获得便于进行数值计算的队长稳态分布的递推表达式在系统容量的优化设计中所具有的清晰应用前景, 并且考察了系统的空闲率 $p^+_{_{0}}$ $E[L^+]$
2 模型描述和预备知识
2.1 模型描述
考虑一个 Geo/G/1 离散时间排队系统, 时间轴被分割成间隔时间相等的时隙序列, 表示为 $0, 1, 2, \cdots$ . 假设
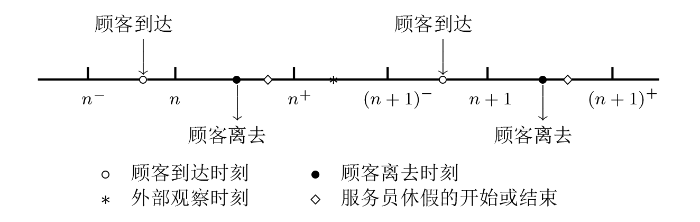
1) 本文讨论的模型为晚到达延迟进入系统 (LAS-DA), 即顾客到达只能发生在时隙末端 $(n^{-},n)$ $n=0, 1, 2, \cdots$ $(n, n^{+})$ $n=1, 2, \cdots$ $(n^{-}, n)$ $(n^{-}, n)$ $(n, n^{+})$ 图 1 ).
图 1
2) 顾客相继到达的间隔时间序列 $\{\tau_{_{k}}, k=1, 2, \cdots\}$ $p$ $P\{\tau=j\}=p(1-p)^{j-1}, j=1, 2, \cdots, 0<p<1$ $(n^{-}, n)$ $p$ $1-p$
3) 服务员对每个顾客服务的工作量是指该顾客需要服务员完成的服务项目中所包含的事件数量, 工作量的度量单位可以是计数单位、重量单位等. 例如到达储存钢材的某仓库的一辆卡车, 要求装载 2000 公斤直径为 3cm 的螺纹钢筋, 以及 1000 公斤直径为 2cm 的螺纹钢筋, 那么此时仓库的服务员对这个顾客 (卡车) 服务的工作量就是 3000 公斤. 服务员对第 $k$ $W_{_{k}}$ $\{W_{_{k}}, k=1, 2, \cdots\}$ $P\{W=j\}=w_{_{j}}, j=1, 2, \cdots$ .
4) 系统中只有一个服务台, 服务员完成工作量 $W_{_{k}}$ $\chi_{_{k}}$ $k$ $\{\chi_{_{k}}, k=1, 2, \cdots\}$ $ P\{\chi=j\}=g_{_{j}}, j=1, 2, \cdots$ $G(z)=\sum_{j=1}^\infty g_{_{j}}z^{j}, |z|<1$ $\mu(1 \leqslant \mu< \infty)$
5) 服务员采取空竭服务多级适应性休假机制和系统采取基于顾客数和服务员工作量的修正 Min$(N, D)$ - 控制策略且服务员休假可中断, 即每当系统变空时, 系统管理者根据当前需要完成的辅助工作量, 要求服务员连续进行 $H$ $H$ $P\{H=j\}=h_j, j=1, 2, \cdots$ $H(z)=\sum_{j=1}^\infty h_{_{j}}z^{j}, |z|<1$ $P\{V=j\}=v_{_{j}}, j=0, 1, 2, \cdots$ $V(z)=\sum_{j=1}^\infty v_{_{j}}z^{j}, |z|<1$ $E[V]$ $k$ $k$ $N$ $D$ $V$ ) ; 若在第 $k$ $N$ $D$ $k$ $k$ $k+1$ $H$ $H$
(1) 在服务员休假期间开始一个新的服务员忙期 (假期中有顾客到达, 且系统中的顾客数达到了 $N$ $D$ ) ;
(2) 在服务员的某一次休假结束后, 开始一个新的服务员忙期 (假期中有顾客到达, 但顾客数没有达到 $N$ $D$ ) ;
(3)在服务员闲期开始一个新的服务员忙期 (服务员连续 $H$
6) $\tau$ $\chi$ $W$ $H$ $V$
7) 系统在时刻 $0^+$ $L(0^+)=i(i=0, 1, 2, \cdots)$ $n^+=0^+$ $(N, D)$ - 控制策略, 且服务员也不休假, 即如果在时刻 $0^+$ $0^+$
${\bf注 2.1}$ $L(n^-), L(n), L(n^+)$ $n^-, n, n^+$ $\rho=p\mu, \bar{p}=1-p; f(z)=\dfrac{pz}{1-\bar{p}z}; S_H=V_1+V_2+\cdots+V_H$ $N$ $D$
2.2 预备知识
${\bf定义2.1}$ $\widehat{\tau}_{_{\scriptstyle k}}$ $k$ $p$ $P\{\widehat{\tau}_{_{\scriptstyle k}}=j\}=p(1-p)^{j-1}, j=1, 2, \cdots, k\geq1$ .
${\bf定义2.2}$
${\bf定义2.3}$
在该系统中, 服务员忙期开始时系统中可能有若干个顾客, 如果令 $b$
${\bf引理2.1}$ [1 ] 令 $B(z)=\sum\limits_{j=1}^\infty P\{b=j\}z^{j}, |z|<1$ $B(z)$ $B(z)=G((1-p+pB(z))z)$
又令 $b^{<i>}$ $i$ $b^{<i>}=b_{1}+b_{2}+\cdots+b_{i}, i=1, 2, \cdots$ $b_{1}, b_{2}, \cdots, b_{i}$ $b$ $\sum\limits_{j=i}^\infty P\{b^{<i>}=j\}z^j=[B(z)]^i, i=1, 2, \cdots, |z|<1$ .
设 $Q_{j}(n^+)=P\{b>n^+, L(n^+)=j\}, j=1, 2, \cdots$ $b$ $n^+$ $j$ $n^+=0^+$ $b$ $Q_{1}(0^+)=1, Q_{j}(0^+)=0, j=2, 3, \cdots$ .
${\bf引理2.2}$ [28 ] 对于 $|z|<1$ $q^+_{_{\scriptstyle j}}(z)=\sum\limits_{n=0}^\infty Q_{j}(n^+)z^{n}$ $Q_{j}(n^+)$
其中当 $j<k$ $\sum\limits_{i=k}^j=0$
3 时刻 $n^+$ $z$ - 变换表达式
令条件概率 $P_{ij}(n^+)=P\{L(n^+)=j|L(0^+)=i\}$ $L(0^+)=i$ $n^+$ $j$ $p^+_{_{ij}}(z)=\sum\limits_{n=0}^\infty P_{ij}(n^+)z^{n}$ $P_{ij}(n^+)$ $z$ - 变换, $i, j=0, 1, 2, \cdots$ . 下面我们运用一种直接的概率分析法和 $z$ - 变换工具来讨论队长的瞬态分布, 并给出其 $z$ - 变换表达式.
${\bf定理3.1}$ $|z|<1$
(3.1) $p^+_{_{\scriptstyle 00}}(z)=\dfrac{1}{1-\bar{p}z}\left\{1+\frac{f(z)B(z)[1-V(\bar{p}z)]}{\Delta(z)}\right\}$
(3.2) $p^+_{_{\scriptstyle i0}}(z)=\dfrac{[B(z)]^i[1-V(\bar{p}z)]}{[1-\bar{p}z]\Delta(z)}, i=1, 2, \cdots,$
其中 $B(z)$ $2.1$ $A_m=\sum\limits_{k=1}^m W_{_{\scriptstyle k}}, W^{(m)}(D)=P\{A_m<D\}, W^{(0)}(D)=1,$
${\bf证}$ $S_k=\sum\limits_{i=1}^kV_i$ $k$ $l_k=\sum\limits_{i=1}^k\tau_{_{\scriptstyle i}}$ $k$ $S_0=l_0=0$ . 时刻 $n^+$ $n^+$ $L(0^+)=0$
(3.3) ${ \begin{matrix} &&\hspace{-0.5cm}P_{00}(n^+)=P\{0\leq n^+ <\widehat{\tau}_{_{\scriptstyle1}} \} +P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1\leq n^+ <\widehat{\tau}_{_{\scriptstyle 1}}+b_1+\widehat{\tau}_{_{\scriptstyle 2}}\}+P\{\widehat{\tau}_{_{1}}+b_1+\widehat{\tau}_{_{\scriptstyle 2}}\leq n^+;L(n^+)=0\}\nonumber\\ &&\hspace{0.7cm}=\bar{p}^n+\sum_{t=2}^n P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1=t\}\bar{p}^{n-t}+P\{\widehat{\tau}_{_{1}}+b_1+\widehat{\tau}_{_{\scriptstyle 2}}\leq n^+;L(n^+)=0\}, \end{matrix}}$
其中 $\widehat{\tau}_{_{\scriptstyle k}}$ $L(0^+)=0$ $k(k\geq 1)$ $b_1$
(3.3) 式中的第三项表示 "时刻 $n^+$
${\bf情况 1}$ $H$ $b_2$ 图 2 ). 图中箭头 $\downarrow$ $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}>S_{H}$ $\widehat{\tau}_{_{\scriptstyle 2}}$
图 2
图 2
当 $L(0^+)=0$
${\bf情况 2}$ $k$ $k-1$ $k$ $m(1\leq m \le N-1)$ $m$ $A_m<D$ $k$ $b^{<m>}$ $m$ 图 3 ), 图中 $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}>S_{k-1}$ $\widehat{\tau}_{_{\scriptstyle 2}}$
图 3
图 3
当 $L(0^+)=0$
${\bf情况 3}$ $k$ $k-1$ $k$ $m(1\leq m \le N-1)$ $m$ $A_{m-1}<D\le A_m$ $m$ $k$ $b^{<m>}$ $m$ 图 4 ).
图 4
图 4
当 $L(0^+)=0$
${\bf情况 4}$ $k$ $k-1$ $k$ $N$ $N-1$ $A_{N-1}<D$ $N$ $k$ $b^{<N>}$ $N$ 图 5 ).
图 5
图 5
当 $L(0^+)=0$
(3.4) $\begin{aligned} P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2} \leq n^{+} ; L\left(n^{+}\right)=0\right\}= & P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2}>S_{H} ; L\left(n^{+}\right)=0\right\} \\ & +P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2} \leq S_{H} ; L\left(n^{+}\right)=0\right\}, \end{aligned}$
(3.5) $\begin{aligned} & P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2}>S_{H} ; L\left(n^{+}\right)=0\right\}=\sum_{k=1}^{\infty} h_{k} P\left\{\widehat{\tau}_{1}+b_{1}+S_{k}+\widetilde{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2}>S_{k} ; L\left(n^{+}\right)=0\right\} \\ = & \sum_{k=1}^{\infty} h_{k} \sum_{t=2}^{n-k-1} P\left\{\widehat{\tau}_{1}+b_{1}=t\right\} \sum_{v=k}^{n-t-1} P\left\{S_{k}=v\right\} \bar{p}^{v} \sum_{u=1}^{n-t-v} P\left\{\widetilde{\tau}_{2}=u\right\} P_{10}\left((n-t-v-u)^{+}\right) \end{aligned}, $
其中 $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}>S_{H}$ $\widehat{\tau}_{_{\scriptstyle 2}}$ $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}$
(3.6) $\begin{aligned} & P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2} \leq S_{H} ; L\left(n^{+}\right)=0\right\} \\ = & \sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} P\left\{\widehat{\tau}_{1}+b_{1}+S_{k} \leq n^{+}, S_{k-1}<\widehat{\tau}_{2} \leq S_{k}, l_{m-1} \leq S_{k}-\widehat{\tau}_{2}<l_{m}, A_{m}<D ; L\left(n^{+}\right)=0\right\} \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2}+l_{m-1} \leq n^{+}, S_{k-1}<\widehat{\tau}_{2} \leq S_{k}-l_{m-1}, A_{m-1}<D \leq A_{m} ; L\left(n^{+}\right)=0\right\} \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} P\left\{\widehat{\tau}_{1}+b_{1}+\widehat{\tau}_{2}+l_{N-1} \leq n^{+}, S_{k-1}<\widehat{\tau}_{2} \leq S_{k}-l_{N-1}, A_{N-1}<D ; L\left(n^{+}\right)=0\right\} \end{aligned}$
(3.7) ${ \begin{matrix} &&\hspace{0.1cm}\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}W^{(m)}(D)P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1+S_k\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k, l_{m-1}\leq S_k-\widehat{\tau}_{_{\scriptstyle 2}}<l_{m}; L(n^+)=0\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum_{t=2}^{n-k-m+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1=t\}\sum\limits_{v=k-1}^{n-t-m}P\{S_{k-1}=v\}\nonumber\\ &&\hspace{-0.1cm}\cdot \sum_{u=m}^{n-t-v}P\{V=u\}\binom{u}{m}p^m\bar{p}^{v+u-m}P_{m0}((n-t-v-u)^+), \end{matrix}} $
(3.8) ${ \begin{matrix} &&\hspace{0.1cm}\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}C_m(D)P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1+\widehat{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k-l_{m-1}; L(n^+)=0\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}C_m(D)P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1+S_{k-1}+\widetilde{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},\widetilde{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq V_k; L(n^+)=0\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}C_m(D)\sum_{t=2}^{n-m-k+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1=t\}\sum\limits_{v=k-1}^{n-t-m}P\{S_{k-1}=v\}\nonumber\\ &&\hspace{-0.1cm}\cdot\sum_{r=m}^{n-t-v}\binom{r-1}{m-1}p^m\bar{p}^{v+r-m}\sum_{u=r}^\infty P\{V=u\}P_{m0}((n-t-v-r)^+), \end{matrix}}$
其中 $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}>S_{k-1}$ $\widehat{\tau}_{_{\scriptstyle 2}}$ $\widetilde{\tau}_{_{\scriptstyle 2}}$ $\widehat{\tau}_{_{\scriptstyle 2}}$
(3.9) ${ \begin{matrix} &&\hspace{0.1cm}W^{(N-1)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1+\widehat{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k-l_{N-1}; L(n^+)=0\}\nonumber\\ &&\hspace{-0.3cm}=W^{(N-1)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1+S_{k-1}+\widetilde{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},\widetilde{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq V_k; L(n^+)=0\}\nonumber\\ &&\hspace{-0.3cm}=W^{(N-1)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s \sum_{t=2}^{n-N-k+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b_1=t\}\sum\limits_{v=k-1}^{n-t-N}P\{S_{k-1}=v\}\nonumber\\ &&\hspace{-0.1cm}\cdot\sum_{r=N}^{n-t-v}\binom{r-1}{N-1}p^N\bar{p}^{v+r-N}\sum_{u=r}^\infty P\{V=u\}P_{N0}((n-t-v-r)^+), \end{matrix}} $
将 (3.4)-(3.9) 式代入 (3.3) 式, 并作 $z$ - 变换得
(3.10) $\begin{aligned} p_{00}^{+}(z)= & \frac{1+f(z) B(z)}{1-\bar{p} z}+[f(z)]^{2} B(z) H(V(\bar{p} z)) p_{10}^{+}(z) \\ & +\frac{f(z) B(z)[1-H(V(\bar{p} z))]}{1-V(\bar{p} z)}\left\{\sum_{m=1}^{N-1} W^{(m)}(D) \sum_{u=m}^{\infty} P\{V=u\}\binom{u}{m}(p z)^{m}(\bar{p} z)^{u-m} p_{m 0}^{+}(z)\right. \\ & +\sum_{m=1}^{N-1} C_{m}(D) \sum_{u=m}^{\infty} P\{V=u\} \sum_{r=m}^{u}\binom{r-1}{m-1}(p z)^{m}(\bar{p} z)^{r-m} p_{m 0}^{+}(z) \\ & \left.+W^{(N-1)}(D) \sum_{u=N}^{\infty} P\{V=u\} \sum_{r=N}^{u}\binom{r-1}{N-1}(p z)^{N}(\bar{p} z)^{r-N} p_{N 0}^{+}(z)\right\} \end{aligned}$
当 $L(0^+)=i, i=1, 2, \cdots$
(3.11) $\begin{aligned} P_{i 0}\left(n^{+}\right)= & \sum_{t=i}^{n} P\left\{b^{<i>}=t\right\} \bar{p}^{n-t} \\ & +\sum_{k=1}^{\infty} h_{k} \sum_{t=i}^{n-k-1} P\left\{b^{<i>}=t\right\} \sum_{v=k}^{n-t-1} P\left\{S_{k}=v\right\} \bar{p}^{v} \sum_{u=1}^{n-t-v} P\left\{\widetilde{\tau}_{1}=u\right\} P_{10}\left((n-t-v-u)^{+}\right) \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} W^{(m)}(D) \sum_{t=i}^{n-k-m+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-m} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{u=m}^{n-t-v} P\{V=u\}\binom{u}{m} p^{m} \bar{p}^{v+u-m} P_{m 0}\left((n-t-v-u)^{+}\right) \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} C_{m}(D) \sum_{t=i}^{n-k-m+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-m} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{r=m}^{n-t-v}\binom{r-1}{m-1} p^{m} \bar{p}^{v+r-m} \sum_{u=r}^{\infty} P\{V=u\} P_{m 0}\left((n-t-v-r)^{+}\right) \\ & +W^{(N-1)}(D) \sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{t=i}^{n-N-k+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-N} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{r=N}^{n-t-v}\binom{r-1}{N-1} p^{N} \bar{p}^{v+r-N} \sum_{u=r}^{\infty} P\{V=u\} P_{N 0}\left((n-t-v-r)^{+}\right) \end{aligned}$
其中 $\widetilde{\tau}_{_{\scriptstyle 1}}$ $\widehat{\tau}_{_{\scriptstyle 1}}>S_{H}$ $\widehat{\tau}_{_{\scriptstyle 1}}$ $\widetilde{\tau}_{_{\scriptstyle 1}}$ $\widehat{\tau}_{_{\scriptstyle 1}}$
(3.12) $\begin{aligned} p_{i 0}^{+}(z)= & \frac{[B(z)]^{i}}{1-\bar{p} z}+f(z)[B(z)]^{i} H(V(\bar{p} z)) p_{10}^{+}(z) \\ & +\frac{[B(z)]^{i}[1-H(V(\bar{p} z))]}{1-V(\bar{p} z)}\left\{\sum_{m=1}^{N-1} W^{(m)}(D) \sum_{u=m}^{\infty} P\{V=u\}\binom{u}{m}(p z)^{m}(\bar{p} z)^{u-m} p_{m 0}^{+}(z)\right. \\ & +\sum_{m=1}^{N-1} C_{m}(D) \sum_{u=m}^{\infty} P\{V=u\} \sum_{r=m}^{u}\binom{r-1}{m-1}(p z)^{m}(\bar{p} z)^{r-m} p_{m 0}^{+}(z) \\ & \left.+W^{(N-1)}(D) \sum_{u=N}^{\infty} P\{V=u\} \sum_{r=N}^{u}\binom{r-1}{N-1}(p z)^{N}(\bar{p} z)^{r-N} p_{N 0}^{+}(z)\right\}, \end{aligned}$
由 (3.10) 式和 (3.12) 式可得 $p^+_{_{\scriptstyle 00}}(z)$ $p^+_{_{\scriptstyle i0}}(z)$
(3.13) ${ \begin{matrix} p^+_{_{\scriptstyle i0}}(z)=\dfrac{[B(z)]^{i-1}}{f(z)} \left[p^+_{_{\scriptstyle 00}}(z)-\dfrac{1}{1-\bar{p}z}\right], i=1, 2, \cdots. \end{matrix}}$
将 (3.13) 式代入 (3.10) 式整理可得 (3.1) 式, 再将 (3.1) 式代入 (3.13) 式得 (3.2) 式.
${\bf定理3.2}$ $j=1, 2, \cdots, N-1$ $|z|<1$
(3.14) $p_{0 j}^{+}(z)=f(z)\left\{q_{j}^{+}(z)+\frac{f(z) B(z)[1-V(\bar{p} z)] H(V(\bar{p} z)) q_{j}^{+}(z)+\sigma_{j}(z)+\eta_{j}(z)}{\Delta(z)}\right\},$
(3.15) $\begin{aligned} p_{i j}^{+}(z)= & \sum_{k=1}^{i}[B(z)]^{k-1} q_{j-i+k}^{+}(z) \\ & +\frac{[B(z)]^{i-1}\left\{f(z) B(z)[1-V(\bar{p} z)] H(V(\bar{p} z)) q_{j}^{+}(z)+\sigma_{j}(z)+\eta_{j}(z)\right\}}{\Delta(z)}, i=1,2, \cdots, \end{aligned}$
其中 $B(z)$ $q^+_{_{\scriptstyle j}}(z)$ $\Delta(z)$
${\bf证}$ $j=1, 2, \cdots, N-1$ $N(n^+)=j$ $n^+$ $j$ $n^+$ $j$ $L(0^+)=0$
(3.16) $\begin{aligned} P_{0 j}\left(n^{+}\right)= & P\left\{\widehat{\tau}_{1} \leq n^{+}<\widehat{\tau}_{1}+b ; L\left(n^{+}\right)=j\right\}+P\left\{\widehat{\tau}_{1}+b+\widehat{\tau}_{2} \leq n^{+} ; L\left(n^{+}\right)=j\right\} \\ = & \sum_{t=1}^{n} P\left\{\widehat{\tau}_{1}=t\right\} Q_{j}\left((n-t)^{+}\right)+P\left\{\widehat{\tau}_{1}+b+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2}>S_{H} ; L\left(n^{+}\right)=j\right\} \\ & +P\left\{\widehat{\tau}_{1}+b+\widehat{\tau}_{2} \leq n^{+}, \widehat{\tau}_{2} \leq S_{H} ; L\left(n^{+}\right)=j\right\}, \end{aligned}$
其中 (3.16) 式中的第一项表示 "时刻 $n^+$ $b$ $j$ $H$ $n^+$ $\widehat{\tau}_{_{\scriptstyle 2}}$ $j$ $n^+$ $\widehat{\tau}_{_{\scriptstyle 2}}$ $j$
(3.17) ${ \begin{matrix} &&P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}}\leq n^+,\widehat{\tau}_{_{\scriptstyle 2}}> S_H;L(n^+)=j\} =\sum\limits_{k=1}^\infty h_kP\{\widehat{\tau}_{_{\scriptstyle 1}}+b+S_k+\widetilde{\tau}_{_{\scriptstyle 2}}\leq n^+,\widehat{\tau}_{_{\scriptstyle 2}}> S_k;L(n^+)=j\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{k=1}^\infty h_k\sum_{t=2}^{n-k-1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b=t\}\sum\limits_{v=k}^{n-t-1}P\{S_{k}=v\} \sum_{u=1}^{n-t-v} p\bar{p}^{v+u-1}P_{1j}((n-t-v-u)^+), \end{matrix}}$
(3.18) ${ \begin{matrix} &&\hspace{0.1cm}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}}\leq n^+,\widehat{\tau}_{_{\scriptstyle 2}}\leq S_H;L(n^+)=j\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+S_k\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k,l_{m-1}\leq S_k-\widehat{\tau}_{_{\scriptstyle 2}}<l_{m}, A_m<D;L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k-l_{m-1},A_{m-1}<D\leq A_m;L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k-l_{N-1},A_{N-1}<D; L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}}\leq n^+<\widehat{\tau}_{_{\scriptstyle 1}}+b+S_k,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},l_{j-1}\leq n^+-(\widehat{\tau}_{_{\scriptstyle 1}}+b+\widehat{\tau}_{_{\scriptstyle 2}})<l_{j},A_j<D\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}W^{(m)}(D)P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+S_k\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}}\leq S_k,l_{m-1}\leq S_k-\widehat{\tau}_{_{\scriptstyle 2}}<l_{m};L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}C_m(D)P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+S_{k-1}+\widetilde{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},\widetilde{\tau}_{_{\scriptstyle 2}}+l_{m-1}\leq V_k;L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+W^{(N-1)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widehat{\tau}_{_{\scriptstyle 1}}+b+S_{k-1}+\widetilde{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq n^+,S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},\widetilde{\tau}_{_{\scriptstyle 2}}+l_{N-1}\leq V_k;L(n^+)=j\}\nonumber\\ &&\hspace{-0.1cm}+W^{(j)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s P\{\widetilde{\tau}_{_{\scriptstyle 2}}\leq n^+-(\widehat{\tau}_{_{\scriptstyle 1}}+b+S_{k-1})<V_k,\\ && S_{k-1}<\widehat{\tau}_{_{\scriptstyle 2}},l_{j-1}\leq n^+-(\widehat{\tau}_{_{\scriptstyle 1}}+b+S_{k-1}+\widetilde{\tau}_{_{\scriptstyle 2}})<l_{j}\}\nonumber\\ &&\hspace{-0.3cm}=\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum_{t=2}^{n-k-m+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b=t\}\sum\limits_{v=k-1}^{n-t-m}P\{S_{k-1}=v\}\nonumber\\ && \cdot \sum_{u=m}^{n-t-v}P\{V=u\}\binom{u}{m}p^m\bar{p}^{v+u-m}P_{mj}((n-t-v-u)^+)\nonumber\\ && +\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum\limits_{m=1}^{N-1}C_m(D)\sum_{t=2}^{n-m-k+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b=t\}\sum\limits_{v=k-1}^{n-t-m}P\{S_{k-1}=v\}\nonumber\\ && \cdot\sum_{r=m}^{n-t-v}\binom{r-1}{m-1}p^m\bar{p}^{v+r-m}\sum_{u=r}^\infty P\{V=u\}P_{mj}((n-t-v-r)^+)\nonumber\\ && +W^{(N-1)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s \sum_{t=2}^{n-N-k+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b=t\}\sum\limits_{v=k-1}^{n-t-N}P\{S_{k-1}=v\}\nonumber\\ && \cdot\sum_{r=N}^{n-t-v}\binom{r-1}{N-1}p^N\bar{p}^{v+r-N}\sum_{u=r}^\infty P\{V=u\}P_{Nj}((n-t-v-r)^+)\nonumber\\ && +W^{(j)}(D)\sum\limits_{s=1}^\infty h_s\sum\limits_{k=1}^s\sum_{t=2}^{n-k-j+1}P\{\widehat{\tau}_{_{\scriptstyle 1}}+b=t\}\sum\limits_{v=k-1}^{n-t-j}P\{S_{k-1}=v\}\nonumber\\ && \cdot\binom{n-t-v}{j}p^j\bar{p}^{n-t-j}\sum_{u=n-t-v+1}^\infty P\{V=u\}, \end{matrix}}$
其中 ${\tau}_{_{k}}, k\geq 1$ $\widetilde{\tau}_{_{\scriptstyle 2}}$
将 (3.17) 式和 (3.18) 式代入 (3.16) 式, 并作 $z$ - 变换得
(3.19) $\begin{aligned} p_{0 j}^{+}(z)= & f(z) q_{j}^{+}(z)+[f(z)]^{2} B(z) H(V(\bar{p} z)) p_{1 j}^{+}(z) \\ & +\frac{f(z) B(z)[1-H(V(\bar{p} z))]}{1-V(\bar{p} z)}\left\{\sum_{m=1}^{N-1} W^{(m)}(D) \sum_{u=m}^{\infty} P\{V=u\}\binom{u}{m}(p z)^{m}(\bar{p} z)^{u-m} p_{m j}^{+}(z)\right. \\ & +\sum_{m=1}^{N-1} C_{m}(D) \sum_{u=m}^{\infty} P\{V=u\} \sum_{r=m}^{u}\binom{r-1}{m-1}(p z)^{m}(\bar{p} z)^{r-m} p_{m j}^{+}(z) \\ & +W^{(N-1)}(D) \sum_{u=N}^{\infty} P\{V=u\} \sum_{r=N}^{u}\binom{r-1}{N-1}(p z)^{N}(\bar{p} z)^{r-N} p_{N j}^{+}(z) \\ & \left.+W^{(j)}(D) \sum_{u=j+1}^{\infty} P\{V=u\} \sum_{k=j}^{u-1}\binom{k}{j}(p z)^{j}(\bar{p} z)^{k-j}\right\} \end{aligned}$
当 $L(0^+)=i, i=1, 2, \cdots$
(3.20) $\begin{aligned} P_{i j}\left(n^{+}\right)= & \sum_{k=1}^{i} \sum_{t=k-1}^{n} P\left\{\sum_{m=1}^{k-1} b_{m}=t\right\} Q_{j-i+k}\left((n-t)^{+}\right) \\ = & \sum_{k=1}^{\infty} h_{k} \sum_{t=i}^{n-k-1} P\left\{b^{<i>}=t\right\} \sum_{v=k}^{n-t-1} P\left\{S_{k}=v\right\} \sum_{u=1}^{n-t-v} p \bar{p}^{v+u-1} P_{1 j}\left((n-t-v-u)^{+}\right) \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} W^{(m)}(D) \sum_{t=i}^{n-k-m+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-m} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{u=m}^{n-t-v} P\{V=u\}\binom{u}{m} p^{m} \bar{p}^{v+u-m} P_{m j}\left((n-t-v-u)^{+}\right) \\ & +\sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{m=1}^{N-1} C_{m}(D) \sum_{t=i}^{n-k-m+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-m} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{r=m}^{n-t-v}\binom{r-1}{m-1} p^{m} \bar{p}^{v+r-m} \sum_{u=r}^{\infty} P\{V=u\} P_{m j}\left((n-t-v-r)^{+}\right) \\ + & W^{(N-1)}(D) \sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{t=i}^{n-N-k+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-N} P\left\{S_{k-1}=v\right\} \\ & \cdot \sum_{r=N}^{n-t-v}\binom{r-1}{N-1} p^{N} \bar{p}^{v+r-N} \sum_{u=r}^{\infty} P\{V=u\} P_{N j}\left((n-t-v-r)^{+}\right) \\ + & W^{(j)}(D) \sum_{s=1}^{\infty} h_{s} \sum_{k=1}^{s} \sum_{t=i}^{n-k-j+1} P\left\{b^{<i>}=t\right\} \sum_{v=k-1}^{n-t-N} P\left\{S_{k-1}=v\right\} \\ & \cdot\binom{n-t-v}{j} p^{j} \bar{p}^{n-t-j} \sum_{u=n-t-v+1}^{\infty} P\{V=u\}. \end{aligned}$
(3.21) $\begin{aligned} p_{i j}^{+}(z)= & \sum_{k=1}^{i}[B(z)]^{k-1} q_{j-i+k}^{+}(z)+f(z)[B(z)]^{i} H(V(\bar{p} z)) p_{1 j}^{+}(z) \\ & +\frac{[B(z)]^{i}[1-H(V(\bar{p} z))]}{1-V(\bar{p} z)}\left\{\sum_{m=1}^{N-1} W^{(m)}(D) \sum_{u=m}^{\infty} P\{V=u\}\binom{u}{m}(p z)^{m}(\bar{p} z)^{u-m} p_{m j}^{+}(z)\right. \\ & +\sum_{m=1}^{N-1} C_{m}(D) \sum_{u=m}^{\infty} P\{V=u\} \sum_{r=m}^{u}\binom{r-1}{m-1}(p z)^{m}(\bar{p} z)^{r-m} p_{m j}^{+}(z) \\ & +W^{(N-1)}(D) \sum_{u=N}^{\infty} P\{V=u\} \sum_{r=N}^{u}\binom{r-1}{N-1}(p z)^{N}(\bar{p} z)^{r-N} p_{N j}^{+}(z) \\ & \left.+W^{(j)}(D) \sum_{u=j+1}^{\infty} P\{V=u\} \sum_{k=j}^{u-1}\binom{k}{j}(p z)^{j}(\bar{p} z)^{k-j}\right\} \end{aligned}$
由 (3.19) 式和 (3.21) 式可得 $p^+_{_{0j}}(z)$ $p^+_{_{ij}}(z)$
(3.22) ${ \begin{matrix} p^+_{_{ij}}(z)=\sum_{k=1}^{i} [B(z)]^{k-1}q^+_{_{j-i+k}}(z) +\dfrac{[B(z)]^{i-1}}{f(z)}\big\{p^+_{_{0j}}(z)-f(z)q^+_{_{j}}(z)\big\}, i=1, 2, \cdots. \end{matrix} }$
将 (3.22) 式代入 (3.19) 式, 整理可得 (3.14) 式, 再将 (3.14) 式代入 (3.22) 式可得 (3.15) 式.
${\bf定理3.3}$ $j=N, N+1, N+2, \cdots $ $|z|<1$
(3.23) $p^+_{_{ 0j}}(z)=f(z)\left\{q^+_{_{ j}}(z)+\dfrac{f(z)B(z)[1-V(\bar{p}z)]H(V(\bar{p}z))q^+_j(z)+\gamma_j(z)}{\Delta(z)}\right\},$
(3.24) $ p^+_{_{ ij}}(z)=\sum_{k=1}^{i}[B(z)]^{k-1}q^+_{_{ {j-i+k}}}(z)\nonumber+\dfrac{[B(z)]^{i-1}\{f(z)B(z)[1-V(\bar{p}z)]H(V(\bar{p}z))q^+_j(z)+\gamma_j(z)\}}{\Delta(z)}, i=1, 2, \cdots, $
其中 $B(z)$ $q^+_{_{j}}(z)$ $\Delta(z)$
${\bf证}$ $j=N, N+1, N+2, \cdots$ $N(n^+)=j$ $n^+$ $j$
4 队长的稳态分布
下面以时刻 $n^+$ $n^+$
4.1 时刻 $n^+$
${\bf定理4.1}$ $p^+_{_{j}}=\lim\limits_{n\to \infty}P\{N(n^+)=j\}, j=0, 1, 2, \cdots$ $n^+$ $j$ $n^+$ $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
(1) 当 $\rho\geq1$ $p^+_{_{j}}=0, j=0, 1, 2, \cdots$ $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
(2) 当 $\rho<1$ $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
(4.1) $p^+_{_{0}}=\dfrac{(1-\rho)[1-V(\bar{p})]}{[1-V(\bar{p})]H(V(\bar{p}))+[1-H(V(\bar{p}))]\Delta},$
(4.2) $p^+_{_{j}}= \dfrac{p(1-\rho)\left\{[1-V(\bar{p})]H(V(\bar{p}))q^+_{_{j}}+[1-H(V(\bar{p}))](\sigma_j+\eta_j)\right\}}{[1-V(\bar{p})]H(V(\bar{p}))+[1-H(V(\bar{p}))]\Delta}, j=1, 2, \cdots, N-1,$
(4.3) $p^+_{_{j}}=\dfrac{p(1-\rho)\left\{[1-V(\bar{p})]H(V(\bar{p}))q^+_{_{j}}+[1-H(V(\bar{p}))]\gamma_j\right\}}{[1-V(\bar{p})]H(V(\bar{p}))+[1-H(V(\bar{p}))]\Delta},j=N, N+1, N+2, \cdots,$
此时 $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
${\bf证}$ (1) 首先用归纳法证明下面的公式
(4.4) $\begin{aligned} T(m)= & \sum_{k=1}^{m} \sum_{u=k}^{\infty} P\{V=u\} \sum_{r=k}^{u}\binom{r-1}{k-1} p^{k-1} \bar{p}^{r-k}-E[V] \\ & +\sum_{u=m}^{\infty} P\{V=u\} \sum_{r=m}^{u}(u-r)\binom{r-1}{m-1} p^{m} \bar{p}^{r-m}=0. \end{aligned}$
假设当 $m=n(n>1)$ $T(n)=0$ $m=n+1$
(2) 根据 $z$ - 变换极限理论 [29 ] 知 $p^+_{_{j}}=\lim\limits_{z\to 1^{-}}(1-z)p^+_{_{ij}}(z)$ . 因此, 对于 $p^+_{_{0}}$ $p^+_{_{0}}=\lim\limits_{z\to 1^{-}}(1-z)p^+_{_{i0}}(z)$
同理, 当 $j=1,2,\cdots,N-1$
类似地, 当 $j=N,N+1,\cdots$
于是当 $z\to 1^{-}$ $\dfrac{1-z}{\Delta(z)}$ $\dfrac{0}{0}$
(4.5) ${ \begin{matrix} &&\lim\limits_{z\to 1^{-}}\left[-{\dfrac{{\mathrm{d}}\Delta(z)}{{\mathrm{d}} z}}\right] \\ &=&[1-H(V(\bar{p}))]\sum\limits_{u=1}^\infty u\bar{p}^uP\{V=u\}+[1-V(\bar{p})]H(V(\bar{p}))\left(\dfrac{1}{p}+E[b]\right)\nonumber\\ && +E[b][1-H(V(\bar{p}))]\Bigg\{NW^{(N-1)}(D)\sum\limits_{u=N}^{\infty}P\{V=u\}\sum\limits_{r=N}^{u}\binom{r-1}{N-1}p^N\bar{p}^{r-N}\nonumber\\ && +\sum\limits_{m=1}^{N-1}C_{m}(D)\sum\limits_{u=m}^\infty P\{V=u\}\sum\limits_{r=m}^{u}m\binom{r-1}{m-1}p^m\bar{p}^{r-m}\\ &&+\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m}^{\infty}mP\{V=u\}\binom{u}{m}p^m\bar{p}^{u-m}\Bigg\}\nonumber\\ && +[1-H(V(\bar{p}))]\Bigg\{W^{(N-1)}(D)\sum\limits_{u=N}^{\infty}P\{V=u\}\sum\limits_{r=N}^{u}r\binom{r-1}{N-1}p^N\bar{p}^{r-N}\nonumber\\ && +\!\sum\limits_{m=1}^{N-1}C_{m}(D)\sum\limits_{u=m}^\infty P\{V\!=\!u\}\sum\limits_{r=m}^{u}r\binom{r-1}{m-1}p^m\bar{p}^{r-m} \!+\!\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m}^{\infty}uP\{V\!=\!u\}\binom{u}{m}p^m\bar{p}^{u-m}\Bigg\}\nonumber\\ & =&[1-H(V(\bar{p}))]\sum\limits_{u=1}^\infty u\bar{p}^uP\{V=u\}+[1-V(\bar{p})]H(V(\bar{p}))\left(\dfrac{1}{p}+E[b]\right)\nonumber\\ && +E[b][1-H(V(\bar{p}))]\Bigg\{NW^{(N-1)}(D)\sum\limits_{u=N}^{\infty}P\{V=u\}\sum\limits_{r=N}^{u}\binom{r-1}{N-1}p^N\bar{p}^{r-N}\nonumber\\ && +\sum\limits_{m=1}^{N-1}[W^{(m-1)}(D)-W^{(m)}(D)]\sum\limits_{u=m}^\infty P\{V=u\}\sum\limits_{r=m}^{u}m\binom{r-1}{m-1}p^m\bar{p}^{r-m}\nonumber\\ && +\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m}^{\infty}P\{V=u\}m\Bigg[\sum\limits_{r=m}^{u}\binom{r-1}{m-1}p^m\bar{p}^{r-m}-\sum\limits_{r=m+1}^{u}\binom{r-1}{m}p^{m+1}\bar{p}^{r-m-1}\Bigg]\Bigg\}\nonumber\\ && +[1-H(V(\bar{p}))]\Bigg\{W^{(N-1)}(D)\sum\limits_{u=N}^{\infty}P\{V=u\}\sum\limits_{r=N}^{u}r\binom{r-1}{N-1}p^N\bar{p}^{r-N}\nonumber\\ && +\sum\limits_{m=1}^{N-1}[W^{(m-1)}(D)-W^{(m)}(D)]\sum\limits_{u=m}^\infty P\{V=u\}\sum\limits_{r=m}^{u}r\binom{r-1}{m-1}p^m\bar{p}^{r-m}\nonumber\\ && +\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m}^{\infty}uP\{V=u\}\Bigg[\sum\limits_{r=m}^{u}\binom{r-1}{m-1}p^m\bar{p}^{r-m}-\sum\limits_{r=m+1}^{u}\binom{r-1}{m}p^{m+1}\bar{p}^{r-m-1}\Bigg]\Bigg\}\nonumber\\ &=&\dfrac{[1-V(\bar{p})][1-H(V(\bar{p}))]}{p}+[1-V(\bar{p})]H(V(\bar{p}))\left(\dfrac{1}{p}+E[b]\right)\nonumber\\ && +E[b][1-H(V(\bar{p}))]\sum\limits_{m=1}^{N}W^{(m-1)}(D)\sum\limits_{u=m}^\infty P\{V=u\}\sum\limits_{r=m}^{u}\binom{r-1}{m-1}p^m\bar{p}^{r-m}\nonumber\\ && +[1-H(V(\bar{p}))]\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m}^\infty P\{V=u\}\sum\limits_{r=m}^u(u-r)\binom{r-1}{m-1}p^{m}\bar{p}^{r-m}\nonumber\\ && +[1-H(V(\bar{p}))]\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m+1}^{\infty}P\{V=u\}\sum\limits_{r=m+1}^{u}(r-u)\binom{r-1}{m}p^{m+1}\bar{p}^{r-m-1}\nonumber\\ &=&\dfrac{[1-V(\bar{p})][1-H(V(\bar{p}))]}{p}+[1-V(\bar{p})]H(V(\bar{p}))\left(\dfrac{1}{p}+E[b]\right)+E[b][1-H(V(\bar{p}))]\Delta\nonumber\\ && -[1-H(V(\bar{p}))]\sum\limits_{m=1}^{N-1}W^{(m)}(D)\Bigg[\sum\limits_{k=1}^m\sum\limits_{u=k}^\infty P\{V=u\}\sum\limits_{r=k}^u\binom{r-1}{k-1}p^{k-1}\bar{p}^{r-k}-E[V]\Bigg]\nonumber\\ && +[1-H(V(\bar{p}))]\sum\limits_{m=1}^{N-1}W^{(m)}(D)\Bigg[\sum\limits_{k=1}^{m+1}\sum\limits_{u=k}^{\infty}P\{V=u\}\sum\limits_{r=k}^{u}\binom{r-1}{k-1}p^{k-1}\bar{p}^{r-k}-E[V]\Bigg]\nonumber\\ &=&\dfrac{[1-V(\bar{p})][1-H(V(\bar{p}))]}{p}+[1-V(\bar{p})]H(V(\bar{p}))\left(\dfrac{1}{p}+E[b]\right)+E[b][1-H(V(\bar{p}))]\Delta\nonumber\\ && +[1-H(V(\bar{p}))]\sum\limits_{m=1}^{N-1}W^{(m)}(D)\sum\limits_{u=m+1}^\infty P\{V=u\}\sum\limits_{r=m+1}^u\binom{r-1}{m}p^{m}\bar{p}^{r-m-1}\nonumber\\ &=&\left\{[1-V(\bar{p})]H(V(\bar{p}))+[1-H(V(\bar{p}))]\Delta\right\}\left(\dfrac{1}{p}+E[b]\right). \end{matrix}}$
由引理 2.1 知, 当 $\rho \geq 1$ $E[b]=\infty$ $\lim\limits_{z\to 1^{-}}\left[-{\dfrac{{\mathrm{d}}\Delta(z)}{{\mathrm{d}} z}}\right]=\infty$ . 则当 $\rho \geq 1$ $p^+_{_{j}}=0, j=0, 1, 2, \cdots$ .
当 $\rho < 1$ $E[b]=\dfrac{\rho}{p(1-\rho)}$
再使用 L'Hospital 法则, 并经过一些代数运算可得 $p^+_{_{j}}, j=0, 1, 2, \cdots$
下面证明当 $\rho<1$ $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
${\bf推论4.1}$ $\pi^+(z)=\sum\limits_{j=0}^\infty p^+_{_{j}}z^j, |z|<1$ $n^+$ $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$ $E[L^+]$ $n^+$ $\rho<1$
(4.6) $\begin{aligned} \pi^{+}(z)= & \frac{(1-\rho)(1-z) G(\bar{p}+p z)}{G(\bar{p}+p z)-z} \\ & \cdot \frac{1-V(\bar{p})+[1-H(V(\bar{p}))] \sum_{m=1}^{N-1} z^{m} W^{(m)}(D) \sum_{u=m+1}^{\infty} P\{V=u\} \sum_{r=m+1}^{u}\binom{r-1}{m} p^{m+1} \bar{p}^{r-m-1}}{[1-V(\bar{p})] H(V(\bar{p}))+[1-H(V(\bar{p}))] \Delta} \end{aligned} $
(4.7) $\begin{aligned} E\left[L^{+}\right]= & \rho+\frac{p^{2}}{2(1-\rho)} E\left[\chi^{2}-\chi\right] \\ & +\frac{[1-H(V(\bar{p}))] \sum_{m=1}^{N-1} m W^{(m)}(D) \sum_{u=m+1}^{\infty} P\{V=u\} \sum_{r=m+1}^{u}\binom{r-1}{m} p^{m+1} \bar{p}^{r-m-1}}{[1-V(\bar{p})] H(V(\bar{p}))+[1-H(V(\bar{p}))] \Delta} \end{aligned}$
其中 $E[\chi^2]=\sum\limits_{j=1}^\infty j^2g_j$ $\Delta$
${\bf证}$
(4.8) $\begin{aligned} \pi^{+}(z)= & \frac{p(1-\rho)}{[1-V(\bar{p})] H(V(\bar{p}))+[1-H(V(\bar{p}))] \Delta}\left\{\frac{1-V(\bar{p})}{p}+[1-V(\bar{p})] H(V(\bar{p})) \sum_{j=1}^{\infty} q_{j}^{+} z^{j}\right. \\ & \left.+[1-H(V(\bar{p}))]\left[\sum_{j=1}^{N-1} \eta_{j} z^{j}+\sum_{j=1}^{N-1} \sigma_{j} z^{j}+\sum_{j=N}^{\infty} \gamma_{j} z^{j}\right]\right\}, \end{aligned}$
(4.9) $\sum\limits_{j=1}^{\infty} q_{_{j}}^{+}z^j=\dfrac{z[1-G(\bar{p}+pz)]}{p[G(\bar{p}+pz)-z]},$
(4.10) $\sum\limits_{j=1}^{N-1}\eta_{_{j}}z^j=\dfrac{-1+V(\bar{p})}{p}+\dfrac{1}{p}\sum\limits_{m=1}^Nz^{m-1}W^{(m-1)}(D)\sum\limits_{u=m}^\infty P\{V=u\}\sum_{r=m}^{u}\binom{r-1}{m-1}p^m\bar{p}^{r-m},$
(4.11) $\sum\limits_{j=1}^{N-1}\sigma_{_{j}}z^j+\sum\limits_{j=N}^\infty\gamma_{_{j}}z^j=\sum\limits_{j=1}^{\infty} q_{_{j}}^{+}z^j\sum\limits_{m=1}^Nz^{m-1}W^{(m-1)}(D)\sum\limits_{u=m}^\infty P\{V=u\}\sum_{r=m}^{u}\binom{r-1}{m-1}p^m\bar{p}^{r-m}.$
将 (4.9) 式、(4.10) 式和 (4.11) 式代入 (4.8) 式, 可得 (4.6) 式. 再运用 $E[L^+]=\left.{\left[\dfrac{{\mathrm{d}}\pi^+(z)}{{\mathrm{d}} z}\right]} \right|_{z=1}$ $(4.7)$
${\bf推论4.2}$ $n^+$ $L_d^+$
其中, $m=1, 2, \cdots, N-1.$
${\bf证}$ $n^+$
则附加队长 $L_d^+$ $P\{L_d^+=m\}=\dfrac{1}{m!}\left.{\left[{\dfrac{{\mathrm{d^m}}\pi_d^+(z)}{{\mathrm{d}} z^m}} \right]}\right|_{z=0}$
一些离散时间排队系统是本文讨论的排队模型的特例, 可以通过选择参数的不同取值直接获得.
${\bf推论4.3}$ $D\rightarrow\infty$ $P\{H=\infty\}=1$ $(N,V)$ - 策略控制的 Geo/G/1 离散时间排队系统. 当 $\rho<1$
${\bf推论 4.4}$ $D\rightarrow\infty$ $P\{H=1\}=1$ $(N,V)$ - 策略控制的 Geo/G/1 离散时间排队系统. 当 $\rho<1$
${\bf推论 4.5}$ $D\rightarrow\infty$ $(N,V)$ - 策略控制的 Geo/G/1 离散时间排队系统. 当 $\rho<1$
${\bf推论 4.6}$ $P\{H=1\}=1$ $(N,D)$ - 策略的 Geo/G/1 离散时间排队系统. 当 $\rho<1$
${\bf推论 4.6}$ $P\{H=\infty\}=1$ $(N,D)$ - 策略的 Geo/G/1 离散时间排队系统. 当 $\rho<1$
4.2 时刻 $n^-$ $n$
下面讨论时刻 $n^-$ $n$
令 $P_{ij}(n^-)=P\{N(n^-)=j|N(0^-)=i \}, P_{ij}(n)=P\{N(n)=j|N(0)=i \}$ $p^-_{_{ j}}=\lim\limits_{n\to \infty}P\{N(n^-)$ $=j\}, p_{_{j}}=\lim\limits_{n\to \infty}P\{N(n)=j\}$ . 假设系统在 $(0^-, 0)$ $(0, 0^+)$ $P\{N(0^-)=i\}=P\{N(0)=i \}=P\{N(0^+)=i \}$ .
${\bf定理4.2}$ $\rho<1$
${\bf证}$ $i, j=0, 1, 2, \cdots, n=1, 2, \cdots$ 图 2.1 可得
(4.12) ${ \begin{matrix} &&\hspace{-1cm}P_{ij}(n^-)=P\{N(n^-)=j|N(0^-)=i\} =P\{N((n-1)^+)=j|N(0^+)=i\} =P_{ij}((n-1)^+). \end{matrix}}$
对 (4.12) 式求 $n\rightarrow\infty$
${\bf定理4.3}$ $\rho<1$
${\bf证}$ $p_{_{0}}=(1-p)p^-_{_{0}}, p_{_{j}}=pp^-_{_{j-1}}+(1-p)p^-_{_{j}}, j=1, 2, \cdots$
${\bf注 4.1}$ $n^-$ $n^+$ $n$
下面讨论在系统外部观测点处队长的稳态分布 $p^{out}_j$ . 外部观察点处队长的分布在研究系统指标方面起着关键的作用. 比如, 要想使用 Little 公式来获得排队系统中的平均等待时间, 则需要外部观察时刻点的平均顾客数. 对于 LAS-DA 系统, 外部观测点落在间隔 $(n^+, (n+1)^-)$ $n=0, 1, 2, \cdots$ . 由于在时刻 $n^+$ $(n+1)^-$ $n^+$ $(n+1)^-$ $\rho<1$
5 数值实例
5.1 系统的空闲率 $p^+_{_{0}}$ $E[L^+]$
在本节中, 根据定理 4.1 和推论 4.1 得出的重要结论, 通过数值计算实例来分析系统的空闲率 $p^+_{_{0}}$ $E[L^+]$ $\rho$ $N$ $D$ $V$ $H$
${\bf例 5.1}$ $\chi$ $P\{\chi=j\}=\dfrac{1}{\mu}\left(1-\dfrac{1}{\mu}\right)^{j-1}, j=1, 2, \cdots$ $W$ $P\{W=j\}=\theta(1-\theta)^{j-1}, j=1, 2, \cdots$ $V$ $P\{V=j\}=q(1-q)^j, j=0, 1, 2, \cdots$ $H$ $P\{H=j\}=h(1-h)^{j-1}, j=1, 2, \cdots$ . 依据 (4.1) 式和 (4.7) 式, 运用 Matlab 软件编程作图, 图 6 和图 7 反映了随着 $\rho$ $N$ $p^+_{_{0}}$ $E[L^+]$ 图 8 和图 9 反映了随着 $\rho$ $D$ $p^+_{_{0}}$ $E[L^+]$
图 6
图 6
$p^+_{_{0}}$ $\rho$ $N$
图 7
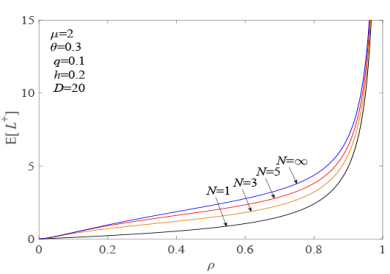
图 7
$\mathrm{E}[L^+]$ $\rho$ $N$
图 8
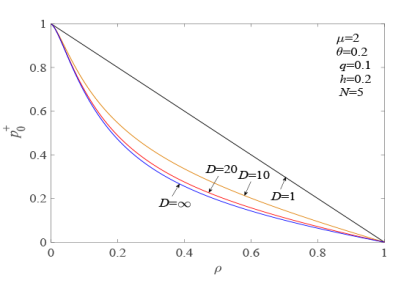
图 8
$p^+_{_{0}}$ $\rho$ $D$
图 9
图 9
$\mathrm{E}[L^+]$ $\rho$ $D$
由图 6 和图 8 可以看出, $p^+_{_{0}}$ $\rho$ $N$ $D$ $N$ $D$ ) 不变, $\rho$ $p^+_{_{0}}$ $\rho$ $N$ $D$ ) 越大, 服务员忙期开始时的初始顾客数越多, 系统的忙期越长, 从而使得系统的空闲率 $p^+_{_{0}}$
由图 7 和图 9 中的曲线表明, $E[L^+]$ $\rho$ $N$ $D$ $N$ $D$ ) 不变, $\rho$ $\rho$ $N$ $D$ ) 越大, 累积在系统中等待服务的顾客数越多, 从而使得系统的平均队长 $E[L^+]$
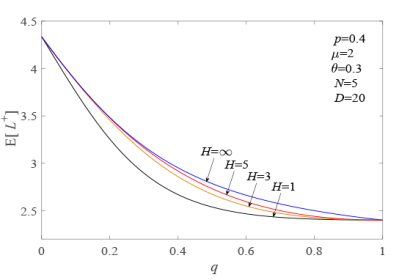
${\bf例 5.2}$ $\chi$ $W$ $V$ $H$ $P\{H=J\}=1$ . 依据 (4.1) 式和 (4.7) 式, 运用 Matlab 软件编程作图, 图 10 和图 11 反映了随着 $q$ $H$ $p^+_{_{0}}$ $E[L^+]$
图 10
图 10
$p^+_{_{0}}$ $q$ $H$
图 11
图 11
$\mathrm{E}[L^+]$ $q$ $H$
由图 10 可以看出, $p^+_{_{0}}$ $q$ 图 11 可以看出, $E[L^+]$ $q$ $q$ $E[V]=\dfrac{1-q}{q}$ $p^+_{_{0}}$ $E[L^+]$ $H=5$ $H=\infty$
5.2 队长稳态分布 $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$
下面依据定理 4.1 给出的便于作数值计算的队长稳态分布的递推公式, 通过数值计算实例, 定量探讨系统容量的优化设计.
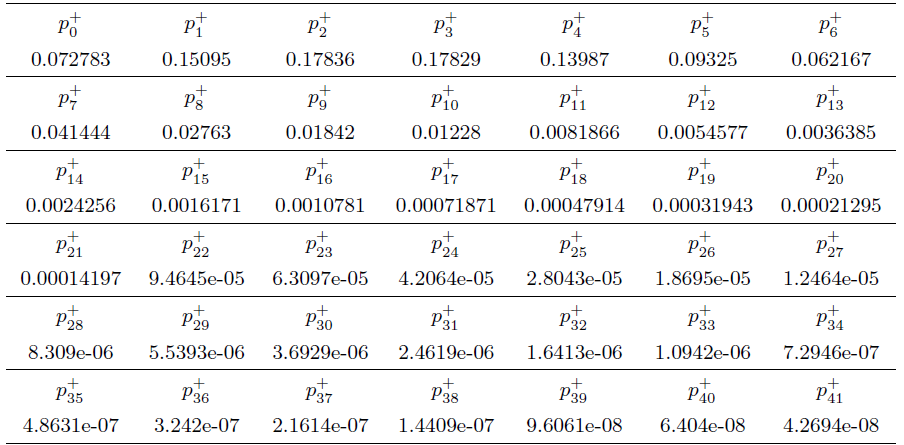
${\bf例 5.3}$ $\chi$ $W$ $V$ $H$ $p=0.4, \mu=2, h=0.2, q=0.1, \theta=0.3, N=4, D=20$ 表 1 给出了队长稳态分布 $\{p^+_{_{j}}, j=0, 1, 2, \cdots\}$ $E[L^+]=3.5603$ .
由表 1 可知, 当 $j$ $p^+_{_{j}}$ 表1 中的数据, (5.1) 式给出了系统中顾客数超过平均稳态队长的概率, 这意味着如果只以平均稳态队长为参考标准来设计系统容量, 到达的顾客由于系统无法容纳而流失的概率将达到 41.9617%, 进一步由 (5.2) 式可得即使以比平均稳态队长大1个单位为参考标准设计, 到达顾客的流失概率也达到了27.9747%, 此时, 顾客的流失概率也是相当大的! 因此, 在设计系统容量时, 不能仅仅以平均稳态队长作为参考依据.
(5.1) $P\{L^+>E[L^+]\}=1-\sum_{j=0}^{E[L^+]} p^+_{_{j}}=1-\sum_{j=0}^3 p^+_{_{j}}=0.419617,$
(5.2) $P\{L^+>E[L^+]+1\}=1-\sum_{j=0}^{E[L^+]+1} p^+_{_{j}}=1-\sum_{j=0}^4 p^+_{_{j}}=0.279747.$
为了减少顾客的流失率, 现在来计算合理的系统容量 $M$ . 如果要求到达的顾客流失的概率不超过万分之一, 即
那么根据表 1 的数据可得 $M\geq 24$ $M=24$ . 由此可见, 使用队长稳态分布 (系统中有 $j$
6 费用结构模型下的最优控制策略
(1) 在一个更新周期内, 系统由于启动等因素产生的固定消耗费用为 $a$
(2) 一个顾客在系统中逗留 (包括等待和服务) 单位时间所需的费用为 $b$
(3) 在服务员忙期内向服务员支付的单位时间服务费为 $c$
${\bf定理6.1}$ $\rho<1$
(6.1) $F(N, D)=\frac{a p(1-\rho)[1-V(\bar{p})]}{[1-H(V(\bar{p}))][V(\bar{p})+\Delta]}+b E\left[L^{+}\right]+c \rho.$
其中 $V(\bar{p})=\sum_{k=0}^{\infty}\bar{p}^kP\{V=k\}$ $\Delta $ $E[L^+]$
${\bf证}$ $Q_b$ $Q_b$
因此, 服务员忙期开始时系统中的平均顾客数 $E[Q_b]$
设 $C$ $B$ $I$ $E(C), E(I), E(B)$ $C, B$ $I$
(6.2) $E[B]=E[b] E\left[Q_{b}\right]=\frac{\rho[1-H(V(\bar{p}))][V(\bar{p})+\Delta]}{p(1-\rho)[1-V(\bar{p})]}, \rho<1.$
另外, 由于服务员忙期开始时在系统内的顾客数为上一个 "服务员非忙期" 内到达的顾客数, 且顾客的到达间隔时间服从参数为 $p$
服务员忙期和服务员非忙期形成了系统的一个更新周期, 则系统的一个更新周期的平均长度为
(6.3) ${ \begin{matrix} E[C]=E(I)+E(B)=\dfrac{[1-H(V(\bar{p}))][V(\bar{p})+\Delta]}{p(1-\rho)[1-V(\bar{p})]}, \rho<1. \end{matrix}}$
于是由更新报酬过程理论知, 系统长期运行下单位时间内所产生的期望总费用为
(6.4) ${ \begin{matrix} F(N,D)=\dfrac{\mbox{一个更新周期内的期望费用}}{\mbox{一个更新周期的平均长度}}=\dfrac{a}{E[C]}+bE[L^+]+\dfrac{cE[B]}{E[C]}. \end{matrix}}$
将 (6.2) 式和 (6.3) 式代入 (6.4) 式, 可得 (6.1) 式.
${\bf例 6.1}$ $\chi$ $W$ $V$ $H$ $F(N, D)$
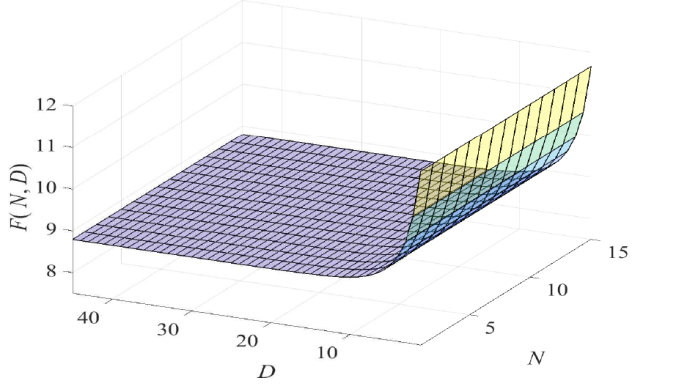
由上式可知, $F(N, D)$ $N$ $D$ $(N^*, D^*)$ . 由表 2 给出了当 $p=0.3, \mu=2, h=0.2, q=0.1, \theta=0.3, a=100, b=1, c=2$ $N$ $N$ $F(N, D^*_N)$ $D^*_N$ $N$ $F(N, D^*_N)$ $(N^*, D^*)$ .
表 2 中数据表明, 随着 $N$ $F(N, D^*_N)$ 图 12 ). 同时可知, 期望费用的最小值为 $F(5, 42)=7.5112$ $(N^*, D^*)=(5,42)$ . 于是, 当系统中顾客数达到 5 个或者到达系统等待服务的顾客所需服务的总工作量不小于 42 时, 无论哪一个先发生, 处于休假的服务员立即中断休假回到系统开始为顾客服务.
图 12
图 12
$F(N,D)$ $N$ $D$
${\bf例 6.2}$ $\chi$ $W$ $V$ $H$ $P\{H=J\}=1$ . 于是由 (6.1) 式可得 $F(N, D, J)$
由上式可知, 如果服务员连续休假 $J$ $P\{H=J\}=1$ $\rho<1$ $F(N, D, J)$ $N$ $D$ $J$ $(N^*, D^*, J^*)$ . 由表 3 给出了当 $p=0.3, \mu=2, q=0.1, \theta=0.3, a=100, b=1, c=2$ $N$ $N$ $F(N, D, J)$ $F(N, D^*_N, J^*_N)$ $(D^*_N, J^*_N)$ $N$ $F(N, D^*_N, J^*_N)$ $(N^*, D^*,, J^*_N)$ .
表 3 中数据可知, 随着 $N$ $F(N, D^*_N, J^*_N)$ $F(5, 41, 10)=7.2766$ $(N^*, D^*, J^*_N)=(5, 41, 10)$ . 也就是说, 当服务员至少连续休假 10 次时, 若系统中顾客数达到 5 个或者到达系统等待服务的顾客所需服务的总工作量不小于 41 时, 无论哪一个先发生, 正在休假的服务员立即中断休假回到系统开始为顾客服务.
7 结论
本文以获得系统队长概率分布的具体表达式为重点内容展开研究, 从任意初始状态出发, 得到时刻 $n^+$ $z$ - 变换表达式 (不需要首先假定系统处于平稳状态) 和稳态分布 (系统中有 $j$ $n^-$ $n$ $n^+$ $p^+_{_{0}}$ $E[L^+]$
参考文献
View Option
[1]
Bruneel H Kim B G Discrete-Time Models for Communication Systems Including ATM . Boston : Kluwer Academic , 1993
[本文引用: 2]
[2]
田乃硕 , 徐秀丽 , 马占友 . 离散时间排队论 . 北京 : 科学出版社 , 2008
[本文引用: 1]
Tian N S Xu X L Ma Z Y Discrete-Time Queueing Theory . Beijing : Science Press , 2008
[本文引用: 1]
[3]
Ma Z Y Wang W B Hu L M Performance evaluation and analysis of a discrete queue system with multiple working vacations and non-preemptive priority
Journal of Industrial & Management Optimization , 2020 , 16 3 ): 1135 -1148
[4]
Li J H Zhang Z G Chen X F A note on customer joining strategy in a discrete-time Geo/G/1 queue with server vacations-a simple mean value analysis
Queueing Models and Service Management , 2022 , 5 2 ): 45 -61
[5]
张恒 , 刘力维 . 带有负顾客和 $N$ - 策略的 Geo/Geo/1 排队模型均衡策略分析
应用数学 , 2024 , 37 2 ): 289 -302
Zhang H Liu L W Analysis of Geo/Geo/1 Queueing model equilibrium strategy with negative customer and $N$ - Policy
Mathematica Applicata , 2024 , 37 2 ): 289 -302
[6]
曹灿 , 刘再明 , 高珊 , 伍逸凡 . 具有风险敏感性顾客的离散时间排队系统策略研究
应用数学学报 , 2024 , 47 2 ): 284 -311
DOI:10.20142/j.cnki.amas.202401022
The research on customer strategy behavior in queueing system combined with game theory is a hot topic in the current queueing theory. This paper studies the strategic behavior of risk-sensitive customers in discrete-time queueing systems. Different from the classical economics of queues, the utility function in this paper is an expectation-variance quadratic utility function. Based on the Nash equilibrium and Markov process theory, we study the game behavior of <i>Geo</i>/<i>Geo</i>/1 queueing system with risk-sentitive customers under fully observable case and fully unobservable case, respectively. The individual optimal joining strategy, the joining strategy for the social net welfare and the server’s profit optimization are obtained. It is found that the smaller the risk sensitivity coefficient is, the more customers like to take risks and the stronger the willingness to join the system. Some numerical experiments are provided to illustrate the effect of the risk sensitivity coefficient on the customer strategic behavior.
Cao C Liu Z M Gao S Wu Y F Strategies research on the discrete-time queueing system with risk-sensitive customers
Acta Mathematicae Applicatae Sinica , 2024 , 47 2 ): 284 -311
DOI:10.20142/j.cnki.amas.202401022
The research on customer strategy behavior in queueing system combined with game theory is a hot topic in the current queueing theory. This paper studies the strategic behavior of risk-sensitive customers in discrete-time queueing systems. Different from the classical economics of queues, the utility function in this paper is an expectation-variance quadratic utility function. Based on the Nash equilibrium and Markov process theory, we study the game behavior of <i>Geo</i>/<i>Geo</i>/1 queueing system with risk-sentitive customers under fully observable case and fully unobservable case, respectively. The individual optimal joining strategy, the joining strategy for the social net welfare and the server’s profit optimization are obtained. It is found that the smaller the risk sensitivity coefficient is, the more customers like to take risks and the stronger the willingness to join the system. Some numerical experiments are provided to illustrate the effect of the risk sensitivity coefficient on the customer strategic behavior.
[7]
Shen Y G Ma Z Y Jiang Z S Li Y H Qin G L Performance analysis of P2P network based on differentiated service Geo/Geo/1+1 queue
Cluster Computing , 2024 , 27 7 ): 9837 -9849
[本文引用: 1]
[8]
Lee H W Seo W J The performance of the M/G/ 1 queue under the dyadic Min$(N, D)$ - policy and its cost optimization
Performance Evaluation , 2008 , 65 10 ): 742 -758
[本文引用: 1]
[9]
魏瑛源 , 唐应辉 , 余玅妙 . 基于 Min$(N, D)$ - 策略的 M/G/1 排队系统的队长分布及最优策略
系统科学与数学 , 2015 , 35 6 ): 729 -744
DOI:10.12341/jssms12594
[本文引用: 1]
考虑基于 Min $(N, D)$-策略的M/G/1排队系统, 运用全概率分解技术和拉普拉斯变换工具, 获得了队长瞬态分布的拉普拉斯变换的递推表达式和稳态队长分布的递推表达式, 进一步通过数值实例, 讨论了稳态队长分布对系统参数的敏感性, 并阐述了稳态队长分布的表达式在系统容量优化设计中的重要价值. 最后, 建立了费用模型, 对最优 Min $(N, D)$-策略与单一的最优$N$-策略和单一的最优$D$-策略进行了比较分析.
Wei Y Y Tang Y H Yu M M Queue length distribution and optimum policy for M/G/1 queueing system under Min$(N, D)$ - policy
Journal of Systems Science and Mathematical Sciences , 2015 , 35 6 ): 729 -744
DOI:10.12341/jssms12594
[本文引用: 1]
考虑基于 Min $(N, D)$-策略的M/G/1排队系统, 运用全概率分解技术和拉普拉斯变换工具, 获得了队长瞬态分布的拉普拉斯变换的递推表达式和稳态队长分布的递推表达式, 进一步通过数值实例, 讨论了稳态队长分布对系统参数的敏感性, 并阐述了稳态队长分布的表达式在系统容量优化设计中的重要价值. 最后, 建立了费用模型, 对最优 Min $(N, D)$-策略与单一的最优$N$-策略和单一的最优$D$-策略进行了比较分析.
[10]
Gu J X Wei Y Y Tang Y H Yu M M Queue size distribution of Geo/G/1 queue under the Min$(N, D)$ - policy
Journal of Systems Science and Complexity , 2016 , 29 3 ): 752 -771
[本文引用: 1]
[11]
Liu R B Alfa A S Yu M M Optimal power consumption control of sensor node based on $(N, D)$ - policy discrete-time queues
RAIRO-Operations Research , 2019 , 53 3 ): 937 -962
[本文引用: 1]
[12]
Wang R X Queue size distribution on a new $ND$
Discrete Dynamics in Nature and Society , 2021 , 9 1 -16
[本文引用: 1]
[13]
Divya V Krishnamoorthy A Vishnevsky V M Kozyrev D V On a queueing system with processing of service items under vacation and $N$ - policy with impatient customers
Queueing Models and Service Management , 2020 , 3 2 ): 167 -201
[本文引用: 2]
[14]
Ayyappan G Karpagam S A bulk queueing system with starting failure and repair, multiple vacation, stand-by server, closedown and $N$ - policy
Thai Journal of Mathematics , 2022 , 20 2 ): 905 -936
[本文引用: 1]
[15]
王勋 , 徐秀丽 . 带 N-策略的双阶段休假 M/M/1 排队系统驱动的流体模型性能分析
运筹学学报 (中英文) , 2024 , 28 1 ): 29 -39
[本文引用: 1]
Wang X Xu X L Performance analysis of a fluid model driven by M/M/1 queue with $N$ - policy and two-stage vacation
Operations Research Transactions , 2024 , 28 1 ): 29 -39
[本文引用: 1]
[16]
He Y X TangY H Yu M M Wu W Q Performance and optimization analysis of a queue with delayed uninterrupted multiple vacation and N-policy
Methodology and Computing in Applied Probability , 2024 , 26 Art 21
[本文引用: 1]
[17]
唐应辉 , 吴文青 , 刘云颇 , 刘晓云 . 基于多重休假的 Min$(N, V)$ - 策略 M/G/1 排队的队长分布
系统工程理论与实践 , 2013 , 33 1 ): 1 -14
[本文引用: 1]
Tang Y H Wu W Q Liu Y P Liu X Y The queue length distribution of M/G/1 queueing system with min$(N, V)$ - policy based on multiple server vacations
Systems Engineering---Theory & Practice , 2013 , 33 1 ): 1 -14
[本文引用: 1]
[18]
唐应辉 , 吴文青 , 刘云颇 . 基于单重休假的 Min$(N,V)$ - 策略 M/G/1 排队系统分析
应用数学学报 , 2014 , 37 6 ): 976 -995
[本文引用: 1]
Tang Y H Wu W Q Liu Y P Analysis of M/G/1 queueing system with Min$(N, V)$ - policy based on single server vacation
Acta Mathematicae Applicatae Sinica , 2014 , 37 6 ): 976 -995
[本文引用: 1]
[19]
蒋书丽 , 唐应辉 . 具有多级适应性休假和 Min$(N, V)$ - 策略控制的 M/G/1 排队系统
系统科学与数学 , 2017 , 37 8 ): 1866 -1884
DOI:10.12341/jssms13233
[本文引用: 1]
研究了具有多级适应性休假和${\rm Min}(N,V)$-策略控制的$M/G/1$排队系统, 运用全概率分解技术和拉普拉斯(L)变换工具, 研究了从任意时刻出发队长的瞬态分布, 得到了队长瞬态分布的拉普拉斯变换的表达式和稳态队长分布的递推表达式, 同时求出了稳态队长分布的概率母函数和平均队长的表达式. 进一步, 在一些特殊情况下, 例如当休假次数服从几何分布或休假次数为固定正整数值$M$时, 我们获得了相应稳态队长分布更简洁的显示表达式, 并通过数值实例阐述了稳态队长分布的显示表达式在系统容量的优化设计中的重要价值. 最后, 在建立系统费用结构模型基础上, 我们导出了系统长期单位时间的期望费用的显示表达式, 并通过数值实例不但确定了使得系统在长期单位时间内的期望费用最小的控制策略${{N}^{*}}$, 而且还确定了当休假次数为固定正整数值$M$时的联合控制策略$({{N}^{*}},{{M}^{*}})$.
Jiang S L Tang Y H M/G/1 queueing system with multiple adaptive vacations and Min$(N, V)$ - policy
Journal of Systems Science and Mathematical Sciences , 2017 , 37 8 ): 1866 -1884
DOI:10.12341/jssms13233
[本文引用: 1]
研究了具有多级适应性休假和${\rm Min}(N,V)$-策略控制的$M/G/1$排队系统, 运用全概率分解技术和拉普拉斯(L)变换工具, 研究了从任意时刻出发队长的瞬态分布, 得到了队长瞬态分布的拉普拉斯变换的表达式和稳态队长分布的递推表达式, 同时求出了稳态队长分布的概率母函数和平均队长的表达式. 进一步, 在一些特殊情况下, 例如当休假次数服从几何分布或休假次数为固定正整数值$M$时, 我们获得了相应稳态队长分布更简洁的显示表达式, 并通过数值实例阐述了稳态队长分布的显示表达式在系统容量的优化设计中的重要价值. 最后, 在建立系统费用结构模型基础上, 我们导出了系统长期单位时间的期望费用的显示表达式, 并通过数值实例不但确定了使得系统在长期单位时间内的期望费用最小的控制策略${{N}^{*}}$, 而且还确定了当休假次数为固定正整数值$M$时的联合控制策略$({{N}^{*}},{{M}^{*}})$.
[20]
Li J J Liu L W On an M/G/1 queue in random environment with Min$(N, V)$ - policy
RAIRO-Operations Research , 2018 , 52 1 ): 61 -77
[本文引用: 1]
[21]
兰绍军 , 唐应辉 . 具有多重休假和 Min$(N, V)$ - 策略控制的 Geo/G/1 离散时间排队
系统工程理论与实践 , 2015 , 35 3 ): 799 -810
DOI:10.12011/1000-6788(2015)3-799
[本文引用: 2]
考虑服务员具有多重休假和系统采用min(N,V)- 策略控制的离散时间Geo/G/1 排队系统, 使用全概率分解技术和更新过程理论, 研究了系统在任意时刻n<sup>+</sup> 的瞬态队长分布和稳态队长分布, 得到了瞬态队长分布的z- 变换表达式和稳态队长分布的递推表达式. 进一步, 得到了系统在时刻点n, n<sup>-</sup> 和外部观察时刻点的稳态队长分布. 特别地, 本文直接获得了一些特殊离散时间排队系统相应的结果. 最后, 通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
Lan S J Tang Y H Geo/G/1 discrete-time queue with multiple server vacations and Min$(N, V)$ - policy
Systems Engineering---Theory & Practice , 2015 , 35 3 ): 799 -810
DOI:10.12011/1000-6788(2015)3-799
[本文引用: 2]
考虑服务员具有多重休假和系统采用min(N,V)- 策略控制的离散时间Geo/G/1 排队系统, 使用全概率分解技术和更新过程理论, 研究了系统在任意时刻n<sup>+</sup> 的瞬态队长分布和稳态队长分布, 得到了瞬态队长分布的z- 变换表达式和稳态队长分布的递推表达式. 进一步, 得到了系统在时刻点n, n<sup>-</sup> 和外部观察时刻点的稳态队长分布. 特别地, 本文直接获得了一些特殊离散时间排队系统相应的结果. 最后, 通过数值实例阐述了获得便于计算的稳态队长分布的表达式在系统容量设计中的重要价值.
[22]
Lan S J Tang Y H Yu M M System capacity optimization design and optimal threshold $N^*$ $(N, V)$ - policy
Journal of Industrial and Management Optimization , 2016 , 12 4 ): 1435 -1464
[本文引用: 2]
[23]
旷欣宇 , 唐应辉 . 具有多级适应性休假和 Min$(N, V)$ - 策略的 Geo/G/1 排队系统分析
应用数学 , 2024 , 37 4 ): 1133 -1153
[本文引用: 3]
Kuang X Y Tang Y H Analysis of Geo/G/1 queueing system with multiple adaptive vacations and Min$(N, V)$ - policy
Mathematica Applicata , 2024 , 37 4 ): 1133 -1153
[本文引用: 3]
[24]
李丹 , 唐应辉 . 基于 Min$(N, D, V)$ - 策略和单重休假且休假不中断的 M/G/1 排队系统
系统科学与数学 , 2021 , 41 2 ): 533 -556
DOI:10.12341/jssms14148
[本文引用: 1]
研究在 Min$(N,D,V)$- 策略控制下服务员具有单重休假且休假不中断的~$M/G/1$ 排队系统, 其中服务员休假归来如果系统中的顾客数不小于事先给定的正整数阈值~$N$ 或者系统中的顾客所需的服务时间总和不小于事先给定的另一正数阈值~$D$, 服务员就立即开始服务. 应用更新过程理论, 全概率分解技术和拉普拉斯变换工具, 讨论了系统队长的瞬态分布和稳态分布, 得到了队长的瞬态分布关于时间~$t$ 的拉普拉斯变换表达式和稳态队长分布的递推表达式. 进一步给出了稳态队长的随机分解结构和附加队长的显示表达式. 同时, 一些特殊情况, 如~$N\to \infty $, 或~$D\to \infty $, 或~$p\left\{ V=0 \right\}=1$ 等也进行了讨论, 并指出了唐应辉和刘名武(2008)的错误. 最后, 建立费用结构模型, 给出了系统长期运行单位时间内的成本期望费用的显示表达式, 并通过数值计算例子讨论了使得系统长期运行单位时间内的成本期望费用最小的最优控制策略~$({{N}^{*}},{{D}^{*}})$.
Li D Tang Y H M/G/1 queueing system based on Min$(N, D, V)$ - policy and single server vacation without interruption
Journal of Systems Science and Mathematical Sciences , 2021 , 41 2 ): 533 -556
DOI:10.12341/jssms14148
[本文引用: 1]
研究在 Min$(N,D,V)$- 策略控制下服务员具有单重休假且休假不中断的~$M/G/1$ 排队系统, 其中服务员休假归来如果系统中的顾客数不小于事先给定的正整数阈值~$N$ 或者系统中的顾客所需的服务时间总和不小于事先给定的另一正数阈值~$D$, 服务员就立即开始服务. 应用更新过程理论, 全概率分解技术和拉普拉斯变换工具, 讨论了系统队长的瞬态分布和稳态分布, 得到了队长的瞬态分布关于时间~$t$ 的拉普拉斯变换表达式和稳态队长分布的递推表达式. 进一步给出了稳态队长的随机分解结构和附加队长的显示表达式. 同时, 一些特殊情况, 如~$N\to \infty $, 或~$D\to \infty $, 或~$p\left\{ V=0 \right\}=1$ 等也进行了讨论, 并指出了唐应辉和刘名武(2008)的错误. 最后, 建立费用结构模型, 给出了系统长期运行单位时间内的成本期望费用的显示表达式, 并通过数值计算例子讨论了使得系统长期运行单位时间内的成本期望费用最小的最优控制策略~$({{N}^{*}},{{D}^{*}})$.
[25]
王敏 , 唐应辉 , 兰绍军 . 在修正二元 Min$(N, D)$ - 策略下多级适应性休假 M/G/1 排队的性能分析
数学物理学报 , 2021 , 41A 4 ): 1166 -1180
[本文引用: 1]
Wang M Tang Y H Lan S J The performance analysis of the M/G/1 queue with multiple adaptive vacations under the modified dyadic Min$(N, D)$ - policy
Acta Math Sci , 2021 , 41A 4 ): 1166 -1180
[本文引用: 1]
[26]
罗乐 , 唐应辉 , 余玅妙 , 吴文青 . 在修正的 Min$(N, D)$ - 策略控制下延迟多级适应性休假 M/G/1 排队分析
系统科学与数学 , 2021 , 41 9 ): 2549 -2570
[本文引用: 1]
Luo L Tang Y H Yu M M Wu W Q Analysis of the M/G/1 queue with delayed multiple adaptive vacations under the modified Min$(N, D)$ - policy control
Journal of Systems Science and Mathematical Sciences , 2021 , 41 9 ): 2549 -2570
[本文引用: 1]
[27]
Liu Q L Tang Y H Yu M M Wu W Q Analysis of $M^{(\lambda_1, \lambda_2)}$ $D$ - policy
Journal of Industrial & Management Optimization , 2023 , 19 6 ): 4523 -4550
[本文引用: 1]
[28]
Wei Y Y Yu M M Tang Y H Gu J X Queue size distribution and capacity optimum design for $N$ - policy Geo$^{(\lambda_1, \lambda_2, \lambda_3)}$
Mathematical and Computer Modelling , 2013 , 57 1559 -1571
[本文引用: 1]
[29]
Jury E I Theory and Application of the Z -Transform Method . New York : John Wiley and Sons , 1964
[本文引用: 1]
2
1993
... 离散时间排队系统是顺应数字化技术发展趋势而建立起来的一套数学分析模型, 离散时间排队系统理论的不断发展, 不仅丰富和拓展了连续时间排队系统理论, 而且为计算机系统和通信网络的设计优化与性能分析提供了十分有效的数学方法和研究手段, 其精确性和适用性得到了广泛验证. 现有研究成果表明, 离散时间排队系统及其延伸的深入研究, 需要较多的数学工具, 其讨论过程比较复杂和繁琐, 其结果也很冗长和复杂, 更具难度和挑战. 近年来离散时间排队的分析取得了惊人的进展[1 7 ] , 为我们提供了有关离散时间排队的深入研究和广泛应用. ...
... ${\bf引理2.1}$ [1 ] 令 $B(z)=\sum\limits_{j=1}^\infty P\{b=j\}z^{j}, |z|<1$ $B(z)$ $B(z)=G((1-p+pB(z))z)$
1
2008
... 休假排队模型是在处理大量复杂系统的设计和控制问题的实际应用背景中产生的, 随着休假排队理论研究的进展, 所得结果迅速在众多领域取得了卓有成效的应用. 例如, 最优保养策略的拟定和实施、生产过程的经济效益分析、物流与仓储管理、通信网络与数据传输、柔性制造系统的生产调度、异步转换模式中的拥塞问题分析等等. 作为多重休假与单重休假的推广, 多级适应性休假[2 ] 仍以空竭服务规则作为控制休假开始的机制, 而何时终止休假既取决于服务员当前所要从事的辅助工作量的多少, 又适当的受到顾客到达过程的制约, 因此服务员的连续休假次数是不确定的. 多级适应性休假策略体现了在为主队列顾客服务和从事辅助工作之间权衡得失决定整个休假期长度的思想, 为系统的优化设计和运行控制提供了极大的灵活性. ...
1
2008
... 休假排队模型是在处理大量复杂系统的设计和控制问题的实际应用背景中产生的, 随着休假排队理论研究的进展, 所得结果迅速在众多领域取得了卓有成效的应用. 例如, 最优保养策略的拟定和实施、生产过程的经济效益分析、物流与仓储管理、通信网络与数据传输、柔性制造系统的生产调度、异步转换模式中的拥塞问题分析等等. 作为多重休假与单重休假的推广, 多级适应性休假[2 ] 仍以空竭服务规则作为控制休假开始的机制, 而何时终止休假既取决于服务员当前所要从事的辅助工作量的多少, 又适当的受到顾客到达过程的制约, 因此服务员的连续休假次数是不确定的. 多级适应性休假策略体现了在为主队列顾客服务和从事辅助工作之间权衡得失决定整个休假期长度的思想, 为系统的优化设计和运行控制提供了极大的灵活性. ...
Performance evaluation and analysis of a discrete queue system with multiple working vacations and non-preemptive priority
0
2020
A note on customer joining strategy in a discrete-time Geo/G/1 queue with server vacations-a simple mean value analysis
0
2022
带有负顾客和 $N$ -策略的 Geo/Geo/1 排队模型均衡策略分析
0
2024
带有负顾客和 $N$ -策略的 Geo/Geo/1 排队模型均衡策略分析
0
2024
具有风险敏感性顾客的离散时间排队系统策略研究
0
2024
具有风险敏感性顾客的离散时间排队系统策略研究
0
2024
Performance analysis of P2P network based on differentiated service Geo/Geo/1+1 queue
1
2024
... 离散时间排队系统是顺应数字化技术发展趋势而建立起来的一套数学分析模型, 离散时间排队系统理论的不断发展, 不仅丰富和拓展了连续时间排队系统理论, 而且为计算机系统和通信网络的设计优化与性能分析提供了十分有效的数学方法和研究手段, 其精确性和适用性得到了广泛验证. 现有研究成果表明, 离散时间排队系统及其延伸的深入研究, 需要较多的数学工具, 其讨论过程比较复杂和繁琐, 其结果也很冗长和复杂, 更具难度和挑战. 近年来离散时间排队的分析取得了惊人的进展[1 7 ] , 为我们提供了有关离散时间排队的深入研究和广泛应用. ...
The performance of the M/G/ 1 queue under the dyadic Min$(N, D)$ -policy and its cost optimization
1
2008
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
基于 Min$(N, D)$ -策略的 M/G/1 排队系统的队长分布及最优策略
1
2015
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
基于 Min$(N, D)$ -策略的 M/G/1 排队系统的队长分布及最优策略
1
2015
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
Queue size distribution of Geo/G/1 queue under the Min$(N, D)$ -policy
1
2016
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
Optimal power consumption control of sensor node based on $(N, D)$ -policy discrete-time queues
1
2019
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
Queue size distribution on a new $ND$ policy Geo/G/1 queue and its computation designs
1
2021
... 生活在高速发展的社会之中, 人们向现代服务不断提出新的要求, 由此引发了对既满足顾客需求又能保证服务系统经济效益的研究. 为此, 基于现实系统的复杂性和信息时代的快速发展, 根据不同的实际应用背景, 提出并研究了各种具有联合控制策略的排队模型, 不同策略的综合应用显示出了潜在的优势. 在 $N$ - 策略与 $D$ - 策略相结合方面, Lee 等[8 ] 提出了二元 Min $(N,D)$ - 控制策略, 研究了具有 Min $(N,D)$ - 策略的连续时间 M/G/1 排队系统的一些稳态性能指标, 得到了队长稳态分布的概率母函数和平均稳态队长, 同时考虑了两个成本模型 (一个基于平均工作负载, 另一个基于平均队长), 并将最优 Min$(N, D)$ - 策略与最优 $N$ - 策略和最优 $D$ - 策略进行比较. 自此, 一系列后续研究成果不断涌现. 魏瑛源等[9 ] 对 Min $(N,D)$ - 策略下的连续时间 M/G/1 排队系统进行了另一个角度的研究, 运用全概率分解技术、更新过程理论和拉普拉斯变换工具, 得到了队长瞬态分布的拉普拉斯变换表达式和队长稳态分布的递推表达式, 而且利用所得到的便于进行数值计算的队长稳态分布的解析表达式, 讨论了系统容量的优化设计. 顾建雄等[10 ] 、刘仁彬等[11 ] 、王荣秀[12 ] 把问题延伸到离散时间刻画的排队系统, 讨论了基于 Min $(N,D)$ - 策略的 Geo/G/1 排队. ...
On a queueing system with processing of service items under vacation and $N$ -policy with impatient customers
2
2020
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... [13 ]研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
A bulk queueing system with starting failure and repair, multiple vacation, stand-by server, closedown and $N$ -policy
1
2022
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
带 N-策略的双阶段休假 M/M/1 排队系统驱动的流体模型性能分析
1
2024
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
带 N-策略的双阶段休假 M/M/1 排队系统驱动的流体模型性能分析
1
2024
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
Performance and optimization analysis of a queue with delayed uninterrupted multiple vacation and N-policy
1
2024
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
基于多重休假的 Min$(N, V)$ -策略 M/G/1 排队的队长分布
1
2013
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
基于多重休假的 Min$(N, V)$ -策略 M/G/1 排队的队长分布
1
2013
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
基于单重休假的 Min$(N,V)$ -策略 M/G/1 排队系统分析
1
2014
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
基于单重休假的 Min$(N,V)$ -策略 M/G/1 排队系统分析
1
2014
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
具有多级适应性休假和 Min$(N, V)$ -策略控制的 M/G/1 排队系统
1
2017
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
具有多级适应性休假和 Min$(N, V)$ -策略控制的 M/G/1 排队系统
1
2017
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
On an M/G/1 queue in random environment with Min$(N, V)$ -policy
1
2018
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
具有多重休假和 Min$(N, V)$ -策略控制的 Geo/G/1 离散时间排队
2
2015
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... 这与文献 [21 ] 的相应结果一致. ...
具有多重休假和 Min$(N, V)$ -策略控制的 Geo/G/1 离散时间排队
2
2015
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... 这与文献 [21 ] 的相应结果一致. ...
System capacity optimization design and optimal threshold $N^*$ for a Geo/G/1 discrete-time queue with single server vacation and under the control of Min$(N, V)$ -policy
2
2016
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... 这与文献 [22 ] 的相应结果一致. ...
具有多级适应性休假和 Min$(N, V)$ -策略的 Geo/G/1 排队系统分析
3
2024
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... [23 ]将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... 这与文献 [23 ] 的相应结果一致. ...
具有多级适应性休假和 Min$(N, V)$ -策略的 Geo/G/1 排队系统分析
3
2024
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... [23 ]将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
... 这与文献 [23 ] 的相应结果一致. ...
基于 Min$(N, D, V)$ -策略和单重休假且休假不中断的 M/G/1 排队系统
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
基于 Min$(N, D, V)$ -策略和单重休假且休假不中断的 M/G/1 排队系统
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
在修正二元 Min$(N, D)$ -策略下多级适应性休假 M/G/1 排队的性能分析
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
在修正二元 Min$(N, D)$ -策略下多级适应性休假 M/G/1 排队的性能分析
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
在修正的 Min$(N, D)$ -策略控制下延迟多级适应性休假 M/G/1 排队分析
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
在修正的 Min$(N, D)$ -策略控制下延迟多级适应性休假 M/G/1 排队分析
1
2021
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
Analysis of $M^{(\lambda_1, \lambda_2)}$ /G/1 queue with uninterrupted single vacation and server's workload controlled $D$ -policy
1
2023
... 在实际应用中, 由于在休假期间顾客的过度积累会导致系统拥塞, 这不仅使得顾客因长时间等待而不耐烦, 还会降低服务质量和顾客满意度. 此外, 在带有阈值策略的控制排队系统中, 系统在空闲和繁忙之间的频繁切换, 会产生大量的费用成本. 因此, 把休假时间长短和假期中到达的顾客数多少结合起来, 能有效控制队长和等待时间, 解决系统的拥堵问题, 减少不耐烦顾客离开系统造成的损失, 从而提高系统的运行效率和经济效益. 文献 [13 23 ] 是近年来具有 $N$ - 策略的休假排队模型的出色研究工作. Divya 等 [13 ] 研究了一个具有不耐烦顾客和 $N$ - 策略的休假排队系统, 计算了几个系统性能特征; Ayyappan 和 Karpagam [14 ] 对具有服务器启动故障与修复、多重休假及 $N$ - 策略的单服务器批量排队系统进行了分析,并推导出了模型的数值结果; 王勋和徐秀丽[15 ] 基于工厂单装配系统的运行机制, 构建并分析了具有 $N$ - 策略和两种混合休假策略的 M/M/1 排队系统驱动的流体模型; 何亚兴等[16 ] 讨论了具有延迟不间断多重休假和 $N$ - 策略的排队系统性能指标与优化分析. 唐应辉等[17 ,18 ] 、蒋书丽和唐应辉 [19 ] 、还有李建军和刘力维[20 ] 把 $N$ - 策略与服务员休假机制相结合, 分别讨论了基于服务员单重休假、多重休假和多级适应性休假及在 Min$(N,V)$ - 策略控制下的 M/G/1 排队系统, 通过使用全概率分解方法和拉普拉斯变换工具, 研究了在任意初始状态条件下系统队长的瞬态分布, 并给出了队长瞬态分布关于时间 $t$ [21 ,22 ] 、旷欣宇和唐应辉 [23 ] 将 Min$(N,V)$ - 策略引入离散时间 Geo/G/1 排队中, 运用全概率分解技术、更新过程理论和 $z$ - 变换, 得到了队长瞬态分布的 $z$ - 变换表达式和队长稳态分布的递推表达式, 并讨论了使得系统长期运行下单位时间内所产生的期望费用最小的最优策略. 李丹和唐应辉[24 ] 把双阈值 Min$(N, D)$ - 策略与服务员的单重休假相结合, 讨论了三元 Min$(N,D,V)$ - 控制策略下的 M/G/1 排队系统. 此外, 由于经典$D$ - 策略是根据等待顾客需要的总服务时间来设计的, 但顾客的服务时间在服务完成之前是随机的, 是无法确定的. 考虑到顾客在接受服务之前, 其服务时间长度是未知的这一事实, 使得根据经典 $D$ - 策略进行系统的设计和运行管理成为很难执行的一项复杂任务. 因此, 王敏等 [25 ] 、罗乐等 [26 ] 、刘琼琳等[27 ] 对经典的 $D$ - 策略作了改进, 引入服务员对顾客的 "服务工作量" 的概念, 提出 "修正的 Min $(N,D)$ - 控制策略", 其中的 $D$ - 策略是根据服务员对等待顾客需要服务的总工作量来设计的, 这在开始服务顾客前是能够确定的, 克服了经典 $D$ - 策略在实际应用中的局限. ...
Queue size distribution and capacity optimum design for $N$ -policy Geo$^{(\lambda_1, \lambda_2, \lambda_3)}$ /G/1 queue with setup time and variable input rate
1
2013
... ${\bf引理2.2}$ [28 ] 对于 $|z|<1$ $q^+_{_{\scriptstyle j}}(z)=\sum\limits_{n=0}^\infty Q_{j}(n^+)z^{n}$ $Q_{j}(n^+)$
1
1964
... (2) 根据 $z$ - 变换极限理论 [29 ] 知 $p^+_{_{j}}=\lim\limits_{z\to 1^{-}}(1-z)p^+_{_{ij}}(z)$ . 因此, 对于 $p^+_{_{0}}$ $p^+_{_{0}}=\lim\limits_{z\to 1^{-}}(1-z)p^+_{_{i0}}(z)$