1 引言
考虑如下绝对值方程 (AVE) 的求解问题[1 ,2 ]
(1.1) $\begin{equation} Ax-|x|=b, \end{equation}$
其中 $A \in \mathbb{R}^{n\times n}, b \in \mathbb{R}^{n}$ $|x|=(|x_1|,|x_2|,\cdots,|x_n|)^{\rm T}$ . AVE 问题 (1.1) 是如下广义绝对值方程 (GAVE) 的特殊情形[3 ,4 ]
(1.2) $\begin{equation} Ax-B|x|=b, \end{equation}$
其中 $B \in \mathbb{R}^{n\times n}$ . GAVE 问题 (1.2) 在各种科学与工程计算领域都有着重要的应用, 如线性规划问题、凸二次规划问题、线性互补问题等,见文献[5 ,6 ]及其参考文献.
受文献[7 ]的启发, 利用牛顿型单步迭代法作为预测步, 提出了一种两步迭代法, 即积分-牛顿型迭代法. 同时, 充分利用更新规则, 提出了改进的积分-牛顿迭代法.
引理1.1 [8 ] 对角矩阵的奇异值等于对角线元素的绝对值.
引理1.2 [8 ] 当且仅当矩阵 $A^TA$ $B^TB$ $A\in\mathbb{R}^{n \times n}$ $B\in\mathbb{R}^{n \times n}$
2 积分-牛顿型迭代法
首先, 将 GAVE (1.2) 转化为非线性函数
(2.1) $\begin{equation} g'(x)=A-BD(x), \end{equation}$
其中 $D(x)={\rm diag(sign}(x))$ $D(x)x=|x|$ $\xi$
在数值分析中, 著名的 Gauss-Legendre 积分 (GL) 和 Newton-Cotes 积分 (NC) 方法被用于计算各种积分, 具体如下所示
(2.2) $\begin{equation} {\rm GL:} \int_{\eta}^{\xi}\rho(t) g'(t){\rm d}t=(\xi-\eta)\sum_{k=0}^n A_kg'(s_k), \end{equation}$
其中 $\rho(t)$ $A_k$
(2.3) $\begin{equation} {\rm NC:} \int_{\eta}^{\xi} g'(t){\rm d}t=(\xi-\eta)\sum_{k=0}^n C_k^{(n)}g'(s_k), \end{equation}$
其中 $s_k=a+kh,h=\xi-\eta$
(2.2) 和 (2.3) 式的右侧统一定义为 $(\xi-\eta)F(\eta,\xi)$ $(\xi-\eta)F(\eta,\xi)=-g(\eta),$ $\xi=\eta-[F(\eta,\xi)]^{-1}g(\eta).$ $\xi^{k+1}=\eta-[F(\eta,\xi^{k})]^{-1}g(\eta).$
为了使 $\xi^k$ $\eta$ $\eta$
下面研究 $\eta$ $A=M-N$ $A$ $M$ $Mx-Nx-B|x|-b=0.$
(2.4) $\begin{equation} x^{k+1}=M^{-1}(Nx^{k}+B|x^{k}|+b). \end{equation}$
将上述公式的更新规则应用于变量 $\eta$ $\xi$
步骤1 取初始点 $\xi^0,\eta^0\in\mathbb{R}^n$ $N$ $\epsilon$ . 置 $k:=0,1,2,\cdots$ .
(2.5) $\begin{equation} \begin{cases} \eta^{k+1}=M^{-1}(N\eta^{k}+B|\eta^{k}|+b),\\ \xi^{k+1}=\eta^{k+1}-[F(\eta^{k+1},\xi^{k})]^{-1}g(\eta^{k+1}). \end{cases} \end{equation}$
步骤3 若 $| \xi^{k+1} - \xi^k|<\epsilon$
步骤4 若 $k=N$ $\xi^{k+1}:=\xi^{k}, k:= k+1 $
又因为 $\xi$ $\eta$ $\xi$
步骤1 取初始点 $\xi^0\in\mathbb{R}^n$ $N$ $\epsilon$ . 置 $k:=0,1,2,\cdots$ .
(2.6) $\begin{equation} \begin{cases} \eta^{k+1}=M^{-1}(N\xi^{k}+B|\xi^{k}|+b),\\ \xi^{k+1}=\eta^{k+1}-[F(\eta^{k+1},\xi^{k})]^{-1}g(\eta^{k+1}). \end{cases} \end{equation}$
步骤3 若 $| \xi^{k+1} - \xi^k|<\epsilon$
步骤4 若 $k=N$ $\xi^{k+1}:=\xi^{k}, k:= k+1 $
接下来对算法 2.1 和算法 2.2 作一些说明和分析. Wang 在文献[9 ]给出了基于牛顿法的矩阵分裂迭代法的一般形式如下
其中 $M+\Omega$ $\Omega$ $\Omega = 0$ $M$ $N$
(a)当 $M=A, N=0$ [10 ]
(b)当 $M=A+\Omega, N=\Omega$ [9 ]
(c) 当 $M=\dfrac{1}{\omega}A, N=\dfrac{1-\omega}{\omega}A$
(d) 当 $M=D+\Omega, N=\Omega+L+U$ [11 ]
(e) 当 $M=D+\Omega-L, N=\Omega+U$ [11 ]
(f) 当 $M=\dfrac{1}{\alpha}(D+\alpha\Omega-\alpha L), N=\dfrac{1}{\alpha}(\alpha D+(1-\alpha)D+\alpha U)$ [9 ]
(g) 当 $M=\frac{1}{\alpha}(D+\alpha\Omega-\beta L), N=\frac{1}{\alpha}(\alpha D+(1-\alpha)D+(\alpha-\beta)L +\alpha U)$ [9 ]
(h) 当 $M=H, N=-S$ [11 ]
(i) 当 $M=H+\Omega, N=\Omega-S$ [9 ]
注2.1 对于不同的积分方法, $F(\eta,\xi)$ $F(\eta,\xi)$
(2.7) $\begin{equation} F(\eta,\xi)= \begin{aligned} \begin{cases} \dfrac{1}{2}\bigg[g'\bigg(\dfrac{\xi+\eta}{2}+\dfrac{1}{\sqrt{3}}\dfrac{\xi-\eta}{2}\bigg)+g'\bigg(\frac{\xi+\eta}{2}-\dfrac{1}{\sqrt{3}} \dfrac{\xi-\eta}{2}\bigg)\bigg],&n=2,\\[12pt] \dfrac{1}{9}\bigg[4g'\bigg(\dfrac{\xi+\eta}{2}\bigg)+\dfrac{5}{2}g'\bigg(\dfrac{\xi+\eta}{2}+\sqrt{\dfrac{3}{5}}\dfrac{\xi-\eta}{2}\bigg) +\dfrac{5}{2}g'\bigg(\dfrac{\xi+\eta}{2}-\sqrt{\frac{3}{5}}\dfrac{\xi-\eta}{2}\bigg)\bigg],&n=3. \end{cases} \end{aligned} \end{equation}$
(2.8) $\begin{equation} F(\eta,\xi)= \begin{aligned} \begin{cases} \dfrac{1}{2}\big[g'(\xi)+g'(\eta)\big],&n=1,\\[6pt] \dfrac{1}{6}\bigg[g'(\xi)+4g'\bigg(\dfrac{\xi+\eta}{2}\bigg)+g'(\eta)\bigg],&n=2,\\[10pt] \dfrac{1}{8}\bigg[g'(\xi)+3g'\bigg(\dfrac{2\xi+\eta}{3}\bigg)+3g'\bigg(\dfrac{2\eta+\xi}{3}\bigg)+g'(\eta)\bigg],&n=3. \end{cases} \end{aligned} \end{equation}$
为了保证算法 2.1 和算法 2.2 的可行性, 需要讨论 $[F(\eta,\xi)]^{-1}$ $n=1$ ) 为例进行分析. 由于其他情况相似, 故此省略.
定理2.1 当 $A\in\mathbb{R}^{n\times n}$ $\sigma(A)>1$ $[g'(\xi)+g'(\eta)]^{-1}$ $D(x)={\rm diag}({\rm sign}(x))$ .
假设 $g'(\xi)+g'(\eta)$ $(g'(\xi)+g'(\eta))u=0$ $u\neq0$ . 记 $\dfrac{1}{2}(D(\xi)+D(\eta))=\widetilde{D}$ . 根据引理 1.1, $\sigma(\widetilde{D})$ $\sigma(A)>1$ $\lambda_{\min}(A^TA)>\lambda_{\max}$ $(D^TB^TBD)$ ) , 通过简单计算可以得到
这是矛盾的, 因此 $g'(\xi)+g'(\eta)$
3 收敛性分析
本节讨论算法 2.1 和算法 2.2 的收敛性. 考虑 GAVE 问题 (1.2) 和分裂式 $A=M-N$ $\mu:=\|F(\eta^{k+1},\xi^k)^{-1}\|$ .
定理3.1 如果 $\|M^{-1}\|(\|N\|+\|B\|)<1$
证 令 $x^*$ $x^*=M^{-1}(Nx^*+B|x^*|+b)$ . 根据 (2.5) 式的第一个公式, 有
(3.1) $\begin{eqnarray*} \|\eta^{k+1}-x^*\|&=&\|M^{-1}N(\eta^k-x^*)+M^{-1}B(|\eta^k|-|x^*|)\| \nonumber\\ &\le&\|M^{-1}N(\eta^k-x^*)\|+\|M^{-1}B(|\eta^k|-|x^*|)\| \nonumber\\ &\le&\|M^{-1}\|\|N\|\|\eta^k-x^*\|+\|M^{-1}\|\|B\|\||\eta^k|-|x^*|\| \nonumber\\ &\le&\|M^{-1}\|(\|N\|+\|B\|)\|\eta^k-x^*\|. \end{eqnarray*}$
(3.2) $\begin{eqnarray*} \|\xi^{k+1}-x^*\| &=&\|F(\eta^{k+1},\xi^k)^{-1}\left[(F(\eta^{k+1},\xi^k)-A)(\eta^{k+1}-x^*)+B(|\eta^{k+1}|-|x^*|)\right]\| \nonumber\\ &\le&\|F(\eta^{k+1},\xi^k)^{-1}\|(\|F(\eta^{k+1},\xi^k)-A\|+\|B\|)\|\eta^{k+1}-x^*\| \nonumber\\ &\le&\mu(\|F(\eta^{k+1},\xi^k)-A\|+\|B\|)\|M^{-1}\|(\|N\|+\|B\|)\|\eta^k-x^*\|. \end{eqnarray*}$
因此, 定理的已知条件及 (3.2) 式立知算法 2.1 是收敛的.
定理3.2 如果$\mu(\|F(\eta^{k+1},\xi^k)-A\|+\|B\|)\|M^{-1}\|(\|N\|+\|B\|)<1$ $2.2$
证 令 $x^*$ $x^*=M^{-1}(Nx^*+B|x^*|+b)$ . 根据 (2.6) 式的第一个公式, 有
(3.3) $\begin{eqnarray*} \|\eta^{k+1}-x^*\|&=&\|M^{-1}(N\xi^{k}+B|\xi^k|+b)-M^{-1}(Nx^*+B|x^*|+b)\| \nonumber\\ &=&\|M^{-1}N(\xi^k-x^*)+M^{-1}B(|\xi^k|-|x^*|)\| \nonumber\\ &\le&\|M^{-1}\|\|N\|\|\xi^k-x^*\|+\|M^{-1}\|\|B\|\||\xi^k|-|x^*|\| \nonumber\\ &\le&\|M^{-1}\|(\|N\|+\|B\|)\|\xi^k-x^*\|. \end{eqnarray*}$
(3.4) $\begin{equation} \|\xi^{k+1}-x^*\| \le\mu(\|F(\eta^{k+1},\xi^k)-A\|+\|B\|)\|M^{-1}\|(\|N\|+\|B\|)\|\xi^k-x^*\|. \end{equation}$
易见, 若 $\mu(\|F(\eta^{k+1},\xi^k)-A\|+\|B\|)\|M^{-1}\|(\|N\|+\|B\|)<1$ $2.2$
下面以 NC $(n=1)$
其中 $\dfrac{1}{2}(D(\xi)+D(\eta))=\widetilde{D}$ . 对上式两边同时取范数, 得
(3.5) $\begin{equation} \mu=\|F(\eta^{k+1},\xi^k)^{-1}\| \le\frac{\|A^{-1}\|}{1-\|A^{-1}\|\|B\widetilde{D}\|} \le\frac{\|A^{-1}\|}{1-\|A^{-1}\|\|B\|}. \end{equation}$
最后一个不等号成立是因为 $\|\widetilde{D}\|\le1$ . 于是, 我们有下面的推论.
推论3.1 如果 $\|M^{-1}\|\le\dfrac{1-\|A^{-1}\|\|B\|}{2\|A^{-1}\|\|B\|(\|N\|+\|B\|)}$ $2.1$ $2.2$
证 首先, 讨论 $\|F(\eta^{k+1},\xi^k)-A\|+\|B\|$
(3.6) $\begin{equation} \|F(\eta^{k+1},\xi^k)-A\|+\|B\|=\|A-B\widetilde{D}-A\|+\|B\| =\|-B\widetilde{D}\|+\|B\| \le2\|B\|. \end{equation}$
为了算法 $2.1$ $2.2$
(3.7) $\begin{equation} \|M^{-1}\|\le\frac{1-\|A^{-1}\|\|B\|}{2\|A^{-1}\|\|B\|(\|N\|+\|B\|)}. \end{equation}$
4 数值实验
在本节, 通过两个数值实验的迭代步数、CPU 时间和残差 RES 来说明算法 $2.1$ $2.2$ $\eta^{(0)}$ $\xi^{(0)}$
例 4.1 考虑 GAVE (1.2), 其中 $b=Ax^*-B|x^*|$
$x^*=(-1,1,-1,1,\cdots,-1,1)^T\in \mathbb{R}^n$
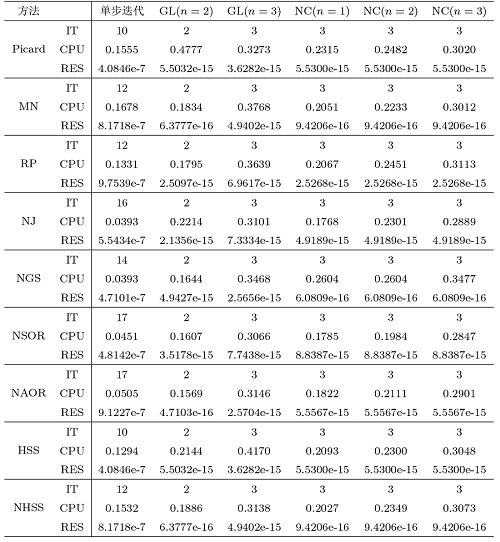
在实验中, MN 法、RP 法、NJ 法、NGS 法和 NHSS 法的参数 $\omega$ $0.8$ $\omega=0.9$ $\alpha=0.9$ $\omega=0.9, \alpha= 0.9$ $\beta=0.6$ . 数值结果如表1.
从表1 可以看出, 在单步迭代法中 Picard 法和 HSS 法的迭代步数最少, 但在这些单步迭代法结合了积分牛顿型方法后, 所有方法的迭代步数都有大幅度减少且同一种积分型结合不同的单步迭代法后的结果是差异较小的. 说明这个数值实验表现出积分牛顿型迭代法对于积分方法的灵敏度不是很高, 不同的积分方法得到的结果是一致的.
下面将用另一个数值实验来证明积分牛顿型迭代法的不同性质.
例 4.2 [12 ] 考虑线性互补问题 LCP, 对于给定的矩阵 $M\in \mathbb{R}^{n\times n}$ $q\in \mathbb{R}^n$ $z,w\in\mathbb{R}^n$
(4.1) $\begin{equation} z\ge0, \quad w=Mz+q\ge0, \quad z^Tw=0. \end{equation}$
(4.2) $\begin{equation} (M+I)x-(M-I)|x|=q, \quad x=\frac{1}{2}((M-I)z+q). \end{equation}$
令 $A=M+I, B=M-I, M=\hat{M}+\mu I\in\mathbb{R}^{n\times n}, q=-Mz^*\in \mathbb{R}^n$
则有 $n=m^2$ $z^*=(1.2,1.2,1.2,\cdots,1.2)^T\in\mathbb{R}^n$ $x^*=(-0.6,-0.6,-0.6,\cdots,-0.6)^T\in\mathbb{R}^n$ .
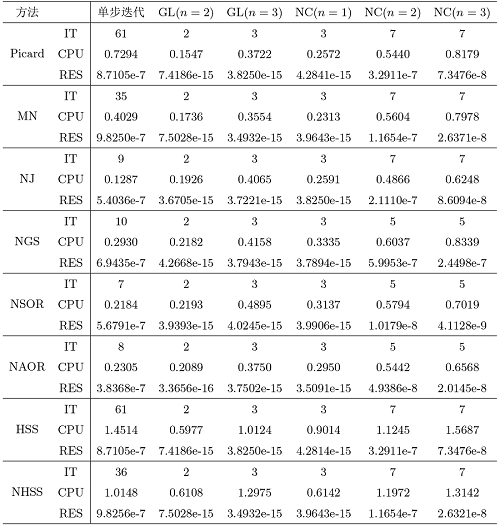
在例4.2 中, 分别取 $\mu=4, \Omega=\hat{M}$ $\mu=4, \Omega=1.5\times\hat{M}$ 表2 和表3 中. 从表格2 中可以看出, RP 法在 $\Omega=\hat{M}$ $(n=2, n=3)$
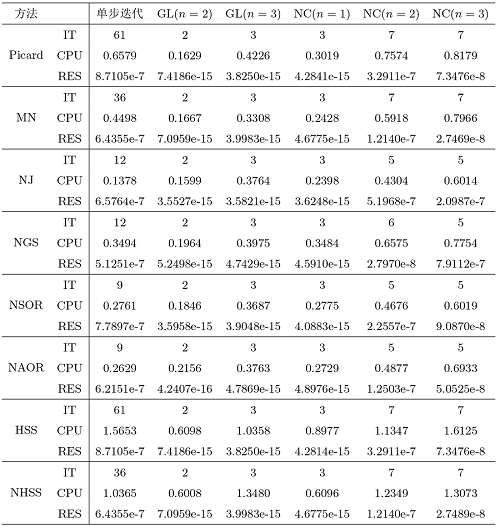
从表3 中可以看出与表2 中实验结果一致, 单步迭代法中, NJ 法、NGS 法、NSOR 法和 NAOR 法优于其他单步迭代法, 结合积分牛顿型迭代法后的结果也大致一样, 但区别于表2 , 在表3 中取 $\Omega=1.5\times\hat{M}$ $n=2, n=3$ ) 方法时, 迭代步数是不一样的, 说明积分牛顿型迭代法在选取不同的积分方法时, 不同的 $n$ $n$ $n$
5 小结
本文将 Gauss-Legendre 和 Newton-Cotes 积分方法结合现有的单步迭代法提出了积分-牛顿型迭代法求解 GAVE (1.2), 对于不同的积分方法和不同的单步迭代法, 得到了相对应的两步迭代方法, 证明了所提方法的收敛性条件, 并通过数值实验去证明了所提方法的优势, 分析了不同积分的选择对迭代情况的影响.
参考文献
View Option
[1]
Rohn J . A theorem of the alternatives for the equation $Ax+B|x|=b$
Linear Multilinear Algebra , 2004 , 52 6 ): 421 -426
[本文引用: 1]
[2]
Hu S L Huang Z H . A note on absolute value equations
Optim Lett , 2010 , 4 (3 ): 417 -424
[本文引用: 1]
[3]
Ketabchi S Moosaei H . An efficient method for optimal correcting of absolute value equations by minimal changes in the right hand side
Comput Math Appl , 2012 , 64 6 ): 1882 -1885
[本文引用: 1]
[4]
Mangasarian O L . A hybrid algorithm for solving the absolute value equation
Optim Lett , 2015 , 9 7 ): 1469 -1474
[本文引用: 1]
[5]
Wu S L Guo P . Modulus-based matrix splitting algorithms for the quasi-complementarity problems
Appl Numer Math , 2018 , 1.2 127 -137
[本文引用: 1]
[6]
Ren H Wang X Tang X B Wang T . The general two-sweep modulus-based matrix splitting iteration method for solving linear complementarity problems
Computers & Mathematics with Applications , 2019 , 77 4 ): 1071 -1081
[本文引用: 1]
[7]
Khan A Iqbal J Akgül A , et al . A Newton-type technique for solving absolute value equations
Alex Engin Jour , 2022 , 64 291 -296
[本文引用: 1]
[8]
Golub G Kahan W . Calculating the singular values and pseudo-inverse of a matrix
J Soc Indust Appl Math B Numer Anal , 1965 , 2 2 ): 205 -224
[本文引用: 2]
[9]
Wang A Cao Y Chen J X . Modified Newton-type iteration methods for generalized absolute value equations
J Optim Theory Appl , 2019 , 1.1 1 ): 216 -230
[本文引用: 5]
[10]
Rohn J Hooshyarbakhsh V Farhadsefat R . An iterative method for solving absolute value equations and sufficient conditions for unique solvability
Optim Lett , 2014 , 8 35 -44
[本文引用: 1]
[11]
Zhou H Y Wu S L Li C X . Newton-based matrix splitting method for generalized absolute value equation
J Comput Appl Math , 2021 , 3.4 : 113578
[本文引用: 3]
[12]
Bai Z Z . Modulus-based matrix splitting iteration methods for linear complementarity problems
Numer Linear Alge Appl , 2010 , 17 917 -933
[本文引用: 1]
A theorem of the alternatives for the equation $Ax+B|x|=b$
1
2004
... 考虑如下绝对值方程 (AVE) 的求解问题[1 ,2 ] ...
A note on absolute value equations
1
2010
... 考虑如下绝对值方程 (AVE) 的求解问题[1 ,2 ] ...
An efficient method for optimal correcting of absolute value equations by minimal changes in the right hand side
1
2012
... 其中 $A \in \mathbb{R}^{n\times n}, b \in \mathbb{R}^{n}$ $|x|=(|x_1|,|x_2|,\cdots,|x_n|)^{\rm T}$ . AVE 问题 (1.1) 是如下广义绝对值方程 (GAVE) 的特殊情形[3 ,4 ] ...
A hybrid algorithm for solving the absolute value equation
1
2015
... 其中 $A \in \mathbb{R}^{n\times n}, b \in \mathbb{R}^{n}$ $|x|=(|x_1|,|x_2|,\cdots,|x_n|)^{\rm T}$ . AVE 问题 (1.1) 是如下广义绝对值方程 (GAVE) 的特殊情形[3 ,4 ] ...
Modulus-based matrix splitting algorithms for the quasi-complementarity problems
1
2018
... 其中 $B \in \mathbb{R}^{n\times n}$ . GAVE 问题 (1.2) 在各种科学与工程计算领域都有着重要的应用, 如线性规划问题、凸二次规划问题、线性互补问题等,见文献[5 ,6 ]及其参考文献. ...
The general two-sweep modulus-based matrix splitting iteration method for solving linear complementarity problems
1
2019
... 其中 $B \in \mathbb{R}^{n\times n}$ . GAVE 问题 (1.2) 在各种科学与工程计算领域都有着重要的应用, 如线性规划问题、凸二次规划问题、线性互补问题等,见文献[5 ,6 ]及其参考文献. ...
A Newton-type technique for solving absolute value equations
1
2022
... 受文献[7 ]的启发, 利用牛顿型单步迭代法作为预测步, 提出了一种两步迭代法, 即积分-牛顿型迭代法. 同时, 充分利用更新规则, 提出了改进的积分-牛顿迭代法. ...
Calculating the singular values and pseudo-inverse of a matrix
2
1965
... 引理1.1 [8 ] 对角矩阵的奇异值等于对角线元素的绝对值. ...
... 引理1.2 [8 ] 当且仅当矩阵 $A^TA$ $B^TB$ $A\in\mathbb{R}^{n \times n}$ $B\in\mathbb{R}^{n \times n}$
Modified Newton-type iteration methods for generalized absolute value equations
5
2019
... 接下来对算法 2.1 和算法 2.2 作一些说明和分析. Wang 在文献[9 ]给出了基于牛顿法的矩阵分裂迭代法的一般形式如下 ...
... (b)当 $M=A+\Omega, N=\Omega$ [9 ] ...
... (f) 当 $M=\dfrac{1}{\alpha}(D+\alpha\Omega-\alpha L), N=\dfrac{1}{\alpha}(\alpha D+(1-\alpha)D+\alpha U)$ [9 ] ...
... (g) 当 $M=\frac{1}{\alpha}(D+\alpha\Omega-\beta L), N=\frac{1}{\alpha}(\alpha D+(1-\alpha)D+(\alpha-\beta)L +\alpha U)$ [9 ] ...
... (i) 当 $M=H+\Omega, N=\Omega-S$ [9 ] ...
An iterative method for solving absolute value equations and sufficient conditions for unique solvability
1
2014
... (a)当 $M=A, N=0$ [10 ] ...
Newton-based matrix splitting method for generalized absolute value equation
3
2021
... (d) 当 $M=D+\Omega, N=\Omega+L+U$ [11 ] ...
... (e) 当 $M=D+\Omega-L, N=\Omega+U$ [11 ] ...
... (h) 当 $M=H, N=-S$ [11 ] ...
Modulus-based matrix splitting iteration methods for linear complementarity problems
1
2010
... 例 4.2 [12 ] 考虑线性互补问题 LCP, 对于给定的矩阵 $M\in \mathbb{R}^{n\times n}$ $q\in \mathbb{R}^n$ $z,w\in\mathbb{R}^n$